Question

Three of six vertices of a regular hexagon are chosen at random. The probability that triangle with three vertices is equilateral, is equal to

Answer 1

Hint: The formula for selecting r different things out of n different things is given by \[{}^{n}{{C}_{r}}\] .
The formula for evaluating probability of any event is
P \[=\dfrac{Favorable\ outcomes}{Total\ outcomes}\] .
Equilateral triangle is a type of triangle in which all three sides are of equal length.

Complete Step-by-step answer:
As mentioned in the question, we need to know how many equilateral triangles are there if we join 3 vertices of a regular hexagon.
Another fact about equilateral triangles is that all the angles of an equilateral triangle is equal to \[{{60}^{\circ }}\] .
Using this fact, we can calculate that there can be only two triangles that are equilateral when we join three vertices of a regular hexagon.

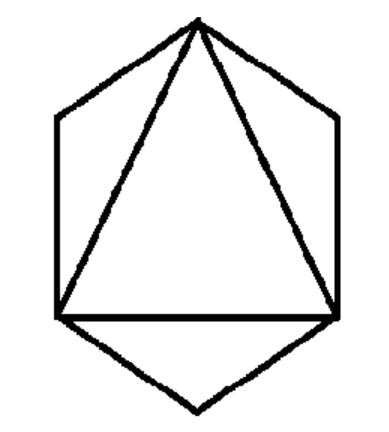
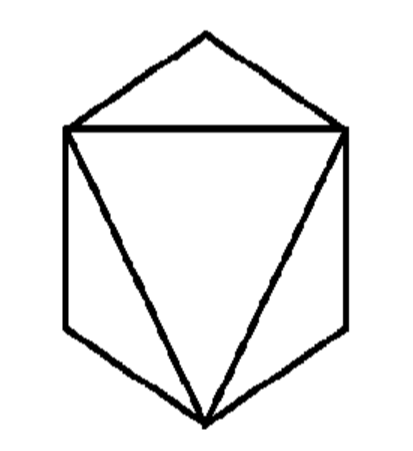
In the figure, the two possible equilateral triangles are marked.
Hence, the total outcomes for the event is given by
\[{}^{6}{{C}_{3}}\] (As the total vertices in a regular hexagon are 6 and the number of vertices that we need to pick are 3)
\[\begin{align}
  & {}^{6}{{C}_{3}}=\dfrac{6!}{3!\left( 6-3 \right)!} \\
 & =20 \\
\end{align}\]
Hence, the total outcomes are 20.
Therefore, the probability of the event to take place is
\[\begin{align}
  & P=\dfrac{Favorable\ outcomes}{Total\ outcomes} \\
 & P=\dfrac{2}{20} \\
\end{align}\]
Hence, the probability is \[\dfrac{1}{10}\] .

Note: The students can make an error in evaluating the number of equilateral triangles that are formed when three vertices of the regular hexagon are selected at random.
Without knowing the property of equilateral triangles that equilateral triangles are those with all the angles of an equilateral triangle is equal to \[{{60}^{\circ }}\] , they would not get to the right answer.