
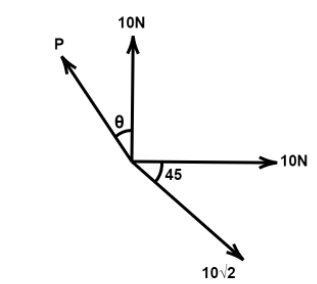
Three vectors acts at a point O as shown in the figure, for the given values of P and $\theta $ the correct options are:-
(A) Resultant is null vector if $\theta = 0,P = 10\sqrt 2 $
(B) Resultant is $10N$if$\theta = 90^\circ,P = 10N$
(C) Resultant is $30\hat iN$if $\theta = \dfrac{{3\pi }}{2},P = 10N$in magnitude
(D) All are correct.
Answer
122.4k+ views
Hint A vector can be resolved into its components along the x and y axes. When they lie on the same axis, the vectors can be added or subtracted like normal numbers. The resultant of a vector can be found by adding two vectors.
Complete step by step solution
From the figure, it is clear that all the three vectors lie in a 2D plane. The correct option can be found by putting the value of P and $\theta $in each option. Suppose a vector makes angle $\theta $from an axis then the two components of this vector can be found by-
Multiplying the magnitude of the vector with the cos of the angle it makes with the axis. (for the base axis)
Multiplying the magnitude of the vector with the sin of the angle it makes with the axis. (for the perpendicular axis)
Resultant of two vectors is given by-
$\Rightarrow$ $\left| {\vec R} \right| = \sqrt {{{\vec A}^2} + {{\vec B}^2} + 2AB\cos \theta } $
For two perpendicular vectors, $\cos 90^\circ = 0$
$\left| {\vec R} \right| = \sqrt {{{\vec A}^2} + {{\vec B}^2}} $
For A, $\theta = 0,P = 10\sqrt 2 $
The first step is to resolve all the components into $\hat i$ and $\hat j$components. Let those values be $x$ and $y$respectively. Then,
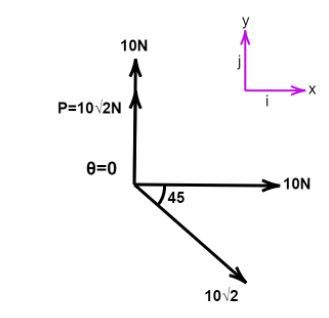
$\Rightarrow$ $x\hat i = 10\hat i + 10\sqrt 2 \cos 45^\circ \hat i$
$\Rightarrow$ $\left\{ {\cos 45^\circ = \dfrac{1}{{\sqrt 2 }}} \right\}$
$\Rightarrow$ $x\hat i = 10\hat i + 10\hat i = 20\hat i$
$y\hat j = 10\hat j + 10\sqrt 2 \hat j - 10\sqrt 2 \sin 45^\circ $
$\Rightarrow$ $y\hat j = 10\sqrt 2 \hat j$
$\Rightarrow$ $\left\{ {\sin 45^\circ = \dfrac{1}{{\sqrt 2 }}} \right\}$
Resultant $\vec R = \sqrt {{{(x\hat i)}^2} + {{(y\hat j)}^2}} $
$\Rightarrow$ $\vec R = \sqrt {{{(20\hat i)}^2} + {{(10\sqrt 2 \hat j)}^2}} $
$\Rightarrow$ $\vec R = \sqrt {400 + 200} $
$\vec R = \sqrt {600} = 10\sqrt 6 $
Resultant is not a null vector, statement is false.
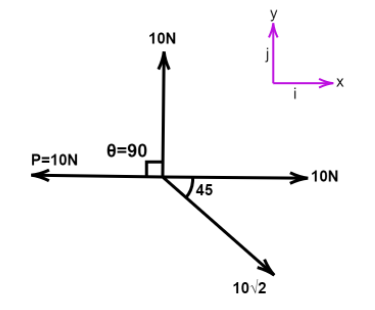
For B, $\theta = 90^\circ,P = 10N$
$x\hat i = 10\hat i + 10\sqrt 2 \cos 45^\circ \hat i - 10\hat i$
$\Rightarrow$ $\left\{ {\cos 45^\circ = \dfrac{1}{{\sqrt 2 }}} \right\}$
$\Rightarrow$ $x\hat i = 10\hat i + 10\hat i - 10\hat i = 10\hat i$
$\Rightarrow$ $y\hat j = 10\hat j - 10\sqrt 2 \sin 45^\circ \hat j$
$\left\{ {\sin 45^\circ = \dfrac{1}{{\sqrt 2 }}} \right\}$
$y\hat j = 10\hat j - 10\hat j$
$y\hat j = 0$
Resultant, $\vec R = \sqrt {{{(x\hat i)}^2} + {{(y\hat j)}^2}} $
$\Rightarrow$ $\vec R = \sqrt {{{(10\hat i)}^2} + {{(0\hat j)}^2} + } $
$\Rightarrow$ $\vec R = \sqrt {100} $
$\vec R = 10$
Resultant is $10N$, statement is true.
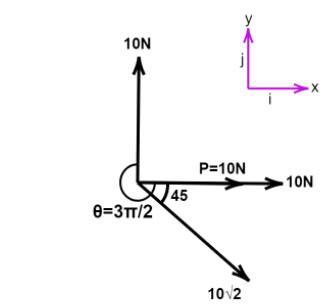
For C, $\theta = \dfrac{{3\pi }}{2},P = 10N$
$\Rightarrow$ $x\hat i = 10\hat i + 10\sqrt 2 \cos 45^\circ \hat i + 10\hat i$ $\Rightarrow$ $\left\{ {\cos 45^\circ = \dfrac{1}{{\sqrt 2 }}} \right\}$
$\Rightarrow$ $x\hat i = 10\hat i + 10\hat i + 10\hat i = 30\hat i$
$y\hat j = 10\hat j - 10\sqrt 2 \sin 45^\circ \hat j$
$\left\{ {\sin 45^\circ = \dfrac{1}{{\sqrt 2 }}} \right\}$
$y\hat j = 10\hat j - 10\hat j = 0$
Resultant, $\vec R = \sqrt {{{(x\hat i)}^2} + {{(y\hat j)}^2}} $
$\Rightarrow$ $\vec R = \sqrt {{{(30\hat i)}^2} + {{(0\hat j)}^2}} $
$\Rightarrow$ $\vec R = \sqrt {900} = 30$
Resultant is $30N$, since all the other components get cancelled out, the direction of this vector is on along x axis or $\hat i$, this statement is also true.
Hence the correct answers are option (B) and (C)
Note To find the resultant of multiple vectors, the best method is to resolve them into their x, y and z components and then find the resultant, this reduces the extra steps which would otherwise be required to find the angle made by the intermediate resultant vectors in the procedure.
Complete step by step solution
From the figure, it is clear that all the three vectors lie in a 2D plane. The correct option can be found by putting the value of P and $\theta $in each option. Suppose a vector makes angle $\theta $from an axis then the two components of this vector can be found by-
Multiplying the magnitude of the vector with the cos of the angle it makes with the axis. (for the base axis)
Multiplying the magnitude of the vector with the sin of the angle it makes with the axis. (for the perpendicular axis)
Resultant of two vectors is given by-
$\Rightarrow$ $\left| {\vec R} \right| = \sqrt {{{\vec A}^2} + {{\vec B}^2} + 2AB\cos \theta } $
For two perpendicular vectors, $\cos 90^\circ = 0$
$\left| {\vec R} \right| = \sqrt {{{\vec A}^2} + {{\vec B}^2}} $
For A, $\theta = 0,P = 10\sqrt 2 $
The first step is to resolve all the components into $\hat i$ and $\hat j$components. Let those values be $x$ and $y$respectively. Then,

$\Rightarrow$ $x\hat i = 10\hat i + 10\sqrt 2 \cos 45^\circ \hat i$
$\Rightarrow$ $\left\{ {\cos 45^\circ = \dfrac{1}{{\sqrt 2 }}} \right\}$
$\Rightarrow$ $x\hat i = 10\hat i + 10\hat i = 20\hat i$
$y\hat j = 10\hat j + 10\sqrt 2 \hat j - 10\sqrt 2 \sin 45^\circ $
$\Rightarrow$ $y\hat j = 10\sqrt 2 \hat j$
$\Rightarrow$ $\left\{ {\sin 45^\circ = \dfrac{1}{{\sqrt 2 }}} \right\}$
Resultant $\vec R = \sqrt {{{(x\hat i)}^2} + {{(y\hat j)}^2}} $
$\Rightarrow$ $\vec R = \sqrt {{{(20\hat i)}^2} + {{(10\sqrt 2 \hat j)}^2}} $
$\Rightarrow$ $\vec R = \sqrt {400 + 200} $
$\vec R = \sqrt {600} = 10\sqrt 6 $
Resultant is not a null vector, statement is false.

For B, $\theta = 90^\circ,P = 10N$
$x\hat i = 10\hat i + 10\sqrt 2 \cos 45^\circ \hat i - 10\hat i$
$\Rightarrow$ $\left\{ {\cos 45^\circ = \dfrac{1}{{\sqrt 2 }}} \right\}$
$\Rightarrow$ $x\hat i = 10\hat i + 10\hat i - 10\hat i = 10\hat i$
$\Rightarrow$ $y\hat j = 10\hat j - 10\sqrt 2 \sin 45^\circ \hat j$
$\left\{ {\sin 45^\circ = \dfrac{1}{{\sqrt 2 }}} \right\}$
$y\hat j = 10\hat j - 10\hat j$
$y\hat j = 0$
Resultant, $\vec R = \sqrt {{{(x\hat i)}^2} + {{(y\hat j)}^2}} $
$\Rightarrow$ $\vec R = \sqrt {{{(10\hat i)}^2} + {{(0\hat j)}^2} + } $
$\Rightarrow$ $\vec R = \sqrt {100} $
$\vec R = 10$
Resultant is $10N$, statement is true.

For C, $\theta = \dfrac{{3\pi }}{2},P = 10N$
$\Rightarrow$ $x\hat i = 10\hat i + 10\sqrt 2 \cos 45^\circ \hat i + 10\hat i$ $\Rightarrow$ $\left\{ {\cos 45^\circ = \dfrac{1}{{\sqrt 2 }}} \right\}$
$\Rightarrow$ $x\hat i = 10\hat i + 10\hat i + 10\hat i = 30\hat i$
$y\hat j = 10\hat j - 10\sqrt 2 \sin 45^\circ \hat j$
$\left\{ {\sin 45^\circ = \dfrac{1}{{\sqrt 2 }}} \right\}$
$y\hat j = 10\hat j - 10\hat j = 0$
Resultant, $\vec R = \sqrt {{{(x\hat i)}^2} + {{(y\hat j)}^2}} $
$\Rightarrow$ $\vec R = \sqrt {{{(30\hat i)}^2} + {{(0\hat j)}^2}} $
$\Rightarrow$ $\vec R = \sqrt {900} = 30$
Resultant is $30N$, since all the other components get cancelled out, the direction of this vector is on along x axis or $\hat i$, this statement is also true.
Hence the correct answers are option (B) and (C)
Note To find the resultant of multiple vectors, the best method is to resolve them into their x, y and z components and then find the resultant, this reduces the extra steps which would otherwise be required to find the angle made by the intermediate resultant vectors in the procedure.
Recently Updated Pages
The ratio of the diameters of two metallic rods of class 11 physics JEE_Main

What is the difference between Conduction and conv class 11 physics JEE_Main

Mark the correct statements about the friction between class 11 physics JEE_Main

Find the acceleration of the wedge towards the right class 11 physics JEE_Main

A standing wave is formed by the superposition of two class 11 physics JEE_Main

Derive an expression for work done by the gas in an class 11 physics JEE_Main

Trending doubts
JEE Mains 2025: Check Important Dates, Syllabus, Exam Pattern, Fee and Updates

JEE Main Login 2045: Step-by-Step Instructions and Details

Class 11 JEE Main Physics Mock Test 2025

JEE Main Chemistry Question Paper with Answer Keys and Solutions

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Keys & Solutions

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

NCERT Solutions for Class 11 Physics Chapter 1 Units and Measurements

NCERT Solutions for Class 11 Physics Chapter 9 Mechanical Properties of Fluids

Units and Measurements Class 11 Notes: CBSE Physics Chapter 1

JEE Advanced 2025: Dates, Registration, Syllabus, Eligibility Criteria and More

NCERT Solutions for Class 11 Physics Chapter 2 Motion In A Straight Line




