Question

To increase the angular magnification of a simple microscope one should increase
a) the focal length of the lens
b) the power of the lens
c) the aperture of the lens
d) the size of the object

Answer 1

Hint: The angular of any lens is given as the ratio of the angle subtended by the image to that of the object. First we will obtain the expression of angular magnification and then see with what quantities it varies. Hence we will manipulate each of the options mentioned above accordingly.

Complete answer: First let us obtain an expression for the angular magnification of the lens in a simple microscope.

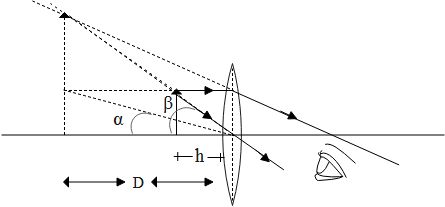
A simple microscope consists of a convex lens of short focal length held close to the eye as shown in the figure above the specimen is kept at a distance h from the lens between the optical centre of the lens and its focal length. Hence the image is formed on the same side of the convex lens at a distance D. A person views the image formed at his least distance of distinct vision.

The angular magnification of the image is given by, $m=\dfrac{\begin{align}
  & \text{Angle Subtended by the image at least } \\
 & \text{distance of distinct vision} \\
\end{align}}

{\begin{align}
  & \text{Angle Subtended by the object at least } \\
 & \text{distance of distinct vision} \\
\end{align}}$

For small angle $\tan \theta \simeq \theta $ Hence, we can write the above equation as $m=\dfrac{\tan \beta }{\tan \alpha }$
From trigonometric definition of $\tan \theta $ we can write the above equation as,
$m=\dfrac{\dfrac{\text{height of the object }}{\text{-h}}}{\dfrac{\text{height of the object}}{-D}}$
$m=\dfrac{-D\text{ }}{\text{-h}}=\dfrac{D\text{ }}{\text{h}}.......(1)$
Let f be the focal length of the convex lens. Using lens formula,
$\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$ where v is the image distance, u is the object distance and f is the focal length.

From the above diagram we know that, v=-D and u=-h. The minus sign indicates that the distance is measured opposite to the direction of the rays. Now let us substitute this in the above formula.

$\dfrac{1}{-D}-\dfrac{1}{-h}=\dfrac{1}{f}$
$\dfrac{1}{h}=\dfrac{1}{f}+\dfrac{1}{D}$
Multiplying D on both the sides of the above equation we get,
$\dfrac{D}{h}=\dfrac{D}{f}+\dfrac{D}{D}$
$\dfrac{D}{h}=\dfrac{D}{f}+1......(2)$
Comparing equation 1 and 2 we get,
$m=\dfrac{D}{f}+1$

Since the power of a lens is given as $P=\dfrac{1}{f}$, we can write the above equation as $m=PD+1.....(3)$
From equation 3 we can conclude angular magnification of the lens can be increased by increasing the power of a lens.
So, the correct answer is “Option b”.

Note:
A person to see the image has to look in the lens at a distance of minimum 25 cm. Going closer to the lens than this the image will not be visible as our least distance of distinct vision is 25cm. The magnification of the image formed also depends on D, which means far from the convex lens the image will be sharper.