Question

Twelve wires each having resistors r, are joined to form a cube as shown in the figure. Find the equivalent resistance between the ends of a face diagonal such as 1 and 8.
             

\[\begin{align}
  & \text{A) r} \\
 & \text{B) }\dfrac{4r}{7} \\
 & \text{C) }\dfrac{3r}{4} \\
 & \text{D) }\dfrac{4r}{5} \\
\end{align}\]

Answer 1

Hint: We need to understand the combination of resistors used in the given network to find the equivalent resistance of the circuit. The face diagonals are the two end points in this case across which we have to find the equivalent resistance.

Complete step by step answer:
We know that the equivalent resistance of a network can be calculated only by identifying the types of combinations involved in the given circuit.
We need to find the equivalent resistance of the network by identifying whether the combination is in series, parallel or series-parallel.
We can do this by simplifying the given network. We need to apply the Wheatstone’s condition to make the situation much easier. According to Wheatstone's condition the resistance in between two pairs of resistances joined by a node doesn’t have any current, if the resistances of the two pairs are in a constant ratio.
                    

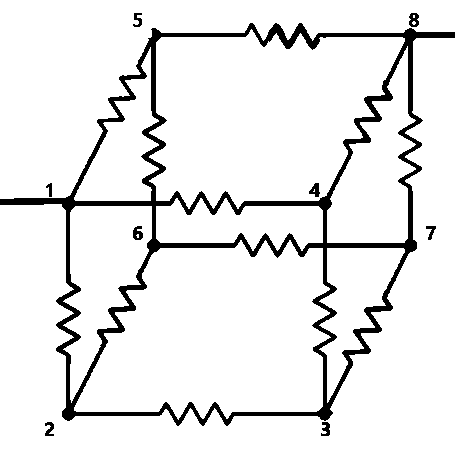
When we consider the given system of circuit, we can easily understand that the points (5, 6) and (4, 7) are equipotential nodes as the resistances at either side of these are in constant ratio. This will simplify the circuit to –

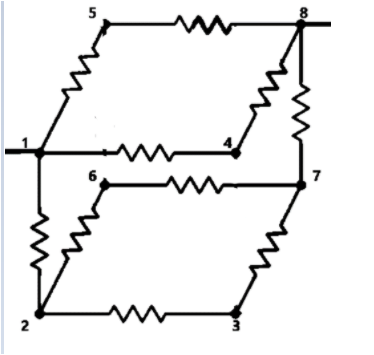
From this we can understand that the series has reduced to a much simpler network of series and parallel connections.
The resistance in the plane 1485 can be found as –
\[\begin{align}
  & \dfrac{1}{{{R}_{1485}}}=\dfrac{1}{{{R}_{15}}+{{R}_{58}}}+\dfrac{1}{{{R}_{14}}+{{R}_{48}}} \\
 & \dfrac{1}{{{R}_{1485}}}=\dfrac{1}{r+r}+\dfrac{1}{r+r} \\
 & \therefore {{R}_{1485}}={{R}_{1}}=r \\
\end{align}\]
The resistance in the plane 2673 is also the same as above.
i.e.,
\[{{R}_{2673}}=r\]
Now the resistors \[{{R}_{12}}\text{ and }{{\text{R}}_{78}}\]are in series with the resistance \[{{R}_{2673}}\].
\[\Rightarrow {{R}_{2}}=r+r+r=3r\]
Now, the resistances between 1 and 8 are \[{{R}_{1}}\text{ and }{{\text{R}}_{2}}\] is parallel. The equivalent resistance between 1 and 8 is given as –
\[\begin{align}
  & \dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}} \\
 & \dfrac{1}{{{R}_{eq}}}=\dfrac{1}{r}+\dfrac{1}{3r} \\
 & \therefore {{R}_{eq}}=\dfrac{3r}{4}\Omega \\
\end{align}\]
The equivalent resistance of the circuit is \[{{R}_{eq}}=\dfrac{3r}{4}\Omega \].
The correct answer is option C.

Note:
The equivalent resistance of the network in this case is taken across the face diagonals of the cube. The value of resistance will vary depending on the points across which the resistance is considered. i.e., the resistance across the body diagonal will not be the same as this.