Answer
110.7k+ views
Hint: All the bodies are in a state of rest and the net force acting on each of them is zero. First find value of $T$ using force balance on 6 kg body and considering frictionless pulley use this value to find ${T_1}$ by considering force balance on 4 kg body.
Complete answer:
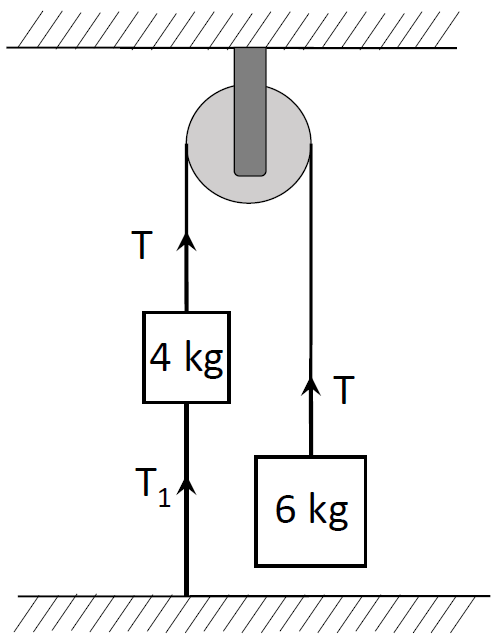
In the above system, all the bodies are in a state of rest. So there is no net acceleration on anybody and thus no net force is acting on both the masses. Let the tension in the string connecting both the masses be $T$. This tension will be an upward force acting on mass 6kg. If we consider the 6 kg mass then we have two forces acting on it. Tension, $T$ is balancing the weight of the mass in downward direction. Both these forces are in the opposite direction. Let the acceleration due to the gravity be $g = 9.8m/{s^2}$. Therefore,
$T = mg$ where $m = 6kg$.
$T = 6 \times 9.8 = 58.8N$
They have not specified any details about pulley, so we will assume it is frictionless and then consider that this tension remains same over it and acts on 4kg mass in the upward direction balancing the tension in the bottom string which connects the 4kg mass to the table and the weight of the mass. Therefore, we can write the force balance for 4kg mass as follows:
${T_1} + {m_1}g = T = 58.8N$, where ${m_1} = 4kg$
$
\Rightarrow {T_1} = 58.8 - 4 \times 9.8 \\
\Rightarrow {T_1} = 19.6N \\
$
Note: Many times, acceleration due to gravity is considered $10m/{s^2}$ for its simplicity in calculations. So better to carry the term till the end and substitute accordingly if the numerical value is required in multiple choice questions.
Complete answer:
In the above system, all the bodies are in a state of rest. So there is no net acceleration on anybody and thus no net force is acting on both the masses. Let the tension in the string connecting both the masses be $T$. This tension will be an upward force acting on mass 6kg. If we consider the 6 kg mass then we have two forces acting on it. Tension, $T$ is balancing the weight of the mass in downward direction. Both these forces are in the opposite direction. Let the acceleration due to the gravity be $g = 9.8m/{s^2}$. Therefore,
$T = mg$ where $m = 6kg$.
$T = 6 \times 9.8 = 58.8N$
They have not specified any details about pulley, so we will assume it is frictionless and then consider that this tension remains same over it and acts on 4kg mass in the upward direction balancing the tension in the bottom string which connects the 4kg mass to the table and the weight of the mass. Therefore, we can write the force balance for 4kg mass as follows:
${T_1} + {m_1}g = T = 58.8N$, where ${m_1} = 4kg$
$
\Rightarrow {T_1} = 58.8 - 4 \times 9.8 \\
\Rightarrow {T_1} = 19.6N \\
$
Note: Many times, acceleration due to gravity is considered $10m/{s^2}$ for its simplicity in calculations. So better to carry the term till the end and substitute accordingly if the numerical value is required in multiple choice questions.
Recently Updated Pages
Write an article on the need and importance of sports class 10 english JEE_Main

Write a composition in approximately 450 500 words class 10 english JEE_Main

Arrange the sentences P Q R between S1 and S5 such class 10 english JEE_Main

If x2 hx 21 0x2 3hx + 35 0h 0 has a common root then class 10 maths JEE_Main

The radius of a sector is 12 cm and the angle is 120circ class 10 maths JEE_Main

For what value of x function fleft x right x4 4x3 + class 10 maths JEE_Main

Other Pages
If a wire of resistance R is stretched to double of class 12 physics JEE_Main

The energy stored is a condenser is in the form of class 12 physics JEE_Main

Excluding stoppages the speed of a bus is 54 kmph and class 11 maths JEE_Main

Electric field due to uniformly charged sphere class 12 physics JEE_Main

In Searles apparatus when the experimental wire is class 11 physics JEE_Main