Question

Two circles touch externally. The sum of their areas is \[130\pi \] sq.cm. and the distance between their centers is 14 cm. Find the radii of the circles.
A) 11cm and 3cm
B) 1cm and 3cm
C) 11cm and 13cm
D) None of these

Answer 1

Hint:
Here, we have to find the radii of the circles. With the given conditions, we can find the radii of the circles by using the area of the circles. First we will use the area of the circle formula to find an equation and the distance between their centers formula to find an equation for either of the radius. Then we will substitute the equation of the radius in the equation we derived from the area of circles formula, after which we will obtain the value of one radius. We will then substitute the radius of one circle in the equation of the radius to obtain the radius of the other circle.

Formula Used:
We will use the following formula:
1) When two circle touch externally then the distance between their centers \[ = \] sum of their radii
\[\left| {{C_1}{C_2}} \right| = {r_1} + {r_2}\] where \[{r_1},{r_2}\] are the radii of two circles
2) Area of the circle is given by \[A = \pi {r^2}\] ​where \[r\] is the radius of the circle.
3) The square of the difference of two numbers is given by \[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab\].

Complete step by step solution:

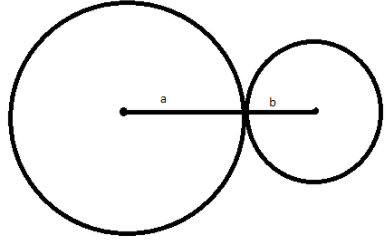
Let us consider the radius of the two circles are \[a\]and \[b\] cm.
Now we will find the distance between the centers of two circles.
The distance between their centers \[ = a + b\]


We are given that the distance between their centers is 14 cm.
Substituting the value of distance, we get

\[ \Rightarrow a + b = 14\]
Rewriting the above equation, we get
\[ \Rightarrow b = 14 - a\] …………………………………………\[\left( 1 \right)\]
By using the area of the circles formula, the sum of their areas with the radius of the two circles as \[a\]and \[b\]cm, we get
\[ \Rightarrow \] Sum of their areas \[ = \pi {a^2} + \pi {b^2}\]
Substituting the value of sum of areas, we get

\[ \Rightarrow \pi {a^2} + \pi {b^2} = 130\pi \]
\[ \Rightarrow \pi \left( {{a^2} + {b^2}} \right) = 130\pi \]
Cancelling the similar term on both the sides, we have
\[ \Rightarrow {a^2} + {b^2} = 130\] …………………………………………\[\left( 2 \right)\]

Substituting equation \[\left( 1 \right)\] in equation \[\left( 2 \right)\], we have

\[ \Rightarrow {a^2} + {\left( {14 - a} \right)^2} = 130\]
Now simplifying the above equation using the identity \[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab\], we get
\[ \Rightarrow {a^2} + {a^2} + 196 - 28a = 130\]

Rewriting the equation and adding the terms, we have
\[ \Rightarrow 2{a^2} + 66 - 28a = 0\]

Dividing both sides by 2, we get
\[ \Rightarrow {a^2} + 33 - 14a = 0\]

By Factorization method, we get
\[ \Rightarrow {a^2} - 11a - 3a + 33 = 0\]
\[ \Rightarrow a(a - 11) - 3(a - 11) = 0\]

Again factoring the equation, we get
\[ \Rightarrow \left( {a - 11} \right)\left( {a - 3} \right) = 0\]
\[ \Rightarrow a = 3,11\]

Now we will find the value of \[b\] when \[a = 3\]. Therefore, we get

\[b = 14 - 3 = 11\]

Now we will find the value of \[b\] when \[a = 11\]. Therefore, we get

\[b = 14 - 11 = 3\]
Therefore, the radius of two circles is 11cm and 3 cm.

Hence, option A is the correct option.

Note:
We have to find the radius of two circles. A radius is a straight line from the center of a circle to the circumference of a circle. If there are two or more of radii, then they are referred to as radii. All radii in a circle will be the same length. A radius can be a line from any point on the circumference to the center of the circle. If we put two radii together, edge to edge, going through the center of a circle, we would get a diameter.