
Two circles touch externally. The sum of their area is
Answer
434.4k+ views
Hint: Here in this question, we are given two circles that touch each other. We are given that the sum of the area of the two circles is
Complete step-by-step answer:
So, there are two touching circles whose sum of area is
Let the radius of the one circle be r and the radius of the other circle be R.
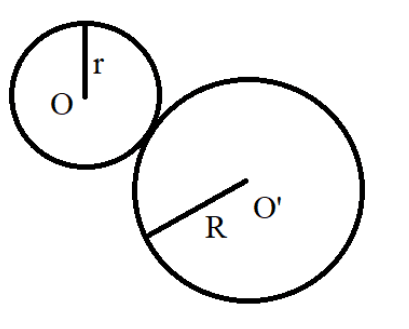
Hence, we have,
Dividing both the sides of the equation by
Also, the distance between the centres of the two circles is
Squaring both sides of the above equation, we get,
Evaluating the square of the left side of the equation, we get,
Now, substituting the value of
Simplifying the equation further, we get,
Now, we can solve for the radii of both the circles using the equation
So, substituting the value of R from the equation
Now, we open the brackets,
Shifting all the terms of the equation to the right side of the equation, we get,
Now, we have to solve this quadratic equation in r so as to find the radii of both the circles. We solve the quadratic equation using splitting the middle term method.
We split the middle term of the quadratic equation into two parts and factorise the equation further.
Taking out r common from the first two terms,
Now, taking out the factor
Now, either
Hence, the value of r is
Now, we know that
If the value of r is
If the value of r is
Hence, the radii of the circle are
Note: A circle is a closed two dimensional figure. The area of a circle is defined as the region occupied by the circular region. It can be determined by using formula
Complete step-by-step answer:
So, there are two touching circles whose sum of area is
Let the radius of the one circle be r and the radius of the other circle be R.
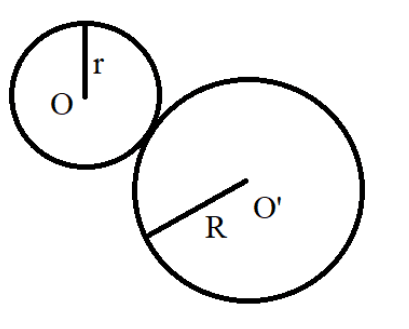
Hence, we have,
Dividing both the sides of the equation by
Also, the distance between the centres of the two circles is
Squaring both sides of the above equation, we get,
Evaluating the square of the left side of the equation, we get,
Now, substituting the value of
Simplifying the equation further, we get,
Now, we can solve for the radii of both the circles using the equation
So, substituting the value of R from the equation
Now, we open the brackets,
Shifting all the terms of the equation to the right side of the equation, we get,
Now, we have to solve this quadratic equation in r so as to find the radii of both the circles. We solve the quadratic equation using splitting the middle term method.
We split the middle term of the quadratic equation into two parts and factorise the equation further.
Taking out r common from the first two terms,
Now, taking out the factor
Now, either
Hence, the value of r is
Now, we know that
If the value of r is
If the value of r is
Hence, the radii of the circle are
Note: A circle is a closed two dimensional figure. The area of a circle is defined as the region occupied by the circular region. It can be determined by using formula
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Differentiate between the Western and the Eastern class 9 social science CBSE




