Question

Two concentric shells have charges$+q$and$-q$as shown in the figure. Choose the correct options:

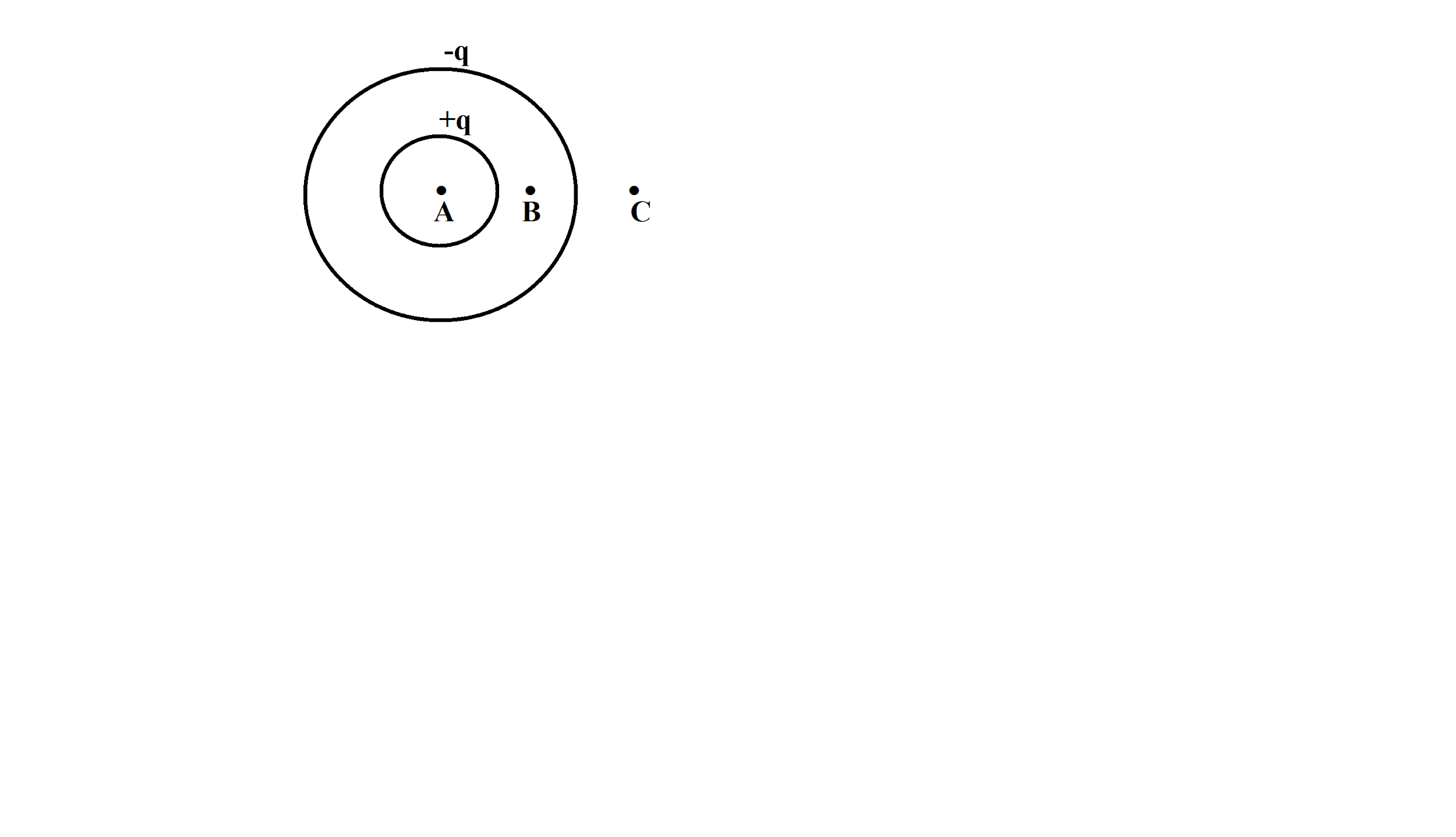
A. At $A$electric field is zero, but electric potential is non-zero
B. At $B$electric field and electric potential both are non-zero
C. At $C$electric field is zero but electric potential is non-zero
D. At $C$electric field and electric potential both are zero

Answer 1

Hint: Electric field intensity is expressed as the strength of electric field at any point. The work done by moving a unit charge in an electric field is stored as electric potential. We will calculate the value of electric field intensity and electric potential at the three given points A, B, and C.

Complete step-by-step answer:
Electric field intensity at a point is described as the force experienced by a unit positive charge placed at that point. Electric field intensity is a vector quantity, meaning it has both magnitude and the direction.
$E=\dfrac{kq}{{{r}^{2}}}$
Where,
\[\begin{align}
  & V=\text{electric field} \\
 & k=\text{Coulomb constant} \\
 & q=\text{charge} \\
 & r=\text{distance of separation} \\
\end{align}\]
Electrical potential is the amount of work needed to move a unit charge from a particular reference point to another specific point inside the electric field without producing any acceleration.
$V=\dfrac{kq}{r}$
Where,
\[\begin{align}
  & V=\text{electric potential} \\
 & k=\text{Coulomb constant} \\
 & q=\text{charge} \\
 & r=\text{distance of separation} \\
\end{align}\]
We are given two concentric shells having charges$+q$and$-q$as shown below:

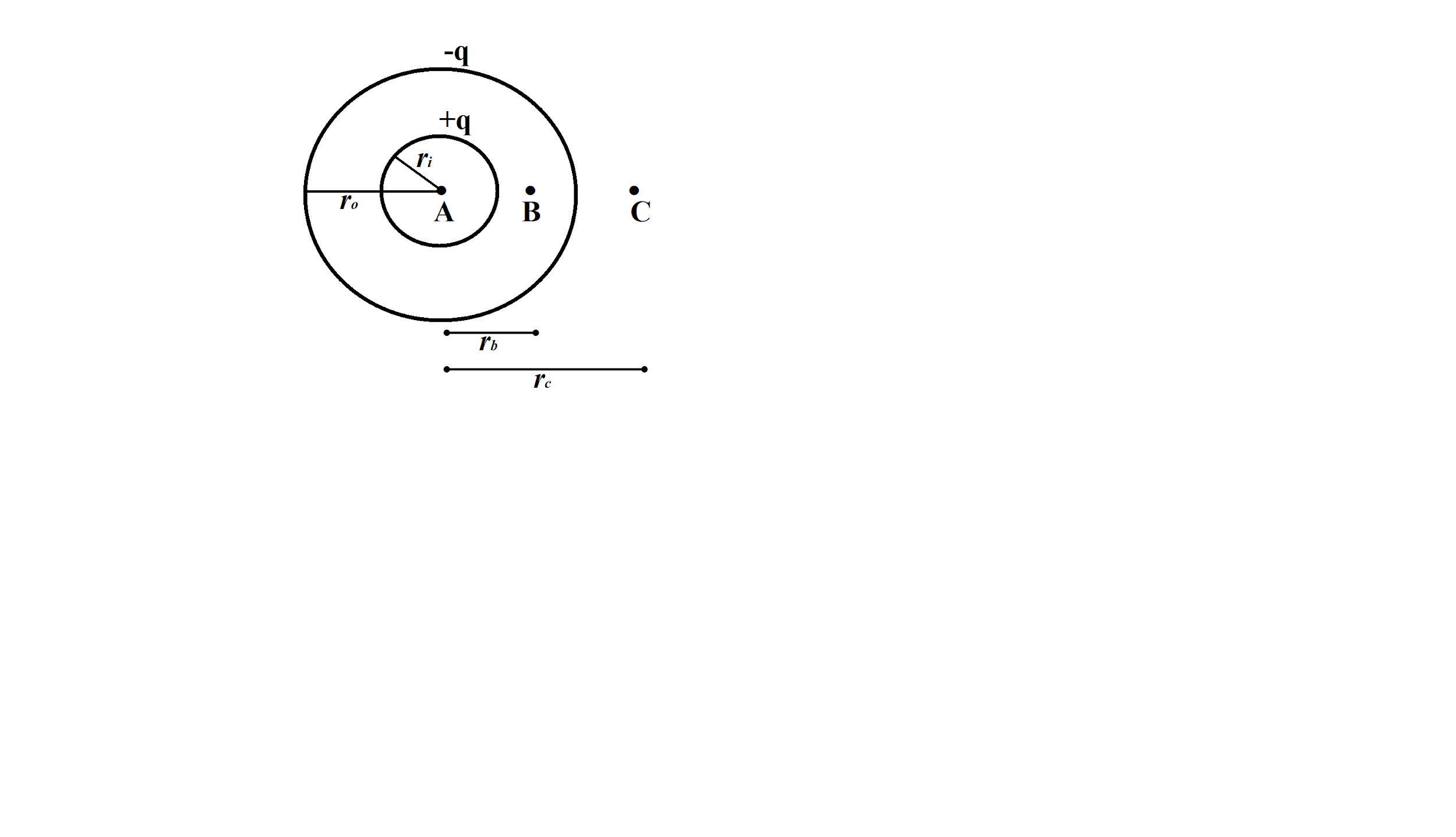
At A
Electric field inside the shell is zero because the charge enclosed by the shell is zero.
${{E}_{A}}=0$
Potential at A is,
${{V}_{A}}=\dfrac{kq}{{{r}_{i}}}-\dfrac{kq}{{{r}_{o}}}$
Where,
${{r}_{i}}$is the radius of inner shell
${{r}_{o}}$ is the radius of outer shell
As ${{r}_{i}}\ne {{r}_{o}}$
Therefore,
${{V}_{A}}\ne 0$
At B
Using Gauss law of electric field, we have,
$\begin{align}
  & {{E}_{B}}\times 4\pi {{\left( {{r}_{b}} \right)}^{2}}=\dfrac{Q}{{{\varepsilon }_{o}}} \\
 & {{E}_{B}}=\dfrac{+q}{4\pi {{\varepsilon }_{o}}{{\left( {{r}_{b}} \right)}^{2}}} \\
\end{align}$
${{E}_{B}}\ne 0$
Potential at B
${{V}_{B}}=\dfrac{kq}{{{r}_{B}}}+\dfrac{k\left( -q \right)}{{{r}_{o}}}$
As ${{r}_{B}}\ne {{r}_{o}}$
Therefore,
${{V}_{B}}\ne 0$
At C
Using Gauss law of electric field, we have,
$\begin{align}
  & {{E}_{C}}\times 4\pi {{r}^{2}}=\dfrac{Q}{{{\varepsilon }_{o}}}=\dfrac{+q-q}{{{\varepsilon }_{o}}} \\
 & {{E}_{C}}=0 \\
\end{align}$
Potential at C
$\begin{align}
  & {{V}_{C}}=\dfrac{kq}{{{r}_{c}}}+\dfrac{k\left( -q \right)}{{{r}_{c}}} \\
 & {{V}_{C}}=0 \\
\end{align}$
Thus,
At A, electric field is zero, but electric potential is non-zero
At B, electric field and electric potential both are non-zero
At C, electric field and electric potential both are zero
Hence, the correct options are A, B, and D.

Note:
While calculating the electric field at any point, direction of the vector should be considered very carefully and the sign of the charge should be taken into account, whether the charge on the body is positive or negative. For calculating electric potential, acceleration of unit charge is assumed to be zero. Also remember that the electric field inside a conducting shell is zero because free charges in conductor reside only on the surface.