Question

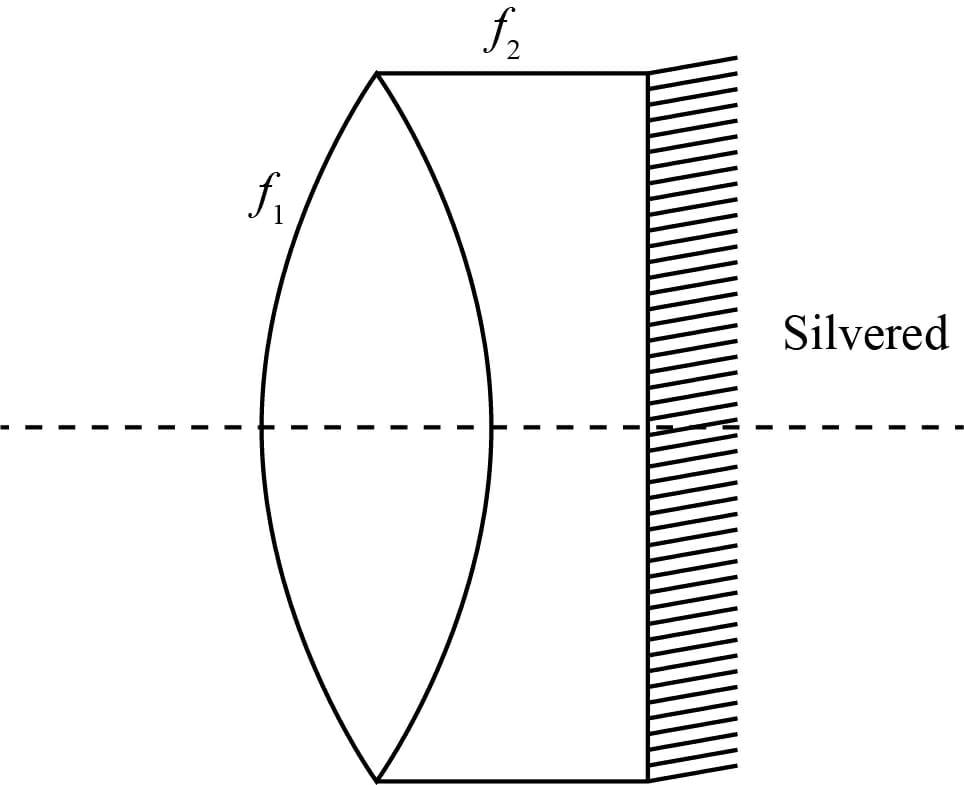
Two lenses of focal length ${{\text{f}}_1} = 10cm$ and ${{\text{f}}_2} = 20cm$ are kept as shown. The resultant power combination will be:

 $\eqalign{
  & {\text{A}}{\text{. - }}10D \cr
  & {\text{B}}{\text{. }}5D \cr
  & {\text{C}}{\text{. - }}5D \cr
  & {\text{D}}{\text{. }}10D \cr} $

Answer 1

Hint: As we know, the power of a lens is defined as the reciprocal of the wavelength, i.e.${\text{P = }}\dfrac{1}{f}$ . The unit of power of a lens is diopters (D). Here we find the power of the combination of a lens is the algebraic sum of the powers of the individual lenses in contact.
$\therefore \dfrac{1}{F} = \dfrac{1}{{{f_1}}} + \dfrac{1}{{{f_2}}} + ........$
Where f is a focal length.
$ \Rightarrow {\text{P = }}{{\text{P}}_1} + {{\text{P}}_2} + ....$

Complete step by step answer:
According to a given diagram
The focal length of the convex lens = $10cm$
The focal length of the concave lens =$ - 20cm$
And the focal length of the plane mirror =$\infty $
So, the resultant power of the combination of lens
$\dfrac{1}{{\text{F}}} = \dfrac{1}{{{f_1}}} + \dfrac{1}{{{f_2}}} + \dfrac{1}{{{f_3}}}$$ \Rightarrow \dfrac{1}{{\text{F}}} = \dfrac{1}{{10}} - \dfrac{1}{{20}} - \dfrac{1}{\infty }$

$\therefore \dfrac{1}{{\text{F}}} = \dfrac{1}{{20}}$
$ \Rightarrow {\text{F = 20cm = 0}}{\text{.2m}}$
Now the power of combination ${\text{P = }}\dfrac{1}{{\text{F}}}$
$ \Rightarrow {\text{P = }}\dfrac{1}{{0.2}} = 5{\text{D}}$

Additional information: The capacity of a lens to bend the rays of light depends upon the focal length. The smaller the focal length, the greater is the bending of a beam of light and vice- versa. Thus the power of a lens to bend the rays of light is inversely proportional to the focal length of the lens.

Note: If two lenses are separated by distance d meter, then the power of a combination of lenses is given by the relation
${\text{P = }}{{\text{P}}_1} + {{\text{P}}_2} - {\text{d}}{\text{.(}}{{\text{P}}_1}{\text{.}}{{\text{P}}_2})$ Here d is the distance.
Always remember the power of a concave lens is negative, and the power of a convex lens is positive. We use a combination of lenses for higher magnification because lens combination multiplies each other's magnification power.