Question

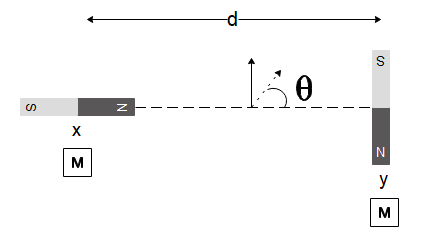
Two magnetic dipoles X and Y are placed at a separation $ d $ , with their axes perpendicular to each other. The dipole moment of Y is twice that of X. A particle of charge $ q $ is passing, through their midpoint P, at an angle $ \theta = 45^\circ $ with the horizontal line, as shown in the figure. What would be the magnitude of the force on the particle at that instant? (d is much larger than the dimensions of the dipole)

A) $ \sqrt 2 \left( {\dfrac{{{\mu _0}}}{{4\pi }}} \right)\dfrac{M}{{{{\left( {d/2} \right)}^3}}} \times qv $
B) $ \left( {\dfrac{{{\mu _0}}}{{4\pi }}} \right)\dfrac{{2M}}{{{{\left( {d/2} \right)}^3}}} \times qv $
C) $ \left( {\dfrac{{{\mu _0}}}{{4\pi }}} \right)\dfrac{M}{{{{\left( {d/2} \right)}^3}}} \times qv $
D) 0

Answer 1

Hint : In this solution, we will use the formula for the magnetic field due to a magnetic dipole taking into account the direction of the magnetic fields due to the two dipoles. Then we will use the formula of Lorentz force to determine the force acting on the charged particle.

Formula used: In this question, we will use the following formula
-Magnetic field due to a magnetic dipole: $ B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2M}}{{{{\left( d \right)}^3}}} $ where $ d $ is the distance of the point from the centre of the dipole
- Lorentz force due to a charge moving in a magnetic field: $ F = q(\vec v \times \vec B) $ where $ v $ is the velocity of the particle and $ B $ is the magnetic field.

Complete step by step answer
In the diagram given to us, we will first determine the net magnetic field at the centre of the two magnetic dipoles. Both the magnetic dipoles will have the same magnetic field since they have the same magnetic moment and the distance of the point is the same from both the magnetic dipoles $ (d/2) $ which are calculated as:
 $ B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2M}}{{{{\left( {d/2} \right)}^3}}} $
Now for the left magnetic dipole, the net magnetic field at the middle point will be in the upwards direction and for the right magnetic dipole, the magnetic field at the middle point will be towards it. Since both of these dipoles have the same magnitude, the net resultant magnetic field at this point will have a direction of $ \theta = 45^\circ $ with the horizontal and have a magnitude
 $ B = \sqrt {{{\left( {\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2M}}{{{{\left( {d/2} \right)}^3}}}} \right)}^2} + {{\left( {\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2M}}{{{{\left( {d/2} \right)}^3}}}} \right)}^2}} $
 $ \Rightarrow B = \sqrt 2 \left( {\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2M}}{{{{\left( {d/2} \right)}^3}}}} \right) $
Now to determine the force acting on a charge moving in a magnetic field, we will use the formula for Lorentz force $ F = q(\vec v \times \vec B) $
Now in the cross-product term, the velocity of the charged particle is given to us as of $ \theta = 45^\circ $ with the horizontal which is the same as the direction of the net magnetic field. As a result, the cross product will be zero $ (\vec v \times \vec B) = 0 $ so the force will be zero.
Hence the correct choice is option (D).

Note
We must be careful to take the direction of the individual magnetic field when calculating the net magnetic field. If we don't take into account the direction, the force will be non-zero and we will get the answer as choice (A) which is wrong.