Question

Two plane mirrors are at right angles to each other. A man stands between them and combs his hair with his hair with his right hand. In how many of the images will he be seen using his right hand:
A. 0
B. 1
C. 2
D. 3

Answer 1

Hint: Multiple images are formed due to multiple reflection when an object is placed in between the two images at an angle ‘$\theta $’. The number of images formed in that case is given by the formula, $n = \dfrac{{360}}{\theta } - 1$, here ‘$\theta $’ is in degrees. We will apply this formula to find the required answer.

Formula Used: $n = \dfrac{{360}}{\theta } - 1$

Complete answer:
According to the question, there are two plane mirrors which are held at right angles, which means they are inclined at an angle of 90 degrees.

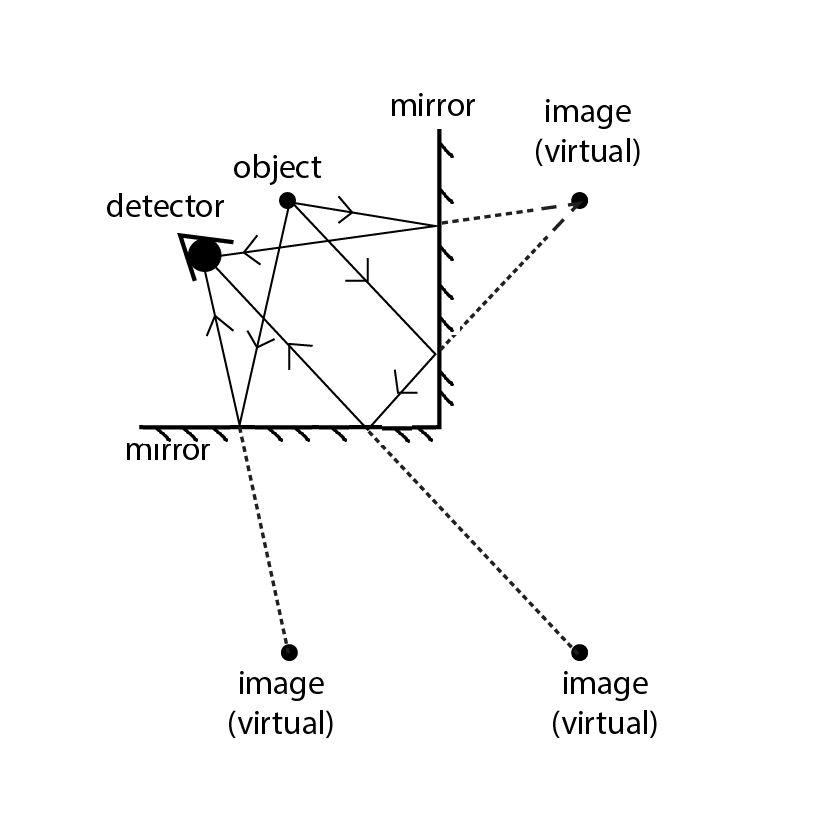
We know that, when 360/90 = 4 is an even number. The number of images would be $\left( {360/90 - 1} \right) = 3$. In the first two images the comb would be in the left hand of the man. The image which appears in between those two images has the comb in its right hand. Therefore, the images in which he will be seen using his right hand is one.

Hence, option (B) is the correct answer.

Additional Information:
An optical instrument consisting of two or more reflecting surfaces is known as a kaleidoscope. In this instrument three surfaces are tilted towards each other at a certain angle for obtaining symmetrical patterns. It is an optical toy consisting of two mirrors at a particular angle. Kaleidoscope works on the principle of law of reflection.

Note:
When light is reflected off one mirror it can then easily be reflected again from another, and many more results in multiple images of a single object. An object when it is placed in between two parallel plane mirrors, infinite images are formed.