Question

Two ships leave a port at the same time. One goes 24 km per hour in the direction \[{\rm{N}}45^\circ {\rm{E}}\] and the other travels 32 km per hour in the direction \[{\rm{S}}75^\circ {\rm{E}}\]. Find the distance between the ships at the end of 3 hours.

Answer 1

Hint: Here, we need to find the distance between the ships at the end of 3 hours. First, we will find the distance travelled by the ships in 3 hours. Then, we will find the angle between the paths taken by the ships. Finally, we will use the law of cosines and the given information to find the distance between the two ships at the end of 3 hours.

Formula Used:
 We will use the following formulas:
1.The distance travelled at a uniform speed in a certain time is given by \[{\rm{Distance}} = {\rm{Speed}} \times {\rm{Time}}\].
2.The law of cosines states that \[{c^2} = {a^2} + {b^2} - 2ab\cos C\], where \[a\], \[b\], and \[c\] are the lengths of the sides of the triangle, and \[C\] is the angle opposite to the side of length \[c\].

Complete step-by-step answer:
First, we will find the distance travelled by the two ships in 3 hours.
The distance travelled at a uniform speed in a certain time is given by \[{\rm{Distance}} = {\rm{Speed}} \times {\rm{Time}}\].
The first ship travels 3 hours at the speed of 24 km per hour.
Therefore, we get
Distance travelled by the first ship in 3 hours \[ = 24 \times 3\]
Multiplying the terms in the expression, we get
\[ \Rightarrow \] Distance travelled by the first ship in 3 hours \[ = 72\] km
The second ship travels 3 hours at the speed of 32 km per hour.
Therefore, we get
Distance travelled by the second ship in 3 hours \[ = 32 \times 3\]
Multiplying the terms in the expression, we get
\[ \Rightarrow \] Distance travelled by the second ship in 3 hours \[ = 96\] km
Now, we will draw the diagram using the given information.

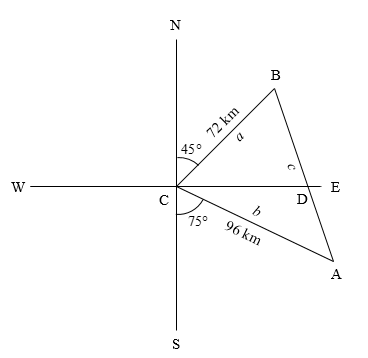
Here, C is the port from where the ships leave. B is the location of the first ship after 3 hours, and A is the location of the second ship after 3 hours.
BC is the distance travelled by the first ship in 3 hours, that is 72 km. AC is the distance travelled by the second ship in 3 hours, that is 96 km.
We need to find the distance between the ships after 3 hours, that is the length of AB.
We know that each of the directions forms a right angle with the adjacent directions.
The angle BCD is the difference in the angle between the directions North and East, and the angle at which the first ship travels North East.
Therefore, we get
\[\angle BCD = 90^\circ - 45^\circ = 45^\circ \]
The angle ACD is the difference in the angle between the directions South and East, and the angle at which the second ship travels South East.
Therefore, we get
\[\angle ACD = 90^\circ - 75^\circ = 15^\circ \]
From the figure, it can be observed that the angle BCA is the sum of the angles BCD and ACD.
Therefore, we get
\[\angle BCA = \angle BCD + \angle ACD\]
Substituting \[\angle BCD = 45^\circ \] and \[\angle ACD = 15^\circ \] in the equation, we get
\[ \Rightarrow \angle BCA = 45^\circ + 15^\circ = 60^\circ \]
Now, we will use the law of cosines to find the distance between the locations of the ships after 3 hours, that is AB.
According to the law of cosine, \[{c^2} = {a^2} + {b^2} - 2ab\cos C\], where \[a\], \[b\], and \[c\] are the lengths of the sides of the triangle, and \[C\] is the angle opposite to the side of length \[c\].
Substituting \[a = BC\], \[b = AC\], and \[c = AB\] in the law of cosines, we get
\[A{B^2} = B{C^2} + A{C^2} - 2\left( {BC} \right)\left( {AC} \right)\cos C\]
Substituting \[BC = 72\] km, \[AC = 96\] km, and \[\angle C = 60^\circ \] in the equation, we get
\[ \Rightarrow A{B^2} = {\left( {72} \right)^2} + {\left( {96} \right)^2} - 2\left( {72} \right)\left( {96} \right)\cos 60^\circ \]
Applying the exponents on the bases, we get
\[ \Rightarrow A{B^2} = 5184 + 9216 - 2\left( {72} \right)\left( {96} \right)\cos 60^\circ \]
We know that the cosine of \[60^\circ \] is \[\dfrac{1}{2}\].
Substituting \[\cos 60^\circ = \dfrac{1}{2}\] in the equation, we get
\[ \Rightarrow A{B^2} = 5184 + 9216 - 2\left( {72} \right)\left( {96} \right)\left( {\dfrac{1}{2}} \right)\]
Simplifying the expression, we get
\[ \Rightarrow A{B^2} = 5184 + 9216 - \left( {72} \right)\left( {96} \right)\]
Multiplying the terms in the expression, we get
\[ \Rightarrow A{B^2} = 5184 + 9216 - 6912\]
Adding and subtracting the terms in the expression, we get
\[ \Rightarrow A{B^2} = 7488\]
Taking the square roots of both sides, we get
\[ \Rightarrow AB \approx \sqrt {7488} \]
Thus, we get
\[\therefore AB\approx 86.5\]
Therefore, we get the distance between the two ships at the end of 3 hours as \[86.5\] km.

Note: We used the law of cosines instead of the law of sines to solve the question. This is because the law of cosines is much easier to use when two sides of a triangle and the angle between them is given.
In any triangle \[ABC\], we can apply three laws of cosines.
(a) \[{a^2} = {b^2} + {c^2} - 2bc\cos A\], where \[a\], \[b\], and \[c\] are the lengths of the sides of the triangle, and \[A\] is the angle opposite to the side of length \[a\].
(b) \[{b^2} = {a^2} + {c^2} - 2ac\cos B\], where \[a\], \[b\], and \[c\] are the lengths of the sides of the triangle, and \[B\] is the angle opposite to the side of length \[b\].
(c) \[{c^2} = {a^2} + {b^2} - 2ab\cos C\], where \[a\], \[b\], and \[c\] are the lengths of the sides of the triangle, and \[C\] is the angle opposite to the side of length \[c\].