Question

How do you use the reference angles to find \[\sin {210^ \circ }\cos {330^ \circ } - \tan {135^ \circ }\]?

Answer 1

Hint: To simplify \[\sin {210^ \circ }\cos {330^ \circ } - \tan {135^ \circ }\] using the reference angle, we will find the value of given angles step by step. Using the concept of reference angle, we will write
\[\sin {210^ \circ } = \sin ({180^ \circ } + {30^ \circ })\],
\[\cos {330^ \circ } = \cos \left( {{{360}^ \circ } - {{30}^ \circ }} \right)\] and
\[\tan {135^ \circ } = \tan \left( {{{180}^ \circ } - {{45}^ \circ }} \right)\].
Then using the value of standard angles, we will find the value of \[\sin {210^ \circ }\cos {330^ \circ } - \tan {135^ \circ }\].

Complete step by step answer:
According to the question, using the reference angles we have to find the value of \[\sin {210^ \circ }\cos {330^ \circ } - \tan {135^ \circ }\]. As we know, the reference angle is the acute angle with the x-axis. Thus, one by one we have to find the value of \[\sin {210^ \circ }\], \[\cos {330^ \circ }\] and \[\tan {135^ \circ }\] using the reference angle.
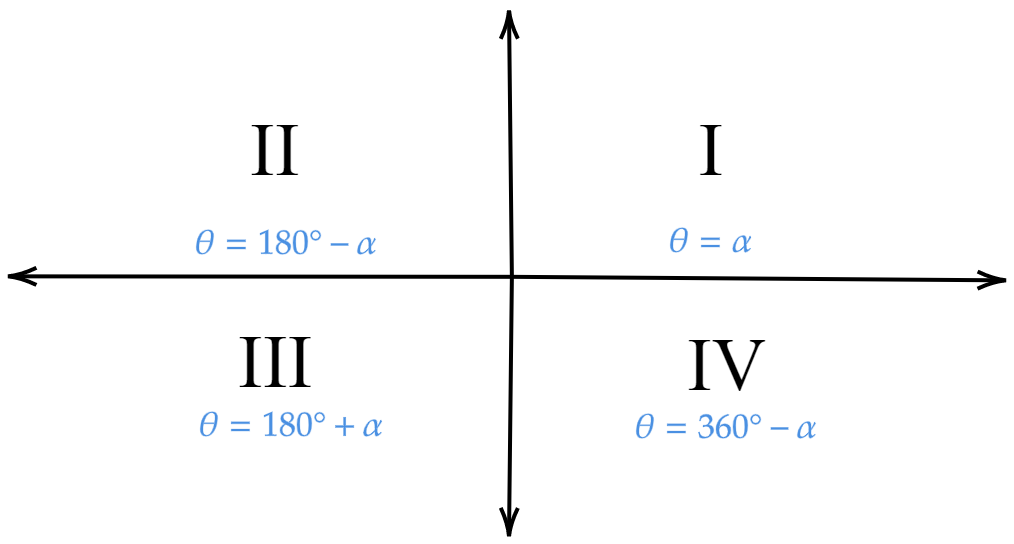
Let us consider the original angle given by \[\theta \] and the auxiliary value is given by \[\alpha \].
For the first quadrant, we have \[\theta = \alpha \].
For the second quadrant, we have \[\theta = {180^ \circ } - \alpha \].
For the third quadrant, we have \[\theta = {180^ \circ } + \alpha \].
For the fourth quadrant, we have \[\theta = {360^ \circ } - \alpha \].

Consider \[\sin {210^ \circ }\]. \[{210^ \circ }\] is in the third quadrant.
Therefore, \[\sin {210^ \circ } = \sin ({180^ \circ } + \alpha )\] i.e., \[\sin {210^ \circ } = \sin ({180^ \circ } + {30^ \circ })\]
In the third quadrant, \[\sin \] is negative.
So,
\[ \Rightarrow \sin ({180^ \circ } + {30^ \circ }) = - \sin {30^ \circ }\]
\[\therefore \sin ({210^ \circ }) = - \dfrac{1}{2}\]
Now, consider \[\cos {330^ \circ }\]. \[{330^ \circ }\] lies in the fourth quadrant.
Therefore, \[\cos {330^ \circ } = \cos \left( {{{360}^ \circ } - {{30}^ \circ }} \right)\].
In the fourth quadrant, \[\cos \] is positive.
So,
\[ \Rightarrow \cos \left( {{{360}^ \circ } - {{30}^ \circ }} \right) = \cos {30^ \circ }\]
\[\therefore \cos \left( {{{330}^ \circ }} \right) = \dfrac{{\sqrt 3 }}{2}\]
Now, consider \[\tan {135^ \circ }\]. \[{135^ \circ }\] lies in the second quadrant.
Therefore, \[\tan {135^ \circ } = \tan \left( {{{180}^ \circ } - {{45}^ \circ }} \right)\].
In the second quadrant, \[\tan \] is negative.
So,
\[ \Rightarrow \tan \left( {{{180}^ \circ } - {{45}^ \circ }} \right) = - \tan {45^ \circ }\]
\[\therefore \tan {135^ \circ } = - 1\]
Putting the values in \[\sin {210^ \circ }\cos {330^ \circ } - \tan {135^ \circ }\], we get
\[ \Rightarrow \sin {210^ \circ }\cos {330^ \circ } - \tan {135^ \circ } = \left( { - \dfrac{1}{2}} \right)\left( {\dfrac{{\sqrt 3 }}{2}} \right) - \left( { - 1} \right)\]
On simplifying, we get
\[ \Rightarrow \sin {210^ \circ }\cos {330^ \circ } - \tan {135^ \circ } = 1 - \dfrac{{\sqrt 3 }}{4}\]
Therefore, the value of \[\sin {210^ \circ }\cos {330^ \circ } - \tan {135^ \circ }\] is \[\left( {1 - \dfrac{{\sqrt 3 }}{4}} \right)\].

Note:
In the first quadrant, all trigonometric functions are positive. In the second quadrant, \[\sin \] and \[\cos ec\] are positive. In the third quadrant, \[\tan \] and \[\cot \] are positive. In the fourth quadrant, \[\cos \] and \[\sec \] are positive. Also, note that here we have used values of some standard angles i.e., \[\sin {30^ \circ } = \dfrac{1}{2}\], \[\cos {30^ \circ } = \dfrac{{\sqrt 3 }}{2}\] and \[\tan {45^ \circ } = 1\].