Question

Use the spherical \[(r,\theta ,\phi )\], polar and cylindrical coordinates to answer the following:
a) Calculate the i) volume ii) Surface area of a sphere of radius R.
b) Calculate the volume and surface area of a cylinder of radius R and length L using integration method. (Use dA and dV elements in their respective coordinate systems).

Answer 1

Hint: We can use the different coordinate systems to calculate the area and volume of a given shape by using proper methods and substitutions. The integration method is much easier than the manual adding of elements to get a total sum. We can use it for all the coordinate systems.

Complete answer:
Let us calculate the volume and surface area of the sphere and cylinder using the appropriate coordinate systems.
a)Volume and Surface area of a sphere of radius R.2
Consider a sphere of radius R as given below:
          

i) We can calculate the volume of it using the spherical coordinate system as –
We should know the conversion from rectangular to spherical coordinates as –
\[{{r}^{2}}={{x}^{2}}+{{y}^{2}}+{{z}^{2}}\]
Now the volume element dV is given by as
\[dV={{r}^{2}}\sin \phi drd\theta d\phi \]
We can do the triple integration of the above element with proper limits as –
\[\begin{align}
  & {{r}^{2}}={{x}^{2}}+{{y}^{2}}+{{z}^{2}} \\
 & \Rightarrow dV={{r}^{2}}\sin \phi drd\theta d\phi \\
 & Volume,V=\int{\int{\int{{{r}^{2}}}}}dV \\
 & \text{By substituting for dV,} \\
 & \Rightarrow \text{Volume,}V=\int_{0}^{R}{dr\int_{0}^{\pi }{{{r}^{2}}\sin \theta d\theta }\int_{0}^{2\pi }{d\phi }} \\
 & \Rightarrow \text{Volume,}V=\int_{0}^{R}{{{r}^{2}}}dr\int_{0}^{\pi }{\sin \theta d\theta }\int_{0}^{2\pi }{d\phi } \\
 & \Rightarrow \text{Volume,}V=-\dfrac{{{R}^{3}}}{3}(-1-1)(2\pi ) \\
 & \therefore V=\dfrac{4}{3}\pi {{R}^{3}} \\
\end{align}\]
The volume of the sphere is \[\dfrac{4}{3}\pi {{R}^{3}}\].
ii) We can find the surface area by integrating over the area element dA which is given as \[{{r}^{2}}\cos \theta d\theta d\phi \]. The surface will be given as –
\[\begin{align}
  & \int{dA=}{{R}^{2}}\int_{-\dfrac{\pi }{2}}^{+\dfrac{\pi }{2}}{\cos \theta d\theta }\int_{0}^{2\pi }{d\phi } \\
 & \Rightarrow \text{Surface area, }A={{R}^{2}}(\sin \dfrac{\pi }{2}-\sin (-\dfrac{\pi }{2}))(2\pi -0) \\
 & \Rightarrow A={{R}^{2}}(1-1)(2\pi ) \\
 & \therefore A=4\pi {{R}^{2}} \\
\end{align}\]
The surface area of the sphere is \[4\pi {{R}^{2}}\].
b) Now, let us use the cylindrical coordinates to find the surface area and volume of the cylinder of length L and radius R.

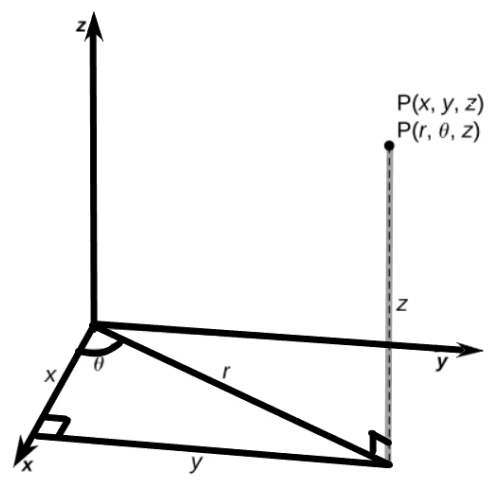
The cylindrical coordinate equivalent for the corner point P \[(r,\theta ,z)\] of the cylinder is as shown in the above figure.
We can find the Surface area of the cylinder with
\[\begin{align}
  & r=R \\
 & z=L \\
\end{align}\]
Where,
\[\begin{align}
  & x=r\cos \theta \\
 & y=r\sin \theta \\
 & z=z \\
 & \text{as,} \\
 & \text{Surface area, }A=\int_{0}^{R}{dr\int_{0}^{2\pi }{d\theta }}\int_{0}^{L}{dz} \\
 & \Rightarrow A=R(2\pi )L \\
 & \therefore A=2\pi RL \\
\end{align}\]
Similarly, we can find the volume of the cylinder by using the given the method –
\[\begin{align}
  & \text{Volume, }V=\int_{0}^{R}{r}\int_{0}^{2\pi }{d\theta \int_{0}^{L}{dz}} \\
 & \Rightarrow V=\dfrac{{{R}^{2}}}{2}(2\pi )L \\
 & \therefore V=\pi {{R}^{2}}L \\
\end{align}\]
Thus, we have found the surface areas and volumes of the sphere and the cylinder using the spherical and cylindrical coordinates respectively.

Note:
The rectangular coordinate is the most easily convertible to any other forms. The cylindrical coordinate is very much similar to the polar coordinates except for that it has a third coordinate. The coordinate systems used effectively makes the calculations much easier.