Question

What is the value of shunt resistance required to convert a galvanometer of resistance $100\Omega$ into an ammeter of range $1A$?
Given: Full scale deflection of the galvanometer is $5mA$.
$\text{A}\text{. }\dfrac{5}{9.95}\Omega $
$\text{B}\text{. }\dfrac{9.95}{5}\Omega $
$\text{C}\text{. 0}\text{.5}\Omega $
$\text{D}\text{. 0}\text{.05}\Omega $

Answer 1

Hint: Resistance in shunt with galvanometer is connected in order to convert galvanometer into an ammeter. Because of parallel combination, potential difference across the galvanometer and shunt resistance remains the same while the current between them gets divided. By using Ohm’s law and current division rule, we can calculate the value of shunt resistance.

Formula used:
Resistance in shunt ${{R}_{S}}=\dfrac{{{I}_{g}}}{\left( I-{{I}_{g}} \right)}\times G$

Complete step by step answer:
A galvanometer is a type of an electromechanical device which is used for detecting and indicating an electric current through a circuit. A galvanometer basically works like an actuator, by producing a rotatory deflection of the pointer, in response to the electric current flowing through a coil placed in a uniform and constant magnetic field. It is a sensitive device which can measure low currents even of the order of a few microamperes.
Principle of working of galvanometer – A current carrying coil when placed in an external magnetic field experiences magnetic torque. The angle by which the coil is deflected due to the effect of the magnetic torque is proportional to the magnitude of current in the coil.
A galvanometer can detect only small currents. Thus, to measure large amounts of currents it is converted into an ammeter. This can be done by connecting a low resistance in parallel to the galvanometer.
Let $G$ be the resistance of the galvanometer and ${{I}_{g}}$ be the current for full scale deflection in the galvanometer.

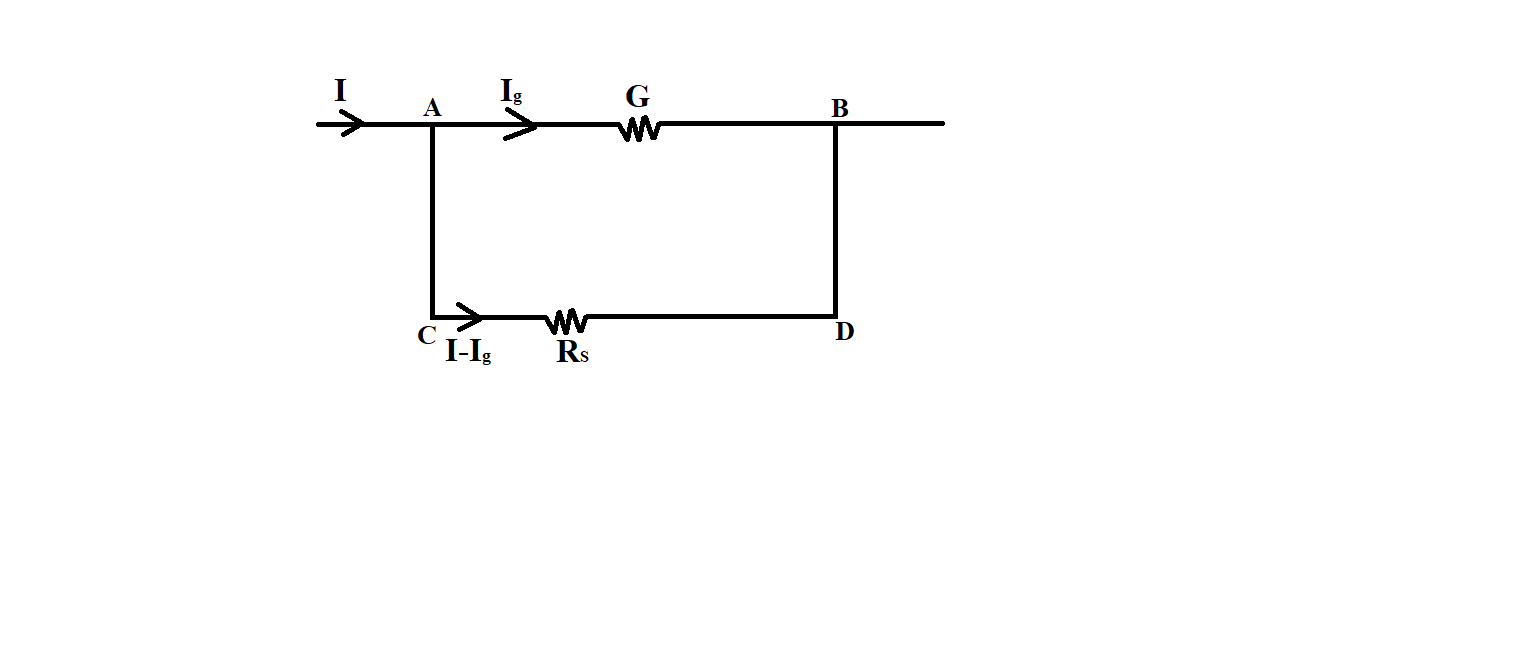
 The value of shunt resistance required to convert the galvanometer into an ammeter of $0$ to $1A$ is,
$\begin{align}
  & I={{I}_{g}}+{{I}_{S}} \\
 & {{I}_{S}}=I-{{I}_{g}} \\
\end{align}$
As the shunt resistance and galvanometer are connected in parallel, therefore, potential difference across galvanometer will be equal to potential difference across shunt
${{I}_{g}}\times G={{I}_{s}}{{R}_{s}}$
We get,
${{I}_{g}}\times G=\left( I-{{I}_{g}} \right)\times {{R}_{s}}$
${{R}_{S}}=\dfrac{{{I}_{g}}}{\left( I-{{I}_{g}} \right)}\times G$
Therefore, to convert galvanometer into an ammeter, we have to connect a resistance in parallel with the galvanometer and value of that shunt resistance is given by ${{R}_{S}}=\dfrac{{{I}_{g}}}{\left( I-{{I}_{g}} \right)}\times G$.
${{I}_{g}}$can be calculated using the equation, ${{I}_{g}}=nK$, where $n$ is the number of divisions on the galvanometer and $K$ is the figure of merit of galvanometer.
For finding figure of merit of galvanometer, we use the equation,
$K=\dfrac{E}{\left( R+S \right)\theta }$
Where,
$E$ is the emf of the cell
$\theta $ is the angle of deflection produced with resistance $R$
Given:
$\begin{align}
  & {{I}_{g}}=5mA=0.005A \\
 & G=100\Omega \\
 & I=1A \\
\end{align}$
Let a shunt resistance ${{R}_{S}}$ is connected to the galvanometer as shown in the figure, to convert the galvanometer into an ammeter.
From figure, we have,
${{V}_{AB}}={{V}_{CD}}$
Therefore,
$\left( I-{{I}_{g}} \right){{R}_{S}}={{I}_{g}}G$
Putting the values, we get,
$\begin{align}
  & \left( 1-0.005 \right){{R}_{S}}=0.005\times 100 \\
 & 0.995{{R}_{S}}=0.5 \\
 & {{R}_{S}}=\dfrac{5}{9.95}\Omega \\
\end{align}$
Hence, the correct option is A.

Note: A resistor having a very small value of resistance is called a Shunt resistance and it is always connected in parallel in a circuit. Shunt resistance is used for converting a galvanometer into ammeter as most of the current will flow through it and only a small fraction of current will flow through the galvanometer, which is sufficient to make a deflection.