Question

What is the value of $\theta $ in the following ray diagram?

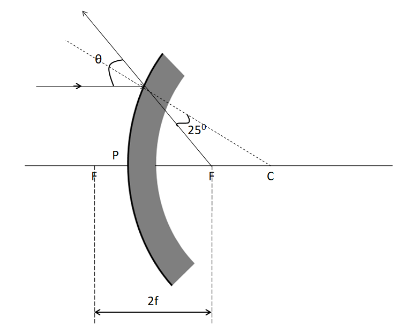
(A) ${25^ \circ }$
(B) ${35^ \circ }$
(C) ${50^ \circ }$
(D) None of these

Answer 1

Hint: To solve this question, we need to use one of the basic properties of reflection which is, the angle of incidence is equal to the angle of refraction. Then, with the application of geometry of the given rays, we can find out the value of the angle.

Complete step by step solution:
The optical instrument given in this question is a mirror. This is because the incident ray after falling on the instrument bounced back. So, it is being reflected back. And since it is polished on the concave side, so its convex side is the reflecting surface. Therefore, it is a convex mirror. Now, considering the diagram given in the question with proper labelling

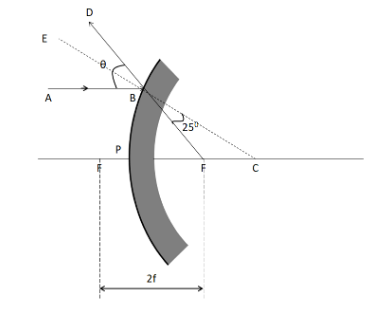
From the above figure, as the dashed line is passing undeflected through the mirror, so it is the normal at the point of incidence B. Now, we know that the angle of incidence is the angle which the incident ray makes with the normal. So the angle of incidence from the above figure is
$\Rightarrow i = \angle ABE$ ……………….(1)
Similarly, the angle of reflection is
$\Rightarrow r = \angle DBE$ ……………..(2)
We know from the properties of reflection that the angle of incidence is equal to the angle of reflection. So, we have
$\Rightarrow i = r$
From (1) and (2) we get
$\Rightarrow \angle ABE = \angle DBE$ ………….(3)
Also, from above figure we can see that
$\Rightarrow \angle ABE + \angle DBE = \theta $ ……………...(4)
Solving (3) and (4) we get
$\Rightarrow \angle ABE = \angle DBE = \dfrac{\theta }{2}$ ……………...(5)
Now, considering the extended lines EC and DF in the above figure, we have
$\Rightarrow \angle DBE = \angle FBC$ (Vertically opposite angles)
According to the question we have
$\Rightarrow \angle FBC = {25^ \circ }$
So we get
$\Rightarrow \angle DBE = {25^ \circ }$ ……………….(6)
From (5) and (6)
$\Rightarrow \dfrac{\theta }{2} = {25^ \circ }$
Multiplying by $2$ both sides, we finally get
$\Rightarrow \theta = {50^ \circ }$
Hence, the correct answer is option C.

Note:
It must be noted that all the information given in the question regarding the distances from the mirror, the type of mirror, are useless. This fact can be appreciated by going through the above solution. We should not try to think from the point of view of the mirror equation. We just needed what type of optical instrument we are given, reflecting or refracting.