
Volume of a hollow sphere is
Answer
473.1k+ views
Hint: A sphere is a ball-shaped three-dimensional object.
The volume of a sphere of radius r units is
The volume of the material used in making a hollow sphere = Volume of outer sphere - Volume of inner sphere.
Assume the inner radius to be x cm, form an equation and solve.
Complete step by step answer:
Let's say that the inside radius of the hollow sphere is x cm and the outside radius is
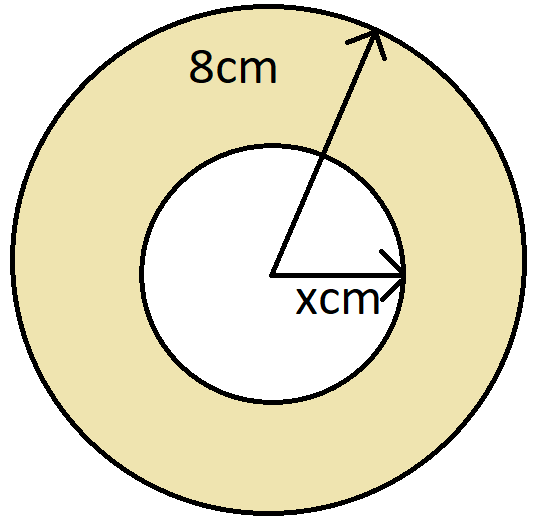
Using the formula
The volume of the hollow sphere (shaded part) will be
According to the question:
Taking out the common factors
⇒
⇒
Note that 11352 is multiple of 11, because
⇒
⇒
⇒
⇒
⇒
Since,
⇒
∴ The inner radius of the sphere is 5 cm.
Note: The same idea can be applied to solids of other shapes. The surface area of a sphere is
The volume of a sphere of radius r units is
The volume of the material used in making a hollow sphere = Volume of outer sphere - Volume of inner sphere.
Assume the inner radius to be x cm, form an equation and solve.
Complete step by step answer:
Let's say that the inside radius of the hollow sphere is x cm and the outside radius is

Using the formula
The volume of the hollow sphere (shaded part) will be
According to the question:
Taking out the common factors
⇒
⇒
Note that 11352 is multiple of 11, because
⇒
⇒
⇒
⇒
⇒
Since,
⇒
∴ The inner radius of the sphere is 5 cm.
Note: The same idea can be applied to solids of other shapes. The surface area of a sphere is
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What are the public facilities provided by the government? Also explain each facility

Difference between mass and weight class 10 physics CBSE

SI unit of electrical energy is A Joule B Kilowatt class 10 physics CBSE




