Question

What is the volume of water in a trough when the depth of the water is d?
A water trough is 6m long and its cross-section is an isosceles trapezoid which is 100cm wide at the bottom and 200cm wide at the top and the height is 50cm.The trough is not full. Give an expression for V, the volume of water in the trough in $c{{m}^{3}}$,when the depth of water is d cm.

Answer 1

Hint: The area of a trapezium is given by:
$A=\dfrac{1}{2}\left( Top+bottom \right)h$
Where,
Top signifies the width at top
Bottom signifies the width at bottom
h is the height of trapezium.
Draw the figure of trapezium to understand it better.

Complete step by step answer:
Given,
Depth of the water is d
Length of water trough is 6m
Cross-section is an isosceles trapezoid.
Width at the bottom is 100cm
Width at the top is 200cm
Height is 50cm
Calculate volume of water in trough?

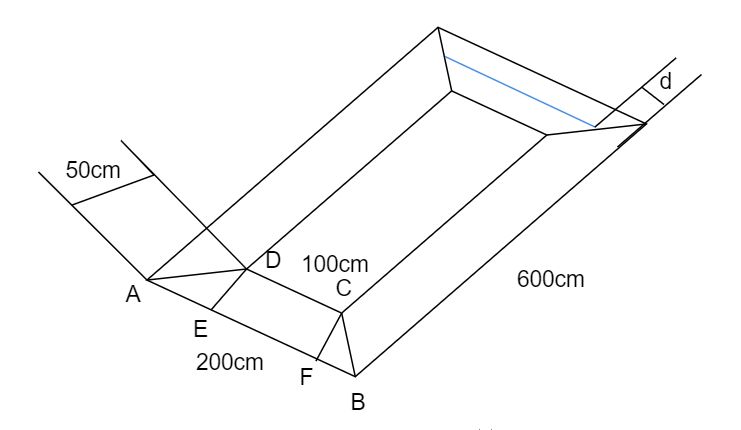
The area of the trapezium is given as:
$\dfrac{1}{2}h\left( {{b}_{1}}+{{b}_{2}} \right)$
Where we have the height of water as d
The width at top is 100
The width at bottom is 100+2d
And the height of trough is d
Therefore, the area of trapezium becomes:
$\begin{align}
  & A=\dfrac{1}{2}\times d\left( 100+100+2d \right) \\
 & \Rightarrow A=d\left( 100+d \right) \\
\end{align}$
Now the volume is given as:
$V=Area\times $Length of water trough
Length of water trough is 6m or 600cm
$\begin{align}
  & V=600d\left( 100+d \right) \\
 & \Rightarrow V=60000d+600{{d}^{2}} \\
\end{align}$
Thus, the volume of trough for the given data is $V=60000d+600{{d}^{2}}$

Note: Here we have calculated the value of depth at top and bottom using the geometry analysis by considering triangles CKJ and DHG which are marked in figure and the rectangle CDGK and the right angled triangle ADE which is also isosceles.
The width at bottom is $HJ=100+2d$
The width at top is $DG=d$
Hence substituting these values in the area formula and then calculating the volume.