
What is the derivative of
Answer
418.5k+ views
Hint:To find the derivative we can use the slope formula, that is
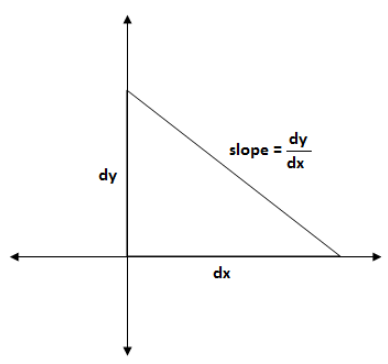
To find the derivative of two variables in multiplication, this formula is used
Mechanically,
Complete step by step answer:
Let us derivate
Substituting the terms
The differentiation of
As the derivation of the function is with respect to
The derivative of
Let us derivate
Substituting the terms
The differentiation of
As the derivation of the function is with respect to
The derivative of
Note:

To find the derivative of two variables in multiplication, this formula is used
Mechanically,
Complete step by step answer:
Let us derivate
Substituting the terms
The differentiation of
As the derivation of the function is with respect to
The derivative of
Let us derivate
Substituting the terms
The differentiation of
As the derivation of the function is with respect to
The derivative of
Note:
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 12 Economics: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

Franz thinks Will they make them sing in German even class 12 english CBSE




