
Which quadrant
Answer
506.1k+ views
Hint: Degree measurement is based on a circle, which is
Complete Step-by-step solution
Here the given angle is
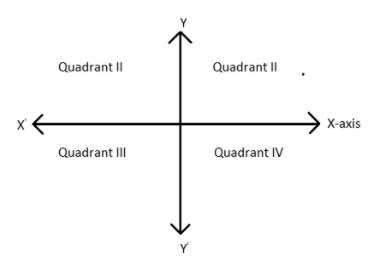
We have the following angle represents in Quadrants:
Quadrant I
Quadrant II
Quadrant III
Quadrant IV
i.e. this lies in Quadrant III as the range of quadrant III is
Initial line: negative
Terminal line: negative
Note: Now let us know look into the concept to make the concept of quadrants simple., i.e. for Quadrant I: -initial side: positive
Terminal side: Positive
Counter-clockwise rotation
We swept angle between

Complete Step-by-step solution
Here the given angle is
We have the following angle represents in Quadrants:
Quadrant I
Quadrant II
Quadrant III
Quadrant IV
i.e. this lies in Quadrant III as the range of quadrant III is
Initial line: negative
Terminal line: negative
Note: Now let us know look into the concept to make the concept of quadrants simple., i.e. for Quadrant I: -initial side: positive
Terminal side: Positive
Counter-clockwise rotation
We swept angle between
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Differentiate between the Western and the Eastern class 9 social science CBSE




