
How do you write $66$ as the product of prime factors?
Answer
533.4k+ views
Hint: Prime factorization is a way to write a composite number as the product of prime
factors. Prime factors are those numbers or factors which are greater than one and have exactly two
factors one is the number itself and other is one . There are basically two ways to find prime factorization namely ,
a) by division method
b) by factor tree
Here, in this question let us try to solve it as the product of prime factors by division method.
Complete step by step solution:
We know that the number $2$ is the smallest prime number. So, in order to find prime factors of $66$ , let us first divide $66$ by least prime number i.e., $2$ .
$66 \div 2 = 33$
Now, we know that $33$ is not divisible by $2$ so we move to the next prime number known to us, which is $3$ , so divide $33$ by $3$ .
$33 \div 3 = 11$
Now, we know that $11$ is not divisible by $3$ so we move to next prime number i.e., $5$ . but again, we know that $11$ is not divisible by $5$ so we move to next prime number i.e., $7$ . but again, we know that $11$ is not divisible by $7$ so we move to next prime number i.e., $11$ . therefore, we get ,
$11 \div 11 = 1$
As now we got 1 as quotient, we can say that the prime factors of $66$ are $2,3,11$ .
In mathematical term the prime factorization of $66$ is written as,
$66 = 2 \times 3 \times 11$ .
Note: Here is another way of calculating prime factors of number $66$ , which is by factor tree. Under
This way, we split the number into its prime factors. It will be clearer through the
following diagram of factor tree.
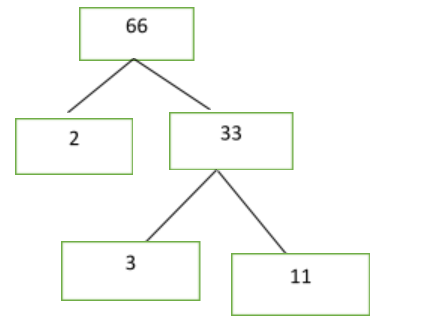
factors. Prime factors are those numbers or factors which are greater than one and have exactly two
factors one is the number itself and other is one . There are basically two ways to find prime factorization namely ,
a) by division method
b) by factor tree
Here, in this question let us try to solve it as the product of prime factors by division method.
Complete step by step solution:
We know that the number $2$ is the smallest prime number. So, in order to find prime factors of $66$ , let us first divide $66$ by least prime number i.e., $2$ .
$66 \div 2 = 33$
Now, we know that $33$ is not divisible by $2$ so we move to the next prime number known to us, which is $3$ , so divide $33$ by $3$ .
$33 \div 3 = 11$
Now, we know that $11$ is not divisible by $3$ so we move to next prime number i.e., $5$ . but again, we know that $11$ is not divisible by $5$ so we move to next prime number i.e., $7$ . but again, we know that $11$ is not divisible by $7$ so we move to next prime number i.e., $11$ . therefore, we get ,
$11 \div 11 = 1$
As now we got 1 as quotient, we can say that the prime factors of $66$ are $2,3,11$ .
In mathematical term the prime factorization of $66$ is written as,
$66 = 2 \times 3 \times 11$ .
Note: Here is another way of calculating prime factors of number $66$ , which is by factor tree. Under
This way, we split the number into its prime factors. It will be clearer through the
following diagram of factor tree.

Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is the Full Form of ISI and RAW

Golden Revolution is related to AFood production BOil class 9 social science CBSE




