Question

Write the formula for calculating wattless current.

Answer 1

Hint: In order to answer the above question, we will refresh our knowledge about a simple LCR circuit which is the most basic circuit. We will be deriving the equation to find out the power consumed by such a circuit. Then we will derive the equation for wattless current.

Complete step by step solution:
First of all we will have a look at an LCR circuit:

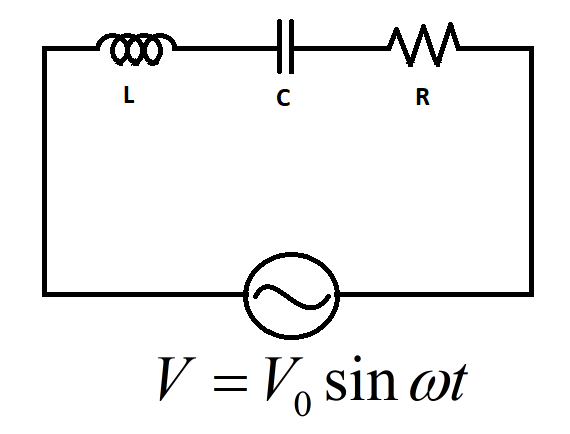
As we can see from the above figure, we have an LCR circuit which comprises an inductor $(L)$, a capacitor $(C)$and a resistor $(R)$. The voltage applied to it is an AC voltage $V={{V}_{0}}\sin \omega t$. The current flowing through this circuit can be given by $I={{I}_{0}}\sin (\omega t+\Phi )$, where $\sin \omega t$is the sinusoidal term and $\Phi $ is the phase difference between current and voltage.
To understand the phase difference properly, we will draw a phase diagram

Now, the work done by the AC source during time interval of $t$ and $t+dt$ is given by
$\begin{align}
  & dW=VIdt \\
 & \Rightarrow dW={{V}_{0}}\sin \omega t\cdot {{I}_{0}}\sin (\omega t+\Phi )\cdot dt \\
 & \Rightarrow dW={{V}_{0}}{{I}_{0}}[\sin \omega t(\sin \omega t\cos \Phi +\cos \omega t\sin \Phi )]dt \\
 & \Rightarrow dW={{V}_{0}}{{I}_{0}}({{\sin }^{2}}\omega t\cos \Phi +\sin \omega t\cos \omega t\sin \Phi )dt \\
\end{align}$
The total work done in one complete cycle is given by taking integral of the above equation over $[0,T]$
$\Rightarrow W={{V}_{0}}{{I}_{0}}\cos \Phi \int\limits_{0}^{T}{{{\sin }^{2}}\omega t\cdot dt+}{{V}_{0}}{{I}_{0}}\sin \Phi \int\limits_{0}^{T}{\sin \omega t\cos \omega t\cdot dt}$
$\Rightarrow W=\dfrac{1}{2}{{V}_{0}}{{I}_{0}}\cos \Phi \int\limits_{0}^{T}{(1-\cos 2\omega t)\cdot dt+\dfrac{1}{2}}{{V}_{0}}{{I}_{0}}\sin \Phi \int\limits_{0}^{T}{\sin 2\omega t\cdot dt}$
$\Rightarrow W=\dfrac{1}{2}{{V}_{0}}{{I}_{0}}T\cos \Phi $
Now, to calculate the average power delivered by the source, we divide the above equation by time period $T$
$\begin{align}
  & P=\dfrac{W}{T} \\
 & \Rightarrow P=\dfrac{1}{2}\dfrac{{{V}_{0}}{{I}_{0}}T\cos \Phi }{T} \\
 & \Rightarrow P=\dfrac{1}{2}{{V}_{0}}{{I}_{0}}\cos \Phi \\
\end{align}$
Simplifying a little
\[\Rightarrow P=\dfrac{{{V}_{0}}}{\sqrt{2}}\dfrac{{{I}_{0}}}{\sqrt{2}}\cos \Phi \]
Now, we know that $\dfrac{{{V}_{0}}}{\sqrt{2}}={{V}_{rms}}$ and $\dfrac{{{I}_{0}}}{\sqrt{2}}={{I}_{rms}}$ represent the $rms$ values for voltage and current. Therefore,
\[\Rightarrow P={{V}_{rms}}{{I}_{rms}}\cos \Phi \]
The above formula is the formula for power dissipated in an AC circuit.
Now, we want to find the formula for wattless current. When the power dissipated or consumed is zero, the current is said to be wattless current or an idle current.
From the above derived formula of power, we can say that the power can only be zero if the value of $\cos \Phi $ is zero or $\Phi =\pm \dfrac{\pi }{2}$. This implies that the phase difference between the current and voltage should be $\dfrac{\pi }{2}$.

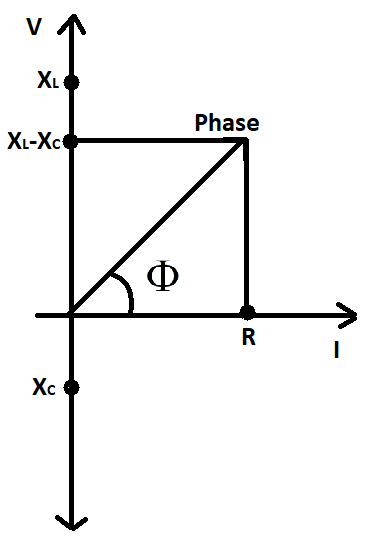
Now as we know that the current in the circuit is given by $I={{I}_{0}}\sin (\omega t+\Phi )$, but for wattless current, the current will be given by
$I={{I}_{0}}\sin \left( \omega t\pm \dfrac{\pi }{2} \right)$

Note:
It is very important to note that the power consumed can be made zero only when a resistance is connected with either a capacitor or an inductor and not with both of them together. The phase angle will become $+\dfrac{\pi }{2}$when only an inductor is connected with a resistor. Whereas, the angle becomes $-\dfrac{\pi }{2}$when only a capacitor is connected with a resistor in a circuit.