Question

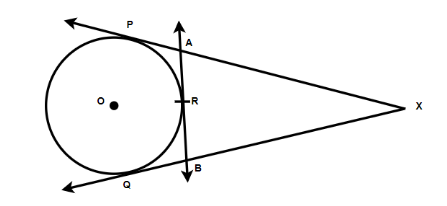
$ XP $ and $ PQ $ are tangents from $ X $ to the circle with a center $ O $ . R is a point on the circle. Prove that, $ XA + AR = XB + BR $

Answer 1

Hint: Here in this question we have to prove $ XA + AR = XB + BR $ and as we know that the lengths of the tangent drawn from the external point to the circle will be equal. So from this, we have the equation and by equating and comparing we will get this question proved.

Complete step-by-step answer:
As we can see from the figure, there is an external point $ X $ and from this point, there are the two tangents which are drawn and named as $ XP $ and $ PQ $
And also $ XP = XQ $
Therefore, as we know that lengths of the tangent drawn from the external point to the circle will be equal. So from this, mathematically we can write it as
 $ \Rightarrow AP = AR $
And similarly,
 $ \Rightarrow BQ = BR $
So from the figure, we will now frame the equation
 $ \Rightarrow XP = XA + AP $ and we will name it equation $ 1 $
 $ \Rightarrow XQ = XB + BQ $ and we will name it equation $ 2 $
By substituting the values, $ AP = AR $ in the equation $ 1 $ and $ BQ = BR $ in the equation $ 2 $ , we will get the equation as
 $ \Rightarrow XP = XA + AR $ and the other equation will become $ XQ = XB + BR $
And we already knew that the tangents are equal which is $ XP $ and $ PQ $ , we get $ XA + AR = XB + BR $ .
Hence, it is proved that $ XA + AR = XB + BR $ .
So, the correct answer is “ $ XA + AR = XB + BR $ ”.

Note: As we know that the two tangents' points are connected by a chord and we can say from this that the radius will cross the midpoint of the chord perpendicularly. And due to the formation of symmetrical lines, there will be two triangles which are congruent right triangles. So, the triangle from that point in time will be termed as the isosceles triangle. By using these we can easily understand the length of tangents drawn from the external point to the circle will be equal.