Question

You are given a wire of length 100 cm and linear resistance of 1 ohm/cm. If it is cut into two parts , so that when they are in parallel , the effective resistance is 24 ohm. The length of the two parts are
A. 30 cm & 70 cm
B. 60 cm & 40 cm
C. 70 cm & 30 cm
D. 20 cm & 80 cm

Answer 1

Hint:-If two wires are connected in parallel the effective resistance of the combination is given by \[R = \dfrac{{{r_1}{r_2}}}{{{r_1} + {r_2}}}\]. Using this relation we get a quadratic equation and by solving the quadratic equation we get the required result.

Complete step-by-step solution:
Length of wire = \[100cm\]
\[l = 100cm\]
Resistance of wire per cm =\[\dfrac{{1\Omega }}{{cm}}\]
Resistance of wire =\[100\Omega \]
Resistance (\[r\])of wire depending upon the resistivity (\[\rho \]), length (\[l\]) and cross- sectional area (\[A\]).
\[r = \dfrac{{\rho l}}{A}\Omega \], where resistivity (\[\rho \]) and cross- sectional area (\[A\]) are constant, only length (\[l\]) is changing.

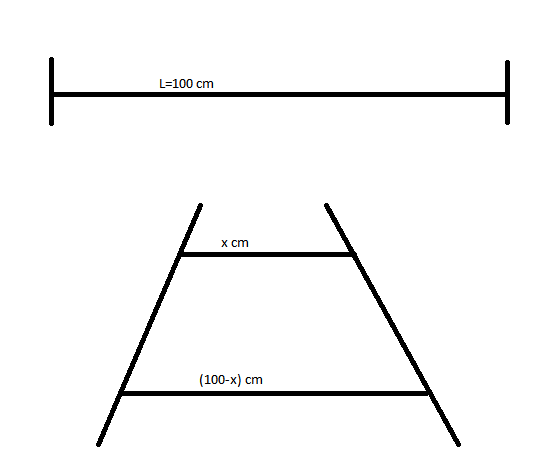
Let the wires be cut into two parts of lengths (x)cm & (100-x)cm respectively and connected in parallel as shown in the above figure.
Then their resistances are \[x\;\Omega \;\& (100 - x)\;\Omega \].
If two resistances \[{r_1}\;\& \;{r_2}\] are connected in parallel then their effective resistance is equal to \[R\]such that
\[R = \dfrac{{{r_1}{r_2}}}{{{r_1} + {r_2}}}\]
Here let
\[\
  {r_1} = x\;\Omega \\
  {r_2} = (100 - x)\;\Omega \\
\ \] & \[R = 24\;\Omega \]
Putting all the values in equation \[R = \dfrac{{{r_1}{r_2}}}{{{r_1} + {r_2}}}\]we get
\[ \Rightarrow 24 = \dfrac{{x(100 - x)}}{{x + (100 - x)}}\]
\[ \Rightarrow 24 = \dfrac{{100x - {x^2}}}{{100}}\]
Converting the equation into quadratic equation we get
\[ \Rightarrow 2400 = 100x - {x^2}\]
Equating the quadratic equation to zero
\[ \Rightarrow {x^2} - 100x + 2400 = 0\]
\[ \Rightarrow {x^2} - 40x - 60x + 2400 = 0\]
Factoring the quadratic equation
\[ \Rightarrow x(x - 40) - 60(x - 40) = 0\]
\[ \Rightarrow (x - 60)(x - 40) = 0\]
The two roots of the quadratic equation are
\[ \Rightarrow x = 60cm\;or\;x = 40cm\]
Hence we can take either of the values of x ,
If x=40 cm then (100-x) = 60 cm
If x=60 cm then (100-x) = 40 cm
Hence option ( B ) is the correct answer.
Hence the length of the two parts are 60 cm & 40 cm respectively.

Note:- When we connect the two resistors in parallel combination the equivalent resistance is less than the both of the individual resistors.
When we connect the two resistors in series combination the equivalent resistance is more than the both of the individual resistors.