NCERT Exemplar for Class 10 Maths Chapter 2 - Polynomials (Book Solutions)

Sample question 1: If one zero of the quadratic polynomial \[{x^2} + 3x + k\] is \[2\], then the value of k is:

a) $10$

b) $ - 10$

c) $5$

d) $ - 5$

Ans: Option b is the correct answer.

\[p\left( x \right) = {x^2} + 3x + k\]

2 is zero of the polynomial. 

So, we have, \[p\left( 2 \right) = {2^2} + 3\left( 2 \right) + k = 0\]

\[ \Rightarrow 10 + k = 0\]

\[ \Rightarrow k =  - 10\]

Sample question 2: Given that two of the zeroes of the cubic polynomial \[a{x^3} + b{x^2} + cx + d\] are $0$, the third zero is: 

a) $ - \dfrac{b}{a}$

b) \[\dfrac{b}{a}\]

c) \[\dfrac{c}{a}\]

d) \[ - \dfrac{d}{a}\]

Ans: Option a is the correct answer. 

Sum of zeroes of a cubic polynomial \[a{x^3} + b{x^2} + cx + d\] is \[ - \dfrac{b}{a}\]. We are given that two of the zeroes are zero. Let the third zero be $\alpha $.

Then, $\alpha  + 0 + 0 =  - \dfrac{b}{a}$

$ \Rightarrow \alpha  =  - \dfrac{b}{a}$

Exercise 2.1

1. If one of the zeroes of the quadratic polynomial $\left( {k - 1} \right){x^2} + kx + 1$ is $ - 3$, then the value of k is: 

A) $\dfrac{4}{3}$

B) $ - \dfrac{4}{3}$

C) $\dfrac{2}{3}$

D) $ - \dfrac{2}{3}$

Ans: Option (A) is the correct answer. 

A number c can only be a root of a polynomial $p\left( x \right)$ if $p\left( c \right) = 0$. 

So, let $p\left( x \right) = \left( {k - 1} \right){x^2} + kx + 1$.

We are given that $ - 3$ is a root of $p\left( x \right) = \left( {k - 1} \right){x^2} + kx + 1$. Then, we have, 

$p\left( { - 3} \right) = \left( {k - 1} \right){\left( { - 3} \right)^2} + k\left( { - 3} \right) + 1 = 0$

\[ \Rightarrow \left( {k - 1} \right){\left( { - 3} \right)^2} + k\left( { - 3} \right) + 1 = 0\]

\[ \Rightarrow 9\left( {k - 1} \right) - 3k + 1 = 0\]

\[ \Rightarrow 9k - 9 - 3k + 1 = 0\]

\[ \Rightarrow 6k = 8\]

\[ \Rightarrow k = \dfrac{4}{3}\]

So, the value of k is \[\dfrac{4}{3}\]. 

2. A quadratic polynomial, whose zeroes are $ - 3$ and \[4\] is:

A) ${x^2} - x - 12$

B) ${x^2} + x + 12$

C) $\dfrac{{{x^2}}}{2} - \dfrac{x}{2} - 6$

D) $2{x^2} + 2x - 24$

Ans: Option A is the correct answer. 

If we are given the zeros of a polynomial as $\alpha $ and $\beta $, then the required polynomial is ${x^2} - \left( {\alpha  + \beta } \right)x + \alpha \beta $.

We are given the zeros of a quadratic polynomial as $ - 3$ and \[4\].

So, the required quadratic polynomial is: ${x^2} - \left( { - 3 + 4} \right)x + \left( { - 3} \right)\left( 4 \right)$

$ = {x^2} - \left( { - 3 + 4} \right)x + \left( { - 3} \right)\left( 4 \right)$

Simplifying the polynomial, we get,

$ = {x^2} - x - 12$

3. If the zeroes of the quadratic polynomial ${x^2} + \left( {a + 1} \right)x + b$ are $2$ and $ - 3$, then 

A) $a =  - 7,b =  - 1$

B) $a =  - 5,b =  - 1$

C) $a = 2,b =  - 6$

D) $a = 0,b =  - 6$

Ans: Option D is the correct answer. 

A number c can only be a root of a polynomial $p\left( x \right)$ if $p\left( c \right) = 0$.

We are given that $2$ and $ - 3$ are the roots of the polynomial. So, we have, $p\left( 2 \right) = 0$ and $p\left( { - 3} \right) = 0$.

So, $p\left( 2 \right) = {2^2} + 2\left( {a + 1} \right) + b = 0$

$ \Rightarrow 4 + 2a + 2 + b = 0$

$ \Rightarrow 2a + b + 6 = 0 -  -  -  - \left( 1 \right)$

So, $p\left( { - 3} \right) = {\left( { - 3} \right)^2} + \left( {a + 1} \right)\left( { - 3} \right) + b = 0$

$ \Rightarrow p\left( { - 3} \right) = 9 - 3a - 3 + b = 0$

$ \Rightarrow b - 3a + 6 = 0 -  -  -  - \left( 2 \right)$

Subtracting equation $\left( 2 \right)$ from equation $\left( 1 \right)$, we get,

$ \Rightarrow \left( {2a + b + 6} \right) - \left( {b - 3a + 6} \right) = 0$

$ \Rightarrow 2a + b + 6 - b + 3a - 6 = 0$

$ \Rightarrow 5a = 0$

$ \Rightarrow a = 0$

Putting $a = 0$ into equation $\left( 1 \right)$,

$ \Rightarrow 2\left( 0 \right) + b + 6 = 0$

$ \Rightarrow b =  - 6$

So, $a = 0$ and $b =  - 6$. 

4. The number of polynomials having zeros as $ - 2$ and $5$ is: 

A) $1$

B) $2$

C) $3$

D) more than $3$

Ans: Option D is the correct answer. 

If we are given the zeros of a polynomial as $\alpha $ and $\beta $, then the required polynomial is ${x^2} - \left( {\alpha  + \beta } \right)x + \alpha \beta $.

We are given the zeros of a polynomial as $ - 2$ and $5$.

So, the required polynomial is: ${x^2} - \left( { - 2 + 5} \right)x + \left( { - 2} \right)\left( 5 \right)$

$ = {x^2} - 3x - 10$

Now, if we divide the obtained polynomial by any constant such as $7$, we get, 

$ = \dfrac{{{x^2}}}{7} - \dfrac{3}{7}x - \dfrac{{10}}{7}$

Now, the polynomials $\dfrac{{{x^2}}}{7} - \dfrac{3}{7}x - \dfrac{{10}}{7}$ and ${x^2} - 3x - 10$ are different from one another but have the same zeroes. So, we can obtain infinitely many such polynomials with zeros as $ - 2$ and $5$.

5. Given that one of the zeroes of the cubic polynomial $a{x^3} + b{x^2} + cx + d = 0$ is zero, the product of the other two zeroes is:

A) $ - \dfrac{c}{a}$

B) $\dfrac{c}{a}$

C) $0$

D) $ - \dfrac{b}{a}$

Ans: Option B is the correct answer. 

We first assume $f\left( x \right) = a{x^3} + b{x^2} + cx + d$.

Let $\alpha ,\beta ,\gamma $ be the zeroes of $f\left( x \right)$. 

Sum of product of zeroes taken two at a time $ = \alpha \beta  + \beta \gamma  + \gamma \alpha  = \left( {\dfrac{c}{a}} \right)$

Now, we are given that one zero of the polynomial is zero. So, let $\gamma  = 0$.

$ \Rightarrow \alpha \beta  + \beta \left( 0 \right) + \left( 0 \right)\alpha  = \left( {\dfrac{c}{a}} \right)$

Simplifying the expression,

 $ \Rightarrow \alpha \beta  = \dfrac{c}{a}$

Hence, the product of the other two zeroes is $\dfrac{c}{a}$. 

6. If one of the zeroes of the polynomial ${x^3} + a{x^2} + bx + c$ is $ - 1$, then the product of other two zeroes is: 

A) $b - a + 1$

B) $b - a - 1$

C) $a - b + 1$

D) $a - b - 1$

Ans: Option A is the correct answer.

We have $f\left( x \right) = {x^3} + a{x^2} + bx + c$

Since $ - 1$ is a zero of $f\left( x \right)$.

So, $f\left( { - 1} \right) = {\left( { - 1} \right)^3} + a{\left( { - 1} \right)^2} + b\left( { - 1} \right) + c = 0$

$ \Rightarrow  - 1 + a - b + c = 0$

$ \Rightarrow c = 1 - a + b -  -  -  - \left( 1 \right)$

Product of all three zeros $ =  - \left( {\dfrac{d}{a}} \right)$

Since $d = c$ and $a = 1$.

Substituting the values, we get,

Product of all three zeroes $ = \alpha \beta \gamma  =  - c$

$ \Rightarrow \alpha \beta \left( { - 1} \right) =  - c$

Using equation $\left( 1 \right)$,

$ \Rightarrow \alpha \beta  = c = 1 + b - a$

7. The zeroes of quadratic polynomial ${x^2} + 99x + 127$ are:

A) both positive

B) both negative

C) one positive one negative

D) both are equal

Ans: Option B is the correct answer.

We have to calculate the discriminant of the quadratic polynomial. 

Let $f\left( x \right) = {x^2} + 99x + 127$.

Compared with $a{x^2} + bx + c$, so $a = 1$, $b = 99$ and $c = 127$.

So, Discriminant $ = D = {b^2} - 4ac$

$ \Rightarrow D = {99^2} - 4\left( 1 \right)\left( {127} \right)$

$ \Rightarrow D = 9801 - 508 = 9293$

Using the quadratic polynomial, roots of the polynomial $ = \dfrac{{ - b \pm \sqrt D }}{{2a}}$

$ \Rightarrow x = \dfrac{{ - 99 \pm \sqrt {9293} }}{2}$

Simplifying the expression,

$ \Rightarrow x = \dfrac{{ - 99 \pm 96.4}}{2}$

This means that both the roots are negative. 

8. The zeroes of the quadratic polynomial \[{x^2} + kx + k\] where $k \ne 0$.

A) cannot both be positive

B) cannot both be negative

C) are always unequal

D) are always equal

Ans: Option A is the correct answer. 

Let \[{x^2} + kx + k\] be \[f\left( x \right)\]. Comparing with \[a{x^2} + bx + c\], we get,

\[a = 1,b = k,c = k\].

Using the quadratic formula, we have, $x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$

$ \Rightarrow x = \dfrac{{ - k \pm \sqrt {{k^2} - 4\left( 1 \right)k} }}{2}$

$ \Rightarrow x = \dfrac{{ - k \pm \sqrt {{k^2} - 4k} }}{2}$

Now, let $k = 4$.

So, $x = \dfrac{{ - 4 \pm \sqrt {{4^2} - 4 \times 4} }}{2}$

$x =  - 2$

Here, both the roots are equal to $ - 2$. Hence, options C and B are not correct.

Now, let $k =  - 1$.

Then, $x = \dfrac{{ - \left( { - 1} \right) \pm \sqrt {{{\left( { - 1} \right)}^2} - 4 \times \left( { - 1} \right)} }}{2}$

\[ \Rightarrow x = \dfrac{{1 \pm \sqrt 5 }}{2}\]

So, one root is positive and one is negative. So, option D is also incorrect.

9. If the zeroes of the quadratic polynomial $a{x^2} + bx + c$, where, $c \ne 0$ are equal then:

A) c and a both have opposite signs

B) c and b have opposite signs

C) c and a have same sign

D) c and b have the same sign

Ans: Option C is the correct answer. 

For a polynomial to have equal roots, Discriminant should be equal to zero.

So, we have, $D = {b^2} - 4ac = 0$

$ \Rightarrow {b^2} = 4ac$

Now, ${b^2}$ is always positive. Hence, a and c should be of the same sign so that their product is positive. 

10. If one of the zeroes of a quadratic polynomial of the form ${x^2} + ax + b$ is the negative of the other then it 

(a) has no linear term and the constant term is negative 

(b) has no linear term and the constant term is positive 

(c) can have a linear term but the constant term is negative 

(d) can have a linear term but the constant term is positive

Ans: Hence, option (a) is the correct answer. 

Let $p\left( x \right) = {x^2} + ax + b$. Suppose $\alpha ,\beta $ are the roots of the polynomial.

So, we have, $\alpha  =  - \beta $

Here, we have, $a = 1,b = a,c = b$.

Now, sum of roots $ =  - \dfrac{b}{a} =  - a$.

$\alpha  + \beta  =  - a$

So, we get, $ - \beta  + \beta  = 0 = a$.

Also, product of zeroes $ = \left( { - \beta } \right)\left( \beta  \right) =  - {\beta ^2}$

We know that $ - {\beta ^2}$ is negative. 

Hence, $p\left( x \right) = {x^2} + ax + b$ has no linear term and the product of zeroes is negative. 

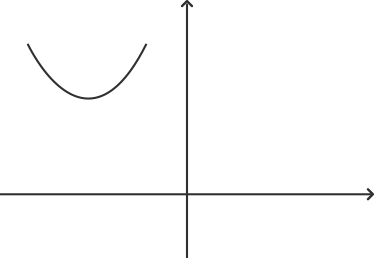
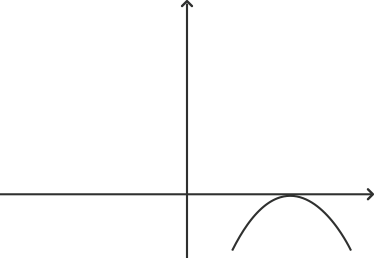
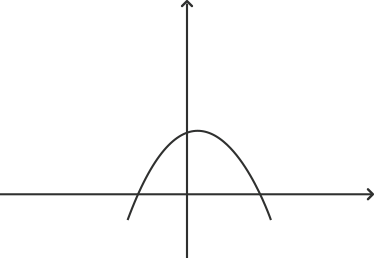
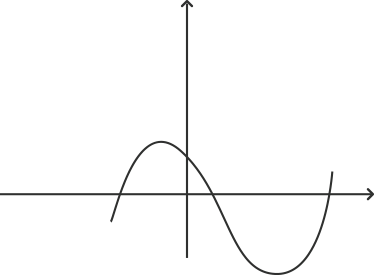
11. Which of the following is not a graph of quadratic polynomials? 

A) 

B) 

C) 

D) 

Ans: option D is the correct answer. 

Graph ‘d’ represents a cubic polynomial as it cuts the x axis at three points. A quadratic polynomial can have at most two real roots. Graph ‘a’ does not intersect the x axis at any point. This means that it has no real root. Graph ‘b’ has coincident roots and graph ‘c’ has two roots. 

Sample question 1: Can $\left( {x - 1} \right)$ be the remainder on division of a polynomial $p\left( x \right)$ by $2x + 3$? Justify your answer. 

Ans: $\left( {x - 1} \right)$ cannot be the remainder of long division when $p\left( x \right)$ is divided by $2x + 3$ since both the remainder and divisor cannot have equal degree. 

Sample question 2: Is the following statement True or False? Justify your answer. 

If the zeroes of a quadratic polynomial $a{x^2} + bx + c$ are both negative, then a, b and c all have the same sign.

Ans: If all the zeroes are negative, then the sum of the two zeroes of the polynomial $a{x^2} + bx + c$ will be negative and the product of the zeroes will be positive. So, we have, $ - \dfrac{b}{a}$ should be negative and $\dfrac{c}{a}$ should be positive. 

Hence, a b and c have the same signs. 

Exercise 2.2

1. Answer the following and justify. 

i) Can ${x^2} - 1$ be the quotient on division of ${x^6} + 2{x^3} + x - 1$ by a polynomial in x of degree $5$? 

Ans: Let $f\left( x \right) = {x^6} + 2{x^3} + x - 1$ and quotient $q\left( x \right) = {x^2} - 1$.

Also, the divisor is a polynomial of degree $5$ in x. 

Let the divisor polynomial be  $g\left( x \right) = a{x^5} + b{x^4} + c{x^3} + d{x^2} + ex + f$.

We know that \[\left( {{\text{Dividend}}} \right){\text{ = }}\left( {{\text{Divisor}}} \right)\left( {{\text{Quotient}}} \right){\text{ + }}\left( {{\text{Remainder}}} \right)\].

Substituting the known polynomials, we have, 

\[\left( {{x^6} + 2{x^3} + x - 1} \right){\text{ = }}\left( {a{x^5} + b{x^4} + c{x^3} + d{x^2} + ex + f} \right)\left( {{x^2} - 1} \right){\text{ + }}\left( {{\text{Remainder}}} \right)\]

Now, we know that the degree of remainder is always less than divisor. 

So, the right hand side of the equation has degree x as \[7\] and the left hand side of equation has degree as \[6\]. This is not possible. 

Hence, ${x^2} - 1$  cannot be the quotient on division of ${x^6} + 2{x^3} + x - 1$ by a polynomial in x of degree $5$.

ii) What will the quotient and remainder be in the division of $a{x^2} + bx + c$ by $p{x^3} + q{x^2} + rx + s$, $p \ne 0$? 

Ans: So, we have, $a{x^2} + bx + c$ as dividend and $p{x^3} + q{x^2} + rx + s$ as the divisor. 

We know that the degree of the dividend should always be greater than the divisor for the division to occur. Since degree of dividend $a{x^2} + bx + c$ is two and degree of divisor $p{x^3} + q{x^2} + rx + s$ is three. 

Hence, the value of the quotient will be zero and the remainder will be equal to $a{x^2} + bx + c$. 

iii) If on division of a non-zero polynomial p(x) by a polynomial g(x), the quotient is zero, what is the relation between the degree of p(x) and g(x)? 

Ans: Here, the dividend is \[p\left( x \right)\] and the divisor is \[g\left( x \right)\].

Also, we are given that quotient \[q\left( x \right) = 0\].

This means that division cannot occur as the degree of divisor is greater than the degree of dividend. Hence, the degree of \[g\left( x \right)\]$ > $ degree of \[p\left( x \right)\].

iv) If on division of a non-zero polynomial p(x) by a polynomial g(x), the remainder is zero, what is the relation between the degree of p(x) and g(x)? 

Ans: There is no remainder when a polynomial \[p\left( x \right)\] is divided by a polynomial \[g\left( x \right)\]. This means \[g\left( x \right)\] is a factor of the dividend \[p\left( x \right)\].

Therefore, degree of \[g\left( x \right)\]$ \leqslant $ degree of \[p\left( x \right)\]

v) Can the quadratic polynomial ${x^2} + kx + k$ have equal zeroes for some odd integer $k > 1$?

Ans: We have the quadratic polynomial ${x^2} + kx + k$. Comparing with $a{x^2} + bx + c$, we get, $a = 1,b = k,c = k$.

For a polynomial to have equal roots, discriminant should be equal to zero. 

Hence, $D = {b^2} - 4ac = 0$.

Substituting the values of a, b, and c.

$ \Rightarrow {k^2} - 4\left( 1 \right)\left( k \right) = 0$

$ \Rightarrow {k^2} - 4k = 0$

$ \Rightarrow k\left( {k - 4} \right) = 0$

Either $k = 0$ or $\left( {k - 4} \right) = 0$

So, $k = 0$ or $k = 4$.

So, the polynomial ${x^2} + kx + k$ cannot have equal roots for any odd integral value of k, $k > 1$.

2. Are the following statements true or false? Justify your answers.

(i) If the zeroes of a quadratic polynomial \[a{x^2} + bx + c\] are both positive, then a, b and c have the same sign. 

Ans: The statement is false.

Let $\alpha $ and $\beta $ be the zeroes of the quadratic polynomial \[a{x^2} + bx + c\]. Now, we are given that both zeroes are positive. So, the sum of the zeroes will also be positive. 

Sum of zeroes \[ =  - \dfrac{b}{a}\]

So, \[ - \dfrac{b}{a} > 0\]

Multiplying both sides of inequality with negative signs and changing signs of inequality.

\[ \Rightarrow \dfrac{b}{a} < 0\]

For division of two numbers to be negative, the numbers have to be of opposite signs. So, a and b cannot have the same sign. 

(ii) If the graph of a polynomial intersects the X-axis at only one point, it cannot be a quadratic polynomial. 

Ans: The statement is false.

A quadratic polynomial can have at most two real roots. This means that a quadratic polynomial may have one real root if the graph of the polynomial touches the x axis at only one point. 

(iii) If the graph of a polynomial intersects the X-axis at exactly two points, it need not be a quadratic polynomial. 

Ans: The statement is false. 

A polynomial of degree greater than two may have non real roots due to which the graph of the polynomial intersects the x axis at only two points. So, it is not necessary for a polynomial to be quadratic if it intersects the X-axis at exactly two points. 

(iv) If two of the zeroes of a cubic polynomial are zero, then it does not have linear and constant terms. 

Ans: The statement is true. 

Let $p\left( x \right) = a{x^3} + b{x^2} + cx + d$ and $\alpha ,\beta ,\gamma $ be the roots of the polynomial. 

We are given that two of the roots are zero. Hence, $\beta  = \gamma  = 0$.

Product of zeroes $ = \alpha \beta \gamma  =  - \dfrac{d}{a}$

$ \Rightarrow  - \dfrac{d}{a} = \alpha \left( 0 \right)\left( 0 \right)$

$ \Rightarrow d = 0$

Sum of product of zeroes taken two at a time $ = \alpha \beta  + \beta \gamma  + \gamma \alpha  = \dfrac{c}{a}$

$ \Rightarrow \alpha \left( 0 \right) + \left( 0 \right)\left( 0 \right) + \left( 0 \right)\alpha  = \dfrac{c}{a}$

$ \Rightarrow c = 0$

Hence, the cubic polynomial does not have linear and constant terms if two roots are zero. 

(v) If all the zeros of a cubic polynomial are negative, then all the coefficients and the constant term of the polynomial have the same sign. 

Ans: The statement is true. 

We have a cubic polynomial $p\left( x \right) = a{x^3} + b{x^2} + cx + d$. Let $\alpha ,\beta ,\gamma $ be the roots of a polynomial. All roots are negative.

So, \[\alpha  + \beta  + \gamma  =  - \dfrac{b}{a}\]

This means that \[ - \dfrac{b}{a}\] is negative. Hence, \[\dfrac{b}{a}\] is positive. So, a and b have the same signs. 

Now, \[\alpha \beta \gamma  =  - \dfrac{d}{a}\]

Multiplication of three negative roots will be negative. So, \[ - \dfrac{d}{a}\] is negative. So, \[\dfrac{d}{a}\] is positive. Therefore, d and a have the same signs. 

Also, \[\alpha \beta  + \beta \gamma  + \gamma \alpha  = \dfrac{c}{a}\]

Multiplication of two negative roots is positive and the sum of positive entities is positive. So, \[\dfrac{c}{a}\] is positive. Hence, c and a have the same signs.

(vi) If all three zeros of a cubic polynomial \[{x^3} + a{x^2} - bx + c\] are positive, then at least one of a, b, and c is non-negative. 

Ans: The statement is false. 

Let \[f\left( x \right) = {x^3} + a{x^2} - bx + c\]. All zeroes of polynomials are positive. So, \[\alpha  > 0,\beta  > 0,\gamma  > 0\].

Now, sum of roots $ = \alpha  + \beta  + \gamma  =  - a$.

Sum of positive roots will also be positive. So, $ - a$ is positive. Hence, a is negative. 

Product of zeroes $ = \alpha \beta \gamma  =  - c$

Product of positive zeroes will also be positive. So, $ - c$ is positive. Hence, c is negative. 

Now, sum of products of zeroes taken two at a time $ = \alpha \beta  + \beta \gamma  + \gamma \alpha  =  - b$

Sum of products of positive roots is positive. So, $ - b$ is positive, So, b is negative.

(vii) The only value of k for which the quadratic polynomial \[k{x^2}{\text{ +  }}x + k\] has equal zeroes is $\dfrac{1}{2}$.

Ans: Let polynomials \[p\left( x \right) = k{x^2}{\text{ +  }}x + k\]. Any polynomial having equal roots has discriminant equal to zero. Hence, $D = {b^2} - 4ac = 0$.

Comparing \[a{x^2}{\text{ +  b}}x + c\], we get \[a = k,b = 1,c = k\].

Substituting these values in expression for D, we get,

\[ \Rightarrow {\left( 1 \right)^2} - 4\left( k \right)\left( k \right) = 0\]

\[ \Rightarrow 4{k^2} = 1\]

\[ \Rightarrow k =  \pm \dfrac{1}{2}\]

So, values of k for which the quadratic polynomial \[k{x^2}{\text{ +  }}x + k\] has equal zeroes are \[\dfrac{1}{2}\] and \[ - \dfrac{1}{2}\].

Sample question 1: Find the zeroes of the polynomial ${x^2} + \dfrac{1}{6}x - 2$, and verify the relation between the coefficients and the roots of the polynomial. 

Ans: ${x^2} + \dfrac{1}{6}x - 2 = \dfrac{1}{6}\left( {6{x^2} + x - 12} \right) = \dfrac{1}{6}\left( {6{x^2} + 9x - 8x - 12} \right)$

$ \Rightarrow {x^2} + \dfrac{1}{6}x - 2 = \dfrac{1}{6}\left[ {3x\left( {2x + 3} \right) - 4\left( {2x + 3} \right)} \right]$

$ \Rightarrow {x^2} + \dfrac{1}{6}x - 2 = \dfrac{1}{6}\left( {2x + 3} \right)\left( {3x - 4} \right)$

So, the zeros of the polynomial are: $x =  - \dfrac{3}{2},\dfrac{4}{3}$.

Now, sum of zeroes $ - \dfrac{3}{2} + \dfrac{4}{3} =  - \dfrac{1}{6}$

Product of zeroes $ =  - \dfrac{3}{2} \times \dfrac{4}{3} =  - 2$

Also, sum of zeroes $ =  - \dfrac{{{\text{Coefficient of x}}}}{{{\text{Coefficient of }}{{\text{x}}^{\text{2}}}}} =  - \dfrac{1}{6}$

Product of zeroes $ = \dfrac{{{\text{Constant term}}}}{{{\text{Coefficient of }}{{\text{x}}^{\text{2}}}}} =  - 2$

Exercise 2.3

Find the zeroes of the following polynomials by factorisation method and verify the relations between the zeroes and coefficients of the polynomials.

1) $4{x^2} - 3x - 1$

Ans: Let $p\left( x \right) = 4{x^2} - 3x - 1$.

Factoring the polynomial using splitting the middle term, we get,

$ \Rightarrow p\left( x \right) = 4{x^2} - 4x + x - 1$

Taking common terms outside the bracket, we get,

\[ \Rightarrow p\left( x \right) = 4x\left( {x - 1} \right) + \left( {x - 1} \right)\]

\[ \Rightarrow p\left( x \right) = \left( {4x + 1} \right)\left( {x - 1} \right)\]

Now, for finding the zeros of the polynomial, we get, 

$ \Rightarrow p\left( x \right) = \left( {4x + 1} \right)\left( {x - 1} \right) = 0$

Either $\left( {4x + 1} \right) = 0$ or $\left( {x - 1} \right) = 0$

$ \Rightarrow x =  - \dfrac{1}{4}$ or $x = 1$

The zeroes are: $x = 1$ and $x =  - \dfrac{1}{4}$.

Sum of zeroes $ = 1 + \left( { - \dfrac{1}{4}} \right) = \dfrac{3}{4}$

Product of zeroes $ = \left( 1 \right) \times \left( { - \dfrac{1}{4}} \right) =  - \dfrac{1}{4}$

$p\left( x \right) = 4{x^2} - 3x - 1$

Compared with $a{x^2} + bx + c$, $a = 4,b =  - 3,c =  - 1$.

Now, we also know that sum of zeroes $ =  - \dfrac{b}{a} =  - \left( {\dfrac{{ - 3}}{4}} \right) = \dfrac{3}{4}$

Also, product of zeroes $ = \dfrac{c}{a} = \left( {\dfrac{{ - 1}}{4}} \right)$

Hence, verified. 

2) $3{x^2} + 4x - 4$

Ans: Let \[p\left( x \right) = 3{x^2} + 4x - 4\].

Factoring the polynomial using splitting the middle term, we get,

$ \Rightarrow p\left( x \right) = 3{x^2} + 6x - 2x - 4$

Taking common terms outside the bracket, we get,

$ \Rightarrow p\left( x \right) = 3x\left( {x + 2} \right) - 2\left( {x + 2} \right)$

$ \Rightarrow p\left( x \right) = \left( {3x - 2} \right)\left( {x + 2} \right)$

Now, for finding the zeros of the polynomial, we get, 

$ \Rightarrow p\left( x \right) = \left( {3x - 2} \right)\left( {x + 2} \right) = 0$

Either $\left( {3x - 2} \right) = 0$ or $\left( {x + 2} \right) = 0$

$ \Rightarrow x = \dfrac{2}{3}$ or $x =  - 2$

The zeroes are: $x = \dfrac{2}{3}$ and $x =  - 2$.

Sum of zeroes $ =  - 2 + \left( {\dfrac{2}{3}} \right) =  - \dfrac{4}{3}$

Product of zeroes $ = \left( { - 2} \right) \times \left( {\dfrac{2}{3}} \right) =  - \dfrac{4}{3}$

\[p\left( x \right) = 3{x^2} + 4x - 4\]

Compared with $a{x^2} + bx + c$, $a = 3,b = 4,c =  - 4$.

Now, we also know that sum of zeroes $ =  - \dfrac{b}{a} =  - \left( {\dfrac{4}{3}} \right) =  - \dfrac{4}{3}$

Also, product of zeroes $ = \dfrac{c}{a} = \left( {\dfrac{{ - 4}}{3}} \right)$

Hence, verified. 

3) $5{t^2} + 12t + 7$

Ans: Let \[f\left( t \right) = 5{t^2} + 12t + 7\].

Factoring the polynomial using splitting the middle term, we get,

$ \Rightarrow f\left( t \right) = 5{t^2} + 5t + 7t + 7$

Taking common terms outside the bracket, we get,

$ \Rightarrow f\left( t \right) = 5t\left( {t + 1} \right) + 7\left( {t + 1} \right)$

$ \Rightarrow f\left( t \right) = \left( {5t + 7} \right)\left( {t + 1} \right)$

Now, for finding the zeros of the polynomial, we get, 

$ \Rightarrow f\left( t \right) = \left( {5t + 7} \right)\left( {t + 1} \right) = 0$

Either $\left( {5t + 7} \right) = 0$ or $\left( {t + 1} \right) = 0$

$ \Rightarrow t =  - \dfrac{7}{5}$ or $t =  - 1$

The zeroes are: $t =  - \dfrac{7}{5}$ and $t =  - 1$.

Sum of zeroes $ =  - \dfrac{7}{5} - 1 =  - \dfrac{{12}}{5}$

Product of zeroes $ = \left( { - 1} \right) \times \left( { - \dfrac{7}{5}} \right) = \dfrac{7}{5}$

\[f\left( t \right) = 5{t^2} + 12t + 7\]

Compared with $a{x^2} + bx + c$, $a = 5,b = 12,c = 7$.

Now, we also know that sum of zeroes 

Also, product of zeroes 

Hence, verified. 

4) ${t^3} - 2{t^2} - 15t$

Ans: Let \[f\left( t \right) = {t^3} - 2{t^2} - 15t\].

Taking t common from all the terms, we get,

\[ \Rightarrow f\left( t \right) = t\left( {{t^2} - 2t - 15} \right)\]

Factoring the polynomial using splitting the middle term, we get,

\[ \Rightarrow f\left( t \right) = t\left( {{t^2} - 5t + 3t - 15} \right)\]

\[ \Rightarrow f\left( t \right) = t\left( {t - 5} \right)\left( {t + 3} \right)\]

Now, for finding the zeros of the polynomial, we get, 

$ \Rightarrow f\left( t \right) = t\left( {t - 5} \right)\left( {t + 3} \right) = 0$

Either $t = 0$, $\left( {t - 5} \right) = 0$ or $\left( {t + 3} \right) = 0$

$ \Rightarrow t = 0$ or $t = 5$ or $t =  - 3$

The zeroes are: $t = 0$, $t = 5$ and $t =  - 3$.

Sum of zeroes \[ = 0 + 5 + \left( { - 3} \right) = 2\]

Product of zeroes $ = \left( 0 \right) \times \left( 5 \right) \times \left( { - 3} \right) = 0$

Sum of products of zeroes taken two at a time$ = \left( 0 \right) \times \left( 5 \right) + \left( { - 3} \right) \times \left( 5 \right) + \left( { - 3} \right) \times \left( 0 \right) = 0 - 15 + 0 =  - 15$

\[f\left( t \right) = {t^3} - 2{t^2} - 15t\]

Compared with $a{x^3} + b{x^2} + cx + d$, $a = 1,b =  - 2,c =  - 15,d = 0$.

Now, we also know that sum of zeroes $ =  - \dfrac{b}{a} =  - \left( {\dfrac{{ - 2}}{1}} \right) = 2$

Also, product of zeroes $ =  - \dfrac{d}{a} =  - \left( 0 \right) = 0$

Sum of products of zeroes taken two at a time $ = \dfrac{c}{a} = \dfrac{{ - 15}}{1} =  - 15$

Hence, verified. 

5) $2{x^2} + \dfrac{7}{2}x + \dfrac{3}{4}$

Ans: Let \[f\left( x \right) = 2{x^2} + \dfrac{7}{2}x + \dfrac{3}{4}\].

Now, for finding the zeros of the polynomial, we get, 

$ \Rightarrow f\left( x \right) = 2{x^2} + \dfrac{7}{2}x + \dfrac{3}{4} = 0$

Multiplying and dividing by four,

$ \Rightarrow f\left( x \right) = \dfrac{1}{4}\left[ {8{x^2} + 14x + 3} \right] = 0$

Factoring using splitting the middle term method, we get,

$ \Rightarrow \dfrac{1}{4}\left[ {8{x^2} + 12x + 2x + 3} \right] = 0$

$ \Rightarrow \dfrac{1}{4}\left[ {4x\left( {2x + 3} \right) + \left( {2x + 3} \right)} \right] = 0$

$ \Rightarrow \dfrac{1}{4}\left( {2x + 3} \right)\left( {4x + 1} \right) = 0$

Either $2x + 3 = 0$ or $4x + 1 = 0$

$ \Rightarrow x =  - \dfrac{3}{2}$ or $x =  - \dfrac{1}{4}$

The zeroes are: $x =  - \dfrac{3}{2}$ and $x =  - \dfrac{1}{4}$.

Sum of zeroes $ =  - \dfrac{1}{4} - \dfrac{3}{2} =  - \dfrac{7}{4}$

Product of zeroes $ = \left( { - \dfrac{3}{2}} \right) \times \left( { - \dfrac{1}{4}} \right) = \dfrac{3}{8}$

Compared with $a{x^2} + bx + c$, $a = 2,b = \dfrac{7}{2},c = \dfrac{3}{4}$.

Now, we also know that sum of zeroes $ =  - \dfrac{b}{a} =  - \dfrac{{\left( {\dfrac{7}{2}} \right)}}{2} =  - \dfrac{7}{4}$

Also, product of zeroes $ = \dfrac{c}{a} = \dfrac{{\left( {\dfrac{3}{4}} \right)}}{2} = \dfrac{3}{8}$

Hence, verified. 

6)  \[4{x^2} + 5\sqrt 2 x - 3\]

Ans: Let \[f\left( x \right) = 4{x^2} + 5\sqrt 2 x - 3\].

Now, for finding the zeros of the polynomial, we get, 

$ \Rightarrow f\left( x \right) = 4{x^2} + 6\sqrt 2 x - \sqrt 2 x - 3 = 0$

$ \Rightarrow 2\sqrt 2 x\left( {\sqrt 2 x + 3} \right) - \left( {\sqrt 2 x + 3} \right) = 0$

$ \Rightarrow \left( {2\sqrt 2 x - 1} \right)\left( {\sqrt 2 x + 3} \right) = 0$

Either $\left( {2\sqrt 2 x - 1} \right) = 0$ or $\left( {\sqrt 2 x + 3} \right) = 0$

$ \Rightarrow x = \dfrac{1}{{2\sqrt 2 }}$ or $ \Rightarrow x =  - \dfrac{3}{{\sqrt 2 }}$

The zeroes are: $x = \dfrac{1}{{2\sqrt 2 }}$ and $x =  - \dfrac{3}{{\sqrt 2 }}$.

Sum of zeroes $ = \dfrac{1}{{2\sqrt 2 }} - \dfrac{3}{{\sqrt 2 }} = \dfrac{{ - 5}}{{2\sqrt 2 }}$

Product of zeroes $ = \dfrac{1}{{2\sqrt 2 }} \times \dfrac{{ - 3}}{{\sqrt 2 }} = \dfrac{{ - 3}}{4}$

\[f\left( x \right) = 4{x^2} + 5\sqrt 2 x - 3\]

Compared with $a{x^2} + bx + c$, \[a = 4,b = 5\sqrt 2 ,c =  - 3\].

Now, we also know that sum of zeroes $ =  - \dfrac{b}{a} =  - \dfrac{{5\sqrt 2 }}{4} =  - \dfrac{5}{{2\sqrt 2 }}$

Also, product of zeroes $ = \dfrac{c}{a} = \left( { - \dfrac{3}{4}} \right)$

Hence, verified. 

7) $2{s^2} - \left( {1 + 2\sqrt 2 } \right)s + \sqrt 2 $

Ans: Let \[f\left( s \right) = 2{s^2} - \left( {1 + 2\sqrt 2 } \right)s + \sqrt 2 \].

Now, for finding the zeros of the polynomial, we get, 

$ \Rightarrow f\left( s \right) = 2{s^2} - \left( {1 + 2\sqrt 2 } \right)s + \sqrt 2  = 0$

Opening brackets,

$ \Rightarrow f\left( s \right) = 2{s^2} - s - 2\sqrt 2 s + \sqrt 2  = 0$

$ \Rightarrow 2s\left( {s - \sqrt 2 } \right) - \left( {s - \sqrt 2 } \right) = 0$

$ \Rightarrow \left( {2s - 1} \right)\left( {s - \sqrt 2 } \right) = 0$

Either $2s - 1 = 0$ or $s - \sqrt 2  = 0$

$ \Rightarrow s = \dfrac{1}{2}$ or $ \Rightarrow s = \sqrt 2 $

The zeroes are: $s = \dfrac{1}{2}$ and $s = \sqrt 2 $.

Sum of zeroes $ = \dfrac{1}{2} + \sqrt 2 $

Product of zeroes $ = \dfrac{1}{2} \times \sqrt 2  = \dfrac{1}{{\sqrt 2 }}$

\[f\left( s \right) = 2{s^2} - \left( {1 + 2\sqrt 2 } \right)s + \sqrt 2 \]

Compared with $a{x^2} + bx + c$, \[a = 2,b =  - \left( {1 + 2\sqrt 2 } \right),c = \sqrt 2 \].

Now, we also know that sum of zeroes $ =  - \dfrac{b}{a} = \dfrac{{1 + 2\sqrt 2 }}{2} = \dfrac{1}{2} + \sqrt 2 $

Also, product of zeroes $ = \dfrac{c}{a} = \dfrac{{\sqrt 2 }}{2} = \dfrac{1}{{\sqrt 2 }}$

Hence, verified. 

8) ${v^2} + 4\sqrt 3 v - 15$

Ans: Let \[f\left( v \right) = {v^2} + 4\sqrt 3 v - 15\].

Now, for finding the zeros of the polynomial, we get, 

$ \Rightarrow f\left( v \right) = {v^2} + 4\sqrt 3 v - 15 = 0$

Splitting the middle term for factorisation, we get,

$ \Rightarrow {v^2} + 5\sqrt 3 v - \sqrt 3 v - 15 = 0$

$ \Rightarrow v\left( {v + 5\sqrt 3 } \right) - \sqrt 3 \left( {v - 5\sqrt 3 } \right) = 0$

$ \Rightarrow \left( {v - \sqrt 3 } \right)\left( {v + 5\sqrt 3 } \right) = 0$

Either $v - \sqrt 3  = 0$ or $v + 5\sqrt 3  = 0$

$ \Rightarrow v = \sqrt 3 $ or $ \Rightarrow v =  - 5\sqrt 3 $

The zeroes are: $v = \sqrt 3 $ and $v =  - 5\sqrt 3 $.

Sum of zeroes $ =  - 5\sqrt 3  + \sqrt 3  =  - 4\sqrt 3 $

Product of zeroes $ = \left( { - 5\sqrt 3 } \right) \times \left( {\sqrt 3 } \right) =  - 15$

${v^2} + 4\sqrt 3 v - 15$

Compared with $a{x^2} + bx + c$, \[a = 1,b = 4\sqrt 3 ,c =  - 15\].

Now, we also know that sum of zeroes $ =  - \dfrac{b}{a} =  - 4\sqrt 3 $

Also, product of zeroes $ = \dfrac{c}{a} =  - 15$

Hence, verified. 

9) ${y^2} + \dfrac{3}{2}\sqrt 5 y - 5$

Ans: Let \[f\left( y \right) = {y^2} + \dfrac{3}{2}\sqrt 5 y - 5\].

Now, for finding the zeros of the polynomial, we get, 

$ \Rightarrow f\left( y \right) = {y^2} + \dfrac{3}{2}\sqrt 5 y - 5 = 0$

Multiplying and dividing by two, 

$ \Rightarrow f\left( y \right) = \dfrac{1}{2}\left( {2{y^2} + 3\sqrt 5 y - 10} \right) = 0$

Splitting the middle term for factorisation, we get,

$ \Rightarrow \dfrac{1}{2}\left( {2{y^2} + 4\sqrt 5 y - \sqrt 5 y - 10} \right) = 0$

$ \Rightarrow \dfrac{1}{2}\left( {2y\left( {y + 2\sqrt 5 } \right) - \sqrt 5 \left( {y + 2\sqrt 5 } \right)} \right) = 0$

$ \Rightarrow \dfrac{1}{2}\left( {2y - \sqrt 5 } \right)\left( {y + 2\sqrt 5 } \right) = 0$

Either $\left( {2y - \sqrt 5 } \right) = 0$ or $\left( {y + 2\sqrt 5 } \right) = 0$

$ \Rightarrow y = \dfrac{{\sqrt 5 }}{2}$ or $ \Rightarrow y =  - 2\sqrt 5 $

The zeroes are: $y = \dfrac{{\sqrt 5 }}{2}$ and $y =  - 2\sqrt 5 $.

Sum of zeroes $ = \dfrac{{\sqrt 5 }}{2} - 2\sqrt 5  =  - \dfrac{3}{2}\sqrt 5 $

Product of zeroes $ = \dfrac{{\sqrt 5 }}{2} \times \left( { - 2\sqrt 5 } \right) =  - 5$

${y^2} + \dfrac{3}{2}\sqrt 5 y - 5$

Compared with $a{x^2} + bx + c$, \[a = 1,b = \dfrac{3}{2}\sqrt 5 ,c =  - 5\].

Now, we also know that sum of zeroes $ =  - \dfrac{b}{a} =  - \dfrac{{\left( {\dfrac{3}{2}\sqrt 5 } \right)}}{1} =  - \dfrac{3}{2}\sqrt 5 $

Also, product of zeroes $ = \dfrac{c}{a} =  - 5$

Hence, verified. 

10) $7{y^2} - \dfrac{{11}}{3}y - \dfrac{2}{3}$

Ans: Let \[f\left( y \right) = 7{y^2} - \dfrac{{11}}{3}y - \dfrac{2}{3}\].

Now, for finding the zeros of the polynomial, we get, 

$ \Rightarrow f\left( y \right) = 7{y^2} - \dfrac{{11}}{3}y - \dfrac{2}{3} = 0$

Multiplying and dividing by three, 

$ \Rightarrow \dfrac{1}{3}\left( {21{y^2} - 11y - 2} \right) = 0$

Splitting the middle term for factorisation, we get,

$ \Rightarrow \dfrac{1}{3}\left( {21{y^2} - 14y + 3y - 2} \right) = 0$

$ \Rightarrow \dfrac{1}{3}\left( {7y\left( {3y - 2} \right) + \left( {3y - 2} \right)} \right) = 0$

$ \Rightarrow \dfrac{1}{3}\left( {3y - 2} \right)\left( {7y + 1} \right) = 0$

Either $3y - 2 = 0$ or $7y + 1 = 0$

$ \Rightarrow y = \dfrac{2}{3}$ or $ \Rightarrow y =  - \dfrac{1}{7}$

The zeroes are: $y = \dfrac{2}{3}$ and $y = \dfrac{1}{7}$.

Sum of zeroes $ = \dfrac{2}{3} - \dfrac{1}{7} = \dfrac{{11}}{{21}}$

Product of zeroes $ = \dfrac{2}{3} \times \left( { - \dfrac{1}{7}} \right) =  - \dfrac{2}{{21}}$

\[f\left( y \right) = 7{y^2} - \dfrac{{11}}{3}y - \dfrac{2}{3}\]

Comparing with $a{x^2} + bx + c$, \[a = 7,b =  - \dfrac{{11}}{3},c =  - \dfrac{2}{3}\].

Now, we also know that sum of zeroes $ =  - \dfrac{b}{a} =  - \dfrac{{\dfrac{{ - 11}}{3}}}{7} = \dfrac{{11}}{{21}}$

Also, product of zeroes $ = \dfrac{c}{a} =  - \dfrac{{\left( {\dfrac{2}{3}} \right)}}{7} =  - \dfrac{2}{{21}}$

Hence, verified. 

Sample question 1: Find quadratic polynomials, the sum and product of whose zeroes are $\sqrt 2 $ and $ - \dfrac{3}{2}$, respectively. Also, find its zeroes.

Ans: A quadratic polynomial whose sum of zeroes is given as ‘s’ and product of zeroes of zeroes is given as ‘p’ can be represented as ${x^2} - sx + p$.

So, required polynomial whose sum and product of zeroes is given as $\sqrt 2 $ and $ - \dfrac{3}{2}$ is ${x^2} - \sqrt 2 x - \dfrac{3}{2}$.

Now, we have to find its zeroes. So, we have, 

${x^2} - \sqrt 2 x - \dfrac{3}{2} = \dfrac{1}{2}\left( {2{x^2} - 2\sqrt 2 x - 3} \right)$

$ \Rightarrow \dfrac{1}{2}\left( {2{x^2} - 3\sqrt 2 x + \sqrt 2 x - 3} \right)$

$ \Rightarrow \dfrac{1}{2}\left( {\sqrt 2 x\left( {\sqrt 2 x - 3} \right) + \left( {\sqrt 2 x - 3} \right)} \right)$

$ \Rightarrow \dfrac{1}{2}\left( {\sqrt 2 x - 3} \right)\left( {\sqrt 2 x + 1} \right)$

So, the zeroes of the polynomial are: $x = \dfrac{3}{{\sqrt 2 }}$ and $x =  - \dfrac{1}{{\sqrt 2 }}$.

Sample question 2: If the remainder on the division of ${x^3} + 2{x^2} + kx + 3$ by $x - 3$ is $21$, find the quotient and the value of k. Hence, find the zeroes of the cubic polynomial ${x^3} + 2{x^2} + kx - 18$.

Ans: Let $p\left( x \right) = {x^3} + 2{x^2} + kx + 3$ and $g\left( x \right) = x - 3$. 

Now, we can find the remainder on dividing the polynomial $p\left( x \right) = {x^3} + 2{x^2} + kx + 3$ by $g\left( x \right) = x - 3$ using the remainder theorem. 

So, remainder $ = p\left( 3 \right) = {\left( 3 \right)^3} + 2{\left( 3 \right)^2} + k\left( 3 \right) + 3 = 27 + 18 + 3k + 3$

$ = 48 + 3k$

We are given the remainder as $21$. Hence, we get, $48 + 3k = 21$

$ \Rightarrow 3k = 21 - 48 =  - 27$

$ \Rightarrow k =  - 9$

So, the value of k is $ - 9$.

Now, let $f\left( x \right) = {x^3} + 2{x^2} + kx - 18 = {x^3} + 2{x^2} - 9x - 18$.

By hit and trial, we see that $ - 2$ is the zero of $f\left( x \right) = {x^3} + 2{x^2} - 9x - 18$.

So, we get, \[f\left( x \right) = {x^2}\left( {x + 2} \right) - 9\left( {x + 2} \right)\]

\[ \Rightarrow \left( {x + 2} \right)\left( {{x^2} - 9} \right)\]

Using the algebraic identity \[\left( {{a^2} - {b^2}} \right) = \left( {a - b} \right)\left( {a + b} \right)\], we get,

\[ \Rightarrow \left( {x + 2} \right)\left( {x - 3} \right)\left( {x + 3} \right)\]

Hence, zeroes of ${x^3} + 2{x^2} + kx - 18$ are: $ - 2$, $3$ and $ - 3$.

Exercise 2.4

1. For each of the following, find a quadratic polynomial whose sum and product respectively of zeroes are as given. Also, find the zeroes of these polynomials by factoring. 

i) $ - \dfrac{8}{3},\dfrac{4}{3}$

Ans: If the zeroes of a quadratic polynomial are given by $\alpha ,\beta $, then the polynomial can be represented as \[{x^2} - \left( {\alpha  + \beta } \right)x + \alpha \beta \].

So, we have, \[\left( {\alpha  + \beta } \right) =  - \dfrac{8}{3}\] and \[\alpha \beta  = \dfrac{4}{3}\]

Then, we have the polynomial as: 

\[{x^2} - \left( {\alpha  + \beta } \right)x + \alpha \beta \]

Substituting the known values, we get,

\[ \Rightarrow {x^2} - \left( { - \dfrac{8}{3}} \right)x + \dfrac{4}{3}\]

\[ \Rightarrow {x^2} + \dfrac{8}{3}x + \dfrac{4}{3}\]

Multiplying and dividing the entire polynomial by three, we get, 

\[ \Rightarrow \dfrac{1}{3}\left( {3{x^2} + 8x + 4} \right)\]

Now, for finding the zeroes of the polynomial, 

\[ \Rightarrow \dfrac{1}{3}\left( {3{x^2} + 8x + 4} \right) = 0\]

Splitting the middle term,

\[ \Rightarrow \dfrac{1}{3}\left( {3{x^2} + 6x + 2x + 4} \right) = 0\]

\[ \Rightarrow \dfrac{1}{3}\left( {3x\left( {x + 2} \right) + 2\left( {x + 2} \right)} \right) = 0\]

\[ \Rightarrow \dfrac{1}{3}\left( {3x + 2} \right)\left( {x + 2} \right) = 0\]

Either \[\left( {3x + 2} \right) = 0\] or \[\left( {x + 2} \right) = 0\]

\[ \Rightarrow x =  - \dfrac{2}{3}\] or \[ \Rightarrow x =  - 2\]

ii) $\dfrac{{21}}{8},\dfrac{5}{{16}}$

Ans: If the zeroes of a quadratic polynomial are given by $\alpha ,\beta $, then the polynomial can be represented as \[{x^2} - \left( {\alpha  + \beta } \right)x + \alpha \beta \].

So, we have, \[\left( {\alpha  + \beta } \right) = \dfrac{{21}}{8}\] and \[\alpha \beta  = \dfrac{5}{{16}}\]

Then, we have the polynomial as: 

\[{x^2} - \left( {\alpha  + \beta } \right)x + \alpha \beta \]

Substituting the known values, we get,

\[ \Rightarrow {x^2} - \left( {\dfrac{{21}}{8}} \right)x + \dfrac{5}{{16}}\]

\[ \Rightarrow {x^2} - \dfrac{{21}}{8}x + \dfrac{5}{{16}}\]

Multiplying and dividing the entire polynomial by \[16\], we get, 

\[ \Rightarrow \dfrac{1}{{16}}\left( {16{x^2} - 42x + 5} \right)\]

Now, for finding the zeroes of the polynomial, 

\[ \Rightarrow \dfrac{1}{{16}}\left( {16{x^2} - 42x + 5} \right) = 0\]

Splitting the middle term,

\[ \Rightarrow \dfrac{1}{{16}}\left( {16{x^2} - 40x - 2x + 5} \right) = 0\]

\[ \Rightarrow \dfrac{1}{{16}}\left( {8x\left( {2x - 5} \right) - \left( {2x - 5} \right)} \right) = 0\]

\[ \Rightarrow \dfrac{1}{{16}}\left( {2x - 5} \right)\left( {8x - 1} \right) = 0\]

Either \[\left( {8x - 1} \right) = 0\] or \[\left( {2x - 5} \right) = 0\]

\[ \Rightarrow x = \dfrac{1}{8}\] or \[ \Rightarrow x = \dfrac{5}{2}\]

iii) $ - 2\sqrt 3 , - 9$

Ans: If the zeroes of a quadratic polynomial are given by $\alpha ,\beta $, then the polynomial can be represented as \[{x^2} - \left( {\alpha  + \beta } \right)x + \alpha \beta \].

So, we have, \[\left( {\alpha  + \beta } \right) =  - 2\sqrt 3 \] and \[\alpha \beta  =  - 9\]

Then, we have the polynomial as: 

\[{x^2} - \left( {\alpha  + \beta } \right)x + \alpha \beta \]

Substituting the known values, we get,

\[ \Rightarrow {x^2} - \left( { - 2\sqrt 3 } \right)x + \left( { - 9} \right)\]

\[ \Rightarrow {x^2} + 2\sqrt 3 x - 9\]

Now, for finding the zeros of the polynomial, 

\[ \Rightarrow {x^2} + 2\sqrt 3 x - 9 = 0\]

Splitting the middle term,

\[ \Rightarrow {x^2} + 3\sqrt 3 x - \sqrt 3 x - 9 = 0\]

\[ \Rightarrow x\left( {x + 3\sqrt 3 } \right) - \sqrt 3 \left( {x + 3\sqrt 3 } \right) = 0\]

\[ \Rightarrow \left( {x - \sqrt 3 } \right)\left( {x + 3\sqrt 3 } \right) = 0\]

Either \[\left( {x - \sqrt 3 } \right) = 0\] or \[\left( {x + 3\sqrt 3 } \right) = 0\]

\[ \Rightarrow x = \sqrt 3 \] or \[ \Rightarrow x =  - 3\sqrt 3 \]

iv) $ - \dfrac{3}{{2\sqrt 5 }}, - \dfrac{1}{2}$

Ans: If the zeroes of a quadratic polynomial are given by $\alpha ,\beta $, then the polynomial can be represented as \[{x^2} - \left( {\alpha  + \beta } \right)x + \alpha \beta \].

So, we have, \[\left( {\alpha  + \beta } \right) =  - \dfrac{3}{{2\sqrt 5 }}\] and \[\alpha \beta  =  - \dfrac{1}{2}\]

Then, we have the polynomial as: 

\[{x^2} - \left( {\alpha  + \beta } \right)x + \alpha \beta \]

Substituting the known values, we get,

\[ \Rightarrow {x^2} - \left( { - \dfrac{3}{{2\sqrt 5 }}} \right)x + \left( { - \dfrac{1}{2}} \right)\]

\[ \Rightarrow {x^2} + \dfrac{3}{{2\sqrt 5 }}x - \dfrac{1}{2}\]

Now, for finding the zeros of the polynomial, 

\[ \Rightarrow {x^2} + \dfrac{3}{{2\sqrt 5 }}x - \dfrac{1}{2} = 0\]

Multiplying and dividing the entire polynomial by \[2\sqrt 5 \], we get,

\[ \Rightarrow \dfrac{1}{{2\sqrt 5 }}\left( {2\sqrt 5 {x^2} + 3x - \sqrt 5 } \right) = 0\]

Splitting the middle term,

\[ \Rightarrow \dfrac{1}{{2\sqrt 5 }}\left( {2\sqrt 5 {x^2} + 5x - 2x - \sqrt 5 } \right) = 0\]

\[ \Rightarrow \dfrac{1}{{2\sqrt 5 }}\left( {\sqrt 5 x\left( {2x + \sqrt 5 } \right) - \left( {2x + \sqrt 5 } \right)} \right) = 0\]

\[ \Rightarrow \dfrac{1}{{2\sqrt 5 }}\left( {2x + \sqrt 5 } \right)\left( {\sqrt 5 x - 1} \right) = 0\]

Either \[\left( {2x + \sqrt 5 } \right) = 0\] or \[\left( {\sqrt 5 x - 1} \right) = 0\]

\[ \Rightarrow x =  - \dfrac{{\sqrt 5 }}{2}\] or \[ \Rightarrow x = \dfrac{1}{{\sqrt 5 }}\]

2. Given that the zeroes of cubic polynomial ${x^3} - 6{x^2} + 3x + 10$ are of the form\[a\], $\left( {a + b} \right)$, and $\left( {a + 2b} \right)$ for some real numbers a and b, find the values of a and b as well as the zeroes of the given polynomial.

Ans: Here, we have, ${x^3} - 6{x^2} + 3x + 10$. Comparing with $a{x^3} + b{x^2} + cx + d$, we get,

$a = 1,b =  - 6,c = 3,d = 10$

So, sum of zeroes $ = a + \left( {a + b} \right) + \left( {a + 2b} \right) =  - \left( {\dfrac{{ - 6}}{1}} \right) = 6$

$ \Rightarrow 3a + 3b = 6$

$ \Rightarrow a + b = 2$

$ \Rightarrow b = 2 - a$

Sum of product of zeroes taken two at a time\[ = a\left( {a + b} \right) + \left( {a + b} \right)\left( {a + 2b} \right) + a\left( {a + 2b} \right) = \dfrac{3}{1} = 3\]

Substituting b as $b = 2 - a$, we get,

\[ \Rightarrow a\left( {a + 2 - a} \right) + \left( {a + 2 - a} \right)\left( {a + 2\left( {2 - a} \right)} \right) + a\left( {a + 2\left( {2 - a} \right)} \right) = 3\]

\[ = 2a + 2\left( {4 - a} \right) + a\left( {4 - a} \right) = 3\]

Opening the brackets, we get,

\[ \Rightarrow 2a + 8 - 2a + 4a - {a^2} = 3\]

\[ \Rightarrow 8 + 4a - {a^2} = 3\]

\[ \Rightarrow {a^2} - 4a - 5 = 0\]

Splitting the middle term, we get,

\[ \Rightarrow {a^2} - 5a + a - 5 = 0\]

\[ \Rightarrow a\left( {a - 5} \right) + \left( {a - 5} \right) = 0\]

\[ \Rightarrow \left( {a + 1} \right)\left( {a - 5} \right) = 0\]

So, either \[\left( {a - 5} \right) = 0\] or \[\left( {a + 1} \right) = 0\]

\[a = 5\] or \[a =  - 1\]

Now, for \[a = 5\], $b = 2 - 5 =  - 3$. So, we get the zeroes as: \[a = 5\], \[a + b = 5 - 3 = 2\], \[a + 2b = 5 - 2\left( 3 \right) =  - 1\].

For \[a =  - 1\], $b = 2 - \left( { - 1} \right) = 3$. So, we get the zeroes as: \[a =  - 1\], \[a + b =  - 1 + 3 = 2\], \[a + 2b =  - 1 + 2\left( 3 \right) = 5\].

Hence, the zeroes in both cases are: $5$, $2$ and $ - 1$. 

3. Given that $\sqrt 2 $ is a zero of a cubic polynomial \[6{x^3} + \sqrt 2 {x^2} - 10x - 4\sqrt 2  = 0\], find its other two zeros.

Ans: So, we have the polynomial \[p\left( x \right) = 6{x^3} + \sqrt 2 {x^2} - 10x - 4\sqrt 2 \] and we are given that  $\sqrt 2 $ is a zero of the polynomial. So, using the factor theorem, we have that $\left( {x - \sqrt 2 } \right)$ is a factor of the polynomial \[p\left( x \right)\].

So, we will factorize the polynomial so as to factor out $\left( {x - \sqrt 2 } \right)$. 

So, we have,  \[p\left( x \right) = 6{x^3} + \sqrt 2 {x^2} - 10x - 4\sqrt 2 \]

\[ \Rightarrow p\left( x \right) = 6{x^3} - 6\sqrt 2 {x^2} + 7\sqrt 2 {x^2} - 14x + 4x - 4\sqrt 2 \]

\[ \Rightarrow p\left( x \right) = 6{x^2}\left( {x - \sqrt 2 } \right) + 7\sqrt 2 x\left( {x - \sqrt 2 } \right) + 4\left( {x - \sqrt 2 } \right)\]

\[ \Rightarrow p\left( x \right) = \left( {x - \sqrt 2 } \right)\left( {6{x^2} + 7\sqrt 2 x + 4} \right)\]

Splitting the idle term of the quadratic expression, we get,

\[ \Rightarrow p\left( x \right) = \left( {x - \sqrt 2 } \right)\left( {6{x^2} + 4\sqrt 2 x + 3\sqrt 2 x + 4} \right)\]

\[ \Rightarrow p\left( x \right) = \left( {x - \sqrt 2 } \right)\left( {2x\left( {3x + 2\sqrt 2 } \right) + \sqrt 2 \left( {3x + 2\sqrt 2 } \right)} \right)\]

\[ \Rightarrow p\left( x \right) = \left( {x - \sqrt 2 } \right)\left( {3x + 2\sqrt 2 } \right)\left( {2x + \sqrt 2 } \right)\]

So, the roots of the polynomial are: \[x =  - \dfrac{{2\sqrt 2 }}{3}\] and \[x =  - \dfrac{1}{{\sqrt 2 }}\].

4. Find k so that ${x^2} + 2x + k$ is a factor of $2{x^4} + {x^3} - 14{x^2} + 5x + 6$. Also, find all the zeroes of the two polynomials. 

Ans: We know that a polynomial is divisible by another polynomial if the remainder in the long division process is zero. 

So, we will carry out the long division. 

Now, equating the remainder to zero, we get,

$ \Rightarrow x\left( {21 + 7k} \right) + \left( {2{k^2} + 8k + 6} \right) = 0$

So, we get, $\left( {21 + 7k} \right) = 0$ and $\left( {2{k^2} + 8k + 6} \right) = 0$

$ \Rightarrow 7k =  - 21$ and $ \Rightarrow {k^2} + 3k + k + 3 = 0$

$ \Rightarrow k =  - \dfrac{{21}}{7}$ and $ \Rightarrow {k^2} + 3k + k + 3 = 0$

$ \Rightarrow k =  - \dfrac{{21}}{7}$ and $ \Rightarrow \left( {k + 1} \right)\left( {k + 3} \right) = 0$

So, value of k is $ - 3$.

Divisor $ = g\left( x \right) = \left( {{x^2} + 2x + k} \right) = \left( {{x^2} + 2x - 3} \right)$

Now, quotient is $q\left( x \right) = 2{x^2} - 3x - 8 - 2\left( { - 3} \right) = 2{x^2} - 3x - 2$.

We know that $f\left( x \right) = g\left( x \right)q\left( x \right) + r\left( x \right)$

$ \Rightarrow f\left( x \right) = \left( {{x^2} + 2x - 3} \right)\left( {2{x^2} - 3x - 2} \right) + 0$

Splitting the middle term, we get,

$ \Rightarrow f\left( x \right) = \left( {{x^2} + 3x - x - 3} \right)\left( {2{x^2} - 4x + x - 2} \right)$

$ \Rightarrow f\left( x \right) = \left( {x\left( {x + 3} \right) - \left( {x + 3} \right)} \right)\left( {2x\left( {x - 2} \right) + \left( {x - 2} \right)} \right)$

$ \Rightarrow f\left( x \right) = \left( {x + 3} \right)\left( {x - 1} \right)\left( {x - 2} \right)\left( {2x + 1} \right)$

So, the zeroes of the polynomial are: $x =  - 3$, $x = 1$, $x = 2$ and $x =  - \dfrac{1}{2}$.

5. Given that $\left( {x - \sqrt 5 } \right)$ is a factor of cubic polynomial ${x^3} - 3\sqrt 5 {x^2} + 13x - 3\sqrt 5 $, find all the zeroes of the polynomial.

Ans: So, we have, $f\left( x \right) = {x^3} - 3\sqrt 5 {x^2} + 13x - 3\sqrt 5 $. We are given that $\left( {x - \sqrt 5 } \right)$ is a factor of the polynomial. 

So, we will factorize the polynomial so as to factor out $\left( {x - \sqrt 5 } \right)$ from the polynomial $f\left( x \right) = {x^3} - 3\sqrt 5 {x^2} + 13x - 3\sqrt 5 $. 

$ \Rightarrow f\left( x \right) = {x^3} - \sqrt 5 {x^2} - 2\sqrt 5 {x^2} + 10x + 3x - 3\sqrt 5 $

$ \Rightarrow f\left( x \right) = {x^2}\left( {x - \sqrt 5 } \right) - 2\sqrt 5 x\left( {x - \sqrt 5 } \right) + 3\left( {x - \sqrt 5 } \right)$

$ \Rightarrow f\left( x \right) = \left( {x - \sqrt 5 } \right)\left( {{x^2} - 2\sqrt 5 x + 3} \right)$

Splitting the middle term, we get,

$ \Rightarrow f\left( x \right) = \left( {x - \sqrt 5 } \right)\left( {{x^2} - \left( {\sqrt 5  - \sqrt 2 } \right)x - \left( {\sqrt 5  + \sqrt 2 } \right)x + \left( {\sqrt 5  - \sqrt 2 } \right)\left( {\sqrt 5  + \sqrt 2 } \right)} \right)$

$ \Rightarrow f\left( x \right) = \left( {x - \sqrt 5 } \right)\left[ {x\left( {x - \left( {\sqrt 5  - \sqrt 2 } \right)} \right) - \left( {\sqrt 5  + \sqrt 2 } \right)\left( {x - \left( {\sqrt 5  - \sqrt 2 } \right)} \right)} \right]$

$ \Rightarrow f\left( x \right) = \left( {x - \sqrt 5 } \right)\left( {x - \left( {\sqrt 5  - \sqrt 2 } \right)} \right)\left( {x - \left( {\sqrt 5  + \sqrt 2 } \right)} \right)$

So, the zeroes of the polynomial are: $x = \sqrt 5 $, $x = \left( {\sqrt 5  + \sqrt 2 } \right)$ and $x = \left( {\sqrt 5  - \sqrt 2 } \right)$.

6. For which values of a and b, are the zeroes of \[q\left( x \right){\text{ = }}{x^3} + 2{x^2} + a\] also the zeroes of the polynomial \[p\left( x \right) = {x^5} - {x^4} - 4{x^3} + 3{x^2} + 3x + b\]? Which zeroes of \[p\left( x \right)\] are not the zeroes of \[q\left( x \right)\]?

Ans: Using the factor theorem, if \[q\left( x \right){\text{ = }}{x^3} + 2{x^2} + a\] is a factor of \[p\left( x \right) = {x^5} - {x^4} - 4{x^3} + 3{x^2} + 3x + b\], then the remainder in the long division process should be zero. So, we have,

Now, $r\left( x \right) = {x^2}\left( { - a - 1} \right) + x\left( {3a + 3} \right) + \left( {b - 2a} \right) = 0$

Now equating coefficients of each power of x to zero, we get,

$ - a - 1 = 0$, $3a + 3 = 0$ and $b - 2a = 0$

Solving these, we have, $a =  - 1$ and $b = 2a =  - 2$.

Now, we have to calculate zeros of \[p\left( x \right) = {x^5} - {x^4} - 4{x^3} + 3{x^2} + 3x + b\].

\[p\left( x \right) = \left( {{x^3} + 2{x^2} + a} \right)\left( {{x^2} - 3x + 2} \right) = 0\]

Substituting the value of a, 

\[ \Rightarrow \left( {{x^3} + 2{x^2} - 1} \right)\left( {{x^2} - 2x - x + 2} \right) = 0\]
\[ \Rightarrow \left( {{x^3} + 2{x^2} - 1} \right)\left( {x\left( {x - 2} \right) - \left( {x - 2} \right)} \right) = 0\]

\[ \Rightarrow \left( {{x^3} + 2{x^2} - 1} \right)\left( {x - 2} \right)\left( {x - 1} \right) = 0\]

So, $x = 1$ and \[x = 2\] are the zeroes of \[p\left( x \right)\]  which are not the zeroes of \[q\left( x \right)\].

• Algebraic Expressions

• Polynomial

• Degree of a Polynomial

• Types Of Polynomials (Based on the number of terms and based on the degree)

• Graphical Representations

• Geometrical Representation of a Linear Polynomial

• Geometrical Representation of a Quadratic Polynomial

• Zeros of a Polynomial

• Factorization of Polynomials

• Relationship between Zeroes and Coefficients of a Polynomial

• Division Algorithm

• Division Algorithm

Number of Exercises under NCERT Exemplar for Class 10 - Polynomials

• Exercise 2.1 (5 Questions)

• Exercise 2.2 (1 Question)

• Exercise 2.3 (5 Questions)

• Exercise 2.4 (4 Questions)

What's the Difference between NCERT Solutions and NCERT Exemplar solutions? 

The NCERT textbooks serve as a foundation for a subject. The Exemplar goes above and beyond the essentials, featuring question twists and questions that are more advanced than those found in the normal NCERT. The Ncert exemplar is published by the National Council for Educational Research and Training (NCERT). These books are intended for students in grades 6 to 12. If you've finished your whole syllabus and properly practiced all of the questions at the end of each chapter, the NCERT Exemplar is the next step to putting the last nail in the coffin.

Why choose Vedantu for NCERT Exemplar for Class 10 Math - Polynomials?

Vedantu is your one-stop solution for all the students finding it hard to navigate through school. We've compiled a step-by-step solution guide for NCERT Exemplar for Class 10 Math - Polynomials with the help of several excellent professors. Our academic pros have solved the solutions in this PDF for a better comprehension of students. By referring to these answers, one can quickly grasp how the problem works and analyze where he or she falls short.

Benefits of solving Problems from NCERT Exemplar for Class 10 Math 

Mathematics is a subject that demands not only a deep understanding of the contents but also frequent practice sessions to master the subject and achieve good grades. As a result, finishing NCERT is insufficient for learning this subject; you will need to have the appropriate study materials in hand. As a result, you should use NCERT Exemplar for Class 10 Math to easily master the topic. Take a look at the benefits of using these NCERT Maths exemplars, which will aid you in your board exam preparation. The following are some of these benefits:

• These NCERT exemplars are written by subject experts after significant research on the subject's issues. They provide in-depth knowledge. You will be able to obtain accurate and reliable information on the subjects. Every detail of each topic in the exemplar is given. You can assess your basic understanding and fully comprehend the in-depth aspects of the topic by answering questions from the NCERT Exemplar.

• Contains a wide range of questions. - However, no matter how much effort you put into the subject, you will not succeed unless you practice a large number of questions. At the end of each chapter of NCERT books, you'll find a variety of questions. Short, long, quizzes, match the following, or fill in the blanks are all possibilities. As a result, if you want to get the best grades in Math, you must tackle all of the different types of questions. This regular practice will assist you in rapidly and simply mastering the subject.

• Clears topic fundamentals- The NCERT books not only cover the whole test syllabus but also offer all of the basics on all topics in plain language. To avoid repeating the same themes, make sure your concepts are crystal clear. To create a clear concept, you must refer to the NCERT Math Exemplar for a complete and extensive study. As a result, you will be required to revise the formulas, terms, and execution during the revision.