NCERT Exemplar for Class 10 Maths Chapter 4 - Quadratic Equations - Free PDF Download

Multiple Choice Questions.

Choose the correct answer from the given four options:

Sample Question 1: Which one of the following is not a quadratic equation?

(A) $ \left( x+2 \right)2 = 2\left( x+3 \right) $ 

(B) $ {{x}^{2}} + 3x =  \left( 1 \right){{\left( 13x \right)}^{2}} $ 

(C) $ (x+2)\left( x-1 \right)={{x}^{2}}-2x-3 $ 

(D) $ {{x}^{3}}-{{x}^{2}} + 2x+1 = {{\left( x + 1 \right)}^{3}} $ 

Ans: Correct option is (c)

Given, options A, B, C and D are the given equation.

Polynomial with degree $ 2 $ is a quadratic equation.

$ (x+2)\left( x1 \right)={{x}^{2}}2x3 $ 

$ {{x}^{2}}-x+2x-2={{x}^{2}}-2x-3 $ 

$ 3x+1=0,\text{ with degree is 1}\text{. } $ 

The degree of the polynomial is not $ 2 $ therefore, it's not a quadratic equation.

Sample Question 2: Which constant should be added and subtracted to solve the quadratic equation $ 4{{x}^{2}}-\sqrt{3}x-5=0 $ by the method of completing the square?

(A) $ \dfrac{9}{16} $ 

(B) $ \dfrac{3}{16} $ 

(C) $ \dfrac{3}{4} $ 

(D) $ \dfrac{\sqrt{3}}{4} $ 

Ans: Correct option is (b)

Given, Quadratic equation $ 4{{x}^{2}}-\sqrt{3}x-5=0 $ 

To solve the quadratic equation by the method of completing the square, add or subtract the third term.

Third term $ ={{\left( \dfrac{1}{2}\times \text{coefficient}\,\text{of}\,x \right)}^{2}} $ 

$ 4{{x}^{2}}-\sqrt{3}x-5=0 $ 

Dividing by $ 4 $ on both the sides we get

$ {{x}^{2}}-\dfrac{\sqrt{3}}{4}x-\dfrac{5}{4}=0 $ 

$ {{x}^{2}}-\dfrac{\sqrt{3}}{4}x=\dfrac{5}{4} $ 

Third term $ ={{\left( \dfrac{1}{2}\times \text{coefficient}\,\text{of}\,x \right)}^{2}} $ 

$ ={{\left( \dfrac{1}{2}\times \dfrac{\sqrt{3}}{4} \right)}^{2}}=\left( \dfrac{3}{64} \right)=\dfrac{3}{64} $ 

$ {{x}^{2}}-\dfrac{\sqrt{3}}{4}x-\dfrac{5}{4}=\dfrac{3}{64} $ 

$ 4{{x}^{2}}-\sqrt{3}x-5=\dfrac{3}{16} $ 

$ 4{{x}^{2}}-\sqrt{3}x-5-\dfrac{3}{16}=0 $ 

$ 4{{\left( x-\dfrac{\sqrt{3}}{8} \right)}^{2}}-5-\dfrac{3}{16}=0 $ 

Therefore, $ \dfrac{3}{16} $ must be added to make $ 4{{x}^{2}}-\sqrt{3}x-5=0 $ complete square.

EXERCISE 4.1

Choose the correct answer from the given four options in the following questions:

1. Which of the following is a quadratic equation?

(A) $ {{x}^{2}}+2x+1={{\left( 4x \right)}^{2}}+3 $ 

(B) $ -2{{x}^{2}}=\left( 5-x \right)\left( 2x-\dfrac{2}{5} \right) $ 

(C) $ \left( k+1 \right){{x}^{2}}+\dfrac{3}{2}x=7, $ where $ k=- 1 $ 

(D) $ {{x}^{3}}-{{x}^{2}}={{\left( x-1 \right)}^{3}} $ 

Ans: Correct option is (d).

A polynomial equation with degree 2 is called a quadratic equation.

By solving given equation:

$ {x^3} - {x^2} = {\left( {x - 1} \right)^3} $ 

$ \Rightarrow {x^3} - {x^2} = \left( {{x^2} - x + 1} \right)\left( {x - 1} \right) $ 

$ \Rightarrow {x^3} - {x^2} = {x^3} - {x^2} - {x^2} - x + x - 1 $ 

$ \Rightarrow  - {x^2} =  - 2{x^2} - 1 $ 

$ \Rightarrow  - {x^2} + 2{x^2} + 1 = 0 $ 

$ \Rightarrow {x^2} + 1 = 0 $ 

So, the degree of the given polynomial is 2 so it’s a quadratic equation.

2. Which of the following is not a quadratic equation?

(a) $ 2{\left( {x-1} \right)^2} = 4{x^2}-2x + 1 $ 

(b) $ 2x - {x^2} = {x^2} + 5 $ 

(c) $ {\left( {\sqrt 2 x + \sqrt 3 } \right)^2} + {x^2} = 3{x^2} - 5x $ 

(d) $ {\left( {{x^2} + 2x} \right)^2} = {x^4} + 3 + 4{x^3} $ 

Ans: Correct option is (c).

A polynomial equation with degree 2 is called a quadratic equation.

$ {\left( {\sqrt 2 x + \sqrt 3 } \right)^2} + {x^2} = 3{x^2} - 5x $ 

$ \Rightarrow 2{x^2} + 2\sqrt 6 x + 3 + {x^2} = 3{x^2} - 5x $ 

$ \Rightarrow 3{x^2} + 2\sqrt 6 x + 3 = 3{x^2} - 5x $ 

$ \Rightarrow 2\sqrt 6 x + 5x + 3 = 0 $ 

$ \Rightarrow 7\sqrt 6 x + 3 = 0,{\text{   degree 1}} $ 

Hence, there is no term with degree $ 2 $ .

So the equation $ {\left( {\sqrt 2 x + \sqrt 3 } \right)^2} + {x^2} = 3{x^2} - 5x $ is not a quadratic equation.

3. Which of the following equations has 2 as a root?

(a) $ {x^2} - 4x + 5 = 0 $ 

(b) $ {x^2} + 3x - 12 = 0 $ 

(c) $ 2{x^2} - 7x + 6 = 0 $ 

(d) $ 3{x^2} - 6x - 2 = 0 $ 

Ans: Correct Option is (c).

By solving with the factorisation method.

$ 2{x^2} - 7x + 6 = 0 $ 

$ \Rightarrow 2{x^2} - 3x - 4x + 6 = 0 $ 

$ \Rightarrow x\left( {2x - 3} \right) - 2\left( {2x - 3} \right) = 0 $ 

$ \Rightarrow \left( {x - 2} \right)\left( {2x - 3} \right) = 0 $ 

$ \Rightarrow x = 2,\dfrac{3}{2} $ 

Therefore, the given equation has $ 2 $ as a root.

4. If $ \dfrac{1}{2} $ is a root of the equation $ {x^2} + kx--\dfrac{5}{4} = 0 $ , then the value of $ k $ is

(a) 2

(b) -2

(c) 14

(d) 12

Ans: Correct option is (a).

$ x = \dfrac{1}{2} $ is a root of the equation so,

$ \Rightarrow x = \dfrac{1}{2} $ is satisfying the given quadratic equation.

Put $ x = \dfrac{1}{2} $ in the equation we get,

$ {x^2} + kx-\dfrac{5}{4} = 0 $ 

$ \Rightarrow {\left( {\dfrac{1}{2}} \right)^2} + k\left( {\dfrac{1}{2}} \right) - \dfrac{5}{4} = 0 $ 

$ \Rightarrow \dfrac{1}{4} + \dfrac{k}{2} - \dfrac{5}{4} = 0 $ 

$ \Rightarrow 1 + 2k - 5 = 0 $ 

$ \Rightarrow 2k = 5 - 1 $ 

$ \Rightarrow k = \dfrac{4}{2} = 2 $ 

Hence the value of $ k $ is $ 2 $.

5. Which of the following equations has the sum of its roots as $ 3 $ ?

(a) $ 2{x^2}-3x + 6 = 0 $ 

(b) $ -{x^2} + 3x-3 = 0 $ 

(c) $ \sqrt 2 {x^2} - \dfrac{3}{{\sqrt 2 }}x + 1 = 0 $ 

(d) $ 3{x^2}-3x + 3 = 0 $ 

Ans: Correct option is (b).

For the quadratic equation $ a{x^2} + bx + c = 0 $ , the sum of the roots $ = \dfrac{{ - b}}{a} $ and product of root $ = \dfrac{c}{a} $ .

Where, $ a = $ coefficient of $ {x^2} $ 

$ b= $ coefficient of $ x $ 

$ c = $ constant

Here $ a =  - 1,b = 3 $ 

Sum of the roots $ = \dfrac{{ - 3}}{{ - 1}} = 3 $ , product of the roots $ = \dfrac{3}{{ - 1}} =  - 3 $ 

Hence, the quadratic equation is  

$ -{x^2} + 3x-3 = 0 $ has sum of the roots $ = 3 $ 

6. Values of $ k $ for which the quadratic equation $ 2{x^2}-kx + k = 0 $ has equal roots is

(a)0 only 

(b) 4

(c) 8 only 

(d) 0, 8

Ans: Correct option is (d).

A quadratic equation has equal roots if $ D = 0 $ 

The given equation $ 2{x^2}-kx + k = 0 $ , 

On comparing with $ a{x^2} + bx + c = 0 $ , 

we get: $ a = 2,b =  - k,c = k $ 

$ D = 0 $ 

$ {b^2} - 4ac = 0 $ 

$ {\left( { - k} \right)^2} - 4\left( 2 \right)\left( k \right) = 0 $ 

$ \Rightarrow {k^2} - 8k = 0 $ 

$ \Rightarrow k\left( {k - 8} \right) = 0 $ 

$ \Rightarrow k = 0,8 $ 

Hence, $ 0,8 $ are the values of $ k $ for which the quadratic equation $ 2{x^2}-kx + k = 0 $ has equal roots.

7. Which constant must be added and subtracted to solve the quadratic equation $ 9{x^2} + \dfrac{3}{4}x-\sqrt 2  = 0 $ by the method of completing the square?

(a) $ \dfrac{1}{8} $ 

(b) $ \dfrac{1}{{64}} $ 

(c) $ \dfrac{1}{4} $ 

(d) $ \dfrac{9}{{64}} $ 

Ans: Correct option is (b).

Given equation is $ 9{x^2} + \dfrac{3}{4}x-\sqrt 2  = 0 $ 

$ 9{x^2} + \dfrac{3}{4}x-\sqrt 2  = 0 $ 

Can also be written as

$ {\left( {3x} \right)^2} + \dfrac{1}{4}\left( {3x} \right) - \sqrt 2  = 0 $ 

Let’s take $ 3x = t $ 

$ {t^2} + \dfrac{1}{4}t - \sqrt 2  = 0 $ 

${\text{Third}}\,{\text{term}}={\left({\dfrac{1}{2}\times {\text{coefficient}}\,{\text{of}}\,x} \right)^2} $ 

$ = {\left( {\dfrac{1}{2} \times \dfrac{1}{4}} \right)^2} = \dfrac{1}{{64}} $ 

$ {t^2} + \dfrac{1}{4}t + \dfrac{1}{{64}} = \sqrt 2  + \dfrac{1}{{64}} $ 

$ \Rightarrow {\left( {t + \dfrac{1}{8}} \right)^2} = \dfrac{{64\sqrt 2  + 1}}{{64}} $ 

Thus, $ \dfrac{1}{{64}} $ must be subtracted or added to make the equation a complete square.

8. The quadratic equation $ 2{x^2} - \sqrt 5 x + 1 = 0 $ has

(a) two distinct real roots

(b) two equal real roots

(c) no real roots 

(d) more than 2 real roots

Ans: Correct option is (c)

The quadratic equation is $ 2{x^2} - \sqrt 5 x + 1 = 0 $ 

On comparing with $ a{x^2} + bx + c = 0 $ , we get

Here, $ a = 2,b =  - \sqrt {5,} c = 1 $ 

$ \Rightarrow {b^2} - 4ac = 0 $ 

$ \Rightarrow {\left( { - \sqrt 5 } \right)^2} - \left( 4 \right)\left( 2 \right)\left( 1 \right) = 0 $ 

$ \Rightarrow 5 - 8 = 0 $ 

$ \Rightarrow  - 3 < 0 $ 

Therefore, equation has no real roots

9. Which of the following equations has two distinct real roots?

(a) $ 2{x^2} - 3\sqrt 2 x + \dfrac{9}{4} = 0 $ 

(b) $ {x^2} + x-5 = 0 $ 

(c) $ {x^2} + 3x + 2\sqrt 2  = 0 $ 

(d) $ 5{x^2}-3x + 1 = 0 $ 

Ans: Correct option is (b).

The quadratic equation is $ {x^2} + x-5 = 0 $ .

On comparing with $ a{x^2} + bx + c = 0 $ , 

we get:

$ a = 1,b = 1,c =  - 5 $ 

Consider, 

$ D = {b^2} - 4ac $ 

$ = {\left( 1 \right)^2} - 4\left( 1 \right)\left( { - 5} \right) $ 

$ = 1 - \left( { - 20} \right) $ 

$ = 1 + 20 $ 

$ = 21 $ 

$ D > 0 $ ,i.e., $ 21 > 0 $ 

Therefore, the equation has two distinct real roots.

10. Which of the following equations has no real roots?

(a) $ {x^2}-4x + 3\sqrt 2  = 0 $ 

(b) $ {x^2} + 4x - 3\sqrt 2  = 0 $ 

(c) $ {x^2}-4x - 3\sqrt 2  = 0 $ 

(d) $ 3{x^2} + 4\sqrt 3 x + 4 = 0 $ 

Ans: Correct option is (a).

The given equation is $ {x^2}-4x + 3\sqrt 2  = 0 $ .

On comparing with $ a{x^2} + bx + c = 0 $ , 

we get:

$ a = 1,b =  - 4,c = 3\sqrt 2 $ 

Consider

$ D = {b^2} - 4ac $ 

$ \Rightarrow {\left( { - 4} \right)^2} - 4\left( 1 \right)\left( {3\sqrt 2 } \right) $ 

$ \Rightarrow 16 - 12\sqrt 2 $ 

$ \Rightarrow 16 - 12\left( {1.41} \right) $ 

$ \Rightarrow 16 - 16.92 =  - 0.92 $ 

$ \Rightarrow  - 0.92 < 0 $ 

Hence, the equation $ {x^2}-4x + 3\sqrt 2  = 0 $ has no real roots.

11. $ {\left( {{x^2} + 1} \right)^2}-{x^2} = 0 $ has

(a) four real roots 

(b) two real roots

(c)no real roots

(d) one real root.

Ans: Correct option is (c).

Given equation is $ {\left( {{x^2} + 1} \right)^2}-{x^2} = 0 $ 

On simplifying;

$ {\left( {{x^2} + 1} \right)^2}-{x^2} = 0 $ 

$ \Rightarrow {x^4} + 2{x^2} + 1 - {x^2} = 0 $ 

$ \Rightarrow {x^4} + {x^2} + 1 = 0...............(i) $ 

Put $ {x^2} = t $ 

Equation (i) becomes

$ {t^2} + t + 1 = 0 $ 

On comparing with $ a{x^2} + bx + c = 0 $ , 

we get:

$ a = 1,b = 1,c = 1 $ 

Consider, $ {b^2} - 4ac $ 

$ \Rightarrow {\left( 1 \right)^2} - 4\left( 1 \right)\left( 1 \right) $ 

$ \Rightarrow  - 3 < 0 $ 

$ \Rightarrow D < 0 $ 

Hence, the equation $ {\left( {{x^2} + 1} \right)^2}-{x^2} = 0 $ has no real roots.

EXERCISE 4.2

1. State whether the following quadratic equations have two distinct real roots.

Justify your answer.

(i) $ {x^2}-3x + 4 = 0 $ 

Ans: On comparing it with standard quadratic equation $ a{x^2} + bx + c = 0 $ 

Here, $ a = 1,b =  - 3,c = 4 $ 

We know

$ D = {b^2} - 4ac $ 

Putting up the values,

$ D = {\left( { - 3} \right)^2} - 4\left( 1 \right)\left( 4 \right) $ 

$ \Rightarrow D = 9 - 16 $ 

$ \Rightarrow D =  - 7 $ 

$ \Rightarrow D < 0 $ 

Therefore, equation $ {x^2}-3x + 4 = 0 $ has no real roots because $ D < 0 $ .

(ii) $ 2{x^2} + x-1 = 0 $ 

Ans: On comparing it with standard quadratic equation $ a{x^2} + bx + c = 0 $ 

Here, $ a = 2,b = 1,c =  - 1 $ 

We know

$ D = {b^2} - 4ac $ 

Putting up the values,

$ D = {b^2} - 4ac $ 

$ \Rightarrow D = {\left( 1 \right)^2} - 4\left( 2 \right)\left( { - 1} \right) $ 

$ \Rightarrow D = 1 - 4\left( { - 2} \right) $ 

$ \Rightarrow D = 1 + 8 $ 

$ \Rightarrow D = 9 $ 

$ \Rightarrow D > 0 $ 

Therefore, the equation $ 2{x^2} + x-1 = 0 $ has two real distinct roots because $ D > 0 $.

(iii) $ 2{x^2}-6x + \dfrac{9}{2} = 0 $ 

Ans: On comparing it with standard quadratic equation $ a{x^2} + bx + c = 0 $ 

$ a = 2,b = 6,c = \dfrac{9}{2} $ 

We know

$ D = {b^2} - 4ac $ 

Putting up the values,

$ D = {\left( { - 6} \right)^2} - 4\left( 2 \right)\left( {\dfrac{9}{2}} \right) $ 

$ \Rightarrow D = 36 - 36 $ 

$ \Rightarrow D = 0 $ 

Therefore, the equation $ 2{x^2}-6x + \dfrac{9}{2} = 0 $ has no real distinct roots. 

(iv) $ 3{x^2}-4x + 1 = 0 $ 

Ans: On comparing it with standard quadratic equation $ a{x^2} + bx + c = 0 $ 

Here, $ a = 3,b =  - 4,c = 1 $ 

We know

$ D = {b^2} - 4ac $ 

Putting up the values,

$ D = {b^2} - 4ac $ 

$ \Rightarrow D = {\left( { - 4} \right)^2} - 4\left( 3 \right)\left( 1 \right) $ 

$ \Rightarrow D = 16 - 12 $ 

$ \Rightarrow D = 4 $ 

$ \Rightarrow D > 0 $ 

Therefore, equation $ 3{x^2}-4x + 1 = 0 $ has two real distinct roots because $ D > 0 $ . 

(v) $ {\left( {x + 4} \right)^2}-8x = 0 $ 

Ans: On simplification, we get:

$ {\left( {x + 4} \right)^2}-8x = 0 $ 

$ \Rightarrow {x^2} + 8x + 16 - 8x = 0 $ 

$ \Rightarrow {x^2} + 16 = 0 $ 

On comparing it with standard quadratic equation $ a{x^2} + bx + c = 0 $ , we get:

$ a = 1,b = 0,c = 16 $ 

We know

$ D = {b^2} - 4ac $ 

Putting up the values,

$ D = 0 - 4\left( 1 \right)\left( {16} \right) $ 

$ \Rightarrow D =  - 64 $ 

$ \Rightarrow D < 0 $ 

Therefore, the equation \[{\left( {x + 4} \right)^2}--8x = 0\]has no real roots because $ D < 0 $ .

(vi) $ {\left( {x-\sqrt 2 } \right)^2}-2\left( {x + 1} \right) = 0 $ 

Ans: On simplification, we get:

$ {\left( {x-\sqrt 2 } \right)^2}-2\left( {x + 1} \right) = 0 $ 

$ \Rightarrow {\left( {x - \sqrt 2 } \right)^2} = 2\left( {x + 1} \right) $ 

$ \Rightarrow {x^2} - 2\sqrt 2 x + 2 = 2x + 2 $ 

$ \Rightarrow {x^2} - 2\sqrt 2 x = 2x $ 

$ \Rightarrow x\left( {x - 2\sqrt 2 } \right) = 2x $ 

$ \Rightarrow x - 2\sqrt 2  = 2 $ 

$ \Rightarrow x - 2\sqrt 2  - 2 = 0 $ 

$ \Rightarrow x - 2\left( {\sqrt 2  + 1} \right) = 0 $ 

On comparing it with standard quadratic equation $ a{x^2} + bx + c = 0 $ 

Here, $ a = 0,b = 1,c =  - 2\left( {\sqrt 2  + 1} \right) $ 

We know

$ D = {b^2} - 4ac $ 

Putting up the values,

$ D = {\left( 1 \right)^2} - 4\left( 0 \right)\left( { - 2\left( {\sqrt 2  + 1} \right)} \right) $ 

$ \Rightarrow D = 1 - 0 $ 

$ \Rightarrow D = 1 $ 

$ \Rightarrow D > 0 $ 

Therefore, equation $ {\left( {x-\sqrt 2 } \right)^2}-2\left( {x + 1} \right) = 0 $ has two real distinct roots because $ D > 0 $ .

(vii) $ \sqrt 2 {x^2} - \dfrac{3}{{\sqrt 2 }}x + \dfrac{1}{{\sqrt 2 }} = 0 $ 

Ans: On simplification, we get:

$ 2{x^2} - 3x + 1 = 0 $ 

On comparing it with standard quadratic equation $ a{x^2} + bx + c = 0 $ 

$ a = 2,b =  - 3,c = 1 $ 

We know

$ D = {b^2} - 4ac $ 

Putting up the values,

$ D = {\left( { - 3} \right)^2} - 4\left( 2 \right)\left( 1 \right) $ 

$ \Rightarrow D = 9 - 8 $ 

$ \Rightarrow D = 1 $ 

$ \Rightarrow D > 1 $ 

Therefore, the equation $ \sqrt 2 {x^2} - \dfrac{3}{{\sqrt 2 }}x + \dfrac{1}{{\sqrt 2 }} = 0 $ has two real distinct roots because $ D > 0 $ .

(viii) $ x\left( {1-x} \right)-2 = 0 $ 

Ans: On simplification,

$ x\left( {1-x} \right)-2 = 0 $ 

$ \Rightarrow x - {x^2} - 2 = 0 $ 

$ \Rightarrow {x^2} - x + 2 = 0 $ 

On comparing it with standard quadratic equation $ a{x^2} + bx + c = 0 $ 

$ a = 1,b =  - 1,c = 2 $ 

We know

$ D = {b^2} - 4ac $ 

Putting up the values,

$ D = {\left( 1 \right)^2} - 4\left( 1 \right)\left( 2 \right) $ 

$ \Rightarrow D = 1 - 8 $ 

$ \Rightarrow D =  - 7 $ 

$ \Rightarrow D < 0 $ 

Therefore, the equation $ x\left( {1-x} \right)-2 = 0 $ has no real roots because $ D < 0 $ .

(ix) $ \left( {x - 1} \right)\left( {x + 2} \right) + 2 = 0 $ 

Ans: On simplification, 

$ \left( {x - 1} \right)\left( {x + 2} \right) + 2 = 0 $ 

$ \Rightarrow {x^2} + 2x - x - 2 + 2 = 0 $ 

$ \Rightarrow {x^2} + x = 0 $ 

On comparing it with standard quadratic equation $ a{x^2} + bx + c = 0 $ 

$ a = 1,b = 1,c = 0 $ 

We know

$ D = {b^2} - 4ac $ 

Putting up the values,

$ D = {\left( 1 \right)^2} - 4\left( 1 \right)\left( 0 \right) $ 

$ \Rightarrow D = 1 - 0 $ 

$ \Rightarrow D = 1 $ 

$ \Rightarrow D > 0 $ 

Therefore, equation $ x\left( {1-x} \right)-2 = 0 $ has two real distinct roots because $ D > 0 $ .

(x) $ \left( {x + 1} \right)\left( {x - 2} \right) + x = 0 $ 

Ans: On simplification,

$ \left( {x + 1} \right)\left( {x - 2} \right) + x = 0 $ 

$ \Rightarrow {x^2} - 2x + x - 2 + x = 0 $ 

$ \Rightarrow {x^2} - 2 = 0 $ 

For the equation to have real and distinct roots discriminant $ D > 0 $ .

On comparing it with standard quadratic equation $ a{x^2} + bx + c = 0 $ 

$ a = 1,b = 0,c =  - 2 $ 

We know

$ D = {b^2} - 4ac $ 

Putting up the values,

$ D = 0 - 4\left( 1 \right)\left( { - 2} \right) $ 

$ \Rightarrow D =  + 8 $ 

$ \Rightarrow D = 8 $ 

$ \Rightarrow D > 0 $ 

Therefore, equation $ \left( {x + 1} \right)\left( {x - 2} \right) + x = 0 $ has two real distinct roots because $ D > 0 $ .

Question 2: Write whether the following statements are true or false. Justify your answers.

(i) Every quadratic equation has exactly one root.

Ans: Consider, $ {x^2} - 1 = 0 $ is a simplest quadratic equation then its roots are $ x =  \pm 1 $ . Hence every quadratic equation has two roots.

Hence, the statement “Every quadratic equation has exactly one root.” is false.

(ii) Every quadratic equation has at least one real root.

Ans: The statement is “Every quadratic equation has at least one real root.”

Consider, $ {x^2} + 4x + 4 = 0 $ is a quadratic equation then

$ {x^2} + 4x + 4 = 0 $ 

$ \Rightarrow {x^2} + 2x + 2x + 4 = 0 $ 

$ \Rightarrow x\left( {x + 2} \right) + 2\left( {x + 2} \right) = 0 $ 

$ \Rightarrow \left( {x + 2} \right)\left( {x + 2} \right) = 0 $ 

$ \Rightarrow x =  - 2, - 2 $ 

$ x =  - 2, - 2 $ are the roots of the equation. Therefore, no real roots.

Hence, the statement “Every quadratic equation has at least one real root.” is false.

(iii) Every quadratic equation has at least two roots.

Ans: The statement “Every quadratic equation has at least two roots.”

Consider, $ {x^2} + 1 = 0 $ 

$ {x^2} + 1 = 0 $ 

$ \Rightarrow {x^2} =  - 1 $ 

$ \Rightarrow x =  \pm \sqrt { - 1} $ 

Here, the quadratic equation $ {x^2} + 1 = 0 $ has two roots.

Hence, the statement “Every quadratic equation has at least two roots.” is false.

(iv) Every quadratic equation has at most two roots.

Ans: We know that,

The degree of quadratic equation is two.

And the number of roots of any polynomial depends on the degree of that polynomial.

Hence, the statement “Every quadratic equation has at most two roots.” is true.

(v) If the coefficient of $ {x^2} $ and the constant term of a quadratic equation have

opposite signs, then the quadratic equation has real roots.

Ans: If $ a{x^2} + bx + c = 0 $ is a quadratic equation,

And given that $ a\,{\text{and }}c $ have opposite signs. 

Consider, 

$ D = {b^2} - 4\left( a \right)\left( { - c} \right) $ 

$ \Rightarrow D = {b^2} + 4ac $ 

$ \Rightarrow D > 0 $ 

We know that, if $ D > 0 $ then the equation has two distinct real roots.

Hence, the statement “If the coefficient of $ {x^2} $ and the constant term of a quadratic equation have opposite signs, then the quadratic equation has real roots.” is true. 

(vi) If the coefficient of $ {x^2} $ and the constant term have the same sign and if the coefficient of $ x $ term is zero, then the quadratic equation has no real roots.

Ans: If $ a{x^2} + bx + c = 0 $ is a quadratic equation,

And given that if $ a\,{\text{and }}c $ have the same sign and b = 0.

Consider, 

$ D = {b^2} - 4\left( a \right)\left( c \right) $ 

$ \Rightarrow D = 0 - 4ac $ 

$ \Rightarrow D =  - 4ac $ 

$ \Rightarrow D < 0 $ 

We know that, if $ D < 0 $ then the equation has no real roots.

Hence, the statement “If the coefficient of $ {x^2} $ and the constant term have the same sign and if the coefficient of $ x $ term is zero, then the quadratic equation has no real roots.” is true. 

3. A quadratic equation with an integral coefficient has integral roots. Justify your answer.

Ans: The statement “A quadratic equation with integral coefficient has integral roots.”

Consider a quadratic equation with integral coefficient $ 8{x^2}-2x-1 = 0 $ .

$ 8{x^2} - 2x-1 = 0 $ 

$ 8x2-{\text{ }}2x{\text{ }}-{\text{ }}1{\text{ }} = {\text{ }}0 $ 

$ \Rightarrow 8{x^2} - 4x + 2x - 1 = 0 $ 

$ \Rightarrow 4x\left( {2x - 1} \right) + 1\left( {2x - 1} \right) = 0 $ 

$ \Rightarrow \left( {4x + 1} \right)\left( {2x - 1} \right) = 0 $ 

$ \Rightarrow x = \dfrac{{ - 1}}{4},\dfrac{1}{2} $ 

Hence, the roots of the equation are $ \dfrac{{ - 1}}{4}{\text{and}}\dfrac{1}{2} $ which are not integers.

Hence, a quadratic equation with integral coefficient may or may not have integral roots.

4. Does there exist a quadratic equation whose coefficients are rational but both of

its roots are irrational? Justify your answer.

Ans: Consider, a quadratic equation whose coefficients are rational $ {x^2} + 5x + 1 = 0 $ 

$ {\text{By quadratic formula:}} $ 

$ x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}} $ 

$ x = \dfrac{{ - \,5 \pm \sqrt {{{\left( 5 \right)}^2} - 4\left( 1 \right)\left( 1 \right)} }}{{2\left( 1 \right)}} $ 

$ \Rightarrow x = \dfrac{{ - \,5 \pm \sqrt {25 - 4} }}{2} $ 

$ \Rightarrow x = \dfrac{{ - 5 \pm \sqrt {21} }}{2} $ 

$ \Rightarrow x = \dfrac{{ - 5 + \sqrt {21} }}{2},\dfrac{{ - 5 - \sqrt {21} }}{2} $ 

The roots of the equation are irrational. So, a quadratic equation with rational coefficients may have irrational roots.

The statement “Does there exist a quadratic equation whose coefficients are rational 

but both of its roots are irrational.” is true.

5. Does there exist a quadratic equation whose coefficients are all distinct irrationals but both the roots are rational? Why?

Ans: Consider, quadratic equation whose coefficients are all distinct irrationals

$ \sqrt 2 {x^2} - 5\sqrt 2 x + 4\sqrt 2  = 0 $ 

By quadratic formula

$ \sqrt 2 {x^2} - 5\sqrt 2 x + 4\sqrt 2  = 0 $ 

$ x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}} $ 

$ \Rightarrow x = \dfrac{{ - \left( { - 5\sqrt 2 } \right) \pm \sqrt {{{\left( { - 5\sqrt 2 } \right)}^2} - 4\left( {\sqrt 2 } \right)\left( {4\sqrt 2 } \right)} }}{{2\sqrt 2 }} $ 

$ \Rightarrow x = \dfrac{{5\sqrt 2  \pm \sqrt {50 - \left( {4 \times 2 \times 4} \right)} }}{{2\sqrt 2 }} $ 

$ \Rightarrow x = \dfrac{{5\sqrt 2  \pm \sqrt {50 - 32} }}{{2\sqrt 2 }} $ 

$ \Rightarrow x = \dfrac{{5\sqrt 2  \pm \sqrt {18} }}{{2\sqrt 2 }} $ 

$ \Rightarrow x = \dfrac{{5\sqrt 2  \pm 3\sqrt 2 }}{{2\sqrt 2 }} $ 

$ \Rightarrow x = \dfrac{{\sqrt 2 \left( {5 \pm 3} \right)}}{{2\sqrt 2 }} = \dfrac{{5 \pm 3}}{2} $ 

$ \Rightarrow x = \dfrac{{5 + 3}}{2},\dfrac{{5 - 3}}{2} $ 

$ \Rightarrow x = \dfrac{8}{2} = 4,1 $ 

The roots of the given equation are $ 4 $ and $ 1 $ which are rational.

The statement “Does there exist a quadratic equation whose coefficients are all distinct irrationals but both the roots are rational?” is true.

6. Is 0.2 a root of the equation $ {x^2-0.4 = 0} $ ? Justify.

Ans: Given, $ 0.2 $ is a root of the equation $ {x^2}-0.4 = 0 $ .

$ \Rightarrow 0.2 $  is satisfying the quadratic equation $ {x^2}-0.4 = 0 $ .

$ x $ = 0.2 in the equation $ {x^2}-0.4 = 0 $ 

$ {\text{LHS}} = {x^2} - 0.4 $ 

$ {\text{= }}{\left( {0.2} \right)^2} - 0.4 $ 

$ {\text{= }}0.04 - 0.4 $ 

$ {\text{}} \ne {\text{ 0}} $ 

$ {\text{ }} \ne {\text{ RHS}} $ 

Therefore, $ 0.2 $ cannot be a root of the equation.

The statement “Is $ 0.2 $ a root of the equation $ {x^2}-0.4 = 0 $ ?” is false.

7. If $ b = 0,c < 0 $ , is it true that the roots of $ {x^2} + bx + c = 0 $ are numerically equal and opposite in sign? Justify.

Ans: Given a quadratic equation $ {x^2} + bx + c = 0 $ with $ b = 0,c < 0 $ .

Consider, 

$ D = {b^2} - 4(1)( - c) $ 

$ \Rightarrow D{\text{  =  0 }} + 4c $ 

$ \Rightarrow {\text{D  =  4c}} $ 

$ \Rightarrow {\text{D  >  0}} $ 

Hence, roots will be equal and opposite in sign.

The statement “If $ b = 0,c < 0 $ , is it true that the roots of $ {x^2} + bx + c = 0 $ are numerically equal and opposite in sign?” is true.

EXERCISE 4.3

Question 1: Find the roots of the quadratic equations by using the quadratic formula in each of the following:

(i) $ 2{x^2} - 3x - 5 = 0 $ 

Ans: The quadratic equation is $ 2{x^2} - 3x - 5 = 0 $ .

On comparing with $ a{x^2} + bx + c = 0 $ , we get:

$ a = 2,b =  - 3,c =  - 5 $ 

We know by quadratic formula,

 $ x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}} $ 

Putting up the values in formula, we have:

$ x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}} $ 

$ x = \dfrac{{ - \left( { - 3} \right) \pm \sqrt {{{\left( { - 3} \right)}^2} - 4\left( 2 \right)\left( { - 5} \right)} }}{{2\left( 2 \right)}} $ 

$ \Rightarrow x = \dfrac{{3 \pm \sqrt {9 - 4\left( { - 10} \right)} }}{4} $ 

$ \Rightarrow x = \dfrac{{3 \pm \sqrt {9 + 40} }}{4} $ 

$ \Rightarrow x = \dfrac{{3 \pm \sqrt {49} }}{4} $ 

$ \Rightarrow x = \dfrac{{3 \pm 7}}{4} $ 

$ \Rightarrow x = \dfrac{{3 + 7}}{4},\dfrac{{3 - 7}}{4} $ 

$ \Rightarrow x = \dfrac{{10}}{4},\dfrac{{ - 4}}{4} $ 

$ \Rightarrow x = \dfrac{5}{2}, - 1 $ 

Therefore, the roots of the equation $ 2{x^2} - 3x - 5 = 0 $ are $ \dfrac{5}{2} $ and $ - 1 $.

(ii) $ 5{x^2} + 13x + 8 = 0 $ 

Ans: The quadratic equation is $ 5{x^2} + 13x + 8 = 0 $ .

On comparing with $ a{x^2} + bx + c = 0 $ , we get:

$ a = 5,b = 13,c = 8 $ 

We know by quadratic formula,

$ x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}} $ 

Putting up the values in formula, we have:

$ x = \dfrac{{ - 13 \pm \sqrt {{{\left( {13} \right)}^2} - 4\left( 5 \right)\left( 8 \right)} }}{{2\left( 5 \right)}} $ 

$ \Rightarrow x = \dfrac{{ - 13 \pm \sqrt {169 - 4\left( {40} \right)} }}{{10}} $ 

$ \Rightarrow x = \dfrac{{ - 13 \pm \sqrt {169 - 160} }}{{10}} $ 

$ \Rightarrow x = \dfrac{{ - 13 \pm \sqrt 9 }}{{10}} $ 

$ \Rightarrow x = \dfrac{{ - 13 \pm 3}}{{10}} $ 

$ \Rightarrow x = \dfrac{{ - 13 + 3}}{{10}},\dfrac{{ - 13 - 3}}{{10}} $ 

$ \Rightarrow x = \dfrac{{ - 10}}{{10}},\dfrac{{ - 16}}{{10}} $ 

$ \Rightarrow x =  - 1,\dfrac{{ - 8}}{5} $ 

Therefore, the roots of the equation $ 5{x^2} + 13x + 8 = 0 $ are $ - 1 $ and $ \dfrac{{ - 8}}{5} $ .

(iii) $ -3{x^2} + 5x + 12 = 0 $ 

Ans: The quadratic equation is $ -3{x^2} + 5x + 12 = 0 $ .

On comparing with $ a{x^2} + bx + c = 0 $ , we get:

$ a =  - 3,b = 5,c = 12 $ 

We know by quadratic formula:

$ x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}} $ 

Putting up the values in formula, we have:

$ x = \dfrac{{ - \left( { - 3} \right) \pm \sqrt {{{\left( 5 \right)}^2} - 4\left( { - 3} \right)\left( {12} \right)} }}{{2\left( { - 3} \right)}} $ 

$ \Rightarrow x = \dfrac{{3 \pm \sqrt {25 - 4\left( { - 36} \right)} }}{{ - 6}} $ 

$ \Rightarrow x = \dfrac{{3 \pm \sqrt {25 + 144} }}{{ - 6}} $ 

$ \Rightarrow x = \dfrac{{3 \pm \sqrt {169} }}{{ - 6}} $ 

$ \Rightarrow x = \dfrac{{3 \pm 13}}{{ - 6}} $ 

$ \Rightarrow x = \dfrac{{3 + 13}}{{ - 6}},\dfrac{{3 - 13}}{{ - 6}} $ 

$ \Rightarrow x = \dfrac{{16}}{{ - 6}},\dfrac{{ - 10}}{{ - 6}} $ 

$ \Rightarrow x =  - \dfrac{8}{3},\dfrac{5}{3} $ 

Therefore, the roots of the equation $ -3{x^2} + 5x + 12 = 0 $ are $ - \dfrac{8}{3} $ and $ \dfrac{5}{3} $ .

(iv) $ - {x^2} + 7x - 10 = 0 $ 

Ans: The quadratic equation is $ - {x^2} + 7x - 10 = 0 $ .

On comparing with $ a{x^2} + bx + c = 0 $ , we get:

$ a=  - 1,b = 7,c =  - 10 $ 

We know by quadratic formula:

$ x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}} $ 

Putting up the values in formula, we have:

$ x = \dfrac{{ - \left( 7 \right) \pm \sqrt {{{\left( 7 \right)}^2} - 4\left( { - 1} \right)\left( { - 10} \right)} }}{{2\left( { - 1} \right)}} $ 

$ \Rightarrow x = \dfrac{{ - 7 \pm \sqrt {49 - 4\left( {10} \right)} }}{{ - 2}} $ 

$ \Rightarrow x = \dfrac{{ - 7 \pm \sqrt {49 - 40} }}{{ - 2}} $ 

$ \Rightarrow x = \dfrac{{ - 7 \pm \sqrt 9 }}{{ - 2}} $ 

$ \Rightarrow x = \dfrac{{ - 7 \pm 3}}{{ - 2}} $ 

$ \Rightarrow x = \dfrac{{ - 7 + 3}}{{ - 2}},\dfrac{{ - 7 - 3}}{{ - 2}} $ 

$ \Rightarrow x = \dfrac{{ - 4}}{{ - 2}},\dfrac{{ - 10}}{{ - 2}} $ 

$ \Rightarrow x = \dfrac{4}{2},\dfrac{{10}}{2} $ 

$ \Rightarrow x = 2,5 $ 

Therefore, the roots of the equation are $ 2 $ and $ 5 $ .

(v) $ {x^2} + 2\sqrt 2 x-6 = 0 $ 

Ans: The quadratic equation is $ {x^2} + 2\sqrt 2 x-6 = 0 $ .

On comparing with $ a{x^2} + bx + c = 0 $ , we get:

$ a = 1,b = 2\sqrt 2 ,c =  - 6 $ 

We know by quadratic formula:

$ x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}} $ 

Putting up the values in formula, we have:

$ x = \dfrac{{ - \left( {2\sqrt 2 } \right) \pm \sqrt {{{\left( {2\sqrt 2 } \right)}^2} - 4\left( 1 \right)\left( { - 6} \right)} }}{{2\left( 1 \right)}} $ 

$ \Rightarrow x = \dfrac{{ - \left( {2\sqrt 2 } \right) \pm \sqrt {\left( {4 \times 2} \right) - 4\left( { - 6} \right)} }}{2} $ 

$ \Rightarrow x = \dfrac{{ - 2\sqrt 2  \pm \sqrt {8 + 24} }}{2} $ 

$ \Rightarrow x = \dfrac{{ - 2\sqrt 2  \pm \sqrt {32} }}{2} $ 

$ \Rightarrow x = \dfrac{{ - 2\sqrt 2  \pm 4\sqrt 2 }}{2} $ 

$ \Rightarrow x = \dfrac{{ - 2\sqrt 2  + 4\sqrt 2 }}{2},\dfrac{{ - 2\sqrt 2  - 4\sqrt 2 }}{2} $ 

$ \Rightarrow x = \dfrac{{2\sqrt 2 \left( { - 1 + 4} \right)}}{2},\dfrac{{2\sqrt 2 \left( { - 1 - 4} \right)}}{2} $ 

$ \Rightarrow x = \sqrt 2 \left( 3 \right),\sqrt 2 \left( { - 5} \right) $ 

$ \Rightarrow x = 3\sqrt 2 , - 5\sqrt 2 $ 

Therefore, the roots of the equation $ - {x^2} + 7x - 10 = 0 $ are $ 3\sqrt 2 $ and $ - 5\sqrt 2 $ .

(vi) $ {x^2}-3\sqrt 5 x + 10 = 0 $ 

Ans: The quadratic equation is $ {x^2}-3\sqrt 5 x + 10 = 0 $ .

On comparing with $ a{x^2} + bx + c = 0 $ , we get:

$ a = 1,b = 3\sqrt 5 ,c = 10 $ 

We know by quadratic formula:

$ x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}} $ 

Putting the values in formula

$ x = \dfrac{{ - \left( {3\sqrt 5 } \right) \pm \sqrt {{{\left( { - 3\sqrt 5 } \right)}^2} - 4\left( 1 \right)\left( {10} \right)} }}{{2\left( 1 \right)}} $ 

$ \Rightarrow x = \dfrac{{ - 3\sqrt 5  \pm \sqrt {\left( {9 \times 5} \right) - 4\left( {10} \right)} }}{2} $ 

$ \Rightarrow x = \dfrac{{ - 3\sqrt 5  \pm \sqrt {45 - 40} }}{2} $ 

$ \Rightarrow x = \dfrac{{ - 3\sqrt 5  \pm \sqrt 5 }}{2} $ 

$ \Rightarrow x = \dfrac{{\sqrt 5 \left( { - 3 \pm 1} \right)}}{2} $ 

$ \Rightarrow x = \dfrac{{\sqrt 5 \left( { - 3 + 1} \right)}}{2},\dfrac{{\sqrt 5 \left( { - 3 - 1} \right)}}{2} $ 

$ \Rightarrow x = \dfrac{{ - 2\sqrt 5 }}{2},\dfrac{{ - 4\sqrt 5 }}{2} $ 

$ \Rightarrow x =  - \sqrt 5 , - 2\sqrt 5 $ 

Therefore, the roots of the equation $ {x^2}-3\sqrt 5 x + 10 = 0 $ are $ - \sqrt 5 $ and $ - 2\sqrt 5 $ .

(vii) $ \dfrac{1}{2}{x^2}-\sqrt {11} x + 1 = 0 $ 

Ans: The given quadratic equation is $ \dfrac{1}{2}{x^2}-\sqrt {11} x + 1 = 0 $ .

$ \Rightarrow {x^2}-2\sqrt {11} x + 2 = 0 $ 

On comparing with $ a{x^2} + bx + c = 0 $ , we get:

$ a = 1,b =  - 2\sqrt {11} ,c = 2 $ 

We know by quadratic formula:

$ x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}} $ 

Putting the values in formula

$ x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}} $ 

$ \Rightarrow x = \dfrac{{ - \left( { - 2\sqrt {11} } \right) \pm \sqrt {{{\left( { - 2\sqrt {11} } \right)}^2} - 4\left( 1 \right)\left( 2 \right)} }}{{2\left( 1 \right)}} $ 

$ \Rightarrow x = \dfrac{{2\sqrt {11}  \pm \sqrt {\left( {4 \times 11} \right) - 8} }}{2} $ 

$ \Rightarrow x = \dfrac{{2\sqrt {11}  \pm \sqrt {44 - 8} }}{2} $ 

$ \Rightarrow x = \dfrac{{2\sqrt {11}  \pm \sqrt {36} }}{2} $ 

$ \Rightarrow x = \dfrac{{2\sqrt {11}  \pm 6}}{2} $ 

$ \Rightarrow x = \dfrac{{2\left( {\sqrt {11}  \pm 3} \right)}}{2} $ 

$ \Rightarrow x = \left( {\sqrt {11}  + 3} \right),\left( {\sqrt {11}  - 3} \right) $ 

Therefore, the roots of the equation $ \dfrac{1}{2}{x^2}-\sqrt {11} x + 1 = 0 $ are $ \left( {\sqrt {11}  + 3} \right) $ and $ \left( {\sqrt {11}  - 3} \right) $ .

Question 2: Find the roots of the following quadratic equations by the factorisation method:

(i) $ 2{x^2} + \dfrac{5}{3}x-2 = 0 $ 

Ans: The given quadratic equation is $ 2{x^2} + \dfrac{5}{3}x-2 = 0 $ .

Solving by factorisation method:

$ 6{x^2} + 5x - 6 = 0 $ 

$ 6{x^2} + 9x - 4x - 6 = 0 $ 

$ \Rightarrow 3x\left( {2x + 3} \right) - 2\left( {2x + 3} \right) = 0 $ 

$ \Rightarrow \left( {3x - 2} \right)\left( {2x + 3} \right) = 0 $ 

$ \Rightarrow x = \dfrac{2}{3},\dfrac{{ - 3}}{2} $ 

Hence, the roots of the equation $ 2{x^2} + \dfrac{5}{3}x-2{\text{ =  }}0 $ are $ \dfrac{2}{3}\,{\text{and}}\,\dfrac{{ - 3}}{2} $ .

(ii) $ \dfrac{2}{5}{x^2}-x-\dfrac{3}{5} = 0 $ 

Ans: The given quadratic equation is 

$ \dfrac{2}{5}{x^2}-x-\dfrac{3}{5} = 0 $ .

On simplifying the given equation:

$ 2{x^2} - 5x - 3 = 0 $ 

Solving by factorisation method:

$ 2{x^2} - 5x - 3 = 0 $ 

$ 2{x^2} - 6x + x - 3 = 0 $ 

$ \Rightarrow 2x\left( {x - 3} \right) + 1\left( {x - 3} \right) = 0 $ 

$ \Rightarrow \left( {2x + 1} \right)\left( {x - 3} \right) = 0 $ 

$ \Rightarrow x = \dfrac{{ - 1}}{2},3 $ 

Hence, the roots of the equation $ \dfrac{2}{5}{x^2}-x-\dfrac{3}{5} = 0 $ are $ - \dfrac{1}{2}{\text{and}}\,3 $ .

(iii) $ 3\sqrt 2 {x^2}-5x-\sqrt 2  = 0 $ 

Ans: The given quadratic equation is 

$ 3\sqrt 2 {x^2}-5x-\sqrt 2  = 0 $ .

Solving by factorisation method:

$ 3\sqrt 2 {x^2}-5x-\sqrt 2  = 0 $ 

$ 3\sqrt 2 {x^2} - 6x + x - \sqrt 2  = 0 $ 

$ \Rightarrow 3\sqrt 2 x\left( {x - \sqrt 2 } \right) + 1\left( {x - \sqrt 2 } \right) = 0 $ 

$ \Rightarrow \left( {3\sqrt 2 x + 1} \right)\left( {x - \sqrt 2 } \right) = 0 $ 

$ \Rightarrow x =  - \dfrac{1}{{3\sqrt 2 }},\sqrt 2 $ 

Hence, the roots of the equation $ 3\sqrt 2 {x^2}-5x-\sqrt 2  = 0 $ are $ - \dfrac{1}{{3\sqrt 2 }} $ and $ \sqrt 2 $ .

(iv) $ 3{x^2} + 5\sqrt 5 x-10 = 0 $ 

Ans: The given quadratic equation is 

$ 3{x^2} + 5\sqrt 5 x-10 = 0 $ .

Solving by factorisation method:

$ 3{x^2} + 5\sqrt 5 x-10 = 0 $ 

$ 3{x^2} + 6\sqrt 5 x - \sqrt 5 x - 10 = 0 $ 

$ \Rightarrow 3x\left( {x + 2\sqrt 5 } \right) - \sqrt 5 \left( {x + 2\sqrt 5 } \right) = 0 $ 

$ \Rightarrow \left( {3x - \sqrt 5 } \right)\left( {x + 2\sqrt 5 } \right) = 0 $ 

$ \Rightarrow x = \dfrac{{\sqrt 5 }}{3}, - 2\sqrt 5 $ 

Hence, the roots of the equation $ 3{x^2} + 5\sqrt 5 x-10 = 0 $ are $ \dfrac{{\sqrt 5 }}{3} $ and $ - 2\sqrt 5 $ .

(v) $ 21{x^2}-2x + \dfrac{1}{{21}} = 0 $ 

Ans: The given quadratic equation is $ 21{x^2}-2x + \dfrac{1}{{21}} = 0 $ .

On simplifying the given equation:

$ 441{x^2} - 42x + 1 = 0 $ 

The equation is $ 441{x^2} - 42x + 1 = 0 $ 

Using factorisation method

$ 441{x^2} - 42x + 1 = 0 $ 

$ 441{x^2} - 21x - 21x + 1 = 0 $ 

$ \Rightarrow 21x\left( {21x - 1} \right) - 1\left( {21x - 1} \right) = 0 $ 

$ \Rightarrow \left( {21x - 1} \right)\left( {21x - 1} \right) = 0 $ 

$ \Rightarrow x = \dfrac{1}{{21}},\dfrac{1}{{21}} $ 

Hence, the roots of the equation $ 21{x^2}-2x + \dfrac{1}{{21}} = 0 $ are $ \dfrac{1}{{21}} $ and $ \dfrac{1}{{21}} $ .

EXERCISE 4.4

Question 1: Find whether the following equations have real roots. If real roots exist, find them.

(i) $ 8{x^2} + 2x-3 = 0 $ 

Ans: The equation $ 8{x^2} + 2x-3 = 0 $ .

On comparing with $ a{x^2} + bx + c = 0 $ , we get:

$ a = 8,b = 2,c =  - 3 $ 

The quadratic equation $ a{x^2} + bx + c = 0 $ has two distinct real roots if $ D = {b^2} - 4ac > 0 $ .

Consider, 

$ D = {b^2} - 4ac $ 

$ D = {\left( 2 \right)^2} - 4\left( 8 \right)\left( { - 3} \right) $ 

$ \Rightarrow D = 4 - 4\left( { - 24} \right) $ 

$ \Rightarrow D = 4 + 96 $ 

$ \Rightarrow D = 100 $ 

$ \therefore D > 0 $ 

So, the equation has real roots.

Finding the roots by factorisation method;

$ 8{x^2} + 2x-3 = 0 $ 

$ 8{x^2} + 6x - 4x - 3 = 0 $ 

$ \Rightarrow 2x\left( {4x + 3} \right) - 4\left( {4x + 3} \right) = 0 $ 

$ \Rightarrow \left( {2x - 4} \right)\left( {4x + 3} \right) = 0 $ 

$ \Rightarrow \left( {2x - 4} \right) = 0 $ 

$ \Rightarrow \left( {4x + 3} \right) = 0 $ 

$ \Rightarrow x = \dfrac{4}{2} = 2\,{\text{or}}\,x = \dfrac{{ - 3}}{4} $ 

Hence, the roots of the equation $ 8{x^2} + 2x-3 = 0 $ are $ 2{\text{ and }}\dfrac{{ - 3}}{4} $ .

(ii) $ -2{x^2} + 3x + 2 = 0 $ 

Ans: The equation $ -2{x^2} + 3x + 2 = 0 $ .

On comparing with $ a{x^2} + bx + c = 0 $ , we get:

$ a =  - 2,b = 3,c = 2 $ 

The quadratic equation $ a{x^2} + bx + c = 0 $ has two distinct real roots if $ D = {b^2} - 4ac > 0 $ .

Consider, 

$ D = {b^2} - 4ac $ 

$ D = {\left( 3 \right)^2} - 4\left( { - 2} \right)\left( 2 \right) $ 

$ \Rightarrow D = 9 - 4\left( { - 4} \right) $ 

$ \Rightarrow D = 9 + 16 $ 

$ \Rightarrow D = 25 $ 

$ \therefore D > 0 $ 

So, the equation has real roots.

Solving by factorisation method;

$ -2{x^2} + 3x + 2 = 0 $ 

$ - 2{x^2} + 4x - x + 2 = 0 $ 

$ \Rightarrow 2x\left( { - x + 2} \right) + 1\left( { - x + 2} \right) = 0 $ 

$ \Rightarrow \left( {2x + 1} \right)\left( {2 - x} \right) = 0 $ 

$ \Rightarrow x = \dfrac{{ - 1}}{2}{\text{ or }}x = 2 $ 

Hence, the roots of the equation $ -2{x^2} + 3x + 2 = 0 $ are $ \dfrac{{ - 1}}{2}{\text{ and 2}} $ .

(iii) $ 5{x^2}-2x-10 = 0 $ 

Ans: The equation $ 5{x^2}-2x-10 = 0 $ .

On comparing with $ a{x^2} + bx + c = 0 $ , we get:

$ a = 5,b =  - 2,c =  - 10 $ 

The quadratic equation $ a{x^2} + bx + c = 0 $ has two distinct real roots if $ D = {b^2} - 4ac > 0 $ .

Consider, 

$ D = {b^2} - 4ac $ 

$ D = {\left( { - 2} \right)^2} - 4\left( 5 \right)\left( { - 10} \right) $ 

$ \Rightarrow D = 4 - 4\left( { - 50} \right) $ 

$ \Rightarrow D = 4 + 200 $ 

$ \Rightarrow D = 204 $ 

$ \therefore D > 0 $ 

So, the equation has real roots.

Solving by quadratic formula:

$ 5{x^2}-2x-10 = 0 $ 

$ x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}} $ 

$ \Rightarrow x = \dfrac{{ - \left( { - 2} \right) \pm \sqrt {{{\left( { - 2} \right)}^2} - 4\left( 5 \right)\left( { - 10} \right)} }}{{2\left( 5 \right)}} $ 

$ \Rightarrow x = \dfrac{{2 \pm \sqrt {4 - 4\left( { - 50} \right)} }}{{10}} $ 

$ \Rightarrow x = \dfrac{{2 \pm 2\sqrt {51} }}{{10}} $ 

$ \Rightarrow x = \dfrac{{2\left( {1 \pm \sqrt {51} } \right)}}{{10}} $ 

$ \Rightarrow x = \dfrac{{1 \pm \sqrt {51} }}{5} $ 

$ \Rightarrow x = \dfrac{{1 + \sqrt {51} }}{5}\,{\text{or}}\,x{\text{ = }}\dfrac{{1 - \sqrt {51} }}{5} $ 

Hence, the roots of the equation $ 5{x^2}-2x-10 = 0 $ are $ \dfrac{{1 + \sqrt {51} }}{5}{\text{and }}\dfrac{{1 - \sqrt {51} }}{5} $ .

(iv) $ \dfrac{1}{2x-3}\ +\ \dfrac{1}{x-5}=1,\ x\ne \dfrac{3}{2},\ 5 $ 

Ans: The given equation is $ \dfrac{1}{{2x - 3}} + \dfrac{1}{{x - 5}} = 1,x \ne \dfrac{3}{2},5 $ 

On simplifying the given equation, we have

$ \dfrac{1}{{2x - 3}} + \dfrac{1}{{x - 5}} = 1 $ 

$ \Rightarrow \left( {x - 5} \right) + \left( {2x - 3} \right) = \left( {2x - 3} \right)\left( {x - 5} \right) $ 

$ \Rightarrow x - 5 + 2x - 3 = 2{x^2} - 10x - 3x + 15 $ 

$ \Rightarrow 3x - 8 = 2{x^2} - 13x + 15 $ 

$ \Rightarrow 2{x^2} - 16x + 23 = 0 $ 

On comparing with $ a{x^2} + bx + c = 0 $ , we get:

$ a = 2,b =  - 16,c = 23 $ 

The quadratic equation $ a{x^2} + bx + c = 0 $ has two distinct real roots if $ D = {b^2} - 4ac > 0 $ .

Consider, 

$ D = {b^2} - 4ac $ 

$ \Rightarrow D = {\left( { - 16} \right)^2} - 4\left( 2 \right)\left( {23} \right) $ 

$ \Rightarrow D = 256 - 4\left( {46} \right) $ 

$ \Rightarrow D = 256 - 184 $ 

$ \Rightarrow D = 72 $ 

$ \therefore D > 0 $ 

The equation has real roots.

On solving by quadratic formula:

$ 2{x^2} - 16x + 23 = 0 $ 

$ x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}} $ 

$ \Rightarrow x = \dfrac{{ - \left( { - 16} \right) \pm \sqrt {{{\left( { - 16} \right)}^2} - 4\left( 2 \right)\left( {23} \right)} }}{{2\left( 2 \right)}} $ 

$ \Rightarrow x = \dfrac{{16 \pm \sqrt {256 - 4\left( {46} \right)} }}{4} $ 

$ \Rightarrow x = \dfrac{{16 \pm \sqrt {256 - 184} }}{4} $ 

$ \Rightarrow x = \dfrac{{16 \pm \sqrt {72} }}{4} $ 

$ \Rightarrow x = \dfrac{{16 \pm 6\sqrt 2 }}{4} $ 

$ \Rightarrow x = \dfrac{{8 \pm 3\sqrt 2 }}{2} $ 

$ \Rightarrow x = \dfrac{{8 + 3\sqrt 2 }}{2}{\text{ or }}x = \dfrac{{8 - 3\sqrt 2 }}{2} $ 

Hence, the roots of the equation $ \dfrac{1}{{2x - 3}} + \dfrac{1}{{x - 5}} = 1,x \ne \dfrac{3}{2},5 $ are $ \dfrac{{8 + 3\sqrt 2 }}{2}{\text{ and}}\dfrac{{8 - 3\sqrt 2 }}{2} $ .

(v) $ {x^2} + 5\sqrt 5 x-70 = 0 $ 

Ans: The equation $ {x^2} + 5\sqrt 5 x-70 = 0 $ .

On comparing with $ a{x^2} + bx + c = 0 $ , we get: $ a = 1,b = 5\sqrt 5 ,c =  - 70 $ 

The quadratic equation $ a{x^2} + bx + c = 0 $ has two distinct real roots if $ D = {b^2} - 4ac > 0 $ .

Consider, 

$ D = {b^2} - 4ac $ 

$ D = {\left( {5\sqrt 5 } \right)^2} - 4\left( 1 \right)\left( { - 70} \right) $ 

$ \Rightarrow D = \left( {25 \times 5} \right) - 4\left( { - 70} \right) $ 

$ \Rightarrow D = 125 + 280 $ 

$ \Rightarrow D = 405 $ 

$ \therefore D > 0 $ 

Solving by quadratic formula:

$ {x^2} + 5\sqrt 5 x--70 = 0 $ 

$ x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}} $ 

$ \Rightarrow x = \dfrac{{ - 5\sqrt 5  \pm \sqrt {{{\left( {5\sqrt 5 } \right)}^2} - 4\left( 1 \right)\left( { - 70} \right)} }}{{2\left( 1 \right)}} $ 

$ \Rightarrow x = \dfrac{{ - 5\sqrt 5  \pm \sqrt {125 - 4\left( { - 70} \right)} }}{2} $ 

Hence, the roots are $ 2\sqrt {5\,} {\text{and }} - {\text{7}}\sqrt 5 $ .

2. Find a natural number whose square diminished by 84 is equal to thrice of 8 more than the given number.

Ans: Let the natural number $ = x $ 

By the given information, we have:

$ x = \dfrac{{ - 5\sqrt 5  \pm \sqrt {125 + 280} }}{2} $ 

$ \Rightarrow x = \dfrac{{ - 5\sqrt 5  \pm \sqrt {405} }}{2} $ 

$ \Rightarrow x = \dfrac{{ - 5\sqrt 5  \pm 9\sqrt 5 }}{2} $ 

$ \Rightarrow x = \dfrac{{\sqrt 5 \left( { - 5 \pm 9} \right)}}{2} $ 

$ x = \dfrac{{\sqrt 5 \left( { - 5 + 9} \right)}}{2} = \dfrac{{\sqrt 5 \left( 4 \right)}}{2} = 2\sqrt 5 $ 

$ {\text{or}} $ 

$ x = \dfrac{{\sqrt 5 \left( { - 5 - 9} \right)}}{2} = \dfrac{{\sqrt 5 \left( { - 14} \right)}}{2} =  - 7\sqrt 5 $ 

$ \Rightarrow x = 2\sqrt 5 , - 7\sqrt 5 $ 

On further solving

$ \Rightarrow {x^2}-84 = 3\left( {x + 8} \right) $ 

$ \Rightarrow {x^2} - 84 = 3x + 24 $ 

$ \Rightarrow {x^2} - 3x - 84 - 24 = 0 $ 

$ \Rightarrow {x^2} - 3x - 108 = 0 $ 

$ \Rightarrow {x^2} - 12x + 9x - 108 = 0 $ 

$ \Rightarrow x\left( {x - 12} \right) + 9\left( {x - 12} \right) = 0\, $ 

$ \Rightarrow \left( {x + 9} \right)\left( {x - 12} \right) = 0 $ 

$ \Rightarrow x =  - 9\,{\text{or}}\,x = 12 $ 

Since, natural numbers cannot be negative. 

Hence, the required number is 12. 

3. A natural number, when increased by 12, equals 160 times its reciprocal. Find the number. 

Ans: Let the natural number be $ x $ 

By the given information, we have: 

$ x + 12 = 160\left( {\dfrac{1}{x}} \right) $ 

Solving the equation further;

$ x + 12 = 160\left( {\dfrac{1}{x}} \right) $ 

$ \Rightarrow {x^2} + 12x = 160 $ 

$ \Rightarrow {x^2} + 12x - 160 = 0 $ 

$ \Rightarrow x\left( {x + 20} \right) - 8\left( {x + 20} \right) = 0 $ 

$ \Rightarrow \left( {x - 8} \right)\left( {x + 20} \right) = 0 $ 

$ x = 8\,{\text{or}}{\text{ }}x =  - 20 $ 

Natural numbers are not negative.

So, the required natural number is 8. 

4. A train, traveling at a uniform speed for 360 km, would have taken 48 minutes less to travel the same distance if its speed were 5 km/h more. Find the original speed of the train.

Ans: We know that $ {\text{time taken}}{\text{ = }}\dfrac{{{\text{distance}}}}{{{\text{speed}}}} $ 

Let the original speed of the train be $ x\,{\text{km/hr}} $ .

So time taken is

 $ {\text{time taken = }}\dfrac{{360}}{x} $ 

Time taken when speed is increased $ = \dfrac{{360}}{{x + 5}} $ 

By the given information, we have:

$ \dfrac{{360}}{x} - \dfrac{{360}}{{x + 5}} = \dfrac{{48}}{{60}} $ 

$ 360\left[ {\dfrac{1}{x} - \dfrac{1}{{x + 5}}} \right] = \dfrac{4}{5} $ 

$ \Rightarrow \dfrac{{1800}}{{{x^2} + 5x}} = \dfrac{4}{5} $ 

$ \Rightarrow 9000 = 4{x^2} + 20x $ 

$ \Rightarrow 4{x^2} + 20x - 9000 = 0 $ 

$ {x^2} + 5x - 2250 = 0 $ 

$ \Rightarrow {x^2} + 50x - 45x - 2250 = 0 $ 

$ x\left( {x + 50} \right) - 45\left( {x + 50} \right) = 0 $ 

$ \Rightarrow \left( {x - 45} \right)\left( {x + 50} \right) = 0 $ 

$ \Rightarrow x = 45\,{\text{or}}\,x =  - 50 $ 

Speed cannot be negative.

So, the original speed of the train $ = 45\,{\text{km/hr}} $ .

5. If Zeba were younger by 5 years than what she really is, then the square of her age (in years) would have been 11 more than five times her actual age. What is her age now?

Ans: Let the present age of Zeba be $ x $ years.

By the given information, we have:

Age of Zeba before $ 5 $ years $ = \left( {x - 5} \right) $ 

Square of her age is equal to $ 11 $ more $ 5 $ times of her actual age

$ \therefore {\left( {x - 5} \right)^2} = 5x + 11 $ 

Solving the equation further, we get

$ {\left( {x - 5} \right)^2} = 5x + 11 $ 

$ \Rightarrow {x^2} + 25 - 10x = 5x + 11 $ 

$ \Rightarrow {x^2} - 15x + 14 = 0 $ 

$ \Rightarrow {x^2} - 14x - x + 14 = 0 $ 

$ \Rightarrow x\left( {x - 14} \right) - 1\left( {x - 14} \right) = 0 $ 

$ \Rightarrow \left( {x - 1} \right)\left( {x - 14} \right) = 0 $ 

$ \Rightarrow x = 1\,{\text{or}}\,x = 14 $ 

Present age of Zeba cannot be equal to $ 1 $ .

So, the present age of Zeba is equal to $ 14 $ years.

6. At present Asha’s age (in years) is 2 more than the square of her daughterNisha’s age. When Nisha grows to her mother’s present age, Asha’s age would be one year less than 10 times the present age of Nisha. Find the present ages of both Asha and Nisha.

Ans: Let the present age of Nisha is $ x $ 

By the given information, we have:

Asha’s age $ = {x^2} + 2 $ 

When Nisha grows to her mother’s age after $ {x^2} + 2 - x $ years.

After $ {x^2} + 2 - x $ years, Asha’s age $ = {x^2} + 2 + {x^2} + 2 - x $ 

Asha’s age would be one year less than $ 10 $ times the present age of Nisha therefore,

$ {x^2} + 2 + {x^2} + 2 - x = 10x - 1 $ 

$ \Rightarrow 2{x^2} + 4 - x = 10x - 1 $ 

$ \Rightarrow 2{x^2} - 11x + 5 = 0 $ 

$ \Rightarrow 2{x^2} - 10x - x + 5 = 0 $ 

$ \Rightarrow 2x\left( {x - 5} \right) - 1\left( {x - 5} \right) = 0 $ 

$ \Rightarrow \left( {2x - 1} \right)\left( {x - 5} \right) = 0 $ 

$ \Rightarrow x = \dfrac{1}{2}\,{\text{or }}x = 5 $ 

Present age Nisha can’t be $ \dfrac{1}{2} $ years.

So, the present age of Nisha and Asha respectively are $ 5{\text{ and }}{{\text{5}}^2} + 2 = 27 $ .

7. In the center of a rectangular lawn of dimensions $ 50\,m \times 40\,m $ , a rectangular pond has to be constructed so that the area of the grass surrounding the pond would be $ 1184\,{m^2} $ . [see Fig. 4.1]. Find the length and breadth of the pond.

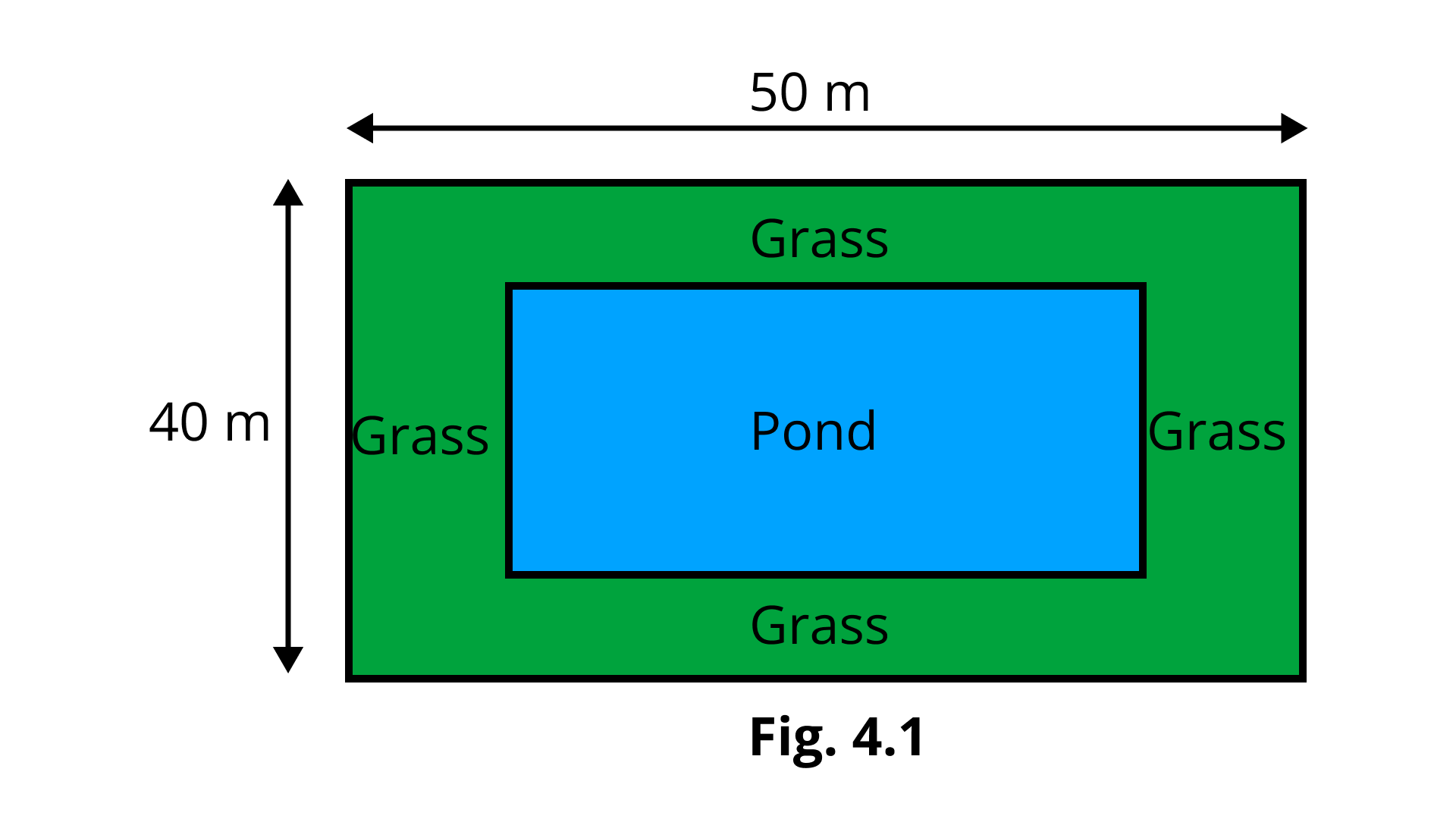
Ans:

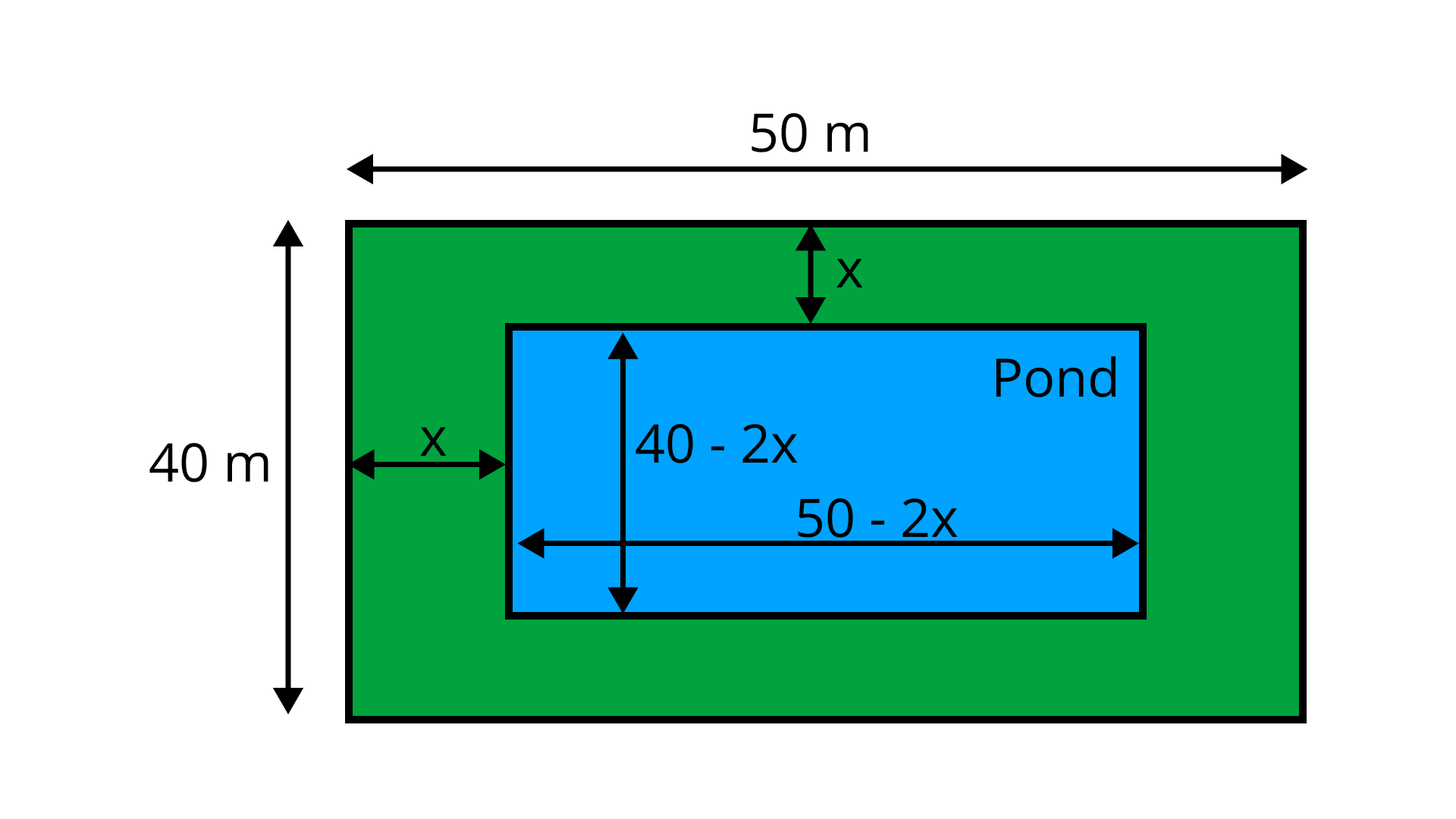
Let $ x\,{\text{m}} $ is the width of the grass area

Width of lawn $ = 40\,{\text{m}} $ 

Length of lawn $ = 50{\text{ m}} $ 

Breadth of pond $ = \left( {40 - 2x} \right){\text{m}} $ 

Length of pond $ = \left( {50 - 2x} \right){\text{m}} $ 

Pond is surrounded by the area of grass $ = 1184{{\text{m}}^2} $ 

Area of rectangular lawn $ - $ Area of pond $ = \,\,1184{{\text{m}}^2} $ 

$ \Rightarrow \left( {50 \times 40} \right) - \left\{ {\left( {50 - 2x} \right) \times \left( {40 - 2x} \right)} \right\} = 1184 $ 

$ \Rightarrow 2000 - \left( {2000 - 80x - 100x + 4{x^2}} \right) = 1184 $ 

$ \Rightarrow 2000 - 2000 + 80x + 100x - 4{x^2} = 1184 $ 

$ \Rightarrow 4{x^2} - 180x + 1184 = 0 $ 

$ \Rightarrow {x^2} - 45x + 296 = 0 $ 

$ \Rightarrow {x^2} - 37x - 8x + 296 = 0 $ 

$ \Rightarrow x\left( {x - 37} \right) - 8\left( {x - 37} \right) = 0 $ 

$ \Rightarrow \left( {x - 8} \right)\left( {x - 37} \right) = 0 $ 

$ \Rightarrow x = 8\,{\text{or}}\,x = 37 $ 

Value of $ x = 37 $ is not possible because then the length of the pond becomes

$ 50 - 2x = 50 - 2\left( {37} \right) =  - 24 $ which is not possible.

So the value of $ x = 8 $ 

Therefore, length of the pond is:

$ \Rightarrow 50 - 2x $ 

$ \Rightarrow 50 - 2\left( 8 \right) $ 

$ \Rightarrow 50 - 16 $ 

$ \Rightarrow 34\,{\text{m}} $ 

And width of the pond is:

$ \Rightarrow 40 - 2x $ 

$ \Rightarrow 40 - 2\left( 8 \right) $ 

$ \Rightarrow 40 - 16 $ 

$ \Rightarrow 24\,{\text{m}} $ 

So, the length and breadth of the pond is 34 m and 24 m.

8. At $ t $ minutes past 2 p. m., the time needed by the minutes hand of a clock to show 3 p. m. was found to be $ 3 $ minutes less than $ \dfrac{{{t^2}}}{4} $ minutes. Find $ t $ .

Ans: We know that $ 1\,{\text{hour}} $ = $ 60 $ minutes

Using the given conditions:

$ \left( {60 - t} \right) = \left( {\dfrac{{{t^2}}}{4} - 3} \right) $ 

$ 4\left( {60 - t} \right) = \left( {{t^2} - 12} \right) $ 

$ 240 - 4t = {t^2} - 12 $ 

$ {t^2} - 4t - 252 = 0 $ 

Using quadratic formula we have,

$ x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}} $ 

$ \therefore t = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}} $ 

$ \Rightarrow t = \dfrac{{ - 4 \pm \sqrt {{{\left( 4 \right)}^2} - 4\left( 1 \right)\left( { - 252} \right)} }}{{2\left( 1 \right)}} $ 

$ \Rightarrow t = \dfrac{{ - 4 \pm \sqrt {16 - \left( { - 1008} \right)} }}{2} $ 

$ \Rightarrow t = \dfrac{{ - 4 \pm \sqrt {16 + 1008} }}{2} $ 

$ \Rightarrow t = \dfrac{{ - 4 \pm \sqrt {1024} }}{2} $ 

$ \Rightarrow t = \dfrac{{ - 4 \pm 32}}{2} $ 

$ \Rightarrow t = \dfrac{{ - 4 + 32}}{2}{\text{ or }}t = \dfrac{{ - 4 - 32}}{2} $ 

$ \Rightarrow t = \dfrac{{28}}{2}{\text{   or }}t = \dfrac{{ - 36}}{2} $ 

$ \Rightarrow t = 14{\text{   or }}t =  - 18 $ 

Because time cannot be negative therefore, $ t = 14\,{\text{mins}} $.

Concepts Included in Class 10 Math - Quadratic Equations

The concepts that are included are:

• Quadratic Polynomial

• Quadratic Equations

• Solving Quadratic Equation by Factorisation

• Solving Quadratic Equation by Completing the Square

• Solving Quadratic Equation by Quadratic Formula

• Nature of Roots

• Graphical Representation of QE

• Sum and Product of Roots of Quadratic Equation

Number of Exercises Under NCERT Exemplar Class 10 Math - Quadratic Equations

• Exercise 4.1 ( 11 Questions)

• Exercise 4.2 (7 Questions)

• Exercise 4.3 (1 Question)

• Exercise 4.4 (8 Questions)

For your exam preparation, Vedantu offers all of the solutions to the problems found in the NCERT Exemplar for Class 10 Math - Quadratic Equations. The questions from each segment are carefully framed and solved by topic specialists. NCERT Exemplar for Class 10 Math - Quadratic Equations is a comprehensive, step-by-step approach to all of the students' questions. If you want to do well on your exams, you should solve the exercises in this chapter with the utmost seriousness. Math is a subject that demands a thorough understanding as well as a great deal of practice. Below are some helpful tips and strategies for solving problems fast and with ease. 

Tips to Remember While Solving Questions from NCERT Exemplar for Class 10 Math:

• Don’t be disheartened if you’re not able to solve the questions. NCERT Exemplar has a curation of comparatively difficult questions from the NCERT textbook. Take your time with each question, try to understand, and make a step to step chart of how you’re going to solve it

• Before starting to address a problem, always take a second look at it - understand the question thoroughly before solving it. A project done in haste may not always yield positive results. So take your time and attempt to comprehend the issue with an open and calm mind.

• Don’t hesitate to ask for help from teachers. As stated above, Exemplar might have some tricky questions, so you can always refer to solved Exemplar problems from Vedantu for some reference.