NCERT Exemplar for Class 11 Maths Chapter 6 - Linear Inequalities (Book Solutions)

Solved Examples

Short Answer Type:

Example 1. Solve the inequality, $3x - 5 < x + 7$, when

(i) $x$ is a natural number

Ans: Given: The inequality $3x - 5 < x + 7$.

First of all solve the given linear inequality for the values of $x$ and then find the possible solution set for each of the subparts of the question.

The provided linear inequality is $3x - 5 < x + 7$, solving it for the values of $x$,

$\Rightarrow 3x - x < 7 + 5$

$\Rightarrow 2x < 12$

$\Rightarrow x < 6$

Now, the natural numbers (also known as the counting numbers) less than $6$ are: - $1$, $2$, $3$, $4$ and $5$. Hence, the solution set is $x \in \left\{ {1,{\text{ }}2,{\text{ }}3,{\text{ }}4,{\text{ }}5} \right\}$.

(ii) $x$ is a whole number

Ans: Given: The inequality $3x - 5 < x + 7$.

First of all solve the given linear inequality for the values of $x$ and then find the possible solution set for each of the subparts of the question.

The provided linear inequality is $3x - 5 < x + 7$, solving it for the values of $x$,

The whole numbers less than $6$ are $0$, $1$, $2$, $3$, $4$ and $5$. Hence, the solution set is $x \in \left\{ {0,{\text{ }}1,{\text{ }}2,{\text{ }}3,{\text{ }}4,{\text{ }}5} \right\}$.

(iii) $x$ is an integer

Ans: Given: The inequality $3x - 5 < x + 7$.

First of all solve the given linear inequality for the values of $x$ and then find the possible solution set for each of the subparts of the question.

The provided linear inequality is $3x - 5 < x + 7$, solving it for the values of $x$,

$\Rightarrow 3x - x < 7 + 5$

$\Rightarrow 2x < 12$

$\Rightarrow x < 6$

The integers less than $6$ will be $0$, $1$, $2$, $3$, $4$, $5$ and all the negative natural numbers. Hence, the solution set will be $x \in \left\{ {... - 4,{\text{ }} - 3,{\text{ }} - 2,{\text{ }} - 1,{\text{ }}0,{\text{ }}1,{\text{ }}2,{\text{ }}3,{\text{ }}4,{\text{ }}5} \right\}$.

(iv) $x$ is a real number

Ans: Given: The inequality $3x - 5 < x + 7$.

First of all solve the given linear inequality for the values of $x$ and then find the possible solution set for each of the subparts of the question.

The provided linear inequality is $3x - 5 < x + 7$, solving it for the values of $x$,

$\Rightarrow 3x - x < 7 + 5$

$\Rightarrow 2x < 12$

$\Rightarrow x < 6$

Real numbers less than $6$ will include all the decimals, integers, rational and irrational numbers that are less than $6$. Hence, the solution set will be $x \in \left( { - \infty ,6} \right)$.

Example 2. Solve $\dfrac{{x - 2}}{{x + 5}} > 2$.

Ans: Given: The inequality $\dfrac{{x - 2}}{{x + 5}} > 2$.

Consider two cases: -

In the first case assume the term $\left( {x + 5} \right) > 0$ and multiply both sides with it leaving the inequality sign as it is. Solve the obtained inequality as per the assumed range of $x$.

In the second case assume the term $\left( {x + 5} \right) < 0$ and multiply both sides with it while reversing the inequality sign. Solve the obtained inequality as per the assumed range of $x$.

Take the union of the sets obtained in the two cases.

The provided linear inequality is $\dfrac{{x - 2}}{{x + 5}} > 2$. Let us assume two cases and find the solution set for each case.

(i) Assuming the term $\left( {x + 5} \right) > 0$, so on multiplying both sides with $\left( {x + 5} \right)$ the direction of the inequality will remain the same.

 $\Rightarrow \left( {x - 2} \right) > 2\left( {x + 5} \right)$

 $\Rightarrow x - 2 > 2x + 10$

 $\Rightarrow 2x - x <  - 2 - 10$

 $\Rightarrow x <  - 12$

However, it is assumed that $\left( {x + 5} \right) > 0$ that means $x >  - 5$. So the solution set are the values of $x$ that are less than $ - 12$ but greater than $ - 5$ and no such real values of $x$ exist. Therefore there is no possible solution set of $x$ in this case.

(ii) Now, assuming the term $\left( {x + 5} \right) < 0$, so on multiplying both sides with $\left( {x + 5} \right)$ the direction of the inequality will get reversed.

 $\Rightarrow \left( {x - 2} \right) < 2\left( {x + 5} \right)$

 $\Rightarrow x - 2 < 2x + 10$

 $\Rightarrow 2x - x >  - 2 - 10$

 $\Rightarrow x >  - 12$

However, it is assumed that $\left( {x + 5} \right) < 0$ that means $x <  - 5$. So the solution set are the values of $x$ that are greater than $ - 12$ but less than $ - 5$. Therefore the solution set in this case is $x \in \left( { - 12, - 5} \right)$.

Hence, the overall solution set of the given inequality is $x \in \left( { - 12, - 5} \right)$.

Example 3. Solve $\left| {3 - 4x} \right| \geqslant 9$.

Ans: Given: The inequality $\left| {3 - 4x} \right| \geqslant 9$.

Use the formula if $\left| {f\left( x \right)} \right| \geqslant a$, where $a$ is a positive real number, then $f\left( x \right) \leqslant  - a$ or $f\left( x \right) \geqslant a$. Solve the inequalities for each case and take the union of the solution sets of $x$.

The provided linear inequality is $\left| {3 - 4x} \right| \geqslant 9$. If $\left| {f\left( x \right)} \right| \geqslant a$, where $a$ is a positive real number, then $f\left( x \right) \leqslant  - a$ or $f\left( x \right) \geqslant a$.

$\Rightarrow \left( {3 - 4x} \right) \leqslant  - 9$ or $\left( {3 - 4x} \right) \geqslant 9$

$\Rightarrow 4x \geqslant 3 + 9$ or $4x \leqslant 3 - 9$

$\Rightarrow 4x \geqslant 12$ or $4x \leqslant  - 6$

$\Rightarrow x \geqslant 3$ or $x \leqslant  - \dfrac{3}{2}$

Hence, the solution set of $x$ can be given as $\left( { - \infty , - \dfrac{3}{2}} \right] \cup \left[ {3,\infty } \right)$.

Example 4. Solve $1 \leqslant \left| {x - 2} \right| \leqslant 3$.

Ans: Given: The inequality $1 \leqslant \left| {x - 2} \right| \leqslant 3$.

Consider two cases: -

In the first case consider the inequality $1 \leqslant \left| {x - 2} \right|$ and use the formula if $\left| {f\left( x \right)} \right| \geqslant a$, where $a$ is a positive real number, then $f\left( x \right) \leqslant  - a$ or $f\left( x \right) \geqslant a$.

In the second case consider the inequality \[\left| {x - 2} \right| \leqslant 3\] and use the formula if $\left| {f\left( x \right)} \right| \leqslant a$, where $a$ is a positive real number, then $ - a \leqslant f\left( x \right) \leqslant a$.

Take the intersection of the sets obtained in the two cases.

The provided linear inequality is $1 \leqslant \left| {x - 2} \right| \leqslant 3$. Let us consider two cases $1 \leqslant \left| {x - 2} \right|$ and $\left| {x - 2} \right| \leqslant 3$.

(i) Considering $1 \leqslant \left| {x - 2} \right|$, if $\left| {f\left( x \right)} \right| \geqslant a$, where $a$ is a positive real number, then $f\left( x \right) \leqslant  - a$ or $f\left( x \right) \geqslant a$.

$\Rightarrow \left( {x - 2} \right) \leqslant  - 1$ or $\left( {x - 2} \right) \geqslant 1$

$\Rightarrow x \leqslant  - 1 + 2$ or $x \geqslant 1 + 2$

$\Rightarrow x \leqslant 1$ or $x \geqslant 3$

Therefore, the solution set is \[\left( { - \infty ,1} \right] \cup \left[ {3,\infty } \right)\].

(ii) Considering \[\left| {x - 2} \right| \leqslant 3\], if $\left| {f\left( x \right)} \right| \leqslant a$, where $a$ is a positive real number, then $ - a \leqslant f\left( x \right) \leqslant a$.

 $\Rightarrow  - 3 \leqslant \left( {x - 2} \right) \leqslant 3$

 $\Rightarrow  - 3 + 2 \leqslant x \leqslant 3 + 2$

 $\Rightarrow  - 1 \leqslant x \leqslant 5$ 

Therefore, the solution set is $\left[ { - 1,5} \right]$.

Hence, the overall solution set of the given inequality can be given as $\left( { - \infty ,1} \right] \cup \left[ {3,\infty } \right) \cap \left[ { - 1,5} \right]$ which can be simplified as $\left[ { - 1,1} \right] \cup \left[ {3,5} \right]$.

Example 5. The cost and revenue functions of a product are given by $C\left( x \right) = 20x + 4000$ and $R\left( x \right) = 60x + 2000$, respectively, where $x$ is the number of items produced and sold. How many items must be sold to realize some profit?

Ans: Given: The cost function $C\left( x \right) = 20x + 4000$

The revenue function $R\left( x \right) = 60x + 2000$

Here $x$ is the number of items produced and sold.

Subtract the cost function $C\left( x \right)$ from the revenue function $R\left( x \right)$ and use the relation $R\left( x \right) - C\left( x \right) > 0$ to solve for the value of $x$.

The formula used is Profit $ = $ Selling price (revenue) $ - $ Cost price.

The profit is the difference of selling price (revenue) and cost price of an article, therefore the profit on the number of products being manufactured and sold is given as Profit $ = R\left( x \right) - C\left( x \right)$.

Since they have to make some profit, this difference must be greater than $0$. Therefore the relation becomes,

$\Rightarrow R\left( x \right) - C\left( x \right) > 0$

$\Rightarrow \left( {60x + 2000} \right) - \left( {20x + 4000} \right) > 0$

$\Rightarrow 40x > 2000$

$\Rightarrow x > 50$

Hence, more than $50$ items must be sold to realize some profit.

Example 6. Solve for $x$, $\left| {x + 1} \right| + \left| x \right| > 3$.

Ans: Given: The inequality $\left| {x + 1} \right| + \left| x \right| > 3$.

Substitute the terms $\left( {x + 1} \right)$ and $x$ equal to $0$ and find the values of $x$. Consider different cases for different intervals of $x$ and remove the modulus function to solve the inequality.

Take the union of all the sets obtained in different cases.

Use the formula $\left| x \right| = x$ if $x > 0$ and $\left| x \right| = \left( { - x} \right)$ if $x < 0$.

The provided linear inequality is \[\left| {x + 1} \right| + \left| x \right| > 3\]. Substituting the terms $\left( {x + 1} \right)$ and $x$ equal to $0$ and finding the critical points, $x =  - 1$ or $0$. Let us consider different intervals of $x$.

Case 1: - When $ - \infty  < x <  - 1$, both $\left( {x + 1} \right)$ and $x$ are less than $0$. $\left| x \right| = \left( { - x} \right)$ if $x < 0$ and $\left| x \right| = x$ if $x > 0$,

$\Rightarrow  - \left( {x + 1} \right) + \left( { - x} \right) > 3$

$\Rightarrow  - 2x - 1 > 3$

$\Rightarrow 2x <  - 4$

$\Rightarrow x <  - 2$ 

However, here the interval $ - \infty  < x <  - 1$ is considered, so the solution set will be $ - \infty  < x <  - 2$.

Case 2: - When $ - 1 \leqslant x < 0$, $\left( {x + 1} \right)$ is greater than $0$ and $x$ is less than $0$,

 $\Rightarrow \left( {x + 1} \right) + \left( { - x} \right) > 3$

 $\Rightarrow 1 > 3$

Clearly the above condition is not possible so there is no solution set for this case.

Case 3:- When $0 \leqslant x < \infty $, both $\left( {x + 1} \right)$ and $x$ are greater than $0$,

$\Rightarrow \left( {x + 1} \right) + \left( x \right) > 3$

$\Rightarrow 2x + 1 > 3$

$\Rightarrow 2x > 2$

$\Rightarrow x > 1$

However, here the interval $0 \leqslant x < \infty $ is considered, so the solution set will be $1 < x < \infty $.

Hence, the solution set for all the three cases can be given as $x \in \left( { - \infty , - 2} \right) \cup \left( {1,\infty } \right)$.

Long Answer Type:

Example 7. Solve for $x$, $\dfrac{{\left| {x + 3} \right| + x}}{{x + 2}} > 1$.

Ans: Given: The inequality $\dfrac{{\left| {x + 3} \right| + x}}{{x + 2}} > 1$.

Take all the terms to the L.H.S and simplify. Consider two cases $\left( {x + 3} \right) < 0$ and $\left( {x + 3} \right) \geqslant 0$ and solve the inequality for each case. Take the union of all the sets obtained in different cases.

Use the formulas: -

$\left| x \right| = x$ if $x > 0$ and $\left| x \right| = \left( { - x} \right)$ if $x < 0$.

If $\dfrac{a}{b} < 0$ then $a$ and $b$ are of opposite sign and if $\dfrac{a}{b} > 0$ then $a$ and $b$ are of the same sign.

The provided linear inequality is $\dfrac{{\left| {x + 3} \right| + x}}{{x + 2}} > 1$, so on simplification,

$\Rightarrow \dfrac{{\left| {x + 3} \right| + x}}{{x + 2}} - 1 > 0$

$\Rightarrow \dfrac{{\left| {x + 3} \right| + x - \left( {x + 2} \right)}}{{x + 2}} > 0$

$\Rightarrow \dfrac{{\left| {x + 3} \right| - 2}}{{x + 2}} > 0$

Substituting the terms $\left( {x + 3} \right)$ equal to $0$ and finding the critical points, $x =  - 3$. Let us consider two different cases.

Case 1: - When $ - \infty  < x <  - 3$, $\left( {x + 3} \right)$ is less than $0$. $\left| x \right| = \left( { - x} \right)$ if $x < 0$,

$\Rightarrow \dfrac{{ - \left( {x + 3} \right) - 2}}{{x + 2}} > 0$

$\Rightarrow \dfrac{{ - \left( {x + 5} \right)}}{{x + 2}} > 0$

Multiplying both the sides with $ - 1$ and reversing the direction of inequality,

$ \Rightarrow \dfrac{{x + 5}}{{x + 2}} < 0$

If $\dfrac{a}{b} < 0$ then $a$ and $b$ are of opposite signs.

$ \Rightarrow$ $(x + 5 < 0 \text{ and } x + 2 > 0)$ or $ (x + 5 > 0 \text{ and } x + 2 < 0)$

$ \Rightarrow$ $(x <  - 5 \text{ and } x >  - 2)$ or $ (x >  - 5 \text{ and }x <  - 2)$

$ \Rightarrow$ $(x <  - 5 \text{ and } x >  - 2)$ or $ (x >  - 5 \text{ and } x <  - 2)$

Now, the condition $(x <  - 5 \text{ and } x > -2)$ is not possible but $(x >  - 5 \text{ and }x <  - 2)$ is possible so the solution set is $x \in \left( { - 5, - 2} \right)$.

However, here the interval $ - \infty  < x <  - 3$ is considered, so the possible solution set for this case is $x \in \left( { - 5, - 3} \right)$.

Case 2:- When $ - 3 \leqslant x < \infty $, $\left( {x + 3} \right)$ is greater than $0$. $\left| x \right| = x$ if $x > 0$,

$\Rightarrow \dfrac{{\left( {x + 3} \right) - 2}}{{x + 2}} > 0$

$\Rightarrow \dfrac{{x + 1}}{{x + 2}} > 0$

If $\dfrac{a}{b} > 0$ then $a$ and $b$ are of the same sign.

$ \Rightarrow$ $(x + 1 > 0 \text{ and } x + 2 > 0)$ or $(x + 1 < 0 \text{ and }x + 2 < 0)$

$ \Rightarrow$ $(x > 1\text{ and } x >  - 2)$ or $(x <  - 1 \text{ and } x <  - 2)$

$ \Rightarrow$ $x \in \left( { - \infty , - 2} \right) \cup \left( {1,\infty } \right)$

However, here the interval $ - 3 \leqslant x < \infty $ is considered, so the possible solution set for this case is $x \in \left[ { - 3, - 2} \right) \cup \left( {1,\infty } \right)$.

Hence, the solution set for both the cases can be given as $x \in \left( { - 5, - 3} \right) \cup \left[ { - 3, - 2} \right) \cup \left( {1,\infty } \right)$ which can be simplified as $x \in \left( { - 5, - 2} \right) \cup \left( {1,\infty } \right)$.

Example 8. Solve the following system of inequalities:

$\dfrac{x}{{2x + 1}} \geqslant \dfrac{1}{4}$, $\dfrac{{6x}}{{4x - 1}} < \dfrac{1}{2}$

Ans :  Given: The system of inequalities $\dfrac{x}{{2x + 1}} \geqslant \dfrac{1}{4}$ and $\dfrac{{6x}}{{4x - 1}} < \dfrac{1}{2}$.

Solve the two inequalities separately by taking all the terms to the L.H.S. and take the intersection of the sets of values of $x$ obtained.

Use the formula: -

If $\dfrac{a}{b} < 0$ then $a$ and $b$ are of opposite sign and if $\dfrac{a}{b} \geqslant 0$ then $a$ and $b$ are of the same sign.

The provided system of linear inequalities are \[\dfrac{x}{{2x + 1}} \geqslant \dfrac{1}{4}\] and $\dfrac{{6x}}{{4x - 1}} < \dfrac{1}{2}$, so on simplification,

$ \Rightarrow \dfrac{x}{{2x + 1}} - \dfrac{1}{4} \geqslant 0$ and $\dfrac{{6x}}{{4x - 1}} - \dfrac{1}{2} < 0$

$ \Rightarrow \dfrac{{4x - \left( {2x + 1} \right)}}{{4\left( {2x + 1} \right)}} \geqslant 0$ and $\dfrac{{12x - \left( {4x - 1} \right)}}{{2\left( {4x - 1} \right)}} < 0$

$ \Rightarrow \dfrac{{2x - 1}}{{2x + 1}} \geqslant 0$ and $\dfrac{{8x + 1}}{{4x - 1}} < 0$

If $\dfrac{a}{b} \geqslant 0$ then $a$ and $b$ are of the same sign and if $\dfrac{a}{b} < 0$ then $a$ and $b$ are of opposite sign.

(1) For the inequality $\dfrac{{2x - 1}}{{2x + 1}} \geqslant 0$ where $\left( {2x + 1 \ne 0} \right)$,

$ \Rightarrow (2x - 1 \leqslant 0$ and $2x + 1 < 0)$ or $(2x - 1 \geqslant 0$ and $2x + 1 > 0)$

$ \Rightarrow (x \leqslant \dfrac{1}{2}$ and $x <  - \dfrac{1}{2})$ or $(x \geqslant \dfrac{1}{2}$ and $x >  - \dfrac{1}{2})$

$ \Rightarrow x \in \left( { - \infty , - \dfrac{1}{2}} \right) \cup \left[ {\dfrac{1}{2},\infty } \right)$

(2) For the inequality $\dfrac{{8x + 1}}{{4x - 1}} < 0$,

$ \Rightarrow (8x + 1 < 0 \text{ and } 4x - 1 > 0)$ or $(8x + 1 > 0 \text{ and } $4x - 1 < 0)$

$ \Rightarrow (x <  - \dfrac{1}{8}$ and $x > \dfrac{1}{4})$ or \[(x >  - \dfrac{1}{8}\] and $x < \dfrac{1}{4})$

Now, the condition $(x <  - \dfrac{1}{8}$ and $x > \dfrac{1}{4})$ is not possible but $(x >  - \dfrac{1}{8}$ and $x < \dfrac{1}{4})$ is possible so the solution set is $x \in \left( { - \dfrac{1}{8},\dfrac{1}{4}} \right)$.

Therefore, the solution set of the given system can be given as $x \in \left( { - \infty , - \dfrac{1}{2}} \right) \cup \left[ {\dfrac{1}{2},\infty } \right) \cap \left( { - \dfrac{1}{8},\dfrac{1}{4}} \right)$ which is a null set $\left( \phi  \right)$.

Example 9. Find the linear inequalities for which the shaded region in the given figure is the solution set.

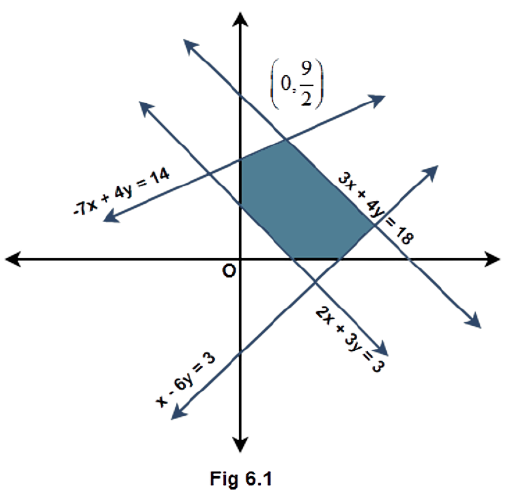
Ans : Given : A shaded portion as the solution set of some linear inequalities.

Consider the given equations of the lines and check the side at which the origin and the shaded portion lie with respect to each line. Form the inequalities accordingly using the equation of the lines.

(1) Considering the line $3x + 4y = 18$, the origin and the shaded area lie on the same side of this line. Substituting the point $\left( {0,0} \right)$ in the L.H.S gives $0$, which is less than $18$ in the R.H.S. Also a solid line is present and not a dashed line. Therefore, the inequality is $3x + 4y \leqslant 18$.

(2) Considering the line $ - 7x + 4y = 14$, the origin and the shaded area lie on the same side of this line. Substituting the point $\left( {0,0} \right)$ in the L.H.S gives $0$, which is less than $14$ in the R.H.S. Therefore, the inequality is $ - 7x + 4y \leqslant 14$.

(3) Considering the line $x - 6y = 3$, the origin and the shaded area lie on the same side of this line. Substituting the point $\left( {0,0} \right)$ in the L.H.S gives $0$ which is less than $3$ in the R.H.S. Therefore, the inequality is $x - 6y \leqslant 3$.

(4) Considering the line $2x + 3y = 3$, the origin and the shaded area lie on the opposite sides of this line. Substituting the point $\left( {0,0} \right)$ in the L.H.S gives $0$ which is less than $3$ in the R.H.S that means the inequality of the side containing the origin is $2x + 3y \leqslant 3$. Therefore, the inequality of the side containing the shaded area is $2x + 3y \geqslant 3$.

(5) At last it can be seen that the shaded area lies in the first quadrant whose inequalities are given as $x \geqslant 0$ and $y \geqslant 0$.

Hence, the inequalities representing the solution set shown in figure 6.1 are: -

$3x + 4y \leqslant 18$, $ - 7x + 4y \leqslant 14$, $x - 6y \leqslant 3$, $2x + 3y \geqslant 3$, $x \geqslant 0$ and $y \geqslant 0$.

Example 10. If $\dfrac{{\left| {x - 2} \right|}}{{x - 2}} \geqslant 0$, then

(A) $x \in \left[ {2,\infty} \right)$

(B) $x \in \left( {2,\infty} \right)$

(C) $x \in \left( { - \infty,2} \right)$

(D) $x \in \left( { - \infty,2} \right]$

Ans : Option (B) is the correct answer.

Given: The inequality $\dfrac{{\left| {x - 2} \right|}}{{x - 2}} \geqslant 0$.

Use the fact that the modulus function is always positive. Apply the rule that if $\dfrac{a}{b} \geqslant 0$ then $a$ and $b$ are of the same sign.

The provided linear inequality is $\dfrac{{\left| {x - 2} \right|}}{{x - 2}} \geqslant 0$. The modulus function is always positive or equal to $0$ so the numerator is always greater than or equal to $0$.

If $\dfrac{a}{b} \geqslant 0$ then $a$ and $b$ are of the same sign that means the denominator $\left( {x - 2} \right)$ will always be greater than $0$ and also for the function to be defined $\left( {x - 2} \right) \ne 0$.

$\Rightarrow x - 2 > 0$

$\Rightarrow x > 2$

$\Rightarrow x \in \left( {2,\infty } \right)$

Correct Answer: B

Example 11. The length of a rectangle is three times the breadth. If the minimum perimeter of the rectangle is $160 cm$, then

(A) breadth $ > 20 cm$

(B) length $ < 20 cm$

(C) breadth 

(D) length $  \leqslant 20 cm$

Ans : Option (C) is the correct answer.

Given: Length of the rectangle = $3 \times $ breadth of the rectangle

Minimum perimeter of the rectangle is $160{\text{ cm}}$.

Assume $l$ and $b$ as the length and breadth of the rectangle and use the relation $P \geqslant 160{\text{ cm}}$ where $P$ is the perimeter of the rectangle. Use the given relation between $l$ and $b$ to solve.

Use the formula $P = 2\left( {l + b} \right)$.

Since the minimum perimeter of the rectangle is $160{\text{ cm}}$ so mathematically,

 $\Rightarrow P \geqslant 160{\text{ cm}}$

 $\Rightarrow 2\left( {l + b} \right) \geqslant 160{\text{ cm}}$

 $\Rightarrow l + b \geqslant 80{\text{ cm}}$

Here, $P = $ perimeter of the rectangle, $l = $ length and $b = $ breadth.

Using the given relation $l = 3b$,

$\Rightarrow 3b + b \geqslant 80{\text{ cm}}$

$\Rightarrow 4b \geqslant 80{\text{ cm}}$

$\Rightarrow b \geqslant 20{\text{ cm}}$

Correct Answer: C

Example 12. Solution of the inequalities comprising a system in variable $x$ are represented on number lines as given below, then

(A) $x \in \left( { - \infty, - 4} \right] \cup \left[ {3,\infty} \right)$

(B) $x \in \left[ { - 3,1} \right]$

(C) $x \in \left( { - \infty, - 4} \right) \cup \left[ {3,\infty} \right)$

(D) $x \in \left[ { - 4,3} \right]$

Ans : Option (A) is the correct answer.

Given: The solutions of a system of linear inequalities in the line representation form.

Write the solution set of the two lines represented in the figure and take the intersection of the two sets to find the common set of solutions of $x$.

Considering the first line the solution set can be written as $x \in \left( { - \infty , - 4} \right] \cup \left[ {3,\infty } \right)$ and similarly for the second line the solution set is $x \in \left( { - \infty , - 3} \right] \cup \left[ {1,\infty } \right)$.

Since the two lines comprise a system of linear inequalities, the solution set will be the set of their common elements. Therefore, the intersection of the two sets is to be taken.

$ \Rightarrow x \in \left( { - \infty , - 4} \right] \cup \left[ {3,\infty } \right)$

Correct Answer: A

Example 13. If $|x+3|\geqslant 10$, then

(A) $x \in \left( { - 13,7} \right]$

(B) $x \in \left[ { - 13,7} \right]$

(C) $x \in \left( { - \infty, - 13} \right] \cup \left[ {7,\infty} \right)$

(D) $x \in \left[ { - \infty, - 13} \right] \cup \left[ {7,\infty} \right)$

Ans: Option (C) is the correct answer.

Given: The inequality $\left| {x + 3} \right| \geqslant 10$.

Use the formula if $\left| {f\left( x \right)} \right| \geqslant a$, where $a$ is a positive real number, then $f\left( x \right) \leqslant  - a$ or $f\left( x \right) \geqslant a$. Solve the inequalities for each case and take the union of the solution sets of $x$.

The provided linear inequality is $\left| {x + 3} \right| \geqslant 10$. If $\left| {f\left( x \right)} \right| \geqslant a$, where $a$ is a positive real number, then $f\left( x \right) \leqslant  - a$ or $f\left( x \right) \geqslant a$.

$\Rightarrow x + 3 \leqslant  - 10$ or $x + 3 \geqslant 10$

$\Rightarrow x \leqslant  - 10 - 3$ or $x \geqslant 10 - 3$

$\Rightarrow x \leqslant  - 13$ or $x \geqslant 7$

Since $ - \infty $ and $\infty $ are not real numbers so the open interval should be marked towards them.

$\Rightarrow x \in \left( { - \infty , - 13} \right] \cup \left[ {7,\infty } \right)$

Correct Answer: C

Example 14. State whether the following statements are True or False.

(i) If $x > y$ and $b < 0$, then $bx < by$

Ans: The given statement is true because if a negative number is multiplied on both the sides of an inequality then the direction of the inequality gets reversed.

(ii) If $xy > 0$, then $x > 0$ and $y < 0$

Ans: The given statement is false because if the numbers are of opposite sign then their product is always negative.

(iii) If $xy < 0$, then $x > 0$ and $y > 0$

Ans: The given statement is false because if the numbers are of the same sign then their product is always positive.

(iv) If $x > 5$ and $x > 2$, then $x \in \left( {5,\infty} \right)$

Ans: The given statement is true because here the intersection of two sets of values of $x$ given is to be taken.

(v) If $\left| x \right| < 5$, then $x \in \left( { - 5,5} \right)$

Ans: The given statement is true because according to the formula if $\left| x \right| < a$ then $ - a < x < a$ where $a$ being any positive real number.

(vi) Graph of $x >  - 2$ is

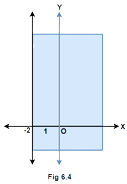
Ans: The given statement is false because the line $x =  - 2$ is represented by a solid line instead of a dashed line in the figure 6.4. This is because the value $x =  - 2$ must not be included.

(vii) Solution set of $x - y  \leqslant 0$ is

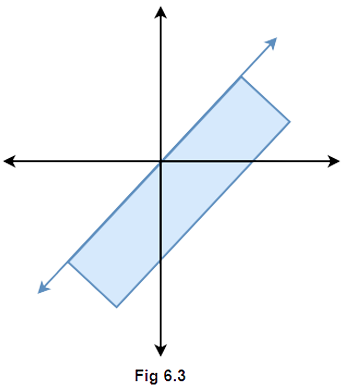
Ans: The given statement is false because if the inequality $x - y \leqslant 0$ is simplified, it gives $x \leqslant y$ that means the shaded portion should be above the line $x = y$ in figure 6.3.

Example 15. Fill in the blanks in the following:

(i) If $x \geqslant -3$, then $x + 5.............2$

Ans: The provided inequality is $x \geqslant  - 3$, so adding $5$ both the sides,

$\Rightarrow x + 5 \geqslant  - 3 + 5$

$\Rightarrow x + 5 \geqslant 2$

(ii) If $- x \leqslant  - 4$, then $2x..............8$

Ans: The provided inequality is $ - x \leqslant  - 4$, so multiplying both the sides with $ - 2$,

 $\Rightarrow \left( { - 2} \right) \times \left( { - x} \right) \geqslant \left( { - 4} \right) \times \left( { - 2} \right)$

 $\Rightarrow 2x \geqslant 8$

(iii) If $\dfrac{1}{{x - 2}} < 0$ then $x...............2$

Ans: The provided inequality is $\dfrac{1}{{x - 2}} < 0$. If $\dfrac{a}{b} < 0$ then $a$ and $b$ are of opposite signs. Since the numerator is positive so $\left( {x - 2} \right) < 0$ which gives $x < 2$.

(iv) If $a < b$ and $c < 0$, then $\dfrac{a}{c}.............\dfrac{b}{c}$

Ans: The provided inequality is $a < b$, since $c$ is a negative number so dividing both the sides by $c$ will change the direction of inequality.

$\Rightarrow \dfrac{a}{c} > \dfrac{b}{c}$

(v) If $\left| {x - 1}\right| \leqslant2$, then $- 1........x........3$

Ans: The provided inequality is $\left| {x - 1} \right| \leqslant 2$. If $\left| x \right| \leqslant a$ then $ - a \leqslant x \leqslant a$ for any positive real number $a$.

$\Rightarrow  - 2 \leqslant x - 1 \leqslant 2$

$\Rightarrow  - 1 \leqslant x \leqslant 3$

(vi) If $\left| {3x - 7} \right| > 2$, then $x.....\dfrac{5}{3}$ or $x.....3$

Ans: The provided inequality is $\left| {3x - 7} \right| > 2$. If $\left| x \right| > a$ then $x <  - a$ or $x > a$ for any positive real number $a$.

$\Rightarrow 3x - 7 <  - 2$ or $3x - 7 > 2$

$\Rightarrow 3x < 5$ or $3x > 9$

$\Rightarrow x < \dfrac{5}{3}$ or $x > 3$

(vii) If $p > 0$ and $q < 0$, then $p + q......p$

Ans: Since $p > 0$ and $q < 0$ so considering the sum $p + q$ means adding a negative number with a positive number. This will reduce some quantity from $p$.

$ \Rightarrow p + q < p$

EXERCISE 6.1

1. Solve for $x$, $\dfrac{4}{{x + 1}}\leqslant 3 \leqslant \dfrac{6}{{x + 1}},\left( {x > 0} \right)$.

Ans: Given: The inequality $\dfrac{4}{{x + 1}} \leqslant 3 \leqslant \dfrac{6}{{x + 1}},\left( {x > 0} \right)$.

Multiply all the terms with $\left( {x + 1} \right)$ and leave the inequality sign as it is. Solve for the values of $x$ to get the solution set.

The provided linear inequality is $\dfrac{4}{{x + 1}} \leqslant 3 \leqslant \dfrac{6}{{x + 1}},\left( {x > 0} \right)$, since $x$ is greater than $0$ so $\left( {x + 1} \right)$ will also be greater than $0$. Multiplying all the terms with $\left( {x + 1} \right)$ will not change the direction of inequality.

$\Rightarrow 4 \leqslant 3\left( {x + 1} \right) \leqslant 6$

$\Rightarrow \dfrac{4}{3} \leqslant \left( {x + 1} \right) \leqslant 2$

$\Rightarrow \dfrac{4}{3} - 1 \leqslant x \leqslant 2 - 1$

 $\Rightarrow \dfrac{1}{3} \leqslant x \leqslant 1$

Therefore, the solution set is $x \in \left[ {\dfrac{1}{3},1} \right]$.

2. Solve for $x$, $\dfrac{{\left| {x - 2}\right| -1}}{{\left|{x - 2}\right| -2}} \leqslant 0$.

Ans : Given: The inequality $\dfrac{{\left| {x - 2} \right| - 1}}{{\left| {x - 2} \right| - 2}} \leqslant 0$.

Use the formula if $\dfrac{a}{b} \leqslant 0$, $\left( {b \ne 0} \right)$ then $a$ and $b$ are of opposite signs and consider two cases.

Now, use the formula if $\left| {f\left( x \right)} \right| > a$, where $a$ is a positive real number, then $f\left( x \right) <  - a$ or $f\left( x \right) > a$ and if $\left| {f\left( x \right)} \right| \leqslant a$, then $ - a \leqslant f\left( x \right) \leqslant a$.

Take the union of the sets obtained in the two cases.

The provided inequality is $\dfrac{{\left| {x - 2} \right| - 1}}{{\left| {x - 2} \right| - 2}} \leqslant 0$. If $\dfrac{a}{b} \leqslant 0$, $\left( {b \ne 0} \right)$ then $a$ and $b$ are of opposite signs , so there are the following two cases,

Case (1): - $\left| {x - 2} \right| - 1 \leqslant 0$ and $\left| {x - 2} \right| - 2 > 0$

$ \Rightarrow \left| {x - 2} \right| \leqslant 1$ and $\left| {x - 2} \right| > 2$

If $\left| {f\left( x \right)} \right| > a$, where $a$ is a positive real number, then $f\left( x \right) <  - a$ or $f\left( x \right) > a$.

$\Rightarrow ( - 1 \leqslant x - 2 \leqslant 1)$ and $(x - 2 <  - 2$ or $x - 2 > 2)$

$\Rightarrow (1 \leqslant x \leqslant 3)$ and $(x < 0$ or $x > 4)$

$\Rightarrow x \in \left[ {1,3} \right] \cap \left( { - \infty ,0} \right) \cup \left( {4,\infty } \right)$

The above set is a null set $\left( \phi  \right)$.

Case (2): - $\left| {x - 2} \right| - 1 \geqslant 0$ and $\left| {x - 2} \right| - 2 < 0$

$\Rightarrow \left| {x - 2} \right| \geqslant 1$ and $\left| {x - 2} \right| < 2$

$\Rightarrow (x - 2 \leqslant  - 1$ or $x - 2 \geqslant 1)$and $( - 2 < x - 2 < 2)$

$\Rightarrow (x \leqslant 1$ or $x \geqslant 3)$ and $(0 < x < 4)$

$\Rightarrow x \in \left( { - \infty ,1} \right] \cup \left[ {3,\infty } \right) \cap \left( {0,4} \right)$

$\Rightarrow x \in \left( {0,1} \right] \cup \left[ {3,4} \right)$

Hence, the overall solution set of the given inequality will be the union of the sets obtained in the two cases which gives $x \in \left( {0,1} \right] \cup \left[ {3,4} \right)$.

3. Solve for $x$, $\dfrac{1}{{\left| x\right| -3}} \leqslant\dfrac{1}{2}$.

Ans : Given: The inequality $\dfrac{1}{{\left| x \right| - 3}} \leqslant \dfrac{1}{2}$.

Simplify the inequality by taking all the terms to the L.H.S. Use the formula if $\dfrac{a}{b} \leqslant 0$, $\left( {b \ne 0} \right)$ then $a$ and $b$ are of opposite signs and consider two cases.

Now, use the formula if $\left| {f\left( x \right)} \right| > a$, where $a$ is a positive real number, then $f\left( x \right) <  - a$ or $f\left( x \right) > a$ and if $\left| {f\left( x \right)} \right| \leqslant a$, then $ - a \leqslant f\left( x \right) \leqslant a$.

Take the union of the sets obtained in the two cases.

The provided inequality is $\dfrac{1}{{\left| x \right| - 3}} \leqslant \dfrac{1}{2}$, so on simplification,

$\Rightarrow \dfrac{1}{{\left| x \right| - 3}} - \dfrac{1}{2} \leqslant 0$

$\Rightarrow \dfrac{{2 - \left( {\left| x \right| - 3} \right)}}{{2\left( {\left| x \right| - 3} \right)}} \leqslant 0$

$\Rightarrow \dfrac{{5 - \left| x \right|}}{{\left| x \right| - 3}} \leqslant 0$

Multiplying both the sides with $ - 1$,

$\Rightarrow \dfrac{{\left| x \right| - 5}}{{\left| x \right| - 3}} \geqslant 0$

If $\dfrac{a}{b} \geqslant 0$, $\left( {b \ne 0} \right)$ then $a$ and $b$ are of the same sign, so there are the following two cases,

Case (1): - $\left| x \right| - 5 \geqslant 0$ and $\left| x \right| - 3 > 0$

$\Rightarrow \left| x \right| \geqslant 5$ and $\left| x \right| > 3$

If $\left| {f\left( x \right)} \right| \geqslant a$, where $a$ is a positive real number, then $f\left( x \right) \leqslant  - a$ or $f\left( x \right) \geqslant a$.

$\Rightarrow (x \leqslant  - 5$ or $x \geqslant 5)$ and $(x <  - 3$ or $x > 3)$

$\Rightarrow x \in \left( { - \infty , - 5} \right] \cup \left[ {5,\infty } \right) \cap \left( { - \infty , - 3} \right] \cup \left[ {3,\infty } \right)$

$\Rightarrow x \in \left( { - \infty , - 5} \right] \cup \left[ {5,\infty } \right)$

Case (2): - $\left| x \right| - 5 \leqslant 0$ and $\left| x \right| - 3 < 0$

$\Rightarrow \left| x \right| \leqslant 5$ and $\left| x \right| < 3$

If $\left| {f\left( x \right)} \right| \leqslant a$, where $a$ is a positive real number, then $ - a \leqslant f\left( x \right) \leqslant a$.

$\Rightarrow ( - 5 \leqslant x \leqslant 5)$ and $( - 3 < x < 3)$

$\Rightarrow x \in \left[ { - 5,5} \right] \cap \left( { - 3,3} \right)$

$\Rightarrow x \in \left( { - 3,3} \right)$

Hence, the overall solution set of the given inequality will be the union of the sets obtained in the two cases which gives $x \in \left( { - \infty , - 5} \right] \cup \left[ {5,\infty } \right) \cup \left( { - 3,3} \right)$.

4. Solve for $|x-1| \leq 5,|x| \geq 2$.

Ans : Given: The system of inequalities $\left| {x - 1} \right| \leqslant 5,\left| x \right| \geqslant 2$.

Solve the two inequalities separately using the formulas: -

If $\left| {f\left( x \right)} \right| \leqslant a$, where $a$ is a positive real number, then $ - a \leqslant f\left( x \right) \leqslant a$.

If $\left| {f\left( x \right)} \right| \geqslant a$, then $f\left( x \right) \leqslant  - a$ or $f\left( x \right) \geqslant a$.

Take the intersection of the sets obtained by solving the two inequalities.

The provided system of inequalities is $\left| {x - 1} \right| \leqslant 5,\left| x \right| \geqslant 2$. Let us solve the two inequalities separately.

(i) Considering $\left| {x - 1} \right| \leqslant 5$, if $\left| {f\left( x \right)} \right| \leqslant a$, where $a$ is a positive real number, then $ - a \leqslant f\left( x \right) \leqslant a$.

 $\Rightarrow  - 5 \leqslant x - 1 \leqslant 5$

 $\Rightarrow  - 4 \leqslant x \leqslant 6$

 $\Rightarrow x \in \left[ { - 4,6} \right]$

(ii) Considering $\left| x \right| \geqslant 2$, if $\left| {f\left( x \right)} \right| \geqslant a$, then $f\left( x \right) \leqslant  - a$ or $f\left( x \right) \geqslant a$.

$\Rightarrow x \leqslant  - 2$ or $x \geqslant 2$

$\Rightarrow x \in \left( { - \infty , - 2} \right] \cup \left[ {2,\infty } \right)$

Hence, the overall solution set of the given inequality will be the intersection sets obtained in the two cases which gives $\left[ { - 4, - 2} \right] \cup \left[ {2,6} \right]$.

5. Solve for $x$, $ - 5 \leqslant\dfrac{{2 - 3x}}{4} \leqslant 9$.

Ans : Given: The inequality $ - 5 \leqslant \dfrac{{2 - 3x}}{4} \leqslant 9$.

Use the fact that if all the terms of an inequality are multiplied or divided by a positive number then the direction of inequality remains the same and if multiplied or divided by a negative number then the direction gets reversed.

The provided linear inequality is $ - 5 \leqslant \dfrac{{2 - 3x}}{4} \leqslant 9$, multiplying all the terms with $4$,

$\Rightarrow  - 20 \leqslant 2 - 3x \leqslant 36$

$\Rightarrow  - 22 \leqslant  - 3x \leqslant 34$

Dividing all the terms by $ - 3$ will change the direction of inequality,

$\Rightarrow \dfrac{{22}}{3} \geqslant x \geqslant  - \dfrac{{34}}{3}$

$\Rightarrow  - \dfrac{{34}}{3} \leqslant x \leqslant \dfrac{{22}}{3}$

Therefore, the solution set is $x \in \left[ { - \dfrac{{34}}{3},\dfrac{{22}}{3}} \right]$.

6. Solve for $x$, $4x + 3\geqslant 2x + 17, 3x – 5 < – 2$.

Ans: Given: The system of inequalities $4x + 3 \geqslant 2x + 17,3x - 5 <  - 2$.

Solve the two inequalities separately and take the intersection of the sets obtained. Use the fact that if all the terms of an inequality are multiplied or divided by a positive number then the direction of inequality remains the same.

The provided system of inequalities is $4x + 3 \geqslant 2x + 17,3x - 5 <  - 2$, solving them separately gives,

$\Rightarrow 4x + 3 \geqslant 2x + 17$ and $3x - 5 <  - 2$

$\Rightarrow 4x - 2x \geqslant 17 - 3$ and $3x < 5 - 2$

$\Rightarrow 2x \geqslant 14$ and $3x < 3$

$\Rightarrow x \geqslant 7$ and $x < 1$

$\Rightarrow x \in \left( { - \infty ,1} \right) \cap \left[ {7,\infty } \right)$

The above solution is a null set $\left( \phi  \right)$.

7. A company manufactures cassettes. Its cost and revenue functions are $C\left( x \right) = 26000 + 30x$ and $R\left( x \right) = 43x$, respectively, where $x$ is the number of cassettes produced and sold in a week. How many cassettes must be sold by the company to realize some profit?

Ans: Given: The cost function $C\left( x \right) = 26000 + 30x$

The revenue function $R\left( x \right) = 43x$

Here $x$ is the number of cassettes produced and sold in a week.

Subtract the cost function $C\left( x \right)$ from the revenue function $R\left( x \right)$ and use the relation $R\left( x \right) - C\left( x \right) > 0$ to solve for the value of $x$.

The formula used is Profit $ = $ Selling price (revenue) $ - $ Cost price.

The profit is the difference of selling price (revenue) and cost price of an article, therefore the profit on the number of cassettes being manufactured and sold is given as Profit $ = R\left( x \right) - C\left( x \right)$

Since the company has to make some profit, this difference must be greater than $0$. Therefore the relation becomes,

$\Rightarrow R\left( x \right) - C\left( x \right) > 0$

$\Rightarrow 43x - \left( {26000 + 30x} \right) > 0$

$\Rightarrow 13x > 26000$

$\Rightarrow x > 2000$

Hence, the company must sell more than $2000$ cassettes or it can be said that a minimum of $2001$ cassettes in a week to realize some profit.

8. The water acidity in a pool is considered normal when the average pH reading of three daily measurements is between $8.2$ and $8.5$. If the first two pH readings are $8.48$ and $8.35$, find the range of pH value for the third reading that will result in the acidity level being normal.

Ans: Given: The first pH reading $ = 8.48$

The second pH reading $ = 8.35$

The normal range of pH reading of water acidity in the pool for the average pH reading of three daily measurements lies in between $8.2$ and $8.5$.

Assume the third pH reading as $x$. Take the average of the three pH readings and make them lie in the range of readings $8.2$ and $8.5$ to solve for the value of $x$.

The average of three numbers ${x_1}$, ${x_2}$ and ${x_3}$ is given by the formula $\dfrac{{\left( {{x_1} + {x_2} + {x_3}} \right)}}{3}$.

Let us assume the third pH reading of the water in the pool is $x$, so the three daily pH readings are $8.48$, $8.35$ and $x$. Therefore the average of these three readings will be given as $\dfrac{{\left( {8.48 + 8.35 + x} \right)}}{3}$.

Since the average reading must lie in the range of readings $8.2$ and $8.5$ for the water acidity to be considered normal so the inequality can be written as,

$\Rightarrow 8.2 < \dfrac{{\left( {8.48 + 8.35 + x} \right)}}{3} < 8.5$

$\Rightarrow 8.2 < \dfrac{{\left( {16.83 + x} \right)}}{3} < 8.5$

Multiplying both the sides with $3$,

$\Rightarrow 24.6 < \left( {16.83 + x} \right) < 25.5$

$\Rightarrow 24.6 - 16.83 < x < 25.5 - 16.83$

$\Rightarrow 7.77 < x < 8.67$

Hence, the pH value for the third reading must lie in between $7.77$ and $8.67$ so that the acidity level of the water in the pool should be considered normal.

9. A solution of $9\% $ acid is to be diluted by adding a $3\%$ acid solution to it. The resulting mixture is to be more than $5\% $ but less than $7\% $ acid. If there is $460$ litres of the $9\% $ solution, how many litres of $3\% $ solution will have to be added?

Ans: Given: Volume of $9\% $ acid solution $ = 460$ litres

Percentage acidic range of the resulting solution $ = \left( {5,7} \right)$

Assume the volume of $3\% $ acid solution to be added as $x$ litres. Add the volumes to find the total volume of the mixture. Use the relation: -

$5\% $ of total volume of mixture $< 3\% $ of $x$ + $9\% $ of $460 < 7\% $ of total volume of mixture, to solve for the value of $x$.

Let us assume the volume of $3\%$ acid solution to be added as $x$ litres. Since volume of $9\%$ solution is $460$ litres,

$ \Rightarrow $ Total volume of the mixture $=\left( {460 + x} \right)$ litres

The resulting mixture is to be more than $5\% $ but less than $7\% $ acidic,

$ \Rightarrow 5\% $ of $\left( {460 + x} \right)< 3\% $ of $x$ + $9\% $ of $460$$ < $$7\% $ of $\left( {460 + x} \right)$

$\Rightarrow \dfrac{5}{{100}} \times \left( {460 + x} \right) < \dfrac{3}{{100}} \times x + \dfrac{9}{{100}} \times 460 < \dfrac{7}{{100}} \times \left( {460 + x} \right)$

$\Rightarrow 2300 + 5x < 3x + 4140 < 3220 + 7x$

Let us solve the system of inequalities separately.

(i) Considering $2300 + 5x < 3x + 4140$,

$\Rightarrow 5x - 3x < 4140 - 2300$

$\Rightarrow 2x < 1840$

$\Rightarrow x < 920$

(ii) Considering $3x + 4140 < 3220 + 7x$,

$\Rightarrow 4140 - 3220 < 7x - 3x$

$\Rightarrow 920 < 4x$

$\Rightarrow x > 230$

Hence, the volume of $3\% $ acid that is to be added must be greater than $230$ litres but less than $920$ litres.

10. A solution is to be kept between $4{0^o}C$ and $4{5^o}C$. What is the range of temperature in degree Fahrenheit, if the conversion formula is ${\text{F}} = \dfrac{9}{5}{\text{C}} + 32$?

Ans: Given: Temperature range (in degree Celsius) of the solution to be stored $ = \left( {40,45} \right)$.

Conversion formula from degree Celsius to degree Fahrenheit ${\text{F}} = \dfrac{9}{5}{\text{C}} + 32$.

From the given formula derive the relation of degree Celsius in terms of degree Fahrenheit. Use the relation ${\text{4}}{{\text{0}}^ \circ } < {\text{C}} < {45^ \circ }$ and find the range of ${\text{F}}$.

From the conversion formula ${\text{F}} = \dfrac{9}{5}{\text{C}} + 32$,

$\Rightarrow {\text{C = }}\dfrac{5}{9}\left( {{\text{F}} - 32} \right)$

Since the temperature of the solution is to be kept between ${40^ \circ }{\text{C}}$ and ${45^ \circ }{\text{C}}$,

$\Rightarrow {\text{4}}{{\text{0}}^ \circ } < \dfrac{5}{9}\left( {{\text{F}} - 32} \right) < {45^ \circ }$

$\Rightarrow {72^ \circ } < {\text{F}} - 32 < {81^ \circ }$

$\Rightarrow {72^ \circ } + {32^ \circ } < {\text{F}} < {81^ \circ } + {32^ \circ }$

$\Rightarrow {104^ \circ } < {\text{F}} < {113^ \circ }$

11. The longest side of a triangle is twice the shortest side and the third side is $2 cm$ longer than the shortest side. If the perimeter of the triangle is more than $166 cm$, then find the minimum length of the shortest side.

Ans: Given: Length of the longest side $ = 2 \times $ length of the shortest side

Length of the third side $ = 2 + $ length of the shortest side

Perimeter of the triangle $ = 166{\text{ cm}}$

Assume the shortest side as $x{\text{ cm}}$ and find the length of the other two sides as per the given information. Take the sum of all the sides and use the relation Perimeter $ \geqslant $$166{\text{ cm}}$ to solve for the value of $x$.

Let us assume the length of the shortest side is $x{\text{ cm}}$,

Length of the longest side $ = 2x{\text{ cm}}$

Length of the third side $ = \left( {x + 2} \right){\text{ cm}}$

Since perimeter of the triangle is more than ${\text{166 cm}}$,

$\Rightarrow x + 2x + \left( {x + 2} \right) \geqslant 166$

$\Rightarrow 4x + 2 \geqslant 166$

$\Rightarrow 4x \geqslant 164$

$\Rightarrow x \geqslant 41$

Hence, the minimum length of the shortest side is $41{\text{ cm}}$.

12. In drilling world’s deepest hole it was found that the temperature ${\text{T}}$ in degree Celsius, $x km$ below the earth’s surface was given by $T = 30+25\left({x - 3} \right),3 \leqslant x \leqslant15$. At what depth will the temperature be between $15{5^o}C$ and $20{5^o}C$?

Ans: Given: Temperature ${\text{T}}$ (in degree Celsius) as a function of depth $x{\text{ km}}$ below the earth’s surface is ${\text{T}} = 30 + 25\left( {x - 3} \right),3 \leqslant x \leqslant 15$.

Use the relation ${155^ \circ }{\text{C}} < {\text{T}} < {205^ \circ }{\text{C}}$ and solve for the range of values of $x$.

Since the temperature at depth $x{\text{ km}}$ is to be between ${155^ \circ }{\text{C}}$ and ${205^ \circ }{\text{C}}$,

$\Rightarrow {155^ \circ }{\text{C}} < {\text{T}} < {205^ \circ }{\text{C}}$

$\Rightarrow 155 < 30 + 25\left( {x - 3} \right) < 205$

$\Rightarrow 125 < 25\left( {x - 3} \right) < 175$

Dividing all the terms by $25$,

$\Rightarrow 5 < \left( {x - 3} \right) < 7$

$\Rightarrow 8 < x < 10$ 

For the temperature to be between ${155^ \circ }{\text{C}}$ and ${205^ \circ }{\text{C}}$ the depth must be between ${\text{8 km}}$ and ${\text{10 km}}$.

13. Solve the following system of inequalities: $\dfrac{{2x + 1}}{{7x - 1}} > 5$, $\dfrac{{x + 7}}{{x - 8}} > 2$.

Ans: Given: The system of inequalities$\dfrac{{2x + 1}}{{7x - 1}} > 5$ and $\dfrac{{x + 7}}{{x - 8}} > 2$.

Solve the two inequalities separately by taking all the terms to the L.H.S. and take the intersection of the sets of values of $x$ obtained.

Use the formula: -

If $\dfrac{a}{b} < 0$ then $a$ and $b$ are of opposite signs.

The provided system of inequalities are $\dfrac{{2x + 1}}{{7x - 1}} > 5$ and $\dfrac{{x + 7}}{{x - 8}} > 2$, so on simplification,

$ \Rightarrow \dfrac{{2x + 1}}{{7x - 1}} - 5 > 0$ and $\dfrac{{x + 7}}{{x - 8}} - 2 > 0$

$ \Rightarrow \dfrac{{\left( {2x + 1} \right) - 5\left( {7x - 1} \right)}}{{7x - 1}} > 0$ and $\dfrac{{\left( {x + 7} \right) - 2\left( {x - 8} \right)}}{{x - 8}} > 0$

\[ \Rightarrow \dfrac{{ - 33x + 6}}{{7x - 1}} > 0\] and $\dfrac{{ - x + 23}}{{x - 8}} > 0$

Multiplying both the inequalities with $ - 1$,

$ \Rightarrow \dfrac{{11x - 2}}{{7x - 1}} < 0$ and $\dfrac{{x - 23}}{{x - 8}} < 0$

If $\dfrac{a}{b} < 0$ then $a$ and $b$ are of opposite signs.

(1) For the inequality $\dfrac{{11x - 2}}{{7x - 1}} < 0$,

$ \Rightarrow (11x - 2 < 0$ and $7x - 1 > 0)$ or $(11x - 2 > 0$ and $7x - 1 < 0)$

$ \Rightarrow (x < \dfrac{2}{{11}}$ and $x > \dfrac{1}{7})$ or $(x > \dfrac{2}{{11}}$ and $x < \dfrac{1}{7})$

The condition $(x > \dfrac{2}{{11}}$ and $x < \dfrac{1}{7})$ is not possible but $(x < \dfrac{2}{{11}}$ and $x > \dfrac{1}{7})$ is possible, so the solution set is $x \in \left( {\dfrac{1}{7},\dfrac{2}{{11}}} \right)$.

(2) For the inequality $\dfrac{{x - 23}}{{x - 8}} < 0$,

$ \Rightarrow (x - 23 < 0$ and $x - 8 > 0)$ or $(x - 23 > 0$ and $x - 8 < 0)$

$ \Rightarrow (x < 23$ and $x > 8)$ or $(x > 23\text{ and } x < 8)$

Now, the condition $(x > 23$ and $x < 8)$ is not possible but $(x < 23$ and $x > 8)$ is possible, so the solution set is $x \in \left( {8,23} \right)$.

Therefore, the solution set of the given system can be given as$x \in \left( {\dfrac{1}{7},\dfrac{2}{{11}}} \right) \cap \left( {8,23} \right)$ which is a null set $\left( \phi  \right)$.

14. Find the linear inequalities for which the shaded region in the given figure is the solution set.

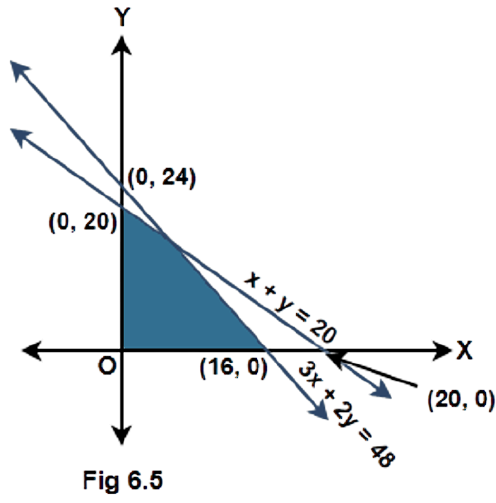
Ans: Given: A shaded portion as the solution set of some linear inequalities.

Consider the given equations of the lines and check the side at which the origin and the shaded portion lie with respect to each line. Form the inequalities accordingly using the equation of the lines.

 (1) Considering the line $x + y = 20$, the origin and the shaded area lie on the same side of this line. Substituting the point $\left( {0,0} \right)$ in the L.H.S gives $0$ which is less than $20$ in the R.H.S. Also there is a solid line and not a dashed line. Therefore, the inequality is $x + y \leqslant 20$.

(2) Considering the line $3x + 2y = 48$, the origin and the shaded area lie on the same side of this line. Substituting the point $\left( {0,0} \right)$ in the L.H.S gives $0$ which is less than $48$ in the R.H.S. Therefore, the inequality is $3x + 2y \leqslant 48$.

(3) At last it can be seen that the shaded area lies in the first quadrant whose inequalities are given as $x \geqslant 0$ and $y \geqslant 0$.

Hence, the inequalities representing the solution set shown in figure 6.5 are: -

$x + y \leqslant 20$, $3x + 2y \leqslant 48$, $x \geqslant 0$ and $y \geqslant 0$.

15. Find the linear inequalities for which the shaded region in the given figure is the solution set.

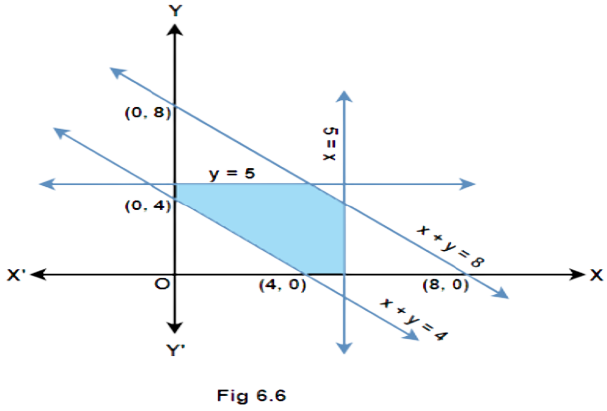
Ans: Given: A shaded portion as the solution set of some linear inequalities.

Consider the given equations of the lines and check the side at which the origin and the shaded portion lie with respect to each line. Form the inequalities accordingly using the equation of the lines.

 (1) Considering the line $x + y = 8$, the origin and the shaded area lie on the same side of this line. Substituting the point $\left( {0,0} \right)$ in the L.H.S gives $0$ which is less than $8$ in the R.H.S. Also there is a solid line and not a dashed line. Therefore, the inequality is $x + y \leqslant 8$.

(2) Considering the line $x = 5$, the origin and the shaded area lie on the same side of this line. Substituting the point $\left( {0,0} \right)$ in the L.H.S gives $0$ which is less than $5$ in the R.H.S. Therefore, the inequality is $x \leqslant 5$.

(3) Considering the line $y = 5$, the origin and the shaded area lie on the same side of this line. Substituting the point $\left( {0,0} \right)$ in the L.H.S gives $0$ which is less than $5$ in the R.H.S. Therefore, the inequality is $y \leqslant 5$.

(4) Considering the line $x + y = 4$, the origin and the shaded area lie on the opposite sides of this line. Substituting the point $\left( {0,0} \right)$ in the L.H.S gives $0$ which is less than $4$ in the R.H.S that means the inequality of the side containing the origin is $x + y \leqslant 4$. Therefore, the inequality of the side containing the shaded area is $x + y \geqslant 4$.

(5) At last it can be seen that the shaded area lies in the first quadrant whose inequalities are given as $x \geqslant 0$ and $y \geqslant 0$.

Hence, the inequalities representing the solution set shown in figure 6.1 are: -

$x + y \leqslant 8$, $x \leqslant 5$, $y \leqslant 5$, $x + y \geqslant 4$, $x \geqslant 0$ and $y \geqslant 0$.

16. Show that the following system of linear inequalities has no solution:

$x + 2y \leqslant 3$, $3x + 4y \geqslant 12$, $x \geqslant 0$, $y \geqslant 1$. 

Ans: Given: The system of linear inequalities:

$x + 2y \leqslant 3$, $3x + 4y \geqslant 12$, $x \geqslant 0$, $y \geqslant 1$

Draw the graphs of all the inequalities on a single graph and check if there is a common region bounded by all of them. If not, then there is no solution to the system.

(1) Considering the inequality $x + 2y \leqslant 3$, the point $\left( {0,0} \right)$ satisfies the inequality that means the origin lies in the region subtended by this inequality.

(2) Considering the inequality $3x + 4y \geqslant 12$, the point $\left( {0,0} \right)$ does not satisfy the inequality that means the origin does not lie in the region subtended by this inequality.

(3) Considering the inequality $x \geqslant 0$, the point $\left( {0,0} \right)$ satisfies the inequality that means the origin lies in the region subtended by this inequality.

(4) Considering the inequality $y \geqslant 1$, the point $\left( {0,0} \right)$ does not satisfy the inequality that means the origin does not lie in the region subtended by this inequality.

The plot of all the inequalities with their subtended region shown by the arrows can be represented as below: -

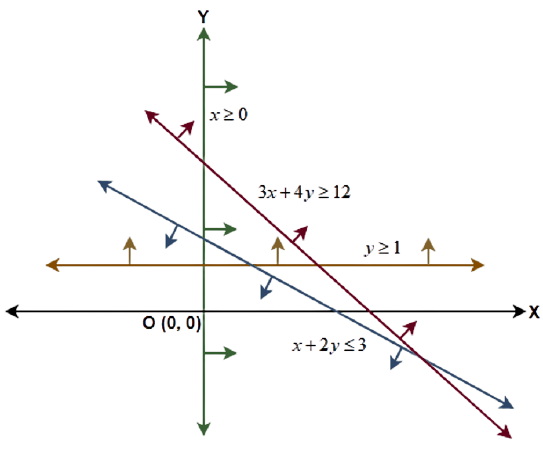
Clearly there is no common region for the given inequalities. Hence, the system has no solution.

Exercise 17. Solve the following system of linear inequalities:

$3x + 2y \geqslant 24$, $3x + y \leqslant 15$, $x \geqslant 4$

Ans: Given: The system of linear inequalities:

$3x + 2y \geqslant 24$, $3x + y \leqslant 15$, $x \geqslant 4$

Draw the graphs of all the inequalities on a single graph and check if there is a common region bounded by all of them. If yes then that region is the solution set. If not, then there is no solution to the system.

(1) Considering the inequality $3x + 2y \geqslant 24$, the point $\left( {0,0} \right)$ does not satisfy the inequality that means the origin does not lie in the region subtended by this inequality.

(2) Considering the inequality $3x + y \leqslant 15$, the point $\left( {0,0} \right)$ satisfies the inequality that means the origin lies in the region subtended by this inequality.

(3) Considering the inequality $x \geqslant 4$, the point $\left( {0,0} \right)$ does not satisfy the inequality that means the origin does not lie in the region subtended by this inequality.

The plot of all the inequalities with their subtended region shown by the arrows can be represented as below:

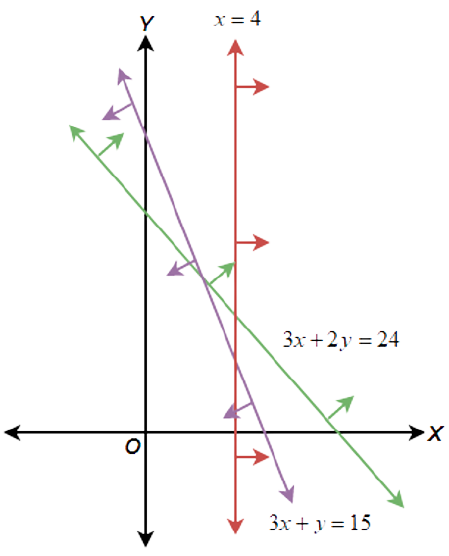
Clearly there is no common region for the given inequalities. Therefore, the system has no solution.

18. Show that the solution set of the following system of linear inequalities is an unbounded region.

Ans: Given: The system of linear inequalities:

$2x + y \geqslant 8$, $x + 2y \geqslant 10$, $x \geqslant 0$, $y \geqslant 0$

Draw the graphs of all the inequalities on a single graph and check the region bounded by them. If $x$ and $y$ values of the bounded region extend up to $\infty $ then the region is unbounded.

 (1) Considering the inequality $2x + y \geqslant 8$, the point $\left( {0,0} \right)$ does not satisfy the inequality that means the origin does not lie in the region subtended by this inequality.

(2) Considering the inequality $x + 2y \geqslant 10$, the point $\left( {0,0} \right)$ does not satisfy the inequality that means the origin does not lie in the region subtended by this inequality.

(3) The inequalities $x \geqslant 0$ and $y \geqslant 0$ means the region is the first quadrant only.

The plot of all the inequalities with their combined bounded region (shown by the arrows) can be represented as below:

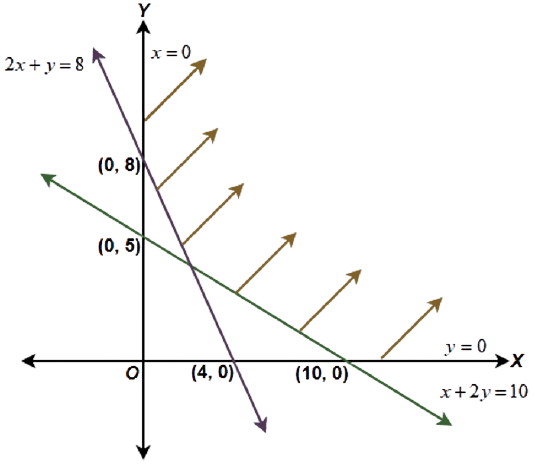
Clearly in the bounded region, the values of $x$ and $y$ are not limited. Hence, the solution set is an unbounded region.

19. If \[x < 5\], then

(A) $ - x <  - 5$

(B) $-x \leqslant -5$

(C) $ - x >  - 5$

(D) $-x \geqslant -5$

Ans: Option (C) is the correct answer.

Given: The inequality $x < 5$.

Use the fact that when a negative number is multiplied on both the sides of an inequality then the direction of the inequality sign gets reversed.

The provided linear inequality is $x < 5$. If a negative number is multiplied on both the sides of an inequality then the direction of the inequality sign gets reversed.

$\Rightarrow \left( { - 1} \right) \times x > \left( { - 1} \right) \times 5$

$\Rightarrow  - x >  - 5$

Correct Answer: C

20. Given that $x,y$ and $b$ are real numbers and $x < y$, $b < 0$, then

(A) $\dfrac{x}{b} < \dfrac{y}{b}$

(B) $\dfrac{x}{b} \geqslant \dfrac{y}{b}$

(C) $\dfrac{x}{b} > \dfrac{y}{b}$

(D) None of these

Ans: Option (C) is the correct answer.

Given: The inequality $x < y$ and $b < 0$.

Use the fact that when both sides of an inequality are divided by a negative number then the direction of the inequality sign gets reversed.

The provided linear inequality is $x < y$ and $b < 0$. That means $b$ is a negative number.

If both sides of an inequality are divided by a negative number then the direction of the inequality sign gets reversed.

$\Rightarrow \dfrac{x}{b} > \dfrac{y}{b}$

Correct Answer: C

21. If $ - 3x + 17 <  - 13$, then

(A) $x \in \left( {10,\infty} \right)$

(B) $x \in \left[ {10,\infty} \right)$

(C) $x \in \left( { - \infty,10} \right]$

(D) $x \in \left[ { - 10,10} \right)$

Ans: Option (A) is the correct answer.

Given: The inequality $ - 3x + 17 <  - 13$.

Use the fact that when both sides of an inequality are divided by a negative number then the direction of the inequality sign gets reversed.

If the endpoint is not included then the symbol for an open interval is used.

The provided linear inequality is $ - 3x + 17 <  - 13$.

$\Rightarrow  - 3x <  - 13 - 17$

$\Rightarrow  - 3x <  - 30$

If both sides of an inequality are divided by a negative number then the direction of the inequality sign gets reversed.

$\Rightarrow \dfrac{{ - 3x}}{{ - 3}} > \dfrac{{ - 30}}{{ - 3}}$

$\Rightarrow x > 10$

$\Rightarrow x \in \left( {10,\infty } \right)$ 

Correct Answer: A

22. If $x$ is a real number and $\left| x \right| < 3$, then

(A) $x \geqslant  3$

(B) $ - 3 < x < 3$

(C) $x \geqslant- 3$

(D) $- 3\geqslant x\geqslant - 3$

Ans: Option (A) is the correct answer.

Given: The inequality $\left| x \right| < 3$.

Use the formula if $\left| x \right| < a$, where $a$ is a positive real number, then $ - a < x < a$.

The provided linear inequality is $\left| x \right| < 3$. If $\left| x \right| < a$, where $a$ is a positive real number, then $ - a < x < a$.

$\Rightarrow  - 3 < x < 3$

Correct Answer: C

23. $x$ and $b$ are real numbers. If $b > 0$ and $\left| x \right| > b$, then

(A) $x \in \left( { - b, - \infty} \right)$

(B) $x \in \left[ { - \infty,b} \right)$

(C) $x \in \left( { - b,b} \right)$

(D) $x \in \left({ -\infty,b} \right)\, \left( {b,\infty} \right)$

Ans: Option (D) is the correct answer.

Given: The inequality $\left| x \right| > b$, where $b > 0$.

Use the formula if $\left| x \right| > a$, where $a$ is a positive real number, then $x <  - a$ or $x > a$.

The provided linear inequality is $\left| x \right| > b$, where $b > 0$. That means $b$ is a positive number.

If $\left| x \right| > a$, where $a$ is a positive real number, then $x <  - a$ or $x > a$.

$\Rightarrow x <  - b$ or $x > b$

$\Rightarrow x \in \left( { - \infty , - b} \right) \cup \left( {b,\infty } \right)$

Correct Answer: D

24. If $\left| {x - 1} \right| > 5$, then

(A) $x \in \left( { - 4,6} \right)$

(B) $x \in \left[ { - 4,6} \right]$

(C) $x \in \left({ - \infty, - 4} \right)\, \left( {6,\infty} \right)$

(D) $x \in \left[ { - \infty, - 4} \right)\, \left[ {6,\infty} \right)$

Ans: Option (C) is the correct answer.

Given: The inequality $\left| {x - 1} \right| > 5$.

Use the formula if $\left| {f\left( x \right)} \right| > a$, where $a$ is a positive real number, then $f\left( x \right) <  - a$ or $f\left( x \right) > a$. Solve the inequalities for each case and take the union of the solution sets of $x$.

The provided linear inequality is $\left| {x - 1} \right| > 5$. If $\left| {f\left( x \right)} \right| > a$, where $a$ is a positive real number, then $f\left( x \right) <  - a$ or $f\left( x \right) > a$.

$\Rightarrow x - 1 <  - 5$ or $x - 1 > 5$

$\Rightarrow x <  - 4$ or $x > 6$

$\Rightarrow x \in \left( { - \infty , - 4} \right) \cup \left( {6,\infty } \right)$

Correct Answer: C

25. If $\left| {x + 2} \right| \leqslant 9$, then

(A) $x \in \left( { - 7,11} \right)$

(B) $x \in \left[ { - 11,7} \right]$

(C) $x \in \left( { - \infty, - 7} \right)\, \left( {11,\infty} \right)$

(D) $x \in \left( { - \infty, - 7} \right)\,\left[ {11,\infty} \right)$

Ans: Option (B) is the correct answer.

Given: The inequality $\left| {x + 2} \right| \leqslant 9$.

Use the formula if $\left| {f\left( x \right)} \right| \leqslant a$, where $a$ is a positive real number, then \[ - a \leqslant f\left( x \right) \leqslant a\].

The provided linear inequality is $\left| {x + 2} \right| \leqslant 9$. If $\left| {f\left( x \right)} \right| \leqslant a$, where $a$ is a positive real number, then \[ - a \leqslant f\left( x \right) \leqslant a\].

$\Rightarrow  - 9 \leqslant x + 2 \leqslant 9$

$\Rightarrow  - 9 - 2 \leqslant x \leqslant 9 - 2$

$\Rightarrow  - 11 \leqslant x \leqslant 7$

$\Rightarrow x \in \left[ { - 11,7} \right]$ 

Correct Answer: B

26. The inequality representing the following graph is:

(A) $\left| x \right| < 5$

(B) $\left| x \right| \leqslant 5$

(C) $\left| x \right| > 5$

(D) $\left| x \right| \geqslant 5$

Ans: Option (A) is the correct answer.

Given: The graph shown below:

Check if the graph is bounded at end points or not. If not, then the end point is not included and an open interval should be used.

If the inequality is of the form $ - a < x < a$, where $a$ is a positive real number, then use the formula $\left| x \right| < a$.

In the given graph the values of $x$ ranges from $ - 5$ to $5$. The graph is not bounded that means the values $ - 5$ and $5$ are not included. Therefore, an open interval will be used.

$ \Rightarrow  - 5 < x < 5$

If $ - a < x < a$, where $a$ is a positive real number, then $\left| x \right| < a$.

$\Rightarrow \left| x \right| < 5$

Correct Answer: A

27. Choose the correct answer for the solution of a linear inequality in variable $x$ represented on a number line.

(A) $x \in \left( { - \infty, 5} \right)$

(B) $x \in \left( { - \infty, 5} \right]$

(C) $x \in \left[ {5,\infty} \right)$

(D) $x \in \left( {5,\infty} \right)$

Ans: Option (D) is the correct answer.

The thick line is running from $5$ to $\infty $ and the point $5$ is not included. So the open interval will be used towards $5$. Also, $\infty $ is not a real number so here an open interval will be used.

Therefore, the solution set is $x \in \left( {5,\infty } \right)$.

Correct Answer: D

28. Choose the correct answer for the solution of a linear inequality in variable $x$ represented on a number line.

(A) $x \in \left( {\dfrac{9}{2}, \infty} \right)$

(B) $x \in \left[ {\dfrac{9}{2}, \infty} \right)$

(C) $x \in \left[ { - \infty , \dfrac{9}{2}} \right)$

(D) $x \in \left( { - \infty, \dfrac{9}{2}} \right]$

Ans: Option (B) is the correct answer.

The thick line is running from $\dfrac{9}{2}$ to $\infty $ and the point $\dfrac{9}{2}$ is included. So the closed interval will be used towards $\dfrac{9}{2}$. Also, $\infty $ is not a real number so here an open interval will be used.

Therefore, the solution set is $x \in \left[ {\dfrac{9}{2},\infty } \right)$.

Correct Answer: B

29. Choose the correct answer for the solution of a linear inequality in variable $x$ represented on a number line.

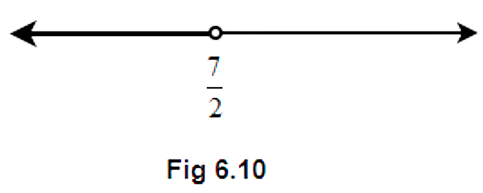
(A) $x \in \left( { - \infty, \dfrac{7}{2}} \right)$

(B) $x \in \left( { - \infty, \dfrac{7}{2}} \right]$

(C) $x \in \left[ {\dfrac{7}{2}, -\infty} \right)$

(D) $x \in \left( {\dfrac{7}{2}, \infty} \right)$

Option (A) is the correct answer.

Ans: The thick line is running from $ - \infty $ to $\dfrac{7}{2}$ and the point $\dfrac{7}{2}$ is not included. So the open interval will be used towards $\dfrac{7}{2}$. Also, $ - \infty $ is not a real number so here an open interval will be used.

Therefore, the solution set is $x \in \left( { - \infty ,\dfrac{7}{2}} \right)$.

Correct Answer: A

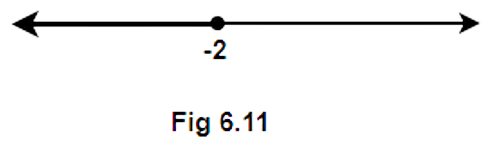
30. Choose the correct answer for the solution of a linear inequality in variable $x$ represented on a number line.

(A) $x \in \left( { - \infty, - 2} \right)$

(B) $x \in \left( { - \infty, - 2} \right]$

(C) $x \in \left( { - 2,\infty} \right]$

(D) $x \in \left[ { - 2,\infty} \right)$

Ans: Option (B) is the correct answer.

The thick line is running from $ - \infty $ to $ - 2$ and the point $ - 2$ is included. So the closed interval will be used towards $ - 2$. Also, $ - \infty $ is not a real number so here an open interval will be used.

Therefore, the solution set is $x \in \left( { - \infty, - 2} \right]$.

31. State whether the following statements are True or False.

(i) If $x < y$ and $b < 0$, then $\dfrac{x}{b} < \dfrac{y}{b}$

Ans: The given statement is false because if both sides of an inequality are divided by a negative number then the direction of the inequality gets reversed.

(ii) If $xy > 0$, then $x > 0$ and $y < 0$

Ans: The given statement is false because if the numbers are of opposite sign then their product is always negative.

(iii) If $xy > 0$, then $x < 0$ and $y < 0$

Ans: The given statement is true because if the numbers are of the same sign then their product is always positive.

(iv) If $xy < 0$, then $x < 0$ and $y < 0$

Ans: The given statement is false because if the numbers are of the same sign then their product is always positive.

(v) If $x <  - 5$ and $x <  - 2$, then $x \in \left( { - \infty, - 5} \right)$

Ans: The given statement is true because here the solution set is the intersection of the sets $x \in \left( { - \;\infty , - \;5} \right)$ and $x \in \left( { - \;\infty , - \;2} \right)$.

(vi) If $x <  - 5$ and $x > 2$, then $x \in \left( { - 5,2} \right)$

Ans: The given statement is false because here the solution set is the intersection of the sets $x \in \left( { - \;\infty , - \;5} \right)$ and $x \in \left( {2,\infty } \right)$ which is a null set $\left( \phi  \right)$.

(vii) If $x >  - 2$ and $x < 9$, then $x \in \left( { - 2,9} \right)$

Ans: The given statement is true because here the solution set is the intersection of the sets $x \in \left( { - \;2,\infty } \right)$ and $x \in \left( { - \;\infty ,9} \right)$.

(viii) If $\left| x \right| > 5$, then $x \in \left( { - \infty, - 5} \right) \cup \left[ {5,\infty} \right)$

Ans: The given statement is false because according to the formula if $\left| x \right| > a$ then $x <  - a$ or $x > a$, where $a$ being any positive real number. Open interval should be used at the end points.

(ix) If $\left| x \right| \leqslant 4$, then $x \in \left[ { - 4,4} \right]$

Ans: The given statement is true because according to the formula if $\left| x \right| \leqslant a$ then $ - a \leqslant x \leqslant a$, where $a$ being any positive real number.Closed intervals should be used at the end points.

(x) Graph of $x < 3$ is

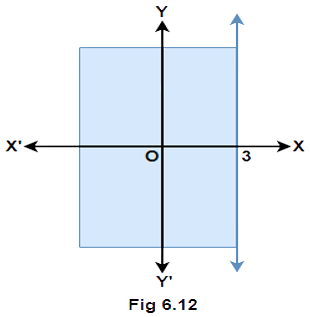
Ans: The given statement is false because the line $x = 3$ is represented by a solid line instead of a dashed line in the figure 6.12. The value $x = 3$ should not be included.

(xi) Graph of $x \geqslant 0$ is

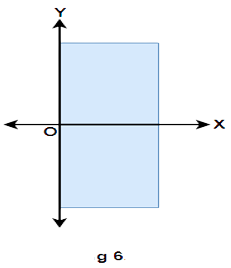
Ans: The given statement is true because in the first and fourth quadrant the values of $x$ is positive and the $y$ axis represents the line $x = 0$.

(xii) Graph of $y \leqslant 0$ is

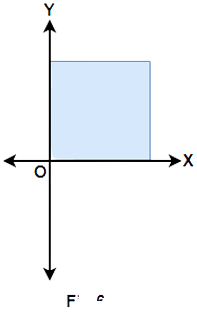
Ans: The given statement is false because in the first and second quadrant $y \geqslant 0$.

(xiii) Solution set of $x \geqslant 0$ and $y \leqslant 0$ is

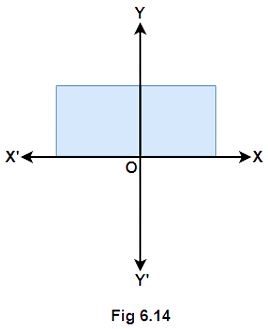
Ans: The given statement is false because in the first quadrant both $x \geqslant 0$ and $y \geqslant 0$.

(xiv) Solution set of $x \geqslant 0$ and $y \leqslant 1$ is

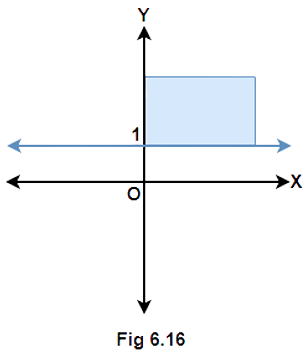
Ans: The given statement is false because the graph in figure 6.16 represents the inequalities $x \geqslant 0$ and $y \geqslant 1$.

(xv) Solution set of $x+y \geqslant 0$ is

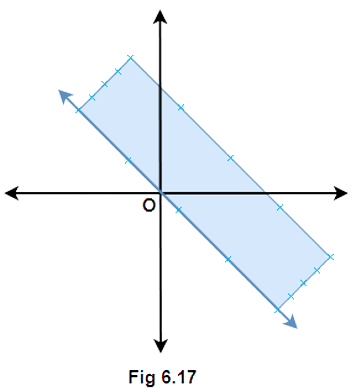
Ans: The given statement is true because if the inequality $x + y \geqslant 0$ is simplified it gives $x \geqslant  - y$ that means the shaded portion must be above the line $x =  - y$.

32. Fill in the blanks in the following:

(i) If $ - 4x \geqslant 12$, then $x... - 3$

Ans: The provided inequality is $ - 4x \geqslant 12$, so dividing both the sides with $ - 4$,

$\Rightarrow \dfrac{{ - 4x}}{{ - 4}} \leqslant \dfrac{{12}}{{ - 4}}$

$\Rightarrow x \leqslant  - 3$ 

(ii) If $\dfrac{{ - 3}}{4}x \leqslant  - 3$, then $x...4$

Ans: The provided inequality is $\dfrac{{ - 3}}{4}x \leqslant  - 3$, multiplying both the sides with $\dfrac{{ - 4}}{3}$,

$\Rightarrow \left( {\dfrac{{ - 4}}{3}} \right) \times \left( {\dfrac{{ - 3}}{4}x} \right) \geqslant \left( {\dfrac{{ - 4}}{3}} \right) \times \left( { - 3} \right)$

$\Rightarrow x \geqslant 4$ 

(iii) If $\dfrac{2}{{x + 2}} > 0$ then $x... - 2$

Ans: The provided inequality is $\dfrac{2}{{x + 2}} > 0$. If $\dfrac{a}{b} > 0$ then $a$ and $b$ are of the same sign. Since the numerator is positive so $\left( {x + 2} \right) > 0$ which gives $x >  - 2$.

(iv) If $x >  - 5$, then $4x... - 20$

Ans: The provided inequality is $x >  - 5$, multiplying both the sides with $4$,

$ \Rightarrow 4x >  - 20$

(v) If $x > y$ and $z < 0$, then $ - xz... - yz$

Ans: The provided inequality is $x > y$ and $z < 0$. Since $z$ is negative, multiplying both the sides with $z$ will change the direction of inequality.

$\Rightarrow xz < yz$

Multiplying both the sides with $ - 1$,

$\Rightarrow  - xz >  - yz$

(vi) If $p > 0$ and $q < 0$, then $p - q…p$

Ans: Since, $p > 0$ and $q < 0$ so considering the difference $p - q$ means subtracting a negative number from a positive number. This will increase some quantity from $p$.

$\Rightarrow p - q > p$

(vii) If $\left| {x + 2} \right| > 5$, then $x... - 7$ or $x...3$

Ans: The provided inequality is $\left| {x + 2} \right| > 5$. If $\left| x \right| > a$ then $x <  -a$ or $x > a$ for any positive real number $a$.

$\Rightarrow x + 2 <  - 5$ or $x + 2 > 5$

$\Rightarrow x <  - 7$ or $x > 3$

(viii) If $ - 2x + 1 \geqslant 9$, then $x... - 4$

Ans: The provided inequality is $ - 2x + 1 \geqslant 9$.

$\Rightarrow  - 2x \geqslant 9 - 1$

$\Rightarrow  - 2x \geqslant 8$

$\Rightarrow \dfrac{{ - 2x}}{{ - 2}} \leqslant \dfrac{8}{{ - 2}}$

$\Rightarrow x \leqslant  - 4$

NCERT Exemplar for Class 11 Math - Linear Inequalities

You must have studied equations of a single variable or two variables in your previous classes. Also, you have solved varied problems/complexities based on it. So, now you are  ready to learn the next level of it via NCERT Exemplar for Class 11 Math Chapter 6 - Linear Inequalities (Book Solutions). 

For this, you must be looking for the best study platform? You can obtain solutions from Vedantu's team along with other study material required to perfect your performance. Math challenges you with varied real-life mathematical equations such as the height of family members. For instance, it is less than 175CM, how many chairs can a room occupy, etc. You may feel stuck here as both of the equations cannot be converted into equations. To find the resolutions of such problems, the signs ‘≤’ (less than or equal than), <' (less than) and  ≥ (greater than are introduced. At Vedantu, the tutors will guide you to comprehend the inequality concept in detail and you will get to know how the inequality concept can be used in the constraints formulations.

Vedantu's experts will describe the chapter in detail for the students where they will learn questions based on inequalities in a single variable or inequalities in two variables. This chapter is helpful in terms of resolving issues such as cost estimation. Thus, the students will be able to grasp the linear inequalities concept with ease with the help of Vedantu's experts.