Free PDF Download of NCERT Exemplar Solutions
FAQs on NCERT Exemplar for Class 12 Maths - Vector Algebra - Free PDF Download
1. Where can students find Exemplar for Class 12 Maths Chapter 10 - Vector Algebra.
Students can easily find a PDF from Chapter 10 - Vector Algebra for Class 12 at Vedantu.com. The Exemplar consists of solutions to the textbooks and additional questions separately to help students to score their best marks. The Exemplar PDF for Class 12 Maths, Chapter - Vector Algebra consists of every step solutions to the textbook problems. In order to increase the conceptual knowledge of students, Exemplars are a good option. The Exemplar is presented in the PDF at Vedantu.com for the students.
2. Is Chapter 10 - Vector Algebra is an important Chapter for a Class 12 student?
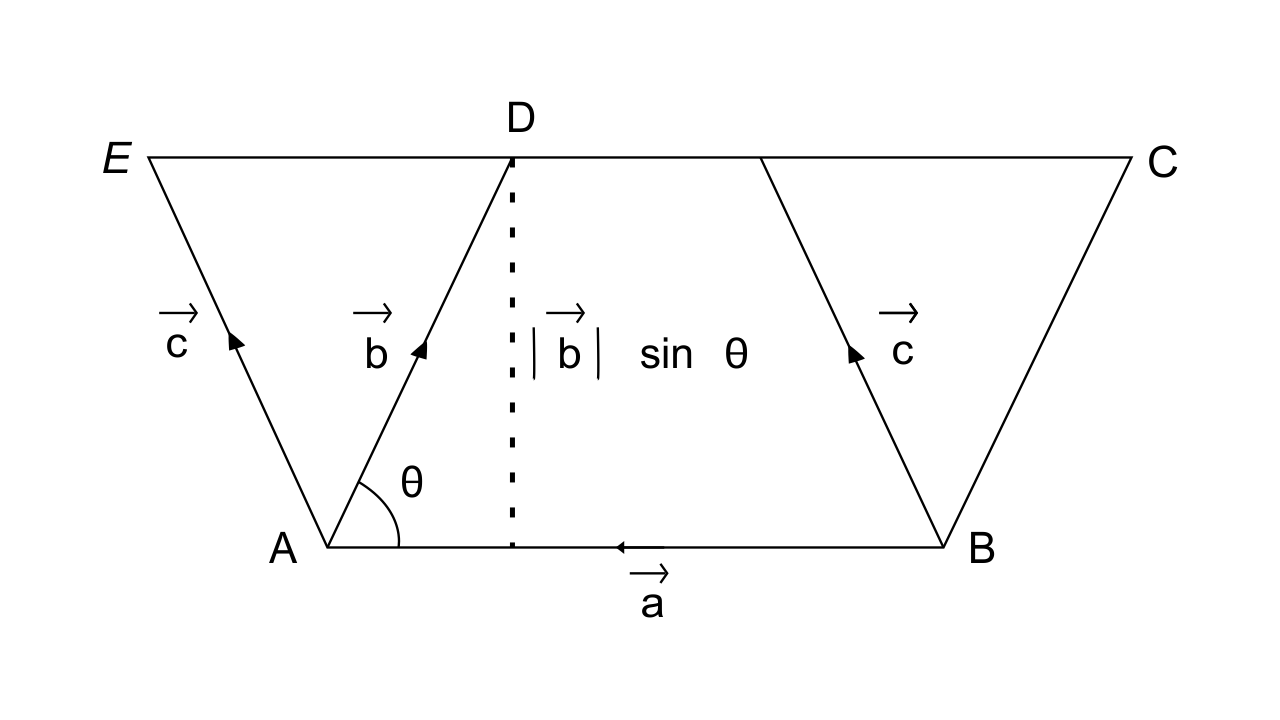
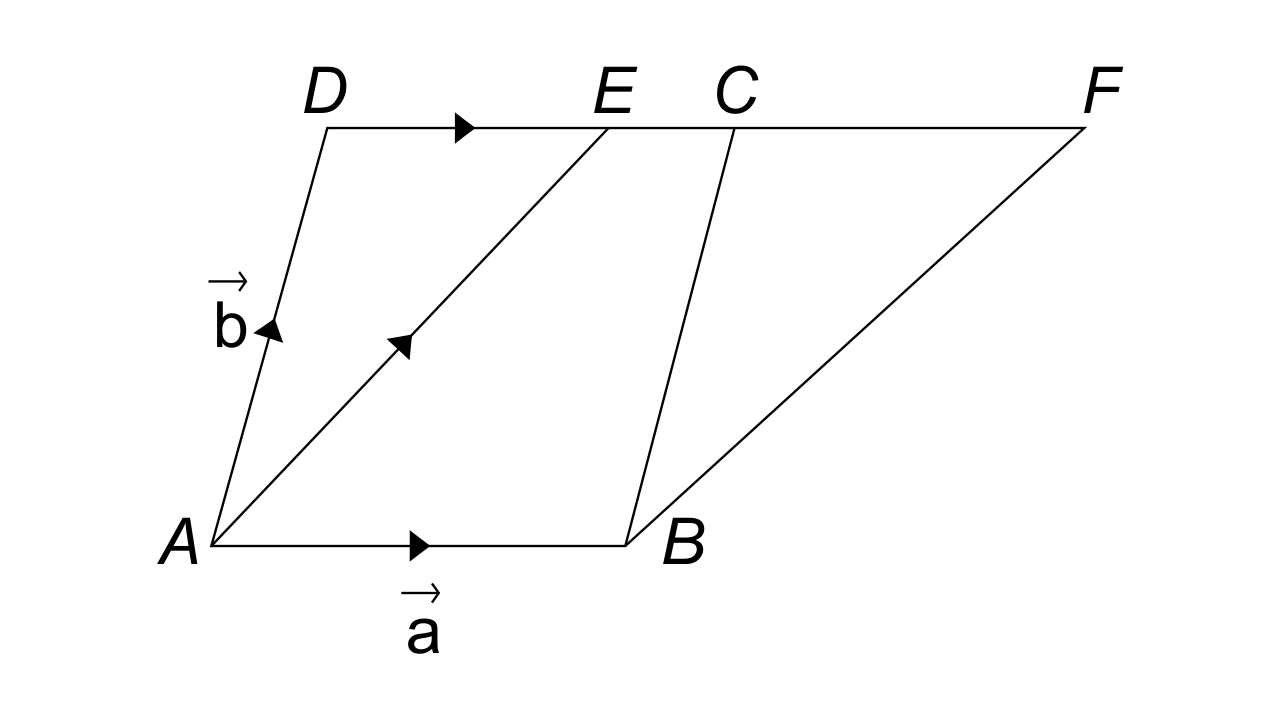
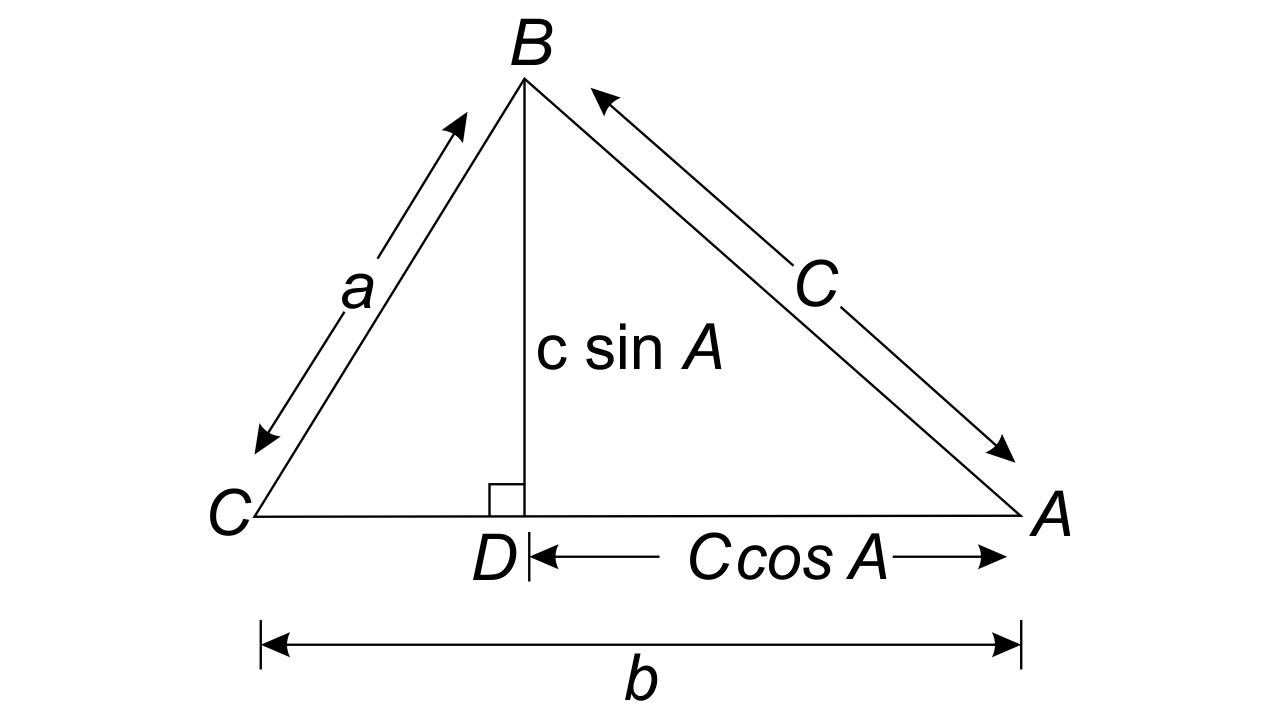
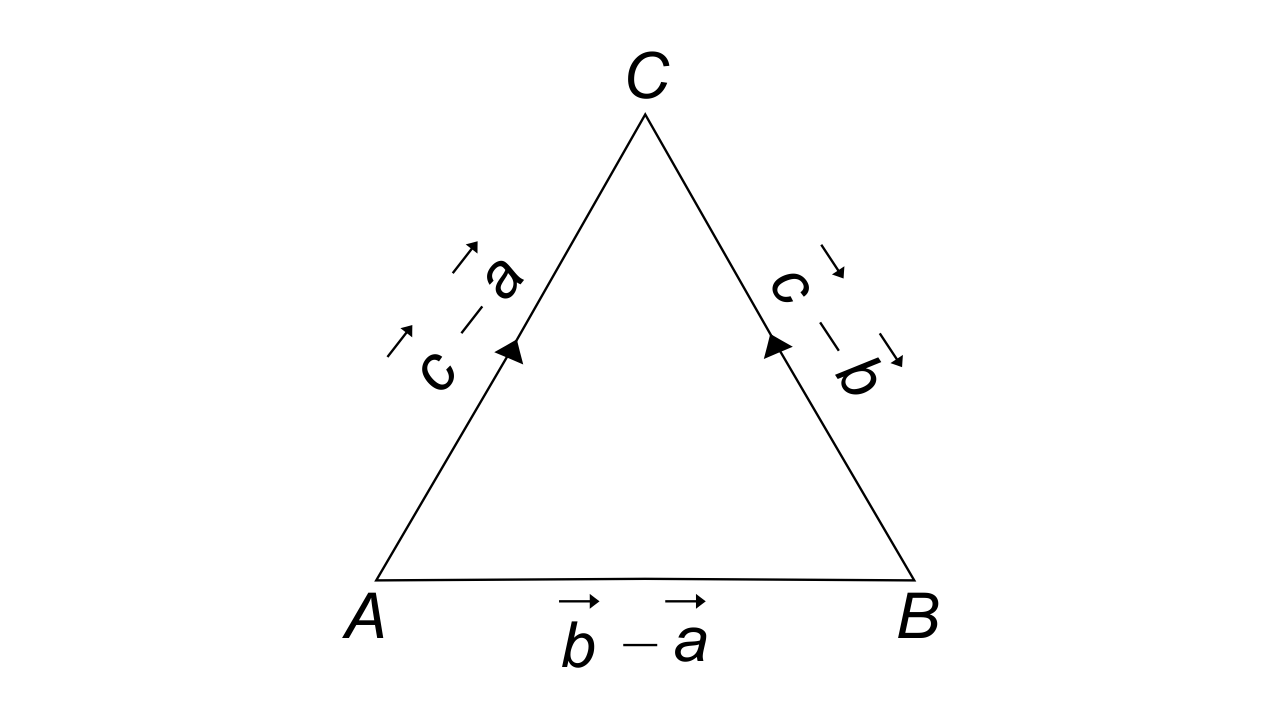
Class 12 is considered to be the most important Class for a student’s life. So all the Chapters are important as they all help students to score their best marks in the Examinations. This Chapter needs special attention, Exemplar sorts a life of a student with full information. This Chapter consists of an introduction to Vectors, types of Vectors, multiplication, and addition performed on Vectors, section formula, components of a Vector, projection of a Vector on a line, scalar product, and Vector product.
3. How the Exemplars are designed by Vedantu for a student?
Exemplars are designed by the expert faculty at Vedantu considering the latest syllabus advised by the Central Board of Secondary Education. The Exemplar PDF for Class 12 Maths, Chapter - Vector Algebra consists of every step solutions to the textbook problems. Students can easily access the NCERT Exemplar PDF available Chapter-wise as well as subject-wise for getting any guidance to solve the problems. Solutions added to the Exemplar PDF are created to help students at various levels of difficulties.
4. Why Exemplars are important for the preparation of students for their Examinations?
Exemplars help students practice more and more to score their best marks. Each question is available with a solution in every Exemplar, so students also can recheck their mistakes and work accordingly. Exemplar has notes that consist of formulas, these formulas are given separately for the students. Students can easily go concept by concept and clear their doubts. Vector Algebra is among the tough Chapters in Maths for Class 12. Students have to work hard for the Chapter to score better marks.