NCERT Exemplar for Class 12 Math - Differential Equations - Free PDF Download

EXAMPLES:

Solved Examples Short Answer Questions:

1. Find the differential equation of the family of curves \[{{y  =  A}}{{{e}}^{{\text{2x}}}}{\text{ + B}}{{{e}}^{{\text{ - 2x}}}}\]

Ans: We are  given that \[{{y  =  A}}{{{e}}^{{\text{2x}}}}{\text{ + B}}{{{e}}^{{\text{ - 2x}}}}\]

Now, differentiate both sides with respect to \[{{x}}\] we get:

${{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  2A}}{{{e}}^{{\text{2x}}}}{\text{ - 2B}}{{{e}}^{{\text{ - 2x}}}}$

${{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{  =  4A}}{{{e}}^{{\text{2x}}}}{\text{ + 4B}}{{{e}}^{{\text{ - 2x}}}}$

${{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{  =  4y}}$

${{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ - 4y  =  0}}$ 

2. Find the general solution of the differential equation \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{y}}}{{{x}}}\]

Ans: We are  given that \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{y}}}{{{x}}}\]

implies \[\dfrac{{{\text{dy}}}}{{{y}}}{\text{  =  }}\dfrac{{{\text{dx}}}}{{{x}}}\]

\[\int {\dfrac{{{\text{dy}}}}{{{y}}}} {\text{  = }}\int {\dfrac{{{\text{dx}}}}{{{x}}}} \]

Now, use formula i.e. \[{\text{logA + logB  =  logAB}}\] in RHS and then remove log, we get:

${\text{log y  =  log x + log c}}$

${{y  =  cx}}$ 

3. Given that \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  y }}{{{e}}^{{x}}}\] and \[{{x  =  0 , y  =  e}}\] . Find the value of \[{{y}}\] when \[{{x  =  1}}\]

Ans: We are  given that \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  y}}{{{e}}^{{x}}}\] which implies

${\dfrac{{{\text{dy}}}}{{{y}}}} {\text{  =  }}\int {{{{e}}^{{x}}}} {\text{dx}}$

${\text{log y  =  }}{{{e}}^{{x}}}{\text{ + c}}$ 

Now, substitute \[{{x  =  0 , y  =  e}}\] we get:

\[{\text{log e  =  }}{{{e}}^{\text{0}}}{\text{ + c}}\]

i.e. \[{\text{c  =  0}}\] as \[{\text{log e  =  1 , }}{{{e}}^0}{\text{  =  1}}\]

So, \[{\text{log y  =  }}{{{e}}^{{x}}}\]

Put \[{{x  =  1}}\] we get

${\text{log y  =  e}}$

${{y  =  }}{{{e}}^0}$ 

4. Solve the differential equation \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + }}\dfrac{{{y}}}{{{x}}}{\text{  =  }}{{{x}}^{\text{2}}}\]

Ans: This equation is of type \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + Py  =  Q}}\] which is a differential equation

I.F. \[{\text{ =  }}\int {\dfrac{{\text{1}}}{{{x}}}} {\text{dx  =  }}{{{e}}^{{\text{log x}}}}{{  =  x \times }}\left( {{{{e}}^{{\text{log(x)}}}}{\text{  =  f(x)}}} \right)\]

So, solution of given differential equation is \[{{yx  =  }}\int {{x}} {{{x}}^{\text{2}}}{\text{dx }} \Rightarrow {\text{ yx  =  }}\dfrac{{{{{x}}^{\text{4}}}}}{{\text{4}}}{\text{ + c}}\]

Thus, \[{{y  =  }}\dfrac{{{{{x}}^{\text{3}}}}}{{\text{4}}}{\text{ + }}\dfrac{{\text{c}}}{{{x}}}\]

5. Find the differential equation of the family of lines through the origin.

Ans: Let \[{{y  =  mx}}\] represents family of lines through origin i.e. \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  m}}\]

Now, Eliminate \[{\text{m}}\] we get:

${{y  =  }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{{ \times x}}$

${{x}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - y  =  0}}$ 

6. Find the differential equation of all non-horizontal lines in a plane.

Ans: Here, general equation of all non-horizontal lines in a plane represents as \[{\text{ax + by  =  c , a}} \ne {\text{0}}\]

Now differentiate both sides with respect to \[{{y}}\] we get:

\[{\text{a}}\dfrac{{{\text{dx}}}}{{{\text{dy}}}}{\text{ + b  =  0}}\]

Again, differentiate with respect to \[{{y}}\] we get:

${\text{a}}\dfrac{{{{\text{d}}^{\text{2}}}{{x}}}}{{{\text{d}}{{{y}}^{\text{2}}}}}{\text{  =  0}}$

${{{\text{d}}{{{x}}^{\text{2}}}}}{{{\text{d}}{{{y}}^{\text{2}}}}}{\text{  =  0}}$ 

7. Find the equation of a curve whose tangent at any point on it, different from origin has slope \[{{y + }}\dfrac{{{y}}}{{{x}}}\]

Ans: We have given that \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  y + }}\dfrac{{{y}}}{{{x}}}{\text{  =  y}}\left( {{\text{1 + }}\dfrac{{\text{1}}}{{{x}}}} \right)\]

implies \[\dfrac{{{\text{dy}}}}{{{y}}}{\text{  =  }}\left( {{\text{1 + }}\dfrac{{\text{1}}}{{{x}}}} \right){\text{dx}}\]

Now, integrate both sides, we get:

${\dfrac{{{\text{dy}}}}{{{y}}}} {\text{  =  }}\int {\left( {{\text{1 + }}\dfrac{{\text{1}}}{{{x}}}} \right)} {\text{dx}}$

${\text{log y  =  x + log x + c}}$

${\text{log}}\left( {\dfrac{{{y}}}{{{x}}}} \right){\text{  =  x + c}}$

${{{y}}}{{{x}}}{\text{  =  }}{{{e}}^{{{x + c}}}}{\text{  =  }}{{{e}}^{{x}}}{{ \times }}{{{e}}^{\text{c}}}$

$y {{x}} =  k \times {{e}}^{{x}}$

${y  =  kx \times } {{e}}^{{x}}$ 

Long Answer Questions

8. Find the equation of a curve which is passing through the point \[(1,1)\] .If the perpendicular distance of the origin from the normal at any point \[{\text{P(x,y)}}\] of the curve is equal to the distance of P form the \[{{x}}\] -axis.

Ans: Here Let equation of normal at \[{\text{P(x,y)}}\] be \[{{y - y  =  }}\dfrac{{{\text{ - dx}}}}{{{\text{dy}}}}{\text{(X - x)}}\]

\[{{y + X}}\dfrac{{{\text{dx}}}}{{{\text{dy}}}}{\text{ - }}\left( {{{y + x}}\dfrac{{{\text{dx}}}}{{{\text{dy}}}}} \right){\text{  =  0}}\]                                 (i)

So, length of perpendicular from origin to (i) be \[\dfrac{{{{y + x}}\dfrac{{{\text{dx}}}}{{{\text{dy}}}}}}{{\sqrt {{\text{1 + }}{{\left( {\dfrac{{{\text{dx}}}}{{{\text{dy}}}}} \right)}^{\text{2}}}} }}\]                                  (ii)

Also, distance between P and \[{{x}}\] -axis is \[{\text{|y|}}\]

Then, we have

\[\dfrac{{{{y + x}}\dfrac{{{\text{dx}}}}{{{\text{dy}}}}}}{{\sqrt {{\text{1 + }}{{\left( {\dfrac{{{\text{dx}}}}{{{\text{dy}}}}} \right)}^{\text{2}}}} }}{\text{  =  |y|}}\]

${\left( {{{y + x}}\dfrac{{{\text{dx}}}}{{{\text{dy}}}}} \right)^{\text{2}}}{\text{  =  }}{{{y}}^{\text{2}}}\left[ {{\text{1 + }}{{\left( {\dfrac{{{\text{dx}}}}{{{\text{dy}}}}} \right)}^{\text{2}}}} \right]$

${{{\text{dx}}}}{{{\text{dy}}}}\left[ {\dfrac{{{\text{dx}}}}{{{\text{dy}}}}\left( {{{{x}}^{\text{2}}}{\text{ - }}{{{y}}^{\text{2}}}} \right){\text{ + 2xy}}} \right]{\text{  =  0}}$

${{{\text{dx}}}}{{{\text{dy}}}}{\text{  =  0}}$

${{{\text{dx}}}}{{{\text{dy}}}}{\text{  =  }}\dfrac{{{\text{2xy}}}}{{{{{y}}^{\text{2}}}{\text{ - }}{{{x}}^{\text{2}}}}}$ 

Case I: \[\dfrac{{{\text{dx}}}}{{{\text{dy}}}}{\text{  =  0 }} \Rightarrow {\text{ dx  =  0}}\]

Now, integrate both sides we have \[{{x  =  k}}\]

Substitute \[{{x  =  1}}\] we get \[{\text{k  =  1}}\]

So, \[{{x  =  1}}\] is an equation of curve which is not possible. Thus, rejected

Case II: \[\dfrac{{{\text{dx}}}}{{{\text{dy}}}}{\text{  =  }}\dfrac{{{\text{2xy}}}}{{{{{y}}^{\text{2}}}{\text{ - }}{{{x}}^{\text{2}}}}}{\text{ }} \Rightarrow {\text{ }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{{{y}}^{\text{2}}}{\text{ - }}{{{x}}^{\text{2}}}}}{{{\text{2xy}}}}\]

Substitute \[{{y  =  vx}}\] we have

${\text{v + x}}\dfrac{{{\text{dv}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{{\text{v}}^{\text{2}}}{{{x}}^{\text{2}}}{\text{ - }}{{{x}}^{\text{2}}}}}{{{\text{2v}}{{{x}}^{\text{2}}}}}$

${{x \times }}\dfrac{{{\text{dv}}}}{{{\text{dx}}}} = \dfrac{{{{\text{v}}^{\text{2}}}{\text{ - 1}}}}{{{\text{2v}}}}{\text{ - v}}$

${{x}}\dfrac{{{\text{dv}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{{\text{v}}^{\text{2}}}{\text{ - 1}}}}{{{\text{2v}}}}{\text{ - v}}$

${\text{ =  }}\dfrac{{{\text{ - }}\left( {{\text{1 + }}{{\text{v}}^{\text{2}}}} \right)}}{{{\text{2v}}}}{\text{ }} \Rightarrow {\text{ }}\dfrac{{{\text{2v}}}}{{{\text{1 + }}{{\text{v}}^{\text{2}}}}}{\text{dv  =  }}\dfrac{{{\text{ - dx}}}}{{{x}}}$ 

Now, integrate both sides

${\text{log}}\left( {{\text{1 + }}{{\text{v}}^{\text{2}}}} \right){\text{  =   - log x + log c}}$

${\text{log}}\left( {{\text{1 + }}{{\text{v}}^{\text{2}}}} \right){\text{(x)  =  log c}}\left( {{\text{1 + }}{{\text{v}}^{\text{2}}}} \right){{x  =  c}}$

${{{x}}^{\text{2}}}{\text{ + }}{{{y}}^{\text{2}}}{\text{  =  cx}}$ 

Substitute \[{{x  =  1 , y  =  1}}\] we have \[{\text{c  =  2}}\]

Thus, \[{{{x}}^{\text{2}}}{\text{ + }}{{{y}}^{\text{2}}}{\text{ - 2x  =  0}}\]

9. Find the equation of a curve passing through \[\left( {{\text{1,}}\dfrac{{{\pi }}}{{\text{4}}}} \right)\] .If the slope of the tangent to the curve at any point \[{\text{P(x,y)}}\] is \[\dfrac{{{y}}}{{{x}}}{\text{ - co}}{{\text{s}}^{\text{2}}}\dfrac{{{y}}}{{{x}}}\]

Ans: Here, slope of tangent \[{\text{m  =  }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}\]

\[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{y}}}{{{x}}}{\text{ - co}}{{\text{s}}^{\text{2}}}\dfrac{{{y}}}{{{x}}}\]  (i)

which is a homogeneous equation

Now, substitute \[{{y  =  vx}}\] we get:

${\text{v + x}}\dfrac{{{\text{dv}}}}{{{\text{dx}}}}{\text{  =  v - co}}{{\text{s}}^{\text{2}}}{\text{v}}$

${{x}}\dfrac{{{\text{dv}}}}{{{\text{dx}}}}{\text{  =   - co}}{{\text{s}}^{\text{2}}}{\text{v}}$

${\text{se}}{{\text{c}}^{\text{2}}}{\text{v dv  =   - }}\dfrac{{{\text{dx}}}}{{{x}}}$

${\text{tan v  =   - log x + c}}\int {{\text{se}}{{\text{c}}^{\text{2}}}} {\text{v dv  =  }}\int {\text{ - }} \dfrac{{{\text{dx}}}}{{{x}}}$ 

\[{\text{tan}}\dfrac{{{y}}}{{{x}}}{\text{ + log x  =  c}}\] (ii)

Again substitute \[{{x  =  1 , y  =  }}\dfrac{{{\pi }}}{{\text{4}}}\] then we get \[{\text{c  =  1}}\]

\[{\text{tan(}}\dfrac{{{y}}}{{{x}}}{\text{) + log x  =  1}}\] is the required equation.

10. Solve \[{{{x}}^{\text{2}}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - xy  =  1 + cos}}\left( {\dfrac{{{y}}}{{{x}}}} \right){\text{ , x}} \ne {\text{0 , x  =  1 , y  =  }}\dfrac{{{\pi }}}{{\text{2}}}\]

Ans: We have \[{{{x}}^{\text{2}}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - xy  =  2co}}{{\text{s}}^{\text{2}}}\left( {\dfrac{{{y}}}{{{\text{2x}}}}} \right){\text{ , x}} \ne {\text{0}}\]

${{{{{x}}^{\text{2}}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - xy}}}}{{{\text{2co}}{{\text{s}}^{\text{2}}}\left( {\dfrac{{{y}}}{{{\text{2x}}}}} \right)}}{\text{  =  1}}$

${{{\text{se}}{{\text{c}}^{\text{2}}}\left( {\dfrac{{{y}}}{{{\text{2x}}}}} \right)}}{{\text{2}}}\left[ {{{{x}}^{\text{2}}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - xy}}} \right]{\text{  =  1}}$ 

Now divide both sides by \[{{{x}}^{\text{3}}}\] we get:

${{{\text{se}}{{\text{c}}^{\text{2}}}\left( {\dfrac{{{y}}}{{{\text{2x}}}}} \right)}}{{\text{2}}}\left[ {\dfrac{{{{x}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - y}}}}{{{{{x}}^{\text{2}}}}}} \right]{\text{  =  }}\dfrac{{\text{1}}}{{{{{x}}^{\text{3}}}}}$

${{\text{d}}}{{{\text{dx}}}}\left[ {{\text{tan}}\left( {\dfrac{{{y}}}{{{\text{2x}}}}} \right)} \right]{\text{  =  }}\dfrac{{\text{1}}}{{{{{x}}^{\text{3}}}}}$ 

Now, integrate both sides

\[\tan \left( {\dfrac{{{y}}}{{{\text{2x}}}}} \right){\text{  =  }}\dfrac{{{\text{ - 1}}}}{{{\text{2}}{{{x}}^{\text{2}}}}}{\text{ + k}}\]

Substitute \[{{x  =  1, y  =  }}\dfrac{{{\pi }}}{{\text{2}}}\] we get \[{\text{k  =  }}\dfrac{{\text{3}}}{{\text{2}}}\]

Thus, we have \[{\text{tan}}\left( {\dfrac{{{y}}}{{{\text{2x}}}}} \right){\text{  =  }}\dfrac{{\text{1}}}{{{\text{2}}{{{x}}^{\text{2}}}}}{\text{ + }}\dfrac{{\text{3}}}{{\text{2}}}{\text{tan}}\left( {\dfrac{{{y}}}{{{\text{2x}}}}} \right){\text{  =  }}\dfrac{{{\text{ - 1}}}}{{{\text{2}}{{{x}}^{\text{2}}}}}{\text{ + }}\dfrac{{\text{3}}}{{\text{2}}}\]

11. State the type of the differential equation for the equation \[{{x dy - y dx  =  }}\sqrt {{{{x}}^{\text{2}}}{\text{ + }}{{{y}}^{\text{2}}}} {\text{ dx}}\] and solve it.

Ans: we have \[{{x dy  =  }}\left( {\sqrt {{{{x}}^{\text{2}}}{\text{ + }}{{{y}}^{\text{2}}}} {\text{ + y}}} \right){\text{dx}}\]

i.e. \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{\sqrt {{{{x}}^{\text{2}}}{\text{ + }}{{{y}}^{\text{2}}}} {\text{ + y}}}}{{{x}}}\] (i)

Thus, RHS is homogeneous of degree zero. Hence this is a homogeneous differential equation.

Now, substitute \[{{y  =  vx}}\] we get

${\text{v + x}}\dfrac{{{\text{dv}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{\sqrt {{{{x}}^{\text{2}}}{\text{ + }}{{\text{v}}^{\text{2}}}{{{x}}^{\text{2}}}} {\text{ + vx}}}}{{{x}}}$

${\text{v + x}}\dfrac{{{\text{dv}}}}{{{\text{dx}}}}{\text{  =  }}\sqrt {{\text{1 + }}{{\text{v}}^{\text{2}}}} {\text{ + v}}$

${{{\text{dv}}}}{{{\text{dx}}}}{\text{  =  }}\sqrt {{\text{1 + }}{{\text{v}}^{\text{2}}}}$ 

\[\dfrac{{{\text{dv}}}}{{\sqrt {{\text{1 + }}{{\text{v}}^{\text{2}}}} }}{\text{  =  }}\dfrac{{{\text{dx}}}}{{{x}}}\] (ii)

Now integrate both sides

$\log \left( {{\text{v + }}\sqrt {{\text{1 + }}{{\text{v}}^{\text{2}}}} } \right){\text{  =  log x + log c}}$

${\text{v + }}\sqrt {{\text{1 + }}{{\text{v}}^{\text{2}}}} {\text{  =  cx}}$

${{{y}}}{{{x}}}{\text{ + }}\sqrt {{\text{1 + }}\dfrac{{{{{y}}^{\text{2}}}}}{{{{{x}}^{\text{2}}}}}} {\text{  =  cx}}$

${{y + }}\sqrt {{{{x}}^{\text{2}}}{\text{ + }}{{{y}}^{\text{2}}}} {\text{  =  c}}{{{x}}^{\text{2}}}$ 

Objective Questions

Choose the correct answer form the given four options in each of the Examples 12 to 21

12. The degree of the differential equation \[{\left( {{\text{1 + }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)^{\text{3}}}{\text{  =  }}{\left( {\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}} \right)^{\text{2}}}\] is

(A) \[{\text{1}}\]

(B) \[{\text{2}}\]

(C) \[{\text{3}}\]

(D) \[{\text{4}}\]

Ans: Correct option (B)

13. The degree of the differential equation \[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + 3}}{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)^{\text{2}}}{\text{  =  }}{{{x}}^{\text{2}}}{\text{log}}\left( {\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}} \right)\] is

(A) \[{\text{1}}\]

(B) \[{\text{2}}\]

(C) \[{\text{3}}\]

(D) Not defined

Ans: Correct option (D) because given differential equation is not a polynomial equation in terms of its derivatives, so its degree is not defined.

14. The order and degree of the differential equation \[{\left[ {{\text{1 + }}{{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)}^{\text{2}}}} \right]^{\text{2}}}{\text{  =  }}\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}\] respectively, are

(A) \[{\text{1,2}}\]

(B) \[{\text{2,2}}\]

(C) \[{\text{2,1}}\]

(D) \[{\text{4,2}}\]

Ans: Correct option (C)

15. The order of the differential equation of all circles of given radius \[{\text{a}}\] is:

(A) \[1\]

(B) \[2\]

(C) \[3\]

(D) \[{\text{4}}\]

Ans: Correct option (B) because Let the equation of given family be \[{{\text{(x - h)}}^{\text{2}}}{\text{ + (y - k}}{{\text{)}}^{\text{2}}}{\text{  =  }}{{\text{a}}^{\text{2}}}\] It has two arbitrary constants \[{\text{h , k}}\] . Therefore, the order of the given differential equation will be two

16. The solution of the differential equation \[{\text{2x}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - y  =  3}}\] represents a family of

(A) straight lines

(B) circles

(C) parabolas

(D) ellipses

Ans: Correct option (C) because Given equation can be written as

${{{\text{2 dy}}}}{{{{y + 3}}}}{\text{  =  }}\dfrac{{{\text{dx}}}}{{{x}}}$

${\text{2 log(y + 3)  =  log x + log c}}$

${{\text{(y + 3)}}^{\text{2}}}{\text{  =  cx}}$ 

which represents the family of parabolas

17. The integrating factor of the differential equation \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{(x logx) + y  =  2 log x}}\] is

(A) \[{{{e}}^{{x}}}\]

(B) \[{\text{log x}}\]

(C) \[{\text{log(log x)}}\]

(D) \[{{x}}\]

Ans: Correct option (B) because given equation can be written as \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + }}\dfrac{{{y}}}{{{{xlogx}}}}{\text{  =  }}\dfrac{{\text{2}}}{{{x}}}\]

Therefore, I.F. \[{\text{ =  }}{{{e}}^{\int {\dfrac{{\text{1}}}{{{{xlogx}}}}{\text{d}}} {{x}}}}{\text{  =  }}{{{e}}^{{\text{log(logx)}}}}{\text{  =  log x}}\]

18. A solution of the differential equation \[{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)^{\text{2}}}{\text{ - x}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y  =  0}}\] is

(A) \[{{y  =  2}}\]

(B) \[{{y  =  2x}}\]

(C) \[{{y  =  2x - 4}}\]

(D) \[{{y  =  2}}{{{x}}^{\text{2}}}{\text{ - 4}}\]

Ans: Correct option ©

19. Which of the following is not a homogeneous function of \[{{x , y}}\]

(A) \[{{{x}}^{\text{2}}}{\text{ + 2xy}}\]

(B) \[{\text{2x - y}}\]

(C) \[{\text{co}}{{\text{s}}^{\text{2}}}\left( {\dfrac{{{y}}}{{{x}}}} \right){\text{ + }}\dfrac{{{y}}}{{{x}}}\]

(D) \[{\text{sin x - cos y}}\]

Ans: Correct option (D)

20. Solution of the differential equation \[\dfrac{{{\text{dx}}}}{{{x}}}{\text{ + }}\dfrac{{{\text{dy}}}}{{{y}}}{\text{  =  0}}\] is

(A) \[\dfrac{{\text{1}}}{{{x}}}{\text{ + }}\dfrac{{\text{1}}}{{{y}}}{\text{  =  c}}\]

(B) \[{{log x \times log y  =  c}}\]

(C) \[{{xy  =  c}}\]

(D) \[{{x + y  =  c}}\]

Ans: Correct option (C) because from the given equation, we get \[{\text{log x + log y  =  log c}}\] giving \[{{xy  =  c}}\]

21. The solution of the differential equation \[{{x}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + 2y  =  }}{{{x}}^{\text{2}}}\] is

(A) \[{{y  =  }}\dfrac{{{{{x}}^{\text{2}}}{\text{ + c}}}}{{{\text{4}}{{{x}}^{\text{2}}}}}\]

(B) \[{{y  =  }}\dfrac{{{{{x}}^{\text{2}}}}}{{\text{4}}}{\text{ + c}}\]

(C) \[{{y  =  }}\dfrac{{{{{x}}^{\text{4}}}{\text{ + c}}}}{{{{{x}}^{\text{2}}}}}\]

(D) \[{{y  =  }}\dfrac{{{{{x}}^{\text{4}}}{\text{ + c}}}}{{{\text{4}}{{{x}}^{\text{2}}}}}\]

Ans: Correct option (D) because I.F. \[{\text{ =  }}{{{e}}^{\int {\dfrac{{\text{2}}}{{{x}}}} {\text{  =  }}{{{e}}^{{\text{2logx}}}}}}{\text{  =  }}{{{e}}^{{\text{log}}{{{x}}^{\text{2}}}}}{\text{  =  }}{{{x}}^{\text{2}}}\]

So, \[{{y \times }}{{{x}}^{\text{2}}}{\text{  =  }}\int {{{{x}}^{\text{2}}}} {{x dx  =  }}\dfrac{{{{{x}}^{\text{4}}}}}{{\text{4}}}{\text{ + k}}\]

i.e. \[{{y  =  }}\dfrac{{{{{x}}^{\text{4}}}{\text{ + c}}}}{{{\text{4}}{{{x}}^{\text{2}}}}}\]

22. Fill in the blanks of the following:

(i) Order of the differential equation representing the family of parabolas \[{{{y}}^{\text{2}}}{\text{  =  4ax}}\] is

Ans: One because \[{\text{a}}\] is the only arbitrary constant.

(ii) The degree of the differential equation \[{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)^{\text{3}}}{\text{ + }}{\left( {\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}} \right)^{\text{2}}}{\text{  =  0}}\] is

Ans: Two because degree of the highest order derivative is two.

(iii) The number of arbitrary constants in a particular solution of the differential equation \[{\text{tan x dx + tan y dy  =  0}}\] is

Ans: Zero because any particular solution of a differential equation has no arbitrary constant.

(iv) \[{\text{F(x,y)  =  }}\dfrac{{\sqrt {{{{x}}^{\text{2}}}{\text{ + }}{{{y}}^{\text{2}}}} {\text{ + y}}}}{{{x}}}\] is a homogeneous function of degree

Ans: Zero

(v) An appropriate substitution to solve the differential equation \[\dfrac{{{\text{dx}}}}{{{\text{dy}}}}{\text{  =  }}\dfrac{{{{{x}}^{\text{2}}}{\text{log}}\left( {\dfrac{{{x}}}{{{y}}}} \right)}}{{{{xylog}}\left( {\dfrac{{{x}}}{{{y}}}} \right)}}\] is 

Ans: \[{{x  =  vy}}\]

(vi) Integrating factor of the differential equation \[{{x}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - y  =  sin x}}\] is

Ans: \[\dfrac{{\text{1}}}{{{x}}}\] ;  given differential equation can be written as \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - }}\dfrac{{{y}}}{{{x}}}{\text{  =  }}\dfrac{{{\text{sin x}}}}{{{x}}}\] and therefore I.F. \[{\text{ =  }}{{{e}}^{\int {\text{ - }} \dfrac{{\text{1}}}{{{x}}}{\text{  =  }}{{{e}}^{{\text{ - logx}}}}}}{\text{  =  }}\dfrac{{\text{1}}}{{{x}}}\]

(vii) The general solution of the differential equation \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}{{{e}}^{{{x - y}}}}\] is

Ans: \[{{{e}}^{{y}}}{\text{  =  }}{{{e}}^{{x}}}{\text{ + c}}\] from given equation, we have \[{{{e}}^{{y}}}{\text{dy  =  }}{{{e}}^{{x}}}{\text{dx}}\]

(viii) The general solution of the differential equation \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + }}\dfrac{{{y}}}{{{x}}}{\text{  =  1}}\] is

Ans: \[{{xy  =  }}\dfrac{{{{{x}}^{\text{2}}}}}{{\text{2}}}{\text{ + c}}\] ; I.F. \[{\text{ =  }}{{{e}}^{\int {\dfrac{{\text{1}}}{{{x}}}} {\text{ + t}}}}{\text{  =  }}{{{e}}^{{\text{log x}}}}{\text{  =  x}}\] and the solution is \[{{yx  =  }}\int {{x}} {\text{.1dx  =  }}\dfrac{{{{{x}}^{\text{2}}}}}{{\text{2}}}{\text{ + C}}\]

(ix) The differential equation representing the family of curves \[{{y  =  a sin x + b cos x}}\]

Ans: \[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + y  =  0}}\] 

Differentiate with respect to \[{{x}}\] we get

${{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  A cos x - B sin x}}$

${{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{  =   - A sin x - B cos x}}$

${{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + y  =  0}}$ 

(x) \[\left( {\dfrac{{{{{e}}^{{\text{ - 2}}\sqrt {\text{5}} }}}}{{\sqrt {{x}} }}{\text{ - }}\dfrac{{{y}}}{{\sqrt {{x}} }}} \right)\dfrac{{{\text{dx}}}}{{{\text{dy}}}}{\text{  =  1 (x}} \ne {\text{0)}}\] when written in the form \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + Py  =  Q}}\] , then \[{\text{P  = }}\]

Ans: \[\dfrac{{\text{1}}}{{\sqrt {{x}} }}\] , given equation equation can be written as

${{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{{{e}}^{{\text{ - 2}}\sqrt {\text{2}} }}}}{{\sqrt {{x}} }}{\text{ - }}\dfrac{{{y}}}{{\sqrt {{x}} }}$

${{{\text{dy}}}}{{{\text{dx}}}}{\text{ + }}\dfrac{{{y}}}{{\sqrt {{x}} }}{\text{  =  }}\dfrac{{{{{e}}^{{\text{ - 2}}\sqrt {{x}} }}}}{{\sqrt {{x}} }}$ 

This is a differential equation of the type \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + Py  =  Q}}\]

23. State whether the following statements are True or False.

(i) Order of the differential equation representing the family of ellipses having centre at origin and foci on \[{{x}}\] -axis is two.

Ans: True because equation represents the given family \[\dfrac{{{{{x}}^{\text{2}}}}}{{{{\text{a}}^{\text{2}}}}}{\text{ + }}\dfrac{{{{{y}}^{\text{2}}}}}{{{{\text{b}}^{\text{2}}}}}{\text{  =  1}}\] , which has two arbitrary constants.

(ii) Degree of the differential equation \[\sqrt {{\text{1 + }}\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}} {\text{  =  x + }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}\] is not defined

Ans: True because it is not a polynomial equation in its derivatives.

(iii) \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y  =  5}}\] is a differential equation of the type \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + Py  =  Q}}\] but it can be solved using variable separable method also.

Ans: True

(iv) \[{\text{F(x,y)  =  }}\dfrac{{{{ycos}}\left( {\dfrac{{{y}}}{{{x}}}} \right){\text{ + x}}}}{{{{xcos}}\left( {\dfrac{{{y}}}{{{x}}}} \right)}}\] is not a homogeneous function.

Ans: True because \[{\text{f}}\left( {{{\lambda x , \lambda y}}} \right){\text{  =  }}{{{\lambda }}^{{^\circ }}}{\text{f(x,y)}}\]

(v) \[{\text{F(x,y)  =  }}\dfrac{{{{{x}}^{\text{2}}}{\text{ + }}{{{y}}^{\text{2}}}}}{{{{x - y}}}}\] is a homogeneous function of degree one

Ans: True

because \[f(\lambda x,\lambda y)~=~{{\lambda }^{'}}f(x,y)\]

(vi) Integrating factor of the differential equation \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - y  =  cos x}}\] is \[{{{e}}^{{x}}}\]

Ans: False because I.F. \[{\text{ =  }}{{{e}}^{\int {\text{ - }} {{1\alpha }}}}{\text{  =  }}{{{e}}^{{\text{ - z}}}}\]

(vii) The general solution of the differential equation \[{{x}}\left( {{\text{1 + }}{{{y}}^{\text{2}}}} \right){\text{dx + y}}\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right){\text{dy  =  0}}\] is \[\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right)\left( {{\text{1 + }}{{{y}}^{\text{2}}}} \right){\text{  =  k}}\]

Ans: True because given equation can be written as

\[\dfrac{{{\text{2x}}}}{{{\text{1 + }}{{{x}}^{\text{2}}}}}{\text{dx  =  }}\dfrac{{{\text{ - 2y}}}}{{{\text{1 + }}{{{y}}^{\text{2}}}}}{\text{dy}}\]

${\text{log}}\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right){\text{  =   - log}}\left( {{\text{1 + }}{{{y}}^{\text{2}}}} \right){\text{ + log k}}$

$\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right)\left( {{\text{1 + }}{{{y}}^{\text{2}}}} \right){\text{  =  k}}$ 

(viii) The general solution of the differential equation \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y sec x  =  tan x}}\] is \[{{y(sec x - tan x)  =  sec x - tan x + x + k}}\]

Ans: False because I.F. \[{\text{ =  }}{{{e}}^{\int {{\text{ sec x dx}}} }}{\text{  =  }}{{{e}}^{{\text{log(secx + tanx)}}}}{\text{  =  secx + tanx}}\]

\[{{y(secx + tanx)  =  }}\int {{\text{(secx + tanx)}}} {\text{tanxdx  =  }}\int {\left( {{\text{secxtanx + se}}{{\text{c}}^{\text{2}}}{{x - 1}}} \right)} {\text{dx  =  secx + tanx - x + k}}\]

(ix) \[{{x + y  =  ta}}{{\text{n}}^{{\text{ - 1}}}}{{y}}\] is a solution of the differential equation \[{{{y}}^{\text{2}}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + }}{{{y}}^{\text{2}}}{\text{ + 1  =  0}}\]

Ans: True because \[{{x + y  =  ta}}{{\text{n}}^{{\text{ - 1}}}}{{y}}\]

${\text{1 + }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{\text{1}}}{{{\text{1 + }}{{{y}}^{\text{2}}}}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}$

${{{\text{dy}}}}{{{\text{dx}}}}\left( {\dfrac{{\text{1}}}{{{\text{1 + }}{{{y}}^{\text{2}}}}}{\text{ - 1}}} \right){\text{  =  1}}$

${{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{\text{ - }}\left( {{\text{1 + }}{{{y}}^{\text{2}}}} \right)}}{{{{{y}}^{\text{2}}}}}$ 

(x) \[{{y  =  x}}\] is a particular solution of the differential equation \[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ - }}{{{x}}^{\text{2}}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + xy  =  x}}\]

Ans: False, \[{{y  =  x}}\] because does not satisfy the given differential equation

16. Solve \[{{{x}}^{\text{2}}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}{{{x}}^{\text{2}}}{\text{ + xy + }}{{{y}}^{\text{2}}}\]

Ans: We have \[{{{x}}^{\text{2}}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}{{{x}}^{\text{2}}}{\text{ + xy + }}{{{y}}^{\text{2}}}\]

Divide both side by \[{{{x}}^{\text{2}}}\] we get \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  1 + }}\dfrac{{{y}}}{{{x}}}{\text{ + }}\dfrac{{{{{y}}^{\text{2}}}}}{{{{{x}}^{\text{2}}}}}\]

Let \[{\text{f(x,y)  =  1 + }}\dfrac{{{y}}}{{{x}}}{\text{ + }}\dfrac{{{{{y}}^{\text{2}}}}}{{{{{x}}^{\text{2}}}}}\]

\[{{f(\lambda x,\lambda y)  =  1 + }}\dfrac{{{{\lambda y}}}}{{{{\lambda x}}}}{\text{ + }}\dfrac{{{{{\lambda }}^{\text{2}}}{{{y}}^{\text{2}}}}}{{{{{\lambda }}^{\text{2}}}{{{x}}^{\text{2}}}}}\]

\[{{f(\lambda x,\lambda y)  =  }}{{{\lambda }}^{\text{0}}}\left( {{\text{1 + }}\dfrac{{{y}}}{{{x}}}{\text{ + }}\dfrac{{{{{y}}^{\text{2}}}}}{{{{{x}}^{\text{2}}}}}} \right){\text{  =  }}{{{\lambda }}^{\text{0}}}{\text{f(x,y)}}\] is a homogeneous equation of degree zero

Put \[{{y  =  vx }} \Rightarrow {\text{ }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  v + x}}\dfrac{{{\text{dv}}}}{{{\text{dx}}}}\]

Now, substitute we get

$\left( {{\text{v + x}}\dfrac{{{\text{dv}}}}{{{\text{dx}}}}} \right){\text{  =  1 + v + }}{{\text{v}}^{\text{2}}}$

${{x}}\dfrac{{{\text{dv}}}}{{{\text{dx}}}}{\text{  =  1 + v + }}{{\text{v}}^{\text{2}}}{\text{ - v}}$

${{x}}\dfrac{{{\text{dv}}}}{{{\text{dx}}}}{\text{  =  1 + }}{{\text{v}}^{\text{2}}}$

${{{\text{dv}}}}{{{\text{1 + }}{{\text{v}}^{\text{2}}}}}{\text{  =  }}\dfrac{{{\text{dx}}}}{{{x}}}$ 

Integrate both sides, we get

${\dfrac{{{\text{dv}}}}{{{\text{1 + }}{{\text{v}}^{\text{2}}}}}} {\text{  =  }}\int {\dfrac{{{\text{dx}}}}{{{x}}}}$

${\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{\text{v  =  log|x| + C}}$

${\text{ta}}{{\text{n}}^{{\text{ - 1}}}}\left( {\dfrac{{{y}}}{{{x}}}} \right){\text{  =  log|x| + C}}$ 

17. Find the general solution of the differential equation \[\left( {{\text{1 + }}{{{y}}^{\text{2}}}} \right){\text{ + }}\left( {{{x - }}{{{e}}^{{\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{y}}}}} \right)\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  0}}\]

Ans: We have \[\left( {{\text{1 + }}{{{y}}^{\text{2}}}} \right){\text{ + }}\left( {{{x - }}{{{e}}^{{\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{y}}}}} \right)\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  0}}\]

  $\left( {{\text{1 + }}{{{y}}^{\text{2}}}} \right){\text{  =   - }}\left( {{{x - }}{{{e}}^{{\text{ta}}{{\text{n}}^1}{{y}}}}} \right)\dfrac{{{\text{dy}}}}{{{\text{dx}}}}$

  $\left( {{\text{1 + }}{{{y}}^{\text{2}}}} \right)\dfrac{{{\text{dx}}}}{{{\text{dy}}}}{\text{  =   - x + }}{{{e}}^{{\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{y}}}}$

  $\left( {{\text{1 + }}{{{y}}^{\text{2}}}} \right)\dfrac{{{\text{dx}}}}{{{\text{dy}}}}{\text{ + x  =  }}{{{e}}^{{\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{y}}}}$

${{{\text{dx}}}}{{{\text{dy}}}}{\text{ + }}\dfrac{{{x}}}{{{\text{1 + }}{{{y}}^{\text{2}}}}}{\text{  =  }}\dfrac{{{{{e}}^{{\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{y}}}}}}{{{\text{1 + }}{{{y}}^{\text{2}}}}}$ 

Now, compare with \[\dfrac{{{\text{dx}}}}{{{\text{dy}}}}{\text{ + Px  =  Q}}\] we get

\[{\text{P  =  }}\dfrac{{\text{1}}}{{{\text{1 + }}{{{y}}^{\text{2}}}}}{\text{ , Q  =  }}\dfrac{{{{{e}}^{{\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{y}}}}}}{{{\text{1 + }}{{{y}}^{\text{2}}}}}\]

IF \[{\text{ =  }}{{{e}}^{\int {\dfrac{{\text{1}}}{{{\text{1 + }}{{{y}}^{\text{2}}}}}} {\text{dy}}}}{\text{  =  }}{{{e}}^{{\text{ta}}{{\text{n}}^{ - 1}}{{y}}}}\]

General solution is 

${{x}}{{{e}}^{{{\tan }^{{\text{ - 1}}}}{{y}}}}{\text{  =  }}\int {\dfrac{{{{{e}}^{{\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{y}}}}}}{{{\text{1 + }}{{{y}}^{\text{2}}}}}} {{{e}}^{{\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{y}}}}{\text{dy + C}}$

${{x}}{{{e}}^{{\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{y}}}}{\text{  =  }}\int {\dfrac{{{{\left( {{{{e}}^{{\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{y}}}}} \right)}^{\text{2}}}}}{{{\text{1 + }}{{{y}}^{\text{2}}}}}} {{ \times dy + C}}$ 

Put \[{\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{y  =  t }} \Rightarrow {\text{ }}\dfrac{{\text{1}}}{{{\text{1 + }}{{{y}}^{\text{2}}}}}{\text{dy  =  dt}}\] we have

\[{{x \times }}{{{e}}^{{\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{y}}}}{\text{  =  }}\int {{{{e}}^{{\text{2t}}}}} {\text{dt + C}}\]

${{x \times }}{{{e}}^{{\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{y}}}}{\text{  =  }}\dfrac{{\text{1}}}{{\text{2}}}{{{e}}^{{\text{2ta}}{{\text{n}}^{{\text{ - 1}}}}{{y}}}}{\text{ + C}}$

${\text{2x}}{{{e}}^{{\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{y}}}}{\text{  =  }}{{{e}}^{{\text{2ta}}{{\text{n}}^{{\text{ - 1}}}}{{y}}}}{\text{ + 2C}}$

${\text{2x}}{{{e}}^{{\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{y}}}}{\text{  =  }}{{{e}}^{{\text{2ta}}{{\text{n}}^{{\text{ - 1}}}}{{y}}}}{\text{ + K}}$ 

18. Find the general solution of \[{{{y}}^{\text{2}}}{\text{dx + }}\left( {{{{x}}^{\text{2}}}{\text{ - xy + }}{{{y}}^{\text{2}}}} \right){\text{dy  =  0}}\]

Ans: We have \[{{{y}}^{\text{2}}}{\text{dx + }}\left( {{{{x}}^{\text{2}}}{\text{ - xy + }}{{{y}}^{\text{2}}}} \right){\text{dy  =  0}}\]

${{{y}}^{\text{2}}}{\text{dx  =   - }}\left( {{{{x}}^{\text{2}}}{\text{ - xy + }}{{{y}}^{\text{2}}}} \right){\text{dy}}$

${{{y}}^{\text{2}}}\dfrac{{{\text{dx}}}}{{{\text{dy}}}}{\text{  =   - }}\left( {{{{x}}^{\text{2}}}{\text{ - xy + }}{{{y}}^{\text{2}}}} \right)$ 

Now, divide by \[{{{y}}^{\text{2}}}\] on both sides, we get:

\[\dfrac{{{\text{dx}}}}{{{\text{dy}}}}{\text{  =   - }}\left( {\dfrac{{{{{x}}^{\text{2}}}}}{{{{{y}}^{\text{2}}}}}{\text{ - }}\dfrac{{{x}}}{{{y}}}{\text{ + 1}}} \right)\] is homogeneous equation

Put \[\dfrac{{{x}}}{{{y}}}{\text{  =  v or x  =  vy}}\] we have

\[\dfrac{{{\text{dx}}}}{{{\text{dy}}}}{\text{  =  v + y}}\dfrac{{{\text{dv}}}}{{{\text{dy}}}}\]

Now, substitute we get:

\[{\text{v + y}}\dfrac{{{\text{dv}}}}{{{\text{dy}}}}{\text{  =   - }}\left[ {{{\text{v}}^{\text{2}}}{\text{ - v + 1}}} \right]\]

${{y}}\dfrac{{{\text{dv}}}}{{{\text{dy}}}}{\text{  =   - }}{{\text{v}}^{\text{2}}}{\text{ + v - 1 - v}}$

${{y}}\dfrac{{{\text{dv}}}}{{{\text{dy}}}}{\text{  =   - }}{{\text{v}}^{\text{2}}}{\text{ - 1}}$

${{{\text{dv}}}}{{{{\text{v}}^{\text{2}}}{\text{ + 1}}}}{\text{  =   - }}\dfrac{{{\text{dy}}}}{{{y}}}$ 

Now, integrate

${\dfrac{{{\text{dv}}}}{{{{\text{v}}^{\text{2}}}{\text{ + 1}}}}} {\text{  =  }}\int {\text{ - }} \dfrac{{{\text{dy}}}}{{{y}}}$

${\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{\text{(v)  =   - log y + C}}$

${\text{ta}}{{\text{n}}^{{\text{ - 1}}}}\left( {\dfrac{{{x}}}{{{y}}}} \right){\text{ + logy  =  C}}$ 

19. Solve \[{\text{(x + y)(dx - dy)  =  dx + dy}}\] (Hint: substitute x + y  =  z after separating {dx , dy} ]

Ans: We have \[{\text{(x + y)(dx - dy)  =  dx + dy}}\]

\[{\text{(x + y)}}\left( {{\text{1 - }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right){\text{  =  1 + }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}\]

Put \[{{x + y  =  z}}\] we have \[{\text{1 + }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{\text{dz}}}}{{{\text{dx}}}}\]

Substitute these values we get:

${\text{z}}\left( {{\text{1 - }}\dfrac{{{\text{dz}}}}{{{\text{dx}}}}{\text{ + 1}}} \right){\text{  =  }}\dfrac{{{\text{dz}}}}{{{\text{dx}}}}$

${\text{z}}\left( {{\text{2 - }}\dfrac{{{\text{dz}}}}{{{\text{dx}}}}} \right){\text{  =  }}\dfrac{{{\text{dz}}}}{{{\text{dx}}}}$ 

\[{\text{2z - z}}\dfrac{{{\text{dz}}}}{{{\text{dx}}}}{\text{ - }}\dfrac{{{\text{dz}}}}{{{\text{dx}}}}{\text{  =  0}}\]

${\text{2z - (z + 1)}}\dfrac{{{\text{dz}}}}{{{\text{dx}}}}{\text{  =  0}}$

${{{\text{dz}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{\text{2z}}}}{{{\text{z + 1}}}}$

$\left( {\dfrac{{{\text{z + 1}}}}{{\text{z}}}} \right){\text{dz  =  2 dx}}$ 

Integrate both sides, we get:

${\left( {{\text{1 + }}\dfrac{{\text{1}}}{{\text{z}}}} \right)} {\text{dz  =  2}}\int {\text{d}} {{x}}$

${\text{z + log z  =  2x - logC}}$

${\text{(x + y) + log(x + y)  =  2x - logC}}$

${\text{2x - x - y  =  logC + log(x + y)}}$

${{x - y  =  log|C(x + y)|}}$

${{{e}}^{{{x - y}}}}{\text{  =  C(x + y)}}$

${\text{(x + y)  =  }}\dfrac{{\text{1}}}{{\text{C}}}{{{e}}^{{{x - y}}}}$

${{x + y  =  K}}{{{e}}^{{{x - y}}}}$ 

20. Solve \[{\text{2(y + 3) - xy}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  0}}\] given that \[{{y(1)  =   - 2}}\]

Ans: We have \[{\text{2(y + 3) - xy}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  0}}\]

${\text{2(y + 3)  =  xy}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}$

${\text{2}}\dfrac{{{\text{dx}}}}{{{x}}}{\text{  =  }}\left( {\dfrac{{{y}}}{{{{y + 3}}}}} \right){\text{dy}}$

${\text{2 \times }}\dfrac{{{\text{dx}}}}{{{x}}}{\text{  =  }}\left( {\dfrac{{{{y + 3 - 3}}}}{{{{y + 3}}}}} \right){\text{dy}}$

${\text{2 \times }}\dfrac{{{\text{dx}}}}{{{x}}}{\text{  =  }}\left( {{\text{1 - }}\dfrac{{\text{3}}}{{{{y + 3}}}}} \right){\text{dy}}$ 

Now, integrate both sides:

${\text{2}} \dfrac{{{\text{dx}}}}{{{x}}}{\text{  =  }}\int {\left( {{\text{1 - }}\dfrac{{\text{3}}}{{{{y + 3}}}}} \right)} {\text{dy}}$

${\text{2 log x  =  y - 3log(y + 3) + C}}$ 

When \[{{x  =  1 , y  =   - 2}}\] then

${\text{2 log1  =   - 2 - 3log( - 2 + 3) + C}}$

${\text{2(0)  =   - 2 - 3(0) + C}}$

${\text{C  =  2}}$ 

Now, substitute we get

${\text{2 log x  =  y - 3log(y + 3) + 2}}$

${\text{2 log x + 3log(y + 3)  =  y + 2}}$

${\text{log}}{{{x}}^{\text{2}}}{\text{ + log(y + 3}}{{\text{)}}^{\text{3}}}{\text{  =  (y + 2)}}$

${\text{log }}{{{x}}^{\text{2}}}{{\text{(y + 3)}}^{\text{3}}}{\text{  =  y + 2}}$

${{{x}}^{\text{2}}}{{\text{(y + 3)}}^{\text{3}}}{\text{  =  }}{{{e}}^{{{y + 2}}}}$ 

21. Solve the differential equation \[{\text{dy  =  cos x(2 - y cosec x)dx}}\] given that \[{{x  =  }}\dfrac{{{\pi }}}{{\text{2}}}\]

Ans: We have \[{\text{dy  =  cos x(2 - y cosec x)dx}}\]

${{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  cosx(2 - y cosec x)}}$

${{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  2cos x - y cosec x cos x}}$

${{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  2cos x - y cot x}}$

${{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y cot x  =  2 cos x}}$ 

which is a differential equation

Now, compare with \[\dfrac{{{\text{dx}}}}{{{\text{dy}}}}{\text{ + Px  =  Q}}\] we get

${\text{P  =  cot x , Q  =  2 cosx}}$

${\text{IF  =   }}{{{e}}^{\int {\text{P}} {\text{dx}}}}{\text{  =  }}{{{e}}^{\int {{\text{cot}}} {\text{ x dx}}}}{\text{  =  }}{{{e}}^{{\text{log sin x}}}}{\text{  =  sin x}}$ 

General solution

${{y \times sin x  =  }}\int {\text{2}} {\text{ cosx sinx dx + C}}$

${{y \times sin x  =  }}\int {{\text{sin}}} {\text{2x dx + C            [sin2x  =  2 sinx cosx]}}$

${{y \times sin x  =   - }}\dfrac{{{\text{cos2x}}}}{{\text{2}}}{\text{ + C}}$ 

When \[{{x  =  }}\dfrac{{{\pi }}}{{\text{2}}}{\text{ , y  =  2}}\] then

${{2 \times sin}}\dfrac{{{\pi }}}{{\text{2}}}{\text{  =   - }}\dfrac{{{\text{cos}}\left( {{\text{2 \times }}\dfrac{{{\pi }}}{{\text{2}}}} \right)}}{{\text{2}}}{\text{ + C}}$

${{2 \times 1  =   + }}\dfrac{{\text{1}}}{{\text{2}}}{\text{ + C}}$

${\text{2 - }}\dfrac{{\text{1}}}{{\text{2}}}{\text{  =  C}}$

${{{\text{4 - 1}}}}{{\text{2}}}{\text{  =  C}}$

${\text{C  =  }}\dfrac{{\text{3}}}{{\text{2}}}$ 

Now, substitute values we get:

\[{{y sin x  =   - }}\dfrac{{\text{1}}}{{\text{2}}}{\text{cos 2x + }}\dfrac{{\text{3}}}{{\text{2}}}\]

22. Form the differential equation by eliminating A and B in \[{\text{A}}{{{x}}^{\text{2}}}{\text{ + B}}{{{y}}^{\text{2}}}{\text{  =  1}}\]

Ans: We have \[{\text{A}}{{{x}}^{\text{2}}}{\text{ + B}}{{{y}}^{\text{2}}}{\text{  =  1}}\]

Differentiate with respect to \[{{x}}\] we get:

${\text{2Ax + 2By}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  0}}$

${\text{2By}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =   - 2Ax}}$ 

${\text{By}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =   - Ax}}$

${{{y}}}{{{x}}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =   - }}\dfrac{{\text{A}}}{{\text{B}}}$ 

Now, again differentiate with respect to \[{{x}}\] we get:

${{{y}}}{{{x}}}{{ \times }}\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{{ \times }}\left( {\dfrac{{{{x}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - y}}}}{{{{{x}}^{\text{2}}}}}} \right){\text{  =  0}}$

${{{y}}}{{{x}}}{{ \times }}\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + }}\dfrac{{{{x}}{{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)}^{\text{2}}}{\text{ - y}}\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)}}{{{{{x}}^{\text{2}}}}}{\text{  =  0}}$

${{xy}}\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + x}}{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)^{\text{2}}}{\text{ - y}}\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right){\text{  =  0}}$

$x y y^{\prime \prime}+x y^{\prime 2}-y y^{\prime}=0$

23. Solve the differential equation \[\left( {{\text{1 + }}{{{y}}^{\text{2}}}} \right){\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{xdx + 2y}}\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right){\text{dy  =  0}}\]

Ans: We have \[\left( {{\text{1 + }}{{{y}}^{\text{2}}}} \right){\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{xdx + 2y}}\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right){\text{dy  =  0}}\]

$\left( {{\text{1 + }}{{{y}}^{\text{2}}}} \right){\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{xdx  =   - 2y}}\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right){\text{dy}}$

${{{\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{xdx}}}}{{{\text{1 + }}{{{x}}^{\text{2}}}}}{\text{  =   - }}\dfrac{{{\text{2y}}}}{{{\text{1 + }}{{{y}}^{\text{2}}}}}{\text{dy}}$ 

Integrate on both sides:

\[\int {\dfrac{{{\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{x}}}}{{{\text{1 + }}{{{x}}^{\text{2}}}}}} {\text{dx  =   - }}\int {\dfrac{{{\text{2y}}}}{{{\text{1 + }}{{{y}}^{\text{2}}}}}} {\text{dy}}\]

Put \[{\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{x  =  t}}\] in LHS we get \[\dfrac{{\text{1}}}{{{\text{1 + }}{{{x}}^{\text{2}}}}}{\text{dx  =  dt}}\]

Put \[{\text{1 + }}{{{y}}^{\text{2}}}{\text{  =  u}}\] in RHS we get:

${\text{2y dy  =  du}}$

${\text{t}} {\text{ dt  =   - }}\int {\dfrac{{\text{1}}}{{\text{u}}}} {\text{du}}$

${{{{\text{t}}^{\text{2}}}}}{{\text{2}}}{\text{  =   - logu + C}}$

${{\text{1}}}{{\text{2}}}{\left( {{\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{x}}} \right)^{\text{2}}}{\text{  =   - log}}\left( {{\text{1 + }}{{{y}}^{\text{2}}}} \right){\text{ + C}}$

${{\text{1}}}{{\text{2}}}{\left( {{\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{x}}} \right)^{\text{2}}}{\text{ + log}}\left( {{\text{1 + }}{{{y}}^{\text{2}}}} \right){\text{  =  C}}$ 

24. Find the differential equation of system of concentric circles with centre \[(1,2)\]

Ans: The family of concentric circles with centre \[(1,2)\] and radius \[{\text{a}}\] is given by

${{\text{(x - 1)}}^{\text{2}}}{\text{ + (y - 2}}{{\text{)}}^{\text{2}}}{\text{  =  }}{{\text{a}}^{\text{2}}}$

${{{x}}^{\text{2}}}{\text{ + 1 - 2x + }}{{{y}}^{\text{2}}}{\text{ + 4 - 4y  =  }}{{\text{a}}^{\text{2}}}$

${{{x}}^{\text{2}}}{\text{ + }}{{{y}}^{\text{2}}}{\text{ - 2x - 4y + 5  =  }}{{\text{a}}^{\text{2}}}$ 

Now differentiate with respect to \[{{x}}\] we get:

${\text{2x + 2y}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - 2 - 4}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  0}}$

${\text{(2x - 4)}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + 2x - 2  =  0}}$

${\text{(y - 2)}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + (x - 1)  =  0}}$ 

Long Answer Questions

25. Solve \[{{y + }}\dfrac{{\text{d}}}{{{\text{dx}}}}{\text{(xy)  =  x(sin x + log x)}}\]

Ans: We have \[{{y + }}\dfrac{{\text{d}}}{{{\text{dx}}}}{\text{(xy)  =  x(sin x + log x)}}\]

\[{{y + x}}\dfrac{{\text{d}}}{{{\text{dx}}}}{\text{ + y  =  x(sinx + logx)y + x}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y  =  x(sin x + log x)}}\]

\[{{x}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + 2y  =  x(sin x + log x)}}\]

Divide by \[{{x}}\] on both sides we get:

\[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + }}\dfrac{{\text{2}}}{{{x}}}{{y  =  sin x + log x}}\] is a linear differential equation

Now, compare with \[\dfrac{{{\text{dx}}}}{{{\text{dy}}}}{\text{ + Px  =  Q}}\] we get

${\text{P  =  }}\dfrac{{\text{2}}}{{{x}}}{\text{ , Q  =  sin x + log x}}$

${\text{IF  =  }}{{{e}}^{\int {\dfrac{{\text{2}}}{{{x}}}} }}{\text{  =  }}{{{e}}^{{\text{2log x}}}}{\text{  =  }}{{{x}}^{\text{2}}}$ 

Complete solution is

\[{{y \times IF  =  }}\int {\text{Q}} {{ \times IFdx + C}}\]

General solution is 

${{y}}{{{x}}^{\text{2}}}{\text{  =  }}\int {{\text{(sinx + logx)}}} {{{x}}^{\text{2}}}{\text{dx + C}}$

${{y}}{{{x}}^{\text{2}}}{\text{  =  }}\int {\left( {{{{x}}^{\text{2}}}{\text{sinx + }}{{{x}}^{\text{2}}}{\text{logx}}} \right)} {\text{dx + C}}$

${{y}}{{{x}}^{\text{2}}}{\text{  =  }}\int {{{{x}}^{\text{2}}}} {\text{sinx dx + }}\int {{{{x}}^{\text{2}}}} {\text{logx dx + C}}$

${{y}}{{{x}}^{\text{2}}}{\text{  =  }}{{\text{I}}_{\text{1}}}{\text{ + }}{{\text{I}}_{\text{2}}}{\text{ + C}}$ 

Let \[{{\text{I}}_{\text{1}}}{\text{  =  }}\int {{{{x}}^{\text{2}}}} {\text{sin x dx}}\] we get

${\text{ =  }}{{{x}}^{\text{2}}}{\text{( - cosx) + }}\int {\text{2}} {\text{ x cos x dx}}$

${\text{ =   - }}{{{x}}^{\text{2}}}{\text{cosx + }}\left[ {{\text{2x(sinx) - }}\int {\text{2}} {\text{sinxdx}}} \right]$

${{\text{I}}_{\text{1}}}{\text{  =   - }}{{{x}}^{\text{2}}}{\text{cosx + 2xsinx + 2cosx}}$ 

Let \[{{\text{I}}_{\text{2}}}{\text{  =  }}\int {{{{x}}^{\text{2}}}} {\text{log x dx}}\] we get

${\text{ =  log x}}\dfrac{{{{{x}}^{\text{3}}}}}{{\text{3}}}{\text{ - }}\int {\dfrac{{\text{1}}}{{{x}}}} \dfrac{{{{{x}}^{\text{3}}}}}{{\text{3}}}{\text{dx}}$

${\text{ =  logx}}\dfrac{{{{{x}}^{\text{3}}}}}{{\text{3}}}{\text{ - }}\dfrac{{\text{1}}}{{\text{3}}}\int {{{{x}}^{\text{2}}}} {\text{dx}}$

${\text{ =  logx}}\dfrac{{{{{x}}^{\text{3}}}}}{{\text{3}}}{\text{ - }}\dfrac{{\text{1}}}{{\text{3}}}\dfrac{{{{{x}}^{\text{3}}}}}{{\text{3}}}$ 

Now, substitute value of \[{{\text{I}}_{\text{1}}}{\text{ , }}{{\text{I}}_{\text{2}}}\] we get

\[{{y}}{{{x}}^{\text{2}}}{\text{  =   - }}{{{x}}^{\text{2}}}{\text{cosx + 2xsinx + 2cosx + }}\dfrac{{{{{x}}^{\text{3}}}}}{{\text{3}}}{\text{logx - }}\dfrac{{\text{1}}}{{\text{9}}}{{{x}}^{\text{3}}}{\text{ + C}}\] 

\[{{y  =   - cosx + }}\dfrac{{{\text{2sinx}}}}{{{x}}}{\text{ + }}\dfrac{{{\text{2cosx}}}}{{{{{x}}^{\text{2}}}}}{\text{ + }}\dfrac{{{x}}}{{\text{3}}}{\text{logx - }}\dfrac{{{x}}}{{\text{9}}}{\text{ + C}}{{{x}}^{{\text{ - 2}}}}\]

26. Find the general solution of \[{\text{(1 + tan y)(dx - dy) + 2x dy  =  0}}\]

Ans: We have \[{\text{(1 + tan y)(dx - dy) + 2x dy  =  0}}\]

Divide by \[{\text{dy}}\] we get:

${\text{(1 + tan y)}}\left( {\dfrac{{{\text{dx}}}}{{{\text{dy}}}}{\text{ - 1}}} \right){\text{ + 2x  =  0}}$

${\text{(1 + tan y)}}\dfrac{{{\text{dx}}}}{{{\text{dy}}}}{\text{ - (1 + tan y) + 2x  =  0}}$

${\text{(1 + tan y)}}\dfrac{{{\text{dx}}}}{{{\text{dy}}}}{\text{ + 2x  =  (1 + tan y)}}$ 

Divide by \[{\text{(1 + tan y)}}\] on both sides we get:

\[\dfrac{{{\text{dx}}}}{{{\text{dy}}}}{\text{ + }}\dfrac{{{\text{2x}}}}{{{\text{1 + tany}}}}{\text{  =  1}}\] is a linear differential equation

Compare with \[\dfrac{{{\text{dx}}}}{{{\text{dy}}}}{\text{ + Px  =  Q}}\] we get

\[{\text{P  =  }}\dfrac{{\text{2}}}{{{\text{1 + tany}}}}{\text{ , Q  =  1}}\]

\[{\text{IF  =  }}{{{e}}^{\int {\dfrac{{\text{2}}}{{{\text{1 + tany}}}}} dy}}{\text{  =  }}{{{e}}^{\int {\dfrac{{{\text{2cosy}}}}{{{\text{cosy + tany}}}}d} {{y}}}}\]  

${\text{ =  }}{{{e}}^{\int {\dfrac{{{\text{cosy + siny + cosy - siny}}}}{{{\text{cosy + siny}}}}} dy}}$

   $= {\text{ }}{{{e}}^{\int {(1 + \dfrac{{\cos y - \sin y}}{{\cos y + \sin y}}} }}$

   $= {\text{ }}{{{e}}^{y + \log x(\cos y + \sin y)}}$ 

\[{\text{ =  }}{{{e}}^{{y}}}{{ \times (cosy + siny)                     }}\left[ {{{{e}}^{{\text{logx}}}}{\text{  =  x}}} \right]\]

General solution is

${{x \times }}{{{e}}^{{y}}}{\text{(cosy + siny)  =  }}\int {\text{1}} {{ \times }}{{{e}}^{{y}}}{\text{(cosy + siny)dy + C}}$

${{x \times }}{{{e}}^{{y}}}{\text{(cosy + siny)  =  }}\int {{{{e}}^{{y}}}} {\text{(siny + cosy)dy + C}}$

$x \times e^{y}(\cos y+\sin y)=e^{y} \sin y+\mathrm{C}$

$\int e^{x} f(x)+f^{\prime}(x) d x=e^{x} f(x)$

${{x(siny + cosy)  =  siny + C}}{{{e}}^{{\text{ - y}}}}$ 

27. Solve \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  cos(x + y) + sin(x + y)}}\]

Ans: We have \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  cos(x + y) + sin(x + y)}}\]

Put \[{{x + y  =  z}}\] we get \[{\text{1 + }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{\text{dz}}}}{{{\text{dx}}}}\]

Substitute values we get

$\left( {\dfrac{{{\text{dz}}}}{{{\text{dx}}}}{\text{ - 1}}} \right){\text{  =  cos z + sin z}}$

${{{\text{dz}}}}{{{\text{dx}}}}{\text{  =  (cos z + sin z + 1)}}$

${{{\text{dz}}}}{{{\text{cosz + sinz + 1}}}}{\text{  =  dx}}$ 

Integrate both sides we get:

\[\int {\dfrac{{{\text{dx}}}}{{{\text{cosz + sinz + 1}}}}} {\text{  =  }}\int {\text{1}} {\text{dx}}\]

${\dfrac{{{\text{dz}}}}{{\dfrac{{{\text{1 - ta}}{{\text{n}}^{\text{2}}}\dfrac{{\text{z}}}{{\text{2}}}}}{{{\text{1 + ta}}{{\text{n}}^{\text{2}}}\dfrac{{\text{z}}}{{\text{2}}}}}{\text{ + }}\dfrac{{{\text{2tan}}\dfrac{{\text{z}}}{{\text{2}}}}}{{{\text{1 + ta}}{{\text{n}}^{\text{2}}}\dfrac{{\text{z}}}{{\text{2}}}}}{\text{ + 1}}}}} {\text{  =  }}\int {\text{d}} {{x}}$

${\dfrac{{{\text{dz}}}}{{{\text{1 - ta}}{{\text{n}}^{\text{2}}}\dfrac{{\text{z}}}{{\text{2}}}{\text{ + 2tan}}\dfrac{{\text{z}}}{{\text{2}}}{\text{ + 1 + ta}}{{\text{n}}^{\text{2}}}\dfrac{{\text{z}}}{{\text{2}}}}}} {\text{  =  }}\int {\text{d}} {{x}}$

${\dfrac{{\left( {{\text{1 + ta}}{{\text{n}}^{\text{2}}}\dfrac{{\text{z}}}{{\text{2}}}} \right)}}{{{\text{2 + 2ta}}{{\text{n}}^{\text{2}}}\dfrac{{\text{z}}}{{\text{2}}}}}} {\text{  =  }}\int {\text{d}} {{x}}$

${\dfrac{{{\text{se}}{{\text{c}}^{\text{2}}}\dfrac{{\text{z}}}{{\text{2}}}{\text{dz}}}}{{{\text{2(1 + tan}}\dfrac{{\text{z}}}{{\text{2}}}{\text{)}}}}} {\text{  =  }}\int {\text{d}} {{x}}$ 

Put \[{\text{1 + tan}}\dfrac{{\text{z}}}{{\text{2}}}{\text{  =  t}}\] we get \[\left( {\dfrac{{\text{1}}}{{\text{2}}}{\text{se}}{{\text{c}}^{\text{2}}}\dfrac{{\text{z}}}{{\text{2}}}} \right){\text{dz  =  dt}}\]

${\dfrac{{{\text{dt}}}}{{\text{t}}}} {\text{  =  }}\int {\text{d}} {{x}}$

${\text{log |t|  =  x + C}}$

${\text{log |1 + tan}}\dfrac{{\text{z}}}{{\text{2}}}{\text{|  =  x + C}}$

${\text{log}}\left| {{\text{1 + tan}}\dfrac{{{\text{(x + y)}}}}{{\text{2}}}} \right|{\text{  =  x + C}}$ 

28. Find the general solution of \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - 3y  =  sin2x}}\]

Ans: We have \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - 3y  =  sin2x}}\] is a linear differential equation

Compare with \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + Py  =  Q}}\] we get

\[{\text{P  =   - 3 , Q  =  sin2x}}\]

\[{\text{IF  =  }}{{{e}}^{{\text{ - 3}}\int {{\text{dx}}} }}{\text{  =  }}{{{e}}^{{\text{ - 3x}}}}\]

General solution is

\[{{y}}{{{e}}^{{\text{ - 3x}}}}{\text{  =  }}\int {{\text{sin}}} {\text{2x}}{{{e}}^{ - 3}}{\text{dx}}\]

Let \[{{y}}{{{e}}^{{\text{ - 3t}}}}{\text{  =  I}}\]

${\text{I  =  }}\int {{{{e}}^{{\text{ - 3x}}}}} {\text{ sin2x}}$

${\text{I  =  sin2x}}\left( {\dfrac{{{{{e}}^{{\text{ - 3x}}}}}}{{{\text{ - 3}}}}} \right){\text{ - }}\int {\text{2}} {\text{cos2x}}\left( {\dfrac{{{{{e}}^{{\text{ - 3x}}}}}}{{{\text{ - 3}}}}} \right){\text{dx + }}{{\text{C}}_{\text{1}}}$

${\text{I  =   - }}\dfrac{{\text{1}}}{{\text{3}}}{{{e}}^{{\text{ - 3x}}}}{\text{sin2x + }}\dfrac{{\text{2}}}{{\text{3}}}\int {{{{e}}^{ - 3{{x}}}}} {\text{cos2xdx + }}{{\text{C}}_{\text{1}}}$

${\text{I  =   - }}\dfrac{{\text{1}}}{{\text{3}}}{{{e}}^{{\text{ - 3x}}}}{\text{sin2x + }}\dfrac{{\text{2}}}{{\text{3}}}\left( {{\text{cos2x}}\dfrac{{{{{e}}^{{\text{ - 3}}}}}}{{{\text{ - 3}}}}{\text{ - }}\int {{\text{( - 2sin2x)}}} \dfrac{{{{{e}}^{{\text{ - 3x}}}}}}{{{\text{ - 3}}}}{\text{dx}}} \right){\text{ + }}{{\text{C}}_{\text{1}}}{\text{ + }}{{\text{C}}_{\text{2}}}$

$\mathrm{I}=-\dfrac{1}{3} e^{-3 \mathrm{x}} \sin 2 \mathrm{x}-\dfrac{2}{9} \cos 2 \mathrm{x} e^{-3 \mathrm{x}}-\dfrac{4}{9} \mathrm{I}+\mathrm{C}^{\prime}$

$\mathrm{I}+\dfrac{41}{9} 2=+e^{-3 \mathrm{x}}\left(-\dfrac{1}{3} \sin 2 \mathrm{x}-\dfrac{2}{9} \cos 2 \mathrm{x}\right)+\mathrm{C}^{\prime}$

$139 \mathrm{I}=e^{-3 \mathrm{x}}\left(-\dfrac{1}{3} \sin 2 \mathrm{x}-\dfrac{2}{9} \cos 2 \mathrm{x}\right)+\mathrm{C}^{\prime}$

$\mathrm{I}+\dfrac{4 \mathrm{I}}{9}=e^{-3 \mathrm{x}}\left(-\dfrac{1}{3} \sin 2 \mathrm{x}-\dfrac{2}{9} \cos 2 \mathrm{x}\right)+\mathrm{C}^{\prime}$

${\text{I  =  }}\dfrac{{\text{9}}}{{{\text{13}}}}{{{e}}^{{\text{ - 3x}}}}\left( {{\text{ - }}\dfrac{{\text{1}}}{{\text{3}}}{\text{sin2x - }}\dfrac{{\text{2}}}{{\text{9}}}{\text{cos2x}}} \right){\text{ + C          }}\left[ {{\text{where C  =  }}\dfrac{{{\text{9C}}}}{{{\text{13}}}}} \right]$

${\text{I  =  }}\dfrac{{\text{3}}}{{{\text{13}}}}{{{e}}^{{\text{ - 3x}}}}\left( {{\text{ - sin2x - }}\dfrac{{\text{2}}}{{\text{3}}}{\text{cos2x}}} \right){\text{ + C}}$ 

${\text{I  =  }}\dfrac{{\text{3}}}{{{\text{13}}}}{{{e}}^{{\text{ - 3x}}}}\dfrac{{{\text{( - 3sin2x - 2cos2x)}}}}{{\text{3}}}{\text{ + C}}$

${\text{ =  }}\dfrac{{{{{e}}^{{\text{ - 3x}}}}}}{{{\text{13}}}}{\text{( - 3sin2x - 2cos2x) + C}}$

${\text{I  =  }}\dfrac{{{{{e}}^{{\text{ - 3x}}}}}}{{{\text{13}}}}{\text{(2cos2x + 3sin2x) + C}}$ 

Substitute values we get

\[{{y}}{{{e}}^{{\text{ - 3x}}}}{\text{  =   - }}\dfrac{{{{{e}}^{{\text{ - 3x}}}}}}{{{\text{13}}}}{\text{(2cos2x + 3sin2x) + C}}\]

\[{{y  =   - }}\dfrac{{\text{1}}}{{{\text{13}}}}{\text{(2cos2x + 3sin2x) + C}}{{{e}}^{{\text{3x}}}}\]

29. Find the equation of a curve passing through \[{\text{(2,1)}}\] . if the slope of the tangent to the curve at any point \[{\text{(x,y)}}\] is \[\dfrac{{{{{x}}^{\text{2}}}{\text{ + }}{{{y}}^{\text{2}}}}}{{{\text{2xy}}}}\]

Ans: The slope of tangent to curve at point \[{\text{(x,y)}}\] is \[\dfrac{{{{{x}}^{\text{2}}}{\text{ + }}{{{y}}^{\text{2}}}}}{{{\text{2xy}}}}\]

${\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)_{{\text{(x,y)}}}}{\text{  =  }}\dfrac{{{{{x}}^{\text{2}}}{\text{ + }}{{{y}}^{\text{2}}}}}{{{\text{2xy}}}}$

${{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{\text{1}}}{{\text{2}}}\left( {\dfrac{{{x}}}{{{y}}}{\text{ + }}\dfrac{{{y}}}{{{x}}}} \right)$ 

Put \[{{y  =  vx}}\] we get \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  v + x}}\dfrac{{{\text{dv}}}}{{{\text{dx}}}}\]

Substitute values we get:

${\text{v + x}}\dfrac{{{\text{dv}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{\text{1}}}{{\text{2}}}\left( {\dfrac{{\text{1}}}{{\text{v}}}{\text{ + v}}} \right)$

${\text{v + x}}\dfrac{{{\text{dv}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{\text{1}}}{{\text{2}}}\left( {\dfrac{{{\text{1 + }}{{\text{v}}^{\text{2}}}}}{{\text{v}}}} \right)$

${{x}}\dfrac{{{\text{dv}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{\text{1 + }}{{\text{v}}^{\text{2}}}}}{{{\text{2v}}}}{\text{ - v}}$

${{x}}\dfrac{{{\text{dv}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{\text{1 + }}{{\text{v}}^{\text{2}}}{\text{ - 2}}{{\text{v}}^{\text{2}}}}}{{{\text{2v}}}}$

${{x}}\dfrac{{{\text{dv}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{\text{1 - }}{{\text{v}}^{\text{2}}}}}{{{\text{2v}}}}$

${{{\text{2v}}}}{{{\text{1 - }}{{\text{v}}^{\text{2}}}}}{\text{dv  =  }}\dfrac{{{\text{dx}}}}{{{x}}}$ 

Integrate both sides we get:

\[\int {\dfrac{{{\text{2v}}}}{{{\text{1 - }}{{\text{v}}^{\text{2}}}}}} {\text{dv  =  }}\int {\dfrac{{{\text{dx}}}}{{{x}}}} \]

Put \[{\text{1 - }}{{\text{v}}^{\text{2}}}{\text{  =  t}}\] in LHS we get:

${\text{ - 2vdv  =  dt}}$

${\text{ - }}\int {\dfrac{{{\text{dt}}}}{{\text{t}}}} {\text{  =  }}\int {\dfrac{{{\text{dx}}}}{{{x}}}}$

${\text{ - log t  =  log x + logC}}$

${\text{ - log}}\left( {{\text{1 - }}{{\text{v}}^{\text{2}}}} \right){\text{  =  log x + log C}}$

${\text{ - log}}\left( {{\text{1 - }}\dfrac{{{{{y}}^{\text{2}}}}}{{{{{x}}^{\text{2}}}}}} \right){\text{  =  logx + logC}}$ 

${\text{ - log}}\left( {\dfrac{{{{{x}}^{\text{2}}}{\text{ - }}{{{y}}^{\text{2}}}}}{{{{{x}}^{\text{2}}}}}} \right){\text{  =  logx + logC}}$

${\text{log}}\left( {\dfrac{{{{{x}}^{\text{2}}}}}{{{{{x}}^{\text{2}}}{\text{ - }}{{{y}}^{\text{2}}}}}} \right){\text{  =  logx + logC}}$

${{{{{x}}^{\text{2}}}}}{{{{{x}}^{\text{2}}}{\text{ - }}{{{y}}^{\text{2}}}}}{\text{  =  Cx}}$ 

As curve passes through point \[{\text{(2,1)}}\]

${{{{{\text{(2)}}}^{\text{2}}}}}{{{{{\text{(2)}}}^{\text{2}}}{\text{ - (1}}{{\text{)}}^{\text{2}}}}}{\text{  =  C(2)}}$

${\text{C  =  }}\dfrac{{\text{2}}}{{\text{3}}}$ 

Required solution is \[{\text{2}}\left( {{{{x}}^{\text{2}}}{\text{ - }}{{{y}}^{\text{2}}}} \right){\text{  =  3x}}\]

30. Find the equation of the curve through the point \[{\text{(1,0)}}\] if the slope of the tangent to the curve at any point \[{\text{(x,y)}}\] is \[\dfrac{{{{y - 1}}}}{{{{{x}}^{\text{2}}}{\text{ + x}}}}\]

Ans: It is given that, slope of tangent to the curve at any point \[{\text{(x,y)}}\] is \[\dfrac{{{{y - 1}}}}{{{{{x}}^{\text{2}}}{\text{ + x}}}}\]

${\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)_{{\text{(x,y)}}}}{\text{  =  }}\dfrac{{{{y - 1}}}}{{{{{x}}^{\text{2}}}{\text{ + x}}}}$

${{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{{y - 1}}}}{{{{{x}}^{\text{2}}}{\text{ + x}}}}$

${{{\text{dy}}}}{{{{y - 1}}}}{\text{  =  }}\dfrac{{{\text{dx}}}}{{{{{x}}^{\text{2}}}{\text{ + x}}}}$ 

${\dfrac{{{\text{dy}}}}{{{{y - 1}}}}} {\text{  =  }}\int {\dfrac{{{\text{dx}}}}{{{{{x}}^{\text{2}}}{\text{ + x}}}}}$

${\dfrac{{{\text{dy}}}}{{{{y - 1}}}}} {\text{  =  }}\int {\dfrac{{{\text{dx}}}}{{{{x(x + 1)}}}}}$

${\dfrac{{{\text{dy}}}}{{{{y - 1}}}}} {\text{  =  }}\int {\left( {\dfrac{{\text{1}}}{{{x}}}{\text{ - }}\dfrac{{\text{1}}}{{{{x + 1}}}}} \right)} {\text{ dx}}$

${\text{log(y - 1)  =  log x - log (x + 1) + logC}}$

${\text{log(y - 1)  =  log}}\left( {\dfrac{{{{xC}}}}{{{{x + 1}}}}} \right)$ 

As given curve passes through point \[{\text{(1,0)}}\]

${\text{0 - 1  =  }}\dfrac{{{\text{1}}{\text{.C}}}}{{{\text{1 + 1}}}}$

${\text{C  =   - 2}}$ 

Particular solution is 

${{y - 1  =  }}\dfrac{{{\text{ - 2x}}}}{{{{x + 1}}}}$

${\text{(y - 1)(x + 1)  =   - 2x}}$

${\text{(y - 1)(x + 1) + 2x  =  0}}$ 

31. Find the equation of a curve passing through origin if the slope of the tangent to the curve at any point \[{\text{(x,y)}}\] is equal to the square of the difference of the abscissa and ordinate of the point.

Ans: Slope of tangent to the curve \[{\text{ =  }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}\]

and difference of abscissa and ordinate \[{\text{ =  x - y}}\]

According to the question \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  (x - y}}{{\text{)}}^{\text{2}}}\]

Put \[{{x - y  =  z}}\]

${\text{1 - }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{\text{dz}}}}{{{\text{dx}}}}$

${{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  1 - }}\dfrac{{{\text{dz}}}}{{{\text{dx}}}}$ 

Substitute values we get

${\text{1 - }}\dfrac{{{\text{dz}}}}{{{\text{dx}}}}{\text{  =  }}{{\text{z}}^{\text{2}}}$

${\text{1 - }}{{\text{z}}^{\text{2}}}{\text{  =  }}\dfrac{{{\text{dz}}}}{{{\text{dx}}}}$

${\text{dx  =  }}\dfrac{{{\text{dz}}}}{{{\text{1 - }}{{\text{z}}^{\text{2}}}}}$ 

Integrate both sides, we get:

${\text{d}} {{x  =  }}\int {\dfrac{{{\text{dz}}}}{{{\text{1 - }}{{\text{z}}^{\text{2}}}}}}$

${{x  =  }}\dfrac{{\text{1}}}{{\text{2}}}{\text{log}}\left| {\dfrac{{{\text{1 + z}}}}{{{\text{1 - z}}}}} \right|{\text{ + C}}$

${\text{tx  =  }}\dfrac{{\text{1}}}{{\text{2}}}{\text{log}}\left| {\dfrac{{{\text{1 + x - y}}}}{{{\text{1 - x + y}}}}} \right|{\text{ + C}}$ 

As curve passes through origin

${\text{0  =  }}\dfrac{{\text{1}}}{{\text{2}}}{\text{log}}\left| {\dfrac{{{\text{1 + 0 - 0}}}}{{{\text{1 - 0 + 0}}}}} \right|{\text{ + C}}$

${\text{C  =  0}}$ 

${{x  =  }}\dfrac{{\text{1}}}{{\text{2}}}{\text{log}}\left| {\dfrac{{{\text{1 + x - y}}}}{{{\text{1 - x + y}}}}} \right|$

${\text{2x  =  log}}\left| {\dfrac{{{\text{1 + x - y}}}}{{{\text{1 - x + y}}}}} \right|$

${{{e}}^{{\text{2x}}}}{\text{  =  }}\left| {\dfrac{{{\text{1 + x - y}}}}{{{\text{1 - x + y}}}}} \right|$

${\text{(1 - x + y)}}{{{e}}^{{\text{2x}}}}{\text{  =  1 + x - y}}$ 

32. Find the equation of a curve passing through the point \[{\text{(1,1)}}\] . If the tangent drawn at any point \[{\text{P(x,y)}}\] on the curve meets the co-ordinate axes at A and B such that P is the mid-point of AB

Ans: The below figure obtained by the given information

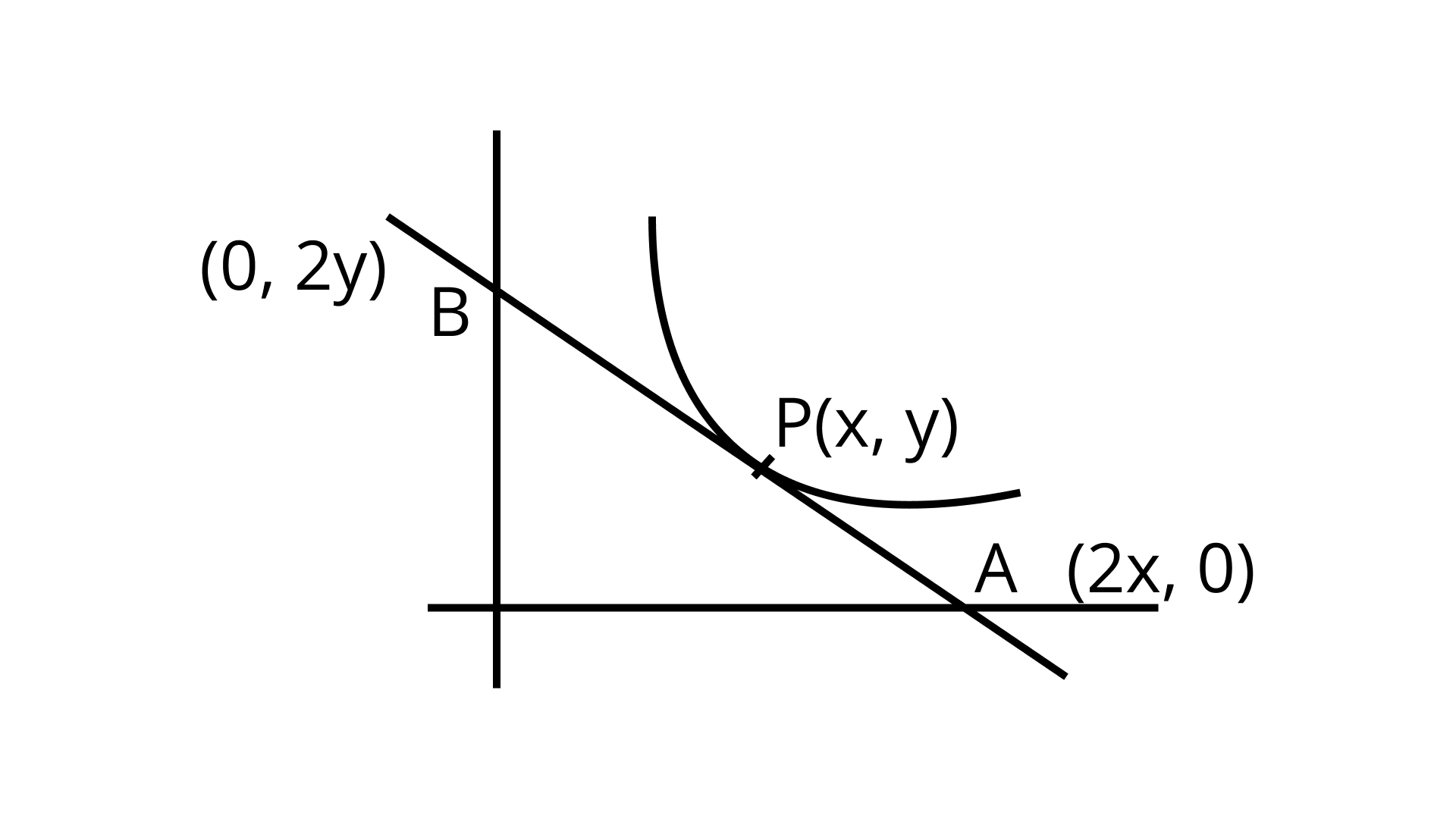
Let the coordinate of the point P is \[{\text{(x,y)}}\] . It is given that, P is mid-point of AB

So, the coordinates of points A and B are \[{\text{(2x,0) , (0,2y)}}\] , respectively.

Slope of AB \[{\text{ =  }}\dfrac{{{\text{0 - 2y}}}}{{{\text{2x - 0}}}}{\text{  =   - }}\dfrac{{{y}}}{{{x}}}\]

Since, the segment AB is a tangent to the curve at P

\[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =   - }}\dfrac{{{y}}}{{{x}}}\]

\[\dfrac{{{\text{dy}}}}{{{y}}}{\text{  =   - }}\dfrac{{{\text{dx}}}}{{{x}}}\]

Integrate both sides we get:

${\text{log y  =   - log x + logC}}$

${\text{log y  =  log}}\dfrac{{\text{C}}}{{{x}}}$ 

As given curve passes through \[{\text{(1,1)}}\]

${\text{log1  =  log}}\dfrac{{\text{C}}}{{\text{1}}}$

${\text{0  =  logC}}$

${\text{c  =  1}}$

${\text{logy  =  log}}\dfrac{{\text{1}}}{{{x}}}$

${{y  =  }}\dfrac{{\text{1}}}{{{x}}}$

${{xy  =  1}}$ 

33. Solve \[{{x}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  y(logy - logx + 1)}}\]

Ans: We have \[{{x}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  y(logy - logx + 1)}}\]

${{x}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  ylog}}\left( {\dfrac{{{y}}}{{{x}}}{\text{ + 1}}} \right){{x}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  y}}\left( {{\text{log}}\dfrac{{{y}}}{{{x}}}{\text{ + 1}}} \right)$

${{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{y}}}{{{x}}}\left( {{\text{log}}\dfrac{{{y}}}{{{x}}}{\text{ + 1}}} \right)$ 

which is a homogeneous equation

Put \[\dfrac{{{y}}}{{{x}}}{\text{  =  v or y  =  vx}}\]

\[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  v + x}}\dfrac{{{\text{dv}}}}{{{\text{dx}}}}\]

Substitute values we have

${\text{v + x}}\dfrac{{{\text{dv}}}}{{{\text{dx}}}}{\text{  =  v(logv + 1)}}$

${{x}}\dfrac{{{\text{dv}}}}{{{\text{dx}}}}{\text{  =  v(logv + 1 - 1)}}$

${{x}}\dfrac{{{\text{dv}}}}{{{\text{dx}}}}{\text{  =  v(logv)}}$

${{{\text{dv}}}}{{{\text{vlogv}}}}{\text{  =  }}\dfrac{{{\text{dx}}}}{{{x}}}$ 

Integrate both sides

\[\int {\dfrac{{{\text{dv}}}}{{{\text{vlogv}}}}} {\text{  =  }}\int {\dfrac{{{\text{dx}}}}{{{x}}}} \]

Put \[{\text{log v  =  u}}\] in LHS we get

${{\text{1}}}{{\text{v}}}{{ \times dv  =  du}}$

${\dfrac{{{\text{du}}}}{{\text{u}}}} {\text{  =  }}\int {\dfrac{{{\text{dx}}}}{{{x}}}}$ 

${\text{log u  =  logx + logC}}$

${\text{log u  =  logCx}}$

${\text{u  =  Cx}}$

${\text{log v  =  Cx}}$

${\text{log}}\left( {\dfrac{{{y}}}{{{x}}}} \right){\text{  =  Cx}}$ 

Objective Questions

Choose the correct answer from the given four options in each of the Exercises from 34 to 75 (M.C.Q)

34. The degree of the differential equation \[{\left( {\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}} \right)^{\text{2}}}{\text{ + }}{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)^{\text{2}}}{\text{  =  xsin}}\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)\] is:

(A) \[{\text{1}}\]

(B) \[{\text{2}}\]

(C) \[{\text{3}}\]

(D) Not defined

Ans: Correct option (D) as degree of the differential equation is not defined because when we expand \[{\text{sin}}\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)\] we get an infinite series in the increasing power of \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}\] Therefore, its degree is not defined.

35. The degree of the differential equation \[{\left[ {{\text{1 + }}{{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)}^{\text{2}}}} \right]^{\dfrac{3}{{\text{2}}}}}{\text{  =  }}\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}\] is

(A) \[{\text{4}}\]

(B) \[\dfrac{{\text{3}}}{{\text{2}}}\]

(C) Not defined

(D) \[{\text{2}}\]

Ans: Correct option (D)

As given that \[{\left[ {{\text{1 + }}{{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)}^{\text{2}}}} \right]^{\dfrac{{\text{3}}}{{\text{2}}}}}{\text{  =  }}\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}\]

Squaring both sides:

\[{\left[ {{\text{1 + }}{{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)}^{\text{2}}}} \right]^{\text{3}}}{\text{  =  }}{\left( {\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}} \right)^{\text{2}}}\]

Thus, degree is two

36. The order and degree of the differential equation \[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + }}{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)^{\dfrac{{\text{1}}}{{\text{4}}}}}{\text{ + }}{{{x}}^{\dfrac{{\text{1}}}{{\text{3}}}}}{\text{  =  0}}\] , respectively, are

(A) \[{\text{2}}\] and not defined

(B) \[{\text{2 , 2}}\]

(C) \[{\text{2 , 3}}\]

(D) \[{\text{3 , 3}}\]

Ans: Correct option (A) Given that \[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + }}{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)^{\dfrac{{\text{1}}}{{\text{4}}}}}{\text{ =   - }}{{{x}}^{\dfrac{{\text{1}}}{{\text{3}}}}}\]

\[{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)^{\dfrac{1}{4}}}{\text{  =   - }}\left( {{{{x}}^{\dfrac{1}{5}}}{\text{ + }}\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}} \right)\]

Squaring both sides

\[{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)^{\dfrac{{\text{1}}}{{\text{2}}}}}{\text{  =  }}{\left( {{{{x}}^{\dfrac{{\text{1}}}{{\text{5}}}}}{\text{ + }}\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}} \right)^{\text{2}}}\]

Again squaring both sides

\[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}{\left( {{{{x}}^{\dfrac{1}{5}}}{\text{ + }}\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}} \right)^{\text{4}}}\]

Order is two, degree does not defined when we expand \[{\left( {{{{x}}^{\dfrac{{\text{1}}}{{\text{5}}}}}{\text{ + }}\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}} \right)^{\text{4}}}\] , it cannot be in polynomial expansion.

37. If \[{{y  =  }}{{{e}}^{{\text{ - x}}}}{\text{(Acosx + Bsinx)}}\] then \[{{y}}\] is a solution of

(a)\[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + 2}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  0}}\]

(b)\[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ - 2}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + 2y  =  0}}\]

(c) \[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + 2}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + 2y  =  0}}\]

(d) \[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + 2y  =  0}}\]

Ans: Correct option (c) 

As we have \[{{y  =  }}{{{e}}^{{\text{ - x}}}}{\text{(Acosx + Bsinx)}}\]

Differentiate both sides

${{{\text{dy}}}}{{{\text{dx}}}}{\text{  =   - }}{{{e}}^{{\text{ - x}}}}{\text{(Acosx + Bsinx) + }}{{{e}}^{{\text{ - x}}}}{\text{( - Asinx + Bcosx)}}$

${{{\text{dy}}}}{{{\text{dx}}}}{\text{  =   - y + }}{{{e}}^{{\text{ - x}}}}{\text{( - Asinx + Bcosx)}}$ 

Again differentiate both sides

\[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{  =  }}\dfrac{{{\text{ - dy}}}}{{{\text{dx}}}}{\text{ + }}{{{e}}^{{\text{ - x}}}}{\text{( - cosx - Bsinx) - }}{{{e}}^{{\text{ - x}}}}{\text{( - Asinx + Bcosx)}}\]

${{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{  =  }}\dfrac{{{\text{ - dy}}}}{{{\text{dx}}}}{\text{ - y - }}\left[ {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y}}} \right]$

${{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{  =   - }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - y - }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - y}}$

${{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{  =   - 2}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - 2y}}$

${{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + 2}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + 2y  =  0}}$ 

38. The differential equation for \[{{y  =  Acos\alpha x + Bsin\alpha x}}\] where A and B are arbitrary constants is

(a) \[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ - }}{{{\alpha }}^{\text{2}}}{{y  =  0}}\]

(b) \[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + }}{{{\alpha }}^{\text{2}}}{{y  =  0}}\]

(c) \[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + \alpha y  =  0}}\]

(d) \[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ - \alpha y  =  0}}\]

Ans: Correct option (b)

As we have \[{{y  =  Acos\alpha  + Bsin\alpha }}\]

\[\dfrac{{{{dy}}}}{{{{dx}}}}{{  =   - \alpha Asin\alpha x + \alpha Bcos\alpha x}}\]

Differentiate both sides:

\[\dfrac{{{{{d}}^{{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{{  =   - A}}{{{\alpha }}^{{2}}}{{cos\alpha x - }}{{{\alpha }}^{{2}}}{{Bsin\alpha x}}\]

${{{{{d}}^{{2}}}{{y}}}}{{{{d}}{{{x}}^{{2}}}}}{{  =   - }}{{{\alpha }}^{{2}}}{{(Acos\alpha x - Bsin\alpha x)}}$

${{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{{  =   - }}{{{\alpha }}^{\text{2}}}{{y}}$

${{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + }}{{{\alpha }}^{\text{2}}}{{y  =  0}}$ 

39. Solution of differential equation \[{{x dy - y dx  =  0}}\] represents:

(A) a rectangular hyperbola

(B) parabola whose vertex is at origin

(C) straight line passing through origin

(D) a circle whose centre is at origin

Ans: Correct option (c)

As we have \[{{x dy - y dx  =  0}}\]

${{x dy  =  y dx}}$

${{{\text{dy}}}}{{{y}}}{\text{  =  }}\dfrac{{{\text{dx}}}}{{{x}}}$ 

Integrate both sides:

${\dfrac{{{\text{dy}}}}{{{y}}}} {\text{  =  }}\int {\dfrac{{{\text{dx}}}}{{{x}}}}$

${\text{log y  =  log x + log C}}$

${\text{log y  =  logCx}}$

${{y  =  Cx}}$ 

which is a straight line passing through origin

40. Integrating factor of the differential equation \[{\text{cos x}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y sin x  =  1}}\] is

(A) \[{\text{cos x}}\]

(B) \[{\text{tan x}}\]

(C) \[{\text{sec x}}\]

(D) \[{\text{sin x}}\]

Ans: Correct option (c)

As we have \[{\text{cos x}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y sin x  =  1}}\]

Divide both side by \[{\text{cos x}}\] we get:

${{{\text{dy}}}}{{{\text{dx}}}}{\text{ + ytanx  =  secx}}$

${\text{Here P  =  tanx , Q  =  secx}}$

${\text{IF  =  }}{{{e}}^{\int {{\text{P dx}}} }}{\text{  =  }}{{{e}}^{\int {{\text{tanxdx}}} }}{\text{  =  }}{{{e}}^{{\text{log secx}}}}{\text{  =  sec x}}$ 

41. Solution of the differential equation \[{\text{tan y se}}{{\text{c}}^{\text{2}}}{{xdx + tan x se}}{{\text{c}}^{\text{2}}}{{ydy  =  0}}\] is

(a) \[{\text{tanx + tany  =  k}}\]

(b) \[{\text{tanx - tany  =  k}}\]

(c) \[\dfrac{{{\text{tanx}}}}{{{\text{tany}}}}{\text{  =  k}}\]

(d) \[{\text{tan x tan y  =  k}}\]

Ans: Correct option (d)

We have \[{\text{tan y se}}{{\text{c}}^{\text{2}}}{{xdx + tan x se}}{{\text{c}}^{\text{2}}}{{ydy  =  0}}\]

${\text{tan y se}}{{\text{c}}^{\text{2}}}{{x dx  =   - tan x se}}{{\text{c}}^{\text{2}}}{{y dy}}$

${{{\text{se}}{{\text{c}}^{\text{2}}}{{x}}}}{{{\text{tanx}}}}{\text{dx  =  }}\dfrac{{{\text{ - se}}{{\text{c}}^{\text{2}}}{{y}}}}{{{\text{tany}}}}{\text{dy}}$ 

Integrate both sides:

\[\int {\dfrac{{{\text{se}}{{\text{c}}^{\text{2}}}{{x}}}}{{{\text{tanx}}}}} {\text{dx  =   - }}\int {\dfrac{{{\text{se}}{{\text{c}}^{\text{2}}}{{y}}}}{{{\text{tany}}}}} {\text{dy}}\]

Put \[{\text{tan x  =  t}}\] in LHS we get

${\text{se}}{{\text{c}}^{\text{2}}}{{x dx  =  dt}}$

${\text{se}}{{\text{c}}^{\text{2}}}{{x dx  =  dt}}$ 

Put \[{\text{tan y  =  u}}\] in RHS we get

\[{\text{se}}{{\text{c}}^{\text{2}}}{{y dy  =  du}}\]

Substitute values we get:

${\dfrac{{{\text{dt}}}}{{\text{t}}}} {\text{  =   - }}\int {\dfrac{{{\text{du}}}}{{\text{u}}}}$

${\text{log t  =   - log u + log k}}$

${\text{log(t}}{\text{.u)  =  log k}}$

${\text{log(tan x tan y)  =  log k}}$

${\text{tan x tan y  =  k}}$ 

42. Family \[{{y  =  Ax + }}{{\text{A}}^{\text{3}}}\] of curves is represented by the differential equation of degree

(a) \[{\text{1}}\]

(b) \[{\text{2}}\]

(c) \[{\text{3}}\]

(d) \[{\text{4}}\]

Ans: Correct option (a)

We have \[{{y  =  Ax + }}{{\text{A}}^{\text{3}}}\]

\[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  A}}\] with degree one

43. Integrating factor of \[\dfrac{{{{x dy}}}}{{{\text{dx}}}}{\text{ - y  =  }}{{{x}}^{\text{4}}}{\text{ - 3x}}\] is 

(a) \[{{x}}\]

(b) \[{\text{log x}}\]

(c) \[\dfrac{{\text{1}}}{{{x}}}\]

(d) \[{\text{ - x}}\]

Ans: Correct option (c) 

We have \[\dfrac{{{{x dy}}}}{{{\text{dx}}}}{\text{ - y  =  }}{{{x}}^{\text{4}}}{\text{ - 3x}}\]

Divide both sides by \[{{x}}\] we get

${{{\text{dy}}}}{{{\text{dx}}}}{\text{ - }}\dfrac{{{y}}}{{{x}}}{\text{  =  }}{{{x}}^{\text{3}}}{\text{ - 3}}$

${\text{Here P  =   - }}\dfrac{{\text{1}}}{{{x}}}{\text{ , Q  =  }}{{{x}}^{\text{3}}}{\text{ - 3}}$

${\text{IF =  e}}{{\text{ }}^{\int {\text{P}} {\text{dx}}}}{\text{  =  }}{{{e}}^{{\text{ - }}\int {\dfrac{{\text{1}}}{{{x}}}} {\text{dx}}}}{\text{  =  }}{{{e}}^{{\text{ - logx}}}}{\text{  =  }}\dfrac{{\text{1}}}{{{x}}}$ 

44. Solution of \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - y  =  1 , y(0)  =  1}}\] is given by

(a) \[{{xy  =   - }}{{{e}}^{{x}}}\]

(b) \[{{xy  =   - }}{{{e}}^{{\text{ - x}}}}\]

(c) \[{{xy  =   - 1}}\]

(d) \[{{y  =  2}}{{{e}}^{{x}}}{\text{ - 1}}\]

Ans: Correct option (b)

We have \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - y  =  1}}\]

${{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  1 + y}}$

${{{\text{dy}}}}{{{\text{1 + y}}}}{\text{  =  dx}}$ 

Integrate both sides:

${\dfrac{{{\text{dy}}}}{{{\text{1 + y}}}}} {\text{  =  }}\int {\text{d}} {{x}}$

${\text{log(1 + y)  =  x + C}}$ 

When \[{{x  =  0 , y  =   - 1}}\] then 

${\text{log2  =  0 + c}}$

${\text{C  =  log2}}$ 

Required solution 

${\text{log(1 + y)  =  x + log2}}$

${\text{log}}\left( {\dfrac{{{\text{1 + y}}}}{{\text{2}}}} \right){\text{  =  x}}$

${{{\text{1 + y}}}}{{\text{2}}}{\text{  =  }}{{{e}}^{{x}}}$

${\text{1 + y  =  2}}{{{e}}^{{x}}}$

${{y  =  2}}{{{e}}^{{x}}}{\text{ - 1}}$ 

45. The number of solutions of \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{{y + 1}}}}{{{{x - 1}}}}{\text{ , y(1)  =  2}}\] is

(a) none

(b) one

(c) two

(d) infinite

Ans: Correct option (b)

As we have \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{{y + 1}}}}{{{{x - 1}}}}\]

\[\dfrac{{{\text{dy}}}}{{{{y + 1}}}}{\text{  =  }}\dfrac{{{\text{dx}}}}{{{{x - 1}}}}\]

Integrate both sides

${\dfrac{{{\text{dy}}}}{{{{y + 1}}}}} {\text{  =  }}\int {\dfrac{{{\text{dx}}}}{{{{x - 1}}}}}$

${\text{log(y + 1)  =  log(x - 1) - logC}}$

${\text{C(y + 1)  =  (x - 1)}}$

${\text{C  =  }}\dfrac{{{{x - 1}}}}{{{{y + 1}}}}$ 

When \[{{x  =  1 , y  =  2 }} \Rightarrow {\text{ C  =  0}}\]

The required solution is \[{{x - 1  =  0}}\]

Thus, one solution exists.

46. Which of the following is a second order differential equation

(a) $y^{\prime 2}+x=y^{2}$

(b) $y^{\prime} y^{\prime \prime}+y=\sin x$

(c) $y^{\prime \prime \prime}+y^{\prime \prime 2}+\mathrm{y}=0$

(d) $y^{\prime}=y^{2}$

Ans: Correct option (b)

47. Integrating factor of the differential equation \[\left( {{\text{1 - }}{{{x}}^{\text{2}}}} \right)\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - xy  =  1}}\] is

(a) \[{\text{ - x}}\]

(b) \[\dfrac{{{x}}}{{{\text{1 + }}{{{x}}^{\text{2}}}}}\]

(c) \[\sqrt {{\text{1 - }}{{{x}}^{\text{2}}}} \]

(d) \[\dfrac{{\text{1}}}{{\text{2}}}{\text{log}}\left( {{\text{1 - }}{{{x}}^{\text{2}}}} \right)\]

Ans: Correct option (c) 

We have \[\left( {{\text{1 - }}{{{x}}^{\text{2}}}} \right)\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - xy  =  1}}\]

Divide both sides by \[\left( {{\text{1 - }}{{{x}}^{\text{2}}}} \right)\] we get

\[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - }}\dfrac{{{x}}}{{{\text{1 - }}{{{x}}^{\text{2}}}}}{{y  =  }}\dfrac{{\text{1}}}{{{\text{1 - }}{{{x}}^{\text{2}}}}}\] is a linear differential equation

\[{\text{IF  =  }}{{{e}}^{{\text{ - }}\int {\dfrac{{{x}}}{{{\text{1 - }}{{{x}}^{\text{2}}}}}} {\text{dx}}}}\]

Put \[{\text{1 - }}{{{x}}^{\text{2}}}{\text{  =  t}}\]

${\text{ - 2x dx  =  dt}}$

${{x dx  =   - }}\dfrac{{{\text{dt}}}}{{\text{2}}}$ 

Now, \[{\text{IF  =  }}{{{e}}^{\dfrac{{\text{1}}}{{\text{2}}}\int {\dfrac{{{\text{dt}}}}{{\text{t}}}} }}{\text{  =  }}{{{e}}^{\dfrac{{\text{1}}}{{\text{2}}}{\text{logt}}}}{\text{  =  }}{{{e}}^{\dfrac{{\text{1}}}{{\text{2}}}{\text{log}}\left( {{\text{1 - }}{{{x}}^{\text{2}}}} \right)}}{\text{  =  }}\sqrt {{\text{1 - }}{{{x}}^{\text{2}}}} \]

48. \[{\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{x + ta}}{{\text{n}}^{{\text{ - 1}}}}{{y  =  c}}\] is the general solution of the differential equation

(a) \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{\text{1 + }}{{{y}}^{\text{2}}}}}{{{\text{1 + }}{{{x}}^{\text{2}}}}}\]

(b) \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{\text{1 + }}{{{x}}^{\text{2}}}}}{{{\text{1 + }}{{{y}}^{\text{2}}}}}\]

(c) \[\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right){\text{dy + }}\left( {{\text{1 + }}{{{y}}^{\text{2}}}} \right){\text{dx  =  0}}\]

(d) \[\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right){\text{dx + }}\left( {{\text{1 + }}{{{y}}^{\text{2}}}} \right){\text{dy  =  0}}\]

Ans: Correct option (c)

We have \[{\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{x + ta}}{{\text{n}}^{{\text{ - 1}}}}{{y  =  c}}\]

Differentiate both sides we get:

${{\text{d}}}{{{\text{dx}}}}\left( {{\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{x + ta}}{{\text{n}}^{{\text{ - 1}}}}{{y}}} \right){\text{  =  }}\dfrac{{\text{d}}}{{{\text{dx}}}}{\text{c}}$

${{\text{1}}}{{{\text{1 + }}{{{x}}^{\text{2}}}}}{\text{ + }}\dfrac{{\text{1}}}{{{\text{1 + }}{{{x}}^{\text{2}}}}}{{ \times }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  0}}$ 

${{\text{1}}}{{{\text{1 + }}{{{x}}^{\text{2}}}}}{\text{ + }}\dfrac{{\text{1}}}{{{\text{1 + }}{{{y}}^{\text{2}}}}}{{ \times }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  0}}$

${{\text{1}}}{{{\text{1 + }}{{{y}}^{\text{2}}}}}{{ \times }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =   - }}\dfrac{{\text{1}}}{{{\text{1 + }}{{{x}}^{\text{2}}}}}$

$\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right){\text{dy + }}\left( {{\text{1 + }}{{{y}}^{\text{2}}}} \right){\text{dx  =  0}}$ 

49. The differential equation \[{{y}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + x  =  c}}\] represents:

(A) Family of hyperbolas

(B) Family of parabolas

(C) Family of ellipses

(D) Family of circles

Ans: Correct option (D) Given that \[{{y}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + x  =  c}}\]

${{y}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  C - x}}$

${{y dy  =  (C - x) dx}}$ 

Integrate both sides

${{y}} {\text{ dy  =  }}\int {{\text{(C - x)}}} {\text{dx}}$

${{{{{y}}^{\text{2}}}}}{{\text{2}}}{\text{  =  Cx - }}\dfrac{{{{{x}}^{\text{2}}}}}{{\text{2}}}{\text{ + k}}$

${{{{{x}}^{\text{2}}}}}{{\text{2}}}{\text{ + }}\dfrac{{{{{y}}^{\text{2}}}}}{{\text{2}}}{\text{  =  Cx + K}}$

${{{{{x}}^{\text{2}}}}}{{\text{2}}}{\text{ + }}\dfrac{{{{{y}}^{\text{2}}}}}{{\text{2}}}{\text{ - Cx  =  k}}$ 

represents family of circles

50. The general solution of \[{{{e}}^{\text{2}}}{\text{cos y dx - }}{{{e}}^{{x}}}{\text{sin y dy  =  0}}\] is

(a) \[{{{e}}^{{x}}}{\text{cos y  =  k}}\]

(b) \[{{{e}}^{{x}}}{\text{sin y  =  k}}\]

(c) \[{{{e}}^{{x}}}{\text{  =  k cos y}}\]

(d) \[{{{e}}^{{x}}}{\text{  =  k sin y}}\]

Ans: Correct option (a) 

We have \[{{{e}}^{{x}}}{\text{cosydx - }}{{{e}}^{{x}}}{\text{sinydy  =  0}}\]

${{{e}}^{{x}}}{\text{cos y dx  =  }}{{{e}}^{{x}}}{\text{sin y dy  =  0}}$

${{{e}}^{{x}}}{\text{cos y dx  =  }}{{{e}}^{{x}}}{\text{sin y dy}}$

${{{\text{dx}}}}{{{\text{dy}}}}{\text{  =  tan y}}$

${\text{dx  =  tan y dy}}$ 

Integrate both sides

${\text{d}} {{x  =  }}\int {{\text{tan }}} {{y dy}}$

${{x  =  log sec y + C}}$

${{x - C  =  log sec y}}$

${\text{sec y  =  }}{{{e}}^{{{x - c}}}}$

${\text{sec y  =  }}{{{e}}^{{x}}}{{{e}}^{{\text{ - c}}}}$

${{\text{1}}}{{{\text{cos y}}}}{\text{  =  }}\dfrac{{{{{e}}^{{x}}}}}{{{{{e}}^{\text{c}}}}}$

${{{e}}^{{x}}}{\text{cos y  =  }}{{{e}}^{\text{c}}}$

${{{e}}^{{x}}}{\text{cos y  =  K                }}\left[ {{\text{where K  =  }}{{{e}}^{\text{c}}}} \right]$ 

51. The degree of the differential equation \[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + }}{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)^{\text{3}}}{\text{ + 6}}{{{y}}^{\text{5}}}{\text{  =  0}}\] is

(a) \[{\text{1}}\]

(b) \[{\text{2}}\]

(c) \[{\text{3}}\]

(d) \[{\text{5}}\]

Ans: Correct option (a) we have \[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + }}{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)^{\text{3}}}{\text{ + 6}}{{{y}}^{\text{5}}}{\text{  =  0}}\]

As we know degree of differential equation is exponent of highest order derivative

So, degree is \[{\text{1}}\]

52. The solution of \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y  =  }}{{{e}}^{{\text{ - x}}}}{\text{ , y(0)  =  0}}\]

(a) \[{{y  =  }}{{{e}}^{{x}}}{\text{(x - 1)}}\]

(b) \[{{y  =  x}}{{{e}}^{{\text{ - x}}}}\]

(c) \[{{y  =  x}}{{{e}}^{{\text{ - x}}}}{\text{ + 1}}\]

(d) \[{{y  =  (x + 1)}}{{{e}}^{{\text{ - x}}}}\]

Ans: Correct option (b)

We have \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y  =  }}{{{e}}^{{\text{ - x}}}}\]

Here \[{\text{P  =  1 , Q  =  }}{{{e}}^{{\text{ - x}}}}\]

IF \[{\text{ =  }}{{{e}}^{\int {\text{P}} {\text{dx}}}}{\text{  =  }}{{{e}}^{\int {\text{d}} {{x}}}}{\text{  =  }}{{{e}}^{{x}}}\]

General solution is

${{y \times }}{{{e}}^{{x}}}{\text{  =  }}\int {{{{e}}^{{\text{ - x}}}}} {{{e}}^{{x}}}{\text{dx + C}}$

${{y \times }}{{{e}}^{{x}}}{\text{  =  }}\int {\text{d}} {{x + C}}$

${{y \times }}{{{e}}^{{x}}}{\text{  =  x + C}}$ 

When \[{{x  =  0 , y  =  0 }} \Rightarrow {\text{ 0  =  C}}\]

We have 

${{y \times }}{{{e}}^{{x}}}{\text{  =  x}}$

${{y  =  x}}{{{e}}^{{\text{ - x}}}}$ 

53. Integrating factor of the differential equation \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y tan x - sec x  =  0}}\]

(a) \[{\text{cos x}}\]

(b) \[{\text{sec x}}\]

(c) \[{{{e}}^{{\text{cosx}}}}\]

(d) \[{{{e}}^{\sec x}}\]

Ans: Correct option (b) we have \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y tan x - sec x  =  0}}\]

${{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y tan x  =  secx}}$

${\text{Here P  =  tan x , Q  =  sec x}}$

${\text{IF  =  }}{{{e}}^{\int {\text{P}} {\text{dx}}}}{\text{  =  }}{{{e}}^{{\text{(log sec x)}}}}{\text{  =  sec x}}$ 

54. The Solution of the differential equation \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{\text{1 + }}{{{y}}^{\text{2}}}}}{{{\text{1 + }}{{{x}}^{\text{2}}}}}\] is

(a) \[{{y  =  ta}}{{\text{n}}^{{\text{ - 1}}}}{{x}}\]

(b) \[{{y - x  =  k(1 + xy)}}\]

(c) \[{{x  =  ta}}{{\text{n}}^{{\text{ - 1}}}}{{y}}\]

(d) \[{\text{tan(xy)  =  k}}\]

Ans: Correct option (b) we have \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{\text{1 + }}{{{y}}^{\text{2}}}}}{{{\text{1 + }}{{{x}}^{\text{2}}}}}\]

\[\dfrac{{{\text{dy}}}}{{{\text{1 + }}{{{y}}^{\text{2}}}}}{\text{  =  }}\dfrac{{{\text{dx}}}}{{{\text{1 + }}{{{x}}^{\text{2}}}}}\]

Integrate both sides we get:

${\dfrac{{{\text{dy}}}}{{{\text{1 + }}{{{y}}^{\text{2}}}}}} {\text{  =  }}\int {\dfrac{{{\text{dx}}}}{{{\text{1 + }}{{{x}}^{\text{2}}}}}}$

${\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{y  =  ta}}{{\text{n}}^{{\text{ - 1}}}}{{x + C}}$ 

${\text{ta}}{{\text{n}}^{{\text{ - 1}}}}{{y - ta}}{{\text{n}}^{{\text{ - 1}}}}{{x  =  C}}$

${\text{ta}}{{\text{n}}^{{\text{ - 1}}}}\left( {\dfrac{{{{y - x}}}}{{{\text{1 + xy}}}}} \right){\text{  =  C}}$

${{{{y - x}}}}{{{\text{1 + xy}}}}{\text{  =  tanC}}$

${{y - x  =  tanC(1 + xy)}}$

${{y - x  =  K(1 + xy)            where k  =  tanC}}$ 

55. The integrating factor of the differential equation \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y  =  }}\dfrac{{{\text{1 + y}}}}{{{x}}}\] is

(a) \[\dfrac{{{x}}}{{{{{e}}^{{x}}}}}\]

(b) \[\dfrac{{{{{e}}^{{x}}}}}{{{x}}}\]

(c) \[{{x}}{{{e}}^{{x}}}\]

(d) \[{{{e}}^{{x}}}\]

Ans: Correct option (b) we have \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y  =  }}\dfrac{{{\text{1 + y}}}}{{{x}}}\]

${{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{\text{1 + y}}}}{{{x}}}{\text{ - y}}$

${{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{\text{1 + y - xy}}}}{{{x}}}$ 

${{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{\text{1}}}{{{x}}}{\text{ + }}\dfrac{{{{y(1 - x)}}}}{{{x}}}$

${{{\text{dy}}}}{{{\text{dx}}}}{\text{ - }}\left( {\dfrac{{{\text{1 - x}}}}{{{x}}}} \right){{y  =  }}\dfrac{{\text{1}}}{{{x}}}$

${\text{Here P  =  }}\dfrac{{{\text{ - (1 - x)}}}}{{{x}}}{\text{ , Q  =  }}\dfrac{{\text{1}}}{{{x}}}$

${\text{IF  =  }}{{{e}}^{\int {\text{P}} {\text{dx}}}}{\text{  =  }}{{{e}}^{{\text{ - }}\int {\dfrac{{{\text{1 - x}}}}{{{x}}}} {\text{dx}}}}{\text{  =  }}{{{e}}^{\int {\dfrac{{{{x - 1}}}}{{{x}}}} {\text{dx}}}}{\text{  =  }}{{{e}}^{\int {\left( {{\text{1 - }}\dfrac{{\text{1}}}{{{x}}}} \right)} {\text{dx}}}}{\text{  =  }}{{{e}}^{{x}}}{{ \times }}{{{e}}^{{\text{log}}\left( {\dfrac{{\text{1}}}{{{x}}}} \right)}}{\text{  =  }}{{{e}}^{{x}}}{{ \times }}\dfrac{{\text{1}}}{{{x}}}$ 

56. \[{{y  =  a}}{{{e}}^{{\text{mx}}}}{\text{ + b}}{{{e}}^{{\text{ - mx}}}}\] satisfies which of the following differential equation

(a) \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + my  =  0}}\]

(b) \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - my  =  0}}\]

(c) \[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ - }}{{\text{m}}^{\text{2}}}{{y  =  0}}\]

(d) \[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + }}{{\text{m}}^{\text{2}}}{{y  =  0}}\]

Ans: Correct option (c) we have \[{{y  =  a}}{{{e}}^{{\text{mx}}}}{\text{ + b}}{{{e}}^{{\text{ - mx}}}}\]

Differentiate both sides we get:

\[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  ma}}{{{e}}^{{\text{mx}}}}{\text{ - bm}}{{{e}}^{{\text{ - mx}}}}\]

Again differentiate both sides

${{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{  =  }}{{\text{m}}^{\text{2}}}{\text{a}}{{{e}}^{{\text{mx}}}}{\text{ + b}}{{\text{m}}^{\text{2}}}{{{e}}^{{\text{ - mx}}}}$

${{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{  =  }}{{\text{m}}^{\text{2}}}\left( {{\text{a}}{{{e}}^{{\text{mx}}}}{\text{ + b}}{{{e}}^{{\text{ - mx}}}}} \right)$

${{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{  =  }}{{\text{m}}^{\text{2}}}{{y}}$

${{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ - }}{{\text{m}}^{\text{2}}}{{y  =  0}}$ 

57. The solution of the differential equation \[{\text{cos x sin y dx + sin x cos y dy  =  0}}\] is 

(a) \[\dfrac{{{{sin x}}}}{{{{sin y}}}}{\text{  =  C}}\]

(b) \[{{sin x sin y  =  C}}\]

(c) \[{{sin x + sin y  =  C}}\]

(d) \[{{cos x cos y  =  C}}\]

Ans: Correct option (b) we have \[{\text{cos x sin y dx + sin x cos y dy  =  0}}\]

${\text{cos x sin y dx  =   - sin x cos y dy}}$

${{{\text{cos x}}}}{{{\text{sin x}}}}{\text{dx  =   - }}\dfrac{{{\text{cos y}}}}{{{\text{sin y}}}}{\text{dy}}$

${\text{cot x dx  =   - cot y dy}}$ 

Integrate both sides

${{\text{cot }}} {{x dx  =  }}\int {\text{ - }} {\text{cot y dy}}$

${\text{log sin x  =   - log sin y + logC}}$

${{log sin x sin y  =  logC}}$

${{sin x \times sin y  =  C}}$ 

58. The solution of \[{{x}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y  =  }}{{{e}}^{{x}}}\] is

(a) \[{{y  =  }}\dfrac{{{{{e}}^{{x}}}}}{{{x}}}{\text{ + }}\dfrac{{\text{k}}}{{{x}}}\]

(b) \[{{y  =  x}}{{{e}}^{{x}}}{\text{ + cx}}\]

(c) \[{{y  =  x}}{{{e}}^{{x}}}{\text{ + k}}\]

(d) \[{{x  =  }}\dfrac{{{{{e}}^{{y}}}}}{{{y}}}{\text{ + }}\dfrac{{\text{k}}}{{{y}}}\]

Ans: Correct option (a) we have \[{{x}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y  =  }}{{{e}}^{{x}}}\]

Divide both sides by \[{{x}}\] we get:

\[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + }}\dfrac{{{y}}}{{{x}}}{\text{  =  }}\dfrac{{{{{e}}^{{x}}}}}{{{x}}}\] is a linear differential equation

\[{\text{IF  =  }}{{{e}}^{\int {\dfrac{{\text{1}}}{{{x}}}} {\text{dx}}}}{\text{  =  }}{{{e}}^{{\text{(logx)}}}}{\text{  =  x}}\]

General solution is \[{{y}}{\text{.x  =  }}\int {\left( {\dfrac{{{{\text{d}}^{{x}}}}}{{{x}}}{{x}}} \right)} {\text{dxy}}{\text{.x = }}\int {\left( {\dfrac{{{{{e}}^{{x}}}}}{{{x}}}{{ \times x}}} \right)} {\text{dx}}\]

${{y \times x  =  }}\int {{{{e}}^{{x}}}} {\text{dx}}$

${{y \times x  =  }}{{{e}}^{{x}}}{\text{ + k}}$

${{y  =  }}\dfrac{{{{{e}}^{{x}}}}}{{{x}}}{\text{ + }}\dfrac{{\text{k}}}{{{x}}}$ 

59. The differential equation of the family of curves \[{{{x}}^{\text{2}}}{\text{ + }}{{{y}}^{\text{2}}}{\text{ - 2ay  =  0}}\] where \[{\text{a}}\] is arbitrary constant is

(a) \[\left( {{{{x}}^{\text{2}}}{\text{ - }}{{{y}}^{\text{2}}}} \right)\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  2xy}}\]

(b) \[{\text{2}}\left( {{{{x}}^{\text{2}}}{\text{ + }}{{{y}}^{\text{2}}}} \right)\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  xy}}\]

(c) \[{\text{2}}\left( {{{{x}}^{\text{2}}}{\text{ - }}{{{y}}^{\text{2}}}} \right)\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  xy}}\]

(d) \[\left( {{{{x}}^{\text{2}}}{\text{ + }}{{{y}}^{\text{2}}}} \right)\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  2xy}}\]

Ans: Correct option (a) we have \[{{{x}}^{\text{2}}}{\text{ + }}{{{y}}^{\text{2}}}{\text{ - 2ay  =  0}}\]

\[\dfrac{{{{{x}}^{\text{2}}}{\text{ + }}{{{y}}^{\text{2}}}}}{{{y}}}{\text{  =  2a}}\]

Differentiate both sides, we get:

${{{{y}}\left( {{\text{2x + 2y}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right){\text{ - }}\left( {{{{x}}^{\text{2}}}{\text{ + }}{{{y}}^{\text{2}}}} \right)\dfrac{{{\text{dy}}}}{{{\text{dx}}}}}}{{{{{y}}^{\text{2}}}}}{\text{  =  0}}$

${\text{2xy + 2}}{{{y}}^{\text{2}}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - }}\left( {{{{x}}^{\text{2}}}{\text{ + }}{{{y}}^{\text{2}}}} \right)\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  0}}$ 

$\left( {{\text{2}}{{{y}}^{\text{2}}}{\text{ - }}{{{x}}^{\text{2}}}{\text{ - }}{{{y}}^{\text{2}}}} \right)\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =   - 2xy}}$

$\left( {{{{y}}^{\text{2}}}{\text{ - }}{{{x}}^{\text{2}}}} \right)\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =   - 2xy}}$ 

\[\left( {{{{x}}^{\text{2}}}{\text{ - }}{{{y}}^{\text{2}}}} \right)\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  2xy}}\]

60. Family \[{{y  =  Ax + }}{{\text{A}}^3}\] of curves will correspond to a differential equation of order

(a) \[3\]

(b) \[2\]

(c) \[1\]

(d) not defined

Ans: Correct option (c) we have \[{{y  =  Ax + }}{{\text{A}}^3}\]

\[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  A}}\]

Replace A by \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}\] we have 

\[{{y  =  x}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + }}{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)^{\text{3}}}\]

So, order is \[{\text{1}}\]

61. The general solution is \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  2x}}{{{e}}^{{{{x}}^{\text{2}}}{\text{ - y}}}}\]

(a) \[{{{e}}^{{{{x}}^{\text{2}}}{\text{ - y}}}}{\text{  =  c}}\]

(b) \[{{{e}}^{{\text{ - y}}}}{\text{ + }}{{{e}}^{{{{x}}^{\text{2}}}}}{\text{  =  c}}\]

(c) \[{{{e}}^{{y}}}{\text{  =  }}{{{e}}^{{{{x}}^{\text{2}}}}}{\text{ + c}}\]

(d) \[{{{e}}^{{{{x}}^{\text{2}}}{\text{ + y}}}}{\text{  =  c}}\]

Ans: Correct option (c) we have \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  2x}}{{{e}}^{{{{x}}^{\text{2}}}{\text{ - y}}}}{\text{  =  2x}}{{{e}}^{{{{x}}^{\text{2}}}}}{{ \times }}{{{e}}^{{\text{ - y}}}}\]

${{{e}}^{{y}}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  2x}}{{{e}}^{{{{x}}^{\text{2}}}}}$

${{{e}}^{{y}}}{\text{dy  =  2x}}{{{e}}^{{{{x}}^{\text{2}}}}}{\text{dx}}$ 

Integrate both sides:

\[\int {{{{e}}^{{y}}}} {\text{dy  =  2}}\int {{x}} {{{e}}^{{{{x}}^{\text{2}}}}}{\text{dx}}\]

Put \[{{{x}}^{\text{2}}}{\text{  =  t}}\] in RHS we get

${\text{2x dx  =  dt}}$

${{{{e}}^{{y}}}} {\text{dy  =  }}\int {{{{e}}^{\text{t}}}} {\text{dt}}$

${{{e}}^{{y}}}{\text{  =  }}{{{e}}^{\text{t}}}{\text{ + C}}$

${{{e}}^{{y}}}{\text{  =  }}{{{e}}^{{{{x}}^{\text{2}}}}}{\text{ + C}}$ 

62. The curve for which the slope of the tangent at any point is equal to the ratio of the abscissa to the ordinate of the point is:

(A) an ellipse

(B) parabola

(C) circle

(D) rectangular hyperbola

Ans: Correct option (D) Slope of tangent to the curve \[{\text{ =  }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}\]

Ratio of abscissa to ordinate \[{\text{ =  }}\dfrac{{{x}}}{{{y}}}\]

Accordingly, \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{x}}}{{{y}}}\]

\[{{y dy  =  x dx}}\]

Integrate both sides:

${{y}} {\text{ dy  =  }}\int {{x}} {\text{ dx}}$

${{{{{y}}^{\text{2}}}}}{{\text{2}}}{\text{  =  }}\dfrac{{{{{x}}^{\text{2}}}}}{{\text{2}}}{\text{ + C}}$

${{{{{y}}^{\text{2}}}}}{{\text{2}}}{\text{ - }}\dfrac{{{{{x}}^{\text{2}}}}}{{\text{2}}}{\text{  =  C}}$ 

\[{{{y}}^{\text{2}}}{\text{ - }}{{{x}}^{\text{2}}}{\text{  =  2C}}\] is an equation of rectangular hyperbola

63. The general solution of the differential equation \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{{{e}}^{\dfrac{{{{{x}}^{\text{2}}}}}{{\text{2}}}}}{\text{ + xy}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}{{{e}}^{\dfrac{{{{{x}}^{\text{2}}}}}{{\text{2}}}}}{\text{ + xy}}\]

(a) \[{{y  =  c}}{{{e}}^{\dfrac{{{\text{ - }}{{{x}}^{\text{2}}}}}{{\text{2}}}}}\]

(b) \[{{y  =  c}}{{{e}}^{\dfrac{{{{{x}}^{\text{2}}}}}{{\text{2}}}}}\]

(c) \[{{y  =  (x + c)}}{{{e}}^{\dfrac{{{{{x}}^{\text{2}}}}}{{\text{2}}}}}\]

(d) \[{{y  =  (c - x)}}{{{e}}^{\dfrac{{{{{x}}^{\text{2}}}}}{{\text{2}}}}}\]

Ans: Correct option (c) we have \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{{{e}}^{\dfrac{{{{{x}}^{\text{2}}}}}{{\text{2}}}}}{\text{ + xy}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}{{{e}}^{\dfrac{{{{{x}}^{\text{2}}}}}{{\text{2}}}}}{\text{ + xy}}\]

\[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - xy  =  }}{{{e}}^{\dfrac{{{{{x}}^{\text{2}}}}}{2}}}\] is a linear differential equation

${\text{Here P  =   - x , Q  =  }}{{{e}}^{\dfrac{{{{{x}}^{\text{2}}}}}{2}}}$

${\text{IF  =  }}{{{e}}^{\int { - {{x dx}}} }}{\text{  =  }}{{{e}}^{\dfrac{{{\text{ - }}{{{x}}^{\text{2}}}}}{2}}}$ 

General solution

${{y}}{{{e}}^{\dfrac{{{\text{ - }}{{{x}}^{\text{2}}}}}{2}}}{\text{  =  }}\int {{{{e}}^{\dfrac{{{\text{ - }}{{{x}}^{\text{2}}}}}{2}}}} {\text{ - }}{{{e}}^{\dfrac{{{{{x}}^{\text{2}}}}}{2}}}{\text{dx + Cy}}{{{e}}^{\dfrac{{{\text{ - }}{{{x}}^{\text{2}}}}}{{\text{2}}}}}{\text{  =  }}\int {{{{e}}^{\dfrac{{{\text{ - }}{{{x}}^{\text{2}}}}}{{\text{2}}}}}} {{ \times }}{{{e}}^{\dfrac{{{{{x}}^{\text{2}}}}}{{\text{2}}}}}{\text{dx + C}}$

${{y}}{{{e}}^{\dfrac{{{\text{ - }}{{{x}}^{\text{2}}}}}{2}}}{\text{  =  }}\int {\text{1}} {\text{ dx + C}}$

${{y \times }}{{{e}}^{\dfrac{{{\text{ - }}{{{x}}^{\text{2}}}}}{2}}}{\text{  =  x + C}}$

${{y  =  x}}{{{e}}^{\dfrac{{{{{x}}^{\text{2}}}}}{2}}}{\text{ + C}}{{{e}}^{\dfrac{{{\text{ - }}{{{x}}^{\text{2}}}}}{2}}}$

${{y  =  (x + C)}}{{{e}}^{\dfrac{{{{{x}}^{\text{2}}}}}{2}}}$ 

64. The solution of the equation \[{\text{(2y - 1)dx - (2x + 3)dy  =  0}}\] is

(a) \[\dfrac{{{\text{2x - 1}}}}{{{\text{2y + 3}}}}{\text{  =  k}}\]

(b) \[\dfrac{{{\text{2y + 1}}}}{{{\text{2x - 3}}}}{\text{  =  k}}\]

(c) \[\dfrac{{{\text{2x + 3}}}}{{{\text{2y - 1}}}}{\text{  =  k}}\]

(d) \[\dfrac{{{\text{2x - 1}}}}{{{\text{2y - 1}}}}{\text{  =  k}}\]

Ans: Correct option (c) we have \[{\text{(2y - 1)dx - (2x + 3)dy  =  0}}\]

\[{\text{(2y - 1)dx  =  (2x + 3)dy}}\]

\[\dfrac{{{\text{dx}}}}{{{\text{2x + 3}}}}{\text{  =  }}\dfrac{{{\text{dy}}}}{{{\text{2y - 1}}}}\]

Integrate both sides:

${\dfrac{{{\text{dx}}}}{{{\text{2x + 3}}}}} {\text{  =  }}\int {\dfrac{{{\text{dy}}}}{{{\text{2y - 1}}}}}$

${{\text{1}}}{{\text{2}}}{{log \times (2x + 3)  =  }}\dfrac{{\text{1}}}{{\text{2}}}{\text{log(2y - 1) + logC}}$

${{\text{1}}}{{\text{2}}}{{[log \times (2x + 3) - log(2y - 1)]  =  logC}}$

${{\text{1}}}{{\text{2}}}{\text{log}}\left( {\dfrac{{{\text{2x + 3}}}}{{{\text{2y - 1}}}}} \right){\text{  =  logC}}$

${\left( {\dfrac{{{\text{2x + 3}}}}{{{\text{2y - 1}}}}} \right)^{\dfrac{1}{2}}}{\text{  =  C}}$

${{{\text{2x + 3}}}}{{{\text{2y - 1}}}}{\text{  =  }}{{\text{C}}^{\text{2}}}$

${{{\text{2x + 3}}}}{{{\text{2y - 1}}}}{\text{  =  k             where K  =  }}{{\text{C}}^{\text{2}}}$ 

65. The differential equation for which \[{{y  =  a cos x + b sin x}}\] is a solution, is

(a) \[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + y  =  0}}\]

(b) \[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ - y  =  0}}\]

(c) \[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + (a + b)y  =  0}}\]

(d) \[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{dx}}}}{\text{ + (a - b)y  =  0}}\]

Ans: Correct option (a) we have \[{{y  =  a cos x + b sin x}}\]

Differentiate both sides we get:

\[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =   - a sin x + b cos x}}\]

Again, differentiate both sides:

${{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{  =   - a sin x + b cos x}}$

${{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{  =   - a cos x - b sinx }}$

${{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{  =   - (a cos x + b sin x)}}$

${{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{  =   - y}}$

${{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + y  =  0}}$ 

66. The solution of \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y  =  }}{{{e}}^{{\text{ - x}}}}{\text{ , y(0)  =  0}}\] is 

(a) \[{{y  =  }}{{{e}}^{{\text{ - x}}}}{\text{(x - 1)}}\]

(b) \[{{y  =  x}}{{{e}}^{{x}}}\]

(c) \[{{y  =  x}}{{{e}}^{{\text{ - x}}}}{\text{ + 1}}\]

(d) \[{{y  =  x}}{{{e}}^{{\text{ - x}}}}\]

Ans: Correct option (d) we have \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y  =  }}{{{e}}^{{\text{ - x}}}}\] is a linear differential equation

${\text{Here P  =  1 , Q  =  }}{{{e}}^{{\text{ - x}}}}$

${\text{IF  =  }}{{{e}}^{{x}}}$ 

General solution is 

${{y \times }}{{{e}}^{{x}}}{\text{  =  }}\int {{{{e}}^{{\text{ - x}}}}} {{ \times }}{{{e}}^{{x}}}{\text{dx + c}}$

${{y}}{{{e}}^{{x}}}{\text{  =  }}\int {\text{d}} {{x + C}}$

${{y}}{{{e}}^{{x}}}{\text{  =  x + C}}$ 

When \[{{x  =  0 , y  =  0 then 0  =  C}}\]

Then, we have 

${{y}}{\text{.}}{{{e}}^{{x}}}{\text{  =  x}}$

${{y  =  x}}{{{e}}^{{\text{ - x}}}}$ 

67. The order and degree of the differential equation \[{\left( {\dfrac{{{{\text{d}}^{\text{3}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{3}}}}}} \right)^{\text{2}}}{\text{ - 3}}\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + 2}}{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)^{\text{4}}}{\text{  =  }}{{{y}}^{\text{4}}}\]

(a) \[{\text{1,4}}\]

(b) \[{\text{3,4}}\]

(c) \[{\text{2,4}}\]

(d) \[{\text{3,2}}\]

Ans: Correct option (d) we have \[{\left( {\dfrac{{{{\text{d}}^{\text{3}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{3}}}}}} \right)^{\text{2}}}{\text{ - 3}}\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + 2}}{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)^{\text{4}}}{\text{  =  }}{{{y}}^{\text{4}}}\]

Order is \[3\] and degree is \[2\]

68. The order and degree of the differential equation \[\left[ {{\text{1 + }}{{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)}^{\text{2}}}} \right]{\text{  =  }}\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}\] are

(a) \[{\text{2,}}\dfrac{3}{2}\]

(b) \[2,3\]

(c) \[2,1\]

(d) \[3,4\]

Ans: Correct option (c) we have \[\left[ {{\text{1 + }}{{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)}^{\text{2}}}} \right]{\text{  =  }}\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}\]

Order is \[2\] and degree is \[1\]

69. The differential equation of the family of curves \[{{{y}}^2}{\text{  =  4a(x + a)}}\]is 

(a) \[{{{y}}^{\text{2}}}{\text{  =  4}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}\left( {{{x + }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)\]

(b) \[{\text{2y}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  4a}}\]

(c) \[{{y}}\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + }}{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)^{\text{2}}}{\text{  =  0}}\]

(d) \[{\text{2x}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y}}{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)^{\text{2}}}{\text{ - y}}\]

Ans: Correct option (d) we have \[{{{y}}^2}{\text{  =  4a(x + a)}}\]

Differentiate both sides we get:

${\text{2y}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  4a}}$

${\text{2y}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  4a}}$

${{y}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  2a}}$

${\text{a  =  }}\dfrac{{\text{1}}}{{\text{2}}}{{y}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}$ 

Now, put values we get

${{{y}}^{\text{2}}}{\text{  =  2y}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\left( {{{x + }}\dfrac{{\text{1}}}{{\text{2}}}{{y}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)$

${{{y}}^{\text{2}}}{\text{  =  2xy}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + }}{{{y}}^{\text{2}}}{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)^{\text{2}}}$

${\text{2x}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y}}{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)^{\text{2}}}{\text{ - y  =  0}}$ 

70. Which of the following is the general solution of \[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ - 2}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y  =  0}}\]

(a) \[{{y  =  (Ax + B)}}{{{e}}^{{x}}}\]

(b) \[{{y  =  (Ax + B)}}{{{e}}^{{\text{ - x}}}}\]

(c) \[{{y  =  A}}{{{e}}^{{x}}}{\text{ + B}}{{{e}}^{{\text{ - x}}}}\]

(d) \[{{y  =  A cos x + B sin x}}\]

Ans: Correct option (a) we have \[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ - 2}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y  =  0}}\]

${{\text{D}}^{\text{2}}}{{y - 2Dy + y  =  0        where D  =  }}\dfrac{{\text{d}}}{{{\text{dx}}}}$

$\left( {{{\text{D}}^{\text{2}}}{\text{ - 2D + 1}}} \right){{y  =  0}}$ 

Auxilliary equation is \[{{\text{m}}^{\text{2}}}{\text{ - 2m + 1  =  0}}\]

${{\text{(m - 1)}}^{\text{2}}}{\text{  =  0}}$

${\text{m  =  1, 1}}$ 

As roots are real and equal

CF \[{\text{ =  (Ax + B)}}{{{e}}^{{x}}}{\text{ }} \Rightarrow {\text{ y  =  (Ax + B)}}{{{e}}^{{x}}}\]

71. General solution of \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y tan x  =  sec x}}\]

(a) \[{{y sec x  =  tan x + c}}\]

(b) \[{{y tan x  =  sec x + c}}\]

(c) \[{\text{tan x  =  y tan x + c}}\]

(d) \[{{x sec x  =  tan y + c}}\]

Ans: Correct answer (a) we have \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y tan x  =  sec x}}\] is a linear differential equation

${\text{Here P  =  tan x , Q  =  sec x}}$

${\text{IF  =  }}{{{e}}^{\int {{\text{tan }}} {{x dx}}}}{\text{  =  }}{{{e}}^{{\text{log|sec x|}}}}{\text{  =  sec x}}$ 

General solution is

${{y \times sec x  =  }}\int {{\text{sec }}} {{x \times sec x + C}}$

${{y \times sec x  =  }}\int {{\text{se}}{{\text{c}}^{\text{2}}}} {{x dx + C}}$

${{y \times sec x  =  tan x + C}}$ 

72. Solution of the differential equation \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + }}\dfrac{{{y}}}{{{x}}}{\text{  =  sinx}}\]

(a) \[{{x(y + cosx)  =  sinx + c}}\]

(b) \[{{x(y - cos x)  =  sin x + c}}\]

(c) \[{{xy cos x  =  sin x + c}}\]

(d) \[{{x(y + cos x)  =  cos x + c}}\]

Ans: Correct option (a) we have \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + }}\dfrac{{{y}}}{{{x}}}{\text{  =  sinx}}\]is a linear differential equation

${\text{Here P  =  }}\dfrac{{\text{1}}}{{{x}}}{\text{ , Q  =  sin x}}$

${\text{IF  =  }}{{{e}}^{\int {\dfrac{{\text{1}}}{{{x}}}} }}{\text{  =  }}{{{e}}^{{\text{log x}}}}{\text{  =  x}}$ 

General solution is

\[{{yx  =  }}\int {{x}} {\text{ sin x dx + C}}\]

Take \[{\text{I  =  }}\int {{x}} {\text{ sin x dx}}\]

${\text{ =   - x cos x - }}\int {\text{ - }} {\text{cos x dx}}$

${\text{ =   - x cos x + sin x}}$ 

Put values we get

${{xy  =   - x cos x + sin x + C}}$

${{x(y + cos x)  =  sin x + C}}$ 

73. The general solution of the differential equation \[\left( {{{{e}}^{{x}}}{\text{ + 1}}} \right){{y dy  =  (y + 1)}}{{{e}}^{{x}}}{\text{dx}}\] is

(a) \[{\text{(y + 1)  =  k}}\left( {{{{e}}^{{x}}}{\text{ + 1}}} \right)\]

(b) \[{{y + 1  =  }}{{{e}}^{{x}}}{\text{ + 1 + k}}\]

(c) \[{{y  =  log}}\left\{ {{\text{k(y + 1)}}\left( {{{{e}}^{{x}}}{\text{ + 1}}} \right)} \right\}\]

(d) \[{{y  =  log}}\left\{ {\dfrac{{{{{e}}^{{x}}}{\text{ + 1}}}}{{{{y + 1}}}}} \right\}{\text{ + k}}\]

Ans: Correct option (c) we have \[\left( {{{{e}}^{{x}}}{\text{ + 1}}} \right){{y dy  =  (y + 1)}}{{{e}}^{{x}}}{\text{dx}}\]

${{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{{{e}}^{{x}}}{\text{(1 + y)}}}}{{\left( {{{{e}}^{{x}}}{\text{ + 1}}} \right){{y}}}}$

${{{\text{dx}}}}{{{\text{dy}}}}{\text{  =  }}\dfrac{{\left( {{{{e}}^{{x}}}{\text{ + 1}}} \right){{y}}}}{{{{{e}}^{{x}}}{\text{(1 + y)}}}}$

${{{\text{dx}}}}{{{\text{dy}}}}{\text{  =  }}\dfrac{{{{{e}}^{{x}}}{{y}}}}{{{{{e}}^{{x}}}{\text{(1 + y)}}}}{\text{ + }}\dfrac{{{y}}}{{{{{e}}^{{x}}}{\text{(1 + y)}}}}$

${{{\text{dx}}}}{{{\text{dy}}}}{\text{  =  }}\dfrac{{{y}}}{{{\text{1 + y}}}}{\text{ + }}\dfrac{{{y}}}{{{\text{(1 + y)}}{{{e}}^{{x}}}}}$

${{{\text{dx}}}}{{{\text{dy}}}}{\text{  =  }}\dfrac{{{y}}}{{{\text{1 + y}}}}\left( {{\text{1 + }}\dfrac{{\text{1}}}{{{{{e}}^{{x}}}}}} \right)$ 

\[\dfrac{{{\text{dx}}}}{{{\text{dy}}}}{\text{  =  }}\dfrac{{{y}}}{{{\text{1 + y}}}}\left( {\dfrac{{{{{e}}^{{x}}}{\text{ + 1}}}}{{{{{e}}^{{x}}}}}} \right)\]

\[\left( {\dfrac{{{y}}}{{{\text{1 + y}}}}} \right){\text{dy  =  }}\left( {\dfrac{{{{{e}}^{{x}}}}}{{{{{e}}^{{x}}}{\text{ + 1}}}}} \right){\text{dx}}\]

Integrate both sides:

\[\int {\dfrac{{{y}}}{{{\text{1 + y}}}}} {\text{dy  =  }}\int {\dfrac{{{{{e}}^{{x}}}}}{{{\text{1 + }}{{{e}}^{{x}}}}}} {\text{dx}}\]

${\dfrac{{{\text{1 + y - 1}}}}{{{\text{1 + y}}}}} {\text{dy  =  }}\int {\dfrac{{{{{e}}^{{x}}}}}{{{\text{1 + }}{{{e}}^{{x}}}}}} {\text{dx}}$

${{\text{1 }}} {\text{dy - }}\int {\dfrac{{\text{1}}}{{{\text{1 + y}}}}} {\text{dy  =  }}\int {\dfrac{{{{{e}}^{{x}}}}}{{{\text{1 + }}{{{e}}^{{x}}}}}} {\text{dx}}$

${{y  =  log(1 + y) + log}}\left( {{\text{1 + }}{{{e}}^{{x}}}} \right){\text{ + log k}}$

${{y  =  log}}\left\{ {{\text{k(1 + y)}}\left( {{\text{1 + }}{{{e}}^{{x}}}} \right)} \right\}$ 

74. The solution of the differential equation \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}{{{e}}^{{{x - y}}}}{\text{ + }}{{{x}}^{\text{2}}}{{{e}}^{{\text{ - y}}}}\] is

(a) \[{{y  =  }}{{{e}}^{{{x - y}}}}{\text{ - }}{{{x}}^{\text{2}}}{{{e}}^{{\text{ - y}}}}{\text{ + c}}\]

(b) \[{{{e}}^{{y}}}{\text{ - }}{{{e}}^{{x}}}{\text{  =  }}\dfrac{{{{{x}}^{\text{3}}}}}{{\text{3}}}{\text{ + c}}\]

(c) \[{{{e}}^{{x}}}{\text{ + }}{{{e}}^{{y}}}{\text{  =  }}\dfrac{{{{{x}}^{\text{3}}}}}{{\text{3}}}{\text{ + c}}\]

(d) \[{{{e}}^{{x}}}{\text{ - }}{{{e}}^{{y}}}{\text{  =  }}\dfrac{{{{{x}}^{\text{3}}}}}{{\text{3}}}{\text{ + c}}\]

Ans: Correct option (b) we have \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}{{{e}}^{{{x - y}}}}{\text{ + }}{{{x}}^{\text{2}}}{{{e}}^{{\text{ - y}}}}\]

${{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}{{{e}}^{{x}}}{{{e}}^{{\text{ - y}}}}{\text{ + }}{{{x}}^{\text{2}}}{{{e}}^{{\text{ - y}}}}$

${{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{{{e}}^{{x}}}{\text{ + }}{{{x}}^{\text{2}}}}}{{{{{e}}^{{y}}}}}$ 

\[{{{e}}^{{y}}}{\text{dy  =  }}\left( {{{{e}}^{{x}}}{\text{ + }}{{{x}}^{\text{2}}}} \right){\text{dx}}\]

Integrate both sides:

${{{{e}}^{{y}}}} {\text{dy  =  }}\int {\left( {{{{e}}^{{x}}}{\text{ + }}{{{x}}^{\text{2}}}} \right)} {\text{dx}}$

${{{e}}^{{y}}}{\text{  =  }}{{{e}}^{{x}}}{\text{ + }}\dfrac{{{{{x}}^{\text{3}}}}}{{\text{3}}}{\text{ + C}}$

${{{e}}^{{y}}}{\text{ - }}{{{e}}^{{x}}}{\text{  =  }}\dfrac{{{{{x}}^{\text{3}}}}}{{\text{3}}}{\text{ + C}}$ 

75. The solution of the differential equation \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + }}\dfrac{{{\text{2xy}}}}{{{\text{1 + }}{{{x}}^{\text{2}}}}}{\text{  =  }}\dfrac{{\text{1}}}{{{{\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right)}^{\text{2}}}}}\] is

(a) \[{{y}}\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right){\text{  =  c + ta}}{{\text{n}}^{{\text{ - 1}}}}{{x}}\]

(b) \[\dfrac{{{y}}}{{{\text{1 + }}{{{x}}^{\text{2}}}}}{\text{  =  c + ta}}{{\text{n}}^{{\text{ - 1}}}}{{x}}\]

(c) \[{{y log}}\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right){\text{  =  c + ta}}{{\text{n}}^{{\text{ - 1}}}}{{x}}\]

(d) \[{{y}}\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right){\text{  =  c + si}}{{\text{n}}^{{\text{ - 1}}}}{{x}}\]

Ans: Correct option (a) we have \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + }}\dfrac{{{\text{2xy}}}}{{{\text{1 + }}{{{x}}^{\text{2}}}}}{\text{  =  }}\dfrac{{\text{1}}}{{{{\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right)}^{\text{2}}}}}\]

\[{\text{Here P  =  }}\dfrac{{{\text{2x}}}}{{{\text{1 + }}{{{x}}^{\text{2}}}}}{\text{ , Q  =  }}\dfrac{{\text{1}}}{{{{\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right)}^{\text{2}}}}}\] is a linear differential equation

\[{\text{IF  =  }}{{{e}}^{\int {\dfrac{{{\text{2x}}}}{{{\text{1 + }}{{\text{2}}^{\text{2}}}}}} {\text{dx}}}}\]

Put \[{\text{1 + }}{{{x}}^{\text{2}}}{\text{  =  t }} \Rightarrow {\text{ 2x dx  =  dt}}\]

So, \[{\text{IF  =  }}{{{e}}^{\int {\dfrac{{{\text{dt}}}}{{\text{t}}}} }}{\text{  =  }}{{{e}}^{{\text{logt}}}}{\text{  =  }}{{{e}}^{{\text{log}}\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right)}}{\text{  =  1 + }}{{{x}}^{\text{2}}}\]

General solution is

\[{{y \times }}\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right){\text{  =  }}\int {\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right)} \dfrac{{\text{1}}}{{{{\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right)}^{\text{2}}}}}{\text{ + C}}\]

${{y}}\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right){\text{  =  }}\int {\dfrac{{\text{1}}}{{{\text{1 + }}{{{x}}^{\text{2}}}}}} {\text{dx + C}}$

${{y}}\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right){\text{  =  ta}}{{\text{n}}^{{\text{ - 1}}}}{{x + C}}$ 

76. Fill in the blanks of the following (i to xi)

(i) The degree of the differential equation \[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + }}{{{e}}^{\dfrac{{{\text{dy}}}}{{{\text{dx}}}}}}{\text{  =  0}}\] is ________

Ans: Given differential equation is \[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ + }}{{{e}}^{\dfrac{{{\text{dy}}}}{{{\text{dx}}}}}}{\text{  =  0}}\]

Degree of this equation is not defined.

(ii) The degree of the differential equation \[\sqrt {{\text{1 + }}{{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)}^{\text{2}}}} {\text{  =  x}}\] is __________

Ans: Given differential equation is \[\sqrt {{\text{1 + }}{{\left( {\dfrac{{{\text{dy}}}}{{{\text{dx}}}}} \right)}^{\text{2}}}} {\text{  =  x}}\]

So, degree of this equation is two.

(iii) The number of arbitrary constants in the general solution of a differential equation of order three is ______________

Ans: There are three arbitrary constants.

(iv) \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + }}\dfrac{{{y}}}{{{{xlogx}}}}{\text{  =  }}\dfrac{{\text{1}}}{{{x}}}\] is an equation of the type __________

Ans: given differential equation is \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + }}\dfrac{{{y}}}{{{{xlogx}}}}{\text{  =  }}\dfrac{{\text{1}}}{{{x}}}\]

This is of type \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + Py  =  Q}}\]

(v) General solution of the differential equation of the type \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + }}{{\text{P}}_{\text{1}}}{{x  =  }}{{\text{Q}}_{\text{1}}}{\text{ , }}\dfrac{{{\text{dx}}}}{{{\text{dy}}}}{\text{ + }}{{\text{P}}_{\text{1}}}{{x  =  }}{{\text{Q}}_{\text{1}}}\] is given by ________

Ans: Given differential equation is \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + }}{{\text{P}}_{\text{1}}}{{x  =  }}{{\text{Q}}_{\text{1}}}{\text{ , }}\dfrac{{{\text{dx}}}}{{{\text{dy}}}}{\text{ + }}{{\text{P}}_{\text{1}}}{{x  =  }}{{\text{Q}}_{\text{1}}}\]

General solution is

${{x}}{\text{.IF  =  }}\int {\text{Q}} {\text{(IF)dy + C}}$

${{xe}}\int {{\text{P dy}}} {\text{  =  }}\int {\text{Q}} \left\{ {{{{e}}^{\int {\text{P}} {\text{dy}}}}} \right\}{\text{dy + C}}$

${{x}}{\text{.}}{{{e}}^{\int {{{\text{P}}_{\text{1}}}} {\text{dy}}}}{\text{  =  }}\int {{{\text{Q}}_{\text{1}}}} \left\{ {{{{e}}^{\int {{{\text{P}}_{\text{1}}}} {\text{dy}}}}} \right\}{\text{dy + C}}$ 

(vi) The solution of differential solution \[\dfrac{{{{x dy}}}}{{{\text{dx}}}}{\text{ + 2y  =  }}{{{x}}^{\text{2}}}\] is ________

Ans: Given differential equation is \[\dfrac{{{{x dy}}}}{{{\text{dx}}}}{\text{ + 2y  =  }}{{{x}}^{\text{2}}}\] in the form \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + Py  =  Q}}\]

\[{\text{IF  =  }}{{{e}}^{\int {\dfrac{{\text{2}}}{{{x}}}} {\text{dx}}}}{\text{  =  }}{{{e}}^{{\text{2 log x}}}}{\text{  =  }}{{{x}}^{\text{2}}}\]

General solution is

${{y}}{{{x}}^{\text{2}}}{\text{  =  }}\int {{x}} {{{x}}^{\text{2}}}{\text{dx + C}}$

${{y}}{{{x}}^{\text{2}}}{\text{  =  }}\dfrac{{{{{x}}^{\text{4}}}}}{{\text{4}}}{\text{ + C}}$

${{y  =  }}\dfrac{{{{{x}}^{\text{2}}}}}{{\text{4}}}{\text{ + C}}{{{x}}^{\text{2}}}$ 

(vii) The solution of \[\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right)\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + 2xy - 4}}{{{x}}^{\text{2}}}{\text{  =  0}}\] is ___________

Ans: Given differential equation is \[\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right)\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + 2xy - 4}}{{{x}}^{\text{2}}}{\text{  =  0}}\]

Divide both side by \[\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right)\]

${{{\text{dy}}}}{{{\text{dx}}}}{\text{ + }}\dfrac{{{\text{2xy}}}}{{{\text{1 + }}{{{x}}^{\text{2}}}}}{\text{ - }}\dfrac{{{\text{4}}{{{x}}^{\text{2}}}}}{{{\text{1 + }}{{{x}}^{\text{2}}}}}{\text{  =  0}}$

${{{\text{dy}}}}{{{\text{dx}}}}{\text{ + }}\dfrac{{{\text{2x}}}}{{{\text{1 + }}{{{x}}^{\text{2}}}}}{{y  =  }}\dfrac{{{\text{4}}{{{x}}^{\text{2}}}}}{{{\text{1 + }}{{{x}}^{\text{2}}}}}$

${\text{IF  =  }}{{{e}}^{\int {\dfrac{{{\text{2x}}}}{{{\text{1 + }}{{{x}}^{\text{2}}}}}} {\text{dx}}}}$ 

Put \[{\text{1 + }}{{{x}}^{\text{2}}}{\text{  =  t}}\]

\[{\text{2x dx  =  dt}}\]

\[{\text{IF  =  }}{{{e}}^{\int {\dfrac{{{\text{dt }}}}{{\text{2}}}} }}{\text{  =  }}{{{e}}^{{\text{logt}}}}{\text{  =  }}{{{e}}^{{\text{log}}\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right)}}{\text{  =  1 + }}{{{x}}^{\text{2}}}\]

General solution is

${{y \times }}\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right){\text{  =  }}\int {\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right)} \dfrac{{{\text{.4}}{{{x}}^{\text{2}}}}}{{\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right)}}{\text{dx + C}}$

$\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right){{y  =  }}\int {\text{4}} {{{x}}^{\text{2}}}{\text{dx + C}}$

$\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right){{y  =  4}}\dfrac{{{{{x}}^{\text{3}}}}}{{\text{3}}}{\text{ + C}}$

${{y  =  }}\dfrac{{{\text{4}}{{{x}}^{\text{3}}}}}{{{\text{3}}\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right)}}{\text{ + C}}{\left( {{\text{1 + }}{{{x}}^{\text{2}}}} \right)^{{\text{ - 1}}}}$ 

(viii) The solution of the differential equation \[{{y dx + (x + xy)dy  =  0}}\]

Ans: Given differential equation is \[{{y dx + (x + xy)dy  =  0}}\]

${{y dx + x(1 + y)dy  =  0}}$

${{{\text{dx}}}}{{{\text{ - x}}}}{\text{  =  }}\left( {\dfrac{{{\text{1 + y}}}}{{{y}}}} \right){\text{dy}}$

${\dfrac{{\text{1}}}{{{x}}}} {\text{dx  =   - }}\int {\left( {\dfrac{{\text{1}}}{{{y}}}{\text{ + 1}}} \right)} {\text{dy}}$

${\text{log(x)  =   - log(y) - y + logA}}$

${\text{log(x) + log(y) + y  =  logA}}$ 

${\text{log(xy) + y  =  logA}}$

${\text{log xy + log }}{{{e}}^{{y}}}{\text{  =  logA}}$ 

${{xy }}{{{e}}^{{y}}}{\text{  =  A}}$

${{xy  =  A}}{{{e}}^{{\text{ - y}}}}$ 

(ix) General solution of \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y  =  sin x}}\] is __________

Ans: Given differential equation is \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y  =  sin x}}\]

\[{\text{IF  =  }}\int {{{{e}}^{{\text{1 dx}}}}} {\text{  =  }}{{{e}}^{{x}}}\]

General solution is \[{{y \times }}{{{e}}^{{x}}}{\text{  =  }}\int {{{{e}}^{{x}}}} {\text{sin x dx + C}}\]

Let \[\int {{{{e}}^{{x}}}} {\text{ sin x dx}}\]

${\text{I  =  sin x }}{{{e}}^{{x}}}{\text{ - }}\int {{\text{cos }}} {{x }}{{{e}}^{{x}}}{\text{dx}}$

${\text{ =  sin x }}{{{e}}^{{x}}}{\text{ - cos x }}{{{e}}^{{x}}}{\text{ + }}\int {{\text{( - sin x)}}} {{{e}}^{{x}}}{\text{dx}}$

${\text{2I  =  }}{{{e}}^{{x}}}{\text{(sin x - cos x)}}$

${\text{I  =  }}\dfrac{{\text{1}}}{{\text{2}}}{{{e}}^{{x}}}{\text{(sin x - cos x)}}$ 

Then we have

${{y \times }}{{{e}}^{{x}}}{\text{  =  }}\dfrac{{{x}}}{{\text{2}}}{{(sin x - cos x) + C}}$

${{y  =  }}\dfrac{{{1}}}{{{2}}}{{(sin x - cos x) + C \times }}{{{e}}^{{{ - x}}}}$ 

(x) The solution of differential equation \[{\text{cot y dx  =  x dy}}\] is ______

Ans: Given differential equation is \[{\text{cot y dx  =  x dy}}\]

\[\dfrac{{\text{1}}}{{{x}}}{\text{dx  =  tan y dy}}\]

Integrate both sides we get:

${\dfrac{{\text{1}}}{{{x}}}} {\text{dx  =  }}\int {{\text{tan }}} {{y dy}}$

${\text{log(x)  =  log(sec y) + log C}}$

${\text{log}}\left( {\dfrac{{{x}}}{{{\text{sec y}}}}} \right){\text{  =  log C}}$ 

${{{x}}}{{{\text{sec y}}}}{\text{  =  C}}$

${{x  =  C sec y}}$ 

(xi) The integrating factor of \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y  =  }}\dfrac{{{\text{1 + y}}}}{{{x}}}\] is ________

Ans: Given differential equation is \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y  =  }}\dfrac{{{\text{1 + y}}}}{{{x}}}\]

${{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y  =  }}\dfrac{{\text{1}}}{{{x}}}{\text{ + }}\dfrac{{{y}}}{{{x}}}$

${{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y}}\left( {{\text{1 - }}\dfrac{{\text{1}}}{{{x}}}} \right){\text{  =  }}\dfrac{{\text{1}}}{{{x}}}$

${\text{IF  =  }}{{{e}}^{\int {\left( {{\text{1 - }}\dfrac{{\text{1}}}{{{x}}}} \right)} {\text{dx}}}}{\text{  =  }}{{{e}}^{{{x - logx}}}}{\text{  =  }}{{{e}}^{{x}}}{{{e}}^{{\text{ - logx}}}}{\text{  =  }}\dfrac{{{{{e}}^{{x}}}}}{{{x}}}$ 

77. State true or false of the following

(i) Integrating factor of the differential equation of the form \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + }}{{\text{p}}_{\text{1}}}{{x  =  }}{{\text{Q}}_{\text{1}}}\] is given by \[{{{e}}^{\int {{{\text{p}}_{\text{1}}}{\text{dy}}} }}\]

Ans: True

Given differential equation  \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + }}{{\text{p}}_{\text{1}}}{{x  =  }}{{\text{Q}}_{\text{1}}}\]

IF is equal to \[{{{e}}^{\int {{{\text{p}}_{\text{1}}}{\text{dy}}} }}\]

(ii) Solution of the differential equation of the type \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + }}{{\text{p}}_{\text{1}}}{{x  =  }}{{\text{Q}}_{\text{1}}}\] is given by \[{{x I}}{\text{.F}}{\text{.  =  }}\int {{\text{(I}}{\text{.F)}}} {{ \times }}{{\text{Q}}_{\text{1}}}{\text{dy}}\]

Ans: True

(iii) Correct substitution for the solution of the differential equation of the type \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  f(x,y) where f(x,y)}}\] is a homogeneous function of zero degree is \[{{y  =  vx}}\]

Ans: True

(iv) Correct substitution for the solution of the differential equation of the type \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  g(x,y) where g(x,y)}}\] is a homogeneous function of the degree zero is \[{{x  =  vy}}\]

Ans: True

(v) Number of arbitrary constants in the particular solution of a differential equation of order two is two.

Ans: False, There is no arbitrary constant in the particular solution of a differential equation.

(vi) The differential equation representing the family of circles \[{{{x}}^{\text{2}}}{\text{ + (y - a}}{{\text{)}}^{\text{2}}}{\text{  =  }}{{\text{a}}^{\text{2}}}\] will be of order two.

Ans: False, As We know order of differential equation is equal to number of arbitrary constant.

Here, number of arbitrary constant is equal to one. Thus, order is one.

(vii) The solution of \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}{\left( {\dfrac{{{y}}}{{{x}}}} \right)^{\dfrac{{\text{1}}}{{\text{3}}}}}\] is \[{{{y}}^{\dfrac{{\text{2}}}{{\text{3}}}}}{\text{ - }}{{{x}}^{\dfrac{{\text{2}}}{{\text{3}}}}}{\text{  =  c}}\]

Ans: True, given differential equation \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}{\left( {\dfrac{{{y}}}{{{x}}}} \right)^{\dfrac{{\text{1}}}{{\text{3}}}}}\]

${{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{{{y}}^{\dfrac{1}{3}}}}}{{{{{x}}^{\dfrac{1}{3}}}}}$

${{{y}}^{\dfrac{{ - 1}}{3}}}{\text{dy  =  }}{{{x}}^{\dfrac{{ - 1}}{3}}}{\text{dx}}$ 

Integrate both sides:

${{{{y}}^{{\text{ - }}\dfrac{1}{3}}}} {\text{dy  =  }}\int {{{{x}}^{{\text{ - }}\dfrac{1}{3}}}} {\text{dx}}$

${{{{{y}}^{{\text{ - }}\dfrac{1}{3}{\text{ + 1}}}}}}{{\dfrac{{{\text{ - 1}}}}{{\text{3}}}{\text{ + 1}}}}{\text{  =  }}\dfrac{{{{{x}}^{{\text{ - }}\dfrac{1}{3}{\text{ + 1}}}}}}{{\dfrac{{{\text{ - 1}}}}{{\text{3}}}{\text{ + 1}}}}{\text{ + }}{{\text{C}}^{\prime}}$

${{\text{3}}}{{\text{2}}}{{{y}}^{\dfrac{2}{3}}}{\text{  =  }}\dfrac{{\text{3}}}{{\text{2}}}{{{x}}^{\dfrac{2}{3}}}{\text{ + }}{{\text{C}}^{\prime}}$

${{{y}}^{\dfrac{2}{3}}}{\text{ - }}{{{x}}^{\dfrac{2}{3}}}{\text{  =  }}{{\text{C}}^{\prime}}{\text{     }}$ 

(viii) Differential equation representing the family of curves \[{{y  =  }}{{{e}}^{{x}}}{\text{(A cos x + B sin x)}}\] is \[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ - 2}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + 2y  =  0}}\]

Ans: True,

Given that \[{{y  =  }}{{{e}}^{{x}}}{\text{(A cos x + B sin x)}}\]

Differentiate both sides we get:

${{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}{{{e}}^{{x}}}{\text{( - Asinx + Bcosx) + }}{{{e}}^{{x}}}{\text{(Acosx + Bsinx)}}$

${{{\text{dy}}}}{{{\text{dx}}}}{\text{ - y  =  }}{{{e}}^{{x}}}{\text{( - Asinx + Bcosx)}}$ 

Again, differentiate both sides:

${{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ - }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}{{{e}}^{{x}}}{\text{( - Acosx - Bsinx) + }}{{{e}}^{{x}}}{\text{( - Asinx + Bcosx)}}$

${{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ - }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + y  =  }}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ - y}}$ 

\[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{ - 2}}\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{ + 2y  =  0}}\]

(ix) The solution of the differential equation \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{{x + 2y}}}}{{{x}}}\] is \[{{x + y  =  k}}{{{x}}^{\text{2}}}\]

Ans: True, given that \[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{{x + 2y}}}}{{{x}}}\]

${{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  1 + }}\dfrac{{\text{2}}}{{{x}}}{{ \times y}}$

${{{\text{dy}}}}{{{\text{dx}}}}{\text{ - }}\dfrac{{\text{2}}}{{{x}}}{{y  =  1}}$

${\text{IF  =  }}{{{e}}^{\dfrac{{{\text{ - 2}}}}{{{x}}}{\text{dx}}}}{\text{  =  }}{{{e}}^{{\text{ - 2logx}}}}{\text{  =  }}{{{x}}^{{\text{ - 2}}}}$ 

Differential solution is \[{{y \times }}{{{x}}^{{\text{ - 2}}}}{\text{  =  }}\int {{{{x}}^{{\text{ - 2}}}}} {{ \times 1dx + k}}\]

${{{y}}}{{{{{x}}^{\text{2}}}}}{\text{  =  }}\dfrac{{{{{x}}^{{\text{ - 2 + 1}}}}}}{{{\text{ - 2 + 1}}}}{\text{ + k}}$

${{{y}}}{{{{{x}}^{\text{2}}}}}{\text{  =  }}\dfrac{{{\text{ - 1}}}}{{{x}}}{\text{ + k}}$

${{y  =   - x + k}}{{{x}}^{\text{2}}}$

${{x + y  =  k}}{{{x}}^{\text{2}}}$ 

(x) Solution of \[\dfrac{{{{x dy}}}}{{{\text{dx}}}}{\text{  =  y + xtan}}\dfrac{{{y}}}{{{x}}}\] is \[{\text{sin}}\left( {\dfrac{{{y}}}{{{x}}}} \right){\text{  =  cx}}\]

Ans: True, given \[\dfrac{{{{x dy}}}}{{{\text{dx}}}}{\text{  =  y + xtan}}\dfrac{{{y}}}{{{x}}}\]

\[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  }}\dfrac{{{y}}}{{{x}}}{\text{ + tan}}\left( {\dfrac{{{y}}}{{{x}}}} \right)\]

Put \[\dfrac{{{y}}}{{{x}}}{\text{  =  v i}}{\text{.e}}{\text{. y  =  vx}}\]

\[\dfrac{{{\text{dx}}}}{{{x}}}{\text{  =  v + }}\dfrac{{{{xdv}}}}{{{\text{dx}}}}\]

Substitute values we get

${{{{xdv}}}}{{{\text{dx}}}}{\text{ + v  =  v + tan v}}$

${{{\text{dx}}}}{{{x}}}{\text{  =  }}\dfrac{{{\text{dv}}}}{{{\text{tanv}}}}$ 

Integrate both sides

${\dfrac{{\text{1}}}{{{x}}}} {\text{dx  =  }}\int {\dfrac{{\text{1}}}{{{\text{tanv}}}}} {\text{dx}}$

${\text{log(x)  =  log(sinv) + log}}{{\text{C}}^{\prime}}$

${\text{log}}\left( {\dfrac{{{x}}}{{{\text{sinv}}}}} \right){\text{  =  log}}{{\text{C}}^{\prime}}$

${{{x}}}{{{\text{sinv}}}}{\text{  =  }}{{\text{C}}^{\prime}}$

${\text{sin v  =  Cx              }}\left[ {{\text{where C  =  }}\dfrac{{\text{1}}}{{{{\text{C}}^{\prime}}}}} \right]$

${\text{sin}}\dfrac{{{y}}}{{{x}}}{\text{  =  Cx}}$ 

(xi) The differential equation of all non-horizontal lines in a plane is \[\dfrac{{{{\text{d}}^{\text{2}}}{{x}}}}{{{\text{d}}{{{y}}^{\text{2}}}}}{{  =  0 \times }}\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{  =  0}}\]

Ans: True

Let non-horizontal line in a plane is \[{{y  =  mx + c}}\]

Differentiate both sides, we get:

\[\dfrac{{{\text{dy}}}}{{{\text{dx}}}}{\text{  =  m}}\]

Now, again differentiate both sides, we get:

\[\dfrac{{{{\text{d}}^{\text{2}}}{{y}}}}{{{\text{d}}{{{x}}^{\text{2}}}}}{\text{  =  0}}\]

Chapter 9 - Differential Equations is an important Chapter for the students recommended by NCERT. This Chapter consists of concepts related to Differential Equations, such as the order and degree of Differential Equations, formation of Differential Equations with variables separable, linear Differential Equations, and homogeneous linear Equations. Students looking for any guidance to solve the problems related to the questions of the respective Chapter can go through the PDF of the Exemplar available at vedantu.com. 

Vedantu’s interest is in students’ welfare, and how to develop the quality of learning. Class 12 is the most important Class for a student’s life. They have to put their best efforts to score their best in the Examinations. NCERT books as recommended by the Central Board of Secondary education but are not sufficient enough for the maximization of marks. Students have to go for some reference texts that will help them to improve. Exemplars are the best source of practice, the questions asked in the Exemplar enhance the thinking and problem-solving capabilities of a student. Students looking for the best Exemplars can go through the Vedantu website, they will get Exemplars for each and every Chapter for each and every Class. 

Vedantu also offers online study for the respective Chapter like notes, additional questions, sample papers, and last year’s asked questions. Students can easily get an idea of what sort of question they are going to face in Exams. And what they have to practice to score more. There are online sessions and recorded Classes both for students, students must register themselves before taking an online session. Students can resolve their doubts with the best expert faculty teaching at Vedantu, they can revise their Chapter through online Classes very easily. In fact, they discuss their problem-solving techniques and can work on them together with the teachers present.