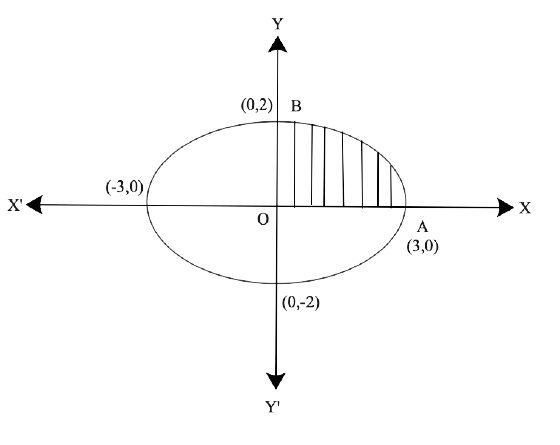
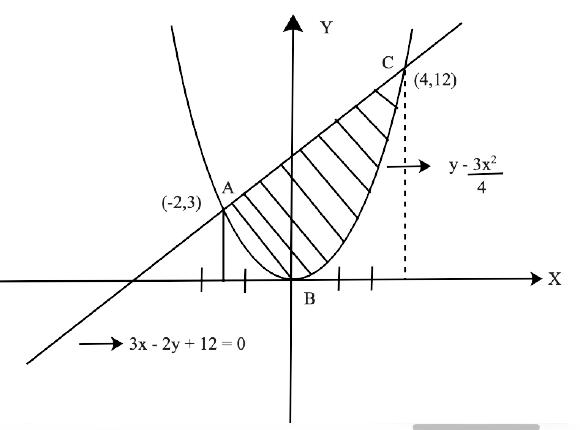
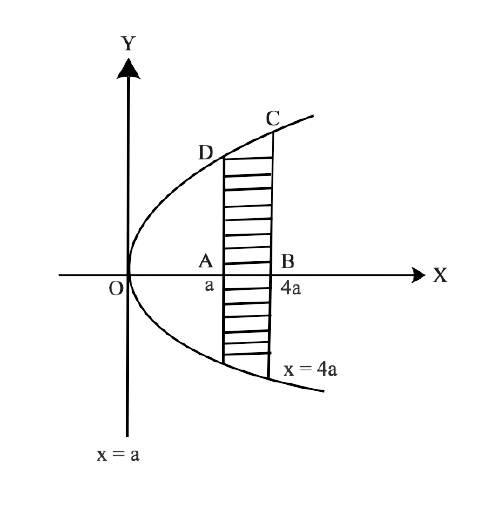
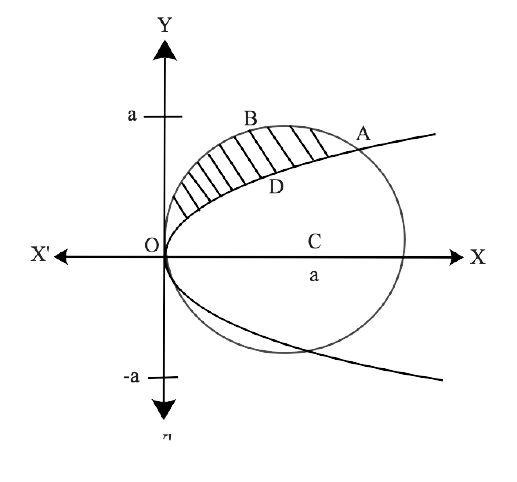
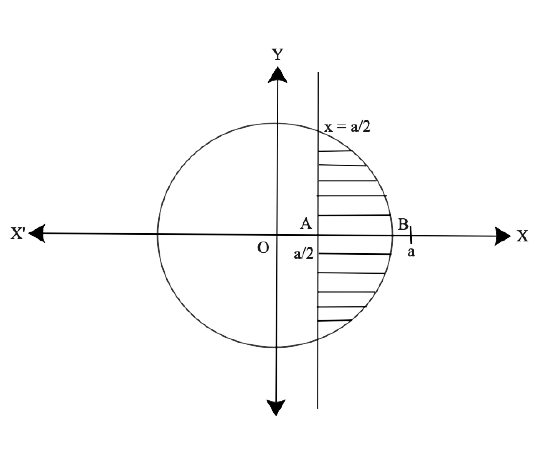
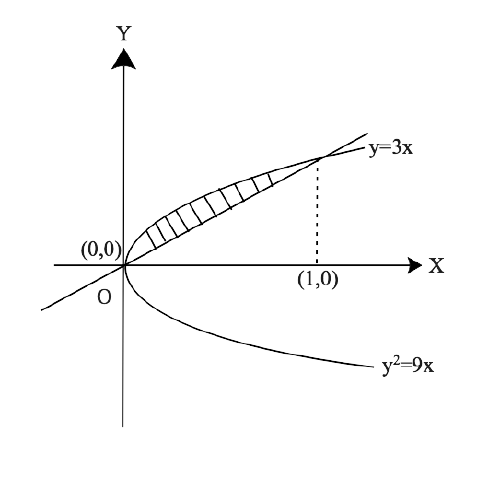
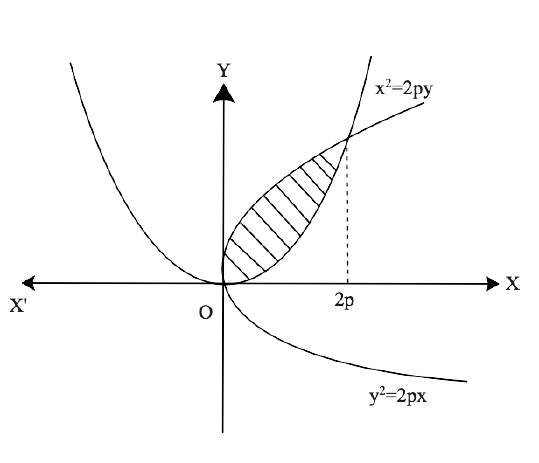
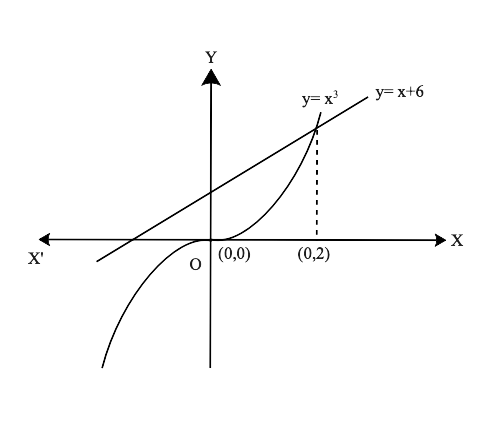
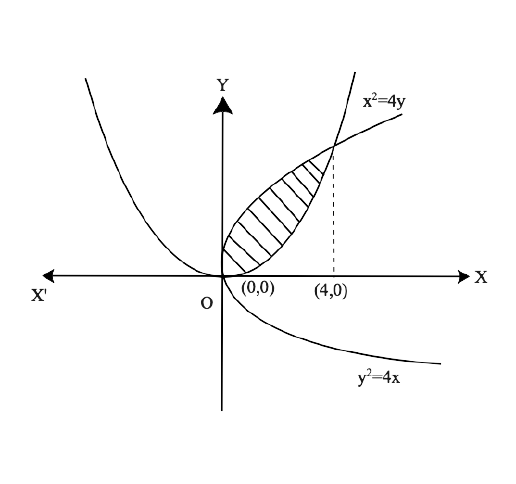
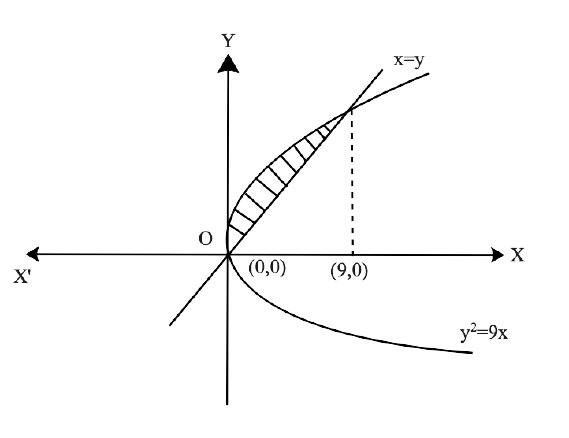
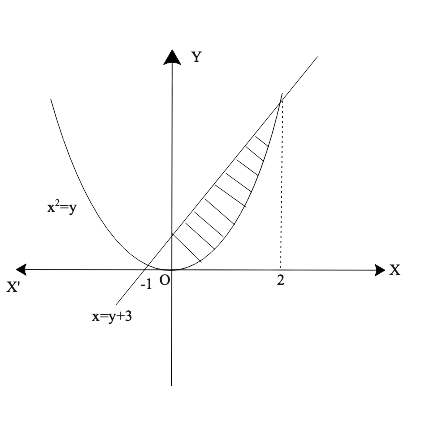
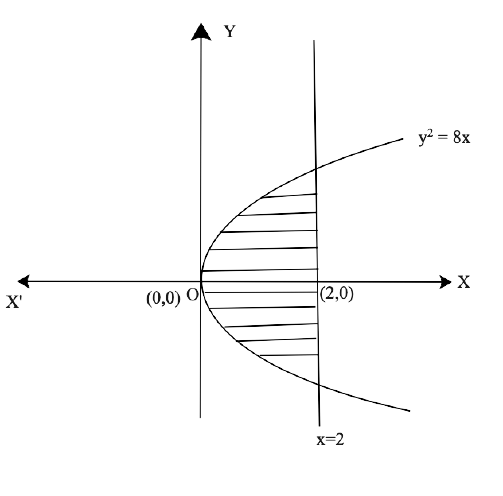
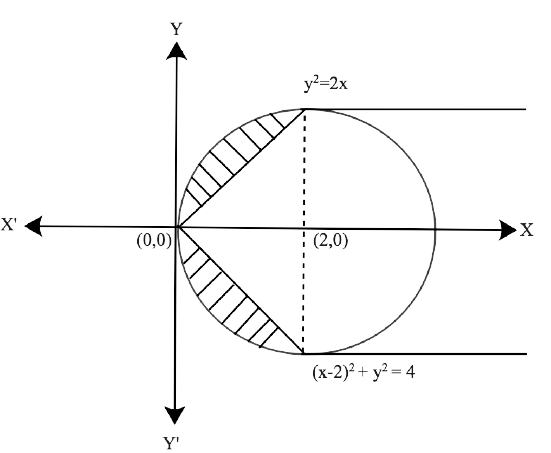
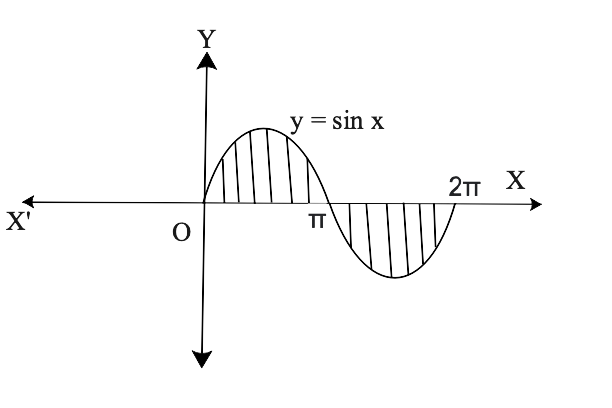
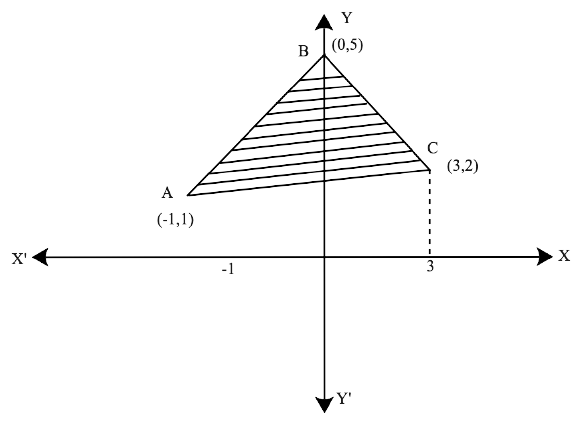
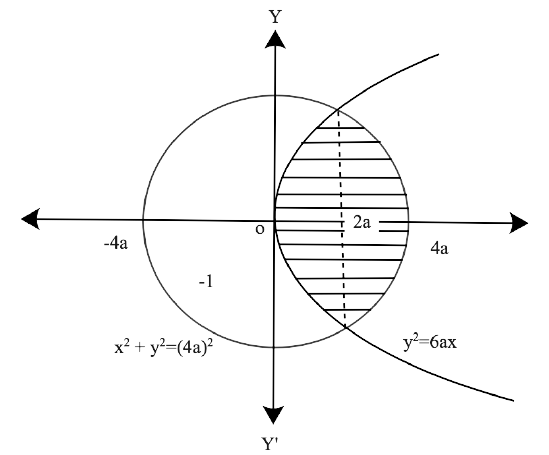
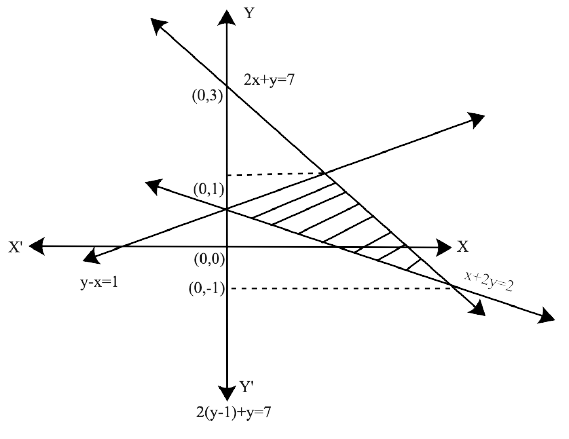
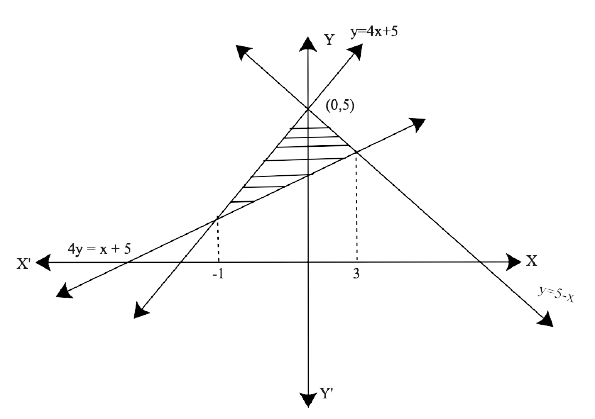
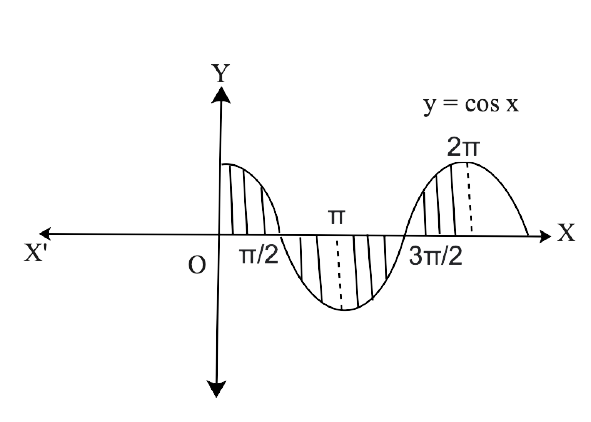
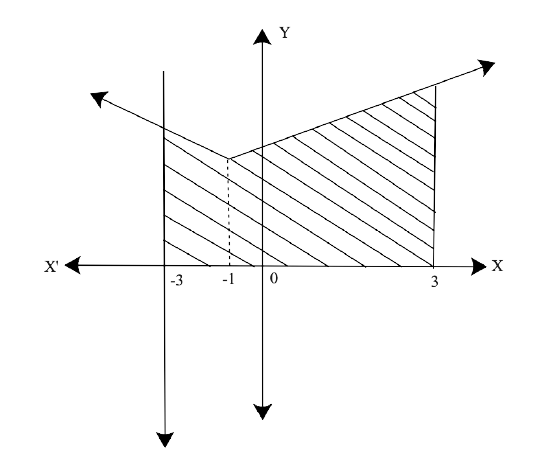
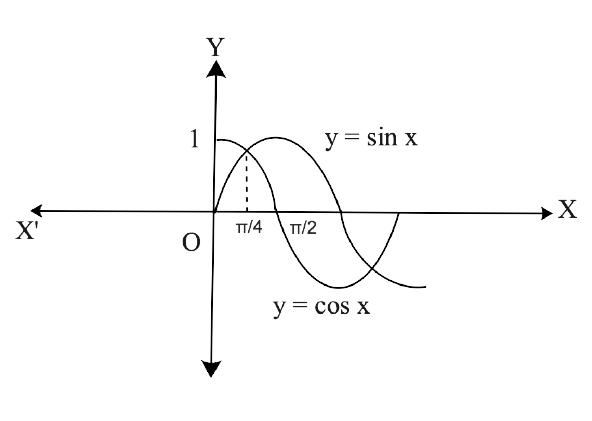
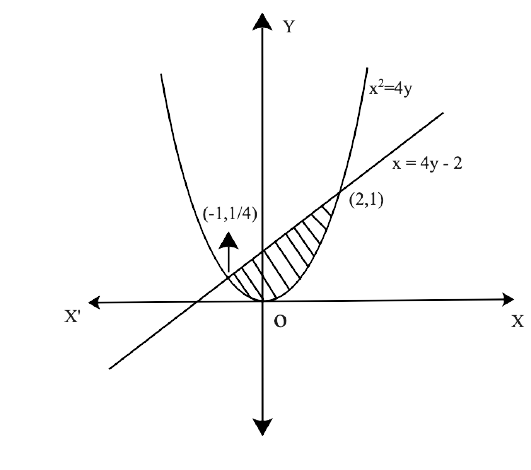
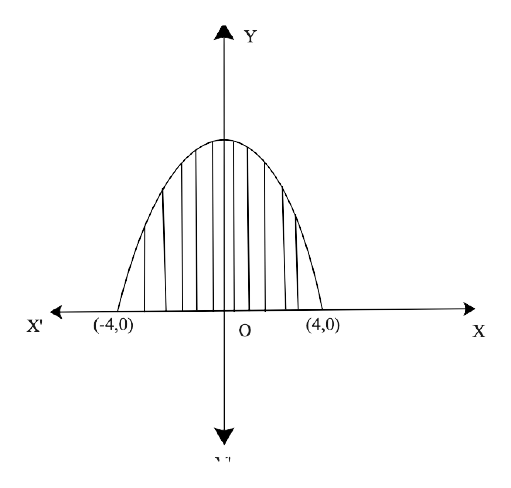
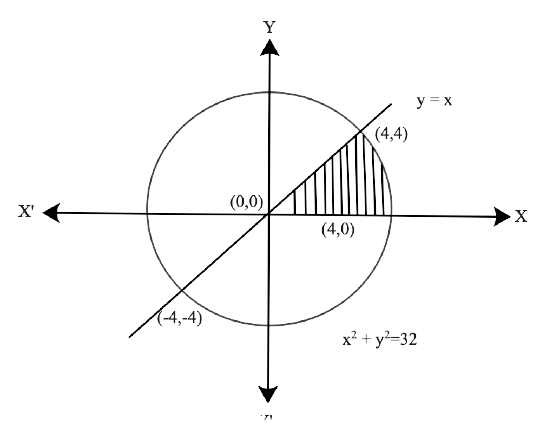
Free PDF download of NCERT Exemplar for Class 12 Maths Chapter 8 - Application of Integrals
FAQs on NCERT Exemplar for Class 12 Maths - ApplicationOf Integrals - Free PDF Download
1. Where can students find the Exemplar PDF for Chapter 8 Application of Integrals, Class 12?
Students can find the Exemplar PDF for Chapter 8 Application Of Integrals, Class 12at Vedantu’s official website i.e. vedantu.com. The Exemplar is available for the students to practice and revise the concepts. This PDF will enhance the advanced knowledge of the respective subject which is important from the Exam’s point of view. The Exemplar PDF consists of problems and additional questions that give an efficient preparation for the students to boost their scores in the Examinations.
2. Why is NCERT Exemplar for Class 12 Maths - ApplicationOf Integrals - Free PDF Download important for the preparation for the subject?
Exemplars are important for the preparation for the subject because Exemplar gives another perspective to the students that help them to realize their plus and minus, which is directly related to their score in the Exam. Students constantly following the Exemplar will notice the change in the question-solving pattern and recognize the concepts they have met earlier but found them tough.
3. How is NCERT Exemplar for Class 12 Maths - ApplicationOf Integrals - Free PDF Download designed for the students of Class 12?
Exemplars are designed in such a way for the students of Class 12 that they can boost their preparation that increases their marks in the Exams directly. The Exemplars help students to attain the utmost knowledge about their respective topic which increases their thinking process and has the upper hand compared to other students. Also, the Exemplar is designed by the expert faculty of Vedantu on the latest guidelines and syllabus pattern advised by the Central Board of Secondary education.
4. Is Chapter 8- Application of Integrals important for a Class 12 student?
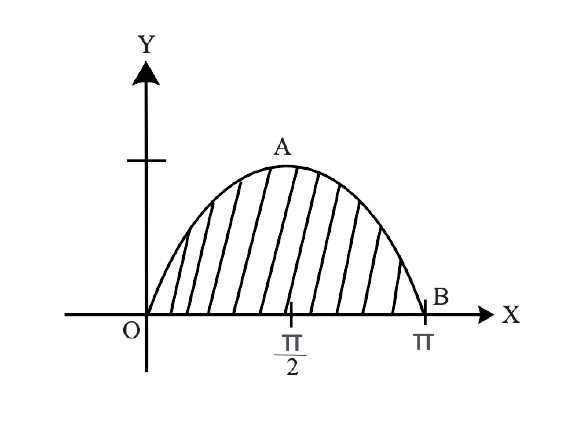
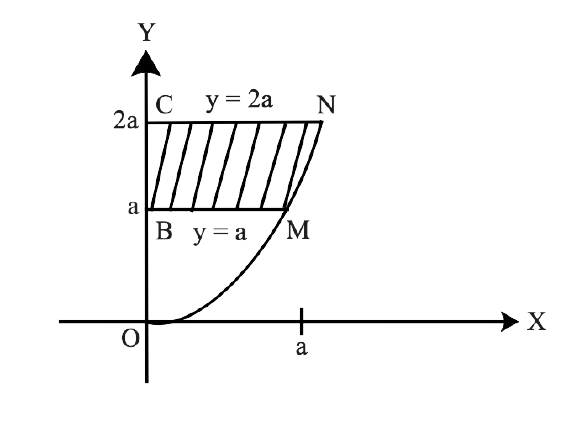
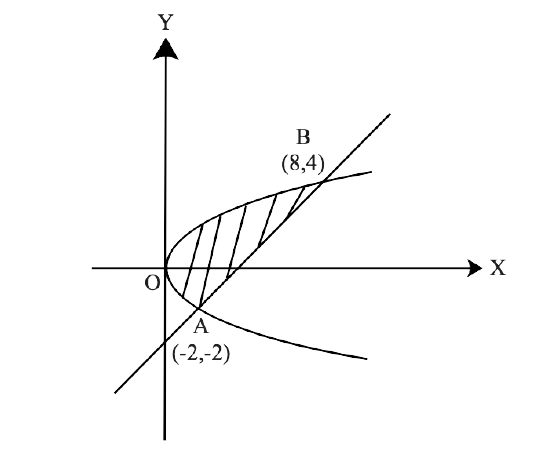
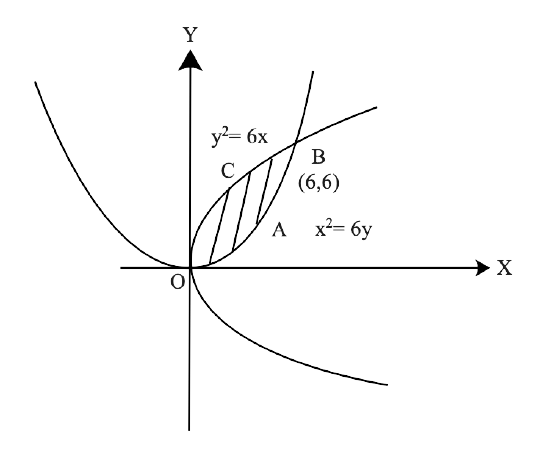
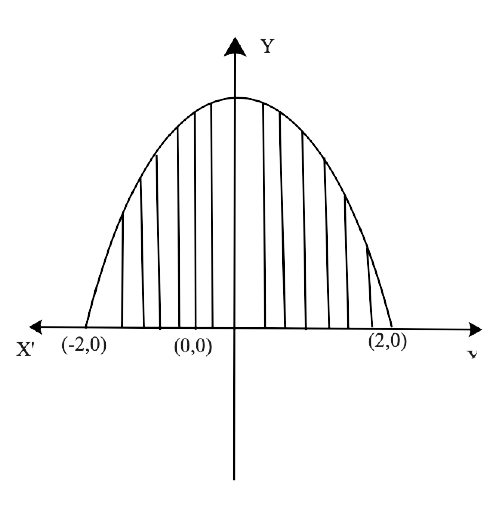
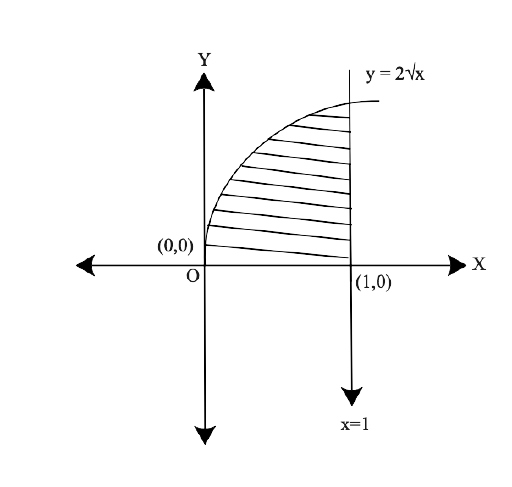
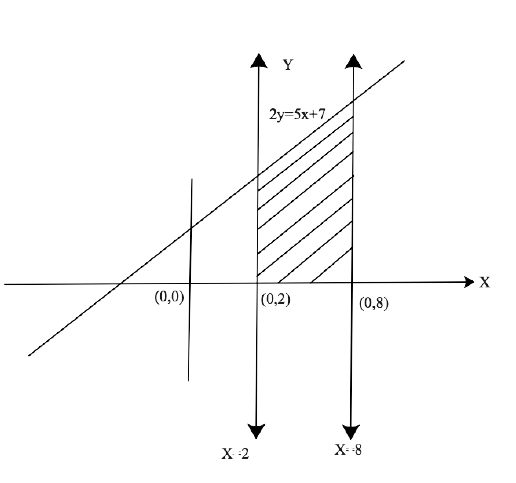
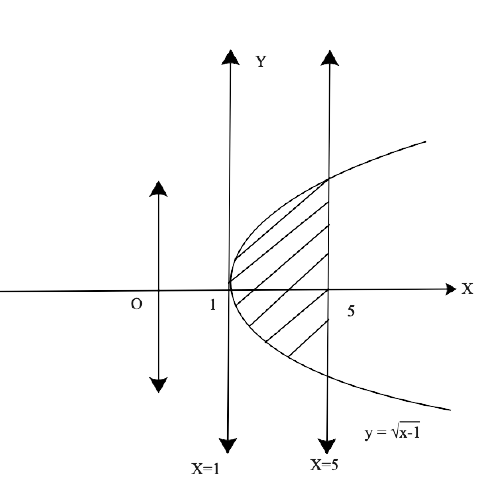
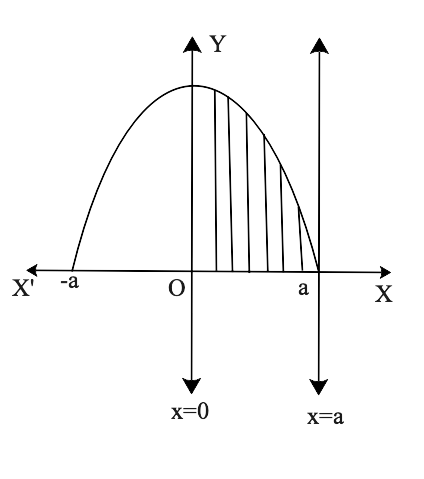
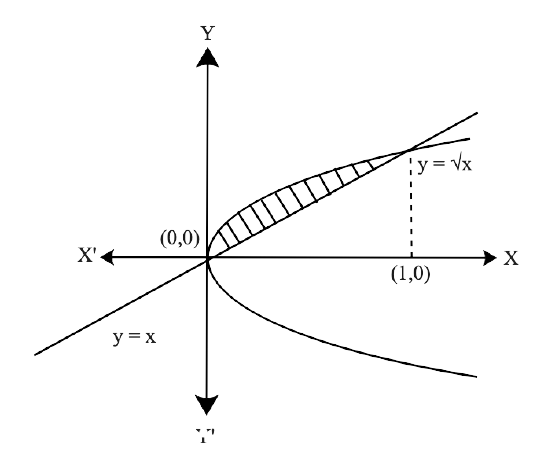
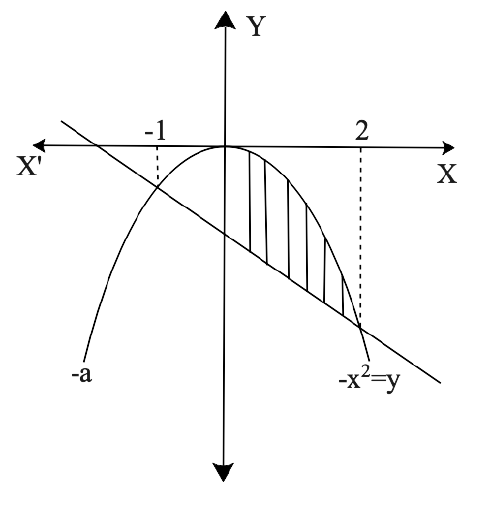
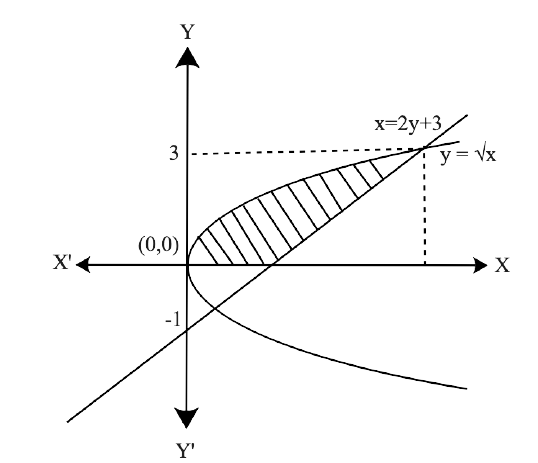
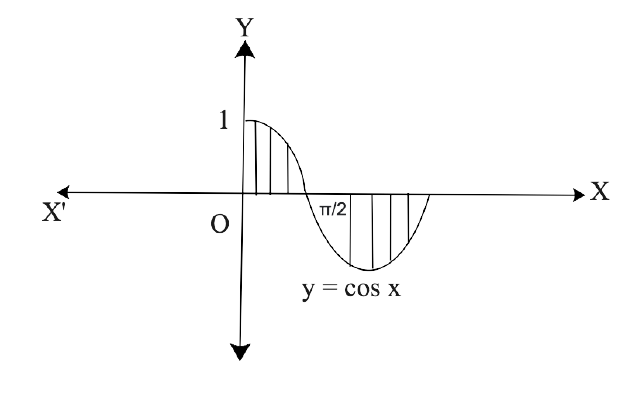
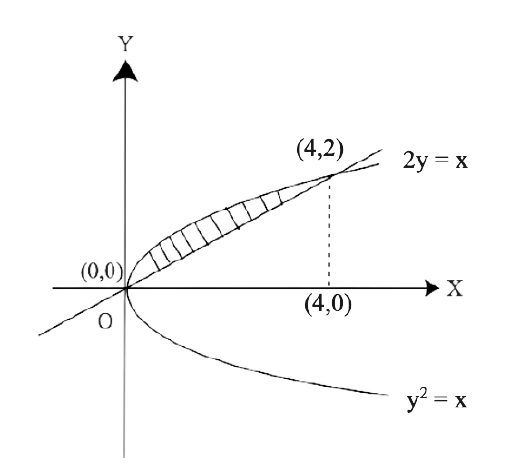
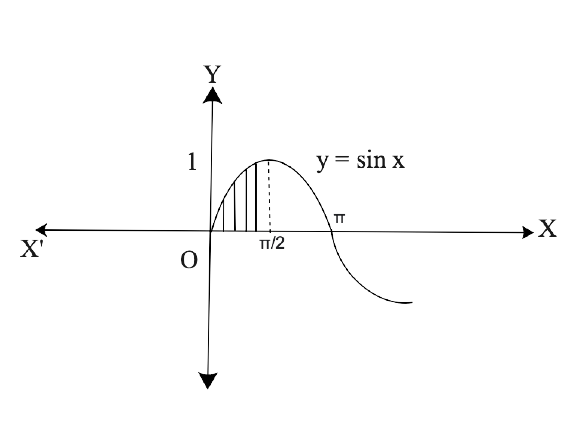
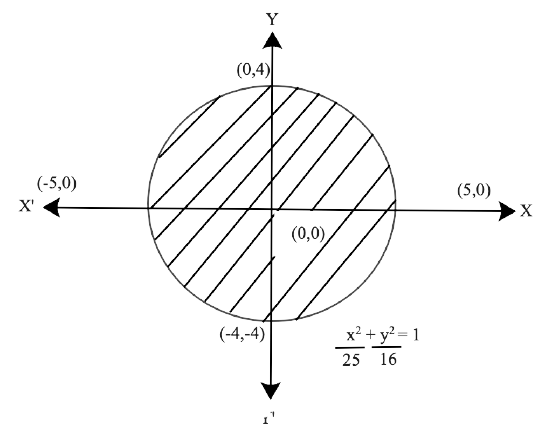
Yes, Chapter 8- Application of Integrals is important for a Class 12 student as this Chapter has a good marks weightage in Exams. Chapter 8 - Application of Integrals is based on the Application of Integrals with the method of finding the area under the simple curves, a line and an area between two curves, and the area region bounded by a curve. The NCERT Exemplar for Class 12 Maths, Chapter 8 Application of Integrals has been developed and designed in such a manner that will increase the thinking process of students to solve the Exercises related to the Chapter.