NCERT Exemplar for Class 12 Physics Chapter-11 (Book Solutions)

Exercise

MULTIPLE CHOICE QUESTIONS-1

1. A particle is dropped from a height $H$. The de Broglie wavelength of the particle as a function of height is proportional to 

(a) $H$

(b) ${H^{\dfrac{1}{2}}}$

 (c) ${H^0}$

(d) ${H^{ - \;\dfrac{1}{2}}}$

Ans: When the body is falling freely from a height, the velocity is

$H = v$

\[ = \sqrt {2gH} \]

according to de-Broglie wavelength 

$\lambda  = \dfrac{h}{p}$

$\lambda  = \dfrac{h}{{mv}}$

$ = \dfrac{h}{{m\sqrt {2gH} }}$

Where, 

$h$, $m$ and $g$ are constant.

$\therefore \dfrac{h}{{m\sqrt {2g} }}$is constant

$ \Rightarrow \lambda  \propto \dfrac{1}{{\sqrt H }}$

$ \Rightarrow \lambda  \propto {H^{ - \,\dfrac{1}{2}}}$

Thus, option (d) is correct.

2. The wavelength of a photon needed to remove a proton from a nucleus which is bound to the nucleus with $1\;MeV$ energy is nearly 

(a) $1.2\,nm$

(b) $1.2 \times {10^{ - 3}}\,nm$

(c) $1.2 \times {10^{ - 6}}\;nm$

(d) $1.2 \times {10^1}\,nm$

Ans:  we know that the energy of the photon should be equal to the binding energy of proton

Thus, energy of photon $ = 1\;MeV$

$ = {10^6} \times 1.6 \times {10^{ - 19}}J$

$\lambda  = \dfrac{{hc}}{E}$

$ \Rightarrow \dfrac{{6.63 \times {{10}^{ - 34}} \times 3 \times {{10}^8}}}{{1.6 \times {{10}^{ - 13}}}}$

$ \Rightarrow \dfrac{{6.63 \times 3}}{{1.60}} \times {10^{ - 26 + 13}}$

$ \Rightarrow \dfrac{{19.89}}{{1.60}} \times {10^{ - 13}}$

$ = 12.4 \times {10^1} \times {10^{ - 13}}$

$ \Rightarrow 1.24 \times {10^{ - 9}} \times {10^{ - 3}}$

$ = 1.24 \times {10^{ - 3}}\;nm$

So, option (b) is correct.

3. Consider a beam of electrons (each electron with energy ${E_0}$ ) incident on a metal surface kept in an evacuated chamber. Then 

(a) no electrons will be emitted as only photons can emit electrons.

(b) electrons can be emitted but all with an energy, ${E_0}$.

(c) electrons can be emitted with any energy, with a maximum of ${E_0}$ – $\phi $($\phi $ is the work function).

(d) electrons can be emitted with any energy, with a maximum of ${E_0}$ .

Ans:  When a beam of electrons in each electron of energy ${E_0}$ incident on the metal surface which is kept in vacuum then because of elastic collisions with electrons on the surface, the energy of incident electrons will be transferred to the emitted electrons. For the emission of electrons below the surface the part of ${E_0}$ of incident electrons is consumed against work function so the energy of emitted electrons becomes less than ${E_0}$. Thus, the maximum energy of emitted electrons can be ${E_0}$. So, the option (d) is correct.

4. Consider \[{{Fig}}.{\text{ }}{{11}}.{{7}}\] in the NCERT text book of physics for Class XII. Suppose the voltage applied to \[{{A}}\] is increased. The diffracted beam will have the maximum at a value of \[{{\theta }}\] that 

(a) will be larger than the earlier value. 

(b) will be the same as the earlier value. 

(c) will be less than the earlier value. 

(d) will depend on the target

Ans:  

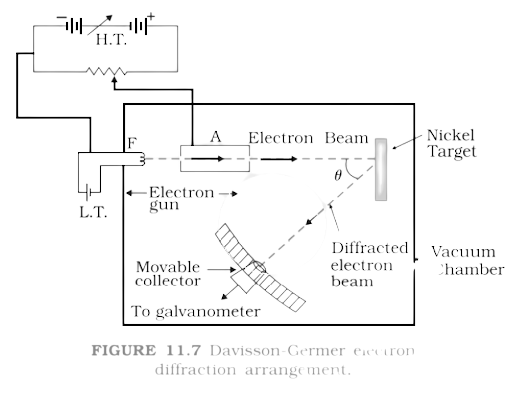
Through Davisson-Germer experiment, we know that diffracted beam of electrons

has the de-Broglie wavelength

${\lambda _d} = \dfrac{{12.27}}{{\sqrt V }}\mathop A\limits^o $ ….(i) 

Here, $V$ is the voltage applied. When there is a maximum of the diffracted electrons at an angle $\theta $, then 

$2d\sin \theta  = \lambda $

From equation (i), as there are increases in the applied voltage in this experiment, the wavelength ${\lambda _d}$ decreases in turn $\sin \theta $ or $\theta $ decreases by relation (ii). Thus, this verifies the option (c).

5. A proton, a neutron, an electron and an α-particle have the same energy. Then their de Broglie wavelengths compare as 

(a) ${\lambda _p} = {\lambda _n} > {\lambda _e} > {\lambda _\alpha }$

(b) ${\lambda _\alpha } < {\lambda _p} = {\lambda _n} > {\lambda _e}$

(c) ${\lambda _e} < {\lambda _p} = {\lambda _n} > {\lambda _\alpha }$

(d) ${\lambda _e} = {\lambda _p} = {\lambda _n} = {\lambda _\alpha }$

Ans:  According to de-Broglie wavelength

${\lambda _d} = \dfrac{h}{p}$

${E_p} = {E_n} = {E_e} = {E_\alpha }$

$K.E. = K = \dfrac{1}{2}m{v^2}$

$ \Rightarrow 2K = m{v^2}$

$ \Rightarrow 2Km = {m^2}{v^2}$

$ \Rightarrow 2mK = {p^2}$

$ \Rightarrow \sqrt {2mK}  = p$

$\therefore {\lambda _d} = \dfrac{h}{p}$

$ \Rightarrow {\lambda _d} = \dfrac{h}{{\sqrt {2mK} }}$

Or ${\lambda _d} = \dfrac{h}{{\sqrt {2mK} }}$

Where, $h$ and $E$$\left( {K.E.} \right)$ is constant.

$\therefore \lambda  \propto \dfrac{1}{{\sqrt m }}$

Thus, 

${m_\alpha } > {m_p} = {m_n} > {m_e}$

So, ${\lambda _\alpha } < {\lambda _p} = {\lambda _n} > {\lambda _e}$, option (b) is correct.

6. An electron is moving with an initial velocity $v = {v_0}\hat i$ and is in a magnetic field $B = {B_0}\hat j$. Then it’s de Broglie wavelength 

(a) remains constant. 

(b) increases with time. 

(c) decreases with time. 

(d) increases and decreases periodically.

Ans:  In the question, it is given that

$v = {v_0}\hat i$

And, $B = {B_0}\hat j$

The force on moving electron is perpendicular magnetic field $B$ is,

$F =  - e\left( {\vec v = \vec B} \right)$

$ =  - e\left[ {{v_0}\hat i \times {B_0}\hat j} \right]$

$ =  - e{v_0}{B_0}\hat i \times \hat j$

$F =  - e{v_0}{B_0}\hat k$

So, here the force is perpendicular to both $v$ and $B$ as it is perpendicular to the velocity. Thus, there will be no change in $v$ or $mv$ so the de-Broglie wavelength remains the same. 

7. An electron (mass $m$) with an initial velocity $v = {v_0}\hat i\left( {{v_0} > 0} \right)$ is in an electric field $E =  - {E_0}\hat i$(${E_0} = {\text{ }}{{constant}}{\text{ }} > {\text{ }}{{0}}$). It’s de-Broglie wavelength at time \[{{t}}\] is given by 

(a) $\dfrac{\lambda }{{\left[ {1 + \dfrac{{e{E_0}}}{m}\dfrac{t}{{{v_0}}}} \right]}}$

(b) ${\lambda _0}\left[ {1 + \dfrac{{e{E_0}}}{{m{v_0}}}t} \right]$

(c) ${\lambda _0}$

(d) ${\lambda _0}t$

Ans:  at initial, de-Broglie wavelength 

${\lambda _0} = \dfrac{h}{{m{v_0}}}$

Force acting on electron

$F = qE$

$F = \left( { - e} \right)\left( { - {E_0}i} \right)$

$ma = e{E_0}\hat i$

$a = \dfrac{{e{E_0}}}{m}\hat i$

After time $t$, velocity of electron is

$v = {v_0} + at$

$v = {v_0}i + \dfrac{{e{E_0}}}{m}i \cdot t$

$v = \left[ {{v_0} + \dfrac{{e{E_0}t}}{m}} \right]\hat i$

$\therefore $New de-Broglie wavelength $\lambda  = \dfrac{h}{{mv}}$

$\lambda  = \dfrac{h}{{m\left[ {{v_0} + \dfrac{{e{E_0}t}}{m}} \right]i}}$

$ = \dfrac{h}{{m{v_0}\left[ {1 + \dfrac{{e{E_0}t}}{{m{v_0}}}} \right]}}$

$\lambda  = \dfrac{{{\lambda _0}}}{{\left[ {1 + \dfrac{{e{E_0}t}}{{m{v_0}}}} \right]}}$$\left( {\because \dfrac{h}{{m{v_0}}} = {\lambda _0}\,\,from\,\,eqn.I} \right)$

8. An electron (mass\[{{m}}\]) with an initial velocity $v = {v_0}\hat i$ is in an electric field $E = {E_0}\hat j$ . If, ${\lambda _0} = \dfrac{h}{{m{v_0}}}$, it’s de-Broglie wavelength at time \[{{t}}\]is given by 

(a) ${\lambda _0}$

(b) ${\lambda _0}\sqrt {1 + \dfrac{{{e^2}E_0^2{t^2}}}{{{m^2}v_0^2}}} $

(c) $\dfrac{{{\lambda _0}}}{{\sqrt {1 + \dfrac{{{e^2}E_0^2{t^2}}}{{{m^2}v_0^2}}} }}$

(d) $\dfrac{{{\lambda _0}}}{{\left[ {1 + \dfrac{{{e^2}E_0^2{t^2}}}{{{m^2}v_0^2}}} \right]}}$

Ans:  We know that de-Broglie wavelength 

${\lambda _0} = \dfrac{h}{{m{v_0}}}$

Force acting on the moving electron due to electric field $E$

$F =  - eE$

$ \Rightarrow F =  - e{E_0}\hat j$

Because of electric field, acceleration in electron due to force,

$ma =  - e{E_0}\hat j$ 

$ \Rightarrow a = \dfrac{{ - e{E_0}}}{m}\hat j$

And acceleration on electron acts along $ - Y$direction, thus the initial velocity of electron along $X - $axis

${v_{{x_0}}} = {v_0}\hat i$

Thus, the initial velocity of electron in $Y$direction is zero

$\therefore {v_{{y_0}}} = 0$

And the velocity of electron after time $t$ along $X - $axis

${v_x} = {v_0}\hat i$

Thus, velocity of electron after $t$along $Y - $axis

$v = u + at$

${v_y} = 0 + \left( {\dfrac{{ - e{E_0}}}{m}\hat j} \right)t$

${v_y} = \dfrac{{ - e{E_0}}}{m}\hat jt$

After time $t$, magnitude of velocity of electron is

$v = \sqrt {v_x^2 + v_y^2} $

$v = \sqrt {v_0^2 + {{\left( {\dfrac{{ - e{E_0}}}{m}\hat jt} \right)}^2}} $

$\left| v \right| = {v_0}\sqrt {1 + {e^2}E_0^2{t^2}} $

$\therefore \lambda ' = \dfrac{h}{{mv}}$

$ = \dfrac{h}{{m{v_0}\sqrt {1 + \dfrac{{{e^2}E_0^2{t^2}}}{{{m^2}v_0^2}}} }}$

$v' = \dfrac{1}{{\sqrt {1 + \dfrac{{{e^2}E_0^2{t^2}}}{{{m^2}v_0^2}}\left( {\because {\lambda _0} = \dfrac{h}{{m{v_0}}}} \right)} }}$

 Thus, option (c) is verified.

MULTIPLE CHOICE

QUESTIONS-II MORE THAN

ONE OPTION

9. Relativistic corrections become necessary when the expression for the kinetic energy$\dfrac{1}{2}m{v^2}$ , becomes comparable with $m{c^2}$ , where \[{{m}}\]is the mass of the particle. At what de Broglie wavelength will relativistic corrections become important for an electron? 

(a) \[{{\lambda }}{\text{ }} = {{10}}\,{{nm}}\]

(b) \[{{\lambda }}{\text{ }} = {{1}}{{{0}}^{--{{1}}}}{{nm}}\]

(c) \[{{\lambda }}{\text{ }} = {{1}}{{{0}}^{--{{4}}}}{{nm}}\]

(d) \[{{\lambda }}{\text{ }} = {{1}}{{{0}}^{--{{6}}}}{{nm}}\]

Ans:  according to de-Broglie wavelength 

$\lambda  = \dfrac{h}{{mv}}$

$ \Rightarrow v = \dfrac{h}{{m\lambda }}$

Here, $h = 6.6 \times {10^{ - 34}}$

$m = 9 \times {10^{ - 31}}\,kg$

$ = \dfrac{{6.6 \times {{10}^{ - 34}}}}{{9 \times {{10}^{ - 31}}\lambda }}$

$ = \dfrac{{6.6 \times {{10}^{ - 34 + 31}}}}{{9\lambda }}$

$ = \dfrac{{0.73 \times {{10}^{ - 3}}}}{\lambda }$

For option

$(a)$ $\lambda  = 10\;nm$

$ = 10 \times {10^{ - 9}}\;m$

$ = {10^{ - 8}}\;m$

$\therefore v = \dfrac{{7.3 \times {{10}^{ - 4}}}}{{{{10}^{ - 8}}}}$

$ = 7.3 \times {10^4}$

$ \approx {10^4} < 3 \times {10^8}$(Speed of light)

$\left( b \right)$$\lambda  = {10^{ - 1}}\;nm$

$ = {10^{ - 1}} \times {10^{ - 9}}\;m$

$ = {10^{ - 10}}\;m$

$\therefore v = \dfrac{{7.3 \times {{10}^{ - 4}}}}{{{{10}^{ - 10}}}}$

$ = 7.3 \times {10^{ - 4 + 10}}$

$ = 7.3 \times {10^6}$

$ \approx {10^7} < {10^8}$(Speed of light)

(c) $\lambda  = {10^{ - 4}}\;nm$

$ = {10^{ - 4}} \times {10^{ - 9}}\;m$

$ = {10^{ - 13}}\;m$

$\therefore v = \dfrac{{7.3 \times {{10}^{ - 4}}}}{{{{10}^{ - 13}}}}$

$ = 7.3 \times {10^{ - 4 + 13}}$

$7.3 \times {10^9}$

$ \approx {10^9} > {10^8}$(Speed of light)

(d) $\lambda  = {10^{ - 6}}\;nm$

$ = {10^{ - 6}} \times {10^{ - 9}}\;m$

$ = {10^{ - 15}}\;m$

$\therefore v = \dfrac{{7.3 \times {{10}^{ - 4}}}}{{{{10}^{ - 15}}}}$

$ = 7.3 \times {10^{11}}\,m$

$ \approx {10^{11}} > {10^8}$(Speed of light)

Here we can see that the velocity of electron is more for option (c) and (d) where the relativistic correction become necessary although the speed of electron is $7.3 \times {10^6}\,m{s^{ - 1}}$ which is comparable with the speed of light, thus the correct answers of this question is option (c) and (d).

10. Two particles\[\;{{{A}}_{{1}}}\]and\[\;{{{A}}_{{2}}}\] of masses\[{{{m}}_{{1}}}\], \[{{{m}}_{{2}}}\](\[{{{m}}_{{1}}}{\text{ }} > {\text{ }}{{{m}}_{{2}}}\]) have the same de-Broglie wavelength. Then 

(a) their momenta are the same. 

(b) their energies are the same. 

(c) energy of \[\;{{{A}}_{{1}}}\] is less than the energy of \[\;{{{A}}_{{2}}}\]. 

(d) energy of \[\;{{{A}}_{{1}}}\] is more than the energy of \[\;{{{A}}_{{2}}}\].

Ans:  We know that de-Broglie wavelength

$\lambda  = \dfrac{h}{p}$

$p = \dfrac{h}{\lambda }$

or $p \propto \dfrac{1}{\lambda }$

$\dfrac{{{p_1}}}{{{p_2}}} = \dfrac{{{\lambda _2}}}{{{\lambda _1}}}$

$\because {\lambda _1} = {\lambda _2} = \lambda $(given)

${p_1} = {p_2}$this verifies option (a)

${E_a} = \dfrac{1}{2}m{v^2}$

$ = \dfrac{1}{2}\dfrac{{{m^2}{v^2}}}{m}$

$ = \dfrac{{{p^2}}}{{2m}}$

$E \propto \dfrac{1}{m}$$\left[ {as\;{p_1} = {p_2} = constant\left( {as\;proved\;above} \right)} \right]$

$\dfrac{{{E_1}}}{{{E_2}}} = \dfrac{{{m_2}}}{{{m_1}}}$

$\dfrac{{{E_1}}}{{{E_2}}} < 1$$\left[ {\because {m_1} > {m_2}\left( {given} \right)} \right]$

$\therefore {E_2} > {E_1}$ this verifies answer (c).

11. The de Broglie wavelength of a photon is twice the de-Broglie wavelength of an electron. The speed of the electron is ${v_e} = \dfrac{c}{{100}}$ Then 

(a) $\dfrac{{{E_e}}}{{{E_p}}} = {10^{ - 4}}$

(b) $\dfrac{{{E_e}}}{{{E_p}}} = {10^{ - 2}}$

(c) $\dfrac{{{p_e}}}{{{m_e}c}} = {10^{ - 2}}$

(d) $\dfrac{{{p_e}}}{{{m_e}c}} = {10^{ - 4}}$

Ans:  de-Broglie wavelength 

$\lambda  = \dfrac{h}{p}$

$\therefore {\lambda _e} = \dfrac{h}{{{m_e}{v_e}}}$

$ = \dfrac{h}{{{m_e}\dfrac{c}{{100}}}}$

$ = \dfrac{{100h}}{{{m_e}c}}$  ….(i)

Now,

$K.E. = \dfrac{1}{2}m{v^2}$

$ \Rightarrow E = \dfrac{{{m^2}{v^2}}}{{2m}}$   ….(ii)

$ \Rightarrow {m_e}{v_e} = \sqrt {2{m_e}{E_e}} $

Now,

${\lambda _e} = \dfrac{h}{{{m_e}{v_e}}}$

$ = \dfrac{h}{{\sqrt {2{m_e}{E_e}} }}$ …[from (ii)]

$ \Rightarrow {E_e} = \dfrac{{{h^2}}}{{2{m_e}\lambda _e^2}}$ ….(iii)

For proton 

${\lambda _p} = 2{\lambda _e}$ [given]

$\therefore {E_p} = \dfrac{{hc}}{{{\lambda _p}}}$

$ = \dfrac{{hc}}{{2{\lambda _e}}}$

Now, $\dfrac{{{E_p}}}{{{E_e}}} = \dfrac{{hc}}{{2{\lambda _e}}} \times \dfrac{{2{m_e}\lambda _e^2}}{{{h^2}}}$

$ = \dfrac{{{\lambda _e}{m_e}c}}{h}$[from (iii)]

$ = \dfrac{{100h}}{{{m_e}c}} \times \dfrac{{{m_e}c}}{h}$

$ = 100$

$ \Rightarrow \dfrac{{{E_e}}}{{{E_p}}} = {10^{ - 2}}$ this verifies option (b)

Now, ${p_e} = {m_e}{v_e}$

$ = {m_e} \times \dfrac{c}{{100}}$$\left( {\because {v_e} = \dfrac{c}{{100}}} \right)$

$ \Rightarrow \dfrac{{{p_e}}}{{{m_e}c}} = \dfrac{1}{{100}}$

$ = {10^{ - 2}}$ this verifies option (c).

12. Photons absorbed in matter are converted to heat. A source emitting \[{{n}}{\text{ }}{{photon}}\;{{se}}{{{c}}^{ - 1}}\]of frequency \[{{\nu }}\]is used to convert \[{{1}}\,{{kg}}\] of ice at \[{{0}}^\circ {{C}}\] to water at\[{{0}}^\circ {{C}}\]. Then, the time\[\;{{T}}\] taken for the conversion 

(a) decreases with increasing\[{{n}}\], with\[\;{{\nu }}\] fixed. 

(b) decreases with \[{{n}}\] fixed, \[\;{{\nu }}\] increasing 

(c) remains constant with \[{{n}}\] and \[\;{{\nu }}\] changing such that \[nv = \] constant. 

(d) increases when the product \[nv\]increases.

Ans:  the amount of heat required to convert $1\;kg$ of ice at ${0^\circ }C$to water at${0^\circ }C$ is

$E = ML$

$E' = nhv$

Where, $n = $no. of photons incident per second.

Let time $T$ be taken by radiation to melt the ice at ${0^\circ }C$. Then,

$E = nhv\,t$

$mL = n\,\,hv\,t$

$t = \dfrac{{mL}}{{nh\,v}}$

$\therefore t \propto \dfrac{1}{n}$and $T \propto \dfrac{1}{v}$

Or $t \propto \dfrac{1}{{nv}}$[$\because m$,$L$and $h$ are constant]

This proves option (a), (b) and (c).

$\therefore $if $nv$ increases, $T$decreases which does not verify option (d).

13. A particle moves in a closed orbit around the origin, due to a force which is directed towards the origin. The de-Broglie wavelength of the particle varies cyclically between two values \[{{{\lambda }}_{{1}}}\]and \[{{{\lambda }}_{{2}}}\]with \[{{{\lambda }}_{{1}}} > {{{\lambda }}_{{2}}}\]. Which of the following statements are true? 

(a) The particle could be moving in a circular orbit with origin as centre 

(b) The particle could be moving in an elliptic orbit with origin as its focus. 

(c) When the de Broglie wavelength is \[{{{\lambda }}_{{1}}}\], the particle is nearer the origin than when its value is\[{{{\lambda }}_{{2}}}\]

(d) When the de-Broglie wavelength is \[{{{\lambda }}_{{2}}}\], the particle is nearer the origin than when its value is \[{{{\lambda }}_{{1}}}\]. 

Ans:  The de-Broglie wavelength varies regularly between two values ${\lambda _1}$ and ${\lambda _2}$ of the particle. This is possible when the particle is operating in an elliptical orbit with origin as one of its focuses then. As if ${\lambda _1}$ and ${\lambda _2}$ are equal, then their speed must be equal and particle must move in circular orbit. Hence this verifies option (b).

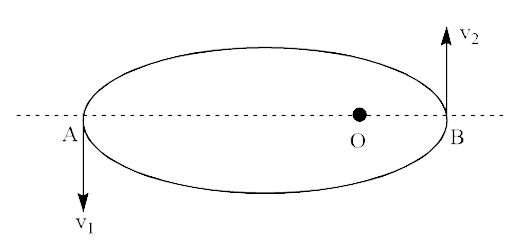
Let ${v_1}$ and ${v_2}$ be the speeds of particles at $A$ and $B$ respectively and origin is at $O$. If particle $A$ and $B$ associated with the de-Broglie wavelengths ${\lambda _1}$ and ${\lambda _2}$ respectively, then

${\lambda _1} = \dfrac{h}{{m{v_1}}}$

And ${\lambda _2} = \dfrac{h}{{m{v_2}}}$ 

So, $\dfrac{{{\lambda _1}}}{{{\lambda _2}}} = \dfrac{{{v_2}}}{{{v_1}}}$$\left[ {\because {\lambda _1} > {\lambda _2}} \right]$

Thus, ${v_1} < {v_2}$  …..(i)

According to the law of conservation of angular momentum, the speed of the particle will be more when it is closer to focus. This proved the option (d).

VERY SHORT ANSWER TYPE

QUESTIONS

14. A proton and an α-particle are accelerated, using the same potential difference. How are the de-Broglie wavelengths \[{{{\lambda }}_{{p}}}\]and \[{{{\lambda }}_\alpha }\]related to each other?

Ans:  The both particles are promoted at the same potential difference so their $K.E.s$ will be equal i.e.,

${K_1} = {K_2} = K = qV$$\left( {\because V = \dfrac{W}{q}} \right)$

So, $\lambda  = \dfrac{h}{{\sqrt {2mK} }}$

${\lambda _d} = \dfrac{h}{{\sqrt {2mqV} }}$

$\therefore \dfrac{{{\lambda _p}}}{{{\lambda _\alpha }}} = \dfrac{h}{{\sqrt {2{m_p}{q_p}{V_p}} }} \times \dfrac{{\sqrt {2{m_\alpha }{q_\alpha }{V_\alpha }} }}{h}$

${m_\alpha } = 4\,{m_p}$; ${q_\alpha } = 2e$; ${q_p} = e$;${V_p} = {V_\alpha } = V$(P.D. applied)

$\dfrac{{{\lambda _p}}}{{{\lambda _\alpha }}} = \sqrt {\dfrac{{2 \times 4{m_p}2eV}}{{2{m_p}eV}}} $

${\lambda _p} = \sqrt 8 {\lambda _\alpha }$

Thus, the de-Broglie wavelength of the proton is $\sqrt 8 $ times of alpha $\left( \alpha  \right)$particle.

15. (i) In the explanation of the photoelectric effect, we assume one photon of frequency\[\;{{\nu }}\] collides with an electron and transfers its energy. This leads to the equation for the maximum energy \[{{{E}}_{{{max}}}}\]of the emitted electron as ${E_{max}} = hv - {\phi _ \circ }$ 

 where ${\phi _0}$ is the work function of the metal. If an electron absorbs 2 photons (each of frequency \[{{\nu }}\]) what will be the maximum energy for the emitted electron? 

(ii) Why is this fact (two photon absorption) not taken into consideration in our discussion of the stopping potential?

Ans:  (i) Here, $2$ photons transfer its energy to one electron as

$E = hv$

$\therefore {E_e} = {E_p}$

$h{v_e} = 2hv$

$\therefore {v_e} = 2v$

Maximum energy of emitted electron is

${E_{\max }} = h{v_e} - {\phi _0}$

$ = h(2v) - {\phi _0}$

$ = 2hv - {\phi _0}$

(ii) the possibility of absorbing $2$photons by electrons is very low due to their mass difference. So, the probability of such emission of electrons is negligible.

16. There are materials which absorb photons of shorter wavelength and emit photons of longer wavelength. Can there be stable substances which absorb photons of larger wavelength and emit light of shorter wavelength. 

Ans:  As we know that as the wavelength of a photon increases, its frequency decreases or energy increases.

Case I: Photons which are of shorter wavelength i.e., those which are of larger energy will effuse the photons of smaller energy. Some energy is utilized against work function. So, it is attainable by law of conservation of energy.

Case II: Photons which are of longer wavelength invariably emit photons of shorter wavelength and photons of smaller energy can never effuse photons of larger energy. Some part of energy $\left( {hv} \right)$ is utilized in the work function $\left( \phi  \right)$ of metal. Or it will repudiate the law of conservation of energy (universal law). So, it is unendurable in stable materials.

17. Do all the electrons that absorb a photon come out as photo-electrons?

Ans:  We can observe that most of the electrons in photoelectric effect pounded by photons are dissipated into the metal by absorbing photons. Thus, some of the energy of photons is absorbed. Generally, one photon cannot emit one electron. Some energy of the photons is consumed against the work function of metal. Thus, some of all electrons which absorb a photon come out from the metal surface.

18. There are two sources of light, each emitting with a power of \[{{100}}{\text{ }}{{W}}\]. One emits X-rays of wavelength \[{{1}}\;{{nm}}\] and the other visible light at \[{{500}}{\text{ }}{{nm}}\]. Find the ratio of the number of photons of X-rays to the photons of visible light of the given wavelength?

Ans:  Let the energies ${E_x}$ and ${E_v}$ given by one photon in X-rays and visible rays then,

${E_x} = h{v_x}$

And ${E_v} = h{v_v}$

Let the number of photons ${n_x}$ and ${n_v}$ X-rays and visible light to give equal energies as both sources (X-rays and visible) emitting same power $100\,W$each so 

${n_x}h{v_x} = {n_v}h{v_v}$

$\dfrac{{{n_x}}}{{{n_v}}} = \dfrac{{{v_v}}}{{{v_x}}}$

$ \Rightarrow \dfrac{{\dfrac{1}{{{\lambda _v}}}}}{{\dfrac{1}{{{\lambda _x}}}}} = \dfrac{{{\lambda _x}}}{{{\lambda _v}}}$$\left( {\because v = \dfrac{c}{\lambda }or\;v = \dfrac{1}{\lambda }} \right)$

$\dfrac{{{n_x}}}{{{n_v}}} = \dfrac{{1\,nm}}{{500\;nm}}$$\left( {\because {\lambda _x} = 1\,nm\;and\,{\lambda _v} = 500\,nm} \right)$

${n_x}:{n_v} = 1:500$

SHORT ANSWER TYPE

QUESTIONS

19. Consider \[{{Fig}}.{{11}}.{{1}}\]for photo-emission. How would you reconcile with momentum conservation? Note light (photons) have momentum in a different direction than the emitted electrons.

Ans:  The transfer of momentum of photons to atoms of metal when photons pound to the metal surface by reducing its own speed up to zero. Photons convey this momentum to the nucleus and electrons of the metal. The direction of emission of excited electrons is roughly contrary to the direction of photons. The total momentum transferred by the photons will be equivalent to the momentum of all electrons and nucleus.

20. Consider a metal exposed to light of wavelength\[{{600}}{\text{ }}{{nm}}\]. The maximum energy of the electron doubles when light of wavelength \[{{400}}{\text{ }}{{nm}}\]is used. Find the work function in\[{{eV}}\].

Ans:  let ${K_1}$ and ${K_2}$ are the maximum energies of emitted electrons when $600\;nm$and $400\,nm$visible light is used according to the question

${K_2} = 2{K_1}$

${K_{\max }} = hv - \phi $

$ = \dfrac{{hc}}{\lambda } - \phi $

${k_1} = \dfrac{{hc}}{{{\lambda _1}}} - \phi $

${k_2} = \dfrac{{hc}}{{{\lambda _2}}} - \phi $

$ = 2{K_1}$

$\dfrac{{hc}}{{{\lambda _2}}} - \phi  = 2\left[ {\dfrac{{hc}}{{{\lambda _1}}} - \phi } \right]$

$ = \dfrac{{2hc}}{{{\lambda _1}}} - 2\phi $

$\phi  = hc\left[ {\dfrac{2}{{{\lambda _1}}} - \dfrac{1}{{{\lambda _2}}}} \right]$$\left( {\because hc = 1240\,ev\,nm} \right)$

$\because \phi  = 1240\left[ {\dfrac{2}{{600}} - \dfrac{1}{{400}}} \right]eV$

$ = \dfrac{{1240}}{{200}}\left[ {\dfrac{2}{3} - \dfrac{1}{2}} \right]$

$ = 6.2\dfrac{{\left( {4 - 3} \right)}}{6}$

The work function $\phi  = \dfrac{{6.2}}{6}$

$ = 1.03\,eV$

21. Assuming an electron is confined to a \[{{1nm}}\] wide region, find the uncertainty in momentum using Heisenberg Uncertainty principle $\left( {\Delta x \times \Delta p \cong h} \right)$. You can assume the uncertainty in position \[{{\Delta x}}\]as\[\;{{1nm}}\]. Assuming\[p \approx \Delta p\], find the energy of the electron in electron volts.

Ans:  As we know that electron revolves in circular path

Thus, $\Delta r = 1\;nm$

$ = {10^{ - 9}}m$

$\Delta x \times \Delta p \cong h$$\left[ {Given} \right]$

$\Delta p = \dfrac{h}{{\Delta x}}$

$ = \dfrac{{6.62 \times {{10}^{ - 34}}}}{{2\pi \Delta r}}JS$

$\therefore \Delta p = \dfrac{{6.62 \times {{10}^{ - 34}}}}{{2 \times 3.14 \times {{10}^{ - 9}}}}kg\,m\,{s^{ - 1}}$

$ \Rightarrow \Delta p = \dfrac{{331}}{{314}} \times {10^{ - 25}}$

$\therefore E = \dfrac{1}{2}m{v^2}$

$ = \dfrac{{{m^2}{v^2}}}{{2m}}$

$ = \dfrac{{\Delta {p^2}}}{{2m}}$

$ = \dfrac{{331 \times 331 \times {{10}^{ - 50 + 31}}}}{{314 \times 314 \times 18.2}}J$

$ = \dfrac{{331 \times 331 \times {{10}^{ - 19}} \times 1.6 \times {{10}^{ - 19}}}}{{314 \times 314 \times 18.2}}e$

$ = \dfrac{{331 \times 331 \times 16}}{{314 \times 314 \times 182}}$

$ = 3.8 \times {10^{ - 2}}eV$

22. Two monochromatic beams \[{{A}}\]and \[{{B}}\]of equal intensity\[{{I}}\], hit a screen. The number of photons hitting the screen by beam is twice that by beam\[{{B}}\]. Then what inference can you make about their frequencies?

Ans:  Given,

${I_A} = {I_B}$

${n_A}h{v_A} = {n_B}h{v_B}$

$\because {n_A} = 2{n_B}$

$\therefore 2{n_B}{v_A} = {n_B}{v_B}$

$ \Rightarrow 2{v_A} = {v_B}$

Thus, the frequency of the source $B$is twice of the frequency of source $A$.

23. Two particles A and B of de Broglie wavelengths \[{{{\lambda }}_{{1}}}\]and \[{{{\lambda }}_{{2}}}\]combine to form a particle\[{{C}}\]. The process conserves momentum. Find the de-Broglie wavelength of the particle \[{{C}}\]. (The motion is one dimensional).

Ans:  According to the de-Broglie wavelengths

$\lambda  = \dfrac{h}{p}$

Or $p = \dfrac{h}{\lambda }$

$ \Rightarrow {p_1} = \dfrac{h}{{{\lambda _1}}}$, ${p_2} = \dfrac{h}{{{\lambda _2}}}$and ${p_3} = \dfrac{h}{{{\lambda _3}}}$

${p_1} + {p_2} = {p_3}$

$\dfrac{h}{{{\lambda _1}}} + \dfrac{h}{{{\lambda _2}}} = \dfrac{h}{{{\lambda _3}}}$(${\lambda _3} = the\;wavelength\;of\,particle\;C$)

$\dfrac{1}{{{\lambda _1}}} + \dfrac{1}{{{\lambda _2}}} = \dfrac{1}{{{\lambda _3}}}$

$\dfrac{{{\lambda _2} + {\lambda _1}}}{{{\lambda _1}{\lambda _2}}} = \dfrac{1}{{{\lambda _3}}}$

Case I: When ${p_1}$and ${p_2}$ are the positive then

${\lambda _3} = \dfrac{{{\lambda _2}{\lambda _1}}}{{{\lambda _1} + {\lambda _2}}}$ 

Case II: When both are negative then

${\lambda _3} = \left| {\dfrac{{ - {\lambda _2}{\lambda _1}}}{{{\lambda _1} + {\lambda _2}}}} \right| = \dfrac{{{\lambda _2}{\lambda _1}}}{{{\lambda _1} + {\lambda _2}}}$

Case III: ${p_A} > 0$, ${p_B} > 0$

$\dfrac{h}{{{\lambda _3}}} = \dfrac{h}{{{\lambda _1}}} - \dfrac{h}{{{\lambda _2}}}$

Or $\dfrac{1}{{{\lambda _3}}} = \dfrac{{{\lambda _2} - {\lambda _1}}}{{{\lambda _1}{\lambda _2}}}$

${\lambda _3} = \dfrac{{{\lambda _1}{\lambda _2}}}{{{\lambda _2} - {\lambda _1}}}$

Case IV: ${p_A} < 0$, ${p_B} > 0$

$\dfrac{h}{{{\lambda _3}}} = \dfrac{h}{{{\lambda _2}}} - \dfrac{h}{{{\lambda _1}}}$

$ \Rightarrow \dfrac{h}{{{\lambda _3}}} = \dfrac{{\left( {{\lambda _1} - {\lambda _2}} \right)h}}{{{\lambda _1}{\lambda _2}}}$

$\therefore {\lambda _3} = \dfrac{{{\lambda _1}{\lambda _2}}}{{{\lambda _1} - {\lambda _2}}}$

24. A neutron beam of energy \[{{E}}\] scatters from atoms on a surface with a spacing\[{{d}}{\text{ }} = {\text{ }}{{0}}.{{1}}\;{{nm}}\]. The first maximum of intensity in the reflected beam occurs at\[{{\theta }}{\text{ }} = {\text{ }}{{30}}^\circ \]. What is the kinetic energy \[{{E}}\]of the beam in\[{{eV}}\]?

Ans:  According to the Bragg’s law of diffraction, condition for $nth$ maxima is

$2d\sin \theta  = n\lambda $

Where,$n = 1$,

So, $\lambda  = 2d\sin \theta $

Where $\theta  = {30^ \circ }$(Given)

$ = 2 \times 0.1 \times {10^{ - 9}}\sin {30^ \circ }\left( {\because d = 0.1\;nm} \right)$

$p = \dfrac{h}{\lambda }$

$ = \dfrac{{6.6 \times {{10}^{ - 34}}}}{{{{10}^{ - 10}}}}$

$ = 6.6 \times {10^{ - 24}}kg\,m\;{s^{ - 1}}$

$E = \dfrac{1}{2}m{v^2}$

$ = \dfrac{1}{2}\dfrac{{{m^2}{v^2}}}{m}$

$ = \dfrac{{{p^2}}}{{2m}}$

\[E = \dfrac{{6.6 \times 6.6 \times {{10}^{ - 48}}}}{{2 \times 1.6 \times {{10}^{ - 27}}}}J\]

$ = \dfrac{{66 \times 66 \times {{10}^{ - 48 + 46}}}}{{2 \times 16{\kern 1pt} \; \times 16}}$

$E = \dfrac{{33 \times 33}}{{126}} \times {10^{ - 2}}$

$ = 8.5 \times {10^{ - 2}}$

$ = 0.085\;eV$

LONG ANSWER TYPE

QUESTIONS

25. Consider a thin target \[\left( {{{1}}{{{0}}^{--{{2}}}}{{m}}{\text{ }}{{square}},{\text{ }}{{1}}{{{0}}^{--{{3}}}}{{m}}{\text{ }}{{thickness}}} \right)\]of sodium, which produces a photo-current of \[100\;\mu A\] when a light of intensity \[{\text{100 W }}\;{m^{ - 2}}{\text{ }}\left( {\lambda  = 660\;nm} \right)\]falls on it. Find the probability that a photo-electron is produced when a photon strikes a sodium atom. \[\left[ {{{Take}}{\text{ }}{{density}}{\text{ }}{{of}}{\text{ }}{{Na}}{\text{ }} = {\text{ }}{{0}}.{{97}}{\text{ }}{{kg}}{{{m}}^{ - {{3}}}}{\text{ }}} \right].\]

Ans:  Area of the square sheet ($A$) $ = {10^{ - 2}} \times {10^{ - 2}}$

$ = {10^{ - 4}}\;{m^2}$

Thickness $\left( d \right)$$ = {10^{ - 3}}\;m$

Current $\left( i \right)$$ = 100\;\mu A = {10^{ - 4}}A$

Intensity $\left( I \right)$$ = 100\;W\;{m^{ - 2}}$

Mass of target $\left( m \right)$=$Volume \times density$

$m = area\;of\,sheet \times thickness \times density$

$ \Rightarrow m = \left( {{{10}^{ - 4}} \times {{10}^{ - 3}}} \right) \times 0.97\;kg$

$ \Rightarrow m = 0.97 \times {10^{ - 7}}kg$

$ \Rightarrow m = 0.97 \times {10^{ - 4}}gm$
$\therefore number\,of\;Na\;atoms\,in\,target = \dfrac{{6.023 \times {{10}^{23}}}}{{23}} \times 0.97 \times {10^{ - 4}}$

$ = 0.254 \times {10^{19}}$

Number of $Na$atoms in $Na$target $ = 2.54 \times {10^{18}}atoms$

Total energy falling per second on target $ = nhv$

\[Intensity \times Area = n \times h \times \dfrac{c}{\lambda }\]

$I \times A = \dfrac{{nhc}}{\lambda }$

$n = \dfrac{{IA\lambda }}{{hc}}$

$ = \dfrac{{100 \times {{10}^{ - 4}} \times 660 \times {{10}^{ - 9}}}}{{6.6 \times {{10}^{ - 34}} \times 3 \times {{10}^8}}}$

$ = \dfrac{{1000 \times 660}}{{66 \times 3}} \times {10^{ - 13 - 8 + 34}}$

$ = \dfrac{{10000}}{3} \times {10^{ - 24 + 34}}$

$ = \dfrac{{10}}{3} \times {10^3} \times {10^{13}}$

Number of photons $\left( n \right)$incident per second on $Na$metal $ = 3.3 \times {10^{16}}$

Assuming $P$is the possibility of emission of photo-electrons per atom per photon.

Number of photo-electrons emitted per second$\left( N \right) = P \cdot n$( here $n$ is no. of sodium atoms)

$N = P \times 3.3 \times {10^{16}} \times 2.54 \times {10^{18}}$

 $i = 100\mu A = {10^{ - 4}}A = Ne$

$ \Rightarrow N = \dfrac{i}{e}$

$P = \dfrac{i}{{e \times 3.3 \times {{10}^{16}} \times 2.54 \times {{10}^{18}}}}$

$P = \dfrac{{{{10}^{ - 4}}}}{{1.6 \times {{10}^{ - 19}} \times 3.3 \times {{10}^{16}} \times 2.54 \times {{10}^{18}}}}$

$ = \dfrac{{{{10}^{ - 4 - 34 + 19}}}}{{13.4}}$

$0.075 \times {10^{ - 19}}$

$P = 7.5 \times {10^{21}}$

26. Consider an electron in front of a metallic surface at a distance d (treated as an infinite plane surface). Assume the force of

attraction by the plate is given as $d = 0.1nm$

Ans: According to the question, $F = \dfrac{1}{4}.\dfrac{{{q^2}}}{{4\pi {\varepsilon _0}{d^2}}}$

Assuming that at any instant electron is at distance x from the metal

surface. Attractional force between metal surface and electron is F.

\[F=\frac{1}{4} \times \frac{q^2}{4\pi\varepsilon _0 x^2}\]

Work done by external in taking

the electron from distance d to infinity is 

$W.D. = \int\limits_d^\infty  {F.dx} $

$ \Rightarrow W.D. = \int\limits_d^\infty  {\dfrac{1}{4} \times \dfrac{{{q^2}}}{{4\pi {\varepsilon _0}{x^2}}}dx} $

\[\Rightarrow W.D. = \frac{1}{4}\times \frac{q^2}{4\pi \varepsilon _0}\int\limits_d^\infty x^{-2}dx\]

\[ \Rightarrow W.D. = \dfrac{1}{4} \times \dfrac{{{q^2}}}{{4\pi {\varepsilon _0}}}\left[ { - \dfrac{1}{x}} \right]_d^\infty \]

\[ \Rightarrow W.D. = \dfrac{1}{4} \times \dfrac{{{q^2}}}{{4\pi {\varepsilon _0}}}\left[ { - \dfrac{1}{\infty } + \dfrac{1}{d}} \right]\]

\[ \Rightarrow W.D. = \dfrac{1}{4} \times \dfrac{{{q^2}}}{{4\pi {\varepsilon _0}}}\left[ { - \dfrac{1}{\infty } + \dfrac{1}{d}} \right]\]

\[ \Rightarrow W.D. = \dfrac{{k{q^2}}}{{4d}}\]

Where $d = 0.1nm = {10^{ - 10}}m$

Work done here is positive

So,  \[W.D.= \frac{9 \times 10^9 \times \left(1.6 \times 10^{-19}\right)^2}{4 \times 10^{-10}}J\]

\[ \Rightarrow W.D. = 5.76 \times {10^{ - 19}}J\]

Converting to eV, we get,

\[ \Rightarrow W.D. = \dfrac{{5.76 \times {{10}^{ - 19}}}}{{1.6 \times {{10}^{ - 19}}}}J\]

\[ \Rightarrow W.D. = \dfrac{{5.76}}{{1.6}}eV\]

\[ \Rightarrow W.D. = 3.6\,eV\]

27. A student performs an experiment on the photoelectric effect, using two materials \[{{A}}\]and\[{{B}}\]. A plot of \[{{\text{V}}_{_{{{stop}}}}}{\text{ vs}}\;{\text{v}}\]is given in Fig. 11.2. 

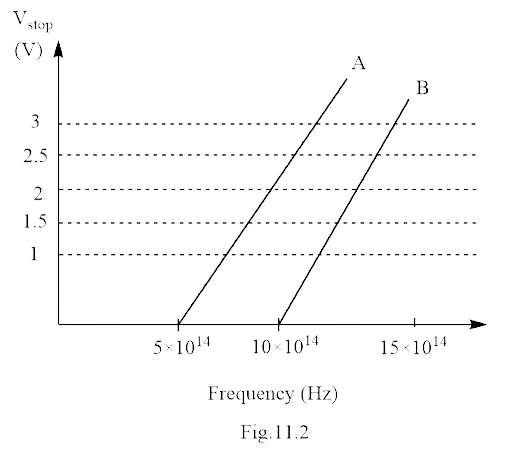
(i) Which material \[{{A}}\] or \[{{B}}\] has a higher work function? 

(ii) Given the electric charge of an electron\[ = {\text{ }}{{1}}.{{6}}{\text{ }} \times {\text{ }}{{1}}{{{0}}^{--{{19}}}}{\text{ }}{{C}}\], find the value of \[{{h}}\]obtained from the experiment for both \[{{A}}\]and \[{{B}}\]. Comment on whether it is consistent with Einstein’s theory:

Ans:  (i) As we know

${\phi _ \circ } = h{v_ \circ }$

Where ${v_ \circ } = $ Threshold frequency 

$h = $ Planck’s constant 

For metal \[A{\text{ }}{v_{ \circ A}} = {\text{ }}5 \times {10^4}{\text{ }}Hz\]

For metal \[B{\text{ }}{v_{ \circ B}} = 10 \times {10^4}{\text{ }}Hz\]

$\dfrac{{{\phi _{ \circ A}}}}{{{\phi _{ \circ B}}}} = \dfrac{{h{v_{ \circ A}}}}{{h{v_{ \circ B}}}}$

$ = \dfrac{{5 \times {{10}^{14}}}}{{10 \times {{10}^{14}}}}$

$\therefore {\phi _{ \circ B}} = 2{\phi _{ \circ A}}$

Thus, the work function of material\[\;B\] is twice of material\[A\]. 

(ii) By the differentiation of potential 

$V = \dfrac{W}{Q}$

If \[W = E\]and \[Q = e\](charge on an electron) 

Then,

$V = \dfrac{E}{e}$

Or\[\;E = eV\] 

\[hv{\text{ }} = {\text{ }}eV{\text{ }}\left( {\because {\text{ }}E = {\text{ }}hv} \right)\]

Differentiating both sides, we get 

\[h.dv = {\text{ }}edV\]

$h = e \cdot \dfrac{{dV}}{{dv}}$

For metal A, 

$h = \dfrac{{1.6 \times {{10}^{ - 19}}\left[ {2 - 0} \right]}}{{\left( {10 - 5} \right) \times {{10}^{14}}}}$

$ = \dfrac{{3.2}}{5} \times {10^{ - 19 + 14}}$

\[ = 0.64 \times {10^{ - 33}}JS\]

\[ = {\text{ }}6.4 \times {10^{ - 33}}{\text{ }}JS\]

\[h = 6 \times {10^{ - 34}}{\text{ }}JS{\text{ }} \ldots  \ldots  \ldots \left( I \right)\]

For metal B, 

$h = \dfrac{{e \times \left( {2.5 - 0} \right)}}{{\left( {10 - 5} \right) \times {{10}^{14}}}}$

$ = \dfrac{{1.6 \times {{10}^{ - 19}} \times 2.5 \times {{10}^{ - 14}}}}{5}$

$ = \dfrac{{4.00}}{5} \times {10^{ - 33}}$

$ = 0.8 \times {10^{ - 33}}$

\[h{\text{ }} = 8 \times {10^{ - 34{\text{ }}}}JS{\text{ }} \ldots .{\text{ }}\left( {II} \right)\]

The Planck’s constant \[\left( h \right)\]’s value for both experimental graphs are not equal, so the experiment is not consistent with Einstein’s theory. 

But because of experimental limitations, values are very close to\[6.6 \times {10^{ - 34}}{\text{ }}JS\], so can be considered consistent with Einstein theory. 

28. A particle \[{{A}}\]with a mass \[{{mA}}\]is moving with a velocity\[\;{{v}}\] and hits a particle\[\;{{B}}\] (mass\[{{mB}}\]) at rest (one dimensional motion). Find the change in the de-Broglie wavelength of the particle\[{{A}}\]. Treat the collision as elastic.

Ans:  Because the collision is elastic, the law of conservation of momentum and kinetic energy are followed.

${m_A}v + {m_B}\left( 0 \right) = {m_A}{v_1} + {m_B}{v_2}$

${m_A}\left( {v - {v_1}} \right) = {m_B}{v_2}.....\left( I \right)$

And $\dfrac{1}{2}{m_A}{v^2} + \dfrac{1}{2}{m_B}{\left( 0 \right)^2} = \dfrac{1}{2}{m_A}v_1^2 + \dfrac{1}{2}{m_B}v_2^2$

${m_A}\left( {{v^2} - v_1^2} \right) = {m_B}v_2^2$

${m_A}\left( {v - v_1^{}} \right)\left( {v + v_1^{}} \right) = {m_B}v_2^2.....(II)$

On dividing (II) by(I) we get,

$v + {v_1} = {v_2}......(III)$

$v = {v_2} - {v_1}$

Putting (III) in (I)

${m_A}v - {m_A}{v_1} = {m_B}\left( {v + {v_1}} \right)$

${m_A}v - {m_A}{v_1} = {m_B}v + {m_B}{v_1}$

${m_A}v - {m_B}v = {m_A}{v_1} + {m_B}{v_1}$

$\left( {{m_A} - {m_B}} \right)v = \left( {{m_A} + {m_B}} \right){v_1}$

${v_1} = \dfrac{{\left( {{m_A} - {m_B}} \right)}}{{\left( {{m_A} + {m_B}} \right)}}v$

From (II),

${v_2} = v + \dfrac{{\left( {{m_A} - {m_B}} \right)}}{{\left( {{m_A} + {m_B}} \right)}}v$

$ = v\left[ {1 + \dfrac{{\left( {{m_A} - {m_B}} \right)}}{{\left( {{m_A} + {m_B}} \right)}}} \right]$

$ = v\left[ {\dfrac{{\left( {{m_A} + {m_B} + {m_A} - {m_B}} \right)}}{{\left( {{m_A} + {m_B}} \right)}}} \right]$

$ = \dfrac{{2{m_A}v}}{{\left( {{m_A} + {m_B}} \right)}}$

${\lambda _{A\;initial}} = \dfrac{h}{{{m_A}v}}$

${\lambda _{A\;final}} = \dfrac{h}{{{m_A}v}}$

${\lambda _{A\;final}} = \dfrac{{h\left( {{m_A} + {m_B}} \right)}}{{{m_A}\left( {{m_A} - {m_B}} \right)v}}$

$\Delta \lambda  = {\lambda _{A\;final}} - {\lambda _{A\;initial}}$

$ = \dfrac{h}{{{m_A}v}}\left[ {\dfrac{{\left( {{m_A} + {m_B}} \right)}}{{\left( {{m_A} - {m_B}} \right)}} - 1} \right]$

$ = \dfrac{h}{{{m_A}v}}\left[ {\dfrac{{\left( {{m_A} + {m_B}} \right) - \left( {{m_A} - {m_B}} \right)}}{{\left( {{m_A} - {m_B}} \right)}}} \right]$

Thus, the change in the de-Broglie wavelength $\Delta \lambda  = \dfrac{{2{m_B}h}}{{{m_A}\left( {{m_A} - {m_B}} \right)v}}$

29. Consider a \[{{20}}{\text{ }}{{W}}\]bulb emitting light of wavelength \[{{5000}}\mathop {\rm A}\limits^ \circ  \] and shining on a metal surface kept at a distance\[{{2m}}\]. Assume that the metal surface has work function of \[{{2}}{\text{ }}{{eV}}\]and that each atom on the metal surface can be treated as a circular disk of radius\[{{1}}.{{5}}\mathop {\rm A}\limits^ \circ  \].

(i) Estimate no. of photons emitted by the bulb per second. [Assume no other losses] 

(ii) Will there be photoelectric emission? 

(iii) How much time would be required by the atomic disk to receive energy equal to work function (\[{{2}}{\text{ }}{{eV}}\])? 

(iv) How many photons would an atomic disk receive within the time duration calculated in (iii) above? 

(v) Can you explain how the photoelectric effect was observed instantaneously?

Ans:  Given, $P = 20\;W$, $\lambda  = 5000\;\mathop {\rm A}\limits^ \circ   = 5000 \times {10^{ - 10}}\;m$, $r = 1.5\;\mathop {\rm A}\limits^ \circ   = 1.5 \times {10^{ - 10}}\;m$(atomic radius) and $\phi  = 2\;eV$

Assuming the number of photons emitted by bulb per second is ${n_1}$ then Power $P$ is 

$P = {n_1}hv$

Or $P = {n_1}\dfrac{c}{\lambda }$

$\therefore {n_1} = \dfrac{{P\lambda }}{{hc}}$

$ = \dfrac{{20 \times 5000 \times {{10}^{ - 10}}}}{{6.62 \times {{10}^{ - 34}} \times 3 \times {{10}^8}}}$

${n_1} = \dfrac{{100000 \times {{10}^{ - 10 - 8 + 34}}}}{{19.86}} \approx \dfrac{{100000}}{{20}} \times {10^{ - 18 + 34}}$

${n_1} = 5 \times {10^{16 + 3}}$

$ = 5 \times {10^{19}}$(no. of photons per second)

Number of photons effused by bulb per second

${n_1} = 5 \times {10^{19}}$

(ii) incident photon’s energy

$E = hv$

$ = \dfrac{{hc}}{\lambda }$

$ = \dfrac{{6.62 \times {{10}^{ - 34}} \times 3 \times {{10}^8}}}{{5000 \times {{10}^{ - 10}}}}J$

$ = \dfrac{{19.86 \times {{10}^{ - 34 + 10 + 8}}}}{{5000 \times 1.6 \times {{10}^{ - 19}}}}eV$

$ = 2.48\,eV$

Energy of photon $ = hv$

$ = \dfrac{{hc}}{\lambda }$

$ = \dfrac{{\left( {6.62 \times {{10}^{ - 34}}} \right)\left( {3 \times {{10}^8}} \right)}}{{5000 \times {{10}^{ - 10}}}}J$

$ \Rightarrow \dfrac{{6.62 \times 3 \times {{10}^{ - 24 + 8}}}}{{5000 \times 1.6 \times {{10}^{ - 19}}}}eV = \dfrac{{19.86 \times {{10}^{ - 16 + 19}}}}{{8000}}$

$Energy\;of\;photon = \dfrac{{20 \times {{10}^3}}}{{8 \times {{10}^3}}}$

$ = \dfrac{5}{2}eV$

$ = 2.5eV$

The photoelectric emission happened because the energy of an incident photon is comparably more than $2\;eV$i.e., metal surface’s work function.

(iii) Assuming $\Delta T$time depleted in getting the energy \[\phi \] (work function of metal) energy sustained by atomic disk in

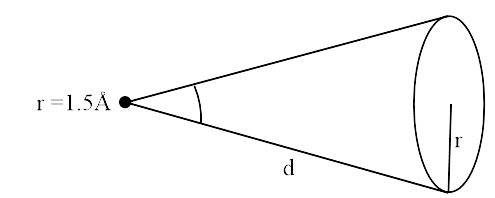
At time $\Delta t$,

$E = P \times A \cdot \Delta t$

Energy transmitted by bulb in full solid angle $4\pi {d^2}$to atoms $ = 4\pi {d^2}\phi $

$\therefore p \times \pi {r^2}\Delta t = 4\pi {d^2}\phi $

$\Delta t = \dfrac{{4{d^2}\phi }}{{{{\Pr }^2}}}\dfrac{{4 \times 2 \times 2 \times 2 \times 1.6 \times {{10}^{ - 19}}}}{{20 \times 1.5 \times 1.5 \times {{10}^{ - 10}} \times {{10}^{ - 10}}}}\sec $

$\Delta t = \dfrac{{12.8 \times {{10}^{ - 19 + 20}}}}{{5 \times 2.25}}$

$ = \dfrac{{128}}{{12.25}}$

$ = 11.4\;\sec $

(iv) Number of photons acquired by one atomic disk in time $\Delta t$

$N = \dfrac{{{n_1}{r^2}\Delta t}}{{4\pi {d^2}}}$

$ = \dfrac{{{n_1}{r^2}\Delta t}}{{4{d^2}}}$

$ = \dfrac{{5 \times {{10}^{19}} \times 1.5 \times 1.5 \times {{10}^{ - 20}} \times 11.4}}{{4 \times 2 \times 2}}$[${n_1}$from part (i) from part (iii)]

$N = \dfrac{{12.25 \times 11.4 \times {{10}^{ - 1}}}}{{8 \times 2 \times 2}} \approx 0.80 \cong 1\;photon\,per\,atom$

$N = 1\,photon\;per\,atom$.

(v) $11.4\;\sec $  is the time of emission of electrons. Thus, photoelectric emission is not an immediate problem. Thus, it takes about $11.4\,\sec $. There is a collision among photon and free electron and nucleus in photoelectric which lasts for very short time interval $\left( {{{10}^{ - 9}}\sec } \right)$therefore we say photoelectric emission is expeditious.