NCERT Exemplar for Class 12 - Free PDF Download (Book Solutions)

MCQ I

5.1 A toroid of n turns, mean radius R and cross-sectional radius a carries current I. It is placed on a horizontal table taken as x-y plane. Its magnetic moment ${\mathbf{m}}$

(a) is non-zero and points in the z-direction by symmetry.

(b) points along the axis of the tortoid $({\mathbf{m}} = m\dot \phi )$.

(c) is zero, otherwise there would be a field falling as $\dfrac{1}{{{r^3}}}$ at large distances outside the toroid.

(d) is pointing radially outwards.

Ans: Option (c) is correct. As there isn't a magnetic field outside of the toroid. 

Outside, the M.F. decreases very quickly because it is inversely related to the third power of the distance from the toroid's center.  

Because there is no current, there is no magnetic moment outside, according to Ampere's circuital law.

5.2 The magnetic field of Earth can be modeled by that of a point dipole placed at the center of the Earth. The dipole axis makes an angle of ${11.3^\circ }$ with the axis of Earth. In Mumbai, declination is nearly zero. Then,

(a) the declination varies between ${11.3^\circ }{\text{W}}$ to${11.3^\circ }{\text{E}}$.

(b) the least declination is ${0^\circ }$.

(c) the plane defined by the dipole axis and Earth axis passes through Greenwich.

(d) declination averaged over Earth must be always negative.

Ans: Option (a) is correct because the magnetic field of the Earth is identical to that of a hypothetical magnetic dipole positioned at the center of the Earth.

The dipole's axis is inclined${11.3^\circ}$ with respect to the earth's axis by ${11.3^\circ}$ on both the east and west sides (South pole of earth towards West and North pole towards east). 

As a result, the declination changes from East to West on both sides of ${11.3^\circ }$ throughout the whole earth's surface.

5.3 In a permanent magnet at room temperature

(a) The magnetic moment of each molecule is zero.

(b) the individual molecules have non-zero magnetic moments which are all perfectly aligned.

(c) domains are partially aligned.

(d) domains are all perfectly aligned.

Ans: Option (c) is correct because, A permanent magnet behaves like a ferromagnetic material at ambient temperature. 

When there is no magnetic field, domains in ferromagnetic substances are randomly distributed. 

As a result, the resulting magnetic moment is close to zero. 

However, when this material is put in a strong magnetic field, certain domains remain aligned in the external field even when the external magnetic field is removed.

5.4 Consider the two idealized systems: (i) a parallel plate capacitor with large plates and small separation and (ii) a long solenoid of length $L \gg R$, radius of cross-section. In (i) ${\mathbf{E}}$ is ideally treated as a constant between plates and zero outside. In (ii) magnetic field is constant inside the solenoid and zero outside. These idealized assumptions, however, contradict fundamental laws as below:

(a) case (i) contradicts Gauss's law for electrostatic fields.

(b) case (ii) contradicts Gauss's law for magnetic fields.

(c) case (i) agrees with $\oint {\mathbf{E}} .{\text{d}}{\mathbf{l}} = 0$.

(d) case (ii) contradicts $\oint {\mathbf{H}} .{\text{d}}{\mathbf{l}} = {I_{en}}$

Ans: Option (b) is correct because, According to Gauss's rule of electrostatic field $\oint_s E  \cdot ds = \dfrac{q}{{{\varepsilon _0}}}$ As the electric field lines do not form a continuous route, it does not contradict. 

Gauss's magnetic field law states that $\oint_S B  \cdot ds = 0$. 

It contradicts the magnetic field since there is a magnetic field inside the solenoid and no field outside the solenoid carrying current, yet magnetic field lines create closed channels.

5.5 A paramagnetic sample shows a net magnetisation of $8{\text{A}}{{\text{m}}^{ - 1}}$ when placed in an external magnetic field of $0.6{\text{T}}$ at a temperature of$4{\text{K}}$. When the same sample is placed in an external magnetic field of $0.2{\text{T}}$ at a temperature of $16{\text{K}}$, the magnetisation will be

(a) $\dfrac{{32}}{3}{\text{A}}{{\text{m}}^{ - 1}}$

(b) $\dfrac{2}{3}{\text{A}}{{\text{m}}^{ - 1}}$

(c) $6{\text{A}}{{\text{m}}^{ - 1}}$

(d)$2.4{\text{A}}{{\text{m}}^{ - 1}}$

Ans: Option (b) is correct because Curie's equation of magnetization states that the magnetization of a substance is directly proportional to magnetic field induction (B) and inversely proportional to absolute temperature t,

$I \propto \dfrac{B}{T}{\text{ or }}\dfrac{{{I_2}}}{{{I_1}}} = \dfrac{{{B_2}{T_1}}}{{{B_1}{T_2}}}$

${{\text{I}}_1} = 8{\text{A}}{{\text{m}}^{ - 1}}$

${{\text{B}}_1} = 0.6{\text{T}}$

${{\text{T}}_1} = 4{\text{k}}{{\text{I}}_2} = ?$

${{\text{B}}_2} = 0.2{\text{T}}$

${{\text{T}}_2} = 16{\text{k}}$

${I_2} = \dfrac{{{B_2}{T_1}}}{{{B_1}{T_2}}}$

${I_1} = \dfrac{{0.2 \times 8 \times 4}}{{0.6 \times 16}} = \dfrac{2}{3}{\text{A}}{{\text{m}}^{ - 1}}$ 

MCQ II

5.6 S is the surface of a lump of magnetic material.

(a) Lines of ${\mathbf{B}}$ are necessarily continuous across S.

(b) Some lines of B must be discontinuous across S.

(c) Lines of ${\mathbf{H}}$ are necessarily continuous across S.

(d) Lines of H cannot all be continuous across S.

Ans: Options (a) and (d) are correct, Because magnetic field lines for magnetic induction (B) create continuous lines, lines of B must be continuous throughout S. 

Also, the magnetic strength (H) to magnetize changes depending on whether the lump is within or outside. 

As a result, the line of H cannot be continuous over S.

5.7 The primary origin(s) of magnetism lies in

(a) atomic currents.

(b) Pauli exclusion principle.

(c) polar nature of molecules.

(d) intrinsic spin of electron.

Ans: Options (a) and (d) are correct, Magnetism is produced by the motion of a charge particle, and the type of magnetism is determined by the nation of motion of the charge particle. In an atom, electrons orbit and spin around the nucleus, producing electricity and, as a result of the magnetic effect of the current, magnetism in the material.

5.8 A long solenoid has \[{\mathbf{1000}}\] turns per meter and carries a current of$1{\text{A}}$. It has a soft iron core of ${\mu _r} = 1000$. The core is heated beyond the Curie temperature, ${T_c}$.

(a) The ${\mathbf{H}}$ field in the solenoid is (nearly) unchanged but the ${\mathbf{B}}$ field decreases drastically.

(b) The ${\mathbf{H}}$ and ${\mathbf{B}}$ fields in the solenoid are nearly unchanged.

(c) The magnetisation in the core reverses direction.

(d) The magnetisation in the core diminishes by a factor of about ${10^8}$.

Ans: Options (a) and (d) are correct because,

$n = 1000{\text{ turns/m }}$

${\mu _r} = 1000$ 

${\text{H}} = {\text{nI}} = 1000 \times 1 = 1000{\text{Amp}}$

It means H is static. Which shows Option (a) is absolutely correct.

${\text{B}} = {\mu _0}\mu ,nI = \left( {{\mu _0}nI} \right){\mu _r} = K{\mu _t}({\text{K}} = {\text{ constant }})$

$B \propto {\mu _r}.$ 

When a ferromagnetic substance is heated above the Curie temperature, it acts like a paramagnetic substance, according to Curie's law. 

Where,

${\left( {{{\text{X}}_{\text{m}}}} \right)_{{\text{ferro }}}} = {10^3}$

${\left( {{{\text{X}}_{\text{m}}}} \right)_{{\text{para }}}} = {10^{ - 5}}$ 

$\therefore \dfrac{{{B_2}}}{{{B_1}}} = \dfrac{{{x_2}}}{{{x_1}}} = \dfrac{{{{10}^{ - 5}}}}{{{{10}^3}}} = {10^{ - 8}}{\text{ or }}{{\text{B}}_2} = {10^{ - 8}}{{\text{B}}_1}$

As a result, magnetization increases by ${10^{ - 8}}$ times or decreases by ${10^8}$ times.

5.9 Essential difference between electrostatic shielding by a conducting shell and magnetostatic shielding is due to

(a) electrostatic field lines can end on charges and conductors have free charges.

(b) lines of ${\mathbf{B}}$ can also end but conductors cannot end them.

(c) lines of ${\mathbf{B}}$ cannot end on any material and perfect shielding is not possible.

(d) shells of high permeability materials can be used to divert lines of ${\mathbf{B}}$ from the interior region.

Ans: Options (a), (c)and (d) are correct, Because conductors have free charge particles, they may halt lines of force, providing a shielding effect. Also monopole magnetic field lines do not exist,  they cannot be halted or shielded. 

Magnetic field lines are impacted by magnetic material and can be resisted by utilizing a magnetic material with a high permeability to provide a zone with no magnetic field.

5.10 Let the magnetic field on earth be modeled by that of a point magnetic dipole at the center of earth. The angle of dip at a point on the geographical equator

(a) is always zero.

(b) can be zero at specific points.

(c) can be positive or negative.

(d) is bounded.

Ans: Options (b), (c)and (d) are correct because the dipole is positioned at an angle of ${11.3^\circ }{\text{W}}$ to ${11.3^\circ }E$ from the geographical N-S axis. 

Its south and north poles are analogous to a fictitious earth magnet. 

The south pole is in the north direction towards ${11.3^\circ}$ towards west, while the north pole is in the south direction towards ${11.3^\circ }$ towards east.

The resultant magnetic field of a dipole will be zero in its equatorial plane but not on the geographical equator, proving the answer (b). When the equatorial plane of the dipole is changed, the angle of dip changes, i.e., where the angle of dip is zero. It does not equal 0 at all sites along the geographic equator. The dip angle is zero. It does not equal 0 at all sites along the geographic equator. Where the geographical equator meets the magnetic equator, the angle of dip is zero. As a result, solution (c) is verified, and (d).

VSA

5.11 A proton has spin and magnetic moment just like an electron. Why then its effect is neglected in magnetism of materials?

Ans: The magnetic moment of a charged particle with charge e and mass m,

${M_e} = \dfrac{{eh}}{{4\pi {m_e}}}{\text{ and }}{M_p} = \dfrac{{eh}}{{4\pi {m_p}}}$

Because the charges on the proton and electron are equivalent in size,

Because the mass of a proton is \[1836\] times that of an electron, the magnetic moment of a proton is 

${M_p} = \dfrac{{{M_e}}}{{{m_p}}}{m_e} = \dfrac{{{M_e} \cdot {m_e}}}{{1836{m_e}}},{M_p} = \dfrac{1}{{1836}}{\text{ of }}{{\text{M}}_{\text{e}}}$

As the magnetic moment of a proton is \[1/1836\]times that of an electron,

it may be ignored.

5.12 A permanent magnet in the shape of a thin cylinder of length $10{\text{cm}}$ has $M = {10^6}{\text{A}}/{\text{m}}$. Calculate the magnetisation current ${I_M}$.

Ans: ${\text{M}} = {10^{ + 6}}$\[ampere/meter\], ${\text{l}} = 10{\text{cm}} = 0.10{\text{m}}$

${{\text{I}}_{\text{M}}} = $ Magnetisation current

$M = \dfrac{{{I_M}}}{I}$

Hence, ${{\text{I}}_{\text{M}}} = {\text{M}} \times {\text{l}} = {10^6} \times 0.1 = {10^5}{\text{ ampere}}{\text{. }}$

5.13 Explain quantitatively the order of magnitude difference between the diamagnetic susceptibility of ${{\text{N}}_2}\left( {5 \times {{10}^{ - 9}}} \right)$ (at STP) and ${\mathbf{Cu}}\left( {{{10}^{ - 5}}} \right)$.

Ans: ${\rho _N} = \dfrac{{28g}}{{22.4lit}} = \dfrac{{28g}}{{22400{\text{ml}}}} = \dfrac{{28}}{{22400}}gper{\text{c}}{{\text{m}}^3}$

${\rho _{cu}} = 8{\text{g}}/{\text{c}}{{\text{m}}^3}$

$\therefore \dfrac{{{\rho _N}}}{{{\rho _{Cu}}}} = \dfrac{{28}}{{22400 \times 8}} = 1.6 \times {10^{ - 4}}$

$\dfrac{{{x_X}}}{{{x_{Cu}}}} = \dfrac{{5 \times {{10}^{ - 9}}}}{{{{10}^{ - 5}}}} = 5 \times {10^{ - 4}}$

$x = \dfrac{{{\text{ Intensity of magnetisation }}(M)}}{{{\text{ Magnetising field intensity }}(H)}}$

Here,

Magnetic moment (m) 

Volume (V)

 $x = \dfrac{m}{{HV}}$ 

Let, ${m^\prime } =$mass

$V =$ Velocity

$\rho =$ density

Then,

$\dfrac{m}{\rho } = V$

$x = \dfrac{{m \times \rho }}{{H{m^\prime }}}$ 

As $x \propto \rho$

$\dfrac{{{x_U}}}{{{x_{Cu}}}} = \dfrac{{{\rho _X}}}{{{\rho _{Cu}}}} = 1.6 \times {10^{ - 4}}$

The main difference in diamagnetic susceptibility of ${{\text{N}}_2}$ gas and solid Cu is related to density differences.

5.14 From molecular view point, discuss the temperature dependence of susceptibility for diamagnetism, paramagnetism and ferromagnetism.

Ans: Because the direction of the external magnetic field H and magnetism M caused by the orbital motion of electrons in a diamagnetic material are opposed, net magnetism is zero. As a result, temperature has little effect on the susceptibility $\chi $ of diamagnetism.

Because the direction of magnetism caused by orbital motion of electrons in paramagnetism and ferromagnetism materials and the direction of the external applied field are in the same direction, net magnetism increases and is greatly impacted by temperature. 

The alignment of atomic magnetism is altered when temperature rises, resulting in a reduction in susceptibility.

5.15 A ball of superconducting material is dipped in liquid nitrogen and placed near a bar magnet. (i) In which direction will it move? (ii) What will be the direction of its magnetic moment?

Ans: Liquid nitrogen and a superconducting material are diamagnetic materials, 

And the superconducting material remains diamagnetic after being immersed in liquid nitrogen.

When an external magnetic field is applied to a superconducting material that has been dipped in liquid nitrogen, the external magnetic field repels the material, and the direction of motion is opposite to the direction of the magnet or magnetic field.

SA

5.16 Verify Gauss's law for magnetic field of a point dipole of dipole moment ${\mathbf{m}}$ at the origin for the surface which is a sphere of radius R.

Ans: Applying Gauss’s Law,

$\oint_s {\vec B}  \cdot \overrightarrow {ds}  = 0$

The magnetic moment, m of a dipole at its origin O, $\vec m = m\hat k$

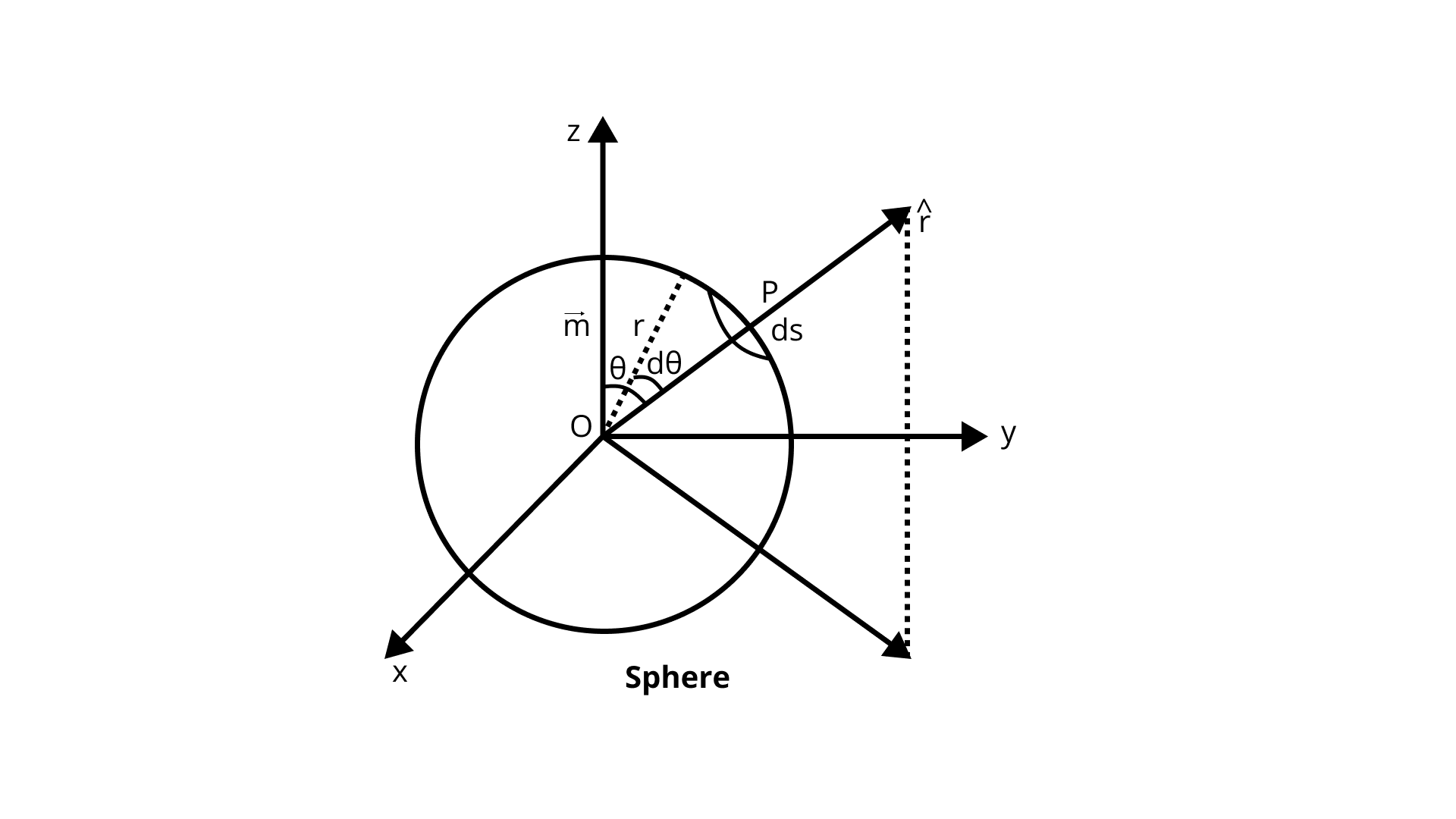
$B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2\bar m\cos \theta }}{{{r^3}}}\hat r$

$\overrightarrow {ds}  = r(r\sin \theta )d\theta \hat r = {r^2}\sin \theta  \cdot d\theta \hat r\left[ {\because d\theta  = \dfrac{{ds}}{{{r^2}}}{\text{ ords }} = {r^2}d\theta } \right]$

$\oint_s {\vec B}  \cdot \overrightarrow {ds}  = \oint {\dfrac{{{\mu _0}}}{{4\pi }}} \dfrac{{2\vec m\cos \theta }}{{{r^3}}}\hat r \cdot \left( {{r^2}\sin \theta  \cdot d\theta \hat r} \right)$

$= \dfrac{{{\mu _0}\bar m}}{{4\pi r}}\int_0^{2\pi } 2 \sin \theta \cos \theta  \cdot d\theta  = \dfrac{{{\mu _0}\bar m}}{{4\pi r}}\int_0^{2\pi r} {\sin } 2\theta  \cdot d\theta $

$= \dfrac{{{\mu _0}\bar m}}{{4\pi r}}\left[ {\dfrac{{ - \cos 2\theta }}{2}} \right]_0^{2\pi }$

$= \dfrac{{{\mu _0}}}{{4\pi r \cdot 2}}[\cos 4\pi  - ( - \cos 0)]$

$= \dfrac{{{\mu _0}}}{{4\pi r \times 2}}[ - \cos 0 + 1]$

$= \dfrac{{{\mu _0}}}{{8\pi r}}[ - 1 + 1]$ 

$\oint B  \cdot ds = 0$

It is proved.

5.17 Three identical bar magnets are riveted together at center in the same plane as shown in Fig. 5.1. This system is placed at rest in a slowly varying magnetic field. It is found that the system of magnets does not show any motion. The north-south poles of one magnet is shown in the Fig. 5.1. Determine the poles of the remaining two.

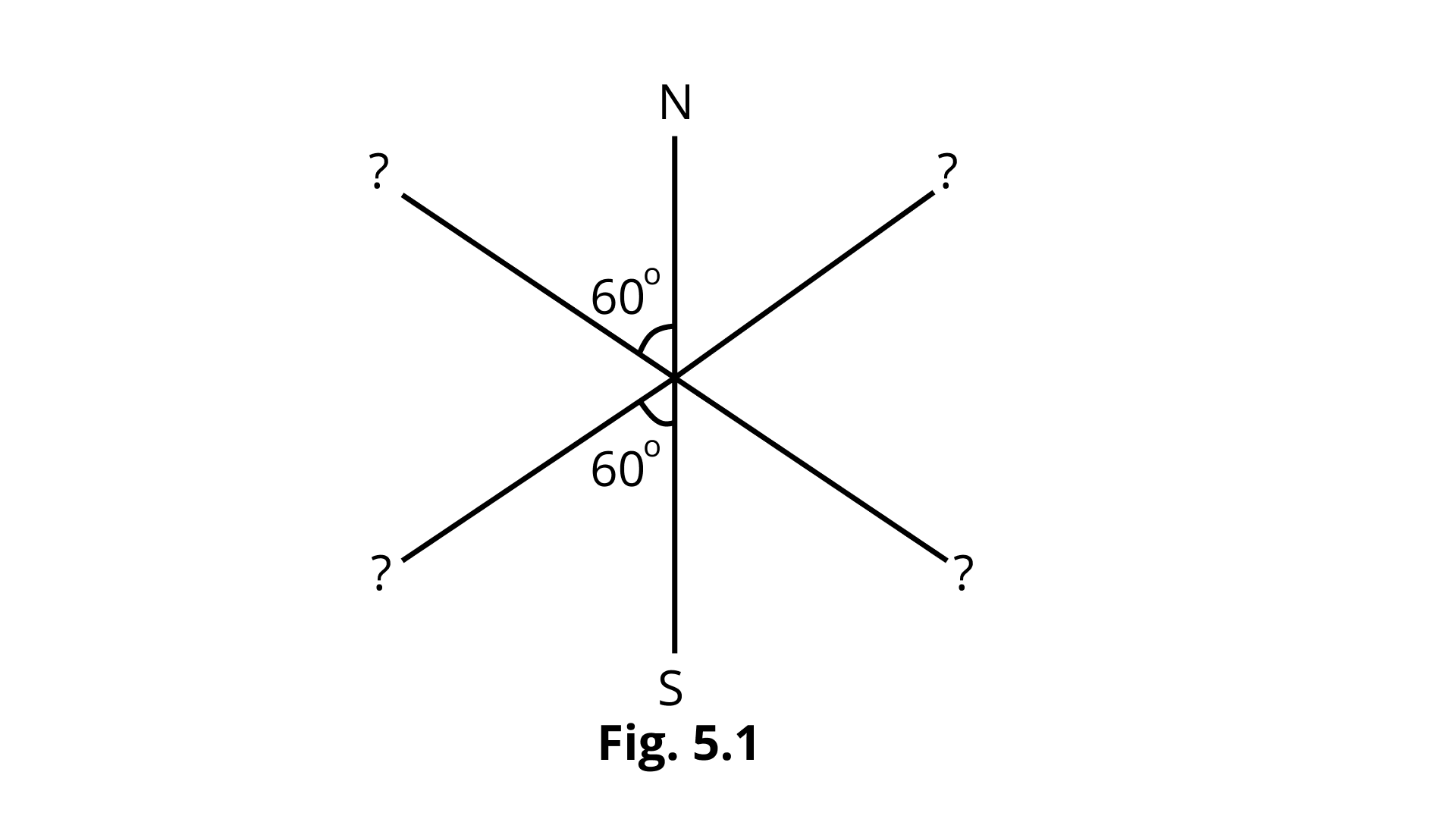
Ans: The poles must be symmetric to each other otherwise a magnet will be formed. 

It is only conceivable if the remaining two magnets' poles are arranged as shown in the illustration.

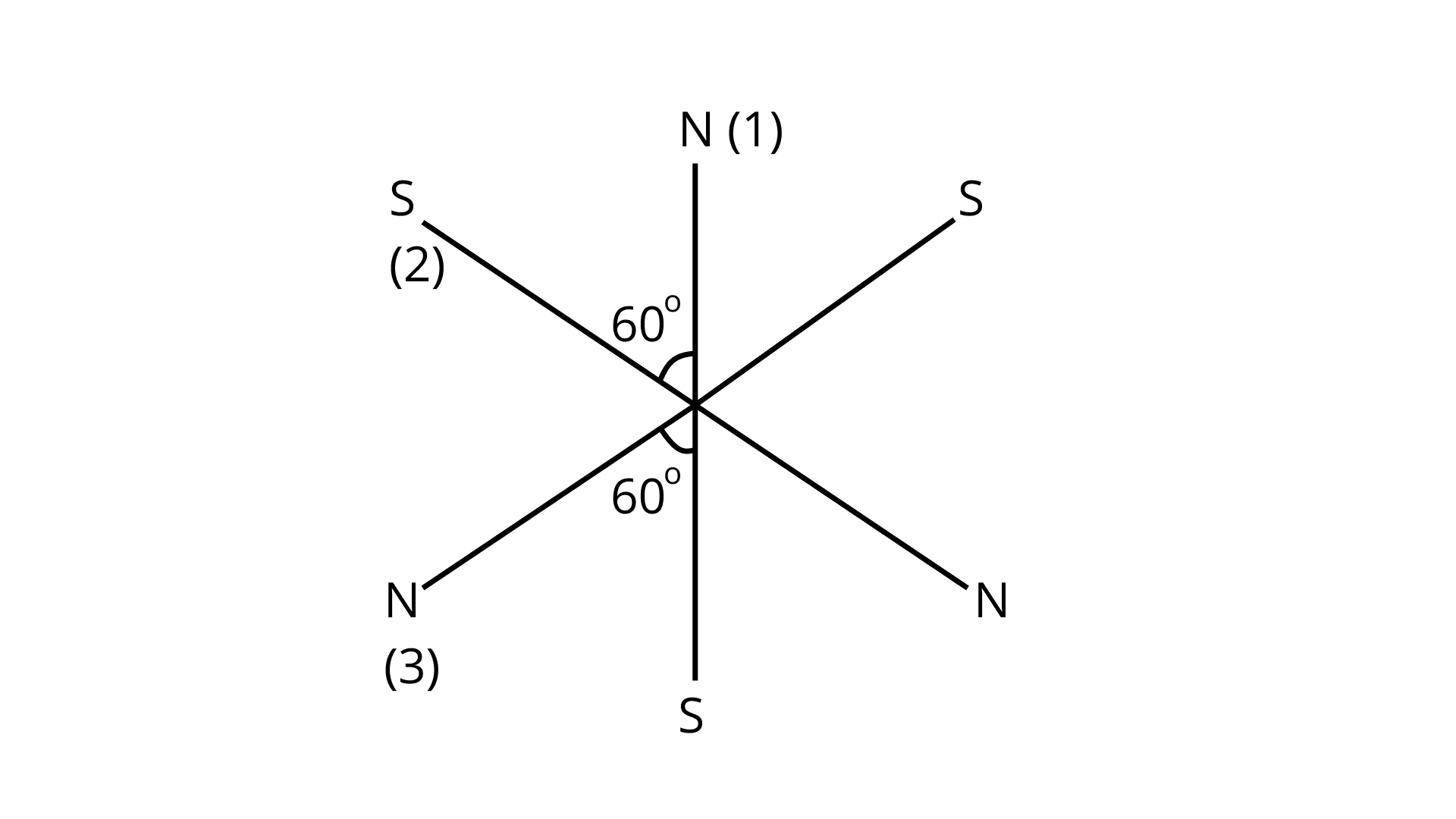
The north pole of magnet \[\left(1\right)\]is equally attracted by the south poles of magnets \[\left(2\right)\]and \[\left(3\right)\]arranged at equal distances apart. 

Similarly, one pole of any one magnet is attracted by the opposing poles of the other two magnets, hence the resultant force or moment of each magnet is zero and it will not move when put on the table.

5.18 Suppose we want to verify the analogy between electrostatic and magnetostatic by an explicit experiment. Consider the motion of (i) electric dipole ${\mathbf{p}}$ in an electrostatic field ${\mathbf{E}}$ and (ii) magnetic dipole ${\mathbf{m}}$ in a magnetic field${\mathbf{B}}$. Write down a set of conditions on${\mathbf{E}}$, ${\mathbf{B}}$, ${\mathbf{p}}$, ${\mathbf{m}}$ so that the two motions are verified to be identical. (Assume identical initial conditions.)

Ans: Assume that the angle between $\vec m{\text{ }}$ and ${\text{ }}\vec B$ is $\theta $.

In a magnetic field, the torque on a magnetic dipole B,

$\tau  = \bar m\bar B\sin \theta  \ldots  \ldots {\text{I}}$

Just like above,

${\tau ^\prime } = \vec p\vec E\sin \theta  \ldots  \ldots .II$

Because if the velocity in I and II of an electric and magnetic dipole is similar,

${\tau ^\prime } = \tau $

$\vec p\vec E\sin \theta  = \vec m\vec B\sin \theta $

$\vec p\vec E = \vec m\vec B......III$ 

$\vec E = \vec c\vec B{\text{ (relation between E and B ) }}..........{\text{IV }}$

In III, substitute the value of E from IV.

$\vec pcB = \vec m\bar B$

$\vec p = \dfrac{{\vec m}}{c}$ 

5.19 A bar magnet of magnetic moment m and moment of inertia I (about center, perpendicular to length) is cut into two equal pieces, perpendicular to length. Let T be the period of oscillations of the original magnet about an axis through the midpoint, perpendicular to length, in a magnetic field${\mathbf{B}}$. What would be the similar period ${T^2}$ for each piece?

Ans: If a magnetic moment magnet is split into n equal pieces,

The magnetic moment of all equal portions is equal to \[nm' = m\]. 

As a result, the magnetic moment of each of the two components of the magnet $ = {m^\prime } = \dfrac{m}{2}.$

$I = \dfrac{{m{l^2}}}{{12}}$

Length of new magnet, ${l^\prime } = \dfrac{l}{2}$

Actual time period, ${\text{T}} = 2\pi \sqrt {\dfrac{I}{{mB}}}$

If M is the mass of the original magnet, then mass of each of the two magnets m' is$\dfrac{M}{2}$.

$\dfrac{T}{{{T^\prime }}} = \dfrac{{2\pi \sqrt {\dfrac{I}{{mB}}} }}{{2\pi \sqrt {\dfrac{{{I^\prime }}}{{{m^\prime }B}}} }} = \sqrt {\dfrac{I}{m} \cdot \dfrac{{{m^\prime }}}{{{I^\prime }}}} {\text{ or }}\dfrac{T}{{{T^\prime }}} = \sqrt {\dfrac{m}{{{m^\prime }}} \cdot \dfrac{{{I^\prime }}}{I}}$

$\dfrac{{{I^\prime }}}{I} = \dfrac{{\dfrac{{{m^\prime }{l^{\prime 2}}}}{{\dfrac{{12}}{{m{l^2}}}}}}}{{\dfrac{{12}}{{\dfrac{m}{2}}}}} = \dfrac{{\dfrac{m}{2} \cdot {{\left( {\dfrac{1}{2}} \right)}^2}}}{{m{l^2}}}$ 

$\dfrac{{{I^\prime }}}{I} = \dfrac{{\dfrac{m}{2} \cdot \dfrac{{{l^2}}}{4}}}{{m{l^2}}} = \dfrac{1}{8}$

$\dfrac{m}{{{m^\prime }}} = \dfrac{m}{{\dfrac{m}{2}}} = \dfrac{2}{1}$

$\therefore \dfrac{T}{{{T^\prime }}} = \sqrt {\dfrac{2}{1} \times \dfrac{1}{8}}  = \sqrt {\dfrac{1}{4}} \dfrac{T}{{{T^\prime }}} = \dfrac{1}{2}{\text{ or }}$

${T^\prime } = \dfrac{T}{2}\sec $ 

5.20 Use (i) the Ampere's law for ${\mathbf{H}}$ and (ii) continuity of lines of${\mathbf{B}}$, to conclude that inside a bar magnet, (a) lines of ${\mathbf{H}}$ run from the N pole to S pole, while (b) lines of ${\mathbf{B}}$must run from the S pole to N pole.

Ans: $\int_P^Q {\vec H}  \cdot \overrightarrow {dl}  = \int_Q^P {\dfrac{{\vec B}}{{{\mu _0}}}} \overrightarrow {dl}$

Where B is the magnetic field and ${{\text{m}}_0}$is dipole moment. As angle between B and dl varies from${90^\circ }$, $0$,${90^\circ }$ from R to T, so $\cos \theta $ is greater than $1$ . So $\int_P^Q {\vec H}  \cdot \overrightarrow {dl}  = \int_Q^P {\dfrac{{\vec B}}{{{\mu _0}}}} \overrightarrow {dl}  > 0$i.e.

Positive.

As a result, the value of B must be adjusted inside the magnet from south pole to north pole.

Applying Ampere’s Law,

$\oint_{PQP} {\vec H}  \cdot \overrightarrow {dl}  = 0$

$\oint_{PQP} {\vec H}  \cdot \overrightarrow {dl}  = \int_P^Q {\vec H}  \cdot \overrightarrow {dl}  + \int_Q^P {\vec H}  \cdot \overrightarrow {dl}  = 0$

Because $\int_P^0 H  \cdot dl > 0$ is outer the magnet,

$\int_Q^pH.dl<0$ is inner the magnet, Because the angle between H and d l is greater than${90^\circ}$ within the magnet,  $cos\theta $ is negative. 

This means that the H lines must travel from north pole to south pole.

LA

5.21 Verify the Ampere's law for magnetic field of a point dipole of dipole moment ${\mathbf{m}} = m{\mathbf{k}}$. Take ${\text{C}}$ as the closed curve running clockwise along 

(i) the z-axis from \[{\mathbf{z}} = {\mathbf{a}} > {\mathbf{0}}\] to$z = R$; 

Ans: In the picture from P to Q, every point on the Z-axis that is on a dipole is in the $\hat k$ direction, 

hence every point on the Z-axis that is on an axial dipole NS is positioned at the origin.

So, $|B| = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2(\bar m)}}{{{z^3}}} = \dfrac{{{\mu _0}\bar m}}{{2\pi {z^3}}}$

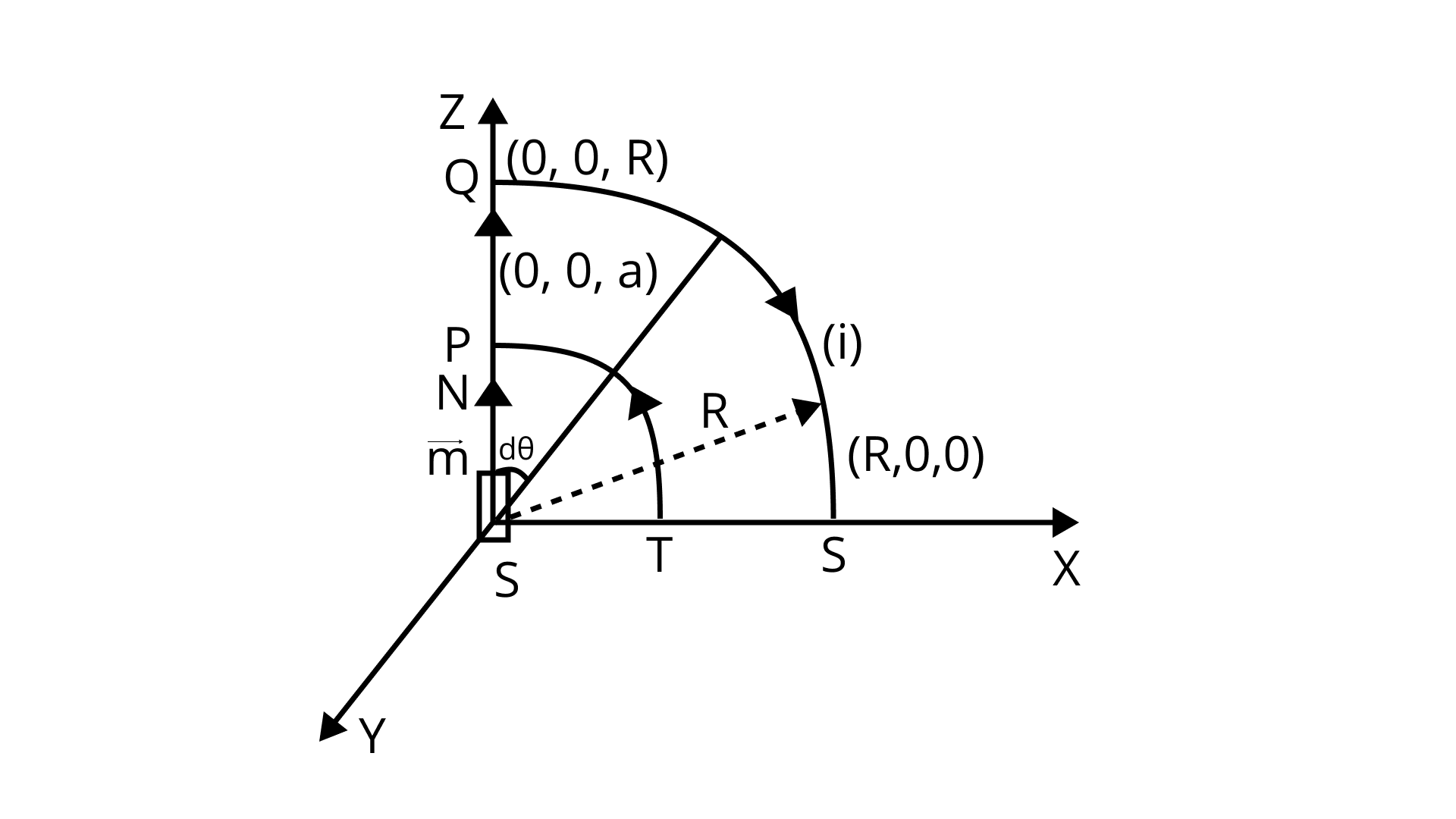
$\oint_P {\vec B}  \cdot \overrightarrow {dl}  = \int_P^Q B dl\cos {0^\circ } = \int_P^Q B dz$

$= \int_P^Q {\dfrac{{{\mu _0}\vec m}}{{2\pi {z^3}}}} dz = \dfrac{{{\mu _0}m}}{{2\pi }}\int_a^R {{z^{ - 3}}} dz$

$= \dfrac{{{\mu _0}\vec m}}{{2\pi }}\left[ {\dfrac{{{z^{ - 2}}}}{{ - 2}}} \right]_a^R = \dfrac{{{\mu _0}\vec m}}{{2\pi ( - 2)}}\left[ {\dfrac{1}{{{R^2}}} - \dfrac{1}{{{a^2}}}} \right]$

${\underline \smallint  _P}B \cdot dl = \dfrac{{{\mu _0}\vec m}}{{4\pi }}\left[ {\dfrac{1}{{{a^2}}} - \dfrac{1}{{{R^2}}}} \right]$ 

(ii) along the quarter circle of radius R and center at the origin, in the first quadrant of x-z plane; 

Ans: Ampere's law is illustrated in the image here along the quarter circle QS of radius R. 

Point A can be thought of as being on the equatorial line of a magnetic dipole of moment$\vec m\sin \theta $.

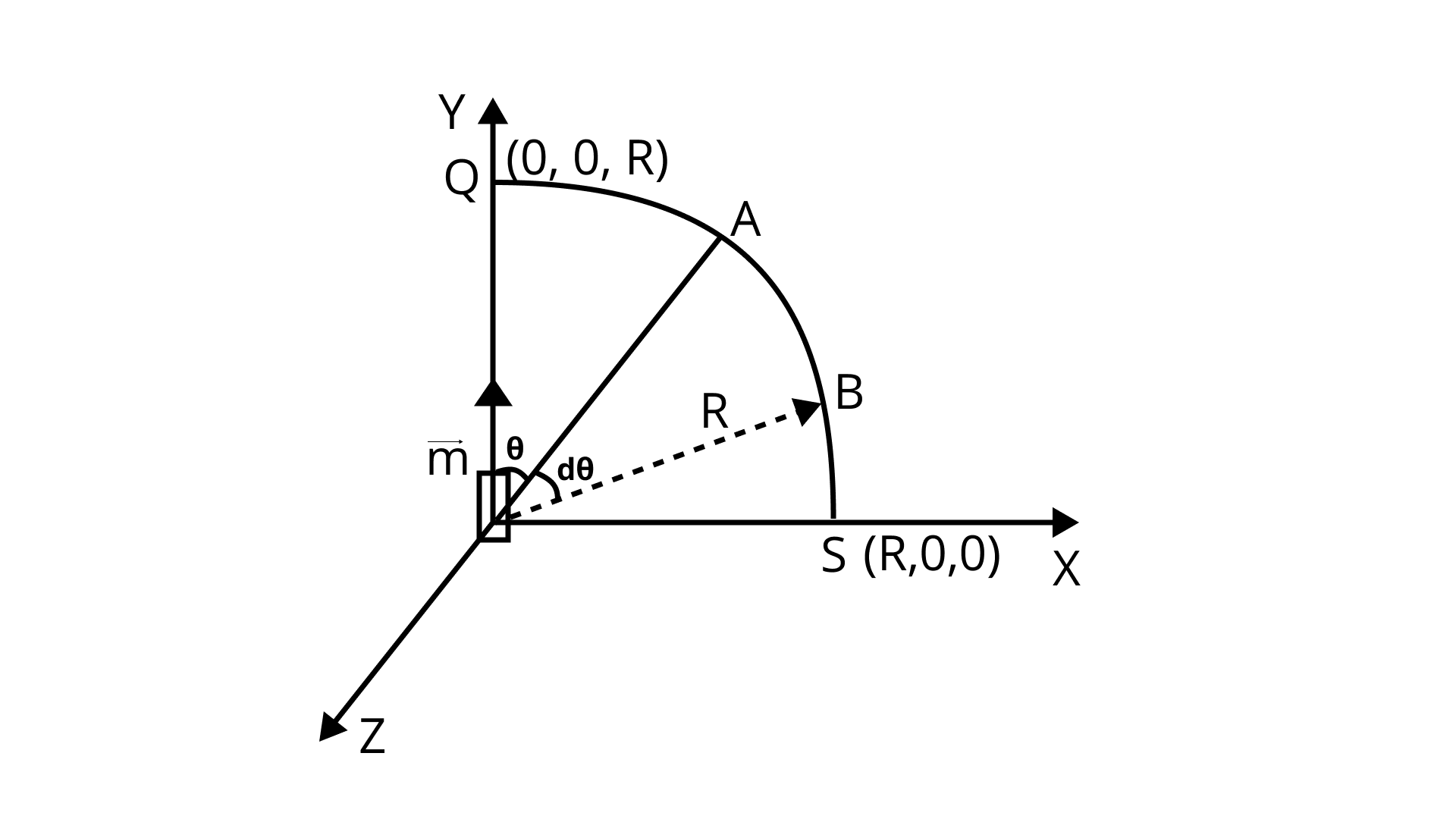
$B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{\bar m\sin \theta }}{{{R^3}}}$

$d\theta  = \dfrac{{dl}}{R} \Rightarrow dl = R \cdot d\theta $ 

Applying Ampere’s Law,

$\int B  \cdot dl = \int B  \cdot dl\cos \theta $

$\int {\vec B}  \cdot \overrightarrow {dl}  = \int_0^{\dfrac{\pi }{2}} {\dfrac{{{\mu _0}}}{{4\pi }}} \dfrac{{\vec m\sin \theta }}{{{R^3}}} \cdot Rd\theta$

$\int {\vec B} {\text{\;}} \cdot dl = \dfrac{{{\mu _0}\vec m}}{{4\pi {R^2}}}[ - \cos \theta ]_0^{\pi /2}$

$= \dfrac{{{\mu _0}\vec m}}{{4\pi {R^2}}}\left[ { - \cos {{90}^\circ } + \cos {0^\circ }} \right]$

$\int B  \cdot dl = \dfrac{{{\mu _0}\vec m}}{{4\pi {R^2}}}$ 

(iii) along the x-axis from \[{\mathbf{x}} = {\mathbf{R}}\] to\[{\mathbf{x}} = {\mathbf{a}}\], and 

Ans: 

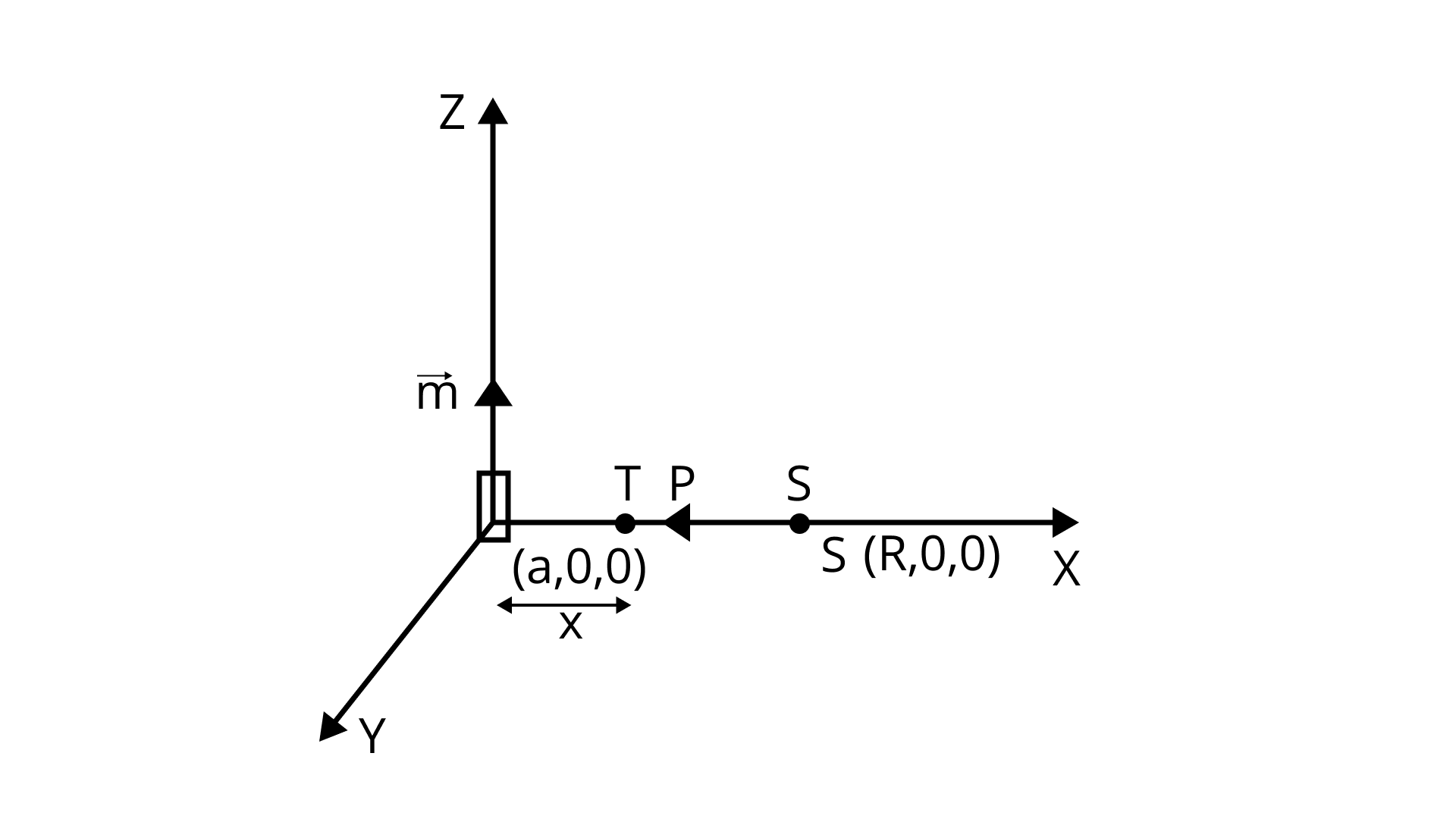
Because all locations from S to T lie on the equatorial line of the magnetic dipole N-S, magnetic field induction occurs at a point P at a distance x from the dipole.

$B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{\vec m}}{{{x^3}}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{\vec m\hat k}}{{{x^3}}}$

$\int {\vec B}  \cdot \overrightarrow {ll}  = \int_R^a {\dfrac{{ - {\mu _0}\vec m\hat k}}{{4\pi {x^3}}}}  \cdot dl\because {\text{ angle between dl and m is }}{90^\circ }{\text{ }}$

$\int {\vec B}  \cdot \overrightarrow {dl}  = \int_R^a {\dfrac{{ - {\mu _0}|\vec m|dl\cos {{90}^\circ }}}{{4\pi {x^3}}}}  = 0$ 

(iv) along the quarter circle of radius a and center at the origin in the first quadrant of x-zplane.

Ans: 

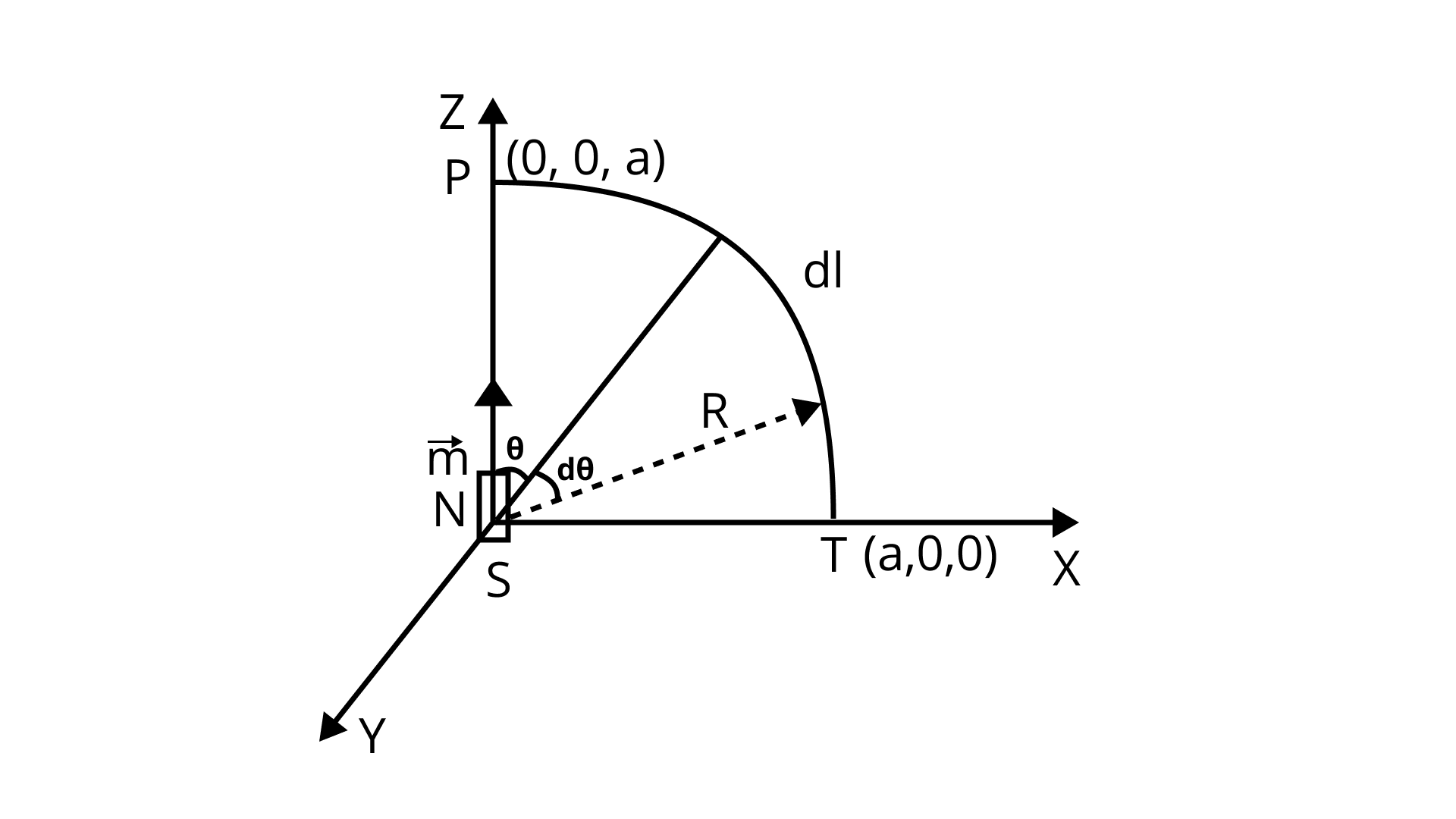
$\int B  \cdot dl = \int_{n = 2}^0 {\dfrac{{{\mu _0}}}{{4\pi }}} \dfrac{{\bar m\sin \theta }}{{{a^3}}} \cdot ad\theta $

$\int B  \cdot dl = \dfrac{{{\mu _0}\bar m}}{{4\pi {a^2}}}[ - \cos \theta ]_{\pi /2}^0$

$\theta  = {\text{ angle from axial line of dipole }}n$

$\int B  \cdot dl = \dfrac{{{\mu _0}\bar m}}{{4\pi {a^2}}}\left[ { - \cos 0 + \cos \dfrac{\pi }{2}} \right] = \dfrac{{{\mu _0}\bar m}}{{4\pi {a^2}}}( - 1 + 0) = \dfrac{{ - {\mu _0}\vec m}}{{4\pi {a^2}}}$ 

Applying Ampere’s Law,

$\oint_{PQST} B  \cdot dl = \int_P^Q {\vec B}  \cdot dl + \int_Q^s {\vec B}  \cdot dl + \int_s^T {\vec B}  \cdot dl + \int_T^P B  \cdot dl$

Using (i), (ii), (iii) values,

$\oint_{PQST} B  \cdot dl = \dfrac{{{\mu _0}\vec m}}{{4\pi }}\left( {\dfrac{1}{{{a^2}}} - \dfrac{1}{{{R^2}}}} \right) + \dfrac{{{\mu _0}\bar m}}{{4\pi {R^2}}} + 0 + \dfrac{{ - {\mu _0}\vec m}}{{4\pi {a^2}}}$

$= \dfrac{{{\mu _0}\bar m}}{{4\pi {a^2}}} - \dfrac{{{\mu _0}\bar m}}{{4\pi {R^2}}} + \dfrac{{{\mu _0}\vec m}}{{4\pi {R^2}}} - \dfrac{{{\mu _0}\bar m}}{{4\pi {a^2}}}$

$\oint_{PQRST} B  \cdot dl = 0$ 

Now, it is proved.

5.22 What are the dimensions of $\chi $, the magnetic susceptibility? Consider an H-atom. Guess an expression for $\chi $, upto a constant by constructing a quantity of dimensions of $\chi $, out of parameters of the atom: $e,m,v,R$ and ${\mu _0}$. Here, m is the electronic mass, v is electronic velocity, R is Bohr radius. Estimate the number so obtained and compare with the value of $|\chi |{10^{ - 5}}$ for many solid materials.

Ans: Because magnetization intensity (M) and magnetizing field (H) have the same unit, i.e. ampere/meter and $\chi=\dfrac{M}{H}$. As a result, susceptibility has no unit.

Using Biot=Savart’s Law,

$dB = \dfrac{{{\mu _0}}}{{4\pi }} = \dfrac{{I.dl\sin \theta }}{{{r^2}}}$

${\text{F}} = {\text{Bqv}}\sin \theta B$

$= \dfrac{F}{{qv\sin \theta }}$

$= \dfrac{{ML{T^{ - 2}}}}{{QL{T^{ - 1}}}}$

$= \left[ {M{L^0}{T^{ - 1}}{Q^{ - 1}}} \right]$

$\therefore {\mu _0} = \dfrac{{\left[ {M{T^1}{Q^{ - 1}}} \right]{L^2}}}{{Q{T^{ - 1}}L}}$

$= \left[ {ML{Q^{ - 2}}} \right]$ 

X is affected by the magnetic moment created when H is turned on. 

Through its charge e, H bonds to atomic electrons. 

The influence on m is caused by current I, which involves another e-factor.

$\chi  = \mu _0^a{e^2}{m^b}{v^c}{R^d}$

$\left[ {{{\text{M}}^0}{{\text{L}}^0}{{\text{T}}^0}{{\text{Q}}^0}} \right] = {\left[ {{\text{ML}}{{\text{Q}}^{ - 2}}} \right]^{\text{a}}}{{\text{Q}}^2}{{\text{M}}^{\text{b}}}{\left[ {{\text{L}}{{\text{T}}^{ - 1}}} \right]^{\text{c}}}{[{\text{L}}]^{\text{d}}}$

${\text{C}} = 0,{\text{a}} + {\text{b}} = 0 - 2{\text{a}} + 2 = 0{\text{a}} + {\text{c}} + {\text{d}} = 0$

$1 + {\text{b}} = 0 - 2{\text{a}} =  - 21 + 0 + {\text{d}} = 0$

${\text{b}} =  - 1{\text{a}} =  + 1{\text{d}} =  - 1$

$\chi  = \left( {{\mu _0}} \right){e^2}{{\text{m}}^{ - 1}}{v^0}{R^{ - 1}}$

$\chi  = \dfrac{{{\mu _0}{e^2}}}{{mR}}$

${\mu _0} = 4\pi  \times {10^{ - 7}}{\text{Tm}}{A^{ - 1}}{\text{e}} = 1.6 \times {10^{ - 19}}$

${\text{m}} = 9.1 \times {10^{ - 31}}{\text{kgR}} = {10^{ - 10}}{\text{m}}$

$\chi  = \dfrac{{\left( {4\pi  \times {{10}^{ - 7}}} \right)\left( {1.6 \times {{10}^{ - 19}}} \right)\left( {1.6 \times {{10}^{ - 19}}} \right)}}{{\left( {9.1 \times {{10}^{ - 31}}} \right) \times {{10}^{ - 10}}}}$

$= \dfrac{{4 \times 3.1 \times 1.6 \times 1.6}}{{9.1}} \times {10^{ - 7 - 19 - 19 + 31 + 10}}$ 

$ = \dfrac{{124 \times 256 \times {{10}^{ - 45 + 41}}}}{{9.1}} = \dfrac{{317.4}}{{91}} \times {10^{ - 4}}$

$= 3.5 \times {10^{ - 4}}\left| {{\chi ^\prime }} \right| = {10^{ - 5}}{\text{ (given)}}$

${\text{ }}\dfrac{\chi }{{\left| {{\chi ^\prime }} \right|}} = \dfrac{{3.5 \times {{10}^{ - 4}}}}{{{{10}^{ - 5}}}} = \dfrac{{3.5 \times {{10}^{ - 4}}}}{{{{10}^{ - 1}} \times {{10}^{ - 4}}}} = 35$

$\chi  = 35\left| {{\chi ^\prime }} \right|$ 

5.23 Assume the dipole model for earth's magnetic field B which is given by ${B_V} = $ vertical component of magnetic field $ = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2m\cos \theta }}{{{r^3}}}{B_H} = $ Horizontal component of magnetic field $ = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{\sin \theta m}}{{{r^3}}}\theta  = {90^\circ } - l$attitude as measured from magnetic equator. Find loci of points for which 

(i) $|{\mathbf{B}}|$is minimum; 

Ans:

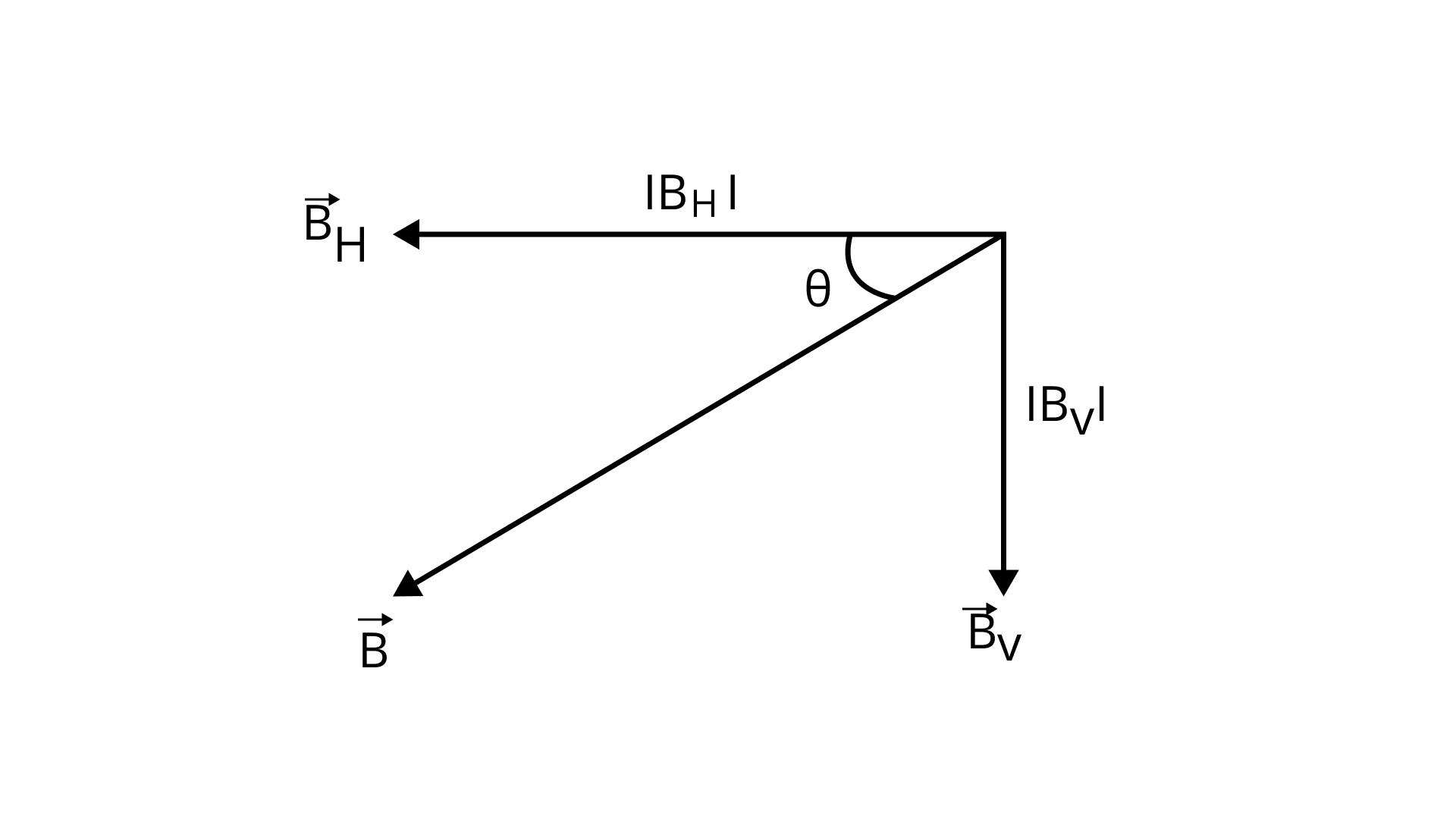
${B^2} + B_V^2 + B_H^2$

$= {\left[ {\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2m\cos \theta }}{{{r^3}}}} \right]^2} + {\left[ {\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{m\sin \theta }}{{{r^3}}}} \right]^2}$ 

According to the question, using values of ${{\text{B}}_{\text{V}}}$ and ${{\text{B}}_{\text{H}}}$.

$= {\left[ {\dfrac{{{\mu _0}}}{{4\pi }}} \right]^2}\dfrac{{{m^2}}}{{{r^6}}}\left[ {4{{\cos }^2}\theta  + {{\sin }^2}\theta } \right]{B^2}$

$= \left( {\dfrac{{{\mu _0}}}{{4\pi }}} \right) \times \dfrac{{{m^2}}}{{{r^6}}}\left[ {3{{\cos }^2}\theta  + 1} \right]B$

$= \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{m}{{{r^3}}}{\left[ {3{{\cos }^2}\theta  + 1} \right]^{12}} \ldots (i)$ 

Using equation (i), the value of B will be minimum when ${\left[ {3{{\cos }^2}\theta  + 1} \right]^{1/2}}$ is minimum which will be at$\theta  = \dfrac{\pi }{2}$. So magnetic equator lies at$\theta  = \dfrac{\pi }{2}$, i.e., from magnetic dipole axis $\theta  = \dfrac{\pi }{2}$ for magnetic equator.

(ii) dip angle is zero; and 

Ans: $\tan \delta  = \dfrac{{{B_V}}}{{{B_H}}} = \dfrac{{\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2m\cos \theta }}{{{r^3}}}}}{{\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{m\sin \theta }}{{{r^3}}}}}$

$\tan \delta  = 2\cot \theta for$

$\delta  = 0,\cot \theta  = 0,\theta  = \dfrac{\pi }{2}$ 

As a result, the angle of dip will be near the magnetic equator.

(iii) dip angle is $\pm {45^\circ }$.

Ans: $\tan \delta  = \dfrac{{{B_V}}}{{{B_H}}} = $angle of dip $\delta  =  \pm {45^\circ }$

$\dfrac{{{B_v}}}{{{B_H}}} = \tan  \pm {45^\circ }$

$\Rightarrow \dfrac{{{B_v}}}{{{B_H}}} = \tan {45^\circ }$ 

$\dfrac{{{B_V}}}{{{B_H}}} = 1$

${B_v} = {B_H}$

$\delta  =  \pm {45^\circ }$

$\tan  \pm {45^\circ } = 2\cos \theta [\because \tan \delta  = 2\cot \theta ]$

$\cot \theta  = \dfrac{1}{2}$

$\tan \theta  = 2$

$\cot \theta  = \dfrac{1}{2}$

$or\tan \theta  = 2\theta  = {\tan ^{ - 1}}2$, here angle of dip is $\delta  =  \pm {45^\circ }$

5.24 Consider the plane S formed by the dipole axis and the axis of the earth. Let P be a point on the magnetic equator and in S. Let ${\text{Q}}$ be the point of intersection of the geographical and magnetic equators. Obtain the declination and dip angles at P and Q.

Ans: Q is the place at where the geographical and magnetic meridian meet.

As a result, the angle dip at P and Q will be 0 with horizontal as the magnetic midpoint remains horizontal. 

The angle formed between the rotation axis of the Earth and the magnetic axis is ${11.3^\circ }$ and their equators are at ${90^\circ }$ with their axes.

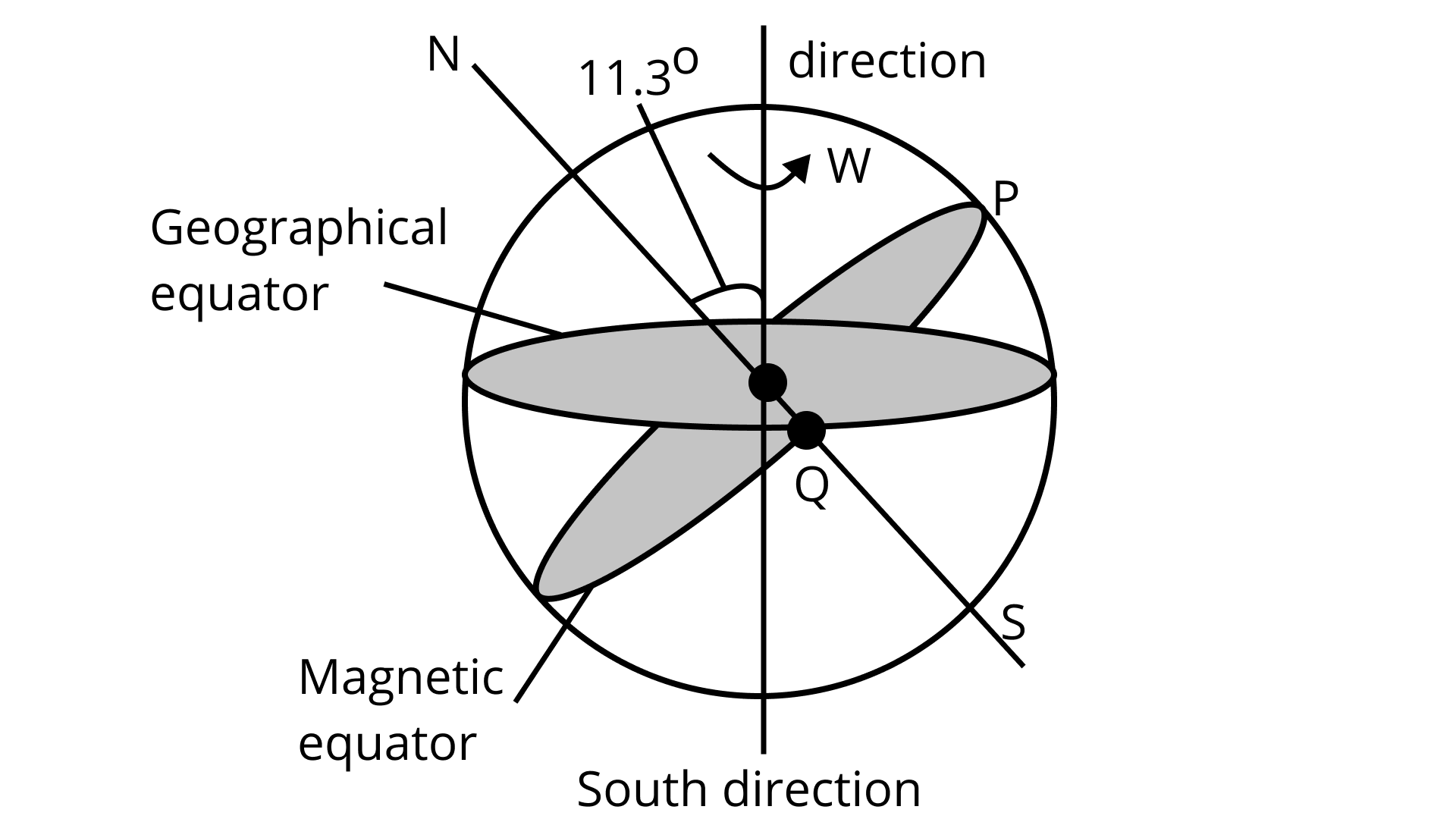
So the angle between the magnetic and geographical planes, i.e. declination, will be ${11.3^\circ }$ at both P and Q.

5.25 There are two current carrying planar coils made each from identical wires of length L. ${{\text{C}}_1}$is circular (radius R ) and ${{\text{C}}_2}$ is square (side a ). They are so constructed that they have same frequency of oscillation when they are placed in the same uniform B and carry the same current. Find a in terms of R.

Ans: Because the frequency $\omega $ for both coils are the same,

${\omega _1} = {\omega _2}$

$\dfrac{{2\pi }}{{{T_1}}} = \dfrac{{2\pi }}{T}$ 

So the time periods of the coils${C_1}$ and ${{\text{C}}_2}$are equal, so

${{\text{T}}_1} = {{\text{T}}_2}$

$2\pi \sqrt {\dfrac{{{I_1}}}{{{m_1}B}}}  = 2\pi \sqrt {\dfrac{{{I_2}}}{{{m_2}B}}}$

$\sqrt {\dfrac{{{I_1}}}{{{m_1}}}}  = \sqrt {\dfrac{{{I_2}}}{{{m_2}}}}$ 

Squaring both sides,

$\dfrac{{{I_1}}}{{{I_2}}} = \dfrac{{{m_1}}}{{{m_2}}}...(i)$

${{\text{I}}_1}$, ${{\text{I}}_2}$ are the moment of inertia of coils ${C_1}$ and ${{\text{C}}_2}$,

${I_1} = \dfrac{{m{R^2}}}{2} \cdots (ii)$

${I_2} = \dfrac{{m{a^2}}}{{12}} \cdots (iii)$ 

Because wire has similar length, then mass will also be similar.

${{\text{m}}_1} = {{\text{n}}_1}{\text{I}}{{\text{A}}_1}$

${m_1} = \dfrac{L}{{2\pi R}} \cdot I \cdot \pi {R^2}\left[ {\because L = 2\pi R{n_1}} \right]$

${m_1} = \dfrac{{LIR}}{2} \ldots (iv)$ 

Magnetic moment for a square-shaped coil

${{\text{m}}_2} = {{\text{n}}_2}{\text{I}}{{\text{A}}_2}$

${m_2} = \dfrac{{LIa}}{4}$

Putting all values in (i),

$=> \dfrac{{\dfrac{{m{R^2}}}{2}}}{{\dfrac{{m{a^2}}}{{12}}}} = \dfrac{{\dfrac{{LIR}}{2}}}{{\dfrac{{LIa}}{4}}}$

$=> \dfrac{{{R^2}}}{2} \times \dfrac{{12}}{{{a^2}}} = \dfrac{R}{2} \times \dfrac{4}{a}$

$=> \dfrac{R}{a} = \dfrac{1}{3}$

$\Rightarrow 3{\text{R}} = {\text{a}}$ 

The NCERT Exemplar for Class 12 Physics Chapter 5 - Magnetism and Matter (Book Solutions) will be a significant help in your exam preparations. Once you are done studying the chapter from the textbook, go through this PDF to know what type of questions related to the chapter can be asked in the exam. It contains a plethora of questions with their answers and explanations to make you understand the concepts of Magnetism and Matter. 

NCERT Class 12 Physics Chapter 5 - Magnetism and Matter Important Concepts 

The NCERT Class 12 Physics Chapter 5 - Magnetism and Matter holds a significant marks weightage in the CBSE board exams. That is why you should be aware of the important concepts of Magnetism and Matter. If you study these topics thoroughly, you will be able to score maximum marks in questions related to the chapter. You can go through the following list to ensure you do not miss any topic while studying: 

• The Magnetic Dipole 

• Coulomb’s Law in Magnetism 

• Magnetic Field Lines 

• Magnetic field due to a bar magnet at axial and on equatorial points

• Torque

• Potential Energy 

• Work Done 

• Current Loop

• Magnetic Dipole 

• Interaction between two magnetic dipoles

• Oscillation of a freely suspended magnet 

• The Electrostatic Analog 

• Gauss’s law of magnetism