NCERT Exemplar for Class 12 Physics Chapter-9 (Book Solutions)

Exercise

MCQ - 1

1. A  beam of light incident at an angle on a prism refracting face generally emerges from the opposite face. The angle of incidence is 5° if the prism is 5° and the prism is built of a material with a refractive index of 1.5.

(a) 7.5°

(b) 5°

(c) 15°

(d) 2.5°

Ans:  (a) 7.5°

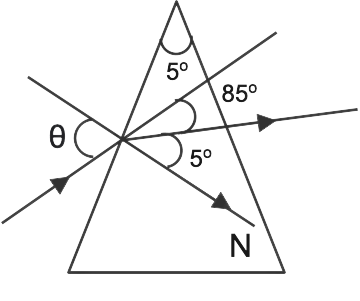
$A = 5^\circ $

μ=1.5

${i_2} = 0^\circ $

${r_2} = 0^\circ $

${r_1} + {r_2} = A$

\[{r_1} = A - {r_2}{\text{ }} = 5 - 0 = 5^\circ \]

\[\mu  = sin{\text{ }}{i_1}sin{\text{ }}{r_1}\]

\[sin{\text{ }}{i_1} = sin{\text{ }}{r_1}\]

=>sini1=μsinr1

=1.5×sin5°

=1.5×sin5°

=1.5×0.087

=1.5×0.087

=0.1305

=7.5°

2. At normal incidence, a brief pulse of white light is incident from the air onto a glass slab. The first colour to appear after passing through the slab is

(a) blue.

(b) green.

(c) violet.

(d) red.

Ans:  (d) red.

Because c=v$\lambda $ and v is constant throughout refraction that is why c $c \propto \lambda $ In glass, the velocity of red colour is at its highest as ${\lambda _R} < {\lambda _V}$

3. A particle approaches a convergent lens from the left at a consistent speed of 5 m/s and comes to a complete stop at the focus. The picture

(a) goes away from the lens at a constant 5 m/s pace.

(b) with a consistent accleration, advances away from the lens.

(c) accelerates away from the lens in a non-uniform manner.

(d) accelerates in a non-uniform manner towards the lens.

Ans:  (c):  accelerates away from the lens in a non-uniform manner.

When an item approaches a lens with uniform speed, its image accelerates non-uniformly away from the lens to infinity.

4. An aircraft passenger will

(a) never witness a rainbow.

(b) perceives the major and secondary rainbows as concentric rings.

(c) A main and secondary rainbow may be seen as concentric arcs via.

(d) is never going to witness a secondary rainbow.

Ans:  (b) perceives the major and secondary rainbows as concentric rings

In an aeroplane, a passenger may observe the primary and secondary rainbows as concentric rings.

5. You are given four light sources, each of which emits a single colour — red, blue, green, and yellow. Assume that the angle of refraction for a yellow light beam corresponding to a certain angle of incidence at the interface of two mediums is 90° If the source of yellow light is changed with that of other lights without modifying the angle of incidence, which of the following assertions is correct?

(a) The red-light beam would be completely internally reflected.

(b) As the red light is refracted via the second medium, it bends back towards normal.

(c) The blue light beam would be completely internalised.

(d) As it passes through the second medium, the green light beam will bend away from the normal.

Ans:  (c): The blue light beam would be completely internalised

 If the angle of refraction is $90^\circ $for the length, then the crucial angle is the incidence angle in this case. As a result, light rays pass through a material that is denser and rarer.

As sin $c = \dfrac{1}{\mu }$so, $c \propto \dfrac{1}{\mu } > {\mu _v} > {\mu _g} > {\mu _Y} > {\mu _R}$

As a result, the critical angle for\[{C_v} < {C_g} < {C_Y} < {C_R}\] i.e., the critical angle of blue and green light is less than that of yellow light, while the critical angle of red light is bigger.

Because the angle of refraction for yellow light is specific to a specific incidence angle. This incidence angle is crucial for yellow, so make it \[{C_Y}\]. In the same way that \[{C_Y} < {C_R}\]. As a result, it will not receive complete internal reflection and\[{C_v} < {C_g} < {C_Y} < {C_R}\].

As a result, blue and green light get 100% internal reflection. So, the right response is (c).

6. A plano-convex lens' curved surface has a radius of curvature of 20 cm. If the lens' material has a refractive index of 1.5, it will 

(a) serve as a convex lens only for objects that fall on its curved side.

(b) serve as a concave lens for items that pass through its curved side.

(c) operate as a convex lens regardless of which side the item is on.

(d) operate as a concave lens regardless of which side the item is on.

Ans:  (c) operate as a convex lens regardless of which side the item is on.

If the item is on the curved side, ${R_1}$ equals +20 cm and ${R_2}$ equals infinity ${\mu _1} = 1,{\mu _2} = 1.5$

$\dfrac{1}{f} = ({\mu _2} - {\mu _1}) = \left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$

$\dfrac{1}{f} = (1.5 - 1) = \left( {\dfrac{1}{{20}} - \dfrac{1}{\infty }} \right) = \dfrac{{0.5}}{{20}} = \dfrac{5}{{200}} = \dfrac{1}{{40}}$

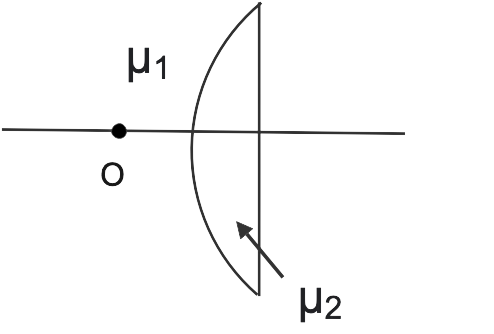
F=+ 40cm

If the item is on the curved side, ${R_1}$  equals infinity and ${R_2}$  equals -20 ${\mu _1} = 1,{\mu _2} = 1.5$

$\dfrac{1}{f} = ({\mu _2} - {\mu _1}) = \left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$

$\dfrac{1}{f} = (1.5 - 1) = \left( {\dfrac{1}{\infty } + \dfrac{1}{{20}}} \right) = \dfrac{{0.5}}{{20}} = \dfrac{5}{{200}} = \dfrac{1}{{40}}$

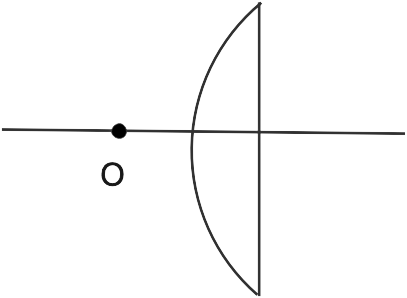
F = +40cm

As a result, regardless of which side the objects are on, the lens will always behave as a convex lens.

7. The mechanisms involved in radio wave reflection by the ionosphere are analogous to

 (a) light reflection by a planar mirror.

(b) during a mirage, entire internal reflection of light in the air.

c) light dispersion by water molecules during the production of a rainbow

(d) light scattering due to air particles.

Ans:  (b) during a mirage, entire internal reflection of light in the air.

The ionosphere is a translucent optical medium that reflects radio waves. Total internal reflection occurs when a radio wave is reflected through a clear surface, resulting in internal reflection of the radio wave

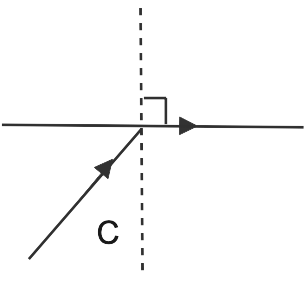
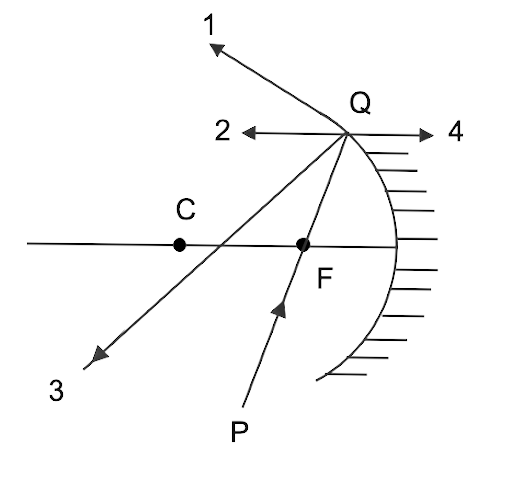
8. PQ depicts the direction of a ray of light incident on a concave mirror, while four rays labelled 1, 2, 3, and 4 depict the directions in which the ray might go after reflection. Which of the four rays appropriately depicts the reflected ray direction?

(a) 1

(b) 2

(c) 3

(d) 4

Ans:  (b) 2

Incidence Because beam PQ enters primary focus F, it must be parallel to the principal axis, i.e., 2 or 4.

Ray (4) is rejected since it cannot get behind the mirror because it is a concave mirror.

Beam 2 is therefore the reflected ray. It confirms the response (b)

We can verify it again by drawing normal QC and find the ∠r = ∠i. So ray (2) is the reflected ray.

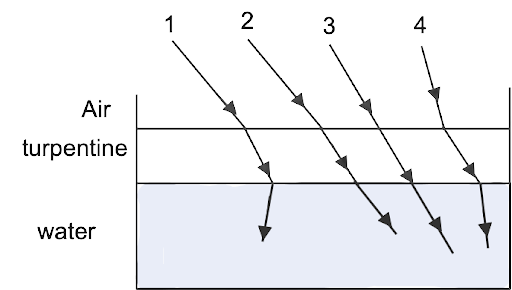
9. Turpentine has a higher optical density than water while having a lower mass density. A layer of turpentine floats on top of water in a container, as shown in Figure. Which of the four rays impacting on turpentine in Figure follows the proper path?

(a) 1

(b) 2

(c) 3

(d) 4

Ans:  (b): 2

\[{\mu _a} < {\mu _T} < {\mu _W}\]

In this case, the incident ray travels from air to turpentine to water, i.e., from rare to denser than denser to rarer, hence it bends towards normal first, then away from normal, resulting in the route illustrated (2).

10. On a straight road, an automobile is travelling at a constant speed of 60 km/h–1. Looking in the rear-view mirror, the driver notices that the automobile behind him is coming at a distance of 100 metres and at a speed of 5 kilometres per hour –1. To maintain track of the automobile in front, the driver alternates between looking in the back and side mirrors of his car every 2 seconds until the other car overtakes. Which of the following statements is/are accurate if the two automobiles maintain their speeds?

(a) The automobile in the back is travelling at 65 km/h.

(b) In the side mirror, the automobile in the rear appears to be approaching the driver of the leading car at a speed of 5 km/h.

(c) As the distance between the cars reduces, the approaching car's speed seems to decrease in the rear-view mirror.

(d) As the distance between the automobiles shrinks, the approaching car's speed appears to rise in the side mirror.

Ans:  (d): As a result, as the back automobile approaches, it seems to be at rest at first since the image is generated at focus. As the automobile gets closer, the speed appears to increase, hence the solution is (d).

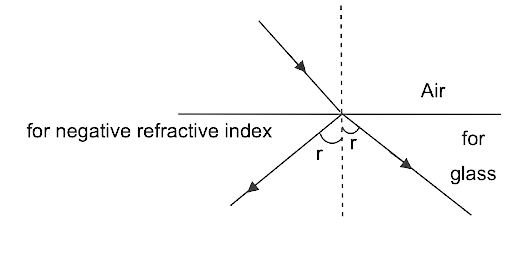
11. Certain materials with a negative refractive index have been created in laboratories (Figure). A beam incident from the air (medium 1) into such a medium (medium 2) must take the route prescribed by

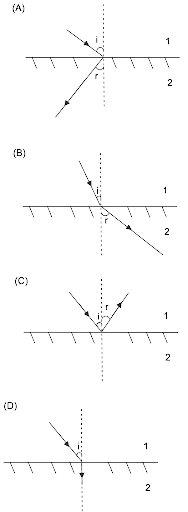
Ans:  (a)

The incoming beam from air (medium 1) refracts or bends differently or opposite and symmetrically to that of the positive refractive index medium in negative refractive index materials. So, the solution is (a).

MCQ -2 

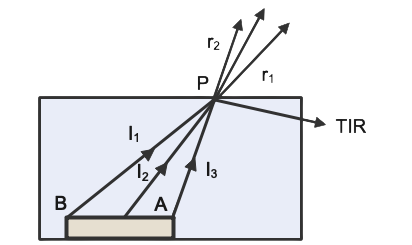
12. Consider a long item submerged in water within a flat trough. When viewed from close to the trough's edge, the item seems deformed because

(a) the apparent depth of the points close to the edge is closer to the water's surface than the ones farther away.

(b) the angle occupied by the item's picture in the eye is less than the actual angle occupied by the object in the air.

(c) Because of 100% internal reflection, some of the object's points far away from the edge may not be seen.

(d) In a trough, water acts as a lens, magnifying the item.

Ans:  (a), (b) and (c)

We know that the shift (h) of an object immersed in liquid from the object is proportional to the actual distance of the object from the liquid's surface.

$h = t\left( {1 - \dfrac{1}{\mu }} \right)$

t=the object's true depth or distance from the liquid's refractive index surface. 

When seen from one edge of the trough, the relative disparities in depth (distance) in water between the two ends of the item are greater than when viewed from the top or away from the edge. The choice is verified by the following calculation, which shows that the distortion of the closer end is lower than the distortion of the further end (a).

The angle occupied by an item under water is greater than its image, and as the image changes upward, choice (b).

Rays from the object to the observer move from a denser to a rarer medium, and the angle of incidence for rays from the object's further end B is greater than the angle of incidence for rays from the object's close end A. The incidence angles for rays coming from end 3 may be greater than the critical angle, causing total internal reflection and preventing the rays from reaching the observer.

13. The refractive index of a rectangular block of glass ABCD is 1.6. A pin is positioned in the middle of the AB figure's face. When seen from the AD side, the pin should-

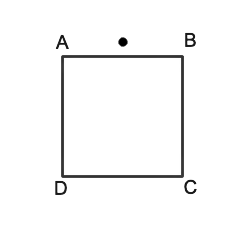
(a) appear to be in close proximity to A.

(b) appear to be in the vicinity of D.

(c) seem to be located at the heart of AD.

(d) go unnoticed at all.

Ans:  (a) appear to be in close proximity to A.

         (b) appear to be in the vicinity of D.

$\sin C = \dfrac{1}{\mu } = \dfrac{1}{{1.6}} = 38.7^\circ $

On the mid-point of face AB, there is a point P. The angle of incidence will be less than critical angle when seen via face AD at point A. \[{i_c} = 38.7^\circ \]. As a result, the image of P will appear at P', and the picture may be viewed at P'. P' is closer to both A and D than P, which validates option (a) (b).

Angle of incidence when observed at point D via face AD \[\;{i_2}{\text{ }} > {\text{ }}{i_c}\]. As a result, there is entire internal reflection and the item cannot be perceived. Option (d) is not confirmed since the item may be seen when viewed close to A.

14. A dark band known as Alexandar's dark band exists between the major and secondary rainbows. This is due to the fact that (a) light diffused into this region interferes in a negative way.

(b) There is no dispersed light in this area.

(c) In this area, light is absorbed.

(d) The dispersed rays make an angle at the eye with regard to the incident light of the sun that is between about 42° and 50°.

Ans:  (d) The dispersed rays make an angle at the eye with regard to the incident light of the sun that is between about 42° and 50°

Between the major and secondary rainbows is Alexandar's black band. The light diffused into this area interferes destructively, causing this to develop. Because the primary and secondary rainbows are at right angles to one other (41° to 42°) and (51° to 54°) The dispersed rays with regard to the incident ray of the sun lie between roughly and at the observer's eye with respect to incident light ray 42° to 50°

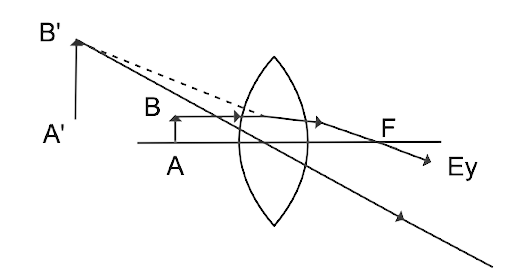
15. Because the item to be examined may be brought closer to the eye than the typical near point, a magnifying glass is needed. As a result

(a) the item near the eye can subtend a bigger angle and so be perceived in more detail 

b) the emergence of a simulated erect image

c) widening of the area of view

(d) At the near point, infinite magnification.

Ans (a) and (b) are the correct answers.

The object is put inside the focal length of a magnifying glass, and the image generated is enlarged and erect. Because the image (A'B') is enlarged, it has a greater angle at the eye than object (AB), allowing it to be seen more clearly.

A magnifying glass is used, as the object to be viewed can be brought closer to the eye than the normal near point.

16.  An astronomical refractive telescope features a 20m focal length objective and a 2cm focal length eyepiece.

(a) The telescope tube is 20.02 metres long.

(b) A magnification of 1000 is used.

(c) The resulting picture is reversed.

(d) A bigger aperture objective will boost the image's brightness while reducing chromatic aberration.

Ans:  (a), (b) and (c)

: The length of the telescope

\[L{\text{ }} = {\text{ }}{f_o}{\text{ }} + {\text{ }}{f_e}{\text{ }} = {\text{ }}20{\text{ }} + {\text{ }}00.02{\text{ }} = {\text{ }}20.02{\text{ }}m\]

\[{\text{m }} = {\text{ }}\dfrac{{{f_o}}}{{{f_e}}}{\text{ }} = {\text{ }}\dfrac{{20.02{\text{ }}m}}{{0.02m}} = \dfrac{{2000}}{2} = 1000\]

Inverted, virtual, and smaller than the object, the final image formed in a telescope (Refracting) is inverted, virtual, and smaller than the object.

VSA

17. Will the focal length of a lens for red light be more, same or less than that for blue light?

Ans:  As we know that \[{\mu _v} > {\mu _r}\]

As a result, 1/f will be big for blue light and tiny for red light. As a result, for red-coloured light, f will be bigger.

18. The typical person near eyesight is 25cm. What should the microscope's power be to examine an item with an angular magnification of 10?

Ans:  D=25 cm to see the final image with clear eyesight

u=-f and v=-25 for eyes lens

$m = \dfrac{v}{u}$

$10 = \dfrac{{ - 25}}{{ - f}}$

$f =  + \dfrac{{25}}{{10}}$ =+2.25 cm =0.025 m

$p = \dfrac{1}{f} = \dfrac{1}{{0.025}} = \dfrac{{1000}}{{25}} = 40D$

19. The image of a point object is formed on the axis of an unsymmetrical double convex thin lens. When the lens is inverted, does the image position change?

Ans:  Altering the u of f or changing the position of the picture in a convex lens affects the image's position. u is constant in this case. and$\dfrac{1}{f} = (\mu  - 1)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$ . Because and the curvature of the lens are the same in this case, f is constant. As a result, inverting the lens has no effect on the image's position or nature.

20.  Three immiscible liquids of densities \[{d_1}{\text{ }} > {d_2}{\text{ }} > {d_3}\] and refractive indices \[\;{\mathbf{\mu }}{{\text{ }}_{\mathbf{1}}}{\text{ }} > {\text{ }}{{\mathbf{\mu }}_2}{\text{ }} > {\text{ }}{{\mathbf{\mu }}_{\mathbf{3}}}\] are put in a beaker. The height of each liquid column is $\dfrac{h}{3}$ . A dot is made at the bottom of the beaker. For near normal vision, find the apparent depth of the dot.

 Ans:  Because the liquids are incompatible, they must be placed

from bottom to top.  ${d_1},{d_2},{d_3}$ with their refractive indices  ${\mu _1},{\mu _2},{\mu _3}$   respectively separated by layers   ${l_1},{l_2}$ Consider the layer   ${l_1}$   . If the object is at P, then the distance between the image of P and the liquid of refractive index from layer is   ${l_1}$ 

\[{x_1} = \dfrac{{\dfrac{h}{3}}}{{_2{\mu _1}}}\]

\[_2{\mu _1} = \dfrac{{{\mu _1}}}{{{\mu _2}}}\]

\[{x_1} = \dfrac{{\dfrac{h}{3}}}{{3\dfrac{{{\mu _1}}}{{{\mu _2}}}}} = \dfrac{h}{3}\dfrac{{{\mu _1}}}{{{\mu _2}}}\]

 This image ${l_1}$ acts as object for liquid of \[{\mu _2}\] and form the image at ${l_2}$. The distance \[{x_2}\] below level ${l_2}$

Real depth

 \[ = \left( {\dfrac{h}{3} + {x_1}} \right)\]

\[{x_2} = \dfrac{{{\text{Real depth}}}}{{_3{\mu _2}}} = \dfrac{{{\text{Real depth}}}}{{\dfrac{{{\mu _1}}}{{{\mu _2}}}}}\]

\[{x_2} = \dfrac{{{\mu _3}}}{{{\mu _2}}}\left[ {\dfrac{h}{3} + {x_1}} \right] = \dfrac{{{\mu _3}}}{{{\mu _2}}}\left[ {\dfrac{h}{3} + \dfrac{h}{3}\dfrac{{{\mu _2}}}{{{\mu _1}}}} \right] = \dfrac{h}{3}\dfrac{{{\mu _3}}}{{{\mu _2}}}\left[ {1 + \dfrac{{{\mu _2}}}{{{\mu _1}}}} \right] = \dfrac{h}{3}\left[ {\dfrac{{{\mu _3}}}{{{\mu _2}}} + \dfrac{{{\mu _3}}}{{{\mu _1}}}} \right]\]

As the point P is seen from

outside

\[{x_3} = \dfrac{{{\mu _0}}}{{{\mu _3}}}\left[ {\dfrac{h}{3} + {x_2}} \right] = \dfrac{1}{{{\mu _3}}}\left[ {\dfrac{h}{3} + \dfrac{h}{3}\left( {\dfrac{{{\mu _3}}}{{{\mu _2}}} + \dfrac{{{\mu _3}}}{{{\mu _1}}}} \right)} \right]\]

Since  \[[{\mu _0} = 1]\] ,refractive index of air

\[ = \dfrac{h}{3}\left[ {\dfrac{1}{{{\mu _3}}} + \dfrac{1}{{{\mu _3}}}\left( {\dfrac{{{\mu _3}}}{{{\mu _2}}} + \dfrac{{{\mu _3}}}{{{\mu _1}}}} \right)} \right] = \dfrac{h}{3}\left[ {\dfrac{1}{{{\mu _3}}} + \dfrac{1}{{{\mu _2}}} + \dfrac{1}{{{\mu _1}}}} \right]\]

\[{X_3}\] is apparent depth.

21. The angle of minimum deviation for a glass prism ($\mu  = \sqrt 3 $) is equal to the prism's angle. Determine the prism's angle.

Ans: The necessary relation for the smallest angle of departure is

$\mu  = \dfrac{{\sin \left( {\dfrac{{A + {\alpha _m}}}{2}} \right)}}{{\sin \dfrac{A}{2}}}$

${\alpha _m} = A$

$\mu  = \dfrac{{\sin \left( A \right)}}{{\sin \dfrac{A}{2}}} = \mu  = \dfrac{{2\sin \left( {\dfrac{A}{2}} \right)\cos \left( {\dfrac{A}{2}} \right)}}{{\sin \dfrac{A}{2}}} = 2\cos \left( {\dfrac{A}{2}} \right)$

$\sqrt 3  = 2\cos \left( {\dfrac{A}{2}} \right)$

 $\cos \dfrac{A}{2} = \dfrac{{\sqrt 3 }}{2} = \cos 30^\circ $

$\dfrac{A}{2} = 30^\circ $

 A = 60° is angle of prism

SA

22. A short item of length L is positioned distant from focus along the major axis of a concave mirror. The distance between the item and the observer is u. What is the length of the picture if the mirror has a focal length  f? You may take L <<|v – f|.

Ans:  Because the object's average distance from the mirror is u,

\[{u_1} = u - \dfrac{L}{2}{\text{ }}\;and{\text{ }}\;{u_2} = (u + \dfrac{L}{2})\]

Allow the picture of the object's two ends to develop at a distance. As a result, the picture length on the principal axis\[\;L\prime ({v_1} - {v_2})\]

$\dfrac{1}{f} = \left( {\dfrac{1}{v} + \dfrac{1}{u}} \right)$

\[\;L\prime  = ({v_1} - {v_2}) = \dfrac{{\left( {u - \dfrac{L}{2}} \right)f}}{{\left( {u - \dfrac{L}{2}} \right) - f}}{\text{  - }}\dfrac{{\left( {u + \dfrac{L}{2}} \right)f}}{{\left( {u + \dfrac{L}{2}} \right) - f}}{\text{  = f -  }}\dfrac{{\left( {u - \dfrac{L}{2}} \right)f}}{{\left( {u - f - \dfrac{L}{2}} \right)}} - \dfrac{{\left( {u + \dfrac{L}{2}} \right)}}{{\left( {u - f + \dfrac{L}{2}} \right)}}\]

\[{\text{  = f}}\left[ {\dfrac{{\left( {u - \dfrac{L}{2}} \right)\left( {u - f + \dfrac{L}{2}} \right){\text{ }} - \left( {u + \dfrac{L}{2}} \right)\left( {u - f - \dfrac{L}{2}} \right)}}{{\left( {u - f - \dfrac{L}{2}} \right)\left( {u - f + \dfrac{L}{2}} \right)}}} \right]\]

\[\therefore L <  < (u - f)\]

\[{L^2} = f\left[ {\dfrac{{\dfrac{{fL}}{2} + \dfrac{{fL}}{2}}}{{{{(u - f)}^2}}}} \right]\]

\[L = \dfrac{{ffL}}{{{{(u - f)}^2}}} = \dfrac{{{f^2}L}}{{{{(u - f)}^2}}}\]

23. Inside an opaque hemispherical bowl of radius 'a', a circular disc of radius 'R' is arranged co-axially and horizontally. When viewed from the bowl's edge, the disc's far edge is barely visible. The bowl is filled with a clear liquid with a high refractive index allowing the discs near edge to be seen. How far below the bowl's rim is the disc positioned?

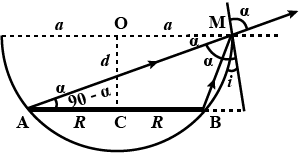
Ans: 

The rays from the ends of disc AB reaching one end of the bowl at M are shown in figures AM and BM. MN is tangent at M, therefore\[{\text{ MN}} \bot {\text{AB  i}}{\text{.e }}\angle {\text{N = 90}}^\circ \]

Using the incident beam BM and the refracted ray MD as examples

BN=CN−CB=OM−CB=a−R

\[MB = \sqrt {{d^2} + (a - {R^2})} \]

\[sini = \dfrac{{BN}}{{BM}} = \dfrac{{a - R}}{{\sqrt {{d^2} + {{(a - R)}^2}} }}\]

\[\angle r = \angle a = \angle AMN\]

\[sinr = cos(90^\circ  - \alpha ) = \dfrac{{AN}}{{AM}}{\text{ }} = \dfrac{{a + R}}{{{d^2} + {{(a + R)}^{2}}}}\]

\[\dfrac{1}{\mu_{1}}=\dfrac{\sin i}{\sin r} \quad\]

\[\dfrac{1}{\mu_{1}}=\dfrac{\dfrac{a-r}{\sqrt{d^{2}+(a+R)^{2}}}}{\dfrac{a+r}{\sqrt{d^{2}+(a-R)^{2}}}}=\dfrac{(a-R) \sqrt{d^{2}+(a+R)^{2}}}{(a-R) \sqrt{d^{2}+(a-R)^{2}}}=\dfrac{\mu\left(a^{2}-d^{2}\right)}{\sqrt{(a+R)^{2}-\mu(a-R)^{2}}}\]

\[ = \dfrac{{(a - R)\sqrt {{d^2} + {{(a + R)}^2}} }}{{(a - R)\sqrt {{d^2} + {{(a - R)}^2}} }}\]

\[ = \dfrac{{\mu ({a^2} - {d^2})}}{{\sqrt {{{(a + R)}^2} - \mu {{(a - R)}^2}} }}\]

24.  0.5 cm above the primary axis, a thin convex lens with a focal length of 25 cm is split into two halves. The top section is at (0,0), whereas the item is at (–50 cm, 0). Find the image's coordinates.

Ans:  The object is 0.5cm above the primary axis.

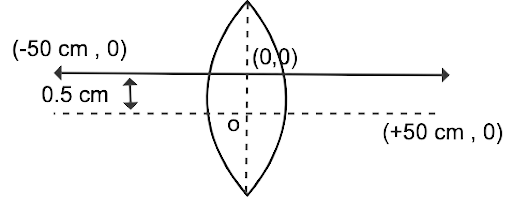
u = -50cm f = +25cm, v =?

$\dfrac{1}{f} = \left( {\dfrac{1}{v} - \dfrac{1}{u}} \right)$

$\dfrac{1}{v} - \dfrac{1}{{ - 50}} = \dfrac{1}{{25}}$

$ = \dfrac{{2 - 1}}{{50}} = \dfrac{1}{{50}}$

v= 50 cm

$m = \dfrac{v}{u} = \dfrac{{50}}{{ - 50}} =  - 1$

= -1

As a result, the picture is the same size as the item, and because m is negative, the image is inverted.

As a result, the picture is located at (50cm, -1cm) and 0.5 cm below the X –X' axis.

25. In many experimental set-ups the source and screen are fixed at a distance say D and the lens is movable. Show that there are two positions for the lens for which an image is formed on the screen. Find the distance between these points and the ratio of the image sizes for these two points.

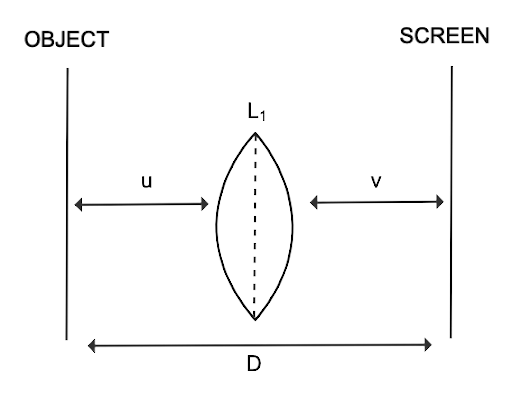
Ans:  

\[u =  - (D - v)\]

\[\dfrac{1}{f}{\text{ }} = \dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{{D - v}}\]$$

\[ = \dfrac{{D - v + v}}{{v(D - v)}} =  - \dfrac{D}{{[vD - {v^2}]}}\]

\[fD = vD - {v^2}\]

\[{v^2} - vD + fD = 0\]

\[v = \dfrac{{ + D \pm \sqrt {{D^2} + 4Df} }}{2} = \dfrac{D}{2} \pm \dfrac{{\sqrt {D{}^2 + 4Df} }}{2}.............(1)\]

\[u =  - (D - v) =  - [D - (\dfrac{D}{2} \pm \dfrac{{\sqrt {{D^2} - 4Df} }}{2})]\]

\[u =  - [\dfrac{D}{2} \pm \dfrac{{\sqrt {D2 - 4Df} }}{2}].............(2)\]

When the location of object \[{u_2}\]is\[ = \dfrac{D}{2}{\text{ }} + \dfrac{{\sqrt {{D^2} + 4Df\;} }}{2}\]

When the location of object \[{v_2}\]is\[ = \dfrac{D}{2}{\text{ }} - \dfrac{{\sqrt {{D^2} - 4Df\;} }}{2}\]

When the location of object \[{u_1}\]is\[ = \dfrac{D}{2}{\text{ }} - \dfrac{{\sqrt {{D^2} - 4Df\;} }}{2}\]

When the location of object \[{u_1}\]is\[ = \dfrac{D}{2}{\text{ }} + \dfrac{{\sqrt {{D^2} - 4Df\;} }}{2}\]

\[\;d = {v_{1}} - v{}_{2}\]

\[d = \left[ {\dfrac{D}{2}{\text{ }} \pm \dfrac{{\sqrt {{D^2} - 4Df\;} }}{2}} \right] - \left[ {\dfrac{D}{2}{\text{ }} \pm \dfrac{{\sqrt {{D^2} - 4Df\;} }}{2}} \right]\]

Case 1 : ${L_1}$

\[{u_1} = \dfrac{D}{2} -  - \dfrac{d}{2}\]

\[{v_1} = \dfrac{D}{2} -  + \dfrac{d}{2}\]

\[{m_1} = \dfrac{{{v_1}}}{{{u_1}}} = \dfrac{{\dfrac{D}{2} - \dfrac{d}{2}}}{{\dfrac{D}{2} + \dfrac{d}{2}}} = \dfrac{{D - d}}{{D + d}}\]

Case 2 : ${L_2}$

\[{u_2} = \dfrac{D}{2}{\text{ }} + \dfrac{d}{2}\]

\[{v_2} = \dfrac{D}{2}{\text{ }} - \dfrac{d}{2}\]

\[{m_2} = \dfrac{{{v_2}}}{{{u_2}}} = \dfrac{{\dfrac{D}{2} - \dfrac{d}{2}}}{{\dfrac{D}{2} + \dfrac{d}{2}}} = \dfrac{{D - d}}{{D + d}}\]

\[\dfrac{{{m_2}}}{{{m_1}}} = \left( {\dfrac{{D - d}}{{D + d}}} \right){^2}\]

26. A clear liquid with a refractive index $(\mu )$is placed in a jar with a height of h. On the bottom surface of the jar, there is a dot in the centre. Find the smallest diameter of a disc that will make a dot invisible when put on the top surface symmetrically around the centre.

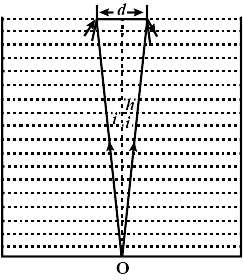
Ans: If the light ray emanating from O does not come out, or if it grazes the surface of a liquid, or if it receives entire internal reflection, the point O will be invisible. Ray OA is incident at A with critical angle ${i_c}$ and a ninety-degree angle of refraction.

If the incidence angle is more than ${i_c}$, the beam will get entire internal reflection from the surface and will not emerge through the liquid.

As a result, a disc with a diameter of d is required to restrict the rays from 'O' escaping the liquid.

$\sin i = \dfrac{1}{\mu }$

$\dfrac{{d/2}}{h} = \tan i$

.$\dfrac{d}{2} = h\tan i = h{[\sqrt {{\mu ^2} - 1} ]^{ - 1}}$

$d = \dfrac{{2h}}{{\sqrt {{\mu ^2} - 1} }}$

27. The far point of a myopic adult is 0.1 m. His accommodation power is 4 dioptres.

(i) How high of a magnification is necessary to observe distant objects?

(ii) Without his spectacles, what is his near point?

(iii) With his glasses on, what is his near point? (Assume a 2 cm image gap between the lens of the eye and the retina.)

Ans: 

i)The lens power necessary to see an item at infinity clearly.

\[U =  - \infty \]

\[\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}\]

\[\dfrac{1}{f} = \dfrac{1}{{ - 10}} - \dfrac{1}{\infty }\]

\[P = \dfrac{1}{f}m\]

\[\dfrac{1}{f} = \dfrac{1}{{10}}\]

\[P = \dfrac{1}{{ - 0.1}}m\]

(ii) if no corrective lenses are worn: Let the eye's capabilities be a \[{p_f}\]and \[{p_n}\]  when the item is far away and a p f and pn when the object is close

​\[{P_{n}} = {P_f} + {P_{a}}\]
When an object is far away, a clear picture is created at the retina 2cm from the eye lens (u=1cm=0.1m, V=2cm=0.02m).

If f is the focal length of an eye lens focused at a distance, then

\[\dfrac{1}{f}{\text{ }} = \dfrac{1}{v} - \dfrac{1}{u}{\text{ }} = \dfrac{1}{{0.02}} - \dfrac{1}{{( - 0.1)}}\]

\[\dfrac{1}{f} = 50 + 10 = 60\]

\[{P_f} = 60D\]

\[\;{P_{n}} = {P_f} + {P_a} = 60 + 4 = 64D\]

\[u = {x_n}\;(v = 2cm = 0.02m)\]

\[\dfrac{1}{f}{\text{ }} = \dfrac{1}{v} - \dfrac{1}{u}\]

\[\dfrac{1}{{0.02}} + \dfrac{1}{{{x_n}}} = Power({P_n})\]

\[50 + \dfrac{1}{{{x_n}}} = 64\]

\[\dfrac{1}{{{x_n}}} = 64 - 50 = 14D\]

\[{x_n} = \dfrac{1}{{14}}m = \dfrac{{100}}{{14}}cm = 7cm\]

(iii) When corrective lenses are used: When corrective lenses are worn, the eye is able to view the object at infinity. P = $\infty $ and v=2cm=0.02m are the eye lens powers in this circumstance.

\[\dfrac{1}{f}{\text{ }} = \dfrac{1}{v} - \dfrac{1}{u}\]

\[{P_{\infty }} = \dfrac{1}{{0.02}}{\text{ }} - \dfrac{1}{\infty } = 50\]

\[{P_n} = {P_{\infty }} + {P_a} = 50 + 4 = 54D\]

\[u =  - {x_{n}}m{\text{ , }}v =  + 2cm = 0.02m\]

\[\dfrac{1}{f}{\text{ }} = 54\]

\[\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}{\text{ }}\]

\[\dfrac{1}{{0.02}} - \dfrac{1}{{{x_n}}} = 54\]

${x_n} = 0.25m$

LA

28. Demonstrate that light incident at any angle on a material with refractive index \[\;\mu  \geqslant \sqrt 2 \]must be steered down a length perpendicular to the incident face.

Ans:  Consider a refractive index \[\;\mu  \geqslant \sqrt 2 \] slab that is rectangular in shape. At the incidence point, an incidence ray incidence at angle I on face PQ. Refracted ray BC collides with face QR, which is perpendicular to PQ and has an incidence angle of\[{i_c}\], causing refracted ray CD to pass normal to the face PQ, as required by the question. As a result, \[{i_c}\] must be a critical viewpoint. 

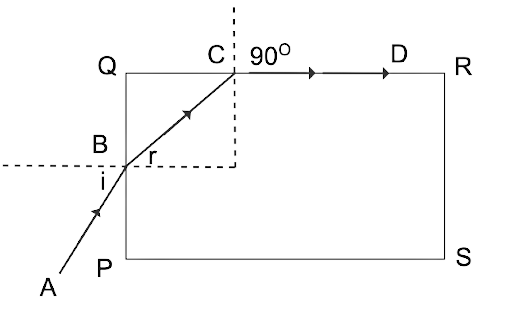
Snell’s law at C

\[\mu  = \dfrac{1}{{sin{i_c}}}\] 

 \[sin{i_c} \geqslant \dfrac{1}{\mu }{\text{ }}[sin{i_c} = \dfrac{1}{\mu }]\]

\[sin(90 - r) \geqslant \dfrac{1}{\mu }\]

\[[\because r + 90 + {i_c} = 180]\]

\[cos{\text{ }}r \geqslant \dfrac{1}{\mu }\]

Square both side

\[co{s^2}r \geqslant \dfrac{1}{{{\mu ^2}}}\]

\[1 - co{s^2}r \leqslant 1 - \dfrac{1}{{{\mu ^2}}}\]

\[si{n^2}r \leqslant co{s^2}r \leqslant 1 - \dfrac{1}{{{\mu ^2}}}.............(1)\]

\[\;sin{\text{ }}i = \mu sin{\text{ }}r \Rightarrow si{n^2}i = {\mu ^2}si{n^2}r\]

\[\dfrac{1}{{{\mu ^2}}}si{n^2}i = sin{}^2r..............(2)\]

Put 2 in 1

\[\dfrac{1}{{\mu {}^2}}si{n^2}i \leqslant 1 - \dfrac{{1}}{{{\mu ^2}}}\]

\[si{n^2}i \leqslant {\mu ^2} - 1\;\]

\[si{n^2}90 \leqslant {\mu ^2} - 1[\because \mu  \geqslant \sqrt 2 ]\]

\[1 + 1 \leqslant {\mu ^2}\]

\[2 \leqslant {\mu ^2}\]

\[\sqrt {2}  \leqslant \mu \]

29. In a long vertical column (i.e., horizontal dimensions vertical dimensions), a mixing of a pure liquid and a solution generates diffusion of solute particles and hence a refractive index gradient along the vertical dimension. A beam of light that enters the column at an angle to the vertical is diverted from its intended course. Determine the deviation when travelling a horizontal distance of d h, the column's height.

Ans:  

Consider a long, translucent vertical column with an unlimited height (h) and thickness (dx). Consider the case of a beam AB that enters at an angle into a liquid column of height y and exits at an angle θ into liquid of height y in column of liquid and emerges at an angle (θ +d θ) at height (y+ dy). 

From Snell’s law,

\[\mu \left( y \right)\sin \theta  = y\left( {y + dy} \right)\sin \left( {\theta  + d\theta } \right)\]

\[\mu \left( y \right)\sin \theta ,\left( {\mu \left( y \right) + \dfrac{{d\mu }}{{dy}}dy} \right)\left( {\sin \theta \cos d\theta  + \cos \theta \sin d\theta } \right)\]

\[\mu \left( y \right)\sin \theta \mu \left( y \right)\cos \theta d\theta  + \dfrac{{d\mu }}{{dy}}dy\sin \theta \]

\[\mu (y)cos\theta d\theta ,\,\dfrac{{d\mu }}{{dy}}dysin\theta d\theta ,\,\dfrac{{ - d\mu }}{{\mu dy}}dytan\theta \]\[\]

\[tan\theta  = \dfrac{{dx}}{{dy}}\]

On solving , we have

\[\therefore \;\:\;\:d\theta  = \dfrac{{ - 1d\mu }}{{\mu dy}}dx\]

Solving this variable separable form of differential equation

.\[\therefore \;\theta  = \dfrac{{ - 1d\mu }}{{\mu dy}}\int_o^d {dx}  = \dfrac{{ - 1d\mu }}{{\mu dy\,}}d\]

30.  When light comes close to a big object, the gravitational interaction bends the beam. This may be explained by a change in the medium's effective refractive index, which is given by

\[n(r) = 1 + \dfrac{{2GM}}{{r{c^2}}}\]

where r is the distance between the point of interest and the large body's mass centre, G is the universal gravitational constant, M is the mass of the body, and c is the speed of light in vacuum. Consider a spherical object and calculate the ray's divergence from its initial path when it grazes the object.

Ans:  Consider two spherical surfaces separated by r and (r + dr) from the centre of a large object with radius R and mass m

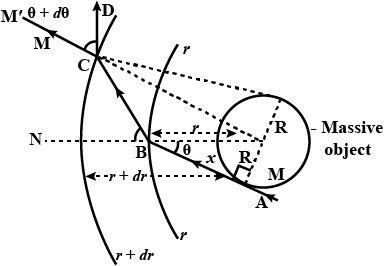
Consider two spherical surface at r and (r+dr) distance from the centre of massive object of mass m and radius R

A ray ABCD incident at B and C on two surface at r and (r+dr) then, by Snell's law

\[\mu \left( r \right)sin\theta  \cong \mu \left( {r + ar} \right)sin\left( {\theta  + d\theta } \right)\mu \left( r \right)\]

\[\mu \left( r \right)sin\theta  \cong [\mu \left( r \right) + \dfrac{{d\mu }}{{dr}}dr](sin\theta .cosd\theta  + cos\theta sin{\text{ }}d\theta )\]

 \[d\theta  \to 0\;{\text{    }}\;cosd\theta  = 1\;and\;d\theta  = 0\]

\[\mu \left( r \right)sin\theta  \cong [\mu \left( r \right) + \dfrac{{d\mu }}{{dr}}dr]\left( {sin\theta  + cos\theta d\theta } \right)\]

\[\mu \left( r \right)sin\theta  \cong \mu \left( r \right)sin\theta  + d\mu sin\theta  + \mu \left( r \right)cos\theta d\theta  + d\mu d\theta cos\theta \]

\[d\mu d\theta cos\theta \]is very small as\[\;d\mu \] and \[d\theta \] are very small

\[\therefore d\mu d\theta cos\theta  \cong 0\]

\[\therefore \mu \left( r \right)sin\theta  \cong \mu \left( r \right)sin\theta  + d\mu sin\theta  + \mu cos\theta .d\theta \]

\[0 \cong d\mu sin\theta  + \mu \left( r \right)cos\theta .d\theta \]

\[ - d\mu sin\theta  = \mu \left( r \right)cos\theta .d\theta \]

Dividing both side by dr

\[ - \dfrac{{d\mu }}{{dr}}sin\theta  = \mu \left( r \right)cos\theta \dfrac{{d\theta }}{{dr}}.............\left( 1 \right)\]

\[\mu \left( r \right) = 1 + \dfrac{{2GM}}{{{c^2}}}.\dfrac{1}{r}\left( {given} \right)\]

\[\dfrac{{d\mu }}{{dr}} = 0 + \dfrac{{2GM}}{{c{}^2}}\left( { - 1} \right){r^{ - 2}}\]

\[ - \dfrac{{d\mu }}{{dr}} = [\dfrac{{2GM}}{{{c^2}{r^2}}}]...............\left( 2 \right)\]

\[\dfrac{{2GMsin\theta }}{{{c^2}{r^2}}} = [1 + \dfrac{{2GM}}{{{c^2}{r^2}}}]cos\theta \dfrac{{d\theta }}{{dr}}\]​

As the G is very small and \[{c^2}\] is very large so

\[\dfrac{{GM}}{{{c^2}{r^2}}}{\text{ }} \to 0\]

\[\dfrac{{2GMcos\theta sin\theta }}{{{c^2}{r^2}}} = \dfrac{{d\theta }}{{dr}}\] ​

\[\dfrac{{2GMtan\theta }}{{{c^2}{r^2}}} \cong drd\theta \]

\[\dfrac{{2GM}}{{c{}^2}}\smallint \dfrac{{tan\theta }}{{{r^2}}}dr = \int\limits_0^{{\theta _0}} {d\theta } \]

\[\;{r^2} = {x^2} + {R^2}\]

Distinguish between the two sides

\[2rdr = 2x.dx\]

\[dr = \dfrac{x}{r}dx\]

∴\[\int\limits_0^{{\theta _0}} {d\theta }  = \dfrac{{2GM}}{{{c^2}}}\int\limits_\infty ^{ - \infty } {\dfrac{1}{{{r^2}}}{\text{ }}} \dfrac{R}{r}(tan\theta  = \dfrac{{R}}{x}) = \dfrac{{2GM}}{{{c^2}}}\int\limits_\infty ^{ - \infty } {\dfrac{1}{{{r^2}}}{\text{ }}} \dfrac{R}{{x{r^3}}}xdx = \dfrac{{2GM}}{{{c^2}}}\int\limits_\infty ^{ - \infty } {\text{ }} \dfrac{R}{{{{({x^2} + R{}^2)}^{3/2}}}}dx\]

\[\int\limits_0^{{\theta _0}} {d\theta }  = \dfrac{{2GM}}{{{c^2}}}\int\limits_\infty ^{ - \infty } R \dfrac{{dx}}{{{{({x^2} + {R^2})}^{3/2}}}}[\because x = Rtan\theta ;dx = Rse{c^2}\theta d\theta ]\]

\[{\theta _0} = \dfrac{{2GM}}{{{c^2}}}\int\limits_{ - \pi /2}^{\pi /2} {\dfrac{{R.Rse{c^2}\theta d\theta }}{{{{({R^2} + ta{n^2}\theta {R^2})}^{3/2}}}}}  = \dfrac{{2GM}}{{{c^2}}}\int\limits_{ - \pi /2}^{\pi /2}  \dfrac{{{R^2}se{c^2}\theta d\theta }}{{{{[{R^2}(1 + ta{n^2}\theta )]}^{3/2}}}}\]\[\int\limits_0^{{\theta _0}} {d\theta }  = \dfrac{{2GM}}{{{c^2}}}\int\limits_{ - \pi /2}^{\pi /2} {\dfrac{{{R^2}se{c^2}\theta d\theta }}{{(R{}^3 + se{c^3}\theta )}}}  = \dfrac{{2GM}}{{{c^2}}}\int\limits_{ - \pi /2}^{\pi /2} {\dfrac{1}{{sec\theta }}} d\theta \]

\[ = \dfrac{{2GM}}{{R{c^2}}}\int\limits_{ - \pi /2}^{\pi /2} {cos\theta d\theta } {\text{ }} = \dfrac{{2GM}}{{R{c^2}}}\left[ {sin\theta } \right]_{ - \pi /2}^{\pi /2} = \dfrac{{2GM}}{{R{c^2}}}[sin\dfrac{\pi }{2} - sin( - \dfrac{\pi }{2})]\]

\[{\theta ^0} = \dfrac{{2GM}}{{R{c^2}}}[1 + sin\dfrac{\pi }{2}] = \dfrac{{2GM}}{{R{c^2}}}\left[ {1 + 1} \right]\]

\[ \Rightarrow {\theta _0} = \dfrac{{4GM}}{{R{c^2}}}\]

31. An infinitely long cylinder of radius R is made of an unusual exotic material with refractive index –1  The cylinder is placed between two planes whose normal are along the y direction. The centre of the cylinder O lies along the y-axis. A narrow laser beam is directed along the y direction from the lower plate. The laser source is at a horizontal distance x from the diameter in the y direction. Find the range of x such that light emitted from the lower plane does not reach the upper plane.

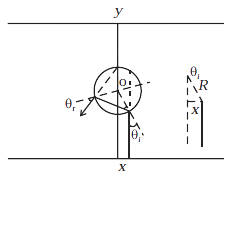
Ans:  Because the cylinder is formed of a material with a refractive index of -1 and is put in air, of μ=1 so, when beam AB collides with cylinder B, ${\theta _r}$ will be negative, implying that the refractive ray will be reflected from the normal. At incidence point C, the same thing happens, and the angle of refraction and incident at B and C will be equal. (${\theta _r}$) as OB=OC=R and of refraction at C is  ${\theta _r}$.${\theta _1} = |{\theta _i}| = |{\theta _r}|$ as reflection takes place

The overall difference between the outgoing and entering rays. 4${\theta _1}$.Rays are not allowed to reach the receiving plane$\dfrac{\pi }{2} \leqslant {\theta _1} \leqslant \dfrac{{3\pi }}{2}$ angles measured from the y axis in a clockwise direction

$\sin {\theta _1} = \dfrac{{3\pi }}{2}$

 $\dfrac{\pi }{8} \leqslant {\sin ^{ - 1}}\dfrac{x}{R} \leqslant \dfrac{{3\pi }}{8}$

As a result, if light produced by the source does not reach the receiving plane,$\dfrac{{R\pi }}{8} \leqslant x \leqslant \dfrac{{3R\pi }}{8}$.

32. (i) Consider a narrow lens in front of a source (S) and an observer (O) (O) Allow the lens thickness to change as needed. $W(b) = {W_0} - \dfrac{{{b^2}}}{\alpha }$ where an is the horizontal distance from the pole and b is the vertical distance from the pole. ${W_0}$  is a fixed value. Find the condition that all paraxial rays beginning from the source will converge at a point 'O' on the axis using Fermat's principle, i.e. the duration of transit for a ray between the source and observer is an extremum. Calculate the focal length.

(ii) A gravitational lens is thought to have a changing form width.

\[W(b) = {K_1}\log \left( {\dfrac{{{K_2}}}{b}} \right)({b_{\min }} < b < {b_{\max }})\]

\[ = {K_1}\log \left( {\dfrac{{{K_2}}}{{b{}_{\min }}}} \right)({b_{\min }} < b)\]

Demonstrate that an observer will view an image of a point item as a ring with an angular radius around the lens's centre.

$\beta  = \sqrt {\dfrac{{(n - 1){K_1}\dfrac{u}{v}}}{{u + v}}} $

Ans:  The time taken by ray from S to \[{P_1}\]

\[{t_1} = \dfrac{{\sqrt {{u^2} + {b^2}} }}{c} = \dfrac{u}{c}{\left( {1 + \dfrac{{{b^2}}}{{{u^2}}}} \right)^{\dfrac{1}{2}}}\]

\[{t_1} = \dfrac{u}{c}\left( {1 + \dfrac{{{b^2}}}{{2{u^2}}}} \right)\] (assuming b <<<u)

Similarly, time required by ray from \[{P_1}\] to 0

\[{t_2} = \dfrac{v}{c}\left( {1 + \dfrac{{{b^2}}}{{2{v^2}}}} \right)\]

The amount of time it takes for a beam to go through the lens

\[{t_3} = \dfrac{{(\mu  - 1)W(b)}}{c}\]

Thus total time by ray from S to O=t=t1+t2+t3

\[t = \dfrac{u}{c}\left( {1 + \dfrac{{{b^2}}}{{2{u^2}}}} \right) + \dfrac{v}{c}\left( {1 + \dfrac{{{b^2}}}{{2{v^2}}}} \right) + \dfrac{{(\mu  - 1)W(b)}}{c}\]

\[ = \dfrac{1}{c}\left[ {u + \dfrac{{{b^2}}}{{2u}} + v + \dfrac{{{b^2}}}{{2v}} + (\mu  - 1)W(b)} \right]\]

\[ = \dfrac{1}{c}\left[ {u + v + \dfrac{{{b^2}}}{2}\left( {\dfrac{1}{u} + \dfrac{1}{v}} \right) + (\mu  - 1)W(b)} \right]\]

If \[\dfrac{1}{D} = \dfrac{1}{v} + \dfrac{1}{u}\]

\[t = \dfrac{1}{c}\left[ {u + v + \dfrac{{{b^2}}}{{2D}} + (\mu  - 1)\left( {{W_o} - \dfrac{{{b^2}}}{\alpha }} \right)} \right]\]

Fermat’s Principle

\[\dfrac{{dt}}{{db}} = \dfrac{1}{c}\left[ {0 + 0 + \dfrac{{2b}}{{2D}} + (\mu  - 1)\left[ {0 - \dfrac{{2b}}{\alpha }} \right]} \right] = \dfrac{b}{{cD}} - (\mu  - 1)\left[ { - \dfrac{{2b}}{\alpha }} \right]\]

But time from S to O remains constant

\[\dfrac{{2(\mu  - 1)b}}{{\alpha c}} = \dfrac{b}{{cD}}\]

\[\alpha  = 2(\mu  - 1)D\]

Thus, the convergence lens is formed \[\alpha =2\left ( \mu -1 \right )D\].

Because it is unaffected by B, all paraxial rays from S will converge at O (for rays b <<u and b <<v).Since \[\dfrac{1}{D} = \dfrac{1}{v} + \dfrac{1}{u}\]

it is equivalent to focal length f

\[\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}\]

\[t = \dfrac{1}{c}\left[ {u + v + \dfrac{{{b^2}}}{{2D}} + (\mu  - 1)W(b)} \right]\]

Here $W(b) = {K_1}{\log _e}\left( {\dfrac{{{K_2}}}{b}} \right)$

\[t = \dfrac{1}{c}\left[ {u + v + \dfrac{{{b^2}}}{{2D}} + (\mu  - 1){K_1}\log \dfrac{{{K_2}}}{b}} \right]\]

\[\dfrac{{dt}}{{db}} = \dfrac{1}{c}\left[ {0 + 0 + \dfrac{{2b}}{{2D}} + (\mu  - 1)\dfrac{b}{{{K_2}}}.{K_1}} \right]\dfrac{d}{{db}}\left( {\dfrac{{{K_2}}}{b}} \right)\]

\[ = \dfrac{1}{c}\left[ {\dfrac{b}{D} + (\mu  - 1)\dfrac{{{K_1}}}{{{K_2}}}b.{K_2}( - 1)\dfrac{1}{{{b^2}}}} \right]\]

Because the period between S and O is constant, so, $\dfrac{{dt}}{{db}} = 0$

So \[0 = \dfrac{1}{c}\left[ {\dfrac{b}{D} - (\mu  - 1)\dfrac{{{K_1}}}{b}} \right]\]

\[(\mu  - 1)\dfrac{{{K_1}}}{b} = \dfrac{b}{D}\]

${b^2} = {K_1}D(\mu  - 1)$

$b = \sqrt {(\mu  - 1){K_1}D} $

As a result, all rays going through at a height of b will contribute to the picture. The beam path is angled.

$\beta  = \dfrac{b}{v} = \dfrac{{\sqrt {(\mu  - 1){K_1}D} }}{v} = \sqrt {\dfrac{{(\mu  - 1){K_1}D}}{{{v^2}}}} $

 $\beta  = \sqrt {\dfrac{{(\mu  - 1){K_1}u}}{{v(u + v)}}} \left( {D = \dfrac{{uv}}{{u + v}}} \right)$

NCERT Exemplar for Class 12 Physics - Ray Optics And Optical Instruments

NCERT Exemplar for Class 12 Physics - Ray Optics And Optical Instruments is a part of the NCERT Exemplar for Class 12 Physics. The complete study material focuses on every chapter given in the NCERT Class 12 Physics textbook. The highly important topics in these chapters are used to create the exercise section of every chapter in the NCERT Class 12 Physics textbook. And the NCERT Exemplar for Class 12 Physics provided by Vedantu provides Class 12 students with answers for those questions. These answers are expert-created and are completely relevant from CBSE's point of view. 

The NCERT Exemplar for Class 12 Physics - Ray Optics And Optical Instruments is a thorough guide that students of Class 12 CBSE should study in order to score high and achieve a good rank in the Class 12 board examination.

On this very page, students can find the NCERT Exemplar for Class 12 Physics - Ray Optics And Optical Instruments in a downloadable PDF form completely free of charge. The study material is created by experts with the goal of providing the crucial knowledge Class 12 students need to perform well in the exams. The solutions given in the NCERT Exemplar for Class 12 Physics Chapter 9 - Ray Optics And Optical Instruments are created keeping in mind the NCERT guidelines and CBSE marking scheme. Any student of any Intelligence Quotient can understand and apply these solutions with ease. That is because the language used to make these solutions is simple and easy to comprehend by any Class 12 student. 

Also, the topics provided in this study gear are organized in an extremely detailed manner. 

The NCERT Exemplar for Class 12 Physics - Ray Optics And Optical Instruments consists of every question given in the exercise section of chapter 9 (Ray Optics And Optical Instruments), which includes multiple-choice questions, questions that require brief answers, and the questions that require long answers. 

Chapter 9 - Ray Optics And Optical Instruments in the NCERT Class 12 Physics textbook is important for Class 12 students to study and understand. A lot of questions from different topics in these chapters are asked in the CBSE Class 12 physical examination. 

Given Below are All the Crucial Topics Available in the Chapter 9:

9.1 Introduction

9.2 Reflection of Light by Spherical Mirrors

9.3 Refraction

9.4 Total Internal Reflection

9.5 Refraction at Spherical Surfaces and by Lenses

9.6 Refraction through a Prism

9.7 Dispersion by a Prism

9.8 Some Natural Phenomena due to Sunlight

9.9 Optical Instruments