Class 8 Maths NCERT Exemplar Solutions Chapter 1 Rational Numbers
Free PDF download of NCERT Exemplar for Class 8 Maths Chapter 1 - Rational Numbers solved by expert Maths teachers on Vedantu.com as per NCERT (CBSE) Book guidelines. All Chapter 1 - Rational Numbers exercise questions with solutions to help you to revise complete syllabus and score more marks in your examinations. NCERT Solutions for Class 8 Maths Chapter 1 provided by Vedantu offers clarifications for the students who can go far but lack the concentration. These solutions help the students to score excellent marks in their exams. Science Students who are looking for NCERT Solutions for Class 8 Science will also find the Solutions curated by our Master Teachers really Helpful.
Download Class 8 Maths NCERT Solutions to help you to revise complete syllabus ans score more marks in your examinations.
Access NCERT Exemplar Solutions for Class 8 Mathematics Chapter 1 – Rational Numbers
In examples 1 to 3 , there are four options out of which one is correct. Choose the correct answer.
Example 1. Which of the following is not true?
(a)
(b)
(c)
(d)
Ans:
(b) is the correct answer.
Subtraction of rational numbers is not commutative.
Thus,
Therefore, (b) is the correct answer.
Example 2. Multiplicative inverse of
(a)
(b)
(c)
(d) not defined
Ans:
(d) is the correct answer.
Reciprocal of
Thus, Multiplicative inverse of
Therefore, (d) is the correct answer.
Example 3. Three rational numbers lying between
(a)
(b)
(c)
(d)
Ans:
(c) is the correct answer.
Three rational numbers lying between
Therefore, the correct answer is (c).
In examples 4 and 5 , fill in the blanks to make the statements true.
Example 4. The product of a non-zero rational number and its reciprocal is________.
Ans:
Let
Then, its reciprocal will be
Now, their product is
The product of a non-zero rational number and its reciprocal is one.
Example 5. If
Ans:
Given that,
Then,
Multiply and divide the numbers,
Take LCM and simplify,
Therefore, If
In examples 6 and 7, state whether the given statements are true or false.
Example 6. Every rational number has a reciprocal.
Ans:
We know that The product of a non-zero rational number and its reciprocal is one.
But, there is no rational number which when multiplied with zero, gives one.
So, the rational number
Therefore, the given statement is false.
Example 7.
Ans:
Make the denominators same:
Multiply and divide
Multiply and divide
Here,
Thus,
Therefore, the given statement is true.
Example 8. Find
Ans:
Rewrite the expression,
Simplify,
Example 9. Using appropriate properties, find
Ans:
Rewrite as,
Example 10. Let
What are the rational numbers represented by the points
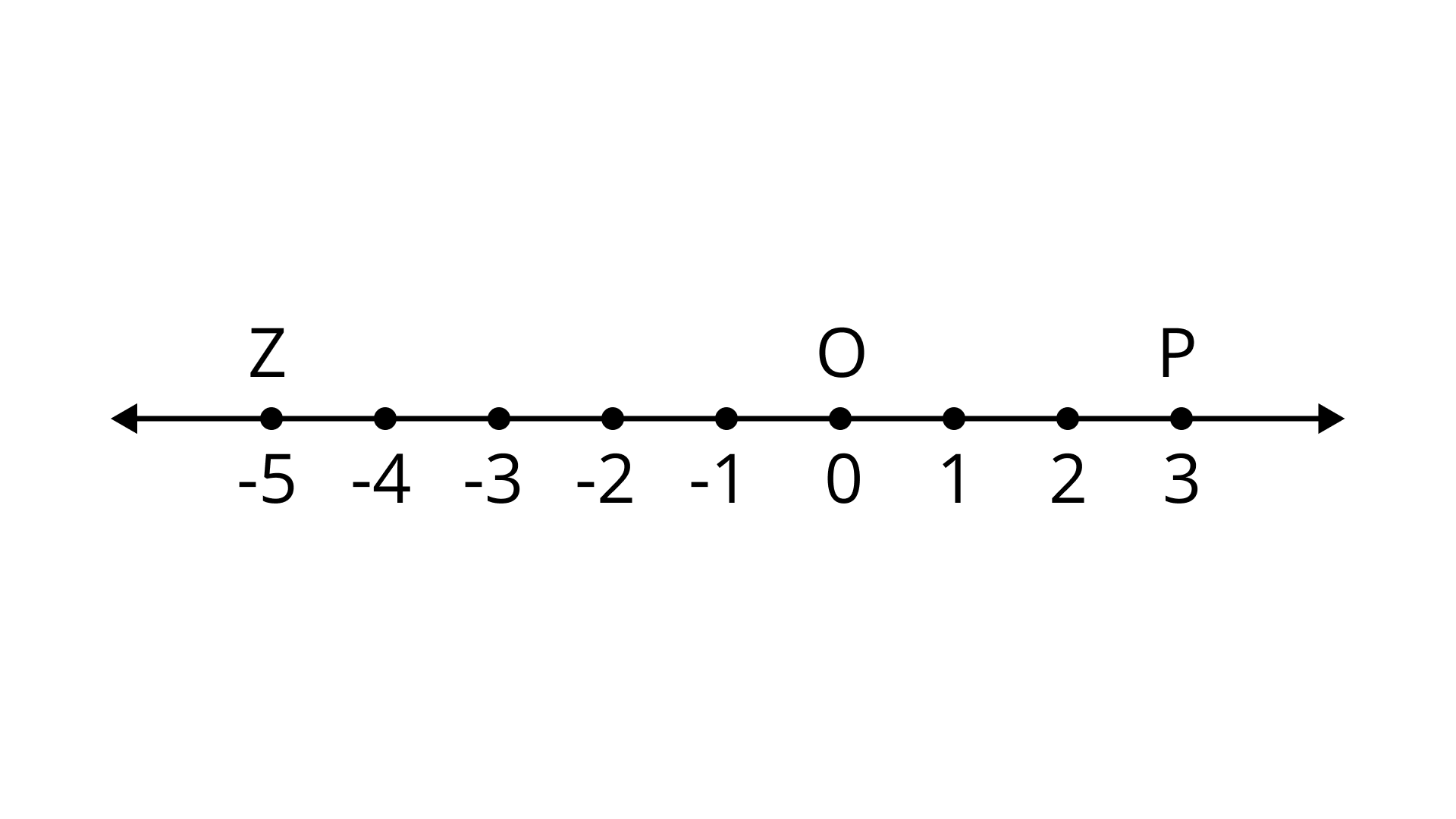
Ans: As
and
therefore
So,
And
Therefore,
Also
So,
Example 11. A farmer has a field of area
Ans:
Each share
Example 12. Let
and
Verify:
(i)
Ans:
So,
Hence, verified.
(ii)
Ans:
So,
Hence, verified.
Example 13. Solve the following questions and write your observations.
(i)
Ans:
When we add zero to a rational number we get the same rational number.
(ii)
Ans:
When we add zero to a rational number we get the same rational number.
(iii)
Ans:
When we add zero to a rational number we get the same rational number.
(iv)
Ans:
When we multiply a rational number by one we get the same rational number.
(v)
Ans:
When we multiply a rational number by one we get the same rational number.
(vi)
Ans:
When we multiply a rational number by one we get the same rational number.
Example 14. Write any
Ans:
Rewrite the numbers,
Thus, rational numbers
Example 15. Identify the rational number which is different from the other three
Ans:
Example 16. The product of two rational numbers is
Ans:
Let the other rational number be
Then,
Now,
Therefore, the other number is
In questions 1 to 25, there are four options out of which one is correct. Choose the correct answer.
1. A number which can be expressed as
(a) Natural number.
(b) Whole number.
(c) Integer.
(d) Rational number.
Ans:
If
Therefore, (d) is the correct answer.
2. A number of the form
(a)
(b)
(c)
(d)
Ans:
A number of the form
Therefore, (b) is the correct answer.
3. The numerical expression
(a) Rational numbers are closed under addition.
(b) Rational numbers are not closed under addition.
(c) Rational numbers are closed under multiplication.
(d) Addition of rational numbers is not commutative.
Ans:
The sum of any two rational numbers is always a rational number.
Here,
Thus, Rational numbers are closed under addition.
Therefore, (a) is the correct answer.
4. Which of the following is not true?
(a) Rational numbers are closed under addition.
(b) Rational numbers are closed under subtraction.
(c) Rational numbers are closed under multiplication.
(d) Rational numbers are closed under division.
Ans:
Rational numbers are not closed under division.
Here,
Therefore, (d) is the correct answer.
5.
(a) Addition of rational numbers is commutative.
(b) Rational numbers are closed under addition.
(c) Addition of rational numbers is associative.
(d) Rational numbers are distributive under addition.
Ans:
Let,
Given that,
So, Addition of rational numbers is commutative.
Therefore, (a) is the correct answer.
6. Which of the following expressions shows that rational numbers are associative under multiplication?
(a)
(b)
(c)
(d)
Ans:
For associative multiplication property-
Let
Then,
Thus,
Therefore, (a) is the correct answer.
7. Zero
(a) The identity for addition of rational numbers.
(b) The identity for subtraction of rational numbers.
(c) The identity for multiplication of rational numbers.
(d) The identity for division of rational numbers.
Ans:
If
Thus, zero is the identity for addition of rational numbers.
Therefore, (a) is the correct answer.
8. One
(a) The identity for addition of rational numbers.
(b) The identity for subtraction of rational numbers.
(c) The identity for multiplication of rational numbers.
(d) The identity for division of rational numbers.
Ans:
If
Thus, one is the identity for multiplication of rational numbers.
Therefore, (c) is the correct answer.
9. The additive inverse of
(a)
(b)
(c)
(d)
Ans:
For any number
That is,
let
Then,
Thus, the additive inverse of
Therefore, (b) is the correct answer.
10. Multiplicative inverse of a negative rational number is
(a) A positive rational number.
(b) A negative rational number.
(c)
(d)
Ans:
Let the rational number be
Then, its multiplicative inverse
Now,
It is observed that the product of the rational number and its multiplicative inverse will be
Thus, the multiplicative inverse of a negative rational number is a negative rational number.
Therefore, (b) is the correct answer.
11. If
(a) Identity for addition of rational numbers.
(b) Additive inverse of
(c) Multiplicative inverse of
(d) Reciprocal of
Ans:
Sum of any rational number and zero is always a rational number.
Therefore, zero is the identity for addition of rational numbers.
Therefore, (a) is the correct answer.
12. To get the product
(a)
(b)
(c)
(d)
Ans:
Let the number be
Divide each side with
Thus, we should multiply
Therefore, (c) is the correct answer.
13.
(a)
(b)
(c)
(d)
Ans:
Therefore, (b) is the correct answer.
14. The multiplicative inverse of
(a)
(b)
(c)
(d)
Ans:
Let the multiplicative inverse is
The product of a rational number and its multiplicative inverse should be
Then,
Divide each side with
Thus, the multiplicative inverse of
Therefore, (d) is the correct answer.
15. If
(a)
(b)
(c)
(d) Not defined
Ans:
It is known that, sum of any rational number and zero is always a rational number.
Then, if
Therefore, (a) is the correct answer.
16. The reciprocal of
(a)
(b)
(c)
(d) Not defined
Ans:
The reciprocal of a number is a number (multiplicative inverse) which when multiplied by the original number yields
Let the reciprocal be
Then,
That is,
Thus, the reciprocal of
Therefore, (a) is the correct answer.
17. The reciprocal of
(a)
(b)
(c)
(d) Not defined
Ans:
The reciprocal of a number is a number (multiplicative inverse) which when multiplied by the original number yields
Let the reciprocal be
Then,
That is,
Thus, the reciprocal of
Therefore, (b) is the correct answer.
18. The reciprocal of
(a)
(b)
(c)
(d) Not defined
Ans:
The reciprocal of a number is a number (multiplicative inverse) which when multiplied by the original number yields
Let the reciprocal be
Then,
That is,
Thus, the reciprocal of
Therefore, (d) is the correct answer.
19. The reciprocal of any rational number
(a)
(b)
(c)
(d)
Ans:
The reciprocal of a number is a number (multiplicative inverse) which when multiplied by the original number yields
Thus, the reciprocal of any rational number
Therefore, (d) is the correct answer.
20. If
(a)
(b)
(c)
(d)
Ans:
The reciprocal of a number is a number (multiplicative inverse) which when multiplied by the original number yields
If
Therefore, (a) is the correct answer.
21. The reciprocal of
(a)
(b)
(c)
(d)
Ans:
Multiply the numbers,
Let
The reciprocal of a number is a number (multiplicative inverse) which when multiplied by the original number yields
Then,
Divide each side with
Thus, the reciprocal of
Therefore, (a) is the correct answer.
22. Which of the following is an example of the distributive property of multiplication over addition for rational numbers?
(a)
(b)
(c)
(d)
Ans:
Distributive property is given as,
Thus,
Therefore, (a) is the correct answer.
23. Between two given rational numbers, we can find
(a) One and only one rational number.
(b) Only two rational numbers.
(c) Only ten rational numbers.
(d) Infinitely many rational numbers.
Ans:
Between two given rational numbers, we can find infinitely many rational numbers.
Therefore, (d) is the correct answer.
24.
(a) Between
(b) Less than
(c) Greater than
(d) Less than
Ans:
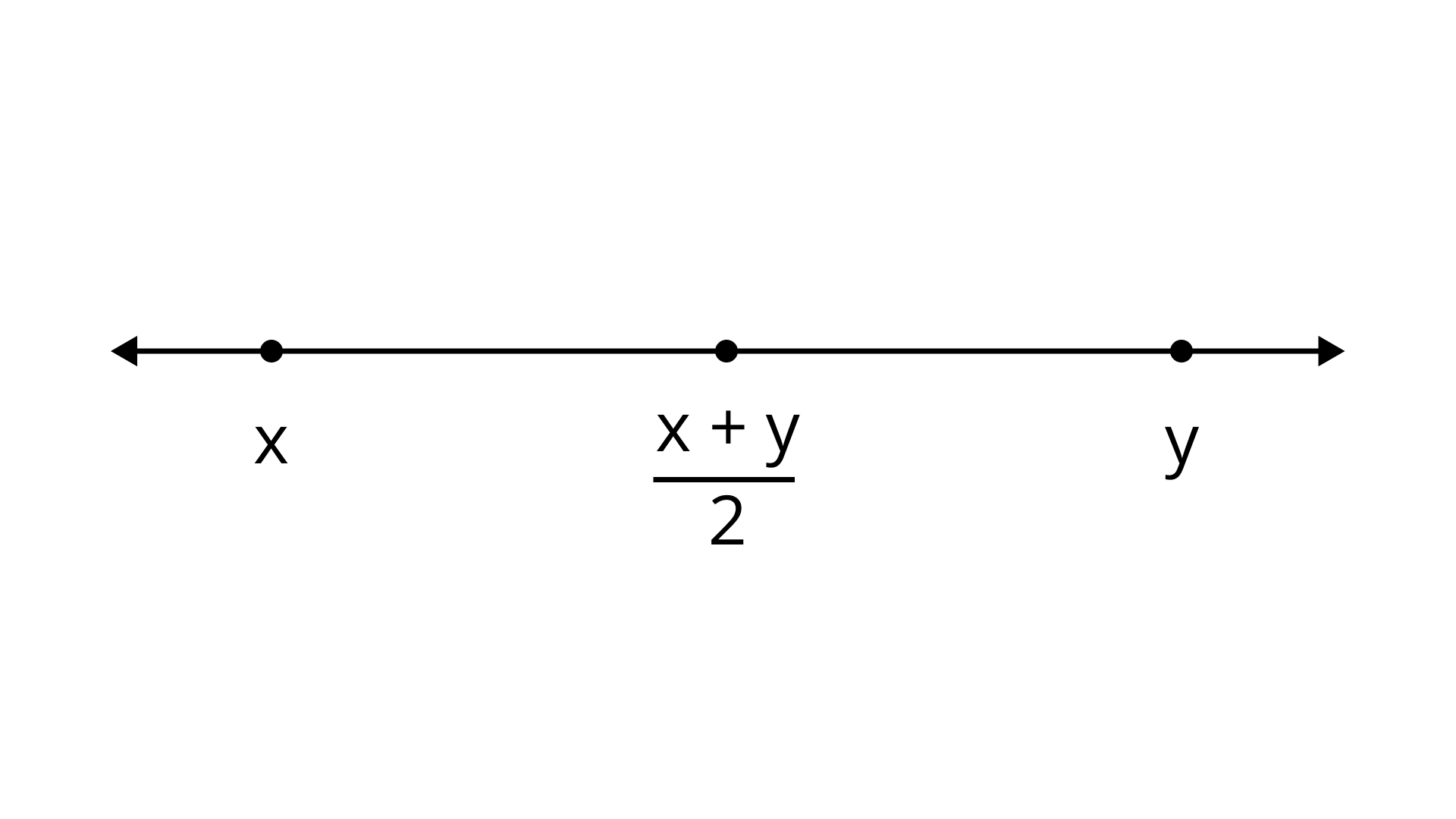
Therefore, (a) is the correct answer.
25. Which of the following statements is always true?
(a)
(b)
(c)
(d)
Ans:
Therefore, (b) is the correct answer.
In questions 26 to 47 , fill in the blanks to make the statements true.
26. The equivalent of
Ans:
To make the numerator
Therefore, the equivalent of
27. The equivalent rational number of
Ans:
To make the denominator
Therefore, the equivalent rational number of
28. Between the numbers
Ans:
Multiplying and dividing
Now, we have to see which is greater in
As we see, the denominator is the same.
So, the number which has a higher numerator value will be greater.
Therefore,
29. The reciprocal of a positive rational number is ________.
Ans:
The reciprocal of a number is a number (multiplicative inverse) which when multiplied by the original number yields
Let
Then,
Thus,
Therefore, the reciprocal of a positive rational number is always a positive rational number.
30. The reciprocal of a negative rational number is ________.
Ans:
The reciprocal of a number is a number (multiplicative inverse) which when multiplied by the original number yields
Let
Then,
Thus,
Therefore, the reciprocal of a negative rational number is always a negative rational number.
31. Zero has ________ reciprocal.
Ans:
The reciprocal of a number is a number (multiplicative inverse) which when multiplied by the original number yields
Let
Then,
Thus,
Therefore, Zero has no reciprocal.
32. The numbers _______ and _______ are their own reciprocal.
Ans:
The reciprocal of a number is a number (multiplicative inverse) which when multiplied by the original number yields
Let
Then,
Thus,
Let
Then,
Thus,
Therefore, the numbers
33. If
Ans:
Given that,
Now,
Therefore, if
34. The reciprocal of
Ans:
Given that the expression is
Rewrite the expression,
The reciprocal of a number is a number (multiplicative inverse) which when multiplied by the original number yields
Therefore, the reciprocal of
35.
Ans:
Let
Then,
Now,
Therefore,
36. The negative of
Ans:
The negative of
37. For rational numbers
Ans:
By distributive property of multiplication over addition,
Therefore, for rational numbers
38.
Ans:
Multiply both the numbers with
Here, we can see that
That is,
39. There are ________ rational numbers between any two rational numbers.
Ans:
There are infinite rational numbers between any two rational numbers.
40. The rational numbers
Ans:
Therefore, the rational numbers
41. The negative of a negative rational number is always a _________ rational number.
Ans:
Let
Then, the negative of this negative rational number is
Therefore, the negative of a negative rational number is always a positive rational number.
42. Rational numbers can be added or multiplied in any ________.
Ans:
Rational numbers are commutative under addition and multiplication.
Therefore, rational numbers can be added or multiplied in any order.
43. The reciprocal of
Ans:
Let
The reciprocal of a number is a number (multiplicative inverse) which when multiplied by the original number yields
Then,
Divide each side with
Therefore, the reciprocal of
44. The multiplicative inverse of
Ans:
Let
The reciprocal of a number is a number (multiplicative inverse) which when multiplied by the original number yields
Then,
Divide each side with
Therefore, the multiplicative inverse of
45. The rational number
Ans:
Multiply and divide
Therefore, the rational number
46.
Ans:
By distributive law,
47. The two rational numbers lying between
Ans:
The two rational numbers lying between
In each of the following, state whether the statements are true (T) or false (F).
48. If
Ans:
If
Therefore, the given statement is false.
49. If
Ans:
If
Therefore, the given statement is false.
50. If
Ans:
It is known that rational numbers are not closed under division.
If
Therefore, the given statement is true.
51.
Ans:
Multiply each number with
Here,
Thus,
Therefore, the given statement is true.
52.
Ans:
Multiply each number with
Here,
Therefore, the given statement is false.
53.
Ans:
Multiply each number with
Here,
Thus,
Therefore, the given statement is true.
54.
Ans:
Multiply each number with
Here,
Thus,
Therefore, the given statement is true.
55. If
Ans:
The multiplicative inverse of a number is a number which when multiplied by the original number yields
Then, if
Therefore, the given statement is true.
56. The multiplicative inverse of
Ans:
Let
The reciprocal of a number is a number (multiplicative inverse) which when multiplied by the original number yields
Then,
Divide each side with
Thus, the multiplicative inverse of
Therefore, the given statement is false.
57. The additive inverse of
Ans:
The additive inverse of a number is the number that, when added to the original number, yields zero.
Let
Then,
That is, additive inverse of
Therefore, the given statement is false.
58. If
Ans:
The additive inverse of a number is the number that, when added to the original number, yields zero.
If
Therefore, the given statement is true.
59. For every rational number
Ans:
For every rational number
Therefore, the given statement is false.
60. 58. If
Ans:
The additive inverse of a number is the number that, when added to the original number, yields zero.
If
Therefore, the given statement is false.
61. The reciprocal of a non-zero rational number
Ans:
The reciprocal of a number is a number (multiplicative inverse) which when multiplied by the original number yields
The reciprocal of a non-zero rational number
Therefore, the given statement is true.
62. If
Ans:
If
Therefore, the given statement is false.
63. The negative of the negative of any rational number is the number itself.
Ans:
If
So, the negative of the negative of any rational number is the number itself.
Therefore, the given statement is true.
64. The negative of
Ans:
Zero has no sign, neither positive nor negative.
So, the negative of
Therefore, the given statement is true.
65. The negative of
Ans:
The negative of
Therefore, the given statement is false.
66. For all rational numbers
Ans:
Subtraction and division are not commutative for rational numbers.
That is, for all rational numbers
Therefore, the given statement is false.
67. For all rational numbers
Ans:
Multiplication is commutative for rational numbers.
That is, for all rational numbers
Therefore, the given statement is true.
68. For every rational number
Ans:
The product of any number and zero will be zero.
Therefore, the given statement is false.
69. For every rational numbers
Ans:
Distributive property of addition over multiplication is not closed in rational numbers.
Therefore, the given statement is false.
70. For all rational numbers
Ans:
According to distributive property of multiplication over addition,
Therefore, the given statement is false,
71.
Ans:
The numbers which are their own reciprocals are
Therefore, the given statement is false.
72.
Ans:
The reciprocal of
Therefore, the given statement is false.
73. For any rational number
Ans:
If
Therefore, the given statement is false.
74. For rational numbers
Ans:
For rational numbers
Therefore, the given statement is false.
75. If
Ans:
If
Therefore, the given statement is true.
76. Between any two rational numbers there are exactly ten rational numbers.
Ans:
Between any two rational numbers there are infinite rational numbers.
Therefore, the given statement is false.
77. Rational numbers are closed under addition and multiplication but not under subtraction.
Ans:
Rational numbers are closed under addition, multiplication and subtraction.
Therefore, the given statement is false.
78. Subtraction of rational numbers is commutative.
Ans:
Subtraction is not commutative for rational numbers because while performing subtraction, if the order of numbers is changed, then the result also changes.
Therefore, the given statement is false.
79.
Ans:
Multiply the numbers by
Here,
Then,
Therefore, the given statement is false.
80.
Ans:
It is known that every integer is a rational number and Zero can be represented as the ratio of two integers.
Therefore, the given statement is true.
81. All positive rational numbers lie between
Ans:
There are infinite positive rational numbers.
Therefore, the given statement is false.
82. The population of India in
Ans:
it is known that every integer is a rational number.
So, the population of India in
Therefore, the given statement is true.
83. There are countless rational numbers between
Ans:
There are infinite positive rational numbers.
Therefore, the given statement is true.
84. The reciprocal of
Ans:
The reciprocal of a number is a number (multiplicative inverse) which when multiplied by the original number yields
Here, both are the same numbers.
Therefore, the given statement is false.
85. The rational number
Ans:
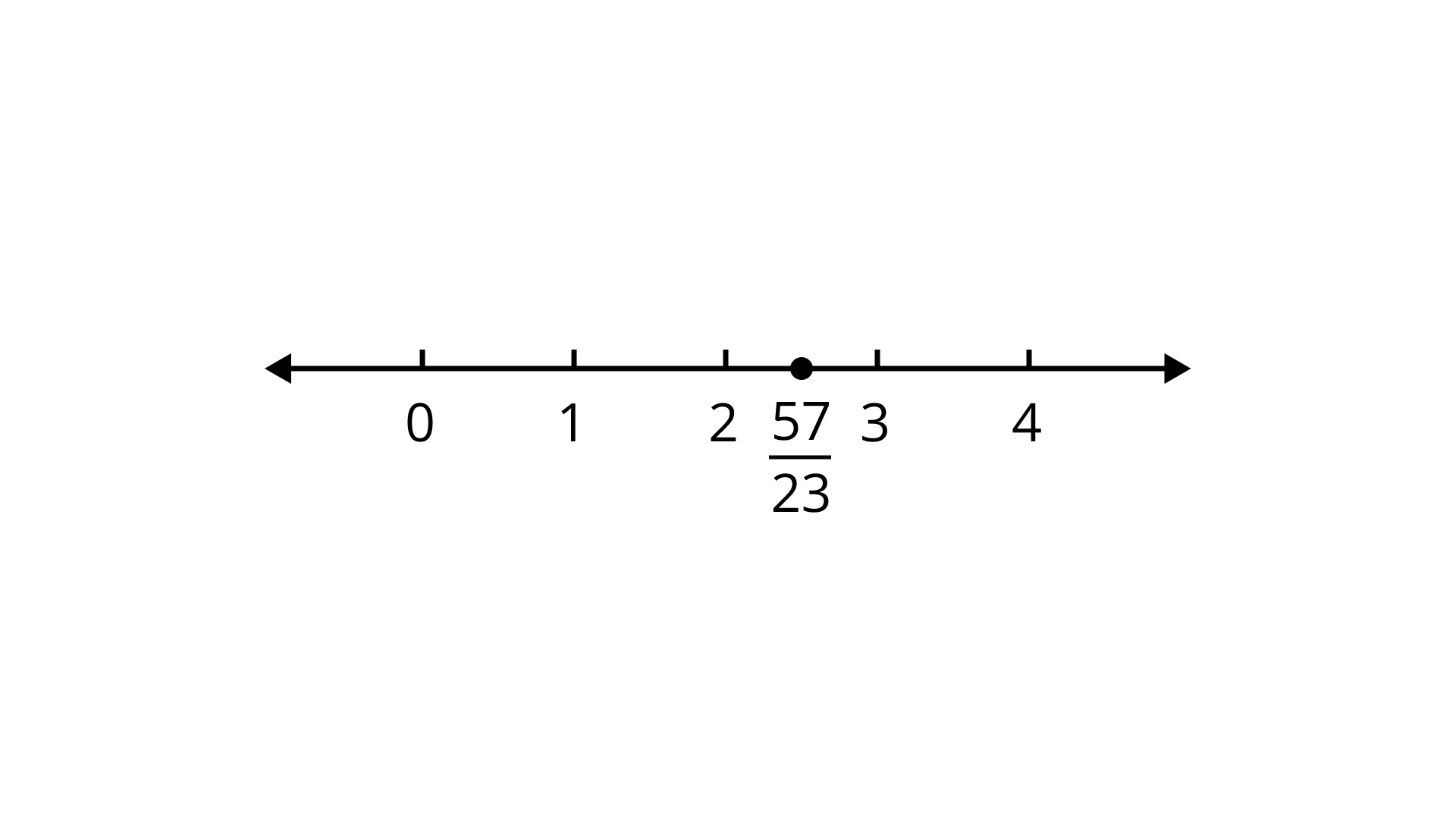
Therefore, the given statement is false.
86. The rational number
Ans:
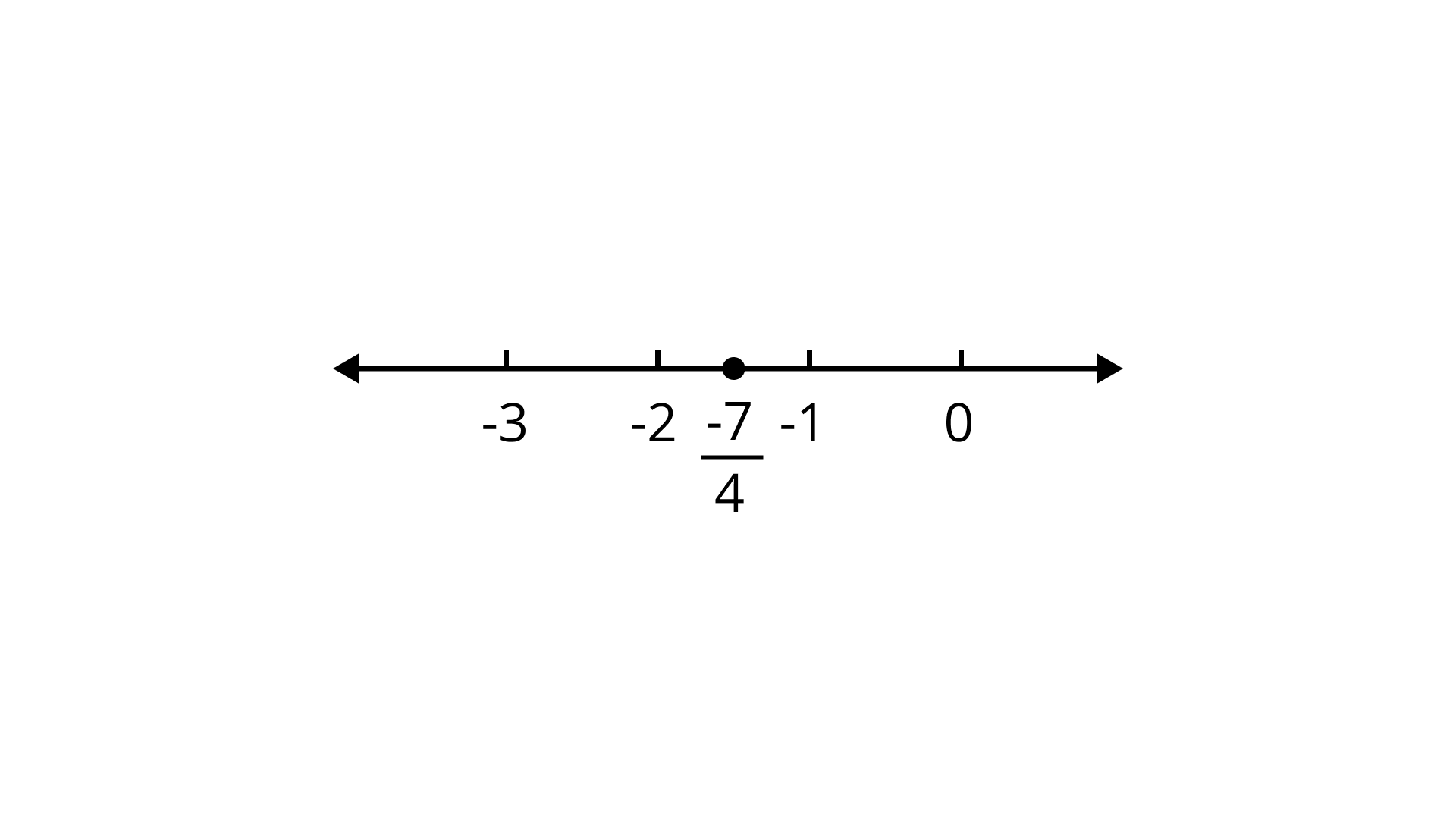
Therefore, the given statement is false.
87. The rational number
Ans:
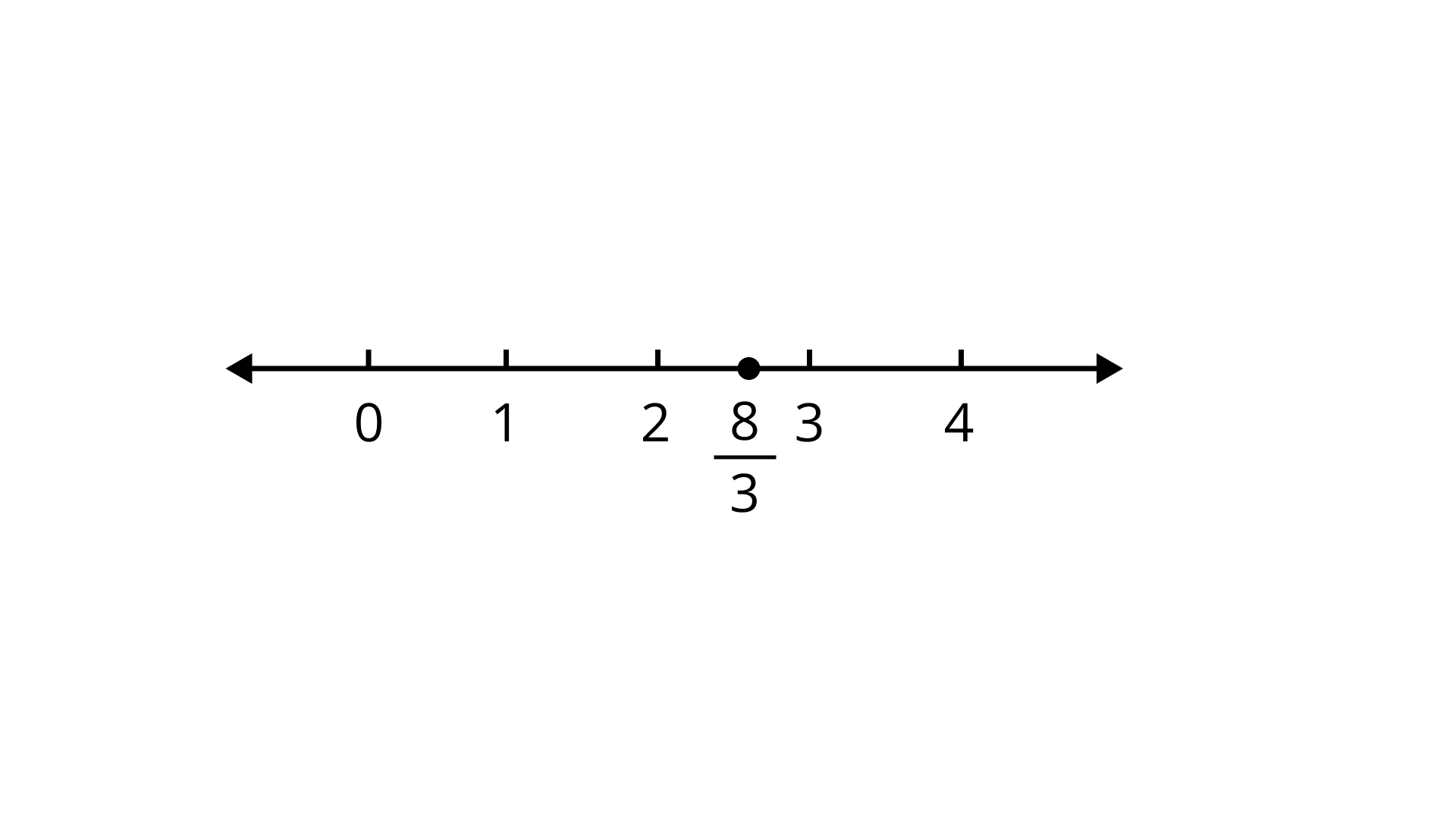
Therefore, the given statement is false.
88. The rational numbers
Ans:
That is,
Therefore, the given statement is true.
89. Every fraction is a rational number.
Ans:
It is known that the rational number is in the form of
Any fraction with non-zero denominators is a rational number.
Therefore, the given statement is true.
90. Every integer is a rational number.
Ans:
We can write integers in the form of
That means, every integer is a rational number.
Therefore, the given statement is true.
91. The rational numbers can be represented on the number line.
Ans:
Rational numbers can be represented on the number line.
Positive rational numbers are represented on the right side of zero and negative on left side of zero.
Therefore, the given statement is true.
92. The negative of a negative rational number is a positive rational number.
Ans:
If
So, the negative of the negative of a rational number is a positive rational number.
Therefore, the given statement is true.
93. If
Ans:
For rational numbers
Therefore, the given statement is true.
94.
Ans:
It is known that the rational number is in the form of
So,
Therefore, the given statement is false.
95. Every whole number is an integer.
Ans:
Whole numbers begin from
That means, every whole number is an integer.
Therefore, the given statement is true.
96. Every whole number is a rational number.
Ans:
Whole numbers begin from
They can be written in the form of
That means, every whole number is a rational number.
Therefore, the given statement is true.
97.
Ans:
it is known that every integer is a rational number and Zero can be represented as the ratio of two integers.
It is also known that, whole numbers begin from
That means, zero is a rational number as well as a whole number.
Therefore, the given statement is false.
98. The rational numbers
Ans:
Therefore, the given statement is true.
99. Rational numbers can be added (or multiplied) in any order
Ans:
Rational numbers are closed under addition multiplication.
That means, they can be added or multiplied in any order.
Therefore, the given statement is true.
100. Solve the following: Select the rational numbers from the list which are also the integers.
Ans:
Integers in the form of
So, the rational numbers which are also the integers are,
101. Select those which can be written as a rational number with denominator
Ans:
102. Using suitable rearrangement and find the sum:
(a)
Ans:
Add first two terms and add next two terms,
Take LCM,
Subtract the numbers,
Divide numerator and denominator by
(b)
Ans:
Rewrite the terms,
Add the first two numbers,
Subtract the numbers,
Take LCM,
Subtract the numbers,
Divide numerator and denominator by
103. Verify
(i)
Ans:
Here,
(ii)
Ans:
Here,
(iii)
Ans:
Here,
104. Give one example each to show that the rational numbers are closed under addition, subtraction, and multiplication. Are rational numbers closed under division? Give two examples in support of your answer.
Ans:
(i) Addition:
(ii) Subtraction:
(iii) Multiplication:
Thus, we see that for addition, subtraction as well as multiplication, the result that we get is itself a rational number. This means that rational numbers are closed under addition, subtraction and multiplication.
Rational Numbers are closed under division except for zero.
105. Verify the property
(a)
Ans:
Substitute
LHS
RHS
Here, LHS
Hence, verified.
(b)
Ans:
Substitute
LHS
RHS
Here, LHS
Hence, verified.
(c)
Ans:
Substitute
LHS
RHS
Here, LHS
Hence, verified.
(d)
Ans:
Substitute
LHS
RHS
Here, LHS
Hence, verified.
106. Simplify each of the following by using suitable property. Also name the property.
(a)
Ans:
Distributive property
(b)
Ans:
Distributive property
(c)
Ans:
Distributive property
107. Tell which property allows you to compute
Ans:
While multiplying three or more rational numbers, they can be grouped in any order.
Therefore, the given computation illustrates Associative property of multiplication.
108. Verify the property
(a)
Ans:
Substitute
LHS
RHS
Here, LHS
Hence, verified.
(b)
Ans:
Substitute
LHS
RHS
Here, LHS
Hence, verified.
(c)
Ans:
Substitute
LHS
RHS
Here, LHS
Hence, verified.
(d)
Ans:
Substitute
LHS
RHS
Here, LHS
Hence, verified.
109. Verify the property
(a)
Ans:
Substitute
LHS
RHS
Here, LHS
Hence, verified.
(b)
Ans:
Substitute
LHS
RHS
Here, LHS
Hence, verified.
(c)
Ans:
Substitute
LHS
RHS
Here, LHS
Hence, verified.
(d)
Ans:
Substitute
LHS
RHS
Here, LHS
Hence, verified.
110. Verify the property
(a)
Ans:
Substitute
LHS
RHS
Here, LHS
Hence, verified.
(b)
Ans:
Substitute
LHS
RHS
Here, LHS
Hence, verified.
(c)
Ans:
Substitute
LHS
RHS
Here, LHS
Hence, verified.
(d)
Ans:
Substitute
LHS
RHS
Here, LHS
Hence, verified.
111. Use the distributive of multiplication of rational numbers over addition to simplify
(a)
Ans:
By the distributive of multiplication of rational numbers over addition,
(b)
Ans:
By the distributive of multiplication of rational numbers over addition,
(c)
Ans:
By the distributive of multiplication of rational numbers over addition,
(d)
Ans:
By the distributive of multiplication of rational numbers over addition,
112. Simplify-
(a)
Ans:
Take LCM,
(b)
Ans:
Rewrite the terms,
(c)
Ans:
Take LCM,
(d)
Ans:
Take LCM,
113. Identify the rational number that does not belong with the other three. Explain your reasoning
Ans:
Whereas
114. The cost of
Ans:
Therefore, Cost of
115. A train travels
Ans:
Given that,
It is known that,
The speed of the train is
116. If
Ans:
Therefore,
117.
Ans:
Let all the Hamid's money is
Therefore, Hamid have Rs.
118. A
Ans:
Given that,
A
Now, Size of rope
Size of small pieces
Number of small pieces
Number of small pieces
Number of small pieces
119.
Ans:
Here,
Then, Total number of below average students
Number of students below average
120.
Ans:
Let the total number of students coming to school be
Students coming by car
Students coming by bus
Remaining students who walk to school
Students walk on their own
Therefore, Total number of students is
121. Huma, Hubna and Seema received a total of Rs.
Seema's share. How much money do the three sisters get individually?
Ans:
Allowances of Seema
Allowances of Hubna
Total amount
Huma's share
Seema's share
Hubna's share
Therefore, Hubna's share is Rs
122. A mother and her two daughters got a room constructed for Rs.
Ans:
Let the share of the mother is
Then, Elder daughter's share
Younger daughter's share
Total amount
That is,
So, Mother contributes Rs.
Elder daughter's share
Younger daughter's share
123. Tell which property allows you to compare
Ans:
Use commutative property of multiplication in
Use associative property of multiplication in
Hence, the statement
124. Name the property used in each of the following-
(i)
Ans:
Two rational numbers can be multiplied in any order. Multiplication is commutative for rational numbers.
In general,
Therefore, the statement
(ii)
Ans:
In general,
Therefore, the statement
(iii)
Ans:
According to Associative Property of Addition
(iv)
Ans:
If we add any rational number with 0, we get that rational number as the sum.
In general,
Here,
Therefore, the statement
(v)
Ans:
If we multiply any rational number with
Here,
Therefore, the statement
125. Find the multiplicative inverse of
(i)
Ans:
Rewrite the fraction as
Let
The reciprocal of a number is a number (multiplicative inverse) which when multiplied by the original number yields
Then,
Divide each side with
Therefore, multiplicative inverse of
(ii)
Ans:
Rewrite the fraction as
Let
The reciprocal of a number is a number (multiplicative inverse) which when multiplied by the original number yields
Then,
Divide each side with
Therefore, multiplicative inverse of
126. Arrange the numbers
Ans:
Let's make their denominator same:
Descending order:
127. The product of two rational numbers is
Ans:
Given that, one number is
Let the other number is
It is also given that, the product of two rational numbers is
Then,
Therefore, the other number is
128. By what numbers should we multiply
Ans:
Let the number is
Then,
Therefore, we should multiply
129. By what number should we multiply
Ans:
Let the number is
Then,
Multiply and divide the numbers,
Therefore, we should multiply
130. The product of two rational numbers is
Ans:
Let the other number is
Then,
Therefore, the other number is
131.Can you find a rational number whose multiplicative inverse is
Ans:
Let
The reciprocal of a number is a number (multiplicative inverse) which when multiplied by the original number yields
Then,
Divide each side with
Therefore, multiplicative inverse of
132. Find five rational numbers between
Ans:
Rational numbers between
(i)
(ii)
(iii)
133. Find two rational numbers whose absolute value is
Ans:
Absolute numbers are the numbers which can be plotted on the number line.
For
134. From a rope
Ans:
Length of one piece
Now, Total number of pieces
135.
Ans:
Length of rope
Number of pieces
Therefore, Length of each piece
136. Write the following rational numbers in the descending order.
Ans:
Let’s make the denominators same:
According to this,
The rational numbers in the descending order is,
137. Find.
(i)
Ans:
Rewrite and simplify the expression,
(ii)
Ans:
Cancel the numbers,
138. On a winter day the temperature at a place in Himachal Pradesh was
Ans:
Temperature in Himanchal Pradesh
Formula to convert in Fahrenheit is,
Cross multiply,
Multiply the numbers,
139. Find the sum of additive inverse and multiplicative inverse of
Ans:
Additive inverse of
Multiplicative inverse of
Now, the sum of additive inverse and multiplicative inverse of
140. Find the product of additive inverse and multiplicative inverse of
Ans:
Additive inverse of
Multiplicative inverse of
Their product is
141. The diagram shows the wingspans of different species of birds. Use the diagram to answer the question given below:
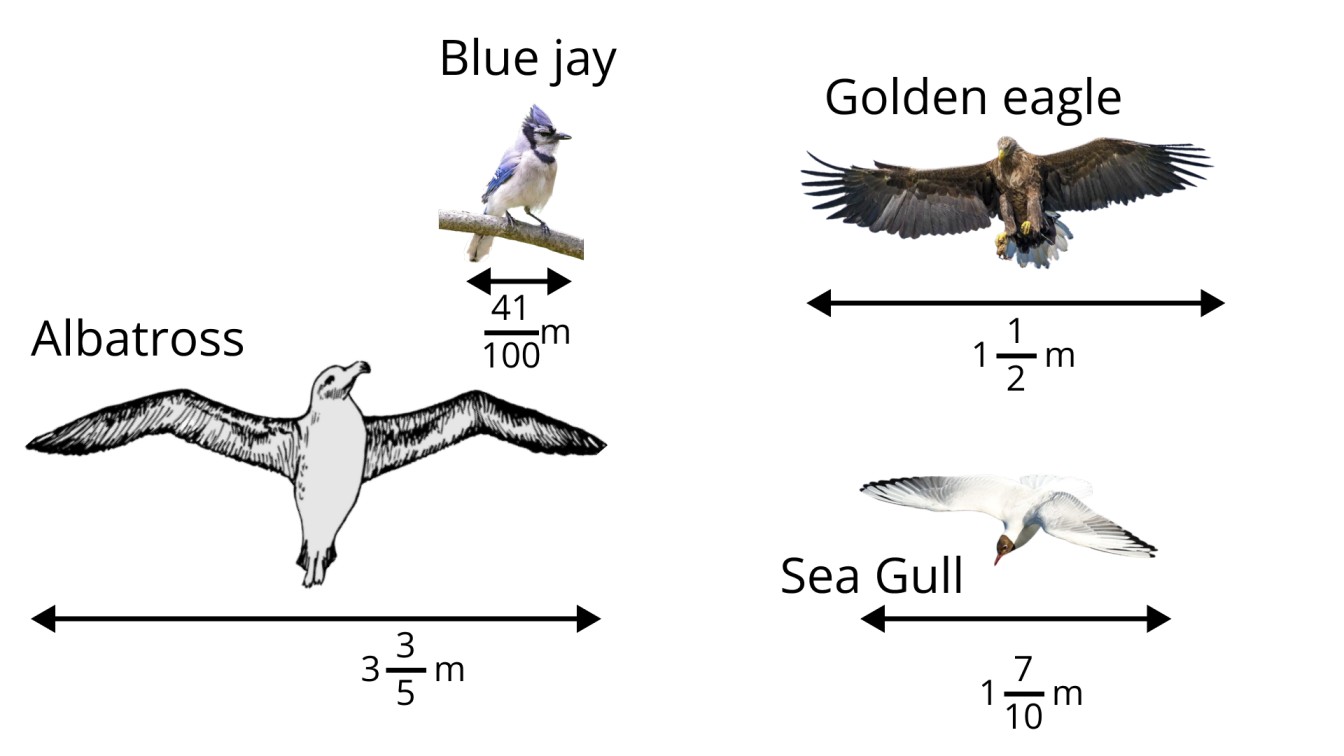
(a) How much longer is the wingspan of an Albatross than the wingspan of a Sea gull?
Ans:
The length of Albatross wing
Length of Sea gull
Difference between the lengths of their wingspan is,
(b) How much longer is the wingspan of a Golden eagle than the wingspan of a Blue jay?
Ans:
Length of Blue ray wings
142. Shalini has to cut out circles of diameter
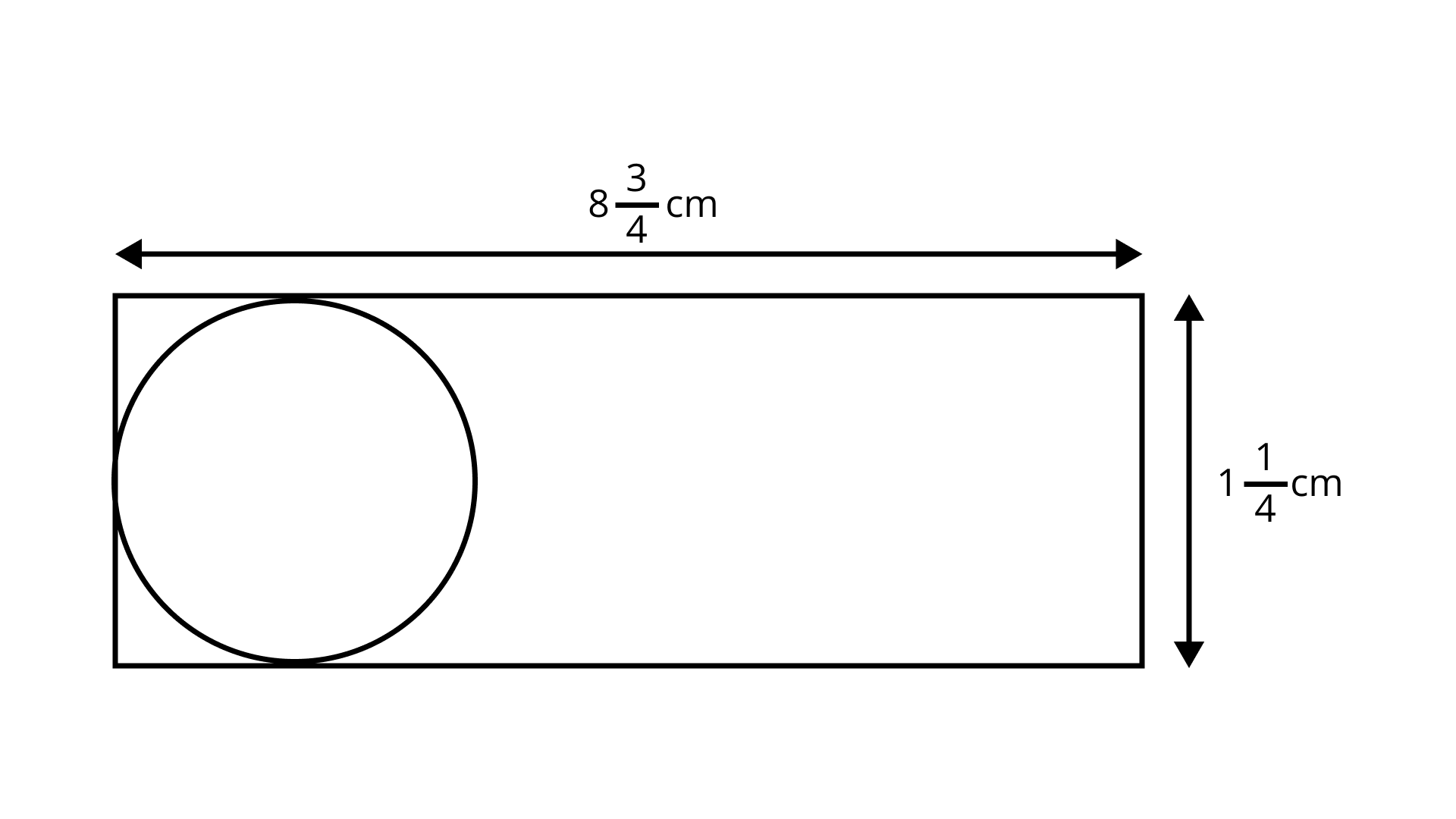
Ans:
Diameter of the circle
Length of Aluminum strip
Width of Aluminium
Number of circles that can be cut
Strip/diameter of circle
Area of aluminium strip
Area of circle
Wastage of aluminium strip
143. One fruit salad recipe requires
Ans:
Requirement for
Same recipe for same fruit
First recipe requires
144. Four friends had a competition to see how far they could hop on one foot. The table given shows the distance covered by each-
Name | Distance Covered |
Seema | |
Nancy | |
Megha | |
Sony |
(a) How farther did Soni hop than Nancy?
Ans:
Distance covered by Soni
Distance covered by Nancy
The distance covered by Soni than Nancy
(b) What is the total distance covered by Seema and Megha?
Ans:
Distance covered by Seema
Distance covered by Megha
Total distance covered by Seema and Megha
(c) Who walked farther, Nancy or Megha?
Ans:
Distance covered by Nancy
Distance covered by Megha
Therefore, Nancy walked further.
145. The table given below shows the distances, in kilometres, between four villages of a state. To find the distance between two villages, locate the square where the row for one village and the column for the other village intersect.
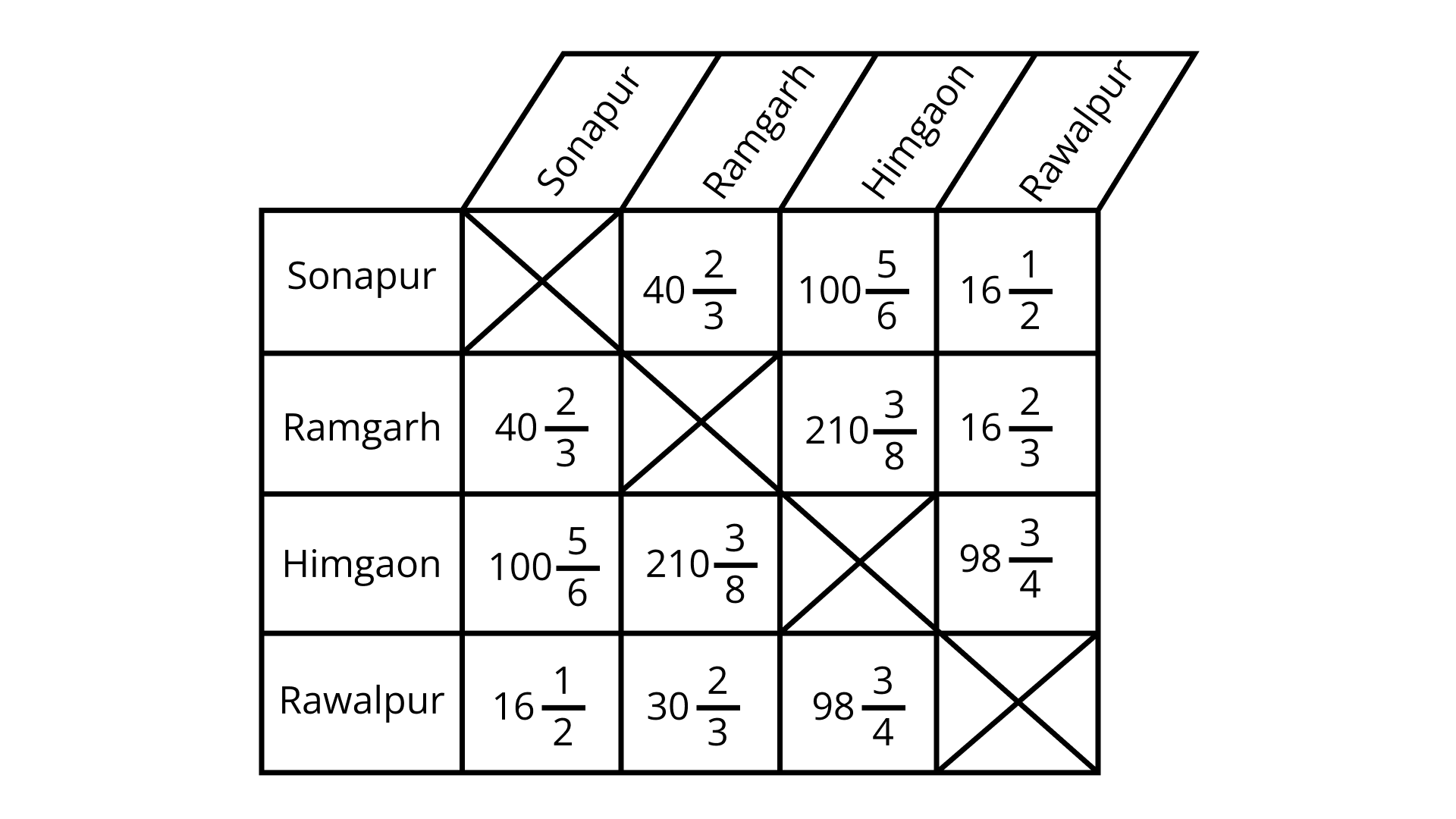
(a) Compare the distance between Himgaon and Rawalpur to Sonapur and Ramgarh?
Ans:
Distance between Himgton and Rawalpur
Distance between sonapur and ramgarh
On subtracting,
Therefore, the distance between Sonapur and Ramgarh is more than from Himgton and Rawalpur
(b) If you drove from Himgaon to Sonapur and then from Sonapur to Rawalpur, how far would you drive?
Ans:
Distance between Himgton to Sonpur
Distance between Sonapur to Rawalpur
Total distance
That is,
146. The table shows the portion of some common materials that are recycled.
Material | Recycled |
Paper | |
Aluminium Cans | |
Glass | |
Scap |
(a) Is the rational number expressing the amount of paper recycled more than
Ans:
Paper recycled
(b) Which items have a recycled amount less than
Ans:
Paper and Glass have a recycled amount less than
(c) Is the quantity of aluminium cans recycled more (or less) than half of the quantity of aluminium cans?
Ans:
The quantity of aluminium cans recycled more than half of the quantity of aluminium
(d) Arrange the rate of recycling the materials from the greatest to the smallest.
Ans:
The rate of recycling the materials from the greatest to the smallest is,
147. The overall width in cm of several wide-screen televisions are
Ans:
Rewrite the numbers as improper fractions,
The arrangement is,
Their ascending order is,
148. Roller Coaster at an amusement park is
Ans:
Height of the roller coaster of the amusement park
The height of new roller coaster is
Then, the height of the new roller coaster
149. Here is a table which gives the information about the total rainfall for several months compared to the average monthly rains of a town. Write each decimal in the form of rational number
Month | Above/Below normal (in cm) |
May | |
June | |
July | |
August |
Ans:
Consider
Multiply and divide the decimal by
Consider
Multiply and divide the decimal by
Consider
Multiply and divide the decimal by
Consider
Multiply and divide the decimal by
150. The average life expectancies of males for several states are shown in the table. Express each decimal in the form
State-wise data are included below; more indicators can be found in the "FACTFILE" section on the homepage for each state.
State | Male | Lowest | |
Andhra Pradesh | |||
Assam | |||
Bihar | |||
Gujarat | |||
Haryana | |||
Himanchal Pradesh | |||
Karnataka | |||
Kerala | |||
Madhya Pradesh | |||
Maharashtra | |||
Orissa | |||
Punjab | |||
Rajasthan | |||
Tamil Nadu | |||
Uttar Pradesh | |||
West Bengal | |||
India |
Source: Registrar General of India (
Ans:
State | Male | Lowest | |
Andhra Pradesh | |||
Assam | |||
Bihar | |||
Gujarat | |||
Haryana | |||
Himanchal Pradesh | |||
Karnataka | |||
Kerala | |||
Madhya Pradesh | |||
Maharashtra | |||
Orissa | |||
Punjab | |||
Rajasthan | |||
Tamil Nadu | |||
Uttar Pradesh | |||
West Bengal | |||
India |
151. A skirt that is
Ans:
Length of skirt
Length of Hem
Total length of skirt
152. Manavi and Kuber each receives an equal allowance. The table shows the fraction of their allowance each deposits into his/her saving account and the fraction each spends at the mall. If the allowance of each is Rs.
Where money goes | Fraction of allowance | |
Manavi | Kuber | |
Saving Account | ||
Spend at mall | ||
Left over | ? | ? |
Ans:
Let the total cost
For Manavi,
Left over
That is,
Amount
For Kuber,
Left over
Amount
NCERT Solutions To Help You To Revise The Complete Syllabus And Score More Marks In Your Examinations
Numbers are often regarded as the most essential building component of mathematics. Students would have learnt about the different sorts of numbers in lower grades, such as natural numbers, whole numbers, integers, and so on. The rational numbers are mentioned in Chapter 1 of Class 8 Math to introduce students to a different set of numbers. This Chapter covers nearly all of the rational number topics that a student in Class 8 is required to master to understand the course. In addition, the method of expressing a rational number on a number line, as well as the method of finding rational numbers between two rational numbers, are described in this Chapter. Continue reading and studying Math Chapter 1 of the NCERT to understand better Rational Numbers and the ideas behind it.
NCERT Exemplar for Class 8 Math Chapter 1 is available online on Vedantu’s website. It is recommended that students complete the questions of each Chapter to achieve good results in the Class 8 Mathematics test. These NCERT Solutions for Class 8 assist the students in gaining a better knowledge of the subjects.
The Main Topics Covered In This Chapter Include
1.1 Introduction
1.2 Properties of Rational Numbers
1.2.1 Closure
1.2.2 Commutativity
1.2.3 Associativity
1.2.4 The role of zero
1.2.5 The role of 1
1.2.6 Negative of a number
1.2.7 Reciprocal
1.2.8 Distributivity of multiplication over addition for rational numbers.
1.3 Representation of Rational Numbers on the Number Line
1.4 Rational Numbers between Two Rational Numbers
FAQs on NCERT Exemplar for Class 8 Maths Solutions Chapter 1 Rational Numbers
1. What are the important things to follow while preparing for Class 8 Math?
To study and excel in mathematics, you must put in the necessary time and effort to understand, solve and practice.
You must read sample papers to have an understanding of the subject.
Concentrate on complex subjects and make sure you fully comprehend all of the principles. Always attempt to do the difficult task first, rather than completing the simpler task first.
Refer to the sample papers and put in a lot of time practicing them. Each idea is given Chapter-by-Chapter in these papers, and students get a fundamental understanding of the subject matter.
When it comes to a specific issue, you must be assured that you have no reservations about it. By removing any ambiguities, you will be able to concentrate on your studies and achieve success.
2. What is the importance of practicing Math from NCERT Exemplar Class 8?
The extensive explanations provided for Class 8 mathematics assist students in grasping the underlying concepts and improving in troublesome areas. Additionally, they present the processes in an easy-to-follow fashion to avoid misunderstanding. Thus, these Exemplars contribute to the establishment of a solid mathematical basis.
These NCERT Class 8 mathematics answers help learners plan their time to study the full course. It also allows them to revise all questions. The answers provide students with a short overview of problem-solving. During exams, students may rapidly browse over the solutions to help them recollect how to approach various question types.
The NCERT Solution Paper for Class 8 mathematics provides students with an understanding of how to solve a problem with great precision and efficiency. They educate learners with strategies and techniques for earning the highest possible grade.
3. When referring to the NCERT Exemplar Class 8 Mathematics, is it necessary to take notes?
It is always good to take notes when studying Math since they serve as guides for students while they revisit and revise specific topics. Additionally, notes assist students in quickly recalling concepts involved in a problem. This significantly decreases the amount of time required to review a topic during examination time. It helps in distinguishing between important elements and details. It helps in quickly grasping a concept if the notes are written in your own words. It also helps in comprehension, concentration and keeps a lasting record. Additionally, taking notes enhances focus and aids in exam preparation. It will be simple to transform your notes into a to-do list for final test revisions.
4. Is it necessary to practise all of the questions in the Class 8 Math NCERT Exemplar?
Because the CBSE school examinations are based on the syllabus included in the NCERT textbooks, students need to practise all of the problems found in the Class 8 mathematics NCERT Exemplar before taking the exam. Practicing questions can also help you enhance your writing and presenting abilities with these papers. After practicing with sample papers, students can assess their level of preparation and identify areas in which they are deficient in their preparation. Regular revision and a dedicated effort will go a long way toward achieving excellent grades in any examination, whether it is a school test or a competitive paper of any kind.
5. Where can I get the NCERT Exemplar for Class 8 Math?
Vedantu's app and website gather all of the relevant information for students taking Class 8 Maths tests and exams. Because they were created by subject-matter experts, the material included in these resources is accurate and trustworthy. Students will have access to review notes and critical questions, as well as question papers and a variety of additional resources. These study resources are completely free of charge, and there are no hidden fees or expenditures related to their usage. The Solutions Paper is available in PDF format. Students can gain access to this material by using the Vedantu app, which is available for download. Registration is entirely voluntary. Make use of these free resources that will unquestionably support you in accomplishing your goals in examinations.
















