Class 8 Maths NCERT Exemplar Solutions Chapter 3 Square-Square Root & Cube-Cube Root
Free PDF download of NCERT Exemplar for Class 8 Maths Chapter 3 - Square-Math & Cube-Cube Root solved by expert Maths teachers on Vedantu.com as per NCERT (CBSE) Book guidelines. All Chapter 3 - Square-Math & Cube-Cube Root exercise questions with solutions to help you to revise the complete syllabus and score more marks in your examinations.
Vedantu is a platform that provides free NCERT Solution and other study materials for students. Science Students who are looking for NCERT Solutions for Class 8 Science will also find the Solutions curated by our Master Teachers Helpful.
You can also Download NCERT Solutions for Class 8 Maths to help you revise the complete Syllabus and score more marks in your examinations.
Access NCERT Exemplar Solutions for NCERT Solutions for Class 8 Mathematics Chapter 3 - Square and Roots
In Examples 1 to 7, out of given four Choices Multiple only one is Correct. Write the Correct Answer
Example 1: Which of the following is the square of an odd number?
(a) 256
(b) 361
(c) 144
(d) 400
Ans: (b) because
Example 2: Which of the following will have
(a)
(b)
(c)
(d)
Ans: (a) because
Example 3: How many natural numbers lie between
(a)
(b)
(c)
(d)
Ans: (d) As
Therefore,
Example 4: Which of the following is not a perfect square?
(a)
(b)
(c)
(d)
Ans: (c) As in
Example 5: A perfect square can never have the following digit at one’s place.
(a)
(b)
(c)
(d)
Ans: (d) digits ending with
Example 6: The value of
(a)
(b)
(c)
(d)
Ans: (b)
Example 7: Given that
(a)
(b)
(c)
(d)
Ans: (c)
Therefore,
In examples 8 to 14, fill in the blanks to make the statements true.
Example 8: There are __________ perfect squares between
Ans: There are
Example 9: The cube of
Ans: Cube of
Example 10: The square of
Ans:
Example 11: The cube of
Ans:
Example 12:
Ans: Because
Example 13: The positive square root of a number
Ans:
Example 14: The least number to be multiplied with
Ans:
In examples 15 to 19, state whether the statements are true (T) or false (F)
Example 15: The square of
Ans: True, because
Example 16: The cube root of
Ans: False because
Example 17: There are
Ans: False because
Example 18: The sum of first
Ans: True, because first seven odd natural numbers are
And their sum:
Example 19: The square root of a perfect square of
Ans: True, as a square root of a perfect square of
Example 20: Express
Ans: successive odd natural numbers are
Example 21: Check whether
Ans: Taking factors of
Example 22: Check whether
Ans: Taking factors of
So,
As all prime factors forms triplets. So,
Example 23: Using distributive law, find the square of
Ans: Finding square using distributive law:
As
So,
Therefore,
Example 24: Write a Pythagorean triplet whose smallest number is
Ans: Given that smallest number is
Pythagorean triplet is given by:
Now,
Therefore, the Pythagorean triplet is
Example 25: Using prime factorisation, find the cube root of
Ans: Prime factors of
Example 26: Evaluate the square root of
Ans: Square root of
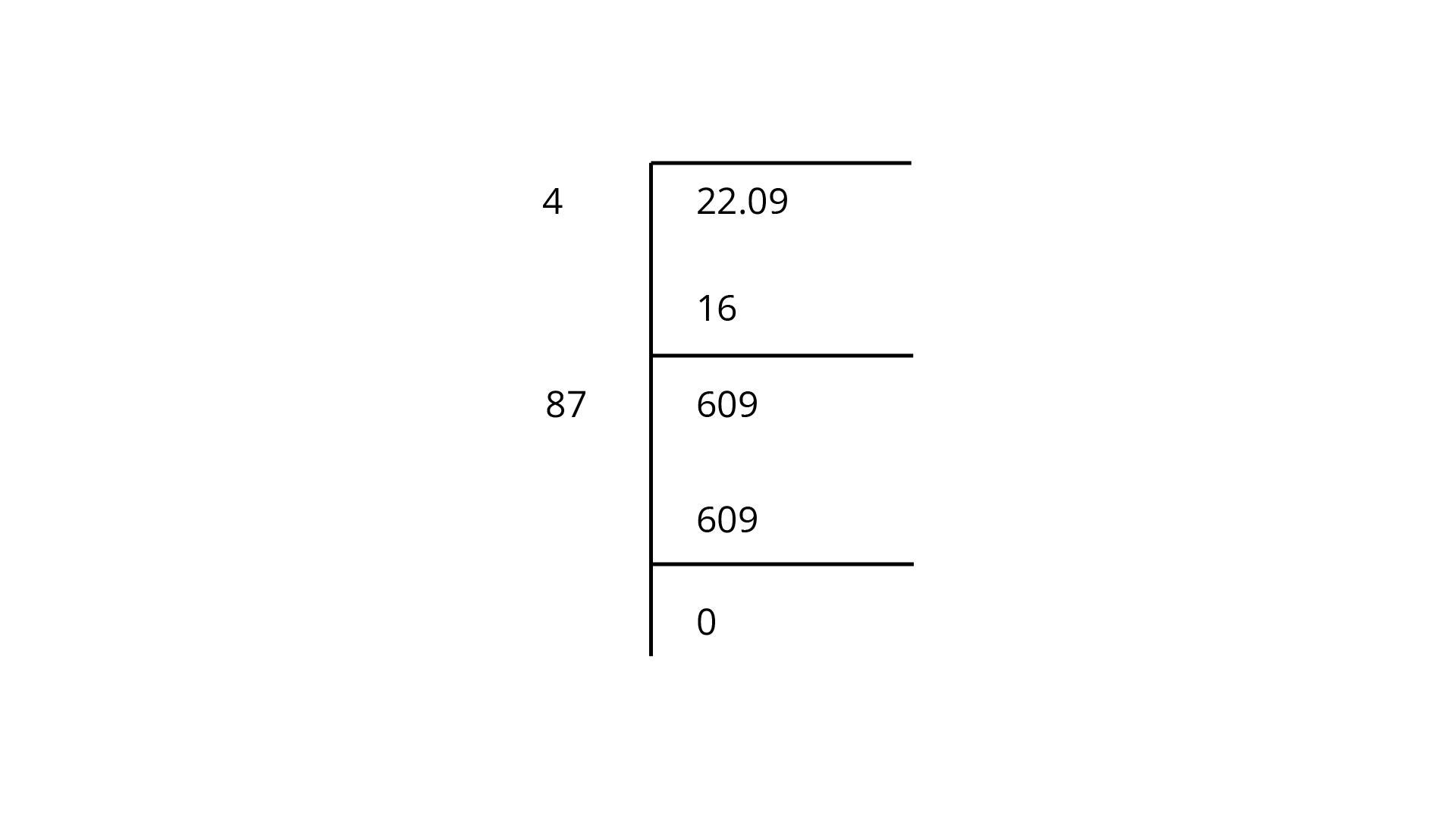
Example 27: Find the smallest perfect square divisible by 3, 4, 5 and 6.
Ans: The least number divisible by
The LCM of
Now,
As
So, the required least square number is
Example 28: A ladder
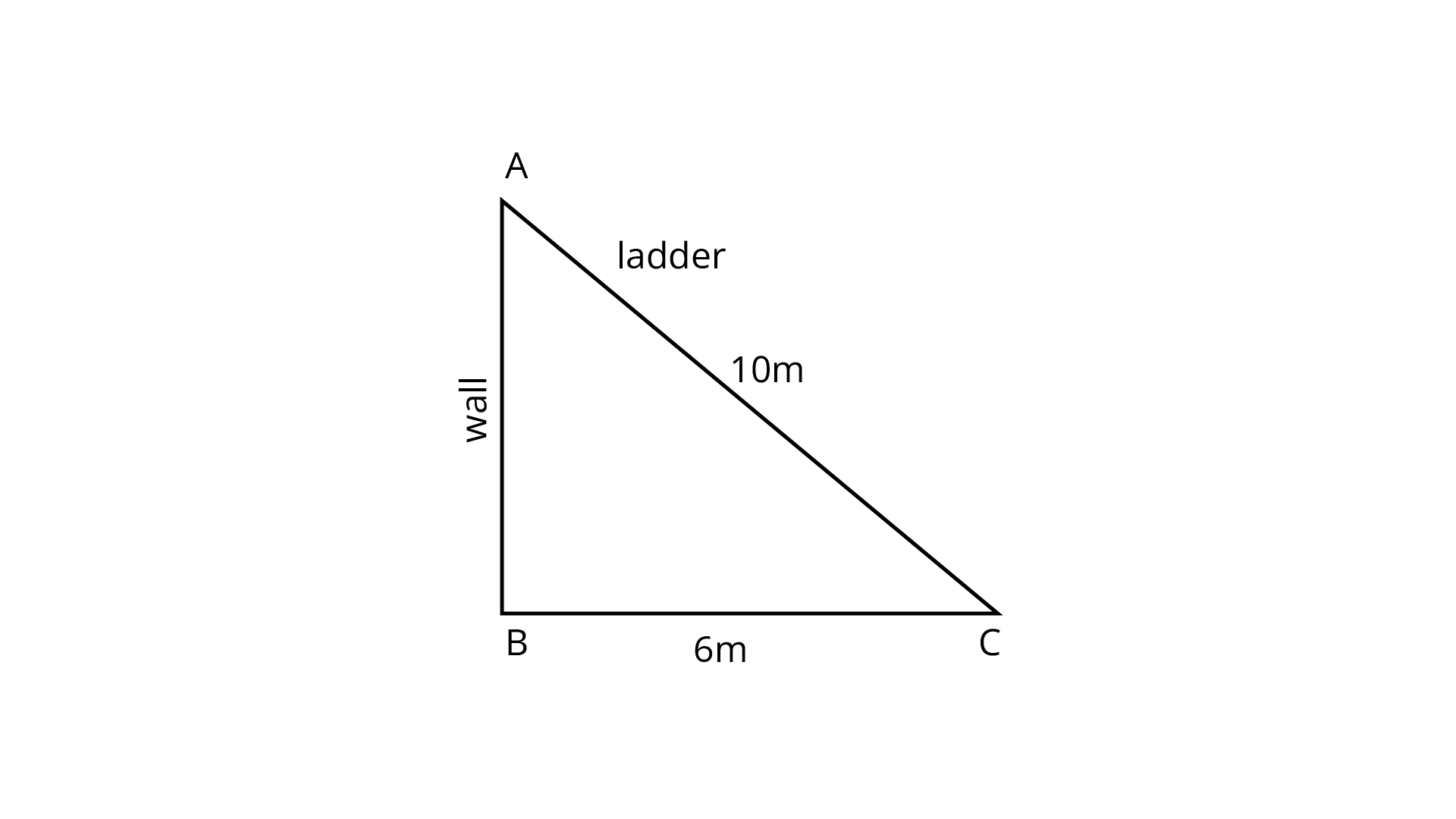
Ans: Let
Given:
Because
Hence, the wall is
Example 29: Find the length of a diagonal of a rectangle with dimensions
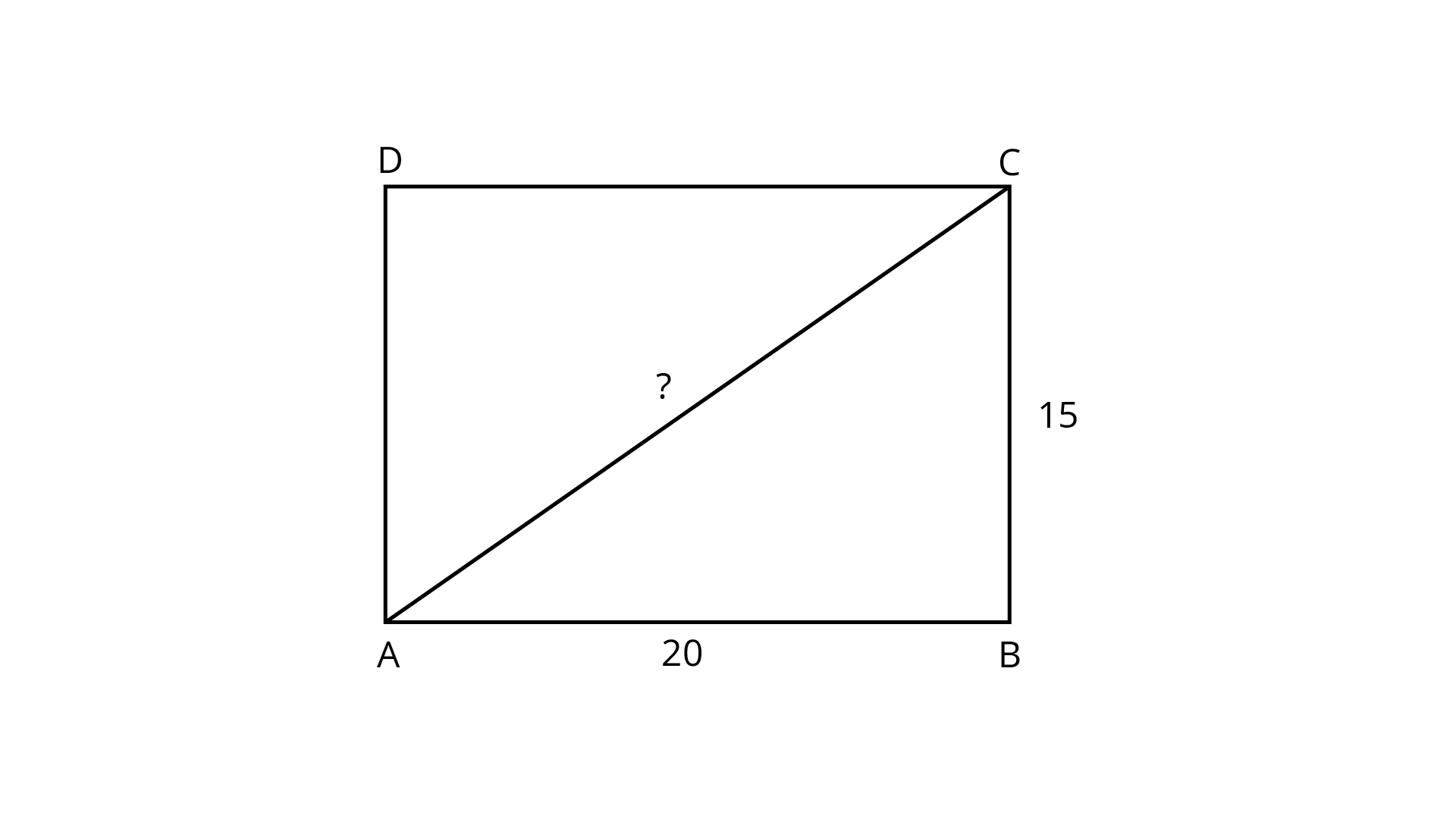
Ans:
By using Pythagoras theorem, we know
Length of diagonal of the rectangle is given by
Thus, the length of diagonal is
Example 30: The area of a rectangular field whose length is twice its breadth is
Ans: If the breadth of the field is
We know, area of the rectangular field
Also given, area is
Therefore,
Therefore, breadth
Now the, perimeter of the field
Example 31: During a mass drill exercise,
Ans: Given total number of students
students forming a square
Thus,
Now let the number of students in each row be
Therefore,
or
So, there are
Example 32: Find the least number that must be added to
Ans:
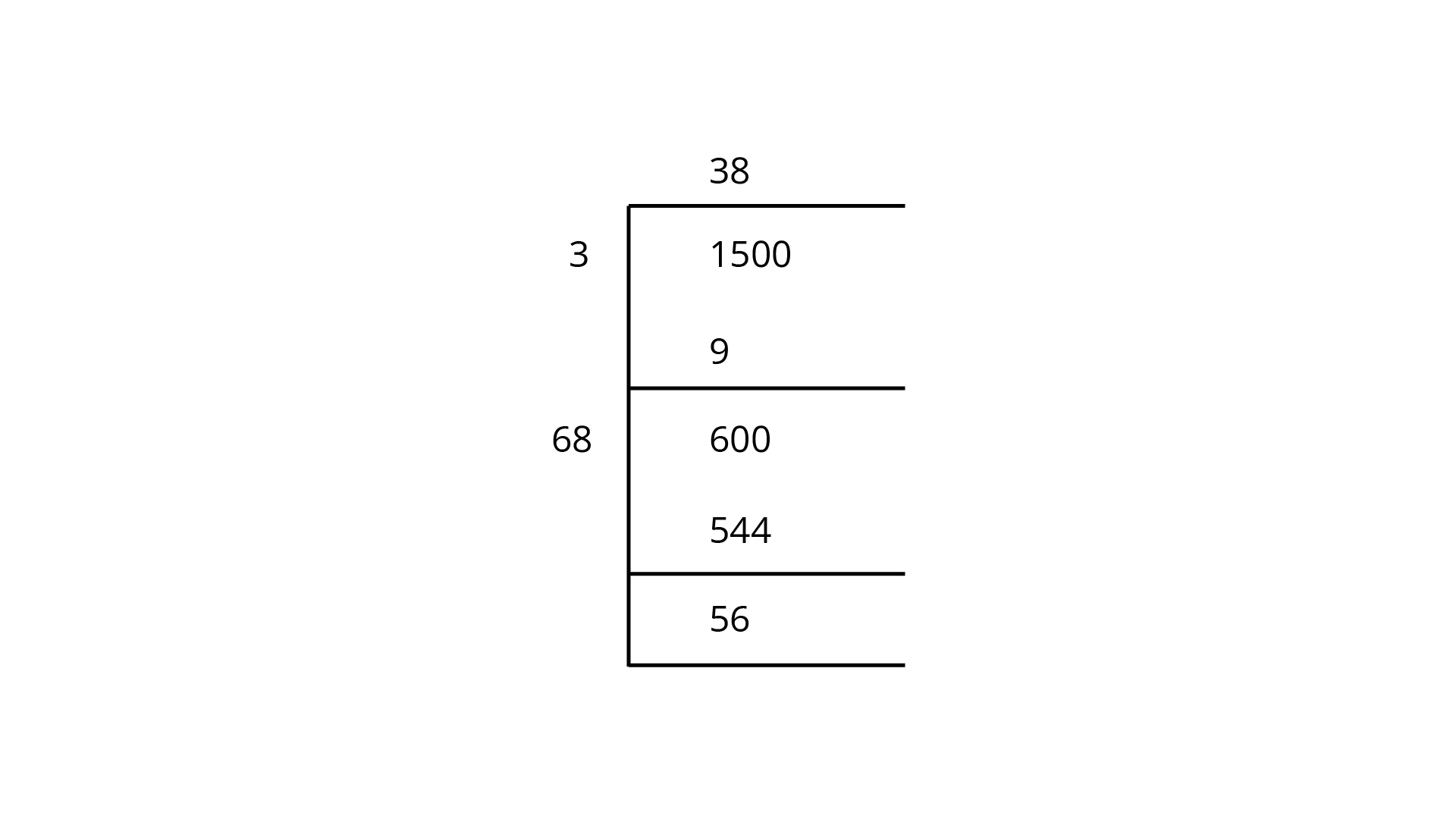
We can see
Hence, the number to be added
=15211500
=21
Therefore, the perfect square
Thus, the required number is
Example 33: Application of problem solving strategies
Finding the smallest number by which
Ans: Understand and Explore:
What information is given in the question? – A number which is not a perfect square.
What are we trying to find? – The smallest number by which
Using prime factorisation to find the product of prime factors of
Pairing the prime factors to see if any factor is left unpaired.
Then the unpaired factor will be the smallest number that must be divided to get a perfect square.
Solve: Prime factorisation of
The product of prime factors
After Pairing these prime factors
We can see that the factor
To check if it is a perfect square. Divide
We can see that on dividing
Multiple question Answer
In each of the questions, 1 to 24, write the correct Answer from the given four options:
1.
a)
b)
c)
d)
Ans: (c),
Breaking
Taking pairs out
Therefore, square root of 196 is 14.
2. Which of the following is a square of an even number?
a)
b)
c)
d)
Ans: (a),
Therefore, square of an even number is:
3. A number ending in
a)
b)
c)
d)
Ans: (c),
We know
Therefore, unit place of a number ending with
4. Which of the following will have 4 at the unit place?
a)
b)
c)
d)
Ans: (b),
Because, unit digit of
Square of
5. How many natural numbers lie between
a) 9
b) 10
c) 11
d) 12
Ans: (b), 10.
We know, natural numbers lie between
31, 32, 33, 34, 35. So there are
6. Which of the following cannot be a perfect square?
a)
b)
c)
d) All of the above
Ans: (c), 198.
7. The one’s digit of the cube of 23 is
a)
b)
c)
d)
Ans: (b),
We know, unit digit of
And cube of
8. A square board has an area of
a)
b)
c)
d)
Ans: (b),
We know,
9. Which letter best represents the location of
a) A
b) B
c) C
d) D
Ans: (c), C
We know, square of
10. If one member of a Pythagorean triplet is
a)
b)
c)
d)
Ans: (b),
Therefore, the formula of Pythagorean triplet is:
11. The sum of successive odd numbers
a)
b)
c)
d)
Ans: (b),
Total numbers are
successive odd numbers
sum of successive odd numbers is
12. The sum of first n odd natural numbers is
a)
b)
c)
d)
Ans: (b),
We know, sum of first n odd natural numbers is given by:
13. Which of the following numbers is a perfect cube?
a)
b)
c)
d)
Ans:(b),
As square of 6 is
14. The hypotenuse of a right triangle with its legs of lengths
a)
b)
c)
d)
Ans: (a),
We know,
15. The next two numbers in the number pattern
a)
b)
c)
d)
Ans: (b),
As the given pattern is a series of perfect squares so the next term will be
16. Which among
a)
b)
c)
d)
Ans: (d),
Because unit digit of
And square of
17. A perfect square can never have the following digit in its ones place.
a)
b)
c)
d)
Ans: (b),
18. Which of the following numbers is not a perfect cube?
a)
b)
c)
d)
Ans: (b),
Factors of
19.
a)
b)
c)
d) None of these
Ans: (a),
20. If m is the square of a natural number n, then n is
a) The square of m
b) Greater than m
c) Equal to m
d)
Ans: (d),
Square of
According to the question:
21. A perfect square number having n digits where n is even will have square root with
a)
b)
c)
d)
Ans: (b),
22. If m is the cube root of n, then n is
a)
b)
c)
d)
Ans: (a),
23. The value of
a)
b)
c)
d)
Ans: (c),
24. Given that
a)
b)
c)
d)
Ans: (d),
As
Also,
And,
Then,
In questions 25 to 48, fill in the blanks to make the statements true.
25. There are _________ perfect squares between
Ans:
Perfect square between
26. There are _________ perfect cubes between
Ans: 8
There are
27. The unit digit in the square of
Ans:
Unit digit in
Therefore, the square of
28. The square of
Ans:
29. There are _________ natural numbers between
Ans:
30. The square root of
Ans:
Number of digits in a square root for odd digit is given by
Number of digits in a given number is
Therefore
31. The square of
Ans:
32. The square root of
Ans: 28.09
33. The cube of
Ans:
34.
Ans:
35.
Ans:
36. Ones digit in the cube of
Ans:
Unit digit is
Therefore, unit digit in the cube of
37. The square of
Ans:
Therefore, square of
38. The sum of first six odd natural numbers is _________.
Ans:
First six odd natural numbers are
Sum of First six odd natural numbers are
39. The digit at the ones place of
Ans:
As unit digit of
40. The sides of a right triangle whose hypotenuse is
Ans:
For Pythagorean triplet sides are given by
Then,
41.
Ans:
42.
Ans:
43. The cube of an odd number is always an _________ number.
Ans: always an odd number
44. The cube root of a number x is denoted by _________.
Ans:
45. The least number by which
Ans: 5
On taking L.C.M we have factors of
On grouping these factors in double of equal factors,
We have only one
So,
46. The least number by which
Ans:
On taking L.C.M we have factors of
On grouping these factors in triple of equal factors,
We have only one
So,
47. The least number by which 72 be divided to make it a perfect cube is _____________.
Ans:
On taking L.C.M we have factors of
On grouping these factors in triple of equal factors,
We have only
So,
48. Cube of a number ending in
Ans:
On taking the cube of number
Therefore, we have
In questions 49 to 86, state whether the statements are true (T) or false (F).
49. The square of
Ans: The given statement is true.
Because square of the number ending with
50. The sum of two perfect squares is a perfect square.
Ans: The given statement is false.
For example: taking two perfect squares,
Here,
So,
51. The product of two perfect squares is a perfect square.
Ans: The given statement is true.
For example, taking two perfect squares,
Here,
So,
52. There is no square number between
Ans: The given statement is true.
53. The square root of
Ans: The given statement is false.
because square of
54. Each prime factor appears
Ans: The given statement is true.
As cubes are represented as the product of triplets of prime factors.
55. The square of
Ans: The given statement is false.
because square of
56. The cube of
Ans: The given statement is true.
57. The square root of
Ans: The given statement is false.
because square of
=
58. The square of every natural number is always greater than the number itself.
Ans: The given statement is false.
Because the square of
59. The cube root of
Ans: The given statement is false.
As,
60. There are five perfect cubes between
Ans: The given statement is false.
There are 8 perfect cubes between
61. There are
Ans: The given statement is true.
62. The sum of first
Ans: The given statement is true.
Sum of first
63.
Ans: The given statement is false.
Factors of
So, 1000 is not a perfect square.
64. A perfect square can have
Ans: The given statement is false.
Because for every digit that ends with an even number either has
65. For every natural number
Ans: The given statement is false.
66. All numbers of a Pythagorean triplet are odd.
Ans: The given statement is false.
Condition for Pythagorean triplet is = square of one should be equal to sum of square of other two.
For example,
Hence,
67. For an integer
Ans: The given statement is false.
If
68. If
Ans: The given statement is false.
If
Suppose,
And
Therefore, clearly
69. Let
Ans: The given statement is true.
If
70. If
Ans: The given statement is false.
If
Then,
71. If
Ans: The given statement is false.
If
Then,
72. The square root of a perfect square of
Ans: The given statement is true.
For example,
73. Square root of a number
Ans: The given statement is true.
74. A number having
Ans: The given statement is false.
As square of
Square of
Square of
And so on.
75. A number having
Ans: The given statement is true.
As cube of
cube of
cube of
And so on.
76. The cube of a one-digit number cannot be a two-digit number.
Ans: The given statement is false.
e.g.
77. Cube of an even number is odd.
Ans: The given statement is false.
For example:
Therefore, cube of an even number is always an even number.
78. Cube of an odd number is even.
Ans: The given statement is false
For example:
Therefore, cube of an odd number is always an odd number.
79. Cube of an even number is even.
Ans: The given statement is true.
For example:
80. Cube of an odd number is odd.
Ans: The given statement is true.
For example:
81.
Ans: The given statement is false.
Factors of 999 =
Therefore,
82.
Ans: The given statement is false.
Breaking
There is only one triplet pair therefore,
83. Cube roots of
Ans: The given statement is false.
Because
84.
Ans: The given statement is false.
As
Which is not equal.
85. There is no cube root of a negative integer.
Ans: The given statement is false.
Let,
86. Square of a number is positive, so the cube of that number will also be positive.
Ans: The given statement is false.
Let,
Square of
Cube of
Solve the Following Questions
87. Write the first five square numbers.
Ans: First five square numbers are:
88. Write cubes of first three multiples of
Ans:
Cube of
Cube of
Cube of
89. Show that
Ans:
There is no pair for
90. Express
Ans:
Now, Sum of first nine consecutive odd numbers
91. Using prime factorisation, find which of the following perfect squares are.
a)
b)
c)
d)
Ans:
On grouping in pairs, there is no unpaired factor left
So,
Therefore,
On grouping in pair, there is no unpaired factor left over. Therefore,
On grouping in pair, there is no unpaired factor left over. Therefore,
92. Using prime factorisation, find which of the following are perfect cubes.
a)
b)
c)
d)
Ans:
Hence, factors of
Hence, factors of
Hence, factors of
Hence, factors of
93. Using distributive law, find the squares of
a)
b)
Ans:
Finding square using distributive law:
Therefore,
Finding square using distributive law:
Therefore,
94. Can a right triangle with sides
Ans: We know the sum of two smaller sides of a triangle is always equal to the square of longer side of a triangle.
Given, Smaller sides
Longer side
As per the rule,
Hence,
95. Write the Pythagorean triplet whose one of the numbers is
Ans: Pythagorean triplets for any natural number greater than
So, if one number is
Given, one number = 4
Then Pythagorean triplets are:
Then,
Also,
Therefore,
96. Using prime factorisation, find the square roots of
a)
b)
Ans:
Hence, factors of
Hence,
Hence, factors of
Hence,
97. Using prime factorisation, find the cube roots of
a)
b)
Ans:
Hence, factors of
Therefore, cube root of is
Hence, factors of
Therefore, cube root of is
98. Are
Ans: Taking factors of
Therefore,
Therefore,
Hence,
99. Is
Ans: Taking factors of
Therefore,
Therefore, on dividing the number by incomplete group of triplet. So, to make
Now, 216 is a perfect cube. Hence, 45 is the smallest number by which it should be
divided to get a perfect cube.
100. Write two Pythagorean triplets each having one of the numbers as
Ans: Sum of two smaller sides in Pythagorean triplet is always equal to the square of longer side. If one of the numbers as
101. By what smallest number should
Ans: Taking factors of
And factors of
Therefore, the smallest number is 36 that should divide
102. By what smallest number should
Ans: Taking factors of
And factors of
Therefore, the smallest number is 60 that should be multiplied so that the quotient is a perfect square.
103. Find the square root of the following by long division method.
a)
b)
Ans: finding square root using long division method:
Therefore, square root of
Therefore, square root of
104. Find the square root of the following by long division method.
a)
b)
Ans:
Finding square root using long division method:
Therefore, square root of
Finding square root using long division method:
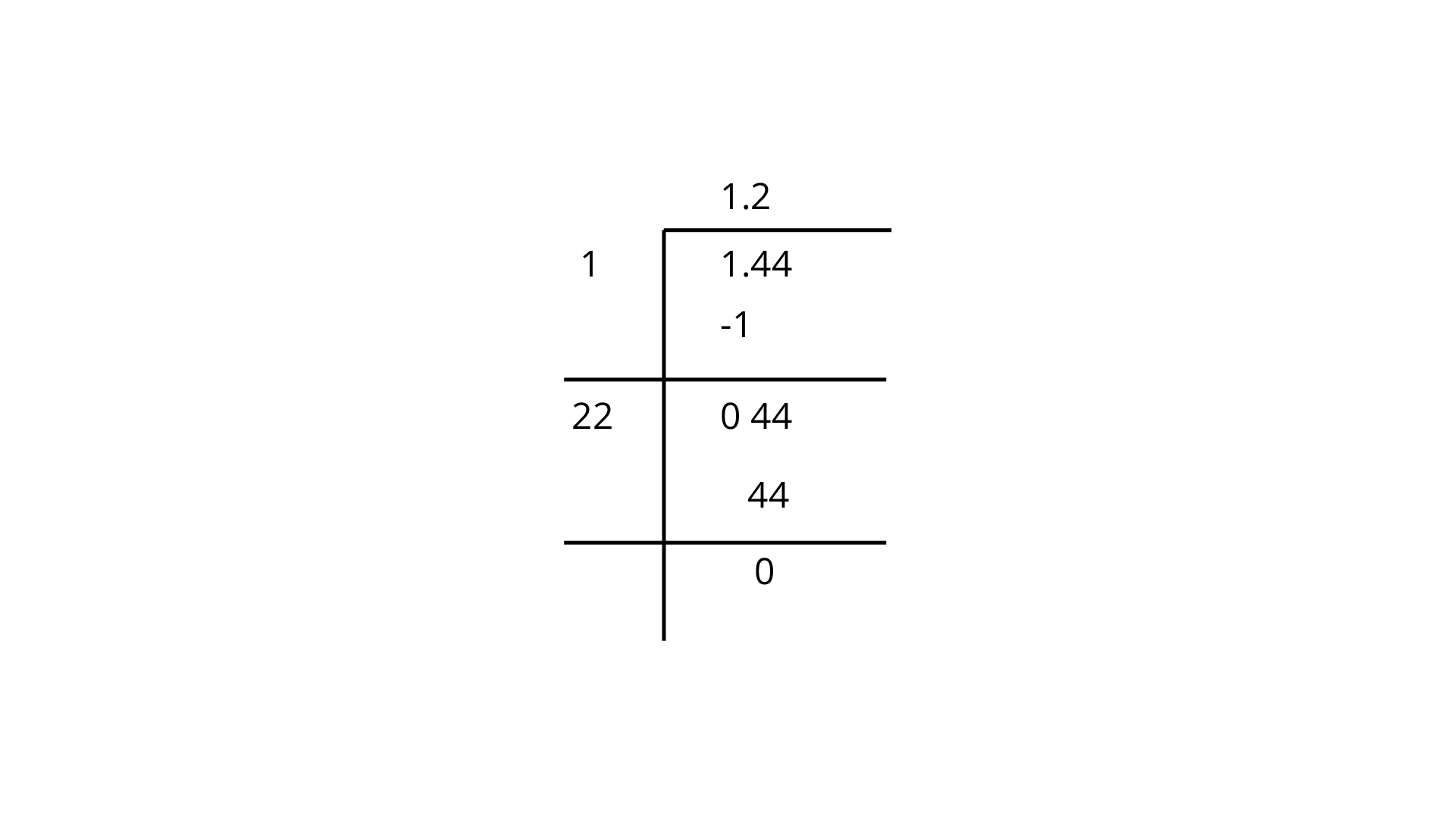
Therefore, square root of
105. What is the least number that should be subtracted from
Ans: finding square root of

We can see that the remainder left is
Hence, the required perfect square number
As
106. What is the least number that should be added to
Ans: finding square root of

We can see that
should be added to
Therefore,
Which is a perfect square.
107. Find the least number of four digits that is a perfect square.
Ans: Least of four-digit number
finding square root of
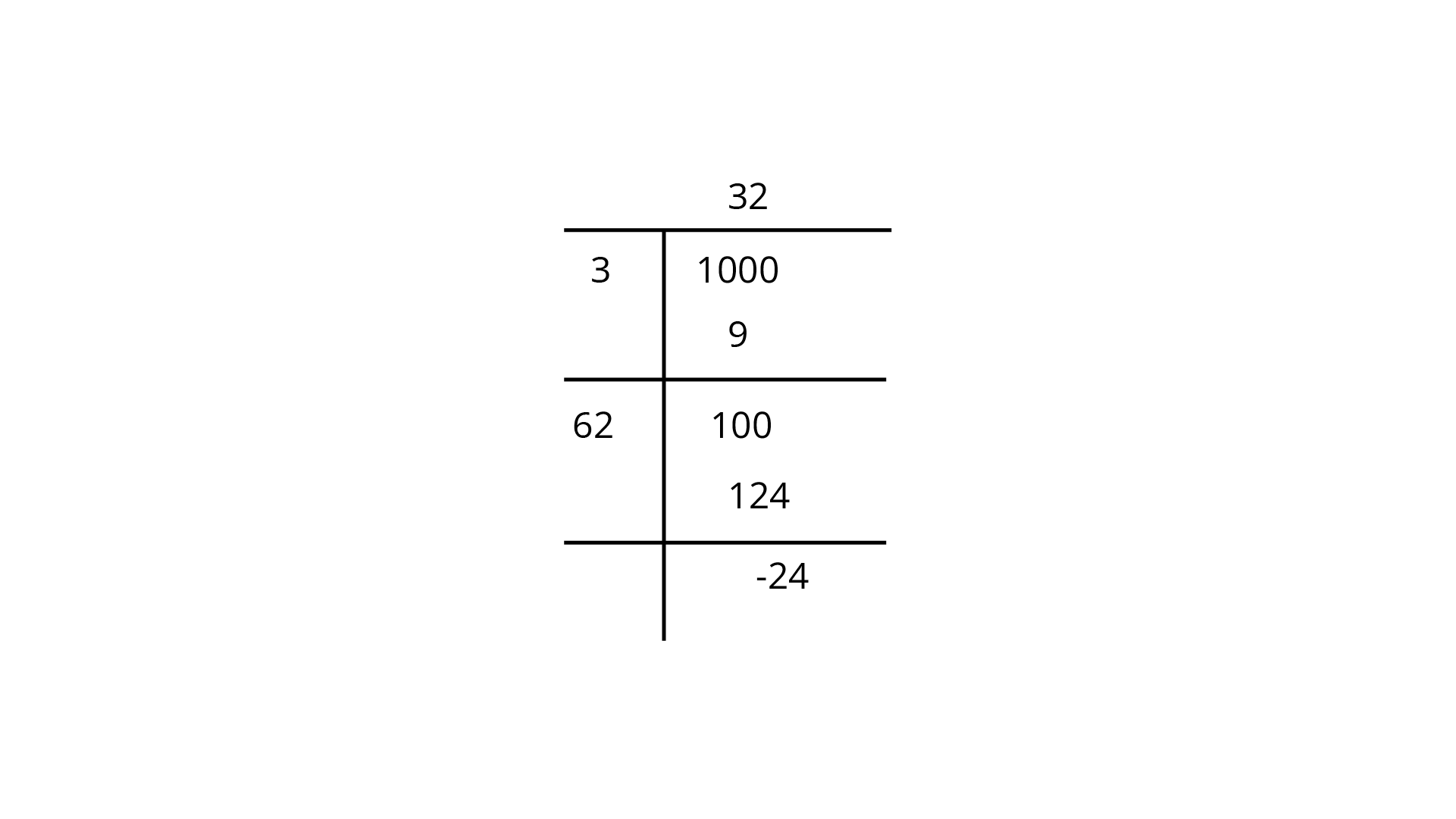
So,
108. Find the greatest number of three digits that is a perfect square.
Ans: Greatest three-digit number
Finding square root of

So,
And
109. Find the least square number which is exactly divisible by
Ans: Taking L.C.M of
L.C.M of
As pair of
Hence, the least square number which is exactly divisible by
110. Find the length of the side of a square if the length of its diagonal is
Ans: Length of diagonal
Now, let the length of side of a square is
Then by Pythagoras theorem:
Therefore, the length of the side of square is
111. A decimal number is multiplied by itself. If the product is
Ans: Given, the product of the number is
Now, let the number be
According to the question:
Now, finding the square root of

112. Find the decimal fraction which when multiplied by itself gives 84.64.
Ans: Given, the product of the number is
Now, let the number be
According to the question:
Now, finding the square root of
113. A farmer wants to plough his square field of side 150m. How much area will he have to plough?
Ans: Given, side of square field
We know, area of square = side x side
114. What will be the number of unit squares on each side of a square graph paper if the total number of unit squares is
Ans: Given,
Total number of unit squares
If the number is
The number of unit square
So, the number of unit square
115. If one side of a cube is
Ans: Given, side of a cube
We know, Volume of cube =
116. The dimensions of a rectangular field are
Ans: Given,
length of a rectangular field (l)
breath of a rectangular field (b)
We know, length of diagonal
117. Find the area of a square field if its perimeter is
Ans: Given, Perimeter of square
We know, Perimeter of a square
Now, the area of square
118. Find the length of each side of a cube if its volume is 512 cm3.
Ans: Given, Side of a cube
We know, Volume of cube =
Therefore,
119. Three numbers are in the ratio
Ans: Let the numbers be
According to the question:
Then the numbers are:
120. How many square metres of carpet will be required for a square room of side
Ans: side of square
Now,
Area of square
121. Find the side of a square whose area is equal to the area of a rectangle with sides
Ans: Given, length of a rectangle
Breadth of a rectangle
We know,
Area of a rectangle
Also given, area of square = area of rectangle
Therefore,
Hence, side
122. Difference of two perfect cubes is
Ans: Given, that the difference of two perfect cubes is
Cube root of the smaller of the two numbers
If cube root of larger number is
Therefore,
Hence, the cube root of the larger number
123. Find the number of plants in each row if
Ans: Total numbers of plants arranged
Let the number of plants is each row
Given, that the number of rows = number of plants in each row
Therefore, the total plants
So, the number of plants in each row is
124. A hall has a capacity of
Ans: Total capacity of hall
Let the number of seats in each row
Given, that the number of rows = number of seats in each row
Therefore, the total seats
Hence, seats in each row
125. A General, wishes to draw up his
Ans: Total number of soldiers
number of soldiers left:
Therefore, number of soldiers left
126.
Ans: Total number of students in each row of the lecture room
Also, the number of rows
Therefore, total students
As per question,
So, the students in each row
127. Rahul walks
Ans: If Rahul walked
By using Pythagoras theorem, in triangle
So, the distance is
128. A
Ans: Let the distance between wall and foot of the ladder
By using Pythagoras theorem,
So, the distance between the wall and the foot of the ladder is 3.3.
129. A king wanted to reward his advisor, a wise man of the kingdom. So he asked the wiseman to name his own reward. The wiseman thanked the king but said that he would ask only for some gold coins each day for a month. The coins were to be counted out in a pattern of one coin for the first day,
Ans: As per question,
Total question at the end
As this is an odd number series.
The number of term ,
We know, Sum of an odd natural numbers
So, the advisor will get
130. Find three numbers in the ratio
Ans: let the three numbers be
According to the question,
Therefore, the three numbers are:
131. Find the smallest square number divisible by each one of the number
Ans: Taking L.C.M. of
Taking pairs
For making it a perfect square, we have to multiple it by the product of incomplete pair
Now,
Hence, the smallest square number is
132. The area of a square plot is
Ans: Given, Area of a square plot
Let the length of square plot
And the area of square
According to the question:
Hence,
133. Find the square root of
Ans: square root of
Now, subtract successive odd numbers starting from 1 as:
The number
So, the
134. Three numbers are in the ratio 2:3:4. The sum of their cubes is 0.334125. Find the numbers.
Ans: Suppose the numbers
Given, the sum of their cubes
According to the question,
Hence, the required numbers are:
135. Evaluate:
Ans:
Now,
Hence, Answer is
136.
Ans: According to the question:
137.
Ans: According to the question:
138. A perfect square number has four digits, none of which is zero. The digits from left to right have values that are: even, even, odd, even. Find the number.
Ans: ABCD is a perfect square.
Here, A = an even number
B = an even number,
C = an odd number,
D = an even number
So,
139. Put three different numbers in the circles so that when you add the numbers at the end of each line you always get a perfect square.
Ans: Three numbers which we add at the end of the line we always give perfect square are
As,
and
Therefore, the complete triangle is
140. The perimeters of two squares are
Ans: Given, that the perimeter of one square
If the length of square
Then,
So, side
Now, area of a square
Given, perimeter of second square
And if the length of second square
Then,
So, side
Now, area of a square
Now the perimeter of another square is equal in area to the sum of the first two square.
So, area of another square
Then, area of a square
Hence, perimeter
141. A three-digit perfect square is such that if it is viewed upside down, the number seen is also a perfect square. What is the number? (Hint: The digits
Ans:
142.
Ans:
i) First pair of number
Also, there square
ii) Second pair of number
Also, there square
NCERT Exemplar for Class 8 Maths Solutions Chapter - 3
Vedantu offers the NCERT Exemplar for Class 8 Maths Solutions Chapter - 3 Square-Math & Cube-Cube Root to the students free of cost. This NCERT Exemplar for Class 8 Maths Solutions Chapter - 3 Square-Math & Cube-Cube Root is provided in PDF format and can be downloaded by the students to study offline anytime anywhere.
The subject matter experts at Vedantu prepared these solutions: The NCERT Exemplar for Class 8 Maths Solutions Chapter - 3 Square-Math & Cube-Cube Root appropriately. All these solutions are made by abiding by the latest NCERT syllabus and guidelines. These solutions are made to help and guide students and prepare them for examinations. These solutions assist students in their homework and assignments as well. Students can top the final exams and ace the subject by practicing these solutions.
In Examples 1 to 7, out of given four Choices Multiple only one is Correct. Write the Correct Answer
Example 1: Which of the following is the square of an odd number?
(a) 256
(b) 361
(c) 144
(d) 400
Ans: (b) because
Example 2: Which of the following will have
(a)
(b)
(c)
(d)
Ans: (a) because
Example 3: How many natural numbers lie between
(a)
(b)
(c)
(d)
Ans: (d) As
Therefore,
Example 4: Which of the following is not a perfect square?
(a)
(b)
(c)
(d)
Ans: (c) As in
Example 5: A perfect square can never have the following digit at one’s place.
(a)
(b)
(c)
(d)
Ans: (d) digits ending with
Example 6: The value of
(a)
(b)
(c)
(d)
Ans: (b)
Example 7: Given that
(a)
(b)
(c)
(d)
Ans: (c)
Therefore,
In examples 8 to 14, fill in the blanks to make the statements true.
Example 8: There are __________ perfect squares between
Ans: There are
Example 9: The cube of
Ans: Cube of
Example 10: The square of
Ans:
Example 11: The cube of
Ans:
Example 12:
Ans: Because
Example 13: The positive square root of a number
Ans:
Example 14: The least number to be multiplied with
Ans:
In examples 15 to 19, state whether the statements are true (T) or false (F)
Example 15: The square of
Ans: True, because
Example 16: The cube root of
Ans: False because
Example 17: There are
Ans: False because
Example 18: The sum of first
Ans: True, because first seven odd natural numbers are
And their sum:
Example 19: The square root of a perfect square of
Ans: True, as a square root of a perfect square of
Example 20: Express
Ans: successive odd natural numbers are
Example 21: Check whether
Ans: Taking factors of
Example 22: Check whether
Ans: Taking factors of
So,
As all prime factors forms triplets. So,
Example 23: Using distributive law, find the square of
Ans: Finding square using distributive law:
As
So,
Therefore,
Example 24: Write a Pythagorean triplet whose smallest number is
Ans: Given that smallest number is
Pythagorean triplet is given by:
Now,
Therefore, the Pythagorean triplet is
Example 25: Using prime factorisation, find the cube root of
Ans: Prime factors of
Example 26: Evaluate the square root of
Ans: Square root of
Example 27: Find the smallest perfect square divisible by 3, 4, 5 and 6.
Ans: The least number divisible by
The LCM of
Now,
As
So, the required least square number is
Example 28: A ladder
Ans: Let
Given:
Because
Hence, the wall is
Example 29: Find the length of a diagonal of a rectangle with dimensions
Ans:
By using Pythagoras theorem, we know
Length of diagonal of the rectangle is given by
Thus, the length of diagonal is
Example 30: The area of a rectangular field whose length is twice its breadth is
Ans: If the breadth of the field is
We know, area of the rectangular field
Also given, area is
Therefore,
Therefore, breadth
Now the, perimeter of the field
Example 31: During a mass drill exercise,
Ans: Given total number of students
students forming a square
Thus,
Now let the number of students in each row be
Therefore,
or
So, there are
Example 32: Find the least number that must be added to
Ans:
We can see
Hence, the number to be added
=15211500
=21
Therefore, the perfect square
Thus, the required number is
Example 33: Application of problem solving strategies
Finding the smallest number by which
Ans: Understand and Explore:
What information is given in the question? – A number which is not a perfect square.
What are we trying to find? – The smallest number by which
Using prime factorisation to find the product of prime factors of
Pairing the prime factors to see if any factor is left unpaired.
Then the unpaired factor will be the smallest number that must be divided to get a perfect square.
Solve: Prime factorisation of
The product of prime factors
After Pairing these prime factors
We can see that the factor
To check if it is a perfect square. Divide
We can see that on dividing
Multiple question Answer
In each of the questions, 1 to 24, write the correct Answer from the given four options:
1.
a)
b)
c)
d)
Ans: (c),
Breaking
Taking pairs out
Therefore, square root of 196 is 14.
2. Which of the following is a square of an even number?
a)
b)
c)
d)
Ans: (a),
Therefore, square of an even number is:
3. A number ending in
a)
b)
c)
d)
Ans: (c),
We know
Therefore, unit place of a number ending with
4. Which of the following will have 4 at the unit place?
a)
b)
c)
d)
Ans: (b),
Because, unit digit of
Square of
5. How many natural numbers lie between
a) 9
b) 10
c) 11
d) 12
Ans: (b), 10.
We know, natural numbers lie between
31, 32, 33, 34, 35. So there are
6. Which of the following cannot be a perfect square?
a)
b)
c)
d) All of the above
Ans: (c), 198.
7. The one’s digit of the cube of 23 is
a)
b)
c)
d)
Ans: (b),
We know, unit digit of
And cube of
8. A square board has an area of
a)
b)
c)
d)
Ans: (b),
We know,
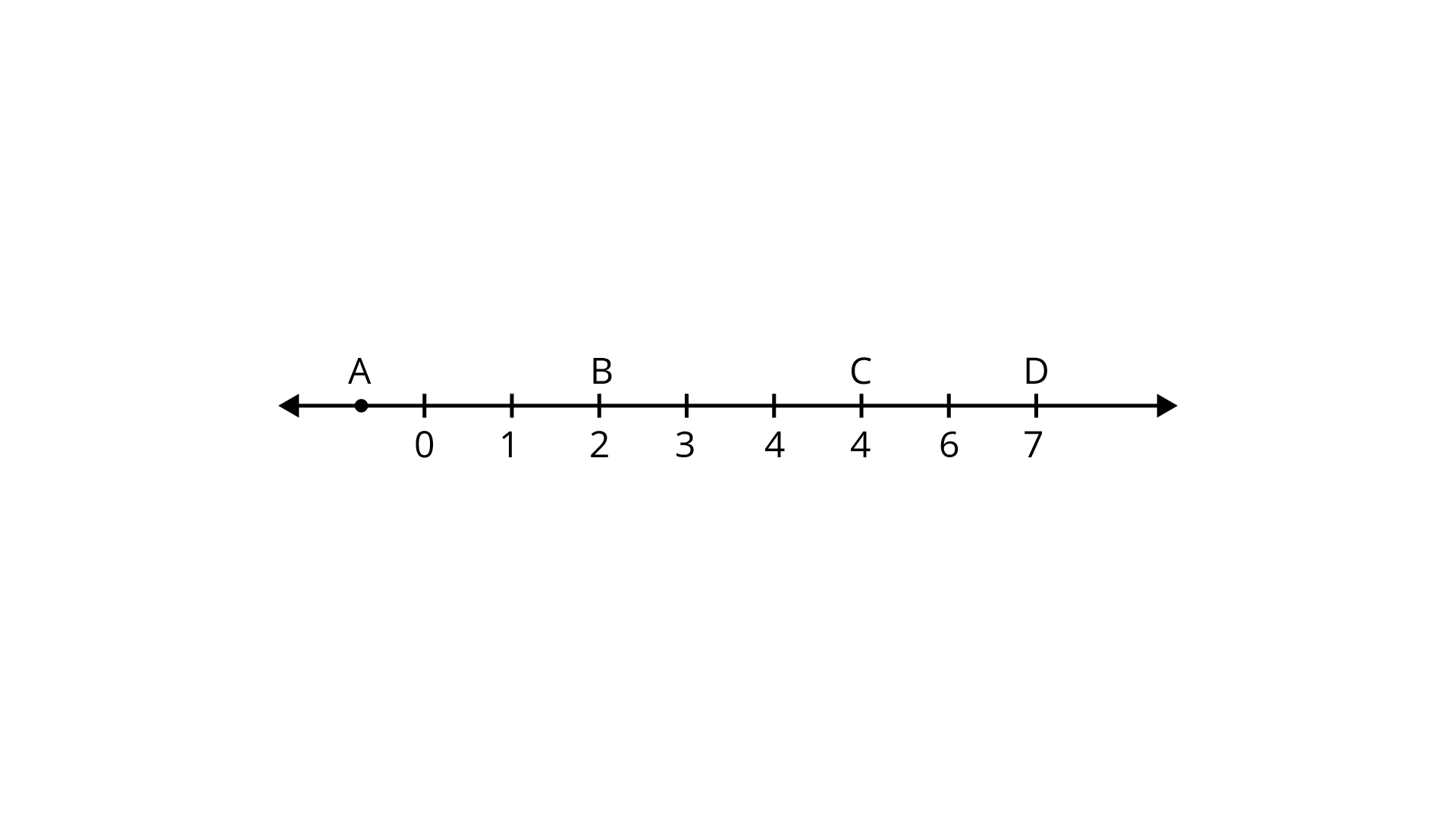
9. Which letter best represents the location of
a) A
b) B
c) C
d) D
Ans: (c), C
We know, square of
10. If one member of a Pythagorean triplet is
a)
b)
c)
d)
Ans: (b),
Therefore, the formula of Pythagorean triplet is:
11. The sum of successive odd numbers
a)
b)
c)
d)
Ans: (b),
Total numbers are
successive odd numbers
sum of successive odd numbers is
12. The sum of first n odd natural numbers is
a)
b)
c)
d)
Ans: (b),
We know, sum of first n odd natural numbers is given by:
13. Which of the following numbers is a perfect cube?
a)
b)
c)
d)
Ans:(b),
As square of 6 is
14. The hypotenuse of a right triangle with its legs of lengths
a)
b)
c)
d)
Ans: (a),
We know,
15. The next two numbers in the number pattern
a)
b)
c)
d)
Ans: (b),
As the given pattern is a series of perfect squares so the next term will be
16. Which among
a)
b)
c)
d)
Ans: (d),
Because unit digit of
And square of
17. A perfect square can never have the following digit in its ones place.
a)
b)
c)
d)
Ans: (b),
18. Which of the following numbers is not a perfect cube?
a)
b)
c)
d)
Ans: (b),
Factors of
19.
a)
b)
c)
d) None of these
Ans: (a),
20. If m is the square of a natural number n, then n is
a) The square of m
b) Greater than m
c) Equal to m
d)
Ans: (d),
Square of
According to the question:
21. A perfect square number having n digits where n is even will have square root with
a)
b)
c)
d)
Ans: (b),
22. If m is the cube root of n, then n is
a)
b)
c)
d)
Ans: (a),
23. The value of
a)
b)
c)
d)
Ans: (c),
24. Given that
a)
b)
c)
d)
Ans: (d),
As
Also,
And,
Then,
In questions 25 to 48, fill in the blanks to make the statements true.
25. There are _________ perfect squares between
Ans:
Perfect square between
26. There are _________ perfect cubes between
Ans: 8
There are
27. The unit digit in the square of
Ans:
Unit digit in
Therefore, the square of
28. The square of
Ans:
29. There are _________ natural numbers between
Ans:
30. The square root of
Ans:
Number of digits in a square root for odd digit is given by
Number of digits in a given number is
Therefore
31. The square of
Ans:
32. The square root of
Ans: 28.09
33. The cube of
Ans:
34.
Ans:
35.
Ans:
36. Ones digit in the cube of
Ans:
Unit digit is
Therefore, unit digit in the cube of
37. The square of
Ans:
Therefore, square of
38. The sum of first six odd natural numbers is _________.
Ans:
First six odd natural numbers are
Sum of First six odd natural numbers are
39. The digit at the ones place of
Ans:
As unit digit of
40. The sides of a right triangle whose hypotenuse is
Ans:
For Pythagorean triplet sides are given by
Then,
41.
Ans:
42.
Ans:
43. The cube of an odd number is always an _________ number.
Ans: always an odd number
44. The cube root of a number x is denoted by _________.
Ans:
45. The least number by which
Ans: 5
On taking L.C.M we have factors of
On grouping these factors in double of equal factors,
We have only one
So,
46. The least number by which
Ans:
On taking L.C.M we have factors of
On grouping these factors in triple of equal factors,
We have only one
So,
47. The least number by which 72 be divided to make it a perfect cube is _____________.
Ans:
On taking L.C.M we have factors of
On grouping these factors in triple of equal factors,
We have only
So,
48. Cube of a number ending in
Ans:
On taking the cube of number
Therefore, we have
In questions 49 to 86, state whether the statements are true (T) or false (F).
49. The square of
Ans: The given statement is true.
Because square of the number ending with
50. The sum of two perfect squares is a perfect square.
Ans: The given statement is false.
For example: taking two perfect squares,
Here,
So,
51. The product of two perfect squares is a perfect square.
Ans: The given statement is true.
For example, taking two perfect squares,
Here,
So,
52. There is no square number between
Ans: The given statement is true.
53. The square root of
Ans: The given statement is false.
because square of
54. Each prime factor appears
Ans: The given statement is true.
As cubes are represented as the product of triplets of prime factors.
55. The square of
Ans: The given statement is false.
because square of
56. The cube of
Ans: The given statement is true.
57. The square root of
Ans: The given statement is false.
because square of
=
58. The square of every natural number is always greater than the number itself.
Ans: The given statement is false.
Because the square of
59. The cube root of
Ans: The given statement is false.
As,
60. There are five perfect cubes between
Ans: The given statement is false.
There are 8 perfect cubes between
61. There are
Ans: The given statement is true.
62. The sum of first
Ans: The given statement is true.
Sum of first
63.
Ans: The given statement is false.
Factors of
So, 1000 is not a perfect square.
64. A perfect square can have
Ans: The given statement is false.
Because for every digit that ends with an even number either has
65. For every natural number
Ans: The given statement is false.
66. All numbers of a Pythagorean triplet are odd.
Ans: The given statement is false.
Condition for Pythagorean triplet is = square of one should be equal to sum of square of other two.
For example,
Hence,
67. For an integer
Ans: The given statement is false.
If
68. If
Ans: The given statement is false.
If
Suppose,
And
Therefore, clearly
69. Let
Ans: The given statement is true.
If
70. If
Ans: The given statement is false.
If
Then,
71. If
Ans: The given statement is false.
If
Then,
72. The square root of a perfect square of
Ans: The given statement is true.
For example,
73. Square root of a number
Ans: The given statement is true.
74. A number having
Ans: The given statement is false.
As square of
Square of
Square of
And so on.
75. A number having
Ans: The given statement is true.
As cube of
cube of
cube of
And so on.
76. The cube of a one-digit number cannot be a two-digit number.
Ans: The given statement is false.
e.g.
77. Cube of an even number is odd.
Ans: The given statement is false.
For example:
Therefore, cube of an even number is always an even number.
78. Cube of an odd number is even.
Ans: The given statement is false
For example:
Therefore, cube of an odd number is always an odd number.
79. Cube of an even number is even.
Ans: The given statement is true.
For example:
80. Cube of an odd number is odd.
Ans: The given statement is true.
For example:
81.
Ans: The given statement is false.
Factors of 999 =
Therefore,
82.
Ans: The given statement is false.
Breaking
There is only one triplet pair therefore,
83. Cube roots of
Ans: The given statement is false.
Because
84.
Ans: The given statement is false.
As
Which is not equal.
85. There is no cube root of a negative integer.
Ans: The given statement is false.
Let,
86. Square of a number is positive, so the cube of that number will also be positive.
Ans: The given statement is false.
Let,
Square of
Cube of
Solve the Following Questions
87. Write the first five square numbers.
Ans: First five square numbers are:
88. Write cubes of first three multiples of
Ans:
Cube of
Cube of
Cube of
89. Show that
Ans:
There is no pair for
90. Express
Ans:
Now, Sum of first nine consecutive odd numbers
91. Using prime factorisation, find which of the following perfect squares are.
a)
b)
c)
d)
Ans:
On grouping in pairs, there is no unpaired factor left
So,
Therefore,
On grouping in pair, there is no unpaired factor left over. Therefore,
On grouping in pair, there is no unpaired factor left over. Therefore,
92. Using prime factorisation, find which of the following are perfect cubes.
a)
b)
c)
d)
Ans:
Hence, factors of
Hence, factors of
Hence, factors of
Hence, factors of
93. Using distributive law, find the squares of
a)
b)
Ans:
Finding square using distributive law:
Therefore,
Finding square using distributive law:
Therefore,
94. Can a right triangle with sides
Ans: We know the sum of two smaller sides of a triangle is always equal to the square of longer side of a triangle.
Given, Smaller sides
Longer side
As per the rule,
Hence,
95. Write the Pythagorean triplet whose one of the numbers is
Ans: Pythagorean triplets for any natural number greater than
So, if one number is
Given, one number = 4
Then Pythagorean triplets are:
Then,
Also,
Therefore,
96. Using prime factorisation, find the square roots of
a)
b)
Ans:
Hence, factors of
Hence,
Hence, factors of
Hence,
97. Using prime factorisation, find the cube roots of
a)
b)
Ans:
Hence, factors of
Therefore, cube root of is
Hence, factors of
Therefore, cube root of is
98. Are
Ans: Taking factors of
Therefore,
Therefore,
Hence,
99. Is
Ans: Taking factors of
Therefore,
Therefore, on dividing the number by incomplete group of triplet. So, to make
Now, 216 is a perfect cube. Hence, 45 is the smallest number by which it should be
divided to get a perfect cube.
100. Write two Pythagorean triplets each having one of the numbers as
Ans: Sum of two smaller sides in Pythagorean triplet is always equal to the square of longer side. If one of the numbers as
101. By what smallest number should
Ans: Taking factors of
And factors of
Therefore, the smallest number is 36 that should divide
102. By what smallest number should
Ans: Taking factors of
And factors of
Therefore, the smallest number is 60 that should be multiplied so that the quotient is a perfect square.
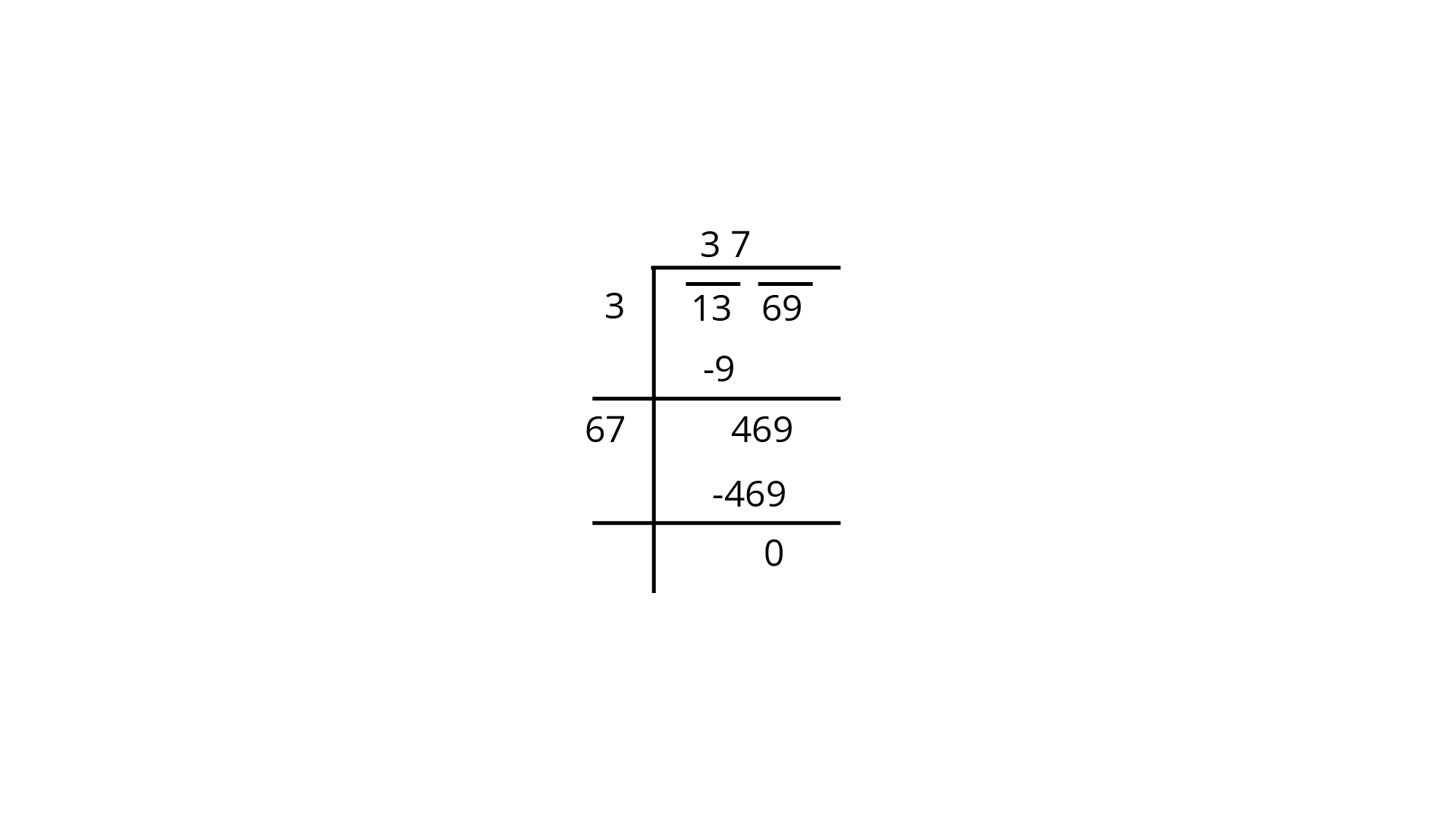
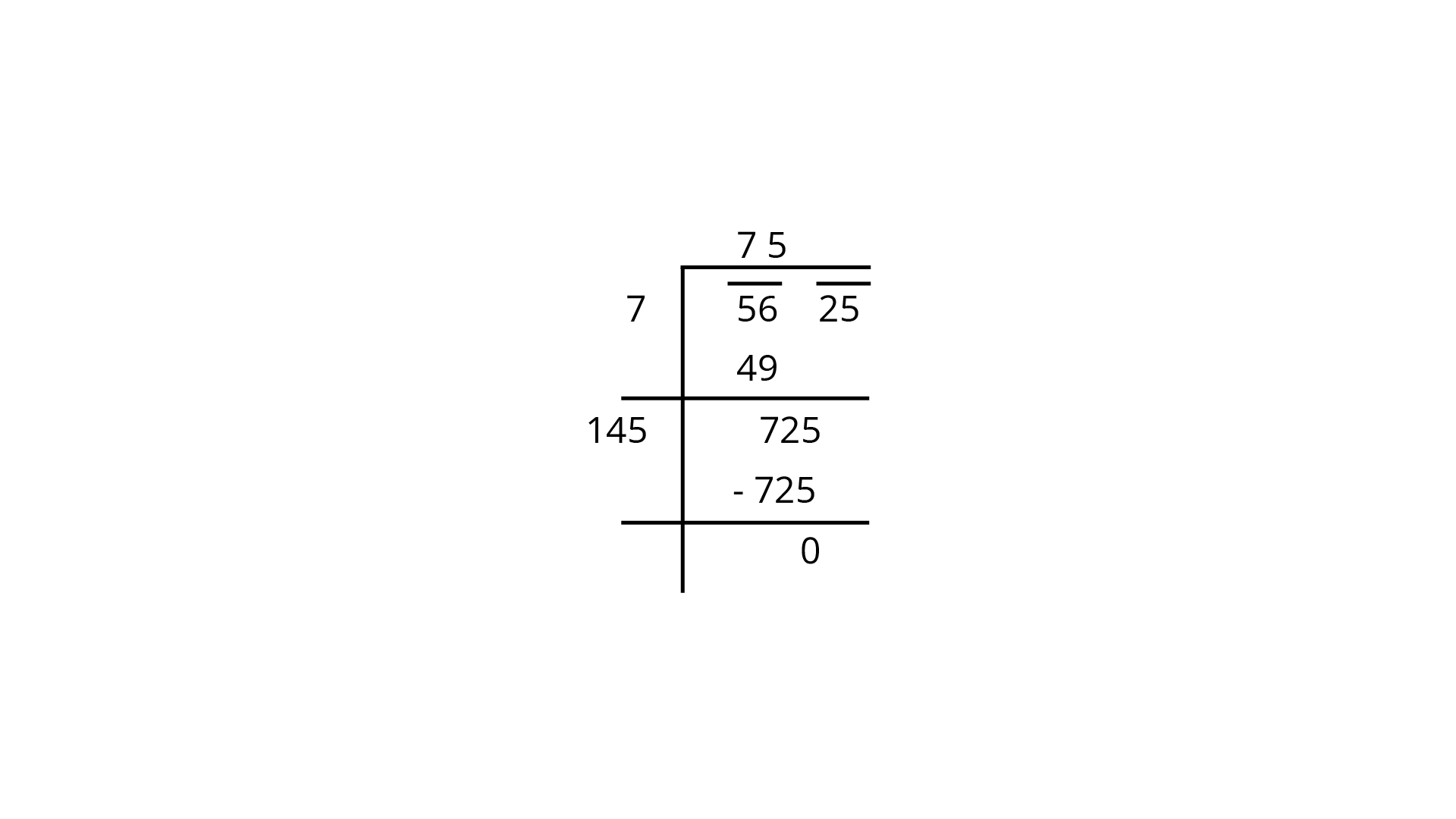
103. Find the square root of the following by long division method.
a)
b)
Ans: finding square root using long division method:
Therefore, square root of
Therefore, square root of
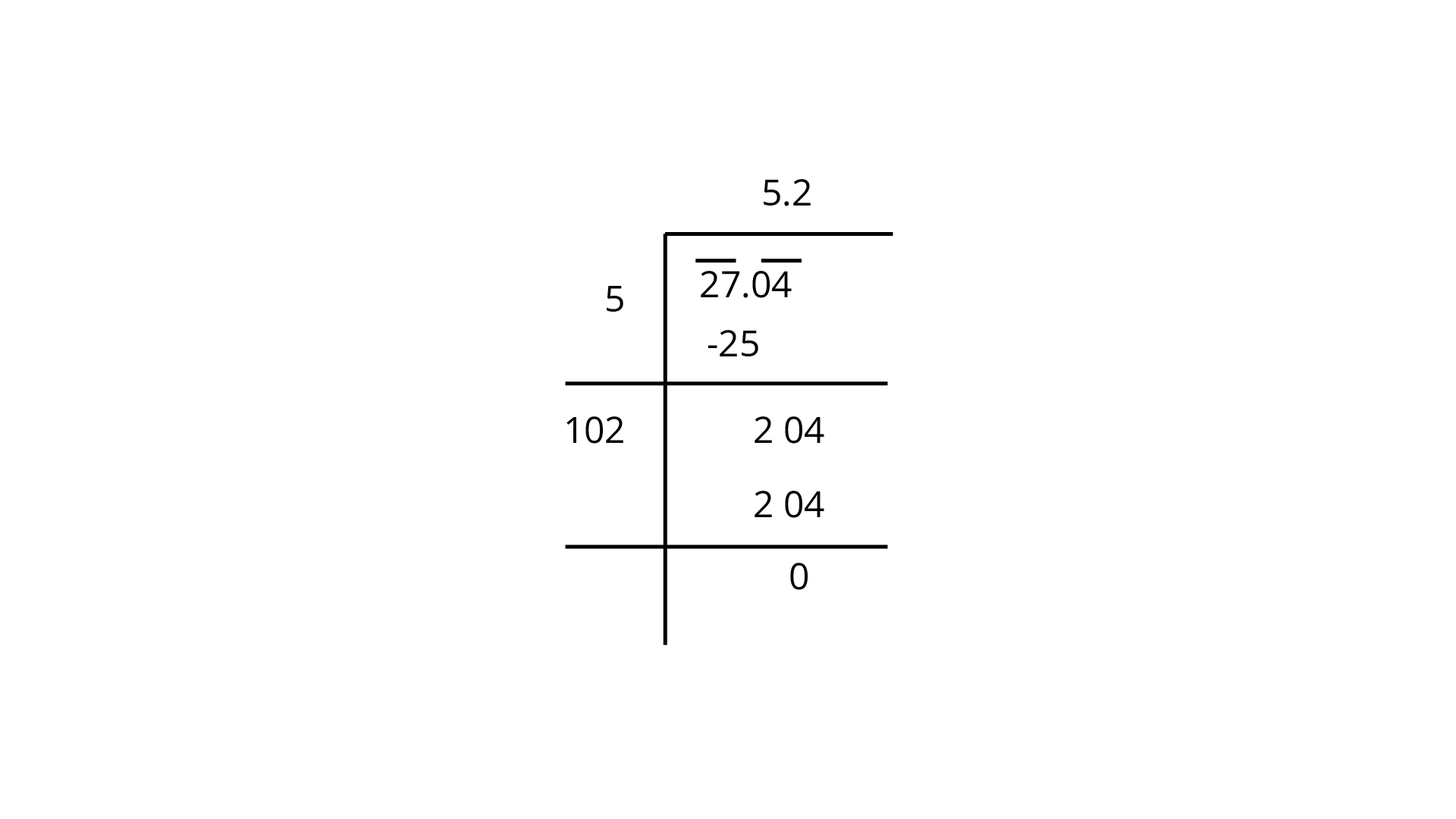
104. Find the square root of the following by long division method.
a)
b)
Ans:
Finding square root using long division method:
Therefore, square root of
Finding square root using long division method:
Therefore, square root of
105. What is the least number that should be subtracted from
Ans: finding square root of
We can see that the remainder left is
Hence, the required perfect square number
As
106. What is the least number that should be added to
Ans: finding square root of
We can see that
should be added to
Therefore,
Which is a perfect square.
107. Find the least number of four digits that is a perfect square.
Ans: Least of four-digit number
finding square root of
So,
108. Find the greatest number of three digits that is a perfect square.
Ans: Greatest three-digit number
Finding square root of
So,
And
109. Find the least square number which is exactly divisible by
Ans: Taking L.C.M of
L.C.M of
As pair of
Hence, the least square number which is exactly divisible by
110. Find the length of the side of a square if the length of its diagonal is
Ans: Length of diagonal
Now, let the length of side of a square is
Then by Pythagoras theorem:
Therefore, the length of the side of square is
111. A decimal number is multiplied by itself. If the product is
Ans: Given, the product of the number is
Now, let the number be
According to the question:
Now, finding the square root of
112. Find the decimal fraction which when multiplied by itself gives 84.64.
Ans: Given, the product of the number is
Now, let the number be
According to the question:
Now, finding the square root of

113. A farmer wants to plough his square field of side 150m. How much area will he have to plough?
Ans: Given, side of square field
We know, area of square $= side \times side$
114. What will be the number of unit squares on each side of a square graph paper if the total number of unit squares is
Ans: Given,
Total number of unit squares
If the number is
The number of unit square
So, the number of unit square
115. If one side of a cube is
Ans: Given, side of a cube
We know, Volume of cube =
116. The dimensions of a rectangular field are
Ans: Given,
length of a rectangular field (l)
breath of a rectangular field (b)
We know, length of diagonal
117. Find the area of a square field if its perimeter is
Ans: Given, Perimeter of square
We know, Perimeter of a square
Now, the area of square
118. Find the length of each side of a cube if its volume is 512 cm3.
Ans: Given, Side of a cube
We know, Volume of cube =
Therefore,
119. Three numbers are in the ratio
Ans: Let the numbers be
According to the question:
Then the numbers are:
120. How many square metres of carpet will be required for a square room of side
Ans: side of square
Now,
Area of square
121. Find the side of a square whose area is equal to the area of a rectangle with sides
Ans: Given, length of a rectangle
Breadth of a rectangle
We know,
Area of a rectangle
Also given, area of square = area of rectangle
Therefore,
Hence, side
122. Difference of two perfect cubes is
Ans: Given, that the difference of two perfect cubes is
Cube root of the smaller of the two numbers
If cube root of larger number is
Therefore,
Hence, the cube root of the larger number
123. Find the number of plants in each row if
Ans: Total numbers of plants arranged
Let the number of plants is each row
Given, that the number of rows = number of plants in each row
Therefore, the total plants
So, the number of plants in each row is
124. A hall has a capacity of
Ans: Total capacity of hall
Let the number of seats in each row
Given, that the number of rows = number of seats in each row
Therefore, the total seats
Hence, seats in each row
125. A General, wishes to draw up his
Ans: Total number of soldiers
number of soldiers left:

Therefore, number of soldiers left
126.
Ans: Total number of students in each row of the lecture room
Also, the number of rows
Therefore, total students
As per question,
So, the students in each row
127. Rahul walks
Ans: If Rahul walked
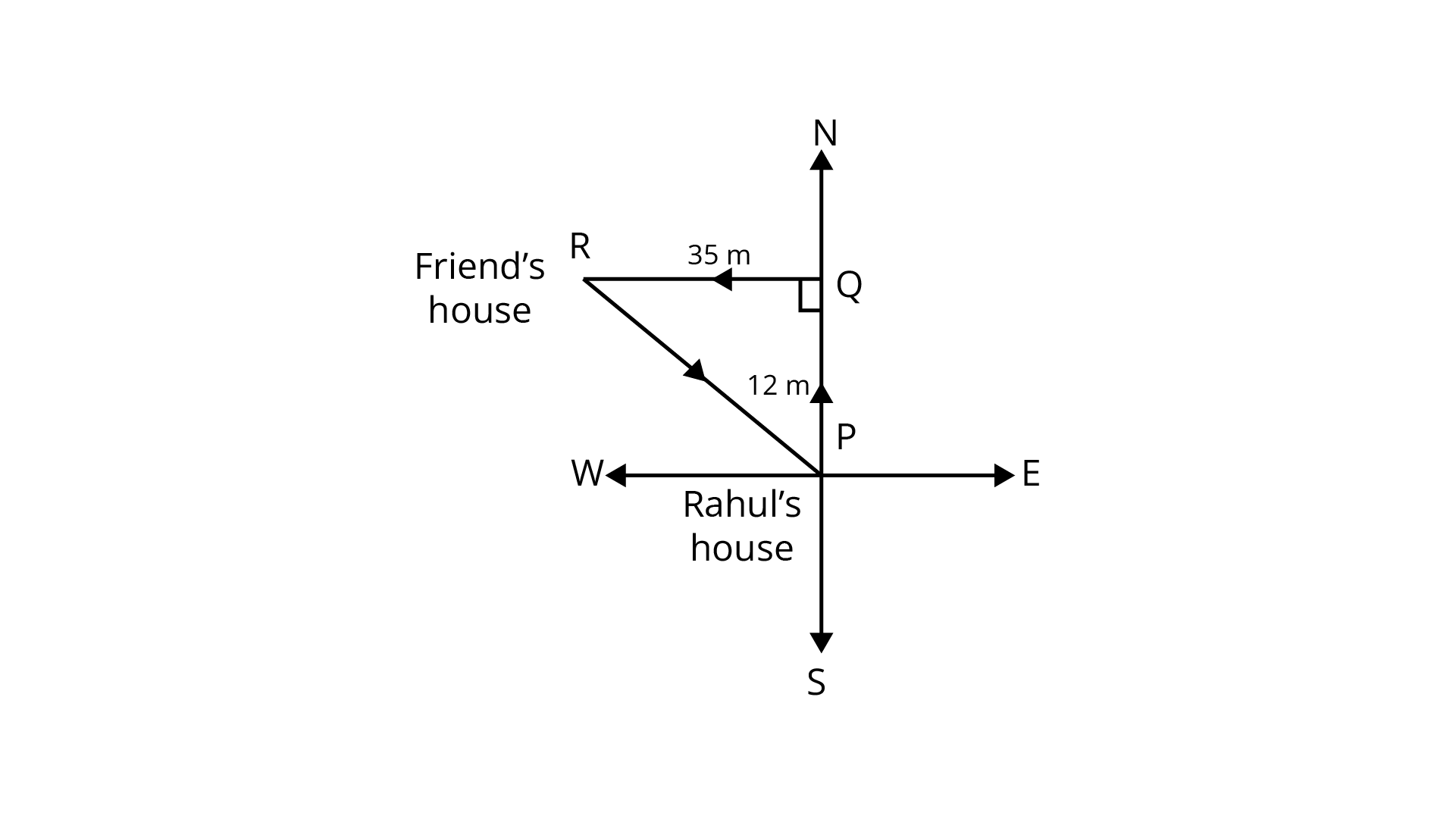
By using Pythagoras theorem, in triangle
So, the distance is
128. A
Ans: Let the distance between wall and foot of the ladder
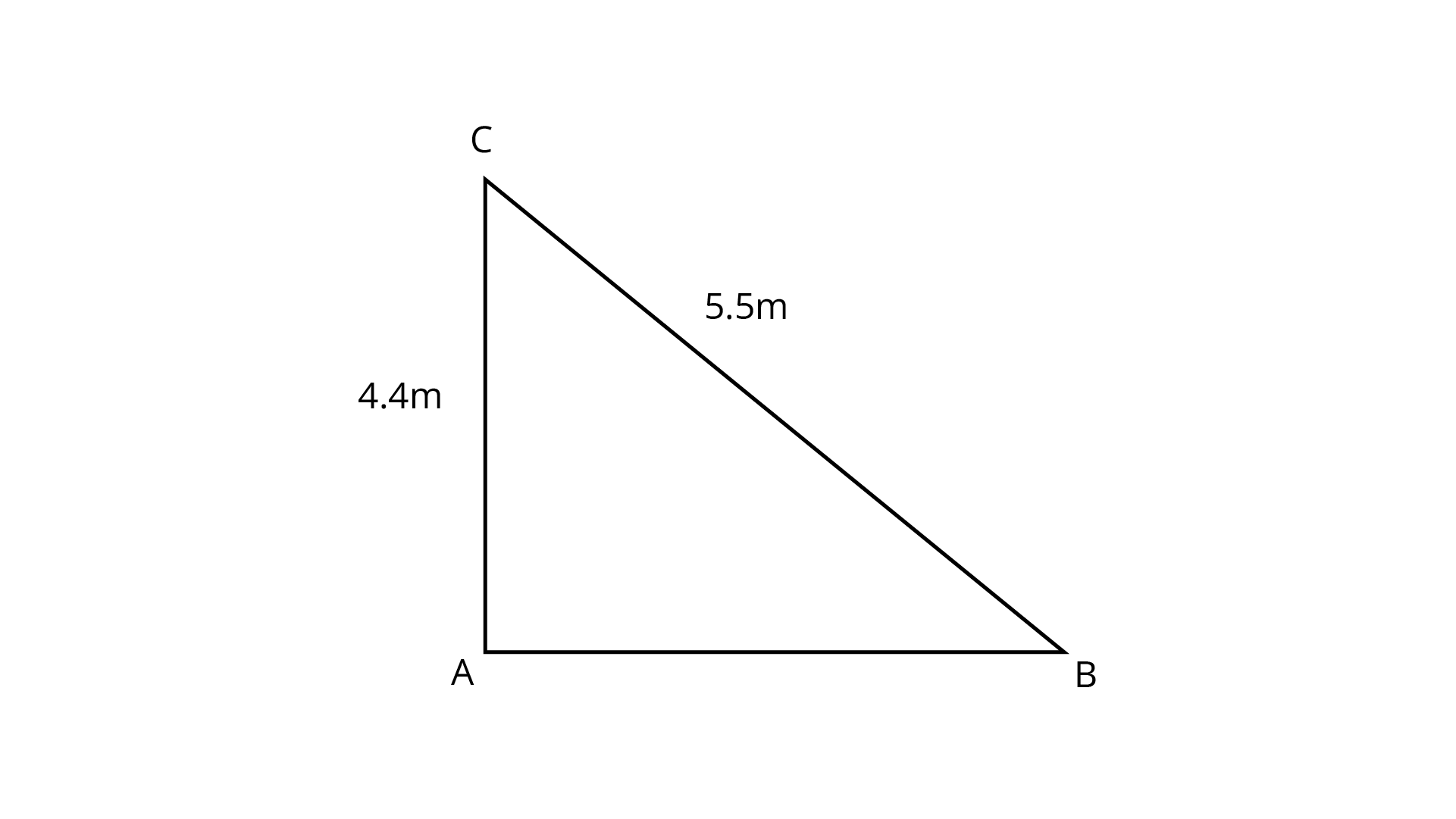
By using Pythagoras theorem,
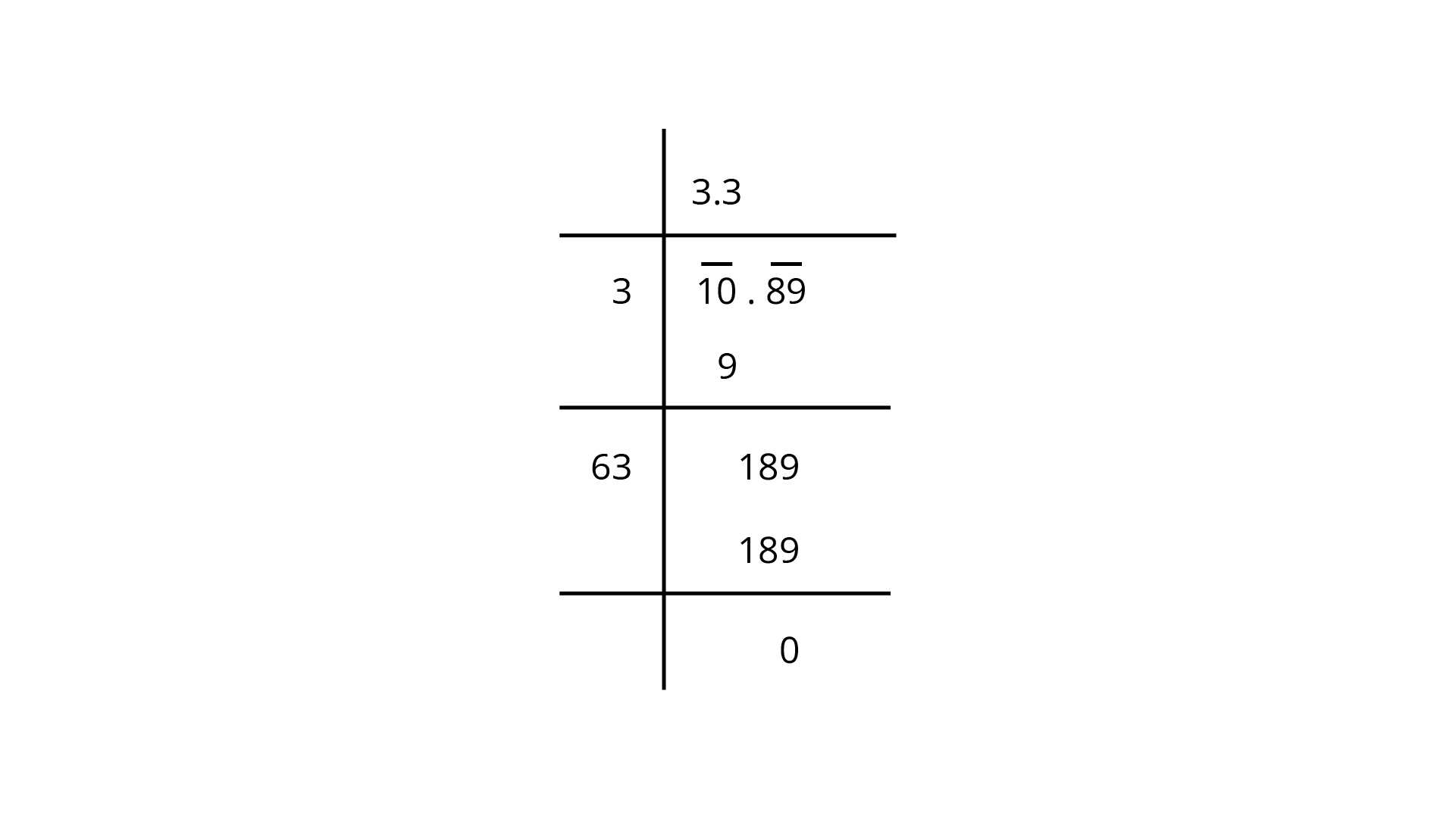
So, the distance between the wall and the foot of the ladder is 3.3.
129. A king wanted to reward his advisor, a wise man of the kingdom. So he asked the wiseman to name his own reward. The wiseman thanked the king but said that he would ask only for some gold coins each day for a month. The coins were to be counted out in a pattern of one coin for the first day,
Ans: As per question,
Total question at the end
As this is an odd number series.
The number of term ,
We know, Sum of an odd natural numbers
So, the advisor will get
130. Find three numbers in the ratio
Ans: let the three numbers be
According to the question,
Therefore, the three numbers are:
131. Find the smallest square number divisible by each one of the number
Ans: Taking L.C.M. of
Taking pairs
For making it a perfect square, we have to multiple it by the product of incomplete pair
Now,
Hence, the smallest square number is
132. The area of a square plot is
Ans: Given, Area of a square plot
Let the length of square plot
And the area of square
According to the question:
Hence,
133. Find the square root of
Ans: square root of
Now, subtract successive odd numbers starting from 1 as:
The number
So, the
134. Three numbers are in the ratio 2:3:4. The sum of their cubes is 0.334125. Find the numbers.
Ans: Suppose the numbers
Given, the sum of their cubes
According to the question,
Hence, the required numbers are:
135. Evaluate:
Ans:
Now,
Hence, Answer is
136.
Ans: According to the question:
137.
Ans: According to the question:
138. A perfect square number has four digits, none of which is zero. The digits from left to right have values that are: even, even, odd, even. Find the number.
Ans: ABCD is a perfect square.
Here, A = an even number
B = an even number,
C = an odd number,
D = an even number
So,
139. Put three different numbers in the circles so that when you add the numbers at the end of each line you always get a perfect square.
Ans: Three numbers which we add at the end of the line we always give perfect square are
As,
and
Therefore, the complete triangle is
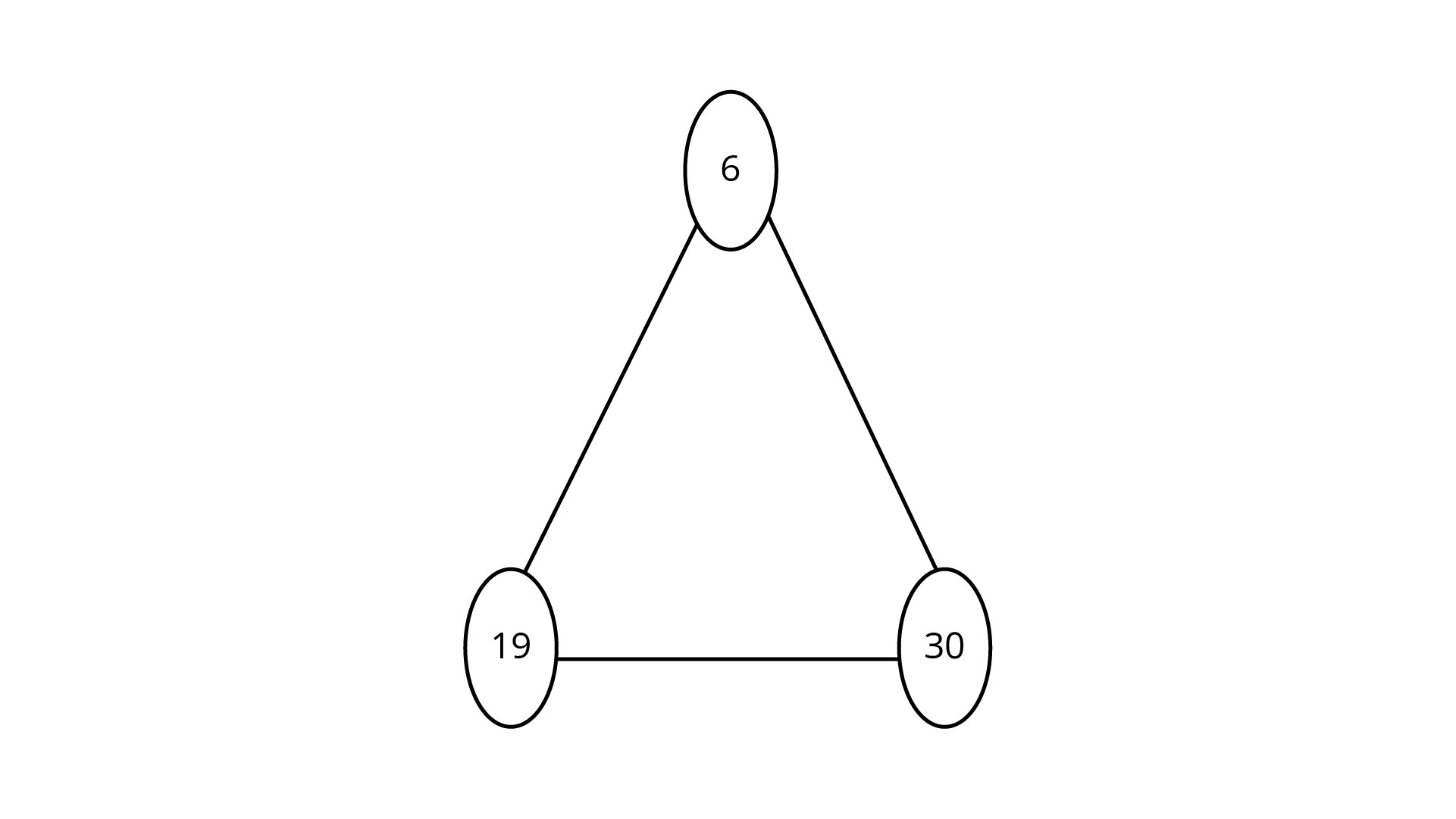
140. The perimeters of two squares are
Ans: Given, that the perimeter of one square
If the length of square
Then,
So, side
Now, area of a square
Given, perimeter of second square
And if the length of second square
Then,
So, side
Now, area of a square
Now the perimeter of another square is equal in area to the sum of the first two square.
So, area of another square
Then, area of a square
Hence, perimeter
141. A three-digit perfect square is such that if it is viewed upside down, the number seen is also a perfect square. What is the number? (Hint: The digits
Ans:
142.
Ans:
i) First pair of number
Also, there square
ii) Second pair of number
Also, there square
NCERT Exemplar for Class 8 Maths Solutions Chapter - 3
Vedantu offers the NCERT Exemplar for Class 8 Maths Solutions Chapter - 3 Square-Math & Cube-Cube Root to the students free of cost. This NCERT Exemplar for Class 8 Maths Solutions Chapter - 3 Square-Math & Cube-Cube Root is provided in PDF format and can be downloaded by the students to study offline anytime anywhere.
The subject matter experts at Vedantu prepared these solutions: The NCERT Exemplar for Class 8 Maths Solutions Chapter - 3 Square-Math & Cube-Cube Root appropriately. All these solutions are made by abiding by the latest NCERT syllabus and guidelines. These solutions are made to help and guide students and prepare them for examinations. These solutions assist students in their homework and assignments as well. Students can top the final exams and ace the subject by practicing these solutions.
FAQs on NCERT Exemplar for Class 8 Maths Solutions Chapter 3 Square-Square Root & Cube-Cube Root
1: Are NCERT Exemplar for Class 8 Maths Solutions Chapter - 3 Square-Math & Cube-Cube Root good to score better in Class 8 examinations?
Yes, NCERT Exemplar for Class 8 Maths Solutions Chapter - 3 Square-Math & Cube-Cube Root can help students to learn more and more of the subject and thus score better grades in the Class 8 examination. This is because, when students practice the solutions mentioned, they learn about all the concepts of the subject deeply. So they are well prepared for the examination. They don't need to be in chaos before the early days of the examination. Also, the learning power of the students is enhanced.
2: Where can I find useful study resources for NCERT Exemplar for Class 8 Maths Solutions Chapter - 3 Square-Math & Cube-Cube Root?
You can find NCERT Exemplar for Class 8 Maths Solutions Chapter - 3 Square-Math & Cube-Cube Root on the Vedantu app or website. You can find the NCERT Exemplar for Class 8 Maths Solutions Chapter - 3 Square-Math & Cube-Cube Root on Vedantu.
Vedantu offers these free resources which are created by the subject matter experts at Vedantu. They are masters in their respective fields and that's why the content is accurate and reliable. Students can find revision notes, important questions, question papers, etc on the site. These study materials are completely free and there is no cost involved. To access these useful study resources, all students have to sign in, and then they will be able to download what they want in PDF format online or offline.
3: Do you have to pay anything for studying NCERT Exemplar for Class 8 Maths Solutions Chapter - 3 Square-Math & Cube-Cube Root on Vedantu?
No, NCERT Exemplar for Class 8 Maths Solutions Chapter - 3 Square-Math & Cube-Cube Root is completely free of cost. Students can access it only by logging in to the Vedantu site which is absolutely free and just preparing for your examination. They don't need to pay anything to access this NCERT Exemplar for Class 8 Maths Solutions Chapter - 3 Square-Math & Cube-Cube Root. These are made for the convenience of the students. They are made not to loot students, but to make students prepare for the examination, to make them more adaptive, and make learning fun and enjoyable for them.
4: How much time does studying NCERT Exemplar for Class 8 Maths Solutions Chapter - 3 Square-Math & Cube-Cube Root involve?
Well, it takes just some time to go through and understand these solutions. They are just made for the convenience of the students. It also depends upon students' memory power and intelligence. Some students can take less time to go through the revision notes while others can take more time also. It also depends upon the difficulty of the subjects and the chapter's concepts. Those with deeper concepts can be difficult to go through by the students while the normal easy-to-understand concepts and chapter revision notes can be easily gone through within a short time.
5: What is NCERT Exemplar?
NCERT Exemplars are books that include extra questions of a higher level. These NCERT Exemplars are made to help students in in-depth learning. The NCERT Exemplar books contain conceptual sums, which cover CBSE board exams and competitive exams (JEE Main and JEE advanced). CBSE board exams sometimes contain in-depth sums.
















