NCERT Exemplar for Class 8 Maths Solutions Chapter 4 Linear Equation In One Variable

Access NCERT Exemplar Solutions for Class 8 Mathematics

Chapter 4 - Linear Equations in One Variable

(Examples, Easy Methods and Step by Step Solutions)

Solved Examples

In examples 1 and 2 , there are four options given out of which one is correct. Choose the correct answer.

Example 1: If $x=a$, then which of the following is not always true for an integer $k$.

(a) $k x=a k$

(b) $\dfrac{x}{a}=\dfrac{a}{k}$

(c) $x-k=a-k$

(d) $x+k=a+k$

Ans: Correct answer is (b).

 $\dfrac{x}{a}=\dfrac{a}{k}$

If $x=a$, then

 $\dfrac{a}{a}=\dfrac{a}{k}$

 $1=\dfrac{a}{k}$

$k=a$

Which is not always true for an integer $k$.

Example 2: If $3 x-4(64-x)=10$, then the value of $x$ is

(a) $-266$

(b) 133

(c) $66.5$

(d) 38

Ans: Correct answer is (d).

$3x - 256 + 4x=10$

$7x=266$

$x=38$

In examples 3 and 4, fill in the blanks to make the statements true.

Example 3: Fifteen added to thrice a whole number gives $93.$ The number is ——.

Ans: $15+3x=93$

$3x=78$

$x=26$

The correct answer is 26 .

Example 4: If $\dfrac{1}{3}-x=-\dfrac{2}{3}$, then $x$ is ——.

Ans: $\dfrac{1}{3}-x=-\dfrac{2}{3}$

$x=1$

The correct answer is 1 .

In examples 5 and 6, state whether the given statements are true (T) or false (F). 

Example 5: Three consecutive even numbers whose sum is 156 are 51,52 and $53 .$

Ans: False.

51 and 53 are not even numbers.

Example $6: x=-12$ is the solution of the linear equation $5 x-3(2 x+1)=21+x$ 

Ans: True.

$5 x-3(2 x+1)=21+x$

$5x-6x-3=21+x$

$-x-x=21+3$

$x=-12$

In examples 7 to 10 solve each of them.

Example 7: Solve :- $\dfrac{x}{2}+\dfrac{x}{4}+\dfrac{x}{5}+10000=x$

Ans: $\dfrac{x}{2}+\dfrac{x}{4}+\dfrac{x}{5}+10000=x$

$\Rightarrow \dfrac{x}{2}+\dfrac{x}{4}+\dfrac{x}{5}-x=-10000$

$\Rightarrow \dfrac{10 x+4 x+5 x-20 x}{20}=-10000$

$\Rightarrow \dfrac{19 x-20 x}{20}=-10000$

$\Rightarrow \dfrac{-x}{20}=-10000$

$\Rightarrow x=200000$

Example 8: The present age of the father is four times the age of his son. After 10 years, the age of father will become three times the age of his son. Find their present ages.

Ans: Let the present age of son be x years

$\therefore$ the present age of father $=4$ x years

After 10 years Age of son $=(x+10)$ years

Age of father $=(4 x+10)$ years

According to the given condition

$4 x+10=3(x+10)$

$\Rightarrow 4 x+10=3 x+30$

$\Rightarrow 4 x-3 x=30-10$

$\Rightarrow x=20$

$\therefore$ Present age of son $=20$ years

Present age of father $=4 x=4 \times 20=80$ years.

Example 9: A steamer goes downstream from one point to another in 7 hours. It covers the same distance upstream in 8 hours. If the speed of the stream be $2 \mathrm{~km} / \mathrm{hr}$, find the speed of the steamer in still water and the distance between the ports.

Ans: Let speed of steamer in still water $=x \mathrm{~km} / \mathrm{hr}$

Speed of stream $=2 \mathrm{~km} / \mathrm{hr}$

Speed downstream $=(x+2) \mathrm{km} / \mathrm{hr}$

Speed upstream $=(x-2) \mathrm{km} / \mathrm{hr}$

Distance covered in 7 hours while downstream $=7(x+2)$ 

Distance covered in 8 hours while upstream $=8(x-2)$

According to the condition

$7(x+2)=8(x-2)$

$\Rightarrow 7 x+14=8 x-16$

$\Rightarrow x=30 \mathrm{~km} / \mathrm{hr}$

$\text { Total Distance } =7(x+2)\mathrm{km}$

$=7(30+2) \mathrm{km}$

$=7 \times 32 \mathrm{~km}$

$=224 \mathrm{~km}$

Example 10: Distance between two stations $A$ and $B$ is $690 \mathrm{~km}$. Two cars start simultaneously from $A$ and $B$ towards each other, and the distance between them after 6 hours is $30 \mathrm{~km}$. If the speed of one car is less than the other by $10 \mathrm{~km} / \mathrm{hr}$, find the speed of each car.

Ans: Let speed of faster car $=x \mathrm{~km} / \mathrm{hr}$

Then speed of other $=(x-10) \mathrm{km} / \mathrm{hr}$

Let 1st one start from $A$ and other from $B$.

$M$ and $N$ be their position after 6 hours.

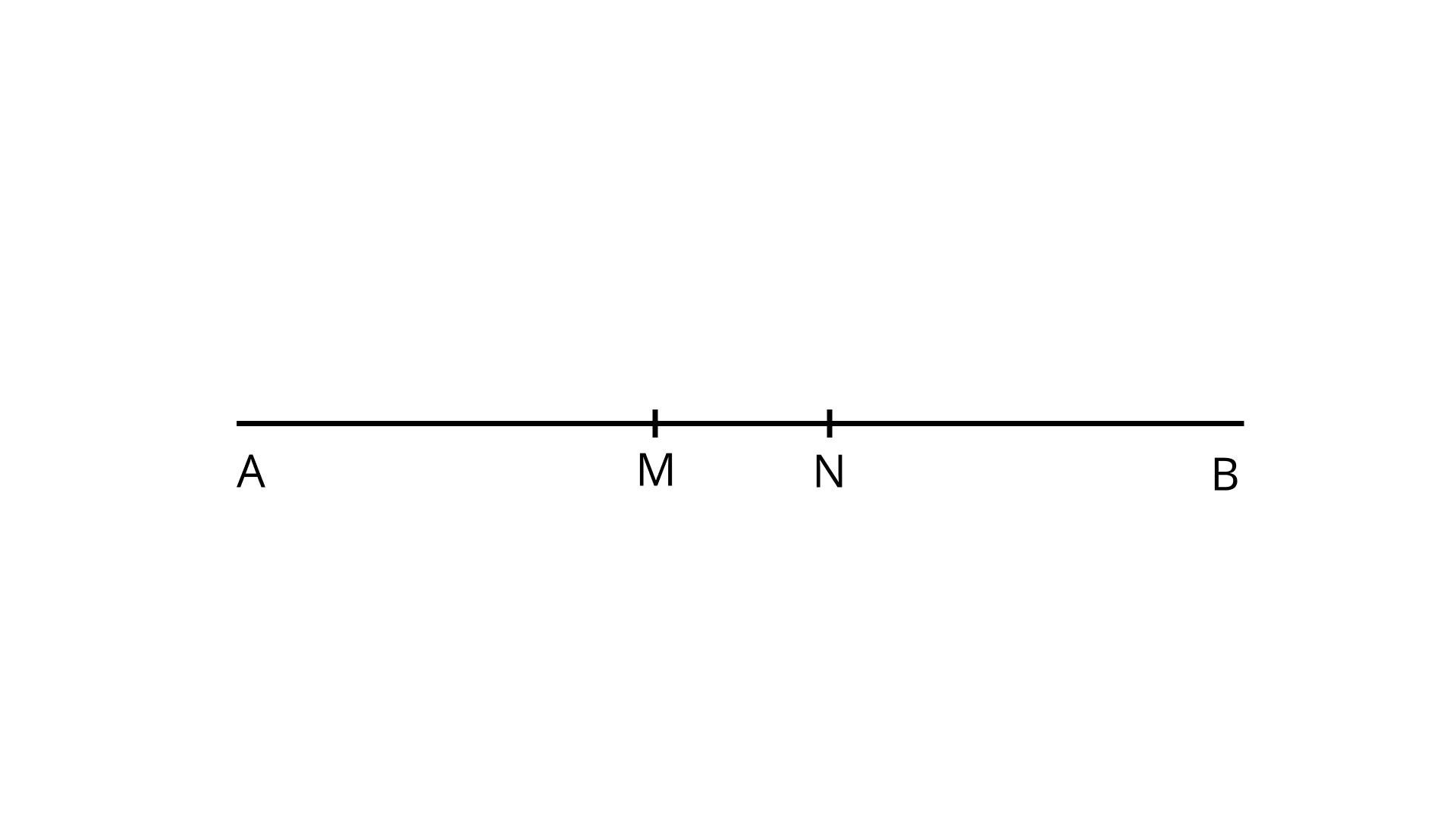
$\mathrm{AM}=6 \mathrm{x},$

$\mathrm{BN}=6(\mathrm{x}-10)$

According to condition,

$6 x+6 x-60 + 30=690$

$\Rightarrow 12 x=690+30$

$\Rightarrow 12 x=720$

$\Rightarrow x=60 \mathrm{~km} / \mathrm{hr}$

Speed of other car $=50 \mathrm{~km} / \mathrm{h}$

Example 11: A home-owner is installing a fence around the square garden. The garden has a perimeter of $6480 \mathrm{~cm}$. Write and solve the equation to find the garden's dimensions.

Ans: Perimeter of square garden $=6480 \mathrm{~cm}$

To find: Side of garden

Fence around square garden. $=$ Perimeter of square garden

$s+s+s+s=6480 \mathrm{~cm}$

$\Rightarrow 4 s=6480 \mathrm{~cm}$

$\Rightarrow s=1620 \mathrm{~cm}$

Thus, side of garden $=1620 \mathrm{~cm}$

Exercise

In questions 1 to 15 out of the four options only one is correct, write the correct answer.

1. The solution of which of the following equations is neither a fraction nor an integer.

(a) $3 x+2=5 x+2$

(b) $4 x-18=2$

(c) $4 x+7=x+2$

(d) $5 x-8=x+4$

Ans: (c)$4 x+7=x+2$ is the correct option.

$\Rightarrow 4 x-x=2-7$              $\text{[transpose x to LHS and 7 to RHS]}$

$\Rightarrow 3 x=-5$

$\Rightarrow x=-\dfrac{5}{3}$           $\text{[This is neither an integer nor a fraction.]}$

2. The solution of the equation $\mathrm{ax}+\mathrm{b}=0$ is

a) $x=a b$

b) $x=-b$

c) $x=-\dfrac{b}{a}$

d) $x=\dfrac{b}{a}$

Ans: (c) $x=-\dfrac{b}{a}$ is the correct option.

Given, $a x+b=0$

$\text{[Transposing b to RHS and it becomes -b]}$

Then,

$a x=-b$

$x=-\dfrac{b}{a}$

3. If $8 x-3=25+17 x$, then $\mathrm{x}$ is

(a) a fraction 

(b) an integer

(c) a rational number 

(d) cannot be solved

Ans: (c) a rational number is the correct option.

Given, $8 x-3=25+17 x$

Transposing $-3$ to the RHS, it becomes 3 and $17 x$ to the LHS, it becomes $-17 x$.

$8 x-17 x=25+3$

$-9 x=28$

$x=-\dfrac{28}{9}$

Therefore, $x$ is a rational number.

4. The shifting of a number from one side of an equation to the other is called

(a) Transposition

(b) Distributivity

(c) Commutativity

(d) Associativity

Ans: (a) Transposition is the correct option.

The shifting of a number from one side of an equation to the other is called transposition.

5. If $\dfrac{5 x}{3}-4=\dfrac{2 x}{5}$, then the numerical value of $2 x-7$ is 

(a) $\dfrac{19}{13}$

(b) $\dfrac{-13}{19}$

(c) 0

(d) $\dfrac{13}{19}$

Ans: (b) $\dfrac{-13}{19}$ is the correct option.

Given, $\dfrac{5 x}{3}-4=\dfrac{2 x}{5}$

$\dfrac{5 x}{3}-\dfrac{2 x}{5}=4$

LCM of 3 and 5 is 15

$\dfrac{25x - 6x}{15}=4$

$19 x=4 \times 15$

$19 x=60$

$x=\dfrac{60}{19}$

Then, substitute the value of $x$ in $2 x-7$

$=(2 \times\dfrac{60}{19})-7$

$=\dfrac{120}{19}-7$

$=\dfrac{120-133}{19}$

$=\dfrac{-13}{19}$

6. The value of $x$ for which the expressions $3 x-4$ and $2 x+1$ become equal is 

(a) -3

(b) 0

(c) 5

(d) $\dfrac{13}{19}$

Ans: (c) 5 is the correct option.

Given, $3 x-4=2 x+1$

Transposing $-4$ to the RHS, it becomes 4 and $2 x$ to the LHS, it becomes $-2 x$.

$3 x-2 x=1+4$

$x=5$

7. If $a$ and $b$ are positive integers, then the solution of the equation $a x=b$ has to be always

(a) positive

(b) negative

(c) one

(d) zero

Ans: (a) positive is the correct option.

Let $a=3, b=4$ 

Then, $a x=b$

$3 x=4$

$x=\dfrac{4}{3}$

8. Linear equation in one variable has

(a) only one variable with any power.

(b) only one term with a variable.

(c) only one variable with power 1 .

(d) only constant term.

Ans: (c) only one variable with power $1 .$

9. Which of the following is a linear expression:

(a) $x^{2}+1$

(b) $y+y^{2}$

(c) 4

(d) $1+z$

Ans: (d) $1+z$ is the correct option.

The linear expression is the one that has the highest power, $1.$

10. A linear equation in one variable has

(a) Only one solution

(b) Two solutions

(c) More than two solutions

(d) No solution

Ans: (a) Only one solution

11. Value of $S$ in $\dfrac{1}{3}+S=\dfrac{2}{5}$

(a) $\dfrac{4}{5}$

(b) $\dfrac{1}{15}$

(c) 10

(d) 0

Ans: (b) $\dfrac{1}{15}$ is the correct option.

Given,

$\dfrac{1}{3}+S=\dfrac{2}{5}$

$S=\dfrac{2}{5}-\dfrac{1}{3}$ 

$S=\dfrac{6-5}{15}$

$S=\dfrac{1}{15}$

12. $\dfrac{-4}{3}y=\dfrac{-3}{4}$, then $y=$

(a) $-{\left(\dfrac{3}{4}\right)}^{2}$

(b) $-{\left(\dfrac{4}{3}\right)}^{2}$

(c) ${\left(\dfrac{3}{4}\right)}^{2}$

(d) ${\left(\dfrac{4}{3}\right)}^{2}$

Ans: (c) ${\left(\dfrac{3}{4}\right)}^{2}$ is the correct option.

Given,

$\dfrac{-4}{3}y=\dfrac{-3}{4}$

$y=\dfrac{-3}{4} \times \dfrac{-3}{4}$

$y=\dfrac{9}{16}$

$y=\dfrac{3 \times 3}{4 \times 4}$

$y={\left(\dfrac{3}{4}\right)}^{2}$

13. The digit in the tens place of a two digit number is 3 more than the digit in the units place. Let the digit at units place be b. Then the number is 

(a) $11 \mathrm{~b}+30$ 

(b) $10 \mathrm{~b}+30$ 

(c) $11 \mathrm{~b}+3$ 

(d) $10 \mathrm{~b}+3$

Ans: (a) $11 \mathrm{~b}+30$ is the correct option.

From the question, it is given that

Let the digit at units place be b.

The digit in the tens place of a two digit number is 3 more than the digit in the units place $=3+b$

So, the number $=10(3+b)+b$

$=30+10 b+b$

$=30+11 b$

14. Arpita's present age is thrice that of Shilpa's. If Shilpa's age three years ago was $x$. Then Arpita's present age is

(a) $3(x-3)$ 

(b) $3 x+3$ 

(c) $3 x-9$ 

(d) $3(x+3)$

Ans: (d) $3(x+3)$ is the correct option.

Given,

Shilpa's age three years ago was $x$

Then, Shilpa's present age is $=x+3$

Arpita's present age is thrice of Shilpa $=3(x+3)$ 

15. The sum of three consecutive multiples of 7 is 357 . Find the smallest multiple.

(a) 112 

(b) 126 

(c) 119 

(d) 116

Ans: (a) 112 is the correct option.

Let us assume the three consecutive multiples of 7 be $7 x,(7 x+7),(7 x+14)$ where $x$ is a natural number.

As per the condition in the question,

$7 x+(7 x+7)+(7 x+14)=357$

$21 x+21=357$

$21(x+1)=357$

$\dfrac{[21(x+1)]}{21}=\dfrac{357}{21}$

$x+1=17$

$X=17-1$

$x=16$

Therefore, the smallest multiple of 7 is,

$7 \times 16=112$

In questions 16 to 32, fill in the blanks to make each statement true.

16. In a linear equation, the ____ power of the variable appearing in the equation is one. 

Ans: In a linear equation, the highest power of the variable appearing in the equation is one.

17. The solution of the equation $3 x-4=1-2 x$ is ____.

Ans: The solution of the equation $3 x-4=1-2 x$ is 1 .

$3 x-4=1-2x$

$3 x+2x=1+4$

$5x=5$

$x=1$

18. The solution of the equation $2 y = 5 y - \dfrac{18}{5}$ is ____.

Ans: The solution of the equation $2 y=5 y-\dfrac{18}{5}$ is $\dfrac{6}{5}$.

$2 y=5 y-\dfrac{18}{5}$

$\dfrac{18}{5}=5 y-2 y$

$\dfrac{18}{5}=3 y$

$y=\dfrac{18}{5} \times\dfrac{1}{3}$

$y=\dfrac{6}{5}$

19. Any value of the variable which makes both sides of an equation equal is known as a ___ of the equation.

Ans: Any value of the variable which makes both sides of an equation equal is known as a solution of the equation.

20. $9 x-\ldots=-21$ has the solution $(-2)$

Ans: $9 x-3=-21$ has the solution $(-2)$

In the question it is given that, $x=-2$

Then, let us assume the missing number be y

$(9 \times(-2))-y=-21$

$-18-y=-21$

$-y=-21+18$

$-y=-3$

$y=3$

21. Three consecutive numbers whose sum is 12 are ____.

Ans: Three consecutive numbers whose sum is 12 are 3,4, and $5 .$

$3+4+5=12$

22. The share of $A$ when Rs 25 is divided between $A$ and $B$ so that $A$ gets Rs. 8 more than $\mathrm{B}$ is ____.

Ans: The share of $A$ when Rs 25 is divided between $A$ and $B$ so that $A$ gets Rs. 8 more than $B$ is Rs $16.50$.

Let us assume $B$ share be $x$

As per the condition in the question, A share be $x+8$

Then,

$x+(x+8)=25$

$\Rightarrow x+x+8=25$

$\Rightarrow 2 x+8=25$

$\Rightarrow 2 x=25-8$

$\Rightarrow 2 x=17$

$\Rightarrow x=\dfrac{17}{2}$

x=8.5

So, $A$ gets $x+8$

$=8.5+8$ $=$ Rs $16.5$

23. A term of an equation can be transposed to the other side by changing its ____.

Ans: A term of an equation can be transposed to the other side by changing its sign. For example:- $2 x+3=0$

Transposing 3 to RHS and it becomes $-3$

$2 x=-3$

$x=\dfrac{-3}{2}$

24. On subtracting 8 from $x$, the result is 2 . The value of $x$ is ____.

Ans: On subtracting 8 from $x$, the result is 2 . The value of $x$ is 10 .

From the question,

On subtracting 8 from $x$, the result is 2 ,

$=x-8=2$

Transposing $-8$ to RHS and it becomes 8

$x=2+8$

$x=10$

25. $\dfrac{x}{5}+30=18$ has the solution as ____.

Ans: $\dfrac{x}{5}+30=18$ has the solution as $-60$.

Given, $\dfrac{x}{5}+30=18$ 

Transposing 30 to RHS and it becomes $-30$.

$\Rightarrow \dfrac{x}{5}=18-30$

$\Rightarrow \dfrac{x}{5}=-12$

$\Rightarrow x=-12 \times 5$

$\Rightarrow x=-60$

26. When a number is divided by 8, the result is $-3$. The number is ____.

Ans: When a number is divided by 8 , the result is $-3$. The number is $-24$.

Let the number be $x$,

Then,

$\dfrac{x}{8}=-3$

$\Rightarrow x=-3 \times 8$

$\Rightarrow x=-24$

27. 9 is subtracted from the product of $p$ and 4 , the result is 11. The value of $p$ is ____.

Ans: 9 is subtracted from the product of $p$ and 4 , the result is 11 . The value of $p$ is 5 .

From the question, it is given that,

9 is subtracted from the product of $p$ and 4 , the result is $4p-9=11$

$4 p-9=11$

Transposing $-9$ to RHS and it becomes $9 .$

$4 p=11+9$

$4 p=20$

$p=\dfrac{20}{4}$

$p=5$

28. If $\dfrac{2}{5}x-2=5-\dfrac{3}{5}x$, then $x=____$.

Ans: If $\dfrac{2}{5} x-2=5-\dfrac{3}{5}x$, then $x=7$

Given,

$\dfrac{2}{5} x-2=5-\dfrac{3}{5}x$

Transposing $-2$ to RHS and it becomes 2 and $-\dfrac{3}{5}x$ to $L H S$ it becomes $\dfrac{3}{5}x$.

$\dfrac{2}{5} x+\dfrac{3}{5} x=5+2$

$\dfrac{2x+3x}{5}=7$

$x=7$

29. After 18 years, Swarnim will be 4 times as old as he is now. His present age is ____.

Ans: After 18 years, Swarnim will be 4 times as old as he is now. His present age is 6 years.

Let us assume swarnim's parent age be x year.

Then, after 18 year, Swarnim's age $=(x+18)$ year

According to the question,

$x+18=4 x$

$x-4 x=-18$

$-3 x=-18$

$\dfrac{-3x}{3}=\dfrac{-18}{3}$

$x=6$

Therefore, swarnim's present age is 6 year.

30. Convert the statement adding 15 to 4 times $x$ is 39 into an equation. 

Ans: Convert the statement Adding 15 to 4 times $x$ is 39 into an equation 

$4 x+15=39$.

31. The denominator of a rational number is greater than the numerator by 10 . If the numerator is increased by 1 and the denominator is decreased by 1, then the expression for the new denominator is ____.

Ans: The denominator of a rational number is greater than the numerator by 10 . If the numerator is increased by 1 and the denominator is decreased by 1 , then the expression for the new denominator is $x+9$.

Let us assume numerator be $x$,

So, denominator $=x+10$

Rational number $=\dfrac{x}{x+10}$

As per the condition given in the question, the numerator is increased by 1 and the denominator is decreased by $1 .$

New rational number $=$ Numerator $+\dfrac{1}{denominator - 1}$

$=\dfrac{x+1}{x+10-1}$

$=\dfrac{x+1}{x+9}$

$\therefore$ the new denominator is $x+9$.

32. The sum of two consecutive multiples of 10 is 210 . The smaller multiple is ____.

Ans: The sum of two consecutive multiples of 10 is 210 . The smaller multiple is 100 .

Let us assume the two consecutive multiples of 10 be $10 x$ and $10 x+10$.

So,

Sum of two consecutive multiples of $10=10 x+10 x+10=210$

$20 x+10=210$

$20 x=210-10$

$20 x=200$

$x=\dfrac{200}{20}$

$x=10$

$\therefore$ the two consecutive multiples of 10 are $10 x=10 \times 10=100$

$10 x+10=(10 \times 10)+10$

$=110$

Hence, the smaller multiple of 10 is 100 .

In questions 33 to 48, state whether the statements are true (T) or false (F).

33. 3 years ago, the age of a boy was y years. His age 2 years ago was $(y-2)$ years

Ans: False.

Because, His age 2 years ago was $(y+1)$ years.

34. Shikha's present age is $\mathrm{p}$ years. Reemu's present age is 4 times the present age of Shikha. After 5 years Reemu's age will be $15 p$ years.

Ans: False.

It is given that, Shikha's present age is p years

Reemu's present age is 4 times the present age of Shikha $=4 p$

After 5 years Reemu's age will be $=(4 p+5)$

35. In a 2 digit number, the units place digit is $x$. If the sum of digits be 9 , then the number is $(10 x-9)$.

Ans: False.

From the question it is given that,

The unit's place digit is $=x$

Sum of two digits $=9$

Then,

Ten's digit $=9-x$

So,

The number $=10(9-x)+x$

$=90-10 x+x$

$=90-9 x$

36. The ages of Anju and her mother are 65 years. If Anju's present age is y years then her mother's age before 5 years is $(60-y)$ years. 

Ans: True.

From the question it is given that,

Anju's present age $=y$ years

The present age of Anju's mother $=(65-y)$ years

Then,

Before 5 years, Anju's mother age $=65-y-5$

$=(60-y)$ years

37. The number of boys and girls in a class are in the ratio $5: 4$. If the number of boys is 9 more than the number of girls, then number of boys is $9 .$

Ans: False.

Let us assume the number of boys be $5 x$ and the number of girls be $4 x$.

From the question,

$5 x-4 x=9$

$x=9$

$\therefore$ Number of boys $=5 x=5 \times 9=45$ boys

Number of girls $=4 x=4 \times 9=36$ girls. 

38. $A$ and $B$ are together 90 years old. Five years ago, $A$ was thrice as old as $B$ was. Hence, the ages of $A$ and $B$ five years back would be $(x-5)$ years and $(85-x)$ years respectively.

Ans: True.

Let us assume A's age is x years.

So, age of $B=(90-x)$ years.

Then,

Before 5 years $A$ 's age $=(x-5)$ years

and $B^{\prime}$ s age $=(90-x-5)=(85-x)$ years.

39. Two different equations can never have the same answer.

Ans: False.

Two different equations can have the same answer.

For example:- (i) $4 x+2=3$

$4 x=3-2$

$x=\dfrac{1}{4}$

(ii) $4 x-6=-5$

$4 x=-5+6$

$x=\dfrac{1}{4}$ 

40. In the equation $3 x-3=9$, transposing $-3$ to RHS, we get $3 x=9$.

Ans: False.

Given, $3 x-3=9$

Transposing $-3$ to the RHS, it becomes 3

$3 x=9+3$

$3 x=12$

41. In the equation $2 x=4-x$, transposing $-x$ to LHS, we get $x=4$.

Ans: False.

Given, $2 x=4-x$

Transposing $-x$ to the LHS, it becomes $x$

$2 x+x=4$

$3 x=4$

$x=\dfrac{4}{3}$

42. If $\dfrac{15}{8}-7 x=9$, then $-7 x=9+\dfrac{15}{8}$

Ans: False.

Given, $\dfrac{15}{8}-7 x=9$

Transposing $\dfrac{15}{8}$ to RHS it becomes $-\dfrac{15}{8}$

$-7 x=9-\dfrac{15}{8}$

43. If $\dfrac{x}{3}+1=\dfrac{7}{15}$, then $\dfrac{x}{3}=\dfrac{6}{15}$

Ans: False.

Given, $\dfrac{x}{3}+1=\dfrac{7}{15}$

Transposing 1 to RHS it becomes - 1

$\dfrac{x}{3}=\dfrac{7}{15}-1$

$\dfrac{x}{3}=\dfrac{7-15}{15}$

$\dfrac{x}{3}=-\dfrac{8}{15}$

44. If $6 x=18$, then $18 x=54$

Ans: True.

Given, $6 x=18$

Multiplying both LHS and RHS by 3 , we get

$6 x \times 3=18 \times 3$ 

$18 x=54$

45. If $\dfrac{x}{11}=15$, then $x=\dfrac{11}{15}$

Ans: False.

Given, $\dfrac{x}{11}=15$

Multiplying both LHS and RHS by 11 , we get

$\dfrac{x}{11} \times 11=15 \times 11$

$x=165$

46. If $x$ is an even number, then the next even number is $2(x+1)$.

Ans: False.

If $x$ is an even number, then the next even number is $(x+2)$

47. If the sum of two consecutive numbers is 93 and one of them is $x$, then the other number is $93-x .$

Ans: True.

From the question, The sum of two consecutive numbers is 93

Two consecutive number are $=x$ and $93-x$

Then, sum of two consecutive numbers $=x+(93-x)=93$

$x+93-x=93$

Transposing 93 to RHS it becomes $-93$

$x-x=93-93$

$0=0$

48. Two numbers differ by 40 , when each number is increased by 8 , the bigger becomes thrice the lesser number. If one number is $x$, then the other number is $(40-$ x).

Ans: False.

From the question it is given that,

One number $=x$

Other number $=40-x$

Let us assume $(40-x)>x$

So, $40-x+8=3(x+8)$

$48-x=3 x+24$

$-x-3 x=24-48$

$-4 x=-24$ 

$x=\dfrac{-24}{-4}$

$x=6$

$\therefore$ One number is $x=6$

Other number is $=40-x$

$=40-6$

$=34$

Difference between numbers $=34-6=28$

Solve the following:

49. $\dfrac{3 x-8}{2 x}=1$

Ans: We have,

$\dfrac{3 x-8}{2 x}=1$

By cross multiplication, we get

$(3 x-8)=2 x$

Transposing $-8$ to RHS it becomes 8 and $2 x$ to LHS it becomes $-2 x$

$3 x-2 x=8$

$x=8$ 

50. $\dfrac{5 x}{2 x-1}=2$

Ans: We have,

$\dfrac{5 x}{2 x-1}=2$

By cross multiplication, we get

$5 x=2 \times(2 x-1)$

$5 x=4 x-2$

Transposing $4 x$ to $L H S$ it becomes $-4 x$

$5 x-4 x=-2$

$x=-2$

51. $\dfrac{2 x-3}{4 x+5}=\dfrac{1}{3}$

Ans: We have,

$\dfrac{2 x-3}{4 x+5}=\dfrac{1}{3}$

By cross multiplication, we get

$3 \times(2 x-3)=1 \times(4 x+5)$

$6 x-9=4 x+5$

Transposing $-9$ to RHS it becomes 9 and $4 x$ to LHS it becomes $-4 x$.

$6 x-4 x=5+9$ 

$2 x=14$

$x=7$

52. $\dfrac{8}{x}=\dfrac{5}{x-1}$

Ans: We have,

$\dfrac{8}{x}=\dfrac{5}{x-1}$

By cross multiplication, we get

$8 \times(x-1)=5 \times x$

$8 x-8=5 x$

Transposing $-8$ to RHS it becomes 8 and $5 x$ to LHS it becomes $-5 x$.

$8 x-5 x=8$

$3 x=8$

$x=\dfrac{8}{3}$

53. $\dfrac{5(1-x)+3(1+x)}{1-2 x}=8$

Ans: We have,

$\dfrac{5(1-x)+3(1+x)}{1-2 x}=8$ 

By cross multiplication, we get

$(5(1-x))+(3(1+x))=8 \times(1-2 x)$

$5-5 x+3+3 x=8-16 x$

$8-2 x=8-16 x$

Transposing 8 to RHS it becomes $-8$ and $-16 x$ to LHS it becomes $16 x$.

$16 x-2 x=8-8$

$14 x=0$

$x=0$

54. $\dfrac{0.2 x+5}{3.5 x-3}=\dfrac{2}{5}$

Ans: We have,

$\dfrac{0.2 x+5}{3.5 x-3}=\dfrac{2}{5}$

By cross multiplication, we get

$5 \times(0.2 x+5)=2 \times(3.5 x-3)$

$x+25=7 x-6$

Transposing $x$ to RHS it becomes $-x$ and $-6$ to LHS it becomes 6 .

$25+6=7 x-x$

$31=6 x$

$x=\dfrac{31}{6}$

55. $\dfrac{y-(4-3 y)}{2 y-(3+4 y)}=\dfrac{1}{5}$

Ans: We have,

$\dfrac{y-(4-3 y)}{2 y-(3+4 y)}=\dfrac{1}{5}$

$\dfrac{y-4+3 y)}{2 y-3-4 y)}=\dfrac{1}{5}$

$\dfrac{-4+4 y)}{-3-2y)}=\dfrac{1}{5}$

By cross multiplication, we get

$5 \times(4 y-4)=1 \times(-2 y-3)$

$20 y-20=-2 y-3$

Transposing $-20$ to RHS it becomes 20 and $-2y$ to LHS it becomes $2 y$.

$20 y+2 y=20-3$

$22 y=17$

$y=\dfrac{17}{22}$

56. $\dfrac{x}{5}=\dfrac{x-1}{6}$

Ans: We have,

 $\dfrac{x}{5}=\dfrac{x-1}{6}$

By cross multiplication, we get

$6x=5(x-1)$

$6x=5 x-5$

Transposing $5 x$ to RHS it becomes $-5 x$

$6 x-5 x=-5$

$x=-5$

57. $0.4(3 x-1)=0.5 x+1$

Ans: We have,

$0.4(3 x-1)=0.5 x+1$

$1.2 x-0.4=0.5 x+1$

Transposing $-0.4$ to RHS it becomes $0.4$ and $0.5 x$ to LHS it becomes $-0.5 x$.

$1.2 x-0.5 x=1+0.4$

$0.7 x=1.4$

$x=2$

58. $8 x-7-3 x=6 x-2 x-3$ 

Ans: We have,

$\Rightarrow 8 x-7-3 x=6 x-2 x-3$

$\Rightarrow 5 x-7=4 x-3$

Transposing $-7$ to RHS it becomes 7 and $4 x$ to LHS it becomes $-4 x$.

$\Rightarrow 5 x-4 x=7-3$

$\Rightarrow x=4$

59. $10 x-5-7 x=5 x+15-8$

Ans: We have,

$10 x-5-7 x=5 x+15-8$

$\Rightarrow 3 x-5=5 x+7$

Transposing $-5$ to RHS it becomes 5 and $5 x$ to LHS it becomes $-5 x$.

$3 x-5 x=7+5$

$\Rightarrow-2 x=12$

$\Rightarrow x=-\dfrac{12}{2}$

$\Rightarrow x=-6$

60. $4 t-3-(3 t+1)=5 t-4$ 

Ans: We have,

$4 t-3-(3 t+1)=5 t-4$

$\Rightarrow 4 t-3-3 t-1=5 t-4$

$\Rightarrow t-4=5 t-4$

Transposing t to RHS it becomes $-\mathrm{t}$ and $-4$ to LHS it becomes 4 .

$4-4=5 t-t$

$\Rightarrow 0=4 t$

$\Rightarrow t=\dfrac{0}{4}$

$\Rightarrow t=0$

61. $5(x-1)-2(x+8)=0$

Ans: We have,

$5(x-1)-2(x+8)=0$

$\Rightarrow 5 x-5-2 x-16=0$

$\Rightarrow 3 x-21=0$

Transposing $-21$ to RHS it becomes $21 .$

$3 x=21$

$\Rightarrow x=\dfrac{21}{3}$

$\Rightarrow x=7$

62.$\dfrac{x}{2}-\dfrac{1}{4}\left(x-\dfrac{1}{3}\right)=\dfrac{1}{6}(x+1)+\dfrac{1}{12}$

Ans: Given equation is,

$\dfrac{x}{2}-\dfrac{1}{4}\left(x-\dfrac{1}{3}\right)=\dfrac{1}{6}(x+1)+\dfrac{1}{12}$

$\Rightarrow \dfrac{x}{2}-\dfrac{x}{4}+\dfrac{1}{12}=\dfrac{x}{6}+\dfrac{1}{6}+\dfrac{1}{12}$

$\Rightarrow \dfrac{2 x-x}{4}+\dfrac{1}{12}=\dfrac{x}{6}+\dfrac{2+1}{12}$

$\Rightarrow \dfrac{x}{4}+\dfrac{1}{12}=\dfrac{x}{6}+\dfrac{3}{12}$

$\Rightarrow \dfrac{x}{4}-\dfrac{x}{6}=\dfrac{3}{12}-\dfrac{1}{12}$

$\Rightarrow \dfrac{6 x-4 x}{24}=\dfrac{3-1}{12}$

$\Rightarrow \dfrac{2 x}{24}=\dfrac{2}{12}$

$\Rightarrow 24 x=48$

$\Rightarrow x=2$

63. $\dfrac{1}{2}(x+1)+\dfrac{1}{3}(x+1)=\dfrac{5}{12}(x-2)$

Ans: Given, 

$\dfrac{1}{2}(x+1)+\dfrac{1}{3}(x+1)=\dfrac{5}{12}(x-2)$

$\dfrac{x}{2}+\dfrac{1}{2}+\dfrac{x}{3}-\dfrac{1}{3}=\dfrac{5 x}{12}-\dfrac{5}{6}$

$\dfrac{x}{2}+\dfrac{x}{3}-\dfrac{5 x}{12}=\dfrac{1}{3}-\dfrac{1}{2}-\dfrac{5}{6}$

$\dfrac{5 x}{12}=\dfrac{-6}{6}$

$5 x \times 6=(-6) \times 12$

$x=\dfrac{(-6) \times 12}{5 \times 6}$

$x=\dfrac{-12}{5}$

64. $\dfrac{x+1}{4}=\dfrac{x-1}{3}$

Ans: $\text { Given that }$

$\dfrac{x+1}{4}=\dfrac{x-1}{3}$

$\Rightarrow 3(x+1)=4(x-1)$

$\Rightarrow 3 x+3=4 x-4$

$\Rightarrow-x=-7$

$\therefore x=7$

65. $\dfrac{2 x-1}{5}=\dfrac{3 x+1}{3}$

Ans: Given that,

$\dfrac{2 x-1}{5}=\dfrac{3 x+1}{3}$

$\Rightarrow 3(2 x-1)=5(3 x+1)$

$\Rightarrow 6 x-3=15 x+5$

$\Rightarrow 6 x-15 x=5+3$

$\Rightarrow-9 x=8$

$\Rightarrow x=-\dfrac{8}{9}$

66. $1-(x-2)-[(x-3)-(x-1)]=0$

Ans: Given that,

$1-(x-2)-[(x-3)-(x-1)]=0$

$\Rightarrow 1-x+2-[x-3-x+1]=0$

$\Rightarrow 3-x-[-2]=0$

$\Rightarrow 3-x+2=0$

$\Rightarrow-x=-2-3$

$\Rightarrow x=5$

67. $3 x-\dfrac{x-2}{3}=4-\dfrac{x-1}{4}$

Ans: Given that,

$3 x-\dfrac{x-2}{3}=4-\dfrac{x-1}{4}$

$\Rightarrow \dfrac{9 x-(x-2)}{3}=\dfrac{16-(x-1)}{4}$

$\Rightarrow 4(9 x-x+2)=3(16-x+1)$

$\Rightarrow 4(8 x+2)=3(-x+17)$

$\Rightarrow 32 x+8=-3 x+51$

$\Rightarrow 32 x+3 x=51-8$

$\Rightarrow 35 x=43$

$\Rightarrow x=\dfrac{43}{35}$

68. $\dfrac{3 t+5}{4}-1=\dfrac{4 t-3}{5}$

Ans: Given that,

$\dfrac{3 t+5}{4}-1=\dfrac{4 t-3}{5}$

$\Rightarrow \dfrac{3 t+5-4}{4}=\dfrac{4 t-3}{5}$

$\Rightarrow 5(3 t+5-4)=4(4 t-3)$

$\Rightarrow 5(3 t+1)=4(4 t-3)$

$\Rightarrow 15 t+5=16 t-12$

$\Rightarrow 15 t-16 t=-12-5$

$\Rightarrow-t=-17$

$\Rightarrow t=17$

69. $\dfrac{2 y-3}{4}-\dfrac{3 y-5}{2}=y+\dfrac{3}{4}$

Ans: $\Rightarrow \left[\dfrac{(2 y-3)-2(3 y-5)}{4}\right]=\dfrac{4 y+3}{4}=y+\dfrac{3}{4}$

$\Rightarrow \dfrac{2 y-3-6 y+10}{4}=\dfrac{4 y+3}{4}$

$\Rightarrow \dfrac{4(-4 y+7)}{4}=\dfrac{4(4 y+3)}{4}$

$\Rightarrow-4 y+7=4 y+3$

$\Rightarrow-8 y==3-7$

$\Rightarrow y=\dfrac{1}{2}$

70. $0.25(4 x-5)=0.75 x+8$

Ans: $\Rightarrow x-1.25=0.75 x+8$

$\Rightarrow x-0.75 x=9.25$

$\Rightarrow x=\dfrac{9.25}{0.25}$

$\Rightarrow x=37$

71. $\dfrac{9-3 y}{1-9 y}=\dfrac{8}{5}$

Ans: Given that,

$\dfrac{9-3 y}{1-9 y}=\dfrac{8}{5}$

$\Rightarrow 5(9-3 y)=8(1-9 y)$

$\Rightarrow 45-15 y=8-72 y$

$\Rightarrow 45-15 y=8-72 y$

$\Rightarrow 72 y-15 y=8-45$

$\Rightarrow 57 y=-37$

$\Rightarrow \dfrac{57 y}{57}=-\dfrac{37}{57}$

$\Rightarrow y=\dfrac{-37}{57}$

72. $\dfrac{3 x+2}{2 x-3}=-\dfrac{3}{4}$

Ans: Given that, $\dfrac{3 x+2}{2 x-3}=-\dfrac{3}{4}$

$\Rightarrow 4(3 x+2)=-3(2 x-3)$

$\Rightarrow 12 x+8=-6 x+9$

$\Rightarrow 12 x+6 x=9-8$

$\Rightarrow 18 x=1$

$\Rightarrow x=\dfrac{1}{18}$

73. $\dfrac{5 x+1}{2 x}=-\dfrac{1}{3}$

Ans: Given that,

$\dfrac{5 x+1}{2 x}=-\dfrac{1}{3}$

$\Rightarrow 3(5 x+1)=-2 x$

$\Rightarrow 15 x+3=-2 x$

$\Rightarrow 15 x+2 x=-3$

$\Rightarrow 17 x=-3$

$\Rightarrow x=-\dfrac{3}{17}$

74. $\dfrac{3 t-2}{3}+\dfrac{2 t+3}{2}=t+\dfrac{7}{6}$

Ans: Given that, 

$\dfrac{3 t-2}{3}+\dfrac{2 t+3}{2}=t+\dfrac{7}{6}$

$\Rightarrow \dfrac{2(3 t-2)+3(2 t+3)}{6}=\dfrac{6 t+7}{6}$

$\Rightarrow 2(3 t-2)+3(2 t+3)=6 t+7$

$\Rightarrow 6 t-4+6 t+9=6 t+7$

$\Rightarrow 6 t=7+4-9$

$\Rightarrow t=\dfrac{1}{3}$

75. $m-\dfrac{m-1}{2}=1-\dfrac{(m-2)}{3}$

Ans: Given that

$m-\dfrac{m-1}{2}=1-\dfrac{(m-2)}{3}$

$\Rightarrow \dfrac{[2 m-(m-1)]}{2}=\dfrac{[3-(m-2)]}{3}$

$\Rightarrow 3(m+1)=2(5-m)$

$\Rightarrow 3 m+3=10-2 m$

$\Rightarrow 3 m+2 m=10-3$

$\Rightarrow 5 m=7$

$\Rightarrow m=\dfrac{7}{5}$

76. $4(3 p+2)-5(6 p-1)=2(p-8)-6(7 p-4)$

Ans: Given that,

$4(3 p+2)-5(6 p-1)=2(p-8)-6(7 p-4)$

$\Rightarrow 12 p+8-30 p+5=2 p-16-42 p+24$

$\Rightarrow-18 p+13=-40 p+8$

$\Rightarrow-18 p+40 p=8-13$

$\Rightarrow 22 p=-5$

$\Rightarrow \mathrm{p}=-\dfrac{5}{22}$

77. $3(5 x-2)+2(9 x-11)=4(8 x-7)-111$

Ans: Given that,

$3(5 x-2)+2(9 x-11)=4(8 x-7)-111$

$\Rightarrow 15 x-6+18 x-22=48 x-28-111$

$\Rightarrow 33 x-43=32 x-139$

$\Rightarrow 33 x-32 x=-139+43$

$\Rightarrow x=-96$

78. $0.16(5 x-2)=0.4 x+7$

Ans: Given that, 

$0.16(5 x-2)=0.4 x+7$

$\Rightarrow 0.8 x-0.32=0.4 x+7$

$\Rightarrow 0.8 x-0.4 x=7+0.32$

$\Rightarrow 0.4 x=7.32$

$\Rightarrow x=\dfrac{7.32}{0.4}$

$\Rightarrow x=18.3$

79. Radha takes some flowers in a basket and visits three temples one-by-one. At each temple, she offers one half of the flowers from the basket. If she is left with 3 flowers at the end, then find the number of flowers she had in the beginning.

Ans: Let total number of flowers be $x$

Then,

Flowers offered in first temple $=\dfrac{x}{2}$

Flowers offered in second temple $=\dfrac{x}{4}$ 

Flowers offered in third temple $=\dfrac{x}{8}$

No. of flowers left in the end $=3$

Now, According to question

$x-\left(\dfrac{x}{2}+\dfrac{x}{4}+\dfrac{x}{8}\right)=3$

$\dfrac{[8 x-(4 x+2 x+x)]}{8}=3$

$8 x-7 x=24$

$x=24$

Hence, the total number of flowers were $24 .$

80. Rs 13500 are to be distributed among Salma, Kiran and Jenifer in such a way that Salma gets Rs 1000 more than Kiran and Jenifer gets Rs 500 more than Kiran. Find the money received by Jenifer.

Ans: Let the money received by Kiran be $x$

Then,

The money received by Salma = Rs $(x+1000)$

Money received by Jenifer $=$ Rs $(x+500)$

According to question

$x+x+1000+x+500=13500$

$3 x+1500=13500$

$3 x=13500-1500$

$x=\dfrac{12000}{3}$

$x=4000$

Hence, the money received by Jenifer $=$ Rs $(4000+500)=$ Rs 4500

81. The volume of water in a tank is twice that of the other. If we draw out 25 liters from the first and add it to the other, the volumes of the water in each tank will be the same. Find the volumes of water in each tank.

Ans: Let volume of water in one tank be $x$

Then, Volume of water in another tank $=2 x$

According to question

$x+25=2 x-25$

$2 x-x=25+25$

$x=50$

Hence, the volume of water in one tank $=50$

82. Anushka and Aarushi are friends. They have an equal amount of money in their pockets. Anushka gave $\dfrac{1}{3}$ of her money to Aarushi as her birthday gift. Then, Aarushi gave a party at a restaurant and cleared the bill by paying half of the total money with her. If the remaining money in Aarushi's pocket is Rs 1600 , then find the sum gifted by Anushka.

Ans: Let Anushka and Arushi have an equal amount of money in the packet, which is Rs. X

After giving $\dfrac{1}{3}$ of money of Anushka to Arushi, Amount of Arushi $=\operatorname{Rs}\left(x+\dfrac{x}{3}\right)$

According to question,

$\left(x+\dfrac{x}{3}\right)-\dfrac{1}{2}\left(x+\dfrac{x}{3}\right)=1600$

$\left(x+\dfrac{x}{3}\right)\left(1-\dfrac{1}{2}\right)=1600$

$\left(x+\dfrac{x}{3}\right) \dfrac{1}{2}=1600$

$\dfrac{3 x+x}{3}=1600 \times 2$

$\dfrac{4 x}{3}=3200$

$x=3200 \times \dfrac{3}{4}$

$x=2400$

So, money gifted by anushka $=\dfrac{1}{3}$ of $2400=\dfrac{1}{3} \times 2400=800$

83. Kaustubh had 60 flowers. He offered some flowers in the temple and found that the ratio of the number of remaining flowers to that of flowers in the beginning is 3 : 5 . Find the number of flowers offered by him in the temple.

Ans: Let number of flowers offered by kaustubh in the temple be $x$ Then,

Remaining flowers $=60-x$

According to the question, $\dfrac{\text { number of remaining flowers }}{\text { number of flowers in beginning }}      = \dfrac{3}{5}$

$\dfrac{60-x}{60}=\dfrac{3}{5}$

$300-5 x=180$

$5 x=300-180$

$5 x=120$

$x=\dfrac{120}{5}$

$x=24$

Hence, number of flowers offered by kaustubh in the temple $=24$

84. The sum of three consecutive even natural numbers is 48 . Find the greatest of these numbers.

Ans: Let the three even consecutive numbers be $x,(x+2),(x+4)$

Now,

According to the question,

$x+(x+2)+(x+4)=48$

$3 x+6=48$

$3 x=42$

$x=\dfrac{42}{3}$

$x=14$ 

Hence, the three even consecutive numbers are 14, 16, 18

Out of these three, 18 is the greatest number.

85. The sum of three consecutive odd natural numbers is $69 .$ Find the prime number out of these numbers.

Ans: Let the three odd consecutive natural numbers be $x,(x+2)$, and $(x+4)$

Now,

According to question,

$x+(x+2)+(x+4)=69$

$3 x+6=69$

$3 x=69-6$

$3 x=63$

$x=\dfrac{63}{3}$

$x=21$

Hence, the three consecutive odd natural numbers are 21, 23, $25 .$

23 is the prime number.

86. The sum of three consecutive numbers is 156 . Find the number which is a multiple of 13 out of these numbers.

Ans: Let the three consecutive numbers be $x, x+1$ and $x+2$ 

According to the question,

$x+(x+1)+(x+2)=156$

$3 x+3=156$

$3 x=156-3$

$3 x=153$

$x=\dfrac{153}{3}$

$x=51$

Hence, three consecutive numbers are $51,52,53 .$

Only 52 is a multiple of $13 .$

87. Find a number whose fifth part increased by 30 is equal to its fourth part decreased by 30 .

Ans: Let the number be $x$

Now,

According to question,

$\dfrac{x}{5}+30=\dfrac{x}{4}-30$

$\dfrac{x}{5}-\dfrac{x}{4}=-30-30$

$\dfrac{4 x-5 x}{20}=-60$

$4 x-5 x=-1200$ 

$x=1200$

Hence, the number is $1200 .$

88. Divide 54 into two parts, such that one part is $\dfrac{2}{7}$ of the other.

Ans: Let the one part be $x$

Then, the other part will be $\dfrac{2 x}{7}$

Now,

According to the question,

$x+\dfrac{2 x}{7}=54$

$\dfrac{7 x+2 x}{7}=54$

$9 x=7 \times 54$

$x=\dfrac{7 \times 54}{9}$

$x=42$

Hence, one part $=\dfrac{42 \times 2}{7}=12$

The other part $=42$

89. Sum of the digits of a two-digit number is 11. The given number is less than the number obtained by interchanging the digits by 9 . Find the number.

Ans: Let the unit's digit be $x$. Then,

The ten's digit $=11-x$

Therefore,

number $=10(11-x)+x=110-10 x+x=110-9 x$

Now, according to the question

$\Rightarrow 9 x+11-(110-9 x)=9$

$\Rightarrow 9 x+11-110+9 x=9$

$\Rightarrow 18 x=108$

$\Rightarrow x=\dfrac{108}{18}$

$\Rightarrow x=6$

So, the unit's digit is 6 and ten's digit is 5 . Hence, the number is 56

90. Two equal sides of a triangle are each $4 \mathrm{~m}$ less than three times the third side. Find the dimensions of the triangle, if its perimeter is $55 \mathrm{~m}$.

Ans: Let the third side be $x$

Then, two equal sides of the triangle $=(3 x-4)$

It's given that

Perimeter $=55 \mathrm{~m}$

Since,

Perimeter of the triangle $=$ Sum of the sides of the triangle

Therefore,

$x+3 x-4+3 x-4=55$

$\Rightarrow 7 x-8=55$

$\Rightarrow 7 x=63$

$\Rightarrow x=\dfrac{63}{7}$

$\Rightarrow x=9$

Hence, the dimensions are $9 \mathrm{~m}, 23 \mathrm{~m}$, and $23 \mathrm{~m}$.

91. After 12 years, Kanwar shall be 3 times as old as he was 4 years ago. Find his present age.

Ans: Let Kanwar's present age be $x$

Kanwar's age after $12 y r s=(x+12) y r$

Kanwar's age 4yrs ago $=(x-4) y r$

Now,

According to the question

$x+12=3(x-4)$

$\Rightarrow 3 x-x=12+12$

$\Rightarrow 2 x=24$

$\Rightarrow x=\dfrac{24}{2}$

$\Rightarrow x=12$

Hence, Kanwar's present age is $12 \mathrm{yrs}$. 

92. Anima left one-half of her property to her daughter, one-third to her son and donated the rest to an educational institute. If the donation was worth Rs 100000 , how much money did Anima have?

Ans: Let Anima's property be $x$

So,

Property left for her daughter $=\dfrac{x}{2}$

Now, remaining property $=x-\dfrac{x}{2}=\dfrac{x}{2}$

Property left for her son $=\dfrac{1}{3}$ of remaining property $=\dfrac{1}{3} \times \dfrac{x}{2}=\dfrac{x}{6}$

Remaining property $=\left[x-\left(\dfrac{x}{2}+\dfrac{x}{6}\right)\right]=x-\left(\dfrac{3 x+x}{6}\right)=\dfrac{6 x-4 x}{6}=\dfrac{x}{3}$

As the remaining property is donated to an educational institution

And donated property $=100000$

Therefore,

$\dfrac{x}{3}=100000$

$\Rightarrow x=300000$

Hence, Anima had Rs. 300000 .

93 If $\dfrac{1}{2}$ is subtracted from a number and the difference is multiplied by 4 , the result is 5. What is the number?

Ans: Let the number be $x$ Now, according to the question,

$4\left(x-\dfrac{1}{2}\right)=5$

$\Rightarrow 4 x-2=5$

$\Rightarrow 4 x=5+2$

$\Rightarrow x=\dfrac{7}{4}$

Therefore, the required number is $\dfrac{7}{4}$

94. The sum of four consecutive integers is $266 .$ What are the integers?

Ans: Let's assume the four consecutive integers be $x, x+1, x+2, x+3$

According to the question,

$x+x+1+x+2+x+3=266$

$\Rightarrow 4 x+6=266$

$\Rightarrow 4 x=260$

$\Rightarrow x=65$

Hence, the four consecutive numbers are $65,66,67,68$.

95. Hamid has three boxes of different fruits. Box $A$ weighs $2 \dfrac{1}{2} \mathrm{~kg}$ more than box $B$ and Box $C$ weighs $10 \dfrac{1}{4} \mathrm{~kg}$ more than box $B$. The total weight of the three boxes is $48 \dfrac{3}{4} \mathrm{~kg}$. How many kilograms does box A weigh?

Ans: Let $x$ kg be the weight of the box A.

According to the question,

Given that Weight of Box A= Weight of Box B+2 $\dfrac{1}{2} \mathrm{~kg}$

weight of box $\mathrm{B}=x-\dfrac{5}{2} \mathrm{~kg}$

And weight of Box C= Weight of Box B+ $\dfrac{41}{4} \mathrm{~kg}$

weight of Box C $=x-\dfrac{5}{2}+\dfrac{41}{4} k g$

$=x+\dfrac{-10+41}{4}$

$=x+\left(\dfrac{31}{4}\right)$

Since,

Total weight of three boxes $=$ Weight of box $A+$ Weight of box $B+$ Weight of box $C$ 

So,

$\dfrac{195}{4}=x+x-\dfrac{5}{2}+x+\dfrac{31}{4}$

$\Rightarrow \dfrac{195}{4}=3 x+\dfrac{31-10}{4}$

$\Rightarrow 3 x=\dfrac{174}{4}$

$\Rightarrow x=\dfrac{29}{2}$

$\Rightarrow x=14 \dfrac{1}{2}$

Hence, weight of box A$=14 \dfrac{1}{2} k g$

96. The perimeter of a rectangle is $240 \mathrm{~cm}$. If its length is increased by $10 \%$ and its breadth is decreased by $20 \%$, then we get the same perimeter. Find the length and breadth of the rectangle. 

Ans: It is given that,

Perimeter $=240 \mathrm{~cm}$

$\Rightarrow 2(l+b)=240 \mathrm{~cm}$

$\Rightarrow l+b=120 \mathrm{~cm}$

Let the length of the rectangle be $x$

Then, breadth $=120-x$

New length $=x+10 \%$ of $x$

$=x+\dfrac{10}{100} x=\dfrac{110}{100} x \mathrm{~cm}$

And

New breadth $=(120-x)-20 \%$ of $(120-x)$

$=(120-x)-\dfrac{20}{100} \times(120-x)$

$=(120-x)\left(1-\dfrac{20}{100}\right)$

$=\dfrac{80}{100}(120-x)$

New perimeter $=240 \mathrm{~cm}$

$2\left[\dfrac{110 x}{100}+\dfrac{80}{100}(120-x)\right]=240$

$\Rightarrow \dfrac{[110 x+9600-80 x]}{100}=\dfrac{240}{2}$

$\Rightarrow 30 x+9600=\dfrac{240}{2} \times 100$

$\Rightarrow 30 x=2400$

$\Rightarrow x=\dfrac{2400}{30}=80$

Therefore, length $=80 \mathrm{~cm}$; breadth $=40 \mathrm{~cm}$

97. The age of $A$ is five years more than that of $B$. 5 years ago, the ratio of their ages was 3 :2. Find their present ages.

Ans: Let the present age of $B$ be $x$

So, the age of $A$ will be $x+5$

Age of $A$, five years ago $=x+5-5=x$

And the age of $B=(x-5)$

According to the question,

$\dfrac{x}{x-5}=\dfrac{3}{2}$

$\Rightarrow 2 x=3 x-15$

$\Rightarrow 3 x-2 x=15$

$\Rightarrow x=15$

Hence, the present age of $B$ and $A$ is $15 y r s$ and $20 y r s$ respectively.

98. If the numerator is 2 less than the denominator of a rational number and when 1 is subtracted from numerator and denominator both, the rational number in its simplest form is $\dfrac{1}{2}$. What is the rational number?

Ans: Let the denominator be $x$

Numerator= denominator - 2

= x - 2

According to the question,

$\dfrac{[(x-2)-1]}{x-1}=\dfrac{1}{2}$

$\Rightarrow 2(x-2-1)=x-1$

$\Rightarrow 2(x-3)=x-1$

$\Rightarrow 2 x-6=x-1$

$\Rightarrow x=5$

Hence, the denominator and numerator are 5 and 3 respectively.

So, the number is $\dfrac{3}{5}$.

99. In a two-digit number, the digit in the unit's place is twice the digit in ten's place. If 27 is added to it, digits are reversed. Find the number.

Ans: Let the ten's digit be $x$

Then, the unit's digit will be $2 x$

Therefore,

Number $=10 x+2 x=10 x+2 x=12 x$

On reversing

New number $=10 \times 2 x+x=20 x+x=21 x$

According to the question,

$12 x+27=21 x$

$\Rightarrow 21 x-12 x=27$

$\Rightarrow 9 x=27$

$\Rightarrow x=3$

Hence the required number $=12 \times 3=36$

100. A man was engaged as typist for the month of February in 2009. He was paid Rs 500 per day, but Rs 100 per day were deducted for the days he remained absent. He received Rs 9100 as salary for the month. For how many days did he work?

Ans: Let the number of working days be $x$

Number of the absent days=(29-x)days

Number of days in February $=29$

Payment per day= Rs. 500

Total paid amount for the working days $=500 x$

Per day deduction $=100$

Total amount deducted $=100 \times(29-x)$

It is given that,

Salary paid= Rs. 9100

Now, according to the question

$500 x-100(29-x)=9100$

$\Rightarrow 500 x-2900+100 x=9100$

$\Rightarrow 600 x=9100+2900$

$\Rightarrow x=\dfrac{12000}{600}$

$\Rightarrow x=20$

Therefore, he worked for 20 days.

101. A steamer goes downstream and covers the distance between two ports in 3 hours. It covers the distance in 5 hours, when it goes upstream. If the stream flows at $3 \mathrm{~km} / \mathrm{h}$, then find what is the speed of the steamer upstream?

Ans: Let the speed of steamer be $x$

Speed of the stream $=3 \mathrm{~km} / \mathrm{h}$

Now,

Speed of the steamer downstream $=x+3$

Speed of the steamer upstream $=x-3$

According to the question,

$3(x+3)=5(x-3)$

$\Rightarrow 3 x+9=5 x-15$

$\Rightarrow 3 x-5 x=-15-9$

$\Rightarrow-2 x=-24$

$\Rightarrow x=12$

Hence, the speed of streamers upstream is $9 \mathrm{~km} / \mathrm{h}$.

102. A lady went to a bank with Rs. 100000 . She asked the cashier to give her Rs 500 and Rs 1000 currency notes in return. She got 175 currency notes in all. Find the number of each kind of currency note.

Ans: Total number of currency $=175$

Let total number of 500 notes be $x$

Total number of notes of $1000=175-x$

According to the question,

$500 x+(175-x) 1000=100000$

$\Rightarrow 500 x+175000-1000 x=100000$

$\Rightarrow-500 x=100000-175000$

$\Rightarrow x=150$

Hence, total number of notes of $500=150$

Total number of notes of $1000=25$

103. There are 40 passengers in a bus, some with Rs 3 tickets and remaining with Rs 10 tickets. The total collection from these passengers is Rs 295. Find how many passengers have tickets worth Rs 3 ?

Ans: Given,

Total number of passengers $=40$

Let number of passengers having tickets of Rs. 3 be $x$

Number of passengers having tickets worth Rs. 10 be $40-x$

Total number of passengers= Rs295

According to the question,

$3 x+10(40-x)$

$\Rightarrow 3 x+400-10 x=295$

$\Rightarrow-7 x=-105$

$\Rightarrow x=15$

Therefore, the number of passengers having tickets of Rs. 3 is 15 .

104. Denominator of a number is 4 less than its numerator. If 6 is added to the numerator, it becomes twice the denominator. Find the fraction.

Ans: Let the numerator be $x$

And denominator is $x-4$

$\therefore$ Fraction $=\dfrac{x}{x-4}$

Now, according to the question,

$x+6=3(x-4)$

$3 x-12=x+6$

$\Rightarrow 3 x-x=6+12$

$\Rightarrow 2 x=18$ 

$\Rightarrow x=\dfrac{18}{2}$

$\Rightarrow x=9$

Therefore, the fraction $=\dfrac{x}{x-4}=\dfrac{9}{9-4}=\dfrac{9}{5}$

105. An employee works in a company on a contract of 30 days on the condition that he will receive Rs 120 for each day he works and he will be fined Rs 10 for each day he is absent. If he receives Rs 2300 in all, for how many days did he remain absent?

Ans: It is given that,

total number of days in contract $=30$

Money received per day for working= Rs. 120

Money received per day for being absent = Rs. 10

Salary received = Rs. 2300

Let $x$ be the number of days the worker was absent.

Now, according to the question,

$120(30-x)-10 x=2300$

$\Rightarrow 3600-120 x-10 x=2300$

$\Rightarrow-130 x=2300-3600$

$\Rightarrow-130 x=-1300$

$\Rightarrow x=10$

Therefore, the employee was absent for 10 days. 

106. Kusum buys some chocolates at the rate of Rs 10 per chocolate. She also buys an equal number of candies at the rate of Rs 5 per candy. She makes a $20 \%$ profit on chocolates and $8 \%$ profit on candies. At the end of the day, all chocolates and candies are sold out and her profit is Rs 240. Find the number of chocolates purchased.

Ans: Let $x$ be the number of chocolates purchased

So, the total cost=Rs. 10x

Then, total number of candies be $x$

Total cost of candies= Rs. $5 x$

Now,

According to the question,

Profit on chocolates $=20 \%$ of $10 x=$ Rs. $2 x$

Profit on candies $=8 \%$ of $5 x=$ Rs. $0.4 x$

Total profit $=2 x+0.4 x=$ Rs. $2.4 x$

But it is given that total profit=Rs. 240

So. According to the question

$2.4 x=240 \Rightarrow \dfrac{240}{2.4}=100$

Therefore, she purchased 100 chocolates.

107. A steamer goes downstream and covers the distance between two ports in 5 hours, while it covers the same distance upstream in 6 hours. If the speed of the stream is $1 \mathrm{~km} / \mathrm{h}$, then find the speed of the steamer in still water.

Ans: Speed of stream $=1 \mathrm{~km} / \mathrm{h}$.

 Let $x$ be the speed of steamer in still water

Speed of steamer downstream $=(x+1)$

Speed of steamer upstream $=(x-1)$

According to the question,

$(x-1) 6=(x+1) 5$

$\Rightarrow 6 x-6=5 x+5$

$\Rightarrow 6 x-5 x=6+5$

$\Rightarrow x=11$

Therefore, the speed of steamer in still water is $11 \mathrm{~km} / \mathrm{h}$.

108. Distance between two places $A$ and $B$ is $210 \mathrm{~km}$. Two cars start simultaneously from $A$ and $B$ in opposite directions and the distance between them after 3 hours is $54 \mathrm{~km}$. If the speed of one car is less than that of another by $8 \mathrm{~km} / \mathrm{h}$, then find the speed of each.

Ans: Let the speed of the car start from A be x $\mathrm{km} / \mathrm{h}$.

Then, speed of car starts from $\mathrm{B}=(x+8) \mathrm{km} / \mathrm{h}$

Given, distance between the cars after $3 \mathrm{~h}=54 \mathrm{~km}$

Now, according to the question,

Total distance between $A$ and $B$-Total distance covered by both cars in $3 h=54$

$210-[3 x+3(x+8)]=54$

$\Rightarrow 210-3 x-3 x-24=54$

$\Rightarrow-6 x=-132$

$\Rightarrow x=\dfrac{132}{6}$

$\Rightarrow x=22$

Hence, the speed of car starts from $A=22 \mathrm{~km} / \mathrm{h}$

and the speed of car starts from $B=22+8=30 \mathrm{~km} / \mathrm{h}$

109. A carpenter charged Rs 2500 for making a bed. The cost of materials used is Rs 1100 and the labor charge is Rs 200 per hour. For how many hours did the carpenter work?

Ans: Let the carpenter work for $x$ hours.

Given, labor charge $=200$ per hour

Then, total labor charge $=200 x$

As, amount charged by carpenter for making a bed = Cost of materials + Total labor charge

$2500=1100+200 x$

$\Rightarrow 200 x=1400$

$\Rightarrow x=\dfrac{1400}{200}$

$\Rightarrow x=7$

Hence, the carpenter worked for 7 hours.

110. For what value of $x$ is the perimeter of shape $77 \mathrm{~cm}$ ?

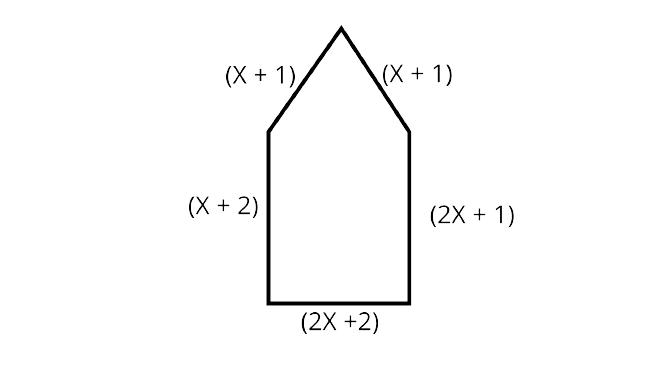
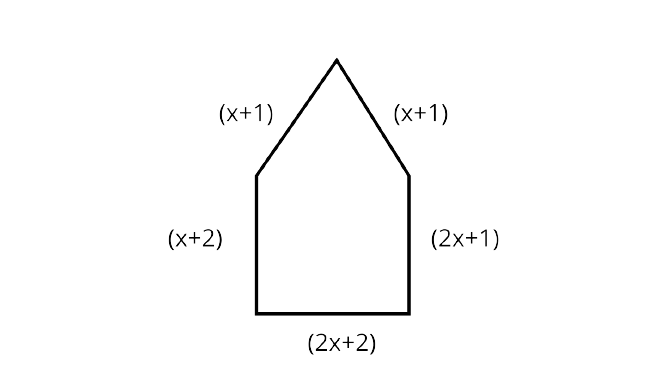
Ans: Perimeter $=77 \mathrm{~cm}$

Sum of all sides $=77$

$\Rightarrow(x+1)+(x+1)+(x+2)+(2 x+1)+(2 x+2)=77$

$\Rightarrow 7 x+7=77$

$\Rightarrow 7 x=70$

$\Rightarrow x=10$

Hence, the value of $\mathrm{x}$ is $10 \mathrm{~cm}$.

111. For what value of $x$ is the perimeter of shape $186 \mathrm{~cm}$ ?

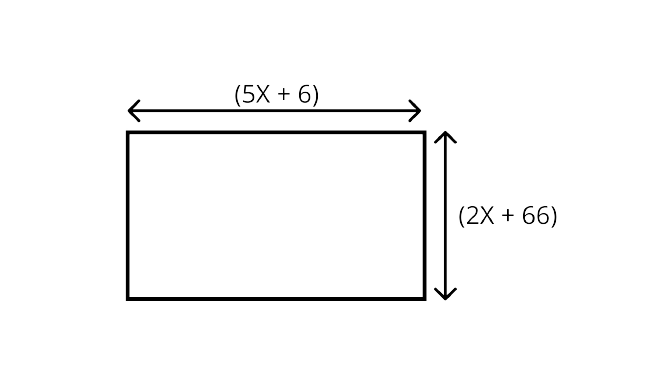
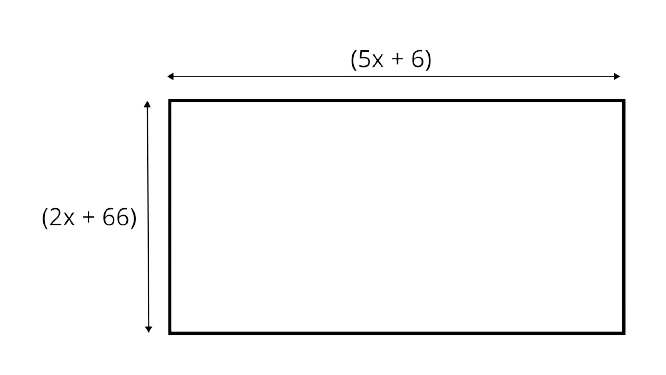
Ans: Given that,

Length of the given figure $=5 x+6$

The breadth of the given figure $=2 x+66$

Perimeter $=186 \mathrm{~cm}$

$2[(5 x+6)+(2 x+66)]=186$

$\Rightarrow 2[7 x+72]=186$

$\Rightarrow 14 x+144=186$

$\Rightarrow 14 x=42$

$\Rightarrow x=3$

Hence, the value of $x=3 \mathrm{~cm}$

112. On dividing Rs 200 between $A$ and $B$, such that twice of $A$ 's share is less than 3 times $B$ 's share by 200 , what is B's share?

Ans: Let B's share be $\mathrm{x}$.

Then, A's share $=(200-x)$

Now,

According to the question,

$2 \times $ (A's share) $=3 \times $(B's share) - 200 

$2(200-x)=3 x-200$

$\Rightarrow 400-2 x=3 x-200$

$\Rightarrow-3 x-2 x=-400-200$

$\Rightarrow-5 x=-600$

$\Rightarrow x=\dfrac{600}{5}$

$\Rightarrow x=120$

Hence, B's share is Rs. 120 .

113. Madhulika thought of a number, doubled it, and added 20 to it. On dividing the resulting number by 25 , she gets 4 . What is the number?

Ans: Let the number be $x$.

According to the question.

$\dfrac{2 x+20}{25}=4$

$\Rightarrow 2 x+20=100$

$\Rightarrow 2 x=80$

$\Rightarrow x=\dfrac{80}{2}$

$\Rightarrow x=40$

Hence, the required number is 40 . 

All these exemplar problems can be easily solved by students if they are clear with the important fundamental concepts of Linear Equation in One Variable. After completing the Linear Equation in One Variable you should be well clear with the following concepts: 

• Solving the equations that have linear expressions on one side and numbers on the other side. 

• Learning to reduce the equations into a simpler form. 

• Applications or word problems based on the linear equation concepts. 

• Solving the equations that have variables on both sides, that is LHS and RHS. 

• Learning to reduce the equations into a linear form. 

Once all the above-mentioned concepts will be clear, students can very easily solve all the exemplar problems on their own. Besides that even if they find any difficulty in any of the problems they can directly take reference from NCERT Exemplar Class 8 Math Solutions Chapter 4 Linear Equation in One Variable. Experts also suggest that students should practice and solve various test papers, sample papers, and revision notes to be well prepared for the examination. 

Benefits of Solving Exemplar Questions for Class 8th Math Linear Equation in One Variable Chapter 

According to the teaching experts of Vedantu, for Class 8th students it is very important to be clear of all concepts. And a chapter like Linear Equation in One Variable if practiced thoroughly can help you score good marks in tests and exams. Talking of exemplar questions, they are also very important and should be solved by every student as they bring more clarity to the concept of any topic. Another amazing benefit of solving exemplar problems is that students also get to know where they need more improvement or clarity in the chapter. After solving all the exemplar solutions, you can verify your answers easily from NCERT Exemplar Class 8 Math Solutions Chapter 4 Linear Equation in One Variable. This important database will help you in checking your preparation of a specific chapter with ease.