NCERT Exemplar Class 8 Math Solutions for Chapter 5: Understanding Quadrilaterals and Practical Geometry
Vedantu provides thorough NCERT Solutions for Class 8 Math, which are updated regularly and is considered to be the most comprehensive study. Students can use these solutions to help them prepare for any level of exam.
These solutions for Class 8 Math, will help students to understand, master the topic and move on with confidence.
In accordance with the CBSE curriculum, these sample problems and solutions are compiled by scholars and cover every topic of Math - Chapter 5.
In brief, the NCERT Exemplar Class 8 Math Solutions Chapter 5 Understanding Quadrilaterals & Practical Geometry includes :
Understanding Quadrilaterals and Practical Geometry
Polygons
Parallelograms
Properties of parallelograms etc
Access NCERT Exemplar Solutions for Class 6 Mathematics Chapter 5 - Understanding Quadrilaterals and Practical Geometry
Sample questions
In examples 1 to 8, there are four options out of which one is correct.
Write the correct answer.
1. The number of diagonals in a polygon of n sides is
(a) \[\dfrac{{n\left( {n - 1} \right)}}{2}\]
(b) \[\dfrac{{n\left( {n - 2} \right)}}{2}\]
(c) \[\dfrac{{n\left( {n - 3} \right)}}{2}\]
(d) \[n\left( {n - 3} \right)\]
Ans: The correct answer is (c).
The sum of all the diagonals of a n-sided polygon is \[ = \dfrac{{n\left( {n - 3} \right)}}{2}\]
2. The angles of a quadrilateral ABCD taken in an order are in the ratio 3 : 7 : 6 : 4. Then ABCD is a
(a) kite
(b) parallelogram
(c) rhombus
(d) trapezium
Ans: The correct answer is (d).
Now the ratio of angles is 3 : 7 : 6 : 4
Sum of ratio of angles = 3 + 7 + 6 + 4 = 20
The angles are:
$\dfrac{3}{{20}} \times 360^\circ = 54^\circ $
$\dfrac{7}{{20}} \times 360^\circ = 126^\circ $
$\dfrac{6}{{20}} \times 360^\circ = 108^\circ $
$\dfrac{4}{{20}} \times 360^\circ = 72^\circ $
Since no angles are equal but $\left( {54^\circ + 126^\circ } \right)$ and $\left( {108^\circ + 72^\circ } \right)$ sum up to become 180°. So, this figure is a trapezium as its adjacent angles are supplementary.
3. If the diagonals of a quadrilateral bisect each other at right angles, it will be a
(a) rhombus
(b) trapezium
(c) rectangle
(d) kite
Ans: The correct answer is (a).
The diagonals of a rhombus bisect each other at right-angle.
4. The sum of the angles of a quadrilateral is
(a) 180°
(b) 270°
(c) 360°
(d) 300°
Ans: The correct answer is (c).
The sum of all the angles of a quadrilateral is 360°.
5. In a square ABCD, the diagonals meet at point O. The $\Delta {\mathbf{AOB}}$ is
(a) isosceles right triangle
(b) equilateral triangle
(c) isosceles triangle but not right triangle
(d) scalene right triangle.
Ans: The correct answer is (a).
The diagonals of a square bisect each other at right-angle. So, the triangle AOB is an isosceles right triangle.
6. ABCD is a quadrilateral in which AB = 5 cm, CD = 8 cm and the sum of angle A and angle D is 180°. What is the name of this quadrilateral?
(a) Parallelogram
(b) Trapezium
(c) Rhombus
(d) Can not be determined
Ans: The correct answer is (b).
This figure is a trapezium as its adjacent angles are supplementary (add up to become 180°) and the opposite sides are not equal.
7. Rukmini has a farm land which is triangular in shape. What is the sum of all the exterior angles taken in an order of the farmland?
(a) 90°
(b) 180°
(c) 360°
(d) Can not be determined.
Ans: The correct answer is (c).
The sum of all the exterior angles of any sided polygon is 360°, it is true for any polygon irrespective of its number of sides.
8. How many sides does an octagon have?
(A) 7
(b) 8
(c) 9
(d) 10
Ans: The correct answer is (b).
Octagons are named from ‘octa’ meaning 8 so octagon has 8 sides.
In examples 9 and 13, fill in the blanks to make the statements true.
9. The diagonals of a rhombus bisect each other at _____ angles.
Ans: Right.
The diagonals of a rhombus bisect each other at right-angle.
10. For getting diagonals through vertex A of a pentagon ABCDE, A is joined to _________.
Ans: C and D.
If A is joined with E or B then it will be the sides of the pentagon. And if A is joined with C and D, it will be the diagonals.
11. For constructing a unique quadrilateral at least __________ measurements are required.
Ans: Five.
We have at least five pieces of information to draw a quadrilateral. We need the information of one angle between the sides or the length of the diagonal in order to draw a quadrilateral.
If we have three sides and two diagonals given to us, we can also draw a unique quadrilateral.
12. If diagonals of a quadrilateral bisect at right angles it is a __________.
Ans: Rhombus (or square).
The diagonals of rhombus and square bisect each other at right-angle.
13. The diagonals of a __________ intersect at right angles.
Ans: Kite or Square or Rhombus.
The diagonals of rhombus, kite and square meet at right-angle. But only the diagonals of rhombus and square bisect each other at right-angle.
In examples 14 to 23, state whether the statements are true (T) or false (F).
14. Every rectangle is a parallelogram.
Ans: True.
Every rectangle is a parallelogram, but every parallelogram is not a rectangle.
15. Every rhombus is a kite.
Ans: True.
The diagonals of rhombus, kite and square meet at right-angle. So, yes, every rhombus is a kite.
16. Every parallelogram is a trapezium.
Ans: True.
The opposite sides are parallel to each other for both trapezium and parallelogram. Thus, every parallelogram is a trapezium but every trapezium is not a parallelogram.
17. Every kite is a trapezium.
Ans: False.
The diagonals of a kite meet at right-angle, but the diagonals of a trapezium don’t meet at a right angle so every kite is not a trapezium.
18. Every kite is a parallelogram.
Ans: False.
The diagonals of a kite meet at right-angle, but the diagonals of a parallelogram don’t necessarily meet at a right angle so every kite is not a parallelogram.
19. Diagonals of a rectangle are perpendicular to each other.
Ans: False.
The diagonals of rhombus, kite and square meet at right-angle. But rectangle diagonals never meet at right-angle.
20. For constructing a unique parallelogram, lengths of only two sides should be given.
Ans: False.
The minimum requirement to draw a unique parallelogram are at least three given information about sides and triangles.
21.

Ans: False.
It is a complex curve with 7 closed figures.
22.

Ans: True.
It is a concave polygon as it has one reflexive angle (angle greater than 180°).
23. A triangle is not a polygon.
Ans: False.
A triangle is a polygon with three sides.
24. The sides AB and CD of a quadrilateral ABCD are extended to points P and Q respectively. Is \[\angle {\mathbf{ADQ}} + \angle {\mathbf{CBP}} = \angle {\mathbf{A}} + \angle {\mathbf{C}}?\] Give reason.
Ans:
Let’s join A to C then we will have two triangles ADC and ABC.
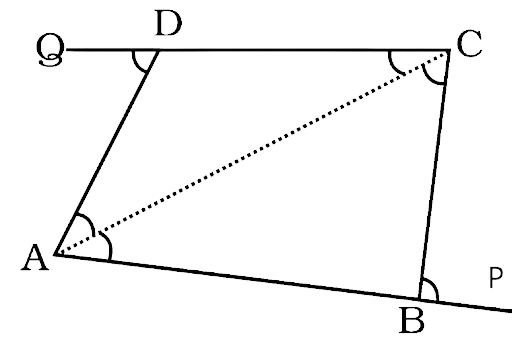
Now in triangle ADC
$\angle ADQ = \angle DAC + \angle DCA$ ….(exterior angles is equal to the sum of two interior opposite angles)
Now in triangle ADC
$\angle CBP = \angle BAC + \angle CAB$ ….(exterior angles is equal to the sum of two interior opposite angles)
Now, $\angle ADQ + \angle CBP = \angle BAC + \angle CAB + \angle DAC + \angle DCA$
$\angle ADQ + \angle CBP = \angle BAC + \angle CAB + \angle DAC + \angle DCA = \angle A + \angle C$
25. If AM and CN are perpendiculars on the diagonal BD of a parallelogram ABCD, Is\[\Delta {\mathbf{AMD}}\; \cong \Delta {\mathbf{CNB}}\]? Give a reason.
Ans:
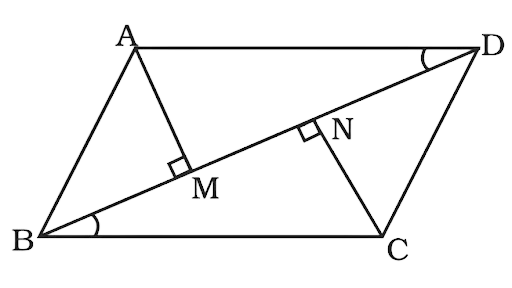
In the triangles ABM and CDN
AB = CD …(ABCD is a parallelogram opposite sides are equal)
$\angle AMB = \angle CND = 90^\circ $
$\angle ABM = \angle NDC$ …(alternate angles)
Thus $\Delta AMD \cong \Delta NCD$
26. Construct a quadrilateral ABCD in which AB = AD = 5cm, BC = CD = 7cm and BD = 6cm. What type of quadrilateral is this?
Ans:
First let’s draw a rough figure:
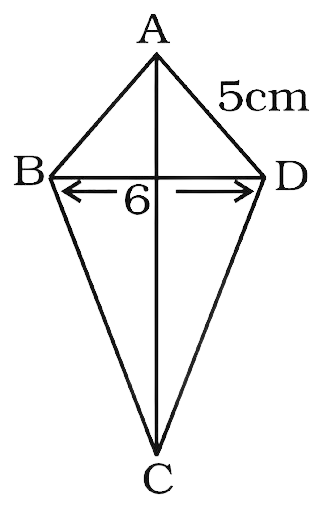
Looking at the rough figure we will draw the quadrilateral.
Steps of construction:
1. Draw a line segment BD of length 6 cm.
2. Taking B and D as centres, we will draw two arcs of radius 5 cm arcs to intersect at the point A.
3. Then again taking B and D as centres, we will draw two arcs of radius 7 cm arcs to intersect at the point C which is on the opposite side of A.
4. Join AB, AD and BC, DC.
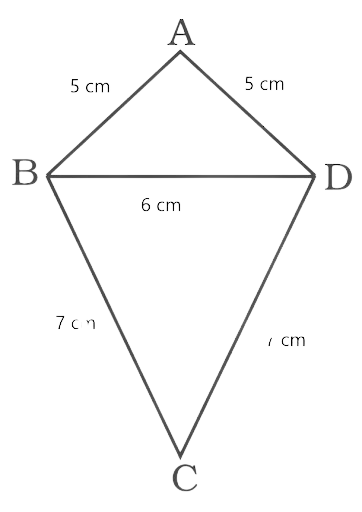
Then ABCD is the required quadrilateral. The quadrilateral formed is a kite.
27. Find x in the following figure.
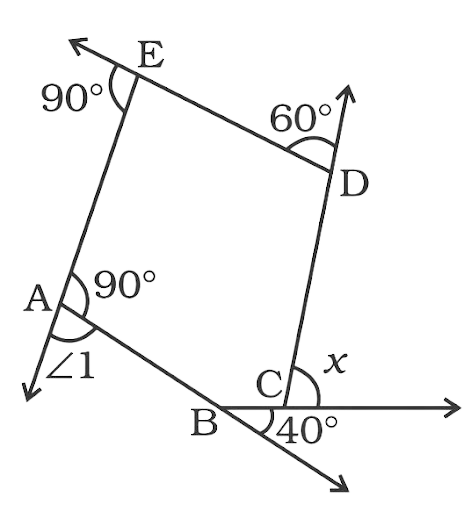
Ans:
Since the sum of all the exterior angles in a polygon is 360°.
$90^\circ + 60^\circ + 40^\circ + x + \angle I = 360^\circ $ …(i)
Now $\angle I = 180^\circ - 90^\circ = 90^\circ $ ….(linear pair of angles in a straight line)
Now equation (i) becomes
$90^\circ + 60^\circ + 40^\circ + 90^\circ + x = 360^\circ $
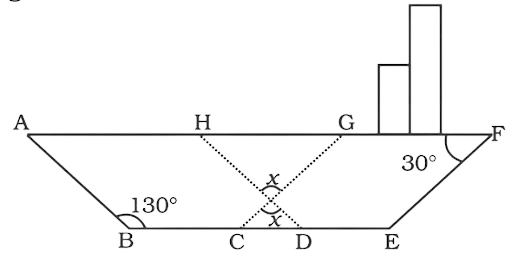
$280^\circ + x = 360^\circ $
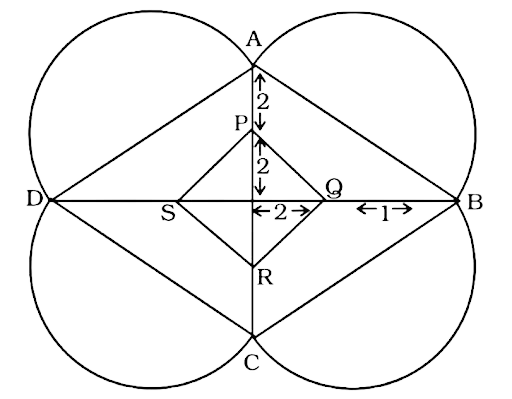
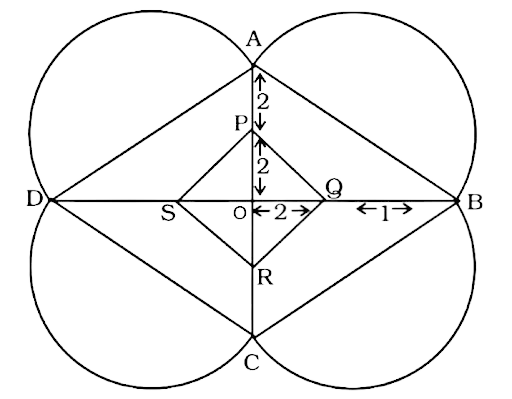
$x = 360^\circ - 280^\circ = 80^\circ $
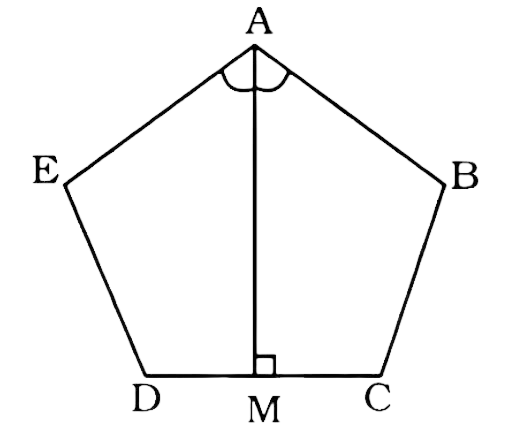
28. Two adjacent angles of a parallelogram are in the ratio 4:5. Find their measures.
Ans:
The adjacent angles of a parallelogram are supplementary the add up to become 180°.
Now the sum of ratio = 4 + 5 = 9
The angles are:
$\dfrac{4}{9} \times 180^\circ = 80^\circ $
$\dfrac{5}{9} \times 180^\circ = 100^\circ $
The angles are 80° and 100°.
29. The four angles of a quadrilateral are in the ratio 3 : 4 : 5 : 6. Find the angles.
Ans:
The sum of all the angles of a quadrilateral is 360°.
Now the sum of ratio = 3 + 4 + 5 + 6 = 18
The angles are:
$\dfrac{3}{{18}} \times 360^\circ = 60^\circ $
$\dfrac{4}{{18}} \times 360^\circ = 80^\circ $
$\dfrac{5}{{18}} \times 360^\circ = 100^\circ $
$\dfrac{6}{{18}} \times 360^\circ = 120^\circ $
The angles are 60°, 80°, 100° and 120°.
30. In a parallelogram PQRS, the bisectors of $\angle {\mathbf{P}}$ and $\angle {\mathbf{Q}}$ meet at O. Find \[\angle {\mathbf{POQ}}\] .
Ans:
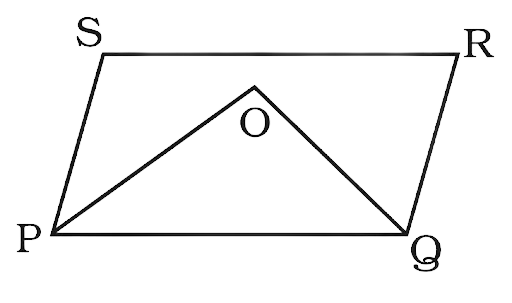
In the triangle POQ the sum of all the angles is 180°.
$\angle POQ + \angle OQP + \angle OPQ = 180^\circ $
Now the angles are:
$\angle OPQ = \dfrac{1}{2} \times \angle P$
$\angle OQP = \dfrac{1}{2} \times \angle Q$
Thus,
$\angle POQ + \angle OQP + \angle OPQ = \angle POQ + \dfrac{1}{2}\angle P + \dfrac{1}{2}\angle Q = 180^\circ $
$\angle POQ = 180^\circ - \left( {\dfrac{1}{2}\angle P + \dfrac{1}{2}\angle Q} \right)$
Now, in a parallelogram the sum of the adjacent angles is 180°. The angles are supplementary.
Thus, $\angle P + \angle Q = 180^\circ $
So $\dfrac{1}{2} \times \angle P + \dfrac{1}{2} \times \angle Q = \dfrac{1}{2} \times 180^\circ = 90^\circ $
So, the equation becomes:
$\angle POQ = 180^\circ - \left( {\dfrac{1}{2}\angle P + \dfrac{1}{2}\angle Q} \right) = 180^\circ - 90^\circ = 90^\circ $
31. Three angles of a quadrilateral are 50°, 40° and 123°. Find its fourth angle.
Ans:
The sum of all the angles of a quadrilateral is 360°.
Since, the first three angles are 50°, 40° and 123°.
The fourth angle is:
$360^\circ - \left( {50^\circ + 40^\circ + 123^\circ } \right) = 360^\circ - 213^\circ = 147^\circ $
32. The ratio of exterior angle to interior angle of a regular polygon is 1 : 4. Find the number of sides of the polygon.
Ans:
For a given vertex the sum of interior and exterior angles is 180°.
The ratio of angles is 1 : 4
The sum of ratios = 1 + 4 = 5
The angles are:
Exterior angle $ = \dfrac{1}{5} \times 180^\circ = 36^\circ $
Interior angle $ = \dfrac{4}{5} \times 180^\circ = 144^\circ $
33. Each interior angle of a polygon is 108°. Find the number of sides of the polygon.
Ans:
The value of the interior angle is = 108°
The value of the exterior angle is = \[180^\circ - 108^\circ = 72^\circ \]
Now the exterior angle is equal to \[\dfrac{{360^\circ }}{n}\] where n is the number of sides of the polygon
Now, \[72^\circ = \dfrac{{360^\circ }}{n}\]
Thus, \[n = \dfrac{{360^\circ }}{{72^\circ }} = 5\]
34. Construct a rhombus PAIR, given that PA = 6 cm and angle \[\angle {\mathbf{A}} = {\mathbf{110}}^\circ \]
Ans:
A rhombus has all its sides equal thus PA = AI = IR = RP = 6cm
The adjacent angles of a rhombus are supplementary
So, \[\angle I = \angle P = 180^\circ - 110^\circ = 70^\circ \]
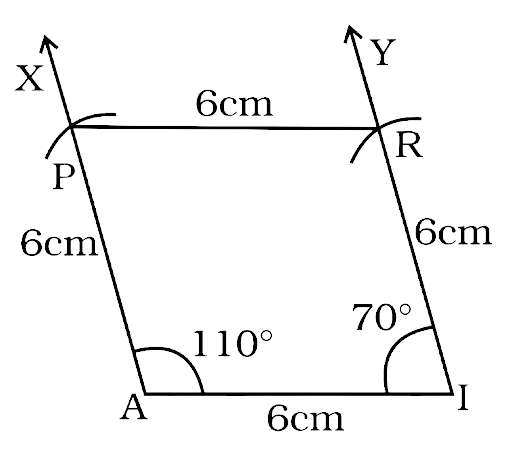
Steps of construction:
1. Draw the line segment AI = 6 cm
2. Draw the ray $\overrightarrow {AX} $ such that $\angle IAX = 110^\circ $ and
3. Now, draw $\overrightarrow {IY} $ such that $\angle AIY{\text{ }} = {\text{ }}70^\circ $.
4. With A and I as centres and draw arcs of radius 6cm which intersects AX and IY at P and R respectively.
4. Join PR.
Thus, PAIR is the required rhombus.
35. One of the diagonals of a rhombus and its sides are equal. Find the angles of the rhombus.
Ans:
Let consider PQRS to be a rhombus such that one of its diagonals (PR) is equal to its side.
Thus, we get PQ = QR = RS = PS = PR
Now in the triangle PSR
RS = PS = PR
So, triangle PSR is an equilateral triangle.
$\angle SPR = \angle SRP = \angle S = 60^\circ $
Since, the adjacent angles of a rhombus are supplementary.
$\angle R = 180^\circ - \angle S = 180^\circ - 60^\circ = 120^\circ $
A rhombus has its opposite angles equal
Thus, the angles are 60°, 120°, 60° and 120°.
36. In the figure, HOPE is a rectangle. Its diagonals meet at G. If HG = 5x + 1 and EG = 4x + 19, find x.
Ans:
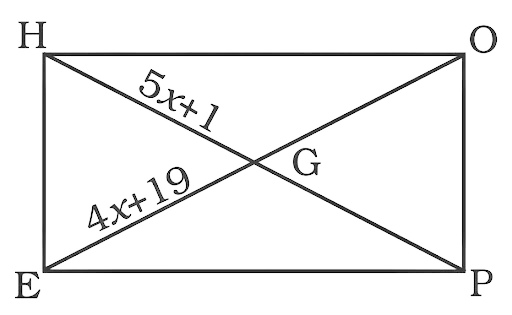
In a rectangle the diagonals are equal and bisect each other.
Since HOPE is a rectangle
HG = GP = EG = GO
Thus HG = EG
$5x + 1 = 4x + 19$
$5x - 4x = 19 - 1$
$x = 18$
37. Application on the problem strategy
RICE is a rhombus. Find x, y, z. Justify your findings. Hence, find the perimeter of the rhombus.
Ans:
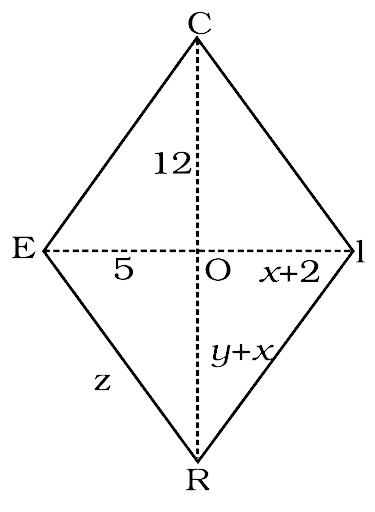
Understand and explore the problem
Now, in the rhombus RICE we are given that OC = 12, OE = 5, OI = x + 2, OR = x + y
And we have to find the values of x, y and z.
Plan a strategy
1. We have to find the lengths of the diagonals. We will use the property that the diagonals of a rhombus bisect each other at right-angle.
2. We have to find the side of the rhombus. We use the property that the diagonals of a rhombus intersect at right angles and we will apply Pythagoras theorem to find the lengths.
3. Since all sides of a rhombus are equal, perimeter of the rhombus = 4 × side.
Solve
1. We have OI = OC
Thus, $x + 2 = 5$
So, $x = 5 - 2 = 3$
And
We have OE = OR
Thus $y + x = 12$
We know that the value of $x = 3$
Thus, $y + 3 = 12$
So, $y = 12 - 3 = 9$
2. Since triangle EOR is a right-angle triangle
$CE = \sqrt {{{\left( {OE} \right)}^2} + {{\left( {OC} \right)}^2}} $
$CE = \sqrt {{{\left( 5 \right)}^2} + {{\left( {12} \right)}^2}} = \sqrt {25 + 144} = \sqrt {169} = 13$
The side of the rhombus is 13 cm
3. Thus the perimeter of the rhombus = 4 × side = 52 cm
We can also find verify the perimeter of a rhombus by using the formula:
Perimeter$ = 2\sqrt {{{\left( {{d_1}} \right)}^2} + {{\left( {{d_2}} \right)}^2}} $
The diagonal RC$ = 2 \times 12 = 24cm$
The diagonal IE $ = 2 \times 5 = 10cm$
Perimeter$ = 2\sqrt {{{\left( {24} \right)}^2} + {{\left( {10} \right)}^2}} = 2\sqrt {576 + 100} = 2\sqrt {676} = 2 \times 26 = 52cm$
Thus, we get the correct perimeter as 52 cm.
38. Application on the problem solution strategy
Construct a rhombus with side 4.5cm and diagonal 6cm.
Ans:
In the rhombus we are given that its side is 4.5 cm and its diagonal is 6 cm
In order to draw a rhombus, we only need a side and one of its diagonals.
Plan a strategy
1. We will use the property of rhombus that all its sides are equal.
2. Make a free hand rough sketch of the rhombus and name it ABCD.
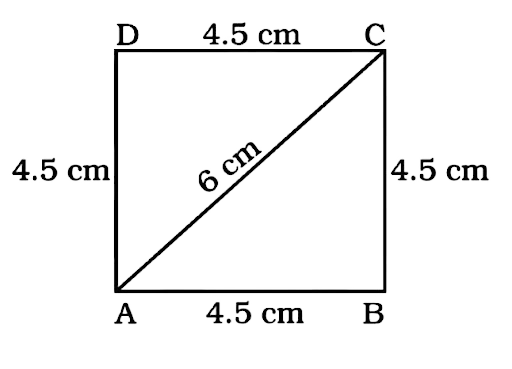
Solve
1. Draw a line segment AB = 4.5 cm.
2. With A as centre draw an arc above AB with radius = 6 cm.
3. With B as centre draw an arc with the radius = 4.5 cm to cut the arc drawn in step 2 at point C.
4. Join AC and BC.
5. With A and C as centre and radius 4.5 cm draw arcs to intersect each other at D.
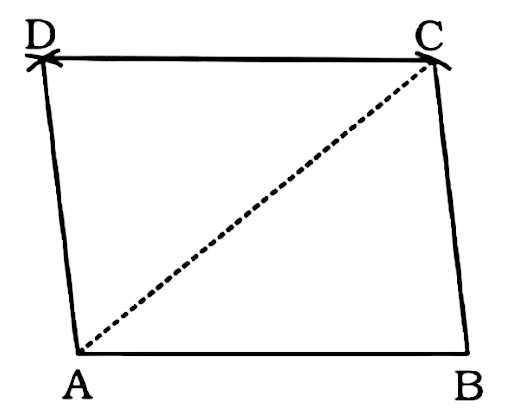
Thus, ABCD is required for rhombus.
Checking:
Given below are some methods that can be helped to verify the diagram we have drawn
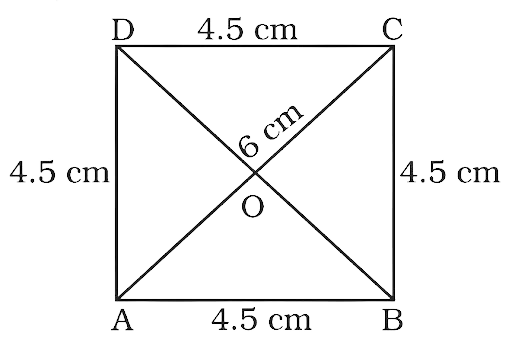
1. Join the point B and D to intersect the diagonal AC at O.
2. Measure the $\angle AOB$ Is it equal to 90°?
3. Measure the parts of the diagonal AC, i.e., OA and OC. Are they equal?
4. Measure the parts of the diagonal BD, i.e., OB and OD. Are they equal?
If your answer to 2, 3, 4 is yes it means that you have constructed the correct diagram.
Exercise
In questions 1 to 52, there are four options, out of which one is correct. Write the correct answer.
1. If three angles of a quadrilateral are each equal to 75°, the fourth angle is
(a) 150°
(b) 135°
(c) 45°
(d) 75°
Ans: (b) 135°
We know that the sum of all the interior angles of a quadrilateral is 360°
Now the three angles are equal to 75°
The fourth angle \[ = 360^\circ - 3 \times 75^\circ = 360^\circ - 225^\circ = 135^\circ \]
2. For which of the following, diagonals bisect each other?
(a) Square
(b) Kite
(c) Trapezium
(d) Quadrilateral
Ans: (a) Square
It is the property of a square that its diagonal bisects each other at 90°.
3. For which of the following figures, all angles are equal?
(a) Rectangle
(b) Kite
(c) Trapezium
(d) Quadrilateral
Ans: (a) Rectangle
All the angles of a rectangle are equal to 90°, with its opposite sides equal. Whereas for others the case is not the same like for rhombus all sides are equal but its opposite angles are only equal.
4. For which of the following figures, diagonals are perpendicular to each other?
(a) Parallelogram
(b) Kite
(c) Trapezium
(d) Rectangle
Ans: (b) Kite
It is the property of a kite that its diagonals meet at 90° to each other, and for the rest of the figures this may or may not remain true all the time.
5. For which of the following figures, diagonals are equal?
(a) Trapezium
(b) Rhombus
(c) Parallelogram
(d) Rectangle
Ans: (d) Rectangle
It is the property of a rectangle that its diagonals are equal to each other, and for the rest figures this may or may not remain true all the time (unequal diagonals).
6. Which of the following figures satisfy the following properties?
- All sides are congruent.
- All angles are right angles.
- Opposite sides are parallel.
(a)

(b)

(c)

(d)

Ans: (c)
Only squares satisfy the criteria that all the sides are congruent to each other, each angle equal to 90° and has its opposite sides parallel.
7. Which of the following figures satisfy the following property?
- Has two pairs of congruent adjacent sides.
(a)

(b)

(c)

(d)

Ans: (c)
The necessary condition for the formation of a lite is that its adjacent sides are equal to each other.
8. Which of the following figures satisfy the following property?
- Only one pair of sides is parallel.
(a)

(b)

(c)

(d)

Ans: (a)
From the above given figures only, trapezium has one pair of sides parallel to one other.
9. Which of the following figures do not satisfy any of the following properties?
- All sides are equal.
- All angles are right angles.
- Opposite sides are parallel.
(a)

(b)

(c)

(d)

Ans: (a)
Only trapezium doesn’t satisfy any of the criteria, the sides are not congruent to each other, each angle not equal to 90° and has only opposite one pair of sides parallel.
10. Which of the following properties describe a trapezium?
(a) A pair of opposite sides is parallel.
(b) The diagonals bisect each other.
(c) The diagonals are perpendicular to each other.
(d) The diagonals are equal
Ans: (a) A pair of opposite sides is parallel.
A trapezium has only one pair of its opposite side parallel to each other.
11. Which of the following is a property of a parallelogram?
(a) Opposite sides are parallel.
(b) The diagonals bisect each other at right angles.
(c) The diagonals are perpendicular to each other.
(d) All angles are equal.
Ans: (a) Opposite sides are parallel.
The necessary condition for the formation of a parallelogram is that it has its opposite sides parallel to each other.
12. What is the maximum number of obtuse angles that a quadrilateral can have?
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (c) 3
Since the sum of all the angles of a quadrilateral is 360°, we can’t have all the angles as obtuse angles. We can only have three obtuse angles and one acute angle, such that the sum will end up to become 360°.
13. How many non-overlapping triangles can we make in a n-gon (polygon having n sides), by joining the vertices?
(a) n –1
(b) n –2
(c) n –3
(d) n –4
Ans: (b) n –2
The number of non-overlapping triangles that is possible from a polygon is always two less than its total number of sides. Like for a square it is 2 non-overlapping triangles.
14. What is the sum of all the angles of a pentagon?
(a) 180°
(b) 360°
(c) 540°
(d) 720°
Ans: (c) 540°
A pentagon has 5 sides.
The formula for the sum of all angles for a polygon of n-sides is $ = \left( {n - 2} \right) \times 180^\circ $
Now putting 5 in place of n we get $ = \left( {5 - 2} \right) \times 180^\circ = 540^\circ $
15. What is the sum of all angles of a hexagon?
(a) 180°
(b) 360°
(c) 540°
(d) 720°
Ans: (d) 720°
A hexagon has 6 sides.
The formula for the sum of all angles for a polygon of n-sides is $ = \left( {n - 2} \right) \times 180^\circ $
Now putting 6 in place of n we get $ = \left( {6 - 2} \right) \times 180^\circ = 720^\circ $
16. If two adjacent angles of a parallelogram are (5x – 5)° and (10x + 35)°, then the ratio of these angles is
(a) 1 : 3
(b) 2 : 3
(c) 1 : 4
(d) 1 : 2
Ans: (a) 1 : 3
The sum of the adjacent angles of a parallelogram is equal to 180°
Now the sum of the angles is:
\[\left( {5x - 5} \right) + \left( {10x + 35} \right) = 180^\circ \]
\[15x + 30^\circ = 180^\circ \]
\[15x = 150^\circ \]
\[x = 10^\circ \]
Now the angles are
\[5x - 5^\circ = 50^\circ - 5^\circ = 45^\circ \] and
$10x + 35^\circ = 100^\circ + 35^\circ = 135^\circ $
Therefore, angles will be in the ratio of \[45^\circ :135^\circ = 1:3\]
17. A quadrilateral whose all sides are equal, opposite angles are equal and the diagonals bisect each other at right angles is a ____.
(a) Rhombus
(b) Parallelogram
(c) Square
(d) Rectangle
Ans: (a) Rhombus
A square and a rhombus both satisfy the above criteria but every square is a rhombus but every rhombus is not a square so the correct answer will be rhombus.
18. A quadrilateral whose opposite sides and all the angles are equal is a
(a) Rectangle
(b) Parallelogram
(c) Square
(d) Rhombus
Ans: (a) Rectangle
A square and a rectangle both satisfy the above criteria but every square is a rectangle but every rectangle is not a square so the correct answer will be rectangle.
19. A quadrilateral whose all sides, diagonals and angles are equal is a
(a) Square
(b) Trapezium
(c) Rectangle
(d) Rhombus
Ans: (a) Square
Only squares satisfy the criteria that all the sides are congruent to each other, each angle equal to 90° and its diagonals are also equal.
20. How many diagonals does a hexagon have?
(a) 9
(b) 8
(c) 2
(d) 6
Ans: (a) 9
The number of diagonals for a polygon of n sides is equal to $ = \dfrac{{n\left( {n - 3} \right)}}{2}$
A hexagon has 6 sides
So, the total number of diagonals is $ = \dfrac{{6\left( {6 - 3} \right)}}{2} = 9$
21. If the adjacent sides of a parallelogram are equal then parallelogram is a
(a) Rectangle
(b) Trapezium
(c) Rhombus
(d) Square
Ans: (c) Rhombus
If the adjacent sides of a parallelogram are equal then the parallelogram has all its sides equal to each other, which means it is a rhombus.
22. If the diagonals of a quadrilateral are equal and bisect each other, then the quadrilateral is a
(a) Rhombus
(b) Rectangle
(c) Square
(d) Parallelogram
Ans: (b) Rectangle
If the diagonals of a quadrilateral are equal and bisect each other, then the quadrilateral is either a rectangle or a square. But every square is a rectangle but every rectangle is not a square so the correct answer will be rectangle.
23. The sum of all exterior angles of a triangle is
(a) 180°
(b) 360°
(c) 540°
(d) 720°
Ans: (b) 360°
The sum of all exterior angles for any sided polygon is 360°.
24. Which of the following is an equiangular and equilateral polygon?
(a) Square
(b) Rectangle
(c) Rhombus
(d) Right triangle
Ans: (a) Square
Equiangular and equilateral polygon means a polygon that has all its angle equal and all its sides equal. Thus, only square satisfies the case.
25. Which one has all the properties of a kite and a parallelogram?
(a) Trapezium
(b) Rhombus
(c) Rectangle
(d) Parallelogram
Ans: (b) Rhombus
A Rhombus has its adjacent sides equal to each other and its opposite sides parallel to one other. Thus, it has both the properties of a kite and a parallelogram.
26. The angles of a quadrilateral are in the ratio 1 : 2 : 3 : 4. The smallest angle is
(a) 72°
(b) 144°
(c) 36°
(d) 18°
Ans: (c) 36°
Let us assume the angles of the quadrilateral are = x, 2x, 3x and 4x
Now the sum of all the angles of a quadrilateral is 360°
\[x + 2x + 3x + 4x = 360^\circ \]
\[10x = 360^\circ \]
\[x = 36^\circ \]
The smallest angle will be equal to x and its value will be = 36°
27. In the trapezium ABCD, the measure of \[\angle {\mathbf{D}}\] is
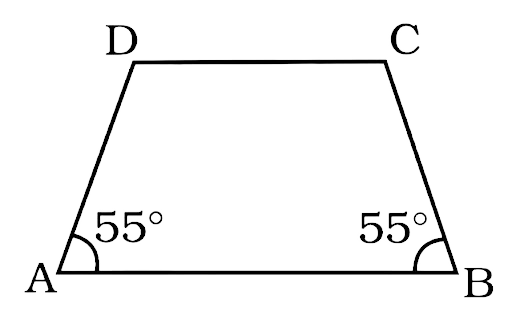
(a) 55°
(b) 115°
(c) 135°
(d) 125°
Ans: (c) 135°
Now the side AB || CD so adjacent angles will be supplementary they will add up to become 180°.
$\angle D + \angle A = 180^\circ $
$\angle D = 180^\circ - \angle A$
$\angle D = 180^\circ - 55^\circ = 135^\circ $
28. A quadrilateral has three acute angles. If each measures 80°, then the measure of the fourth angle is
(a) 150°
(b) 120°
(c) 105°
(d) 140°
Ans: (b) 120°
The sum of all the angles of a quadrilateral is 360°
The sum of the three acute angles is $ = 80^\circ + 80^\circ + 80^\circ = 240^\circ $
The fourth angle is equal to $360^\circ - 240^\circ = 120^\circ $
29. The number of sides of a regular polygon where each exterior angle has a measure of 45° is
(a) 8
(b) 10
(c) 4
(d) 6
Ans: (a) 8
The value of the exterior angle for a n-sided polygon is $ = \dfrac{{360^\circ }}{n}$
We have the exterior angle equal to 45°
Now,
$45^\circ = \dfrac{{360^\circ }}{n}$
$n = \dfrac{{360^\circ }}{{45^\circ }} = 8$
The number of sides for the polygon is 8.
30. In a parallelogram PQRS, if \[\angle {\mathbf{P}} = {\mathbf{60}}^\circ \], then other three angles are
(a) 45°, 135°, 120°
(b) 60°, 120°, 120°
(c) 60°, 135°, 135°
(d) 45°, 135°, 135°
Ans: (b) 60°, 120°, 120°
In parallelogram adjacent angles are supplementary and opposite angles are equal.
The opposite angle is = 60°
The adjacent angle $ = 180^\circ - 60^\circ = 120^\circ $
The angles are 60°, 120° and 120°.
31. If two adjacent angles of a parallelogram are in the ratio 2 : 3, then the measure of angles are
(a) 72°, 108°
(b) 36°, 54°
(c) 80°, 120°
(d) 96°, 144°
Ans: (a) 72°, 108°
In a parallelogram adjacent angles will be supplementary; they will add up to become 180°.
Now
Sum of ratio = 2 + 3 = 5
Now the angles are
$\dfrac{2}{5} \times 180^\circ = 72^\circ $
$\dfrac{3}{5} \times 180^\circ = 108^\circ $
The angles are 72° and 108°.
32. If PQRS is a parallelogram, then \[\angle {\mathbf{P}}--\;\;\angle {\mathbf{R}}\] is equal to
(a) 60°
(b) 90°
(c) 80°
(d) 0°
Ans: (d) 0°
In a parallelogram opposite angles are equal.
$\angle P$ and $\angle R$are equal so their difference will be zero.
33. The sum of adjacent angles of a parallelogram is
(a) 180°
(b) 120°
(c) 360°
(d) 90°
Ans: (a) 180°
Adjacent angles in a parallelogram are supplementary; they sum up to become 180°.
34. The angle between the two altitudes of a parallelogram through the same vertex of an obtuse angle of the parallelogram is 30°. The measure of the obtuse angle is
(a) 100°
(b) 150°
(c) 105°
(d) 120°
Ans: (b) 150°
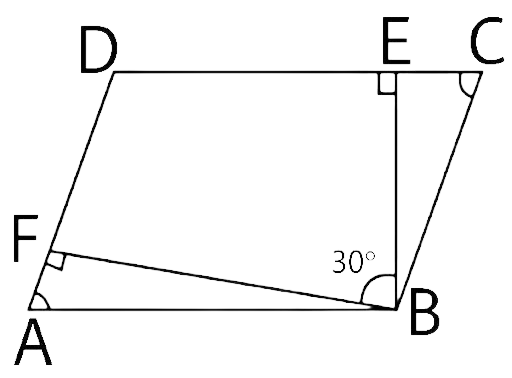
In the quadrilateral DEBF
$\angle FDE = 360^\circ - \left( {90^\circ + 90^\circ + 30^\circ } \right) = 150^\circ $
35. In the given figure, ABCD and BDCE are parallelograms with common base DC. If \[{\mathbf{BC}}\; \bot {\mathbf{BD}}\], then \[\angle {\mathbf{BEC}} = \]
(a) 60°
(b) 30°
(c) 150°
(d) 120
Ans: (a) 60°
In the parallelogram ABCD
$\angle BCD = \angle ADB = 30^\circ $ opposite angles in a parallelogram are equal.
$\angle BDC = 180^\circ - (30^\circ + 90^\circ ) = 60^\circ $
In the parallelogram BDCE
$\angle BEC = \angle BDC = 60^\circ $ opposite angles in a parallelogram are equal.
36. Length of one of the diagonals of a rectangle whose sides are 10 cm and 24 cm is
(a) 25 cm
(b) 20 cm
(c) 26 cm
(d) 3.5 cm
Ans: (c) 26 cm
We will apply Pythagoras theorem to find the diagonal.
$D = \sqrt {{{10}^2} + {{24}^2}} = \sqrt {100 + 576} = \sqrt {676} = 26cm$
37. If the adjacent angles of a parallelogram are equal, then the parallelogram is a
(a) Rectangle
(b) Trapezium
(c) Rhombus
(d) Any of the three
Ans: (a) Rectangle
Adjacent angles are supplementary and if they are equal, it means that each angle is a right angle, and the figure becomes a rectangle.
38. Which of the following can be four interior angles of a quadrilateral?
(a) 140°, 40°, 20°, 160°
(b) 270°, 150°, 30°, 20°
(c) 40°, 70°, 90°, 60°
(d) 110°, 40°, 30°, 180°
Ans: (a) 140°, 40°, 20°, 160°
The addition of all the angles is 360°.
39. The sum of angles of a concave quadrilateral is
(a) More than 360°
(b) less than 360°
(c) Equal to 360°
(d) twice of 360°
Ans: (c) Equal to 360°
The sum of all the angles of a quadrilateral is 360°. It doesn’t matter whether it is a convex or concave quadrilateral.
40. Which of the following can never be the measure of exterior angle of a regular polygon?
(a) 22°
(b) 36°
(c) 45°
(d) 30°
Ans: (a) 22°
The value of the exterior angle for a n-sided polygon is $ = \dfrac{{360^\circ }}{n}$
And we cannot get the value of 22° for any value of n.
41. In the figure, BEST is a rhombus, Then the value of y – x is

(a) 40°
(b) 50°
(c) 20°
(d) 10°
Ans: (a) 40°
Now in the rhombus BEST BE || ST
$\angle TEB = x$ ….(alternate angle)
$y = x + 40^\circ $ …..(in a triangle exterior angle is equal to the sum of two interior opposite angles)
So, $y - x = 40^\circ $
44. The closed curve which is also a polygon is
(a)

(b)
(c)
(d)
Ans: (a)
The figure a is a closed figure surrendered by line segments called edges.
43. Which of the following is not true for an exterior angle of a regular polygon with n sides?
(a) Each exterior angle $ = \dfrac{{360^\circ }}{n}$
(b) Exterior angle = 180° - interior angle
(c) ${\mathbf{n}} = \dfrac{{360^\circ }}{{{\mathbf{Exterior}}{\text{ }}{\mathbf{angle}}}}$
(d) Each exterior angle \[ = \dfrac{{\left( {n - 2} \right) \times 180^\circ }}{n}\]
Ans: (d) Each exterior angle \[ = \dfrac{{\left( {n - 2} \right) \times 180^\circ }}{n}\]
The value of each interior angle is \[ = \dfrac{{\left( {n - 2} \right) \times 180^\circ }}{n}\]
44. PQRS is a square. PR and SQ intersect at O. Then \[\angle {\mathbf{POQ}}\]is a
(a) Right angle
(b) Straight angle
(c) Reflex angle
(d) Complete angle
Ans: (a) Right angle
PR and SQ are the diagonals of the square PQRS.
The diagonals of a square bisect each other at a right angle.
Since they intersect at O the angle $\angle POQ$ is a right angle.
45. Two adjacent angles of a parallelogram are in the ratio 1:5. Then all the angles of the parallelogram are
(a) 30°, 150°, 30°, 150°
(b) 85°, 95°, 85°, 95°
(c) 45°, 135°, 45°, 135°
(d) 30°, 180°, 30°, 180°
Ans: (a) 30°, 150°, 30°, 150°
The ratio of adjacent angles = 1 : 5
Now adjacent angles in a parallelogram add up to become 180°.
Sum of ratio = 1 + 5 = 6
The angles are
$\dfrac{1}{6} \times 180^\circ = 30^\circ $
$\dfrac{5}{6} \times 180^\circ = 150^\circ $
So, the angles are 30°, 150°, 30° and 150°.
46. A parallelogram PQRS is constructed with sides QR = 6 cm, PQ = 4 cm and \[\angle {\mathbf{PQR}} = {\mathbf{90}}^\circ \]. Then PQRS is a
(a) Square
(b) Rectangle
(c) Rhombus
(d) Trapezium
Ans: (b) rectangle
PQRS doesn’t have any of its sides equal.
Now it has one right angle meaning its opposite and adjacent angles will also be a right angle thus PARS is a rectangle.
47. The angles P, Q, R and S of a quadrilateral are in the ratio 1:3:7:9. Then PQRS is a
(a) Parallelogram
(b) Trapezium with PQ || RS
(c) Trapezium with QR||PS
(d) Kite
Ans:
Now the ratio of angles is 1 : 3 : 7 : 9
Sum of ratio of angles = 1 + 3 + 7 + 9 = 20
The angles are:
$\angle P = \dfrac{1}{{20}} \times 360^\circ = 18^\circ $
$\angle Q = \dfrac{3}{{20}} \times 360^\circ = 54^\circ $
$\angle R = \dfrac{7}{{20}} \times 360^\circ = 126^\circ $
$\angle S = \dfrac{9}{{20}} \times 360^\circ = 162^\circ $
Since no angles are equal, $\left( {\angle Q + \angle R} \right)$ and $\left( {\angle P + \angle S} \right)$ sum up to become 180°. So, this figure is a trapezium with PS || QR.
48. PQRS is a trapezium in which PQ || SR and \[\angle {\mathbf{P}} = {\mathbf{130}}^\circ \], \[\angle {\mathbf{Q}} = {\mathbf{110}}^\circ \]. Then \[\angle {\mathbf{R}}\]is equal to:
(a) 70°
(b) 50°
(c) 65°
(d) 55°
Ans: (a) 70°
Since PQ || SR the angles $\angle P,\angle S$ and $\angle Q,\angle R$ will be supplementary.
Now $\angle Q + \angle R = 180^\circ $
$\angle R = 180^\circ - \angle Q$
$\angle R = 180^\circ - 110^\circ = 70^\circ $
49. The number of sides of a regular polygon whose each interior angle is of 135° is
(a) 6
(b) 7
(c) 8
(d) 9
Ans: (c) 8
Sum of interior angles of the polygon \[ = n \times 135^\circ \]
We already know that the sum of interior angles \[ = \left( {2n - 4} \right) \times 90^\circ \]
Equating both the sum of angles as equal we get
\[\left( {2n - 4} \right)90 = 135n\]
\[180n - 360 = 135n\]
\[45n = 360\]
\[n = 8\]
50. If a diagonal of a quadrilateral bisects both the angles, then it is a
(a) Kite
(b) Parallelogram
(c) Rhombus
(d) Rectangle
Ans: (c) rhombus
It is the property of rhombus and square that their diagonals bisect the angles.
51. To construct a unique parallelogram, the minimum number of measurements required is
(a) 2
(b) 3
(c) 4
(d) 5
Ans: (b) 3
The measure of length, breath, diagonal, the angle made by the diagonal or the angle between the two adjacent sides. If we had any three criteria given to us from the above five, we can create a unique parallelogram from it.
52. To construct a unique rectangle, the minimum number of measurements required is
(a) 4
(b) 3
(c) 2
(d) 1
Ans: (c) 2
The measure of length, breath, diagonal or the angle made by the diagonal. If we had any two criteria given to us from the above four, we can create a unique rectangle from it.
In questions 53 to 91, fill in the blanks to make the statements true.
53. In quadrilateral HOPE, the pairs of opposite sides are ________.
Ans: HO, PE and HE, OP.
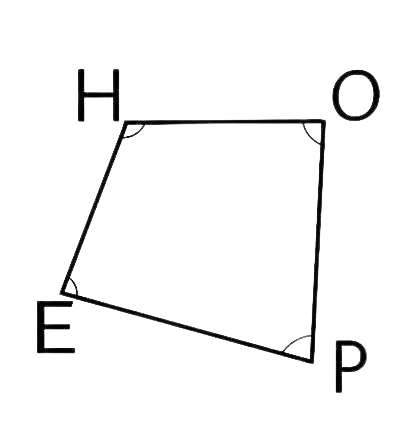
The pair of opposite sides of the above quadrilateral HOPE is HO, PE and HE, OP.
54. In quadrilateral ROPE, the pairs of adjacent angles are________.
Ans: $\left( {\angle R,\angle O} \right)$, $\left( {\angle O,\angle P} \right)$,$\left( {\angle P,\angle E} \right)$and $\left( {\angle E,\angle R} \right)$.
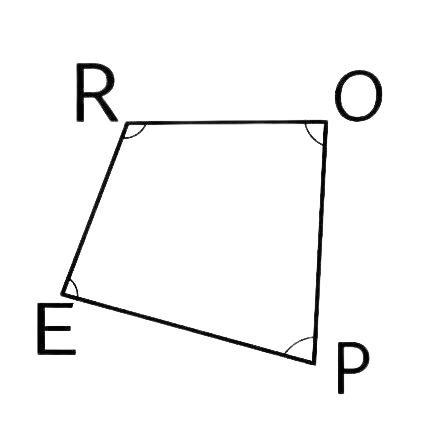
The pair of adjacent angles of the above quadrilateral ROPE is $\angle R,\angle O$ ; $\angle P,\angle E$ ; $\angle E,\angle R$ and $\angle O,\angle P$ .
55. In quadrilateral WXYZ, the pairs of opposite angles are________.
Ans: $\left( {\angle W,\angle Y} \right)$and $\left( {\angle X,\angle Z} \right)$
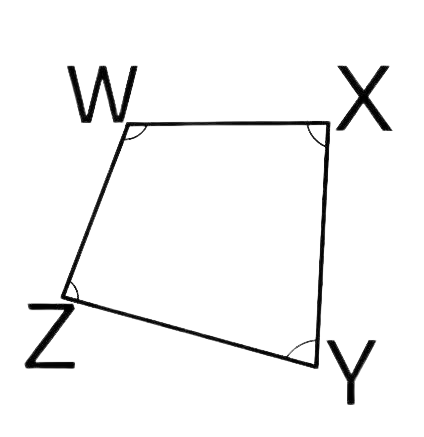
The pair of opposite angles of the above quadrilateral WXYZ is $\angle W,\angle Y$and $\angle X,\angle Z$ .
56. The diagonals of the quadrilateral DEFG are______ and ________.
Ans: DF and EG
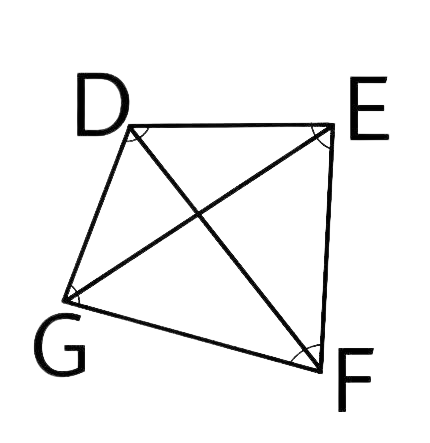
The diagonals of the above quadrilateral DEFG are DF and EG.
56. The sum of all ________ of a quadrilateral is 360°.
Ans: Angles
The sum of all the angles of a quadrilateral is 360°.
57. The measure of each exterior angle of a regular pentagon is_______.
Ans: 72°
The formula for the sum of all angles for a polygon of n-sides is $ = \left( {n - 2} \right) \times 180^\circ $
Now putting 5 in place of n we get $ = \left( {5 - 2} \right) \times 180^\circ = 540^\circ $
Each interior angle of a regular pentagon is = 108°
Each exterior angle of the regular pentagon = 180°-108°=72°
58. Sum of the angles of a hexagon is___________.
Ans: 720°
The formula for the sum of all angles for a polygon of n-sides is $ = \left( {n - 2} \right) \times 180^\circ $
Now putting 6 in place of n we get $ = \left( {6 - 2} \right) \times 180^\circ = 720^\circ $
59. The measure of each exterior angle of a regular polygon of 18 sides is__________.
Ans: 20°
The value of the exterior angle for a n-sided polygon is $ = \dfrac{{360^\circ }}{n}$
Now putting 18 in place of n we get $ = \dfrac{{360^\circ }}{{18}} = 20^\circ $
60. The number of sides of a regular polygon, where each exterior angle has a measure of 36°, is__________.
Ans: 10°
The value of the exterior angle for a n-sided polygon is $ = \dfrac{{360^\circ }}{n}$
We have the exterior angle equal to 36°
Now,
$36^\circ = \dfrac{{360^\circ }}{n}$
$n = \dfrac{{360^\circ }}{{36^\circ }} = 10$
The number of sides for the polygon is 10.
61.
Ans: Concave polygon
This figure is of a concave polygon (hexagon) as two of its vertices are pointing inwards. The inward pointing vertices is a sign that the polygon is a concave polygon.
62. A quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure is_________.
Ans: Kite
The kite has its opposite angles equal to each other whereas its sides are not parallel to one another.
63. The measure of each angle of a regular pentagon is__________.
Ans: 108°
The formula for the sum of all angles for a polygon of n-sides is $ = \left( {n - 2} \right) \times 180^\circ $
Now putting 5 in place of n we get $ = \left( {5 - 2} \right) \times 180^\circ = 540^\circ $
Since, a pentagon has 5 sides the measure of each interior angle \[ = \dfrac{{540^\circ }}{5} = 108^\circ \]
64. The name of the three-sided regular polygon is_________.
Ans: Equilateral triangle
A three-sided regular polygon has three equal sides.
65. The number of diagonals in a hexagon is__________.
Ans: 6
The number of diagonals for a polygon of n sides is equal to $ = \dfrac{{n\left( {n - 3} \right)}}{2}$
A hexagon has 6 sides
So, the total number of diagonals is $ = \dfrac{{6\left( {6 - 3} \right)}}{2} = 9$
66. A polygon is a simple closed curve made up of only____________.
Ans: Line Segments
Polygons are made up from line segments which are known as the sides or edges of the polygon.
67. A regular polygon is a polygon whose all sides are equal and all________are equal.
And: Angles
A regular polygon has both the sides and the angles equal.
68. The sum of interior angles of a polygon of n sides is__________right angles
Ans: 2n-4
The formula for the sum of all angles for a polygon of n-sides is $ = \left( {n - 2} \right) \times 180^\circ = \left( {2n - 4} \right) \times 90^\circ $
It has a sum of 2n-4 right angles.
69. The sum of all exterior angles of a polygon is_________.
Ans: 360°
The sum of all the exterior angles of a polygon remains 360° regardless of the number of sides of the polygon.
70. __________is a regular quadrilateral.
Ans: Square
A regular polygon has both the sides and the angles equal. So a regular quadrilateral is a square.
71. A quadrilateral in which a pair of opposite sides is parallel is________.
Ans: Trapezium
Trapezium has only one of its pairs of sides parallel to each other.
72. If all sides of a quadrilateral are equal, it is a_________.
Ans: Rhombus
Rhombus has all sides equal. Every square is a rhombus but every rhombus is not a square.
73. In a rhombus diagonals intersect at__________angles.
Ans: Right
The diagonals of a rhombus bisect each other at a right angle.
74. __________measurements can determine a quadrilateral uniquely.
Ans: Five
At least five given attributes (measurement) are required for the construction of a unique quadrilateral.
75. A quadrilateral can be constructed uniquely if its three sides and_________angles are given.
Ans: Two included
We need five measurements to create a unique quadrilateral. Apart from three sides we need two included angle measurements to draw a quadrilateral.
76. A rhombus is a parallelogram in which_________sides are equal.
Ans: All
Unlike a parallelogram a rhombus has all its sides equal to each other.
77. The measure of__________angle of the concave quadrilateral is more than 180°.
Ans: One
We can have a maximum of one reflex angle in a quadrilateral, in order to make the sum of all the angles 360°.
78. A diagonal of a quadrilateral is a line segment that joins two__________vertices of the quadrilateral.
Ans: opposite
If consecutive vertices are joined it is termed as a side, and if opposite vertices are joined it is called a diagonal.
79. The number of sides in a regular polygon having measure of an exterior angle as 72° is___________.
Ans: Five
The value of the exterior angle for a n-sided polygon is $ = \dfrac{{360^\circ }}{n}$
We have the exterior angle equal to 72°
Now,
$72^\circ = \dfrac{{360^\circ }}{n}$
$n = \dfrac{{360^\circ }}{{72^\circ }} = 5$
The number of sides for the polygon is 5.
80. If the diagonals of a quadrilateral bisect each other, it is a________.
Ans: Parallelogram
It is the property of a parallelogram that its diagonals bisect each other.
81. The adjacent sides of a parallelogram are 5 cm and 9 cm. Its perimeter is______________.
Ans: 28 cm
The sum of adjacent side length is = 5 cm + 9 cm = 14 cm
Perimeter of a parallelogram is 2 times the adjacent side length
Perimeter = 28 cm
82. A nonagon has_________sides.
Ans: Nine
A nonagon has nine sides and nine vertices.
83. Diagonals of a rectangle are__________.
Ans: Equal
The diagonals of a rectangle are equal and bisect each other.
84. A polygon having 10 sides is known as__________.
Ans: Decagon
A decagon has ten sides and ten vertices.
85. A rectangle whose adjacent sides are equal becomes a________.
Ans: Square
A square is a rectangle with its adjacent sides equal to each other.
86. If one diagonal of a rectangle is 6 cm long, length of the other diagonal is___________.
Ans: 6 cm
A rectangle has equal diagonals.
87. Adjacent angles of a parallelogram are__________.
Ans: Supplementary
The adjacent angles of a parallelogram are supplementary; they add up to become 180°.
88. If only one diagonal of a quadrilateral bisects the other, then the quadrilateral is known as___________.
Ans: Rhombus
It is the property of a rhombus that its diagonals bisect each other at right angles.
89. In trapezium ABCD with AB||CD, if \[\angle {\mathbf{A}} = {\mathbf{100}}^\circ \] , then \[\angle {\mathbf{D}} = \]________.
Ans: 80°
In the trapezium ABCD since AB||CD
$\angle A$ and $\angle D$ are supplementary pairs they add up to become 180°.
$\angle A + \angle D = 180^\circ $
$100^\circ + \angle D = 180^\circ $
$\angle D = 180^\circ - 100^\circ = 80^\circ $
91. The polygon in which the sum of all exterior angles is equal to the sum of interior angles is called__________.
Ans: Quadrilateral
The sum of all the angles of a quadrilateral is 360°.
And the sum of all the exterior angles of a polygon of any side is equal to 360°.
In questions 92 to 131 state whether the statements are true (T) or (F) false.
92. All angles of a trapezium are equal.
Ans: False
All angles are unequal in case of a trapezium, at most two adjacent angles can be equal to each other in case of an isosceles trapezium.
93. All squares are rectangles.
Ans: True
Every square is a rectangle but every rectangle is not a square.
94. All kites are squares.
Ans: False
Kites have only two adjacent sides equal, whereas square has all sides equal.
95. All rectangles are parallelograms.
Ans: True
Every rectangle is a parallelogram but every parallelogram is not a rectangle.
96. All rhombuses are squares.
Ans: False
Every square is a rhombus but every rhombus is not a square.
97. Sum of all the angles of a quadrilateral is 180°.
Ans: False
Sum of all the angles of a quadrilateral is 360°.
98. A quadrilateral has two diagonals.
Ans: True
A quadrilateral has two diagonals, formed by joining any two opposite vertices.
99. Triangle is a polygon whose sum of exterior angles is double the sum of interior angles.
Ans: True
Triangle is a polygon whose sum of exterior angles is 360° which is double the sum of interior angles (180°).
100.

Ans: True
It is a star polygon with 10 edges and 5 pairs of vertices.
101. A kite is not a convex quadrilateral.
Ans: False
A kite is a convex quadrilateral. If we fold the smaller side corner of the kite inwards, we will get a concave quadrilateral.
102. The sum of interior angles and the sum of exterior angles taken in an order are equal in case of quadrilaterals only.
Ans: True
Only for quadrilaterals this remains the same as the sum of exterior and interior angle both are equal to 360°.
For rest polygons the sum of all exterior angles remains the same as 360°.
But the sum of all interior angles varies as $ = \left( {n - 2} \right) \times 180^\circ $ where n is the number of sides.
103. If the sum of interior angles is double the sum of exterior angles taken in an order of a polygon, then it is a hexagon.
Ans: True
For any polygon the sum of all exterior angles remains the same as 360°.
And the sum of the interior angle for a hexagon is 720°.
104. A polygon is regular if all of its sides are equal.
Ans: True
A regular polygon has both its sides and all its angles equal.
105. Rectangle is a regular quadrilateral.
Ans: False
Since, rectangles don’t have all sides equal, they are not regular quadrilaterals.
106. If diagonals of a quadrilateral are equal, it must be a rectangle.
Ans: False
An isosceles trapezium, a square and a rectangle all have equal diagonals.
107. If opposite angles of a quadrilateral are equal, it must be a parallelogram.
Ans: True
Now in the parallelogram ABCD
AB||CD and AD||BC
Now angles on the same side of the transversal sums up to 180°.
So, $\angle BAD + \angle ADC = 180^\circ $
Thus,
$\angle BAD = 180^\circ - \angle ADC$
And the same goes for
$\angle DCB + \angle ADC = 180^\circ $
Thus,
$\angle DCB = 180^\circ - \angle ADC$
Thus, we get $\angle DCB = \angle DAB$
A parallelogram has its opposite sides parallel to each other meaning its opposite sides will be equal to one other.
108. The interior angles of a triangle are in the ratio 1:2:3, then the ratio of its exterior angles is 3:2:1.
Ans: False
The ratio of the angles is 1:2:3
Let’s assume the angles are x, 2x and 3x
Sum of the angles = 6x
Now the sum of all interior angles of a triangle is 180°.
The angles are:
$\dfrac{x}{{6x}} \times 180^\circ = 30^\circ $
$\dfrac{{2x}}{{6x}} \times 180^\circ = 60^\circ $
$\dfrac{{3x}}{{6x}} \times 180^\circ = 90^\circ $
The angles are 30°, 60° and 90°.
Now,
The exterior angle corresponding to 30° is = 150°
The exterior angle corresponding to 60° is = 120°
The exterior angle corresponding to 90° is = 90°
Ratio of the exterior angle is = 150°:120°:90° = 5:4:3
109.

Ans: False
This figure has 6 edges; it is a concave hexagon. A pentagon has 5 sides.
110. Diagonals of a rhombus are equal and perpendicular to each other.
Ans: False
Diagonals of a rhombus are not equal but they are perpendicular to each other.
111. Diagonals of a rectangle are equal.
Ans: True
Diagonals of a rectangle are equal and bisect to each other.
112. Diagonals of rectangles bisect each other at right angles.
Ans: False
Diagonals of a rectangle are equal and bisect to each other, but not at right angle. The diagonals of a square and rhombus bisect each other at right angle.
113. Every kite is a parallelogram.
Ans: False
A kite has no set of parallel sides so its not a parallelogram.
114. Every trapezium is a parallelogram.
Ans: False
A trapezium has only one pair of sides parallel to each other but the other pair is not parallel to the other, thus, a trapezium is not a parallelogram.
115. Every parallelogram is a rectangle.
Ans: False
Every rectangle is a parallelogram, but every parallelogram is not a rectangle.
116. Every trapezium is a rectangle.
Ans: False
A trapezium has a pair of sides parallel to each other but these sides are not equal to one another, whereas rectangles have opposite sides equal to each other.
117. Every rectangle is a trapezium.
Ans: False
A trapezium has a pair of opposite sides non-parallel to each other, whereas a rectangle has opposite sides parallel to each other and all sides are at right angles to each other.
118. Every square is a rhombus.
Ans: True
Every square is a rhombus but every rhombus is not a square.
119. Every square is a parallelogram.
Ans: True
Every square is a parallelogram but every parallelogram is not a square.
120. Every square is a trapezium.
Ans: False
A trapezium has a pair of sides parallel to each other but these sides are not equal to one another, whereas squares have all sides equal to each other.
121. Every rhombus is a trapezium.
Ans: False
A trapezium has a pair of opposite sides non-parallel to each other which are also unequal, whereas a rhombus has opposite sides parallel to each other and all sides are equal and at right angles to each other.
122. A quadrilateral can be drawn if only measures of four sides are given.
Ans: False
We have at least five pieces of information to draw a quadrilateral. We need the information of one angle between the sides or the length of the diagonal in order to draw a quadrilateral.
123. A quadrilateral can have all four angles is obtuse.
Ans: False
A quadrilateral can have a maximum of three angles as obtuse angles, the fourth one should be an acute angle in order to make the sum of all the angles as 360°.
124. A quadrilateral can be drawn if all four sides and one diagonal is known.
Ans: True
We have at least five pieces of information to draw a quadrilateral. We need the information of one angle between the sides or the length of the diagonal in order to draw a quadrilateral.
125. A quadrilateral can be drawn when all the four angles and one side is given.
Ans: False
We need a minimum length of two adjacent sides and the measure of three angles which is included within the given sides in order to draw a quadrilateral.
126. A quadrilateral can be drawn if all four sides and one angle is known.
Ans: True
We have at least five pieces of information to draw a quadrilateral. We need the information of one angle between the sides or the length of the diagonal in order to draw a quadrilateral.
127. A quadrilateral can be drawn if three sides and two diagonals are given.
Ans: True
We have at least five pieces of information to draw a quadrilateral. We need the information of one angle between the sides or the length of the diagonal in order to draw a quadrilateral.
If we have three sides and two diagonals given to us, we can also draw a unique quadrilateral.
128. If diagonals of a quadrilateral bisect each other, it must be a parallelogram.
Ans: True
Diagonals of a parallelogram always bisect each other.
129. A quadrilateral can be constructed uniquely if three angles and any two sides are given.
Ans: False
We need a minimum length of two adjacent sides and the measure of three angles which is included within the given sides in order to draw a quadrilateral.
130. A parallelogram can be constructed uniquely if both diagonals and the angle between them is given.
Ans: True
Diagonals of a parallelogram always bisect each other. So, we can draw the quadrilateral with the given length and angles.
131. A rhombus can be constructed uniquely if both diagonals are given.
Ans: True
We can construct a rhombus as its diagonals bisect each other at 90°.
Solve the following:
132. The diagonals of a rhombus are 8 cm and 15 cm. Find its side.
Ans:
The simple diagram we can draw from the given question is :
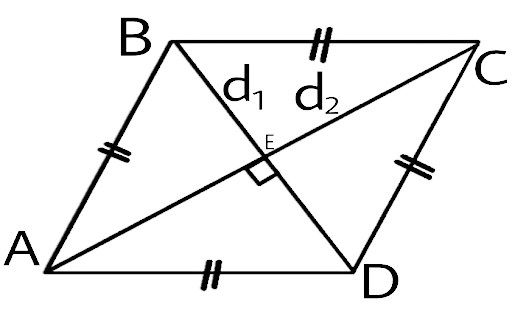
Now the length of the diagonals is:
${d_1} = 8cm$ and ${d_2} = 15cm$
Now these diagonals meet at a right angle and divide the rhombus into four equal right-angle triangles.
Let’s take a look at a triangle ABE
The base of the triangle $ = \dfrac{{{d_2}}}{2} = 7.5cm$
The perpendicular of the triangle $ = \dfrac{{{d_1}}}{2} = 4cm$
And their hypotenuse is equal to the side of the rhombus.
By applying Pythagoras theorem, we will find the hypotenuse.
Hypotenuse $ = \sqrt {{{\left( 4 \right)}^2} + {{\left( {7.5} \right)}^2}} = \sqrt {16 + 56.25} = \sqrt {72.25} = 8.5cm$
Side of the rhombus is 8.5 cm.
133. Two adjacent angles of a parallelogram are in the ratio 1:3. Find its angles.
Ans:
The ratio of the angles of the parallelogram = 1:3
The adjacent angles in a parallelogram are supplementary so the sum of the adjacent angles of the parallelogram = 180°
Now,
The sum of the ratios = 1+3 = 4
The angles are:
$\dfrac{1}{4} \times 180^\circ = 45^\circ $
$\dfrac{3}{4} \times 180^\circ = 135^\circ $
The angles are 45° and 135°.
134. Of the four quadrilaterals - square, rectangle, rhombus and trapezium - one is somewhat different from the others because of its design. Find it and give justification
Ans:
A parallelogram is a quadrilateral that has its opposite sides that are always parallel to each other.
A parallelogram includes figures like square, rectangle and rhombus also.
Now in the case of a trapezium, only one pair of opposite sides are parallel to each other.
Hence, it is not considered as a parallelogram.
From the above points we can clearly see that trapezium is different from square, rectangle and rhombus.
135. In a rectangle ABCD, AB = 25 cm and BC = 15. In what ratio does the bisector of $\angle {\mathbf{C}}$ divide AB?
Ans:
The simple diagram we can draw from the given question is:
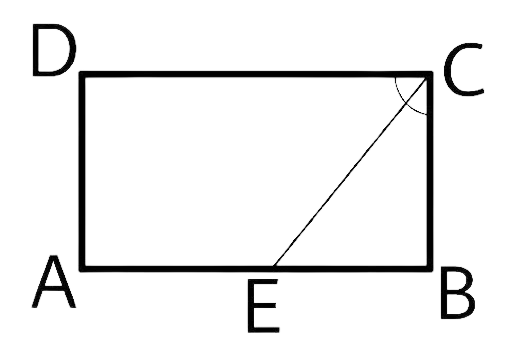
Given, a rectangle ABCD
AB = 25cm
BC = 15cm
Now, CE is the bisector of $\angle C$
Now in triangle BCE
$\angle ECB = \dfrac{{90^\circ }}{2} = 45^\circ $
$\angle CEB = 180^\circ - \left( {\angle ECB + CBE} \right) = 180^\circ - \left( {45^\circ + 90^\circ } \right) = 180^\circ - 135^\circ = 45^\circ $
Now $\angle ECB = \angle CEB$
Which mean triangle BEC is an isosceles triangle
And BE = BC = 15 cm
AE = AB – BE = 25 cm – 15 cm = 10 cm
The ratio of AE to EB = 10 cm : 15 cm = 2 : 3
The bisector of $\angle C$ divides AB in the ratio of 2 : 3 .
136. PQRS is a rectangle. The perpendicular ST from S on PR divides $\angle {\mathbf{S}}$ in the ratio 2:3. Find\[\;\angle {\mathbf{TPQ}}\].
Ans:
The simple diagram we can draw from the given question is:
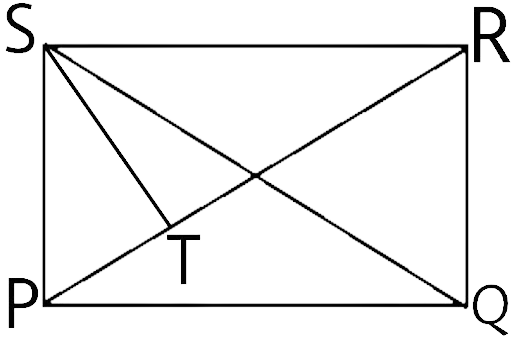
PQRS is a rectangle, so all angles are equal to 90°
Now the line ST divides the angle $\angle PSR$ in the ratio of 2 : 3
Which means $\angle PST:\angle TSR = 2:3$
Now let’s find the angles
The sum of the ratio = 2 + 3 = 5
The angles are:
$\dfrac{2}{5} \times 90^\circ = 36^\circ $
$\dfrac{3}{5} \times 90^\circ = 54^\circ $
Now the angle $\angle PST$ contains 2 parts
So $\angle PST = 36^\circ $
137. A photo frame is in the shape of a quadrilateral. With one diagonal longer than the other. Is it a rectangle? Why or why not?
Ans:
One diagonal is longer than the other which means it is not a rectangle it is a quadrilateral-shaped frame. A rectangle has equal diagonal.
138. The adjacent angles of a parallelogram are (2x – 4)° and (3x – 1)°. Find the measures of all angles of the parallelogram.
Ans:
The adjacent angles in a parallelogram are supplementary so the sum of the adjacent angles of the parallelogram = 180°
Which means
$\left( {2x - 4} \right)^\circ + \left( {3x - 1} \right)^\circ = 180^\circ $
$\left( {5x - 5} \right)^\circ = 180^\circ $
$\left( {5x} \right)^\circ = 185^\circ $
$\left( x \right)^\circ = 37^\circ $
The angle (2x – 4)° = 70°
The angle (3x – 1)° = 110°
139. The point of intersection of diagonals of a quadrilateral divides one diagonal in the ratio 1:2. Can it be a parallelogram? Why or why not?
Ans:
The diagonals of a parallelogram are always bisecting each other.
Which means they are in the ratio 1:1. Therefore, it cannot be a parallelogram.
140. The ratio between exterior angle and interior angle of a regular polygon is 1:5. Find the number of sides of the polygon.
Ans:
The ratio of the angles are = 1 : 5
Now the sum of interior and exterior angles = 180°
Let’s find the angles
The sum of ratio = 1+5 = 6
The angles are:
$\dfrac{1}{6} \times 180^\circ = 30^\circ $
$\dfrac{5}{6} \times 180^\circ = 150^\circ $
The exterior angle is 30°.
The value of the exterior angle for a n-sided polygon is $ = \dfrac{{360^\circ }}{n}$
We have the exterior angle equal to 30°
Now,
$30^\circ = \dfrac{{360^\circ }}{n}$
$n = \dfrac{{360^\circ }}{{30^\circ }} = 12$
The number of sides for the polygon is 12.
141. Two sticks each of length 5 cm are crossing each other such that they bisect each other. What shape is formed by joining their end points? Give a reason.
Ans:
Two sticks each of length 5cm which means they are equal in length.
When a quadrilateral's diagonals are equal and bisect each other, the quadrilateral is a rectangle. As a result, a rectangle formed by combining two sticks.
142 Two sticks each of length 7 cm are crossing each other such that they bisect each other at right angles. What shape is formed by joining their end points? Give a reason.
Ans:
Two sticks each of length 7cm which means they are equal in length, and they bisect each other at right angles.
When a quadrilateral's diagonals are equal and bisect each other at right angles, the quadrilateral is a rhombus. As a result, a rhombus formed by combining two sticks.
143. A playground in the town is in the form of a kite. The perimeter is 106 metres. If one of its sides is 23 metres, what are the lengths of other three sides?
Ans:
A kite has four sides, out of which two adjacent sides are equal to each other and the other two adjacent sides are equal to each other.
Let the lengths are A, A, B and B
Their perimeter = 2A+2B
Given,
Perimeter = 106m
Now let’s assume A = 23 m
$2\left( {23} \right) + 2B = 106$
$2B = 106 - 2\left( {23} \right)$
$B = \dfrac{{106 - 46}}{2} = 30$
The sides are 23m, 23m, 30m, and 30m.
144. In rectangle READ, find $\angle {\mathbf{EAR}}$, $\angle {\mathbf{RAD}}$ and $\angle {\mathbf{ROD}}$
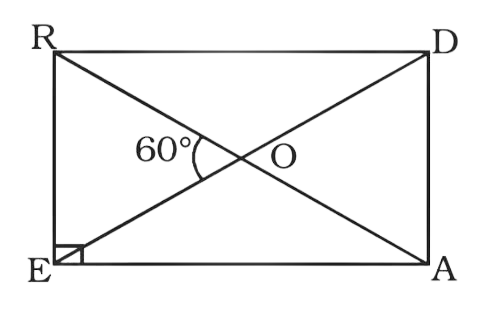
Ans:
The diagonals of a triangle bisect each other.
So, OR = OE = OA = OD
And triangle REO, OEA, OAD and ODR are isosceles triangles.
$\angle ROD = 180^\circ - \angle ROE$ ……..(linear pair of angles)
$\angle ROD = 180^\circ - 60^\circ = 120^\circ $
In triangle OEA which is an isosceles triangle
$\angle OEA = \angle OAE$
Now,
$\angle OEA + \angle OAE = \angle ROE = 60^\circ $ …(exterior angle is equal to the sum of two interior opposite angle)
\[2\angle OAE = 60^\circ \]
\[\angle OAE = \angle EAR = 30^\circ \]
Now,
$\angle EAD = 90^\circ $
\[\angle RAE + \angle RAD = \angle EAD = 90^\circ \]
\[\angle RAD = 90^\circ - \angle RAE = 90^\circ - 30^\circ = 60^\circ \]
145. In rectangle PAIR, find $\angle {\mathbf{ARI}}$ , \[\angle {\mathbf{RMI}}\] and $\angle {\mathbf{PMA}}$ .
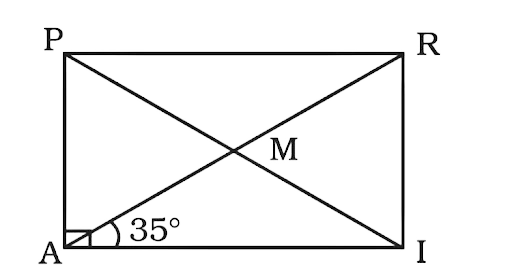
Ans:
The diagonals of a triangle bisect each other.
So, MR = MA = MP = MI
And triangle MAI, MAP, MPR and MRI are isosceles triangles.
Now $\angle MAI = \angle MIA = 35^\circ $
$\angle RMI = \angle MAI + \angle MIA = 35^\circ + 35^\circ = 70^\circ $ ..…(exterior angle is equal to the sum of two interior opposite angle)
$\angle PMA = \angle RMI = 70^\circ $ …..(vertical opposite angle)
In triangle ARI
$\angle RAI = 35^\circ $ and $\angle AIR = 90^\circ $
So, \[\angle ARI = 180^\circ - \left( {\angle RAI + \angle AIR} \right) = 180^\circ - 125^\circ = 55^\circ \]
146. In parallelogram ABCD, find $\angle {\mathbf{B}}$ , $\angle {\mathbf{C}}$ and $\angle {\mathbf{D}}$ .

Ans:
The adjacent angles in a parallelogram are supplementary so the sum of the adjacent angles of the parallelogram = 180°.
So, $\angle A + \angle D = 180^\circ $
And $\angle A + \angle B = 180^\circ $
Now,
$\angle B = \angle D = 180^\circ - \angle A = 180^\circ - 80^\circ = 100^\circ $
And opposite angles of a parallelogram are equal
$\angle A = \angle C = 80^\circ $
147. In parallelogram PQRS, O is the midpoint of SQ. Find $\angle {\mathbf{S}}$, $\angle {\mathbf{R}}$ , PQ, QR and diagonal PR.
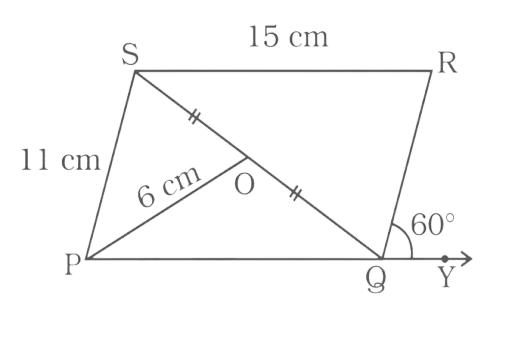
Ans:
$\angle PQR = 180^\circ - 60^\circ = 120^\circ $ ……..(linear pair of angles)
The adjacent angles in a parallelogram are supplementary so the sum of the adjacent angles of the parallelogram = 180°.
So,
$\angle PQR + \angle QRS = 180^\circ $
$\angle PQR = 180^\circ - \angle PQR = 120^\circ $
Now the opposite angles of a parallelogram are equal
$\angle S = \angle PQR = 120^\circ $
A parallelogram has opposite sides equal and parallel to each other
So, PQ = SR = 15 cm
And QR = SP = 11 cm
The diagonals of a parallelogram bisect each other
Since O is the midpoint of diagonal SQ, it will also be the midpoint of diagonal PR
So, diagonal PR = 2(OP) = 12 cm.
148. In rhombus BEAM, find $\angle {\mathbf{AME}}$ and $\angle {\mathbf{AEM}}$.
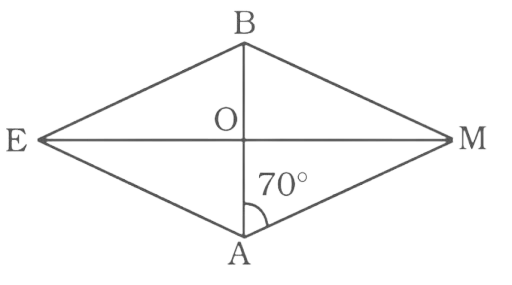
Ans:
Diagonals of a rhombus bisect each other at right angle
So, the angle $\angle AOM = 90^\circ $
In triangle AOM
$\angle AMO = 180^\circ - \left( {\angle OAM + \angle AOM} \right) = 180^\circ - 160^\circ = 20^\circ $
$\angle AME = \angle AMO = 20^\circ $
All sides of a rhombus are equal
So, triangle AEM is an isosceles triangle.
$\angle AEM = \angle AME = 20^\circ $
149. In parallelogram FIST, find $\angle {\mathbf{SFT}}$ , $\angle {\mathbf{OST}}$ and $\angle {\mathbf{STO}}$ .
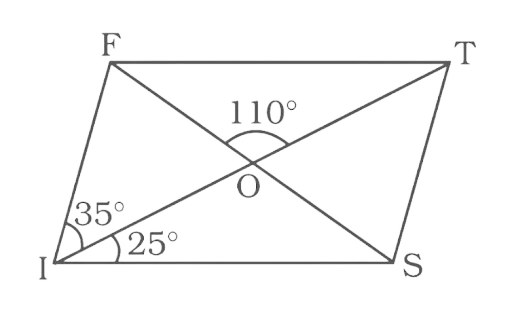
Ans:
The opposite sides of a parallelogram are parallel to each other. And the diagonal bisects each other.
Thus, triangle FOT, IOS, OFI and OTS are isosceles triangles. The sides are parallel so FT || IS and FI || TS.
$\angle OIF = \angle STO = 35^\circ $ …..(alternate angle)
In triangle OIS
$\angle OIA = \angle OSI = 25^\circ $
Now $\angle SFT = \angle OSI = 25^\circ $ …..(alternate angle)
In triangle OIF
$\angle OIF = \angle OFI = 35^\circ $
Now $\angle OST = \angle OFI = 35^\circ $ …..(alternate angle)
150. In the given parallelogram YOUR, $\angle {\mathbf{RUO}} = {\mathbf{120}}^\circ $ and OY is extended to point S such that \[\angle {\mathbf{SRY}} = {\mathbf{50}}^\circ \] . Find $\angle {\mathbf{YSR}}$
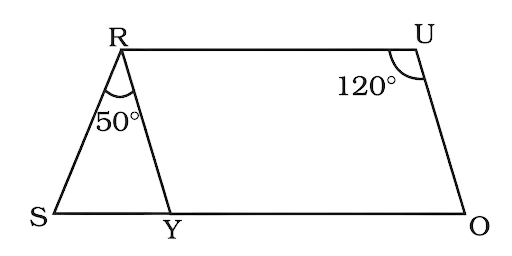
Ans:
In a parallelogram opposite angles are equal
So,
$\angle RYO = \angle RUO = 120^\circ $
Now in triangle SRY
$\angle YSR = \angle RYO - \angle SRY$ …..(exterior angle is equal to the sum of two interior opposite angle)
$\angle YSR = 120^\circ - 50^\circ = 70^\circ $
151. In kite WEAR, $\angle {\mathbf{WEA}} = {\mathbf{70}}^\circ $ and \[\angle {\mathbf{ARW}} = {\mathbf{80}}^\circ .\] .Find the remaining two angles.
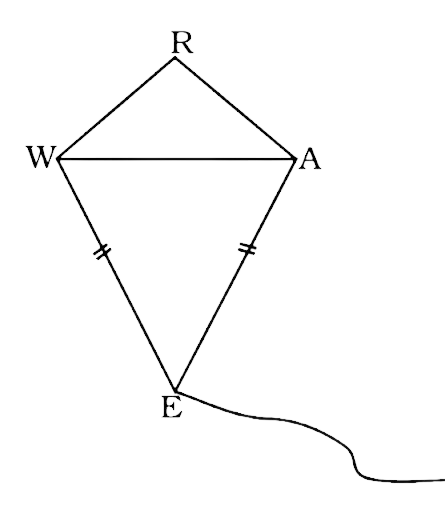
Ans:
In kite adjacent sides are equal, which mean WE = EA and AR = RW
The triangles WEA and WRA are isosceles triangles.
In triangle WEA
\[\angle EWA = \angle EAW = \dfrac{{180^\circ - \angle WEA}}{2}\]
\[\angle EWA = \angle EAW = \dfrac{{180^\circ - 70^\circ }}{2} = 55^\circ \]
In triangle WRA
\[\angle RWA = \angle RAW = \dfrac{{180^\circ - \angle WRA}}{2}\]
\[\angle RWA = \angle RAW = \dfrac{{180^\circ - 80^\circ }}{2} = 50^\circ \]
152. A rectangular MORE is shown below:
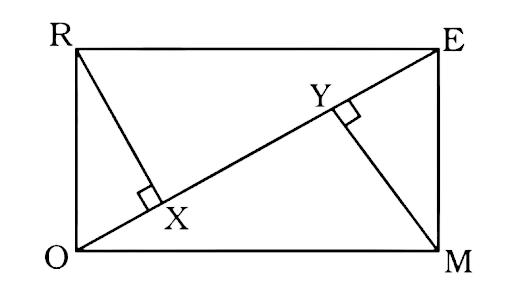
Answer the following questions by giving appropriate reason.
(i) Is RE = OM?
(ii) Is \[\angle {\mathbf{MYO}} = \angle {\mathbf{RXE}}\] ?
(iii) Is \[\angle {\mathbf{MOY}} = \angle {\mathbf{REX}}\] ?
(iv) Is \[\Delta {\mathbf{MOY}} \cong \Delta {\mathbf{REX}}\] ?
(v) Is MY = RX ?
Ans:
Rectangle MORE has its opposite sides equal and parallel to each other.
So, RE = OM
$\angle MYO = \angle MYE = 180^\circ - 90^\circ = 90^\circ $ ……..(Pair of angles in a straight line)
$\angle RXO = \angle RXE = 180^\circ - 90^\circ = 90^\circ $ ……..(Pair of angles in a straight line)
Now, $\angle MYO = \angle RXE = 90^\circ $
Rectangle MORE has its opposite sides equal and parallel to each other.
So, RE || OM and OE is a transversal.
$\angle MOY = \angle REX$ ……..(alternate angles)
In triangle MYO and RXE
$\angle MYO = \angle RXE = 90^\circ $
$\angle MOY = \angle REX$ ……..(alternate angles)
RE = OM
So $\Delta MYO \cong \Delta RXE$
Now MY = RX …(corresponding parts of congruent triangles are equal)
153. In parallelogram LOST, \[{\mathbf{SN}} \bot {\mathbf{OL}}\] and \[{\mathbf{SM}} \bot {\mathbf{LT}}\] . Find \[\angle {\mathbf{STM}}\] , $\angle {\mathbf{SON}}$ and $\angle {\mathbf{NSM}}$ .
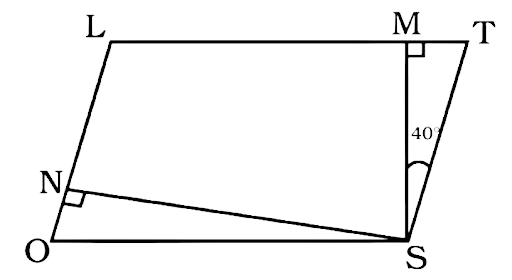
Ans:
In triangle MTS
$\angle STM = 180^\circ - \left( {\angle MST + \angle SMT} \right)$
$\angle STM = 180^\circ - \left( {90^\circ + 40^\circ } \right) = 50^\circ $
Opposite angles of a parallelogram are equal
$\angle SNO = \angle STM = 50^\circ $
In triangle NSO
$\angle NSO = 180^\circ - \left( {\angle ONS + \angle SON} \right)$
$\angle NSO = 180^\circ - \left( {50^\circ + 90^\circ } \right) = 40^\circ $
Since LT || OS and MS is a transversal
$\angle OSM = \angle SMT = 90^\circ $ …….(alternate angle)
$\angle NSM = \angle OSM - \angle NSO = 90^\circ - 40^\circ = 50^\circ $
154. In trapezium HARE, EP and RP are bisectors of $\angle {\mathbf{E}}$ and $\angle {\mathbf{R}}$respectively. Find $\angle {\mathbf{HAR}}$ and $\angle {\mathbf{EHA}}$.
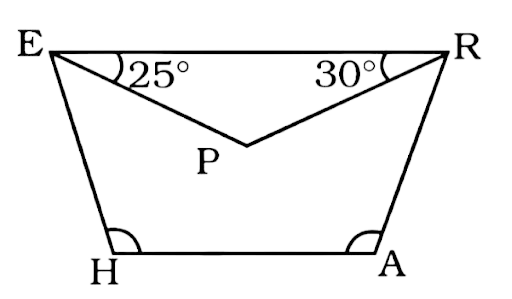
Ans:
\[\angle HER = 2 \times 25^\circ = 50^\circ \]
$\angle ERA = 2 \times 30^\circ = 60^\circ $
Now in trapezium HARE ER || HA
Which means $\left( {\angle HER,\angle EHA} \right)$ and $\left( {\angle ERA,\angle RAH} \right)$ are supplementary, they add up to become 180°.
$\angle EHA = 180^\circ - \angle HER = 180^\circ - 50^\circ = 130^\circ $
$\angle HAR = 180^\circ - \angle ERA = 180^\circ - 60^\circ = 120^\circ $
155. In parallelogram MODE, the bisector of $\angle {\mathbf{M}}$ and $\angle {\mathbf{O}}$ meet at Q, find the measure of $\angle {\mathbf{MQO}}$.
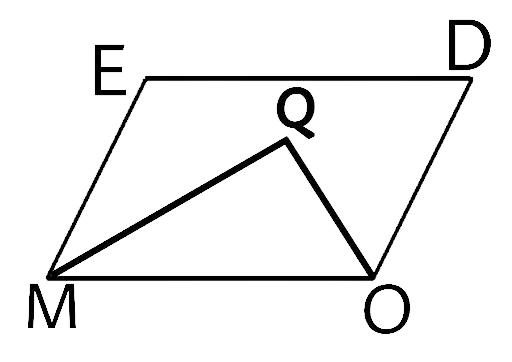
Ans:
In triangle MQO
$\angle MQO = 180^\circ - \left( {\angle QMO + \angle QOM} \right)$
Since MODE is a parallelogram the adjacent angles in a parallelogram are supplementary so the sum of the adjacent angles of the parallelogram =180°.
So, \[\angle EMO + \angle MOD = 180^\circ \]
Now $\angle QMO = \dfrac{1}{2}\angle EMO$
And $\angle QOM = \dfrac{1}{2}\angle MOD$
So,
\[\angle MQO = 180^\circ - \dfrac{1}{2}\left( {\angle EMO + \angle MOD} \right) = 180^\circ - 90^\circ = 90^\circ \]
156. A playground is in the form of a rectangle ATEF. Two players are standing at the points F and B where EF = EB. Find the values of x and y.
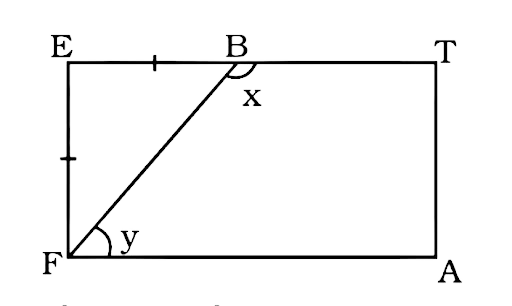
Ans:
ATEF is a rectangle so all angles are equal to 90°.
The triangle EFB is an isosceles triangle as both its sides are equal
Now,
\[\angle EFB = \angle EBF = \dfrac{{180^\circ - 90^\circ }}{2} = 45^\circ \]
$y = 90^\circ - \angle EFB = 45^\circ $
$x = 90^\circ + \angle EFB = 135^\circ $ ….(exterior angle is equal to the sum of interior opposite angles)
157. In the following figure of a ship, ABDH and CEFG are two parallelograms. Find the value of x.
Ans:
Since ABHD is a parallelogram the adjacent angles in a parallelogram are supplementary so the sum of the adjacent angles of the parallelogram =180°.
\[\angle HDC = 180^\circ - \angle ABD = 180^\circ - 130^\circ = 50^\circ \]
Since CEFG is a parallelogram the opposite angles in a parallelogram are equal.
\[\angle GCE = \angle GFE = 30^\circ \]
In the triangle where x is present
$x = 180^\circ - \left( {\angle GCD + \angle HDB} \right) = 180^\circ - \left( {50^\circ + 30^\circ } \right) = 100^\circ $
158. A rangoli has been drawn on the floor of a house. ABCD and PQRS both are in the shape of a rhombus. Find the radius of the semicircle drawn on each side of rhombus ABCD.
Ans:
The diagonals of a rhombus bisects each other at right angles.
So, we can find the length of side AB by applying Pythagoras theorem
Now AO = 4 units
BO = 3 units
$AB = \sqrt {{4^2} + {3^2}} = 5$
Radius of the semicircle = 2.5 units
159. ABCDE is a regular pentagon. The bisector of angle A meets the side CD at M. Find $\angle {\mathbf{AMC}}$ .
Ans: ABCDE is a regular pentagon
Sum of all the angle of an n sided polygon $ = \left( {n - 2} \right) \times 180^\circ $
For pentagon n = 5
Each angle of ABCDE $ = \dfrac{{\left( {5 - 2} \right) \times 180^\circ }}{5} = 108^\circ $
Now in the quadrilateral ABCM. The sum of the angles = 360\[^\circ \]
$\angle MAB = \dfrac{1}{2} \times 108^\circ = 54^\circ $
$\angle AMC = 360^\circ - \left( {\angle ABC + \angle BCM + \angle MAB} \right)$
\[\angle AMC = 360^\circ - \left( {108^\circ + 108^\circ + 54^\circ } \right) = 360^\circ - 270^\circ = 90^\circ \]
160. Quadrilateral EFGH is a rectangle in which J is the point of intersection of the diagonals. Find the value of x if JF = 8x+ 4 and EG = 24x – 8.
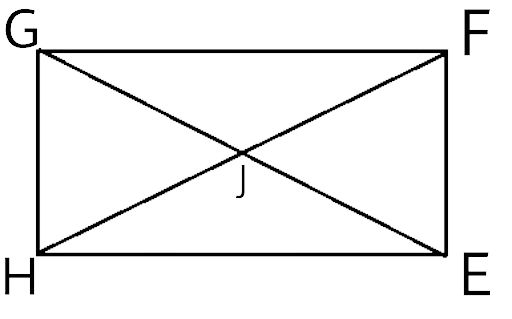
Ans:
The diagonals of a rectangle bisect each other at the intersection point.
So, 2(JF) = EG
$2\left( {8x + 4} \right) = 24x - 8$
$16x + 8 = 24x - 8$
$16 = 8x$
$x = 2$
161. Find the values of x and y in the following parallelogram.
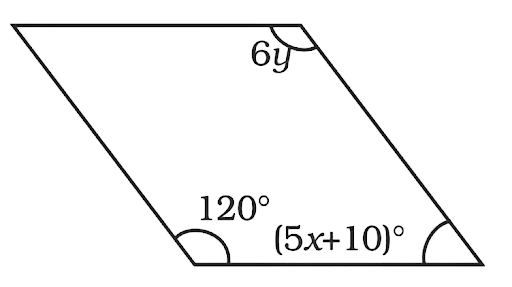
Ans:
In a parallelogram opposite sides are equal and adjacent angles are supplementary; they add up to become 180°.
$6y = 120^\circ $
$y = 20^\circ $
And
\[120^\circ + \left( {5x + 10} \right)^\circ = 180^\circ \]
\[\left( {5x + 10} \right)^\circ = 180^\circ - 120^\circ \]
\[5x = 60^\circ - 10^\circ \]
\[x = 10^\circ \]
162. Find the values of x and y in the following kite.
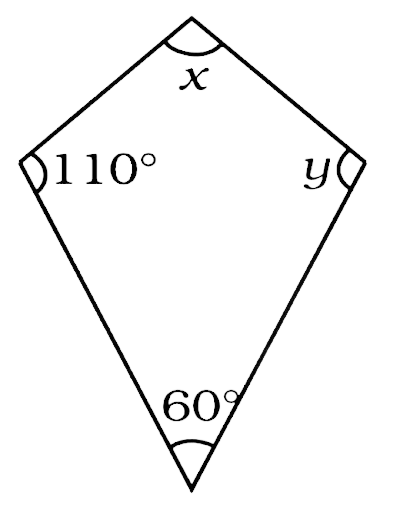
Ans:
One pair of angles in a kite is equal
From the figure $y = 110^\circ $
Now the sum of all the angles in a quadrilateral is 360°.
$x = 360^\circ - \left( {110^\circ + 110^\circ + 60^\circ } \right) = 360^\circ - 280^\circ = 80^\circ $
163. Find the value of x in the trapezium ABCD given below.
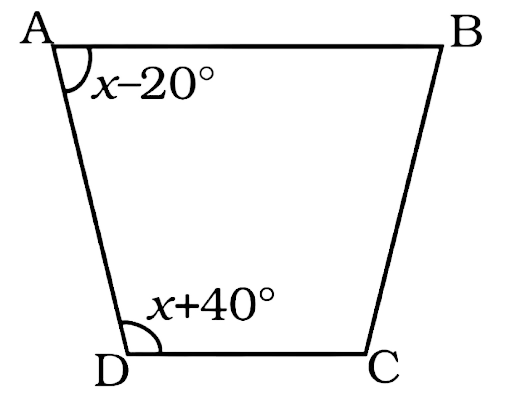
Ans:
In the trapezium ABCD AB || CD
So, the angles $\angle A$ and $\angle D$ will be supplementary; they will add up to become 180°.
$x - 20^\circ + x + 40^\circ = 180^\circ $
$2x + 20^\circ = 180^\circ $
$2x = 160^\circ $
$x = 80^\circ $
164. Two angles of a quadrilateral each measure 75° and the other two angles are equal. What is the measure of these two angles? Name the possible figures so formed
Ans:
We have two pairs of angles. In the first pair both the angles are equal to 75°.
And the second pair of angles are also equal.
Thus, if the equal pair of angles are adjacent then the figure is an isosceles triangle.
If the equal pair of angles are opposite then it is a parallelogram.
165. In a quadrilateral PQRS, P = 50°, Q = 50°, R = 60°. Find $\angle {\mathbf{S}}$ . Is this quadrilateral convex or concave?
Ans:
Sum of all the angles of a quadrilateral is 360°.
$\angle S = 360^\circ - \left( {\angle P + \angle Q + \angle R} \right) = 360^\circ - \left( {50^\circ + 50^\circ + 60^\circ } \right) = 360^\circ - 160^\circ = 200^\circ $
Since $\angle S = 200^\circ > 180^\circ $ it is a concave quadrilateral.
166. Both the pairs of opposite angles of a quadrilateral are equal and supplementary. Find the measure of each angle.
Ans:
Let the quadrilateral be ABCD.
Now $\angle A = \angle C$ and $\angle B = \angle D$
And they are supplementary
So, $\angle A + \angle C = 180^\circ $
Thus, $\angle A = \angle C = 90^\circ $
Now,
$\angle B + \angle D = 180^\circ $
Thus, $\angle B = \angle D = 90^\circ $
Thus, each is at a right angle.
167. Find the measure of each angle of a regular octagon.
Ans:
Sum of all the angle of an n sided polygon $ = \left( {n - 2} \right) \times 180^\circ $
For octagon n = 8
Each angle of the octagon $ = \dfrac{{\left( {8 - 2} \right) \times 180^\circ }}{8} = 120^\circ $
168. Find the measure of an exterior angle of a regular pentagon and an exterior angle of a regular decagon. What is the ratio between these two angles?
Ans:
The value of the exterior angle for a n-sided polygon is $ = \dfrac{{360^\circ }}{n}$
For decagon n = 10
Exterior angle $ = \dfrac{{360^\circ }}{{10}} = 36^\circ $
For pentagon n = 5
Exterior angle $ = \dfrac{{360^\circ }}{5} = 72^\circ $
the ratio between these two angles = $72^\circ :36^\circ = 2:1$
169. In the figure, find the value of x.
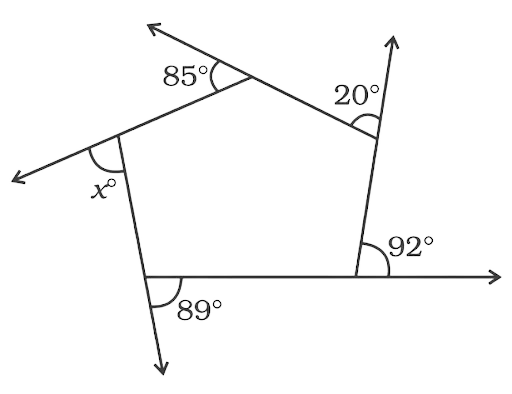
Ans:
Sum of all the exterior angles for any number sided polygon remains 360°.
Now,
$x = 360^\circ - \left( {85^\circ + 20^\circ + 92^\circ + 89^\circ } \right) = 360^\circ - 286^\circ = 74^\circ $
170. Three angles of a quadrilateral are equal. Fourth angle is of measure 120°. What is the measure of equal angles?
Ans:
Sum of all the angles of a quadrilateral is 360°.
Now the remaining three angles are equal
So, the three angles are $ = \dfrac{{360^\circ - 120^\circ }}{3} = 80^\circ $
171. In a quadrilateral HOPE, PS and ES are bisectors of $\angle {\mathbf{P}}$ and $\angle {\mathbf{E}}$ respectively. Give reason
Ans:
Data is not sufficient to solve the question.
172. ABCD is a parallelogram. Find the value of x, y and z.
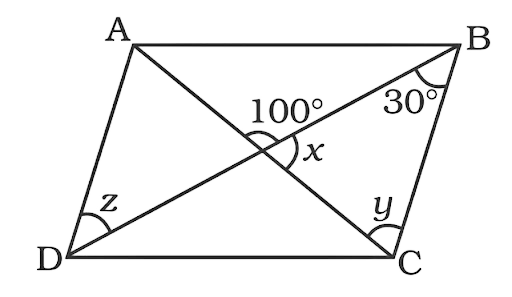
Ans:
Now in parallelogram ABCD the sides AD || BC and BD are the transversal.
$z = 30^\circ $ …..(alternate angles)
$x = 180^\circ - 100^\circ = 80^\circ $ …..(linear pair of angles in a straight line)
In the triangle OBC
$y = 180^\circ - \left( {30^\circ + 80^\circ } \right) = 180^\circ - 110^\circ = 70^\circ $
173. Diagonals of a quadrilateral are perpendicular to each other. Is such a quadrilateral always a rhombus? Give a figure to justify your answer.
Ans:
False, the figure may not only be a rhombus. For a quadrilateral having perpendicular diagonals is not necessary that it is a rhombus, another possible answer like a trapezium exists that has diagonals perpendicular to each other.
For example, the following trapezium ABCD in which AB is parallel to CD
174. ABCD is a trapezium such that AB||CD, $\angle {\mathbf{A}}$ : $\angle {\mathbf{D}}$ = 2 : 1 , $\angle {\mathbf{B}}$ : $\angle {\mathbf{C}}$ = 7 : 5. Find the angles of the trapezium.
Ans:
In the given below diagram ABCD is a trapezium such that AB||CD,
Angle $\angle A$and $\angle D$ will be supplementary, they will add up to become 180°.
Sum of ratio = 2 + 1 = 3
Now the angles are
$\angle A = \dfrac{2}{3} \times 180^\circ = 120^\circ $
And
$\angle D = \dfrac{1}{3} \times 180^\circ = 60^\circ $
Angle $\angle B$and $\angle C$ will be supplementary, they will add up to become 180°.
Sum of ratio = 7 + 5 = 12
Now the angles are
$\angle B = \dfrac{7}{{12}} \times 180^\circ = 105^\circ $
And
$\angle D = \dfrac{5}{{12}} \times 180^\circ = 75^\circ $
175. A line l is parallel to line m and a transversal p intersects them at X, Y respectively. Bisectors of interior angles at X and Y intersect at P and Q. Is PXQY a rectangle? Given reason.
Ans:
Here line l is parallel to line m.
Now,
$\angle YXP = \dfrac{1}{2}\angle YXC$
And
$\angle YXQ = \dfrac{1}{2}\angle YXD$
$\angle YXP + \angle YXQ = \dfrac{1}{2}\left( {\angle YXC + \angle YXD} \right) = \dfrac{1}{2}\left( {180^\circ } \right) = 90^\circ $
The same goes for the line AB.
$\angle XYP = \dfrac{1}{2}\angle XYB$
And
$\angle XYQ = \dfrac{1}{2}\angle XYA$
$\angle XYQ + \angle XYP = \dfrac{1}{2}\left( {XYA + \angle XYB} \right) = \dfrac{1}{2}\left( {180^\circ } \right) = 90^\circ $
Now,
$\angle DXY = \angle XYB$ ..….(alternate angle)
So, $\angle QXY = \angle XYP$
Thus, we can confirm that XQ || YP
And
$\angle CXY = \angle XYA$ ..….(alternate angle)
So, $\angle QYX = \angle YXP$
Thus, we can confirm that YQ || XP.
Now PXQY is a parallelogram with one pair of angles as right angles. Thus, PXQY is a rectangle.
176. ABCD is a parallelogram. The bisector of angle A intersects CD at X and bisector of angle C intersects AB at Y. Is AXCY a parallelogram? Give a reason.
Ans:
Since DC || AB
$\angle XAY = \angle CYB$ …..(corresponding angles)
$\angle CYB = \angle YCX$ ……(alternate angles)
So, $\angle XAY = \angle YCX$
Now XC || AY
Thus, we can conclude that XA || YC and the opposite angles are equal thus, AYCX is a parallelogram.
177. A diagonal of a parallelogram bisects an angle. Will it also bisect the other angle? Give a reason.
Ans:
In the parallelogram ABCD the diagonal AC bisects $\angle A$
Now,
$\angle BAC = \angle CAD$
$\angle BAC = \angle DCA$ ……(alternate angles)
$\angle BAC = \angle BCA$ ……(alternate angles)
Thus, $\angle BAC = \angle CAD = \angle BCA = \angle DCA$
We can see that the diagonal AC also bisects the angle $\angle C$.
178. The angle between the two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 45°. Find the angles of the parallelogram.
Ans:
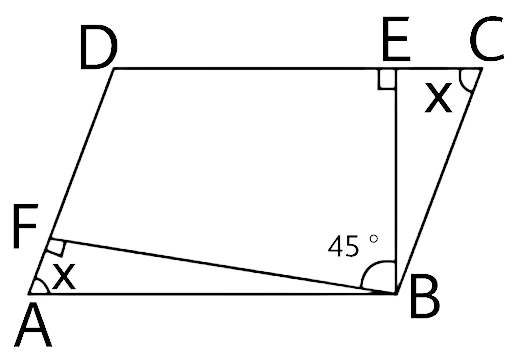
In the quadrilateral DEBF
$\angle FDE = 360^\circ - \left( {90^\circ + 90^\circ + 45^\circ } \right) = 135^\circ $
Now adjacent angles of a parallelogram are supplementary.
$x = 180^\circ - 135^\circ = 45^\circ $
The angles are 45°, 135°, 45° and 135°.
179. ABCD is a rhombus such that the perpendicular bisector of AB passes through D. Find the angles of the rhombus.
(Hint: Join BD. Then ∆ ABD is equilateral.)
Ans:
In the triangles ADE and DEB
DE is the common side.
AE = EB
$\angle AED = \angle DEB = 90^\circ $
So, $\Delta AED \cong \Delta DEB$
So, AD = DB = AB
Thus, ADB is an equilateral triangle.
$\angle DAB = 60^\circ $
Since adjacent angles of a rhombus are supplementary so, $\angle ADC = 120^\circ $.
The angles are 60°, 120°, 60° and 120°.
180. ABCD is a parallelogram. Points P and Q are taken on the sides AB and AD respectively and the parallelogram PRQA is formed. If \[\angle {\mathbf{C}} = {\mathbf{45}}^\circ \] find $\angle {\mathbf{R}}$ .
Ans:
Opposite angles in a parallelogram ABCD are equal so $\angle A = \angle C = 45^\circ $
Now in parallelogram APRQ opposite angles are equal so,
$\angle R = \angle A = 45^\circ $
181. In parallelogram ABCD, the angle bisector of A bisects BC. Will the angle bisector of B also bisect AD? Give a reason.
Ans:
In the parallelogram ABCD the sides AD || BC.
We will draw line EF parallel to AB
Thus, we will have AEFB is a parallelogram, with diagonals EB and AF.
Thus, the diagonals will bisect each other.
$\angle EAF = \angle FAB$
$\angle EAF = \angle AFB$ …..(alternate angle)
Thus, $\angle FAB = \angle AFB$
In the triangle OAB and ABF
$\angle FAB = \angle AFB$
AO = OF
And OB is a common side
Thus, $\Delta AOB \cong \Delta OBF$
So, the $\angle ABO = \angle OBF$ and the diagonal EF is the angle bisector.
Now, FB is equal to EA as ABFE is a parallelogram, which mean AE is half of AD thus the angle bisector bisects the side.
182. A regular pentagon ABCDE and a square ABFG are formed on opposite sides of AB. Find $\angle {\mathbf{BCF}}$ .
Ans:
Now since ABCDE is a regular pentagon its all sides are equal. and its sides are also equal to all the sides of the square ABFG.
Thus, the sides BC and BF are also equal, making the triangle BCF an isosceles triangle.
$\angle ABF = 90^\circ $
Sum of all the angle of a pentagon $ = \left( {n - 2} \right) \times 180^\circ $
For n = 5
Each angle of the polygon $ = \dfrac{{\left( {5 - 2} \right) \times 180^\circ }}{5} = 108^\circ $
$\angle ABC = 108^\circ $
$\angle CBA = 360^\circ - \left( {90^\circ + 108^\circ } \right) = 360^\circ - 198^\circ = 162^\circ $
Now, \[\angle BCF = \dfrac{{180^\circ - 162^\circ }}{2} = 9^\circ \]
183. Find the maximum number of acute angles which a convex, a quadrilateral, a pentagon and a hexagon can have. Observe the pattern and generalise the result for any polygon
Ans:
When an internal angle is acute, the exterior angle is more than 90°.
The sum of all the exterior angles cannot exceed 360°.
So, the maximum number of acute angles will be less than $ < \dfrac{{360^\circ }}{{90^\circ }} = 4$
So, the maximum number of Acute angles that can be present in a polygon is 3.
184. In the following figure, FD||BC||AE and AC||ED. Find the value of x.
Ans:
Now let’s extend FD to G.
In the triangle AGF.
$\angle AGF = \angle ABC = 64^\circ $ …...(corresponding angle)
Now,$\angle AFD = \angle AGF + \angle GAF = 52^\circ + 64^\circ = 116^\circ $ …….(exterior angle is equal to the sum of two interior opposite angles.)
Since, FD || AE and AF || ED so AEDF is a parallelogram.
Opposite angles of a parallelogram are equal
So, $x = 116^\circ $
185. In the following figure, AB||DC and AD = BC. Find the value of x.
Ans:
Let’s draw ED keeping it parallel to side BC.
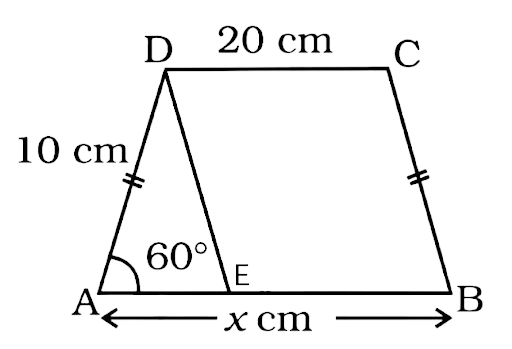
Since DC || EB and BC || DE so EBCD is a parallelogram.
We will have ED = BC and EB = DC = 20 cm
The triangle ADE is an isosceles triangle as ED = AD
So, \[\angle ADE = \angle DEA = 60^\circ \]
Thus $\angle ADE = 60^\circ $
We will have all angles equal so the triangle ADE is an equilateral triangle.
We have AE = DE = AD = 10 cm
Thus, x = AE + EB = 10 cm + 20 cm = 30 cm
186. Construct a trapezium ABCD in which AB||DC, $\angle {\mathbf{A}} = {\mathbf{105}}^\circ $, AD = 3 cm, AB = 4 cm and CD = 8 cm.
Ans:
187. Construct a parallelogram ABCD in which AB = 4 cm, BC = 5 cm and $\angle {\mathbf{B}} = {\mathbf{60}}^\circ $.
Ans:
Since it is a parallelogram AB = CD = 4 cm
And BC = AD = 5 cm
The adjacent angle to $\angle B$ will be equal to $180^\circ - 60^\circ = 120^\circ $
Thus, $\angle A = \angle C = 120^\circ $
Steps of construction:
1. Draw the line AB = 4 cm
2. Draw ray BX such that $\angle ABX = 60^\circ $
3. Mark a point C such that BC = 5cm
4. Draw ray AY such that $\angle BAY = 120^\circ $
5. Mark a point D such that AD = 5 cm
6. Join C and D.
Thus, ABCD is the required parallelogram.
188. Construct a rhombus whose side is 5 cm and one angle is of 60°.
Ans:
Since it is a rhombus AB = BC = CD = AD = 4 cm
The adjacent angle to $\angle B$ will be equal to $180^\circ - 60^\circ = 120^\circ $
Thus, $\angle A = \angle C = 120^\circ $
Steps of construction:
1. Draw the line AB = 5 cm
2. Draw ray BX such that $\angle ABX = 60^\circ $
3. Mark a point C such that BC = 5cm
4. Draw ray AY such that $\angle BAY = 120^\circ $
5. Mark a point D such that AD = 5 cm
6. Join C and D.
Thus, ABCD is the required Rhombus.
189. Construct a rectangle whose one side is 3 cm and a diagonal equal to 5 cm.
Ans:
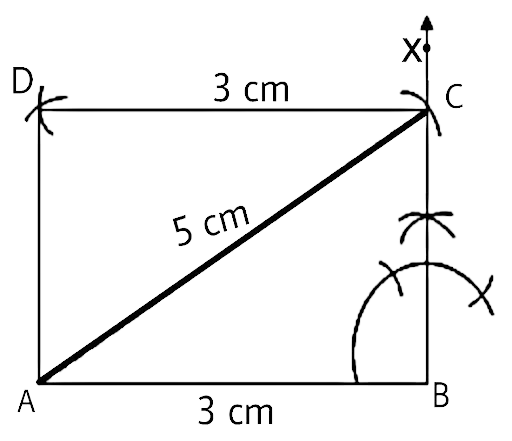
Steps of construction:
1. Draw a line segment with the length AB = 3 cm.
2. Construct an angle $\angle ABX = 90^\circ $ at point B.
3. Make an arc at A with AC = 5cm. which cuts the line BC at C.
4. Draw another 5 cm radius arc with B as the centre.
5. Draw another arc with a radius of 3 cm with centre C that intersects the previous arc at a point D.
6. Join AD and CD.
Thus, we get the required square with sides 4 cm.
190. Construct a square of 4 cm.
Ans:
The sides of a square are equal and all are at right angles.
AB = BC = CD = DA
Steps of construction:
1. Draw a line segment with the length AB = 4 cm.
2. Construct an angle $\angle ABX = 90^\circ $ at point B.
3. From the line BX cut-out BC = 4 cm
4. Draw an arc with a radius of 4cm and with centre C.
5. Draw a new arc with a radius of 4cm and with centre A that intersects the previous arc at D.
6. Join AD and CD.
Thus, we get the required square with sides 4 cm.
191. Construct a rhombus CLUE in which CL = 7.5 cm and LE = 6 cm.
Ans:
We already know that all sides of a rhombus are equal and opposite sides are parallel to each other.
Steps of construction:
1. Draw a line segment with the length CL = 7.5 cm.
2. Draw an arc CE = 7.5 cm with C at the centre.
3. Draw another arc LU = 7.5cm with L at the centre.
4. Draw an arc LE = 6cm with centre L, which cuts off the previous arc CE.
5. Draw an arc UE=7.5cm with E as the centre, cutting off the previous arc LU.
6. Now join UL, CE and EU.
The required rhombus is CLUE.
192. Construct a quadrilateral BEAR in which BE = 6 cm, EA= 7 cm, RB = RE = 5 cm and BA = 9 cm. Measure its fourth side.
Ans:
The steps of construction are:
1. Draw a line segment with the length BE = 6 cm.
2. Draw an arc BR = 5cm with B as the centre and an arc EA = 7cm with E as the centre.
3. Draw a new arc BA = 9cm with B as the centre, which will cut off arc AE.
4. Draw a new arc ER = 5cm with E as the centre, which intersects with arc BR.
5. Join B with R, R with A and E with A.
Thus, we have required quadrilateral BEAR. And the length of AR = 5cm.
193. Construct a parallelogram POUR in which, PO=5.5 cm, OU = 7.2 cm and \[\angle {\mathbf{O}} = {\mathbf{70}}^\circ \].
Ans:
Since, opposite sides of a parallelogram are equal.
Therefore, PO = RU = 5.5cm, OU = RP = 7.2cm
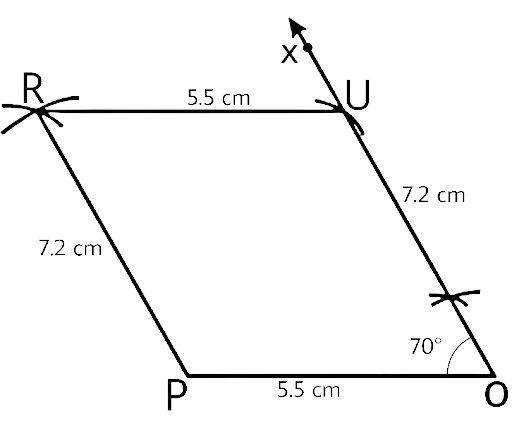
Steps of construction:
1. Draw line PO = 5.5 cm
2. Construct an angle $\angle POX = 70^\circ $
3. Draw an arc with O as the centre and OU = 7.2cm as the radius.
4. Draw an arc with U as the centre and UR = 5.5cm as the radius.
5. Draw an arc to cut the arc drawn in step 4 with P as the centre and PR = 7.2 cm as the radius.
6. Join PR and UP
Hence, the required parallelogram is POUR.
194. Draw a circle of radius 3 cm and draw its diameter and label it as AC. Construct its perpendicular bisector and let it intersect the circle at B and D. What type of quadrilateral is ABCD? Justify your answer.
Ans:
Steps of construction:
This is a cyclic quadrilateral (a square).
1. Draw a circle with the centre O and radius = 3cm.
2. Draw a diameter AC.
3. Draw a perpendicular bisector of AC that cuts the circumference of circle at B and D.
4. Join B and D.
5. Join the line A with B, B with C, C with D and D with A.
This figure formed is a cyclic quadrilateral (a square).
195. Construct a parallelogram HOME with HO = 6 cm, HE = 4 cm and OE = 3 cm.
Ans:
Steps of construction
1. Draw a line HO = 6 cm
2. Draw an arc with H as the centre and a radius of 4cm.
3. Draw an arc with O as the centre and 3cm as the radius, intersecting the arc produced in step 2 at E.
4. With E as the centre and 6cm as the radius. Draw an arc on the opposite side of the HE.
5. Draw an arc with O as the centre and 4cm as the radius, intersecting the arc generated in step IV at M.
6. Join HE, OE, EM and OM.
Hence, HOME is the required parallelogram.
196. Is it possible to construct a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 5.4 cm, DA = 5.9 cm and diagonal AC = 8 cm? If not, why?
Ans: No
Let’s first examine the triangle ABC
AB + BC = 7 cm But AC = 8 cm
The triangle ABC is not possible.
Thus, we can’t form the quadrilateral ABCD with the given conditions.
197. Is it possible to construct a quadrilateral ROAM in which RO=4 cm, OA = 5 cm, $\angle {\mathbf{O}} = {\mathbf{120}}^\circ $ , $\angle {\mathbf{R}} = {\mathbf{105}}^\circ $ and $\angle {\mathbf{A}} = {\mathbf{135}}^\circ $ ? If not, why?
Ans: No
It is impossible to draw a quadrilateral with the above conditions as
$\angle O + \angle R + \angle A = 120^\circ + 105^\circ + 135^\circ = 360^\circ $
Since the sum of three angles is 360° already which makes the fourth angle zero
Hence, this quadrilateral cannot be constructed.
198. Construct a square in which each diagonal is 5cm long.
Ans:
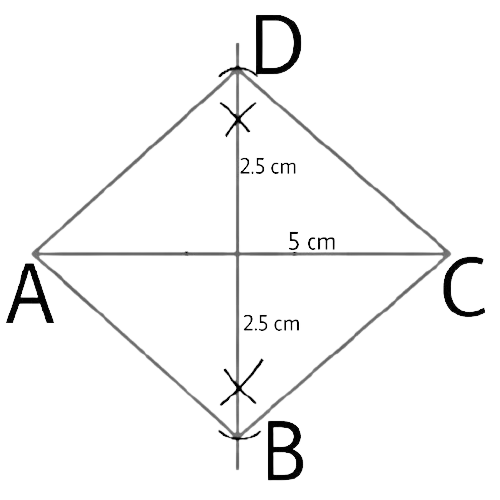
Steps of construction:
1. Draw line AC = 5 cm
2. Draw an arc greater than half of AC above and below the line segment AC with A as the centre.
3. Draw an arc of the same length as the second step above and below the line segment AC that intersects the arcs formed in step two, using C as the centre.
4. Now we will join both the intersection points obtained in step 3 by a line segment which intersects AC at O.
5. With O as centre cut-off point B and D such that OB = OD = 2.5 cm, along the bisector line.
6. Join AD, CD, AB and CB.
Thus, ABCD is the required square.
199. Construct a quadrilateral NEWS in which NE = 7cm, EW = 6 cm,\[\angle {\mathbf{N}} = {\mathbf{60}}^\circ \], \[\angle {\mathbf{E}} = {\mathbf{110}}^\circ \] and \[\angle {\mathbf{S}} = {\mathbf{85}}^\circ \].
Ans:
In order to solve this question, we need to find the angle $\angle W$.
The fourth angle \[ = 360^\circ - \left( {60^\circ + 110^\circ + 85^\circ } \right) = 360^\circ - 255^\circ = 105^\circ \]
$\angle W = 105^\circ $
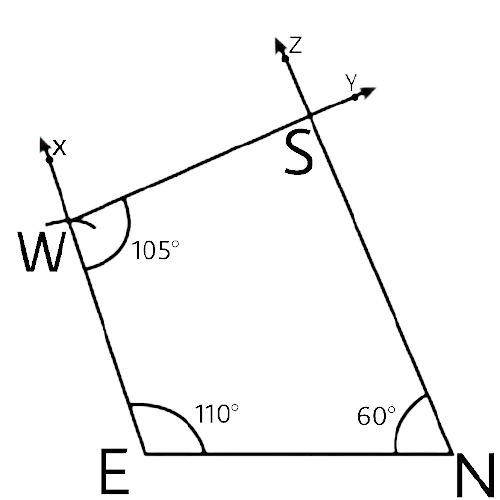
Steps of construction:
1. Draw line NE = 7 cm
2. Make the angle $\angle NEX = 110^\circ $
3. Draw an arc with E as the centre and a radius of 6 cm, cutting EX at W.
4. Now make the angle $\angle EWY = 105^\circ $
5. Make the angle $\angle ENZ = 60^\circ $ at point N, so that the lines NZ and WY both intersect at S.
Thus, NEWS is our required quadrilateral.
200. Construct a parallelogram when one of its sides is 4cm and its two diagonals are 5.6 cm and 7cm. Measure the other side.
Ans:
Steps of construction:
1. Draw the line AB = 4 cm
2. Draw an arc with A as the centre and a radius of 2.8 cm.
3. Draw another arc with B as the centre and a radius of 3.5cm, cutting the previous arc at O.
4. Join point O with A and B.
5. Produce AO to C in such a way that OC = AO and BO to D in such a way that OD = BD.
6. Now join AD, BC, and CD.
Thus, ABCD is the required parallelogram and the other side is 5cm.
201. Find the measure of each angle of a regular polygon of 20 sides?
Ans:
Sum of all the angle of an n-sided polygon $ = \left( {n - 2} \right) \times 180^\circ $
For n = 20
Each angle of the polygon $ = \dfrac{{\left( {20 - 2} \right) \times 180^\circ }}{{20}} = 162^\circ $
202. Construct a trapezium RISK in which RI||KS, RI = 7 cm, IS = 5 cm, RK=6.5 cm and \[\angle {\mathbf{I}} = {\mathbf{60}}^\circ \].
Ans:
In trapezium RISK sides RI || KS which mean angles $\angle I$ and $\angle S$ are supplementary, they add up to become 180°.
Now, $\angle S = 180^\circ - \angle I = 180^\circ - 60^\circ = 120^\circ $
Thus, we can now draw the trapezium.
Steps of construction:
1. Make an arc with RI = 7 cm.
2. Draw an angle $\angle RIX = 60^\circ $
3. Draw an arc with I as the centre and a radius of 5 cm, cutting IX at S.
4. Make another angle at S with $\angle ISY = 120^\circ $
5. Draw an arc cutting SY at K with R as the centre and a radius of 6.5 cm.
6. Join the points K and R.
Thus, the required trapezium is RISK.
203. Construct a trapezium ABCD where AB||CD, AD = BC = 3.2cm, AB = 6.4 cm and CD = 9.6 cm. Measure $\angle {\mathbf{B}}$ and $\angle {\mathbf{A}}$
(Hint: Difference between two parallel sides gives an equilateral triangle.)
Ans:
Now, if we subtract AB from CD, we get DE = 9.6 cm and EC = 3.2 cm
Since we are subtracting (just moving AB to DC) the line segment BC will be equal to AB.
From the figure given below we can make out visualization more clear.
Now since EC = BC = BE = 3.2 cm
Triangle ABC is an equilateral triangle.
Now BE || AD
Thus, $\angle ADE = \angle BEC = 60^\circ $ ….(corresponding angles)
Thus, we can now draw the trapezium
Thus, we have required trapezium ABCD in which
Steps of construction:
1. Draw a line segment with the length DC = 9.6 cm.
2. Draw a 60° angle with D at the centre. Cut it off with a 3.2 cm arc and name it point A.
3. Now draw a line AB parallel to CD.
4. On the previous drawn parallel line, cut an arc B measuring 3.2 cm with C at the centre.
5. Draw a line segment BE = 3.2 cm from the point B to the line CD. Connect the points B to E, and C.
Thus, we have required trapezium ABCD in which $\angle B = 120^\circ $and $\angle A = 120^\circ $.
NCERT Exemplar Class 8 Math Solutions: Highlights
The NCERT Exemplar Solutions have been considered as a comprehensive source of information for many years for the students. It helps them enhance their analytical abilities. These solutions are critical to understanding the coursework and building confidence to succeed in students’ assessments.
The NCERT Exemplar Solutions for Class 8 Math Chapter 5 explains the methods in detail, without leaving out any important components of solving a question. The solutions are written clearly and concisely.
In Addition to the Aforementioned, Here Are Some of the Most Important Highlights:
The NCERT Class 8 Math Solutions are available in a logical and organized manner.
The solutions are organized in a methodical chapter-by-chapter fashion, allowing students to make the most of their limited time.
The key topics have been analyzed rationally to ensure that they are easily absorbed by the learner.
The NCERT solution PDF has all of the NCERT questions and answers at one convenient location.
Free downloads make the PDF accessible to everyone.
Benefits for the Students of Class 8 - Math:
Students will learn how to construct geometric figures such as quadrilaterals and triangles.
Detailed explanations for every problem have been provided which will boost concept-based learning.
Easy usage of language to maximize retrieval of subject matter.
Additional practice questions will assist students in revising their learning repeatedly till they achieve perfection.
Because the solutions to each question are in accordance with the exam requirements, it will help students to gain an understanding of the actual exam format.
Note: For students preparing for the Class 8 Mathematics exam, the NCERT solutions might be extremely beneficial. By utilizing the Exemplar problems for Class 8, students can gain a better understanding of arithmetic Chapter 5 and easily enhance their scores.
FAQs on NCERT Exemplar Class 8 Math Solutions Chapter 5 Understanding Quadrilaterals & Practical Geometry
1. From which website I can download NCERT Class 8 Math Chapter-wise Solutions in PDF Format?
You can refer to Vedantu.com to download the NCERT Class 8 Math Solution Chapter-wise. These solutions have been created in the form of PDFs that correspond to each chapter and may be accessed fast and easily by simply clicking on the specified link(s) on the website.
2. What is the Purpose of NCERT Solutions PDF?
Learners have found NCERT Solutions PDF to be reliable and trustworthy. Students who want to increase their understanding of the subjects and their performance on tests should go through the PDF as often as possible. The PDF categorizes all of your textbook's issues chapter-by-chapter and subject-by-subject to save you time.
3. Can I get good grades if I study from the NCERT Solutions for Class 8 Math textbooks?
All of the exercises from the NCERT Exemplar Class 8 Maths Solutions have been thoroughly covered in Vedantu's solutions to the textbook.
By developing a habit of regular practice and with the help of these solutions, you will be well on your way to achieving a higher grade in your exams.
These solutions are also useful in the preparation of various competitive examinations apart from just Class 8.
4. What is it about Vedantu that attracts the majority of students studying for NCERT Exemplar Class 8 Math Solutions?
Below are the reasons, the majority of students pick Vedantu to refer for NCERT Exemplar Class 8 Math Solutions:
Vedantu has solutions for those who are studying in both English and Hindi.
Students can get the PDF files with the solutions easily from the website.
The content's creators are subject matter experts in their respective fields.
The language that has been used to write the content is really simple to comprehend.
Teachers can assist students anytime in resolving any questions or concerns they may have.
5. What methods should I use to study Math in Class 8?
To begin, you must start with the chapters that will receive the highest number of points in the examination. Then you must concentrate on mastering the fundamentals of each chapter's content. Getting a solid grasp on the fundamental concepts in each chapter is critical since it will aid you in your preparation for competitive exams such as the JEE and NEET.
















