NCERT Exemplar for Class 8 Maths Solutions Chapter 9 Comparing Quantities

(B) Solved Examples

In examples 1 to 4, there are four options out of which one is correct. Write the correct answer.

1. A shirt with marked price Rs 800 was sold at Rs 680. The rate of discount on the shirt is 

(a) 10%                     

(b) 15%                

(c) 20%             

(d) 10%  

Ans: Here, we have marked price (M.P) =   Rs 800

And Selling price (S.P) = Rs 680

Thus, discount $=M.P-S.P$

                            $=800-680$

                             $~=Rs~120$

Now, Rate of discount $=\frac{Discount}{M.P}\times 100$

                              $=\frac{120}{800}\times 100$

                              $=15\%$

Hence, option (b) is the correct answer.

2. If $\frac{7}{3}\%$ of a number is 42, then the number is 

(a) 9800            

(b) 8            

(c) 1800           

(d) 180

Ans: Let required number be $x.$

Now, according to question,

⇒ $\frac{7}{3}\%$ of $x$ = 42

⇒ $\frac{7}{3}~\times $ $x\times \frac{1}{100}$ = 42

⇒ $x$ = $\frac{42\times 100\times 3}{7}$

⇒ $x$ = $1800$

Hence, option (c) is the correct answer.

3. If the cost price of 10 shirts is equal to the selling price of 8 shirts, then which of the following is true for the transaction?

(a) Profit of 25%                                      

(b) Loss of 25%          

(c) Profit of 20%                                       

(d)    Loss of 20%      

Ans: Here, the cost price of 10 shirts is equal to the selling price of 8 shirts.

⇒ $10~CP=8~SP$

⇒ $~CP=\frac{8}{10}~SP$

⇒ $\frac{CP}{SP}=\frac{4}{5}~$

Here, SP > CP, thus there will be profit 

⇒ Profit % = $\frac{S.P-C.P}{C.P}\times 100\%$

                      = $\frac{S.P-\frac{4}{5}~S.P}{\frac{4}{5}~S.P}\times 100\%$

                      = $\frac{\frac{1}{5}~}{\frac{4}{5}~}\times 100\%$

                      = $\frac{1}{4}\times 100\%$

                      = $25\%$

Hence, option (a) is the correct answer.

4. Rs 1600 lent at a compound interest of 5 % per annum, compounded half yearly for one year will amount to: 

(a) Rs 1640                                                     

(b) Rs 1680

(c) Rs 1681                                                     

(d) Rs 1764

Ans: Here, Principle (P) = Rs 1600

⇒ rate of interest (R) = $\frac{5}{2}$ % and time (t) = 1 year. So, n = 2

Now, Amount (A) = $P{{\left( 1+\frac{R}{100} \right)}^{n}}$

                              = $1600{{\left( 1+\frac{5}{2\times 100} \right)}^{2}}$

                              = $1600{{\left( 1+\frac{1}{40} \right)}^{2}}$

                              = $1600{{\left( \frac{41}{40} \right)}^{2}}$

                              = $1600\times \frac{1681}{1600}$

                              = $Rs~1681$

Hence, option (c) is the correct answer.

In examples 5 to 7, fill in the blanks to make the statements true.

5. By selling 50 pens, a shopkeeper lost the amount equal to the selling price of 10 pens. His loss per cent is ………

Ans: let selling price of one pen is $Rs~x.$

So, total selling price (S.P) = Rs $50x$

And loss = Rs $10x$

Thus, total cost price (C.P) = S.P + loss

                                              = $50x$ + $10x$

                                              = $60x$ 

Now, % loss $=~\frac{loss}{CP}\times 100\%$

                      $=~\frac{10x}{60x}\times 100\%$

                      $=~\frac{1}{6}\times 100\%$

                      $=~\frac{50}{3}\%$

Hence, by selling 50 pens, a shopkeeper lost the amount equal to the selling price of 10 pens. His loss per cent is $\frac{50}{3}\%.$

6. The discount percent is calculated on the ……… price of an article.

Ans: As we know that the discount percent is calculated on the Marked price of an article.

7. Amna purchased a toy for Rs 660 including sales tax. If the rate of sales tax is 10 %, then the selling price of the toy is …….

Ans: Let the selling price of the toy be $Rs~x.$

And the rate of sales tax = 10 %

Now, according to question

⇒ $x+x\times 10\times \frac{1}{100}=660$

⇒ $x+\frac{x}{10}=660$

⇒ $\frac{11x}{10}=660$

⇒ $\frac{x}{10}=60$

⇒ $x=Rs~600$

Hence, Amna purchased a toy for Rs 660 including sales tax. If the rate of sales tax is 10 %, then the selling price of the toy is Rs 600.

In Examples 8 to 11, state whether the statements are true (T) or false (F).

8. When the interest is compounded half yearly, the number of conversion periods in a year is four.

Ans: As we know that when the interest is compounded half yearly, the number of conversion periods in a year is two.

Hence, the given statement is False.

9. Arnav buys a book costing Rs 600. If the rate of sales tax is 7 %, then the total amount payable by him is Rs 642.

Ans: Here, cost price = Rs 600 

And sales tax = $600\times 7\times \frac{1}{100}=Rs~42$

Thus, payable amount = C.P + sales tax

                                       = Rs 600 + Rs 42

                                       = Rs 642 

Hence, the given statement is True.

10. After allowing a discount of 15 % on the marked price of an article, it is sold for Rs 680. The marked price of the article is Rs 800.

Ans: let the marked price of article be Rs $x.$

Now, according to question

⇒ $x-15\%~of~x=680$

⇒ $x-~x\times 15\times \frac{1}{100}=680$

⇒ $x-~\frac{3x}{20}=680$

⇒ $~\frac{17x}{20}=680$

⇒ $~\frac{x}{20}=40$

⇒ $~x=Rs~800$

Hence, the given statement is True.

11. Overhead charges, if any, are sometimes included in the cost price.

Ans: As we know that the cost price is the total amount of money that it costs a manufacturer to produce a given article. It is the original cost of the product. It does not include any overhead charges.

Hence, the given statement is False.

12. A number is increased by 20% and then it is decreased by 20%. Find the net increase or decrease percent.

Ans: Let the required number be 100

Now, increase in the number = 20 % of 100 = $20\times 100\times \frac{1}{100}=20$

So, increased number = 100 + 20 = 120

Decrease in the number = 20 % of 120 = $20\times 120\times \frac{1}{100}=24$

So, decreased number = $120-24=96$

Net decrease = $100-96=4$

Thus, net decrease percent = $\frac{4}{100}\times 100\%=4\%$

Hence, the net decrease percent is 4. 

13. Vishakha offers a discount of 20 % on all the items at her shop and still makes a profit of 12 %. What is the cost price of an article marked at Rs 280?

Ans: Here, we have marked price (M.P) = Rs 280

And discount = 20% of Rs 280$~=20\times 280\times \frac{1}{100}=Rs~56$

So, selling price (S.P) = Rs $\left( 280-56 \right)=Rs~224$

Let the cost price (C.P) be Rs 100.

And profit = 12 % of 100 = $12\times 100\times \frac{1}{100}=Rs~12$

So, selling price (S.P) = Rs $\left( 100+12 \right)=Rs~112$

Thus, if the selling price is Rs 112, then cost price = Rs 100

If the selling price is Rs 224, cost price = Rs $\left( \frac{100}{112}\times 224 \right)=Rs~200$

Hence, the required cost price is Rs 200.

14. Find the compound interest on Rs 48,000 for one year at 8 % per annum when compounded half yearly.

Ans: Here, Principal (P) = Rs 48,000

⇒ Rate (R) $=\frac{8}{2}\%=4\%$ and time period (n) = 2

Now, $A=P{{\left( 1+\frac{R}{100} \right)}^{n}}$

⇒ $A=48,000{{\left( 1+\frac{4}{100} \right)}^{2}}$

⇒ $A=48,000{{\left( 1+\frac{1}{25} \right)}^{2}}$

⇒ $A=48,000{{\left( \frac{26}{25} \right)}^{2}}$

⇒ $A=48,000\times \frac{676}{625}$

⇒ $A=Rs~51,916.80~$

Thus, compound interest (C.I) $=A-P$

                                                           $=Rs~51,916.80~-Rs~48000$

                                                             $=Rs~3,916.80$

Hence, the required compound interest is $Rs~3,916.80.$

15. Lemons were bought at Rs 60 a dozen and sold at the rate of Rs 40 per 10. Find the gain or loss percent.

Ans: Here, C.P of 1 dozen lemons = Rs 60

$\therefore C.P$ of 1 lemon = Rs $\frac{60}{12}=Rs~5$

Thus, C.P of 10 lemons = Rs 50

And S.P of 10 lemons = Rs 40

Here, C.P > S.P, it means there will be loss.

Now, % loss $=\frac{C.P-S.P}{C.P}\times 100\%$

                      $=\frac{50-40}{50}\times 100\%$

                      $=\frac{10}{50}\times 100\%$

                      $=20\%$

Hence, the required loss percent is $20\%.$

Multiple Choice Questions 

1. Suppose for the principal P, rate R% and time T, the simple interest is S and compound interest is C. Consider the possibilities

(i) C>S

(ii) C = S

(iii) C <S Then,

(a) only (i) is correct (b) either (i) or (ii) is correct

(c) either (ii) or (iii) is correct (d) only (iii) is correct

Ans: (a) Let the principal (P) = Rs. 100

Rate of interest (R) = 100% and time period (T) = 2 yr

Then, simple interest = $\frac{Px~R~x~T}{100}$ = $\frac{100~x~10~x~2}{100}$ = Rs20

We know that ,

A = $~P~{{\left( 1+~\frac{R}{100} \right)}^{T}}^{{}}$

A = 100 x $\frac{11}{10}$ x $\frac{11}{10}$  = Rs 121

Compound Interest = A - P  = Rs121 - Rs100  = Rs21

so , C > S

Therefore , the correct option is (a).

2. Suppose a certain sum doubles in 2 yr at r% rate of simple interest per annum and R°/o rate of interest per annum compounded annually. Then,

(a) r < R 

(b) R < r

(c) R = r 

(d) Cannot be determined

Ans:  If the total amount received after 2 yr is the same for both simple interest and compound interest on the same principal, then the rate of simple interest is greater than the rate of compound interest.

Hence , R< r

Hence, option (b) is correct.

3. The compound interest on Rs. 50000 at 4% per annum for 2 yr compounded annually is

 (a) Rs. 4000 

 (b) Rs. 4080 

(c) Rs. 4280 

(d) Rs. 4050

Ans:  Principal (P) = Rs. 50000

Rate of interest (R%) = 4% per annum

Time period (T) = 2 yr 

We know that,

A = $P~{{\left( 1+~\frac{R}{100} \right)}^{T}}^{{}}$

    =$~50000~{{\left( 1+~\frac{4}{100} \right)}^{2}}^{{}}$

    = $~50000~{{\left( 1+~\frac{1}{25} \right)}^{2}}^{{}}$

    = $50000$ × $\frac{26}{25}$ × $\frac{26}{25}$  = Rs54080

Compound Interest (CI) = A - P = Rs 54080 - Rs 50000 = Rs 4080

Hence the correct option is (b)

4.If marked price of an article is Rs. 1200 and the discount is 12%, then the selling price of the article is 

(a)Rs. 1056 

(b) Rs. 1344 

(c) Rs. 1212 

(d)Rs.1188

Ans: Marked price of an article = Rs. 1200

 Discount % = 12%

Discount selling price  = Discount %  x marked price

= $\frac{12}{100}$x 1200=12 x 12 = Rs.144

Selling price = Marked price – Discount Selling price

 = Rs.11200 – Rs. 144 

= Rs.1056

Hence the correct option is (a).

5. If 90% of x is 315 km, then the value of x is

(a) 325 km

(b) 350 km

(c) 350 m

Ans: We have, 90% of x = 315 km

$\frac{90}{100}$ $\times $  x = 315

x = 315  $\times $ $\frac{10}{9}$

x = 350

Hence the correct option is (b)

6. To gain 25% after allowing a discount of 10%, the shopkeeper must mark the price of the article which cost him Rs. 360 as

(a) Rs. 500

(b) Rs. 450 

(c) Rs. 460

(d) Rs. 486

Ans: Let the marked price of the article be Rs.x.

Cost price of the article = Rs. 360

 According to the question,

x - x of 10% - $\frac{25~\times ~360~}{100}$ = 360

x - $\frac{x~}{10}$ - 90 = 360

$\frac{9x~}{10}$  = 450

x = $\frac{450~\times 10~~}{9}$

x = 500

So, the Market Price is Rs 500.

Hence the correct option is (a)

7. If a% is the discount percent on marked price x, then discount is

(a)$\frac{x~}{a}$

(b) $\frac{a~}{x}$

(c)$\frac{ax~}{100}$

(d)$\frac{100~}{xa}$

Ans: We know that discount can be calculated always on marked price, when discount percentage is given. 

Discount = Discount % on marked price = a% of x

Discount = $\frac{ax~}{100}$

Hence, option (c) is correct.

8. Ashima took a loan of Rs. 100000 at 12% per annum compounded half-yearly. She paid Rs. 112360. If (1.06)2 is equal to 1.1236, then the period for which she took the loan is

(a) 2 yr 

(b) 1 yr

(c) 6 months

(d) 1$\frac{1~}{2}$

Ans: Principal (P) = Rs.100000

Rate of interest (R%) = 12% per annum compounded half-yearly.

Let m be the time period 

Amount paid = Rs.112360

We know that,

Amount, when interest is compounded half - yearly 

i.e.  A = $~P~{{\left( 1+~\frac{R}{200} \right)}^{2n}}^{{}}$ , where n = time period 

 112360  =  100000$~P~{{\left( 1+~\frac{12}{200} \right)}^{2m}}^{{}}$

\[\Rightarrow \] ${{\left( \frac{53}{50} \right)}^{2m}}$ = $\frac{112360}{100000}$

\[\Rightarrow \] ${{\left( \frac{53}{50} \right)}^{2n}}$ = $\frac{2809}{2500}$

\[\Rightarrow \] ${{\left( \frac{53}{50} \right)}^{2}}$ = ${{\left( \frac{53}{50} \right)}^{2n}}$

On comparing both sides , we get 

 \[\Rightarrow \] 2n = 2

\[\Rightarrow \] n = 1

So the time period is 1yr

Hence option (b) is correct .

9. For calculation of interest compounded half-yearly, keeping the principal the same, which one of the following is true?

(a) Double the given annual rate and half the given number of years

(b) Double the given annual rate as well as the given number of years

(c) Half the given annual rate as well as the given number of years

(d) Half the given annual rate and double the given number of years

Ans: If interest is compounded half-yearly, then R becomes  $\frac{R}{2}$  and T becomes 2T and 2T  = 2n So, we have 

$~P~{{\left( 1+~\frac{R}{200} \right)}^{2n}}^{{}}$

C = A-P

So, half the given annual rate and double the given number of years. 

Hence, option (d) is correct.

10. Shyama purchases a scooter costing Rs. 36450 and the rate of sales tax is 9%, then the total amount paid by her is

(a) Rs. 36490.50 

(b) Rs. 39730.50

(c) Rs. 36454.50 

(d) Rs. 33169.50

Ans: We know that sales tax is charged on the sale of an item by the government and is added to the bill amount. 

Shyama purchase a scooter of costing = Rs. 36450 Sales tax paid =9%

So, total amount paid by her

= Rs. 36450 of 9% +  Rs. 36450

= $\frac{9}{100}$ × 36450 + 36450

= 9 ×  364.5 + 36450 = 3280.5 + 36450 = Rs. 39730.5

Hence, option (b) is correct.

11. The marked price of an article is Rs. 80 and it is sold at Rs. 76, then the discount rate is

(a) 5%

(b) 95%

(c) 10% 

(d) approx 11 %

Ans: The marked price of an article = Rs. 80 

Sold price of the article = Rs. 76

We know that,

Selling price = Marked price – Discount Discount 

\[\Rightarrow \] Marked price – Selling price

\[\Rightarrow \] Discount = Rs.80-Rs.76 = Rs.4

Discount % = $\frac{4}{80}$ × 100  = 5%

Hence, option (a) is correct.

12. A bought a tape recorder for Rs. 8000 and sold it to B. B in turn sold it to C, each earning a profit of 20%. Which of the following is true?

(a) A and B earn the same profit

(b) A earns more profit than B

(c) A earns less profit than < 5 

(d) Cannot be determined

Ans: Cost price of tape recorder for A = Rs.8000

Cost price of tape recorder for B =20% profit on cost price for A

= $\frac{20}{100}$ × 8000 + 8000

=20 × 80 + 8000

=1600 + 8000

=Rs.9600

Cost price of tape recorder for C=20% profit on cost price for B

= $\frac{20}{100}$ × 9600 + 9600

=1929 + 9600

=Rs.11520

Here, profit for A= Rs.1600

 Profit for B = Rs.1920

So, A earns less profit than B.

Hence, option (c) is correct.

13.Question. 13 Latika bought a teapot for Rs. 120 and a set of cups for Rs. 400. She sold teapots at a profit of 5% and cups at a loss of 5%. The amount received by her is

(a) Rs. 494

(b) Rs.7546

(c) Rs. 506 

(d) Rs. 534

Ans: Latika bought a teapot = Rs. 120 

Set of cups = Rs. 400 

She sold teapot at a profit of 5%,  

So, selling price of teapot =$\frac{5}{100}$ x 120 + 120

= $\frac{120}{20}$ +120

= 6 + 120 = Rs.126

 Also, she sold cups at a loss of 5%.

So, selling price of cups = 400 –$\frac{5}{100}$ x 400

= 400 – 20 = Rs. 380

Total amount received by her = Rs. 126 + Rs. 380 = Rs. 506

 Hence, option (c) is correct.

14. A jacket was sold for Rs. 1120 after allowing a discount of 20%. The marked price of the jacket is

(a) Rs. 1440

(b) Rs. 1400 

(c) Rs. 960

(d) Rs. 866.66

Ans: Let the marked price of the jacket be Rs. x.

Discount % on marked price = 20%

Selling Price of jacket  =  Rs1120

Then , 

1120 = x - x $\times \frac{20}{100}$

1120 = x - $\frac{x}{5}$

$\frac{4x}{5}$ = 1120

x = Rs1400

So, market price of the jacket is Rs1400

Hence , option (b) is correct .

15.A sum is taken for two years at 16% per annum. If interest is .compounded after every three months, the number of times for which interest is charged in 2 yrs is

(a) 8 

(b)4

(c) 6 

(d) 9

Ans: Here since the rate of interest is calculated after every three months. Similarly, the time period for the amount in a year will be 4 times.

If the amount is taken for 2 yr, it means 4×2 = 8 times charged in 2 yr.

Hence the correct option is (a)

16. The original price of a washing machine which was bought for Rs. 13500 including of 8% VAT, is

(a) Rs. 12420 

(b) Rs. 14580

 (c) Rs.12500

 (d) Rs. 13492

Ans: The price of the washing machine = Rs.13500

VAT [Value Added Tax] is included in the selling price, which is 8%.

The original price of the washing machine including of 8% VAT

= 13500 -13500 × $\frac{8}{100}$

= 13500-135 × 8 = 13500-1080= Rs.12420 

Hence, option (a) is correct.

17. Avinash bought an electric iron for Rs. 900 and sold it at a gain of 10%. He sold another electric iron at 5% loss which was bought

Rs. 1200. On the transaction, he has a

(a) profit of Rs. 75

(b) loss of Rs. 75

(c) profit of Rs. 30 

(d) loss of Rs. 30

Ans: Avinash bought an electric iron = Rs. 900 

He sold it, at 10% profit.

So, selling price of the electric iron = $\frac{10}{100}$× 900 + 900

= 90+ 900 = Rs. 990

He also sold another electric iron at a 5% loss.

Cost price of another electric iron = Rs.1200

So, selling price of the electric iron = 1200

$\frac{5}{100}$ × 1200

= 1200-60 = Rs.1140

Total amount paid by Avinash for purchasing electric irons = Rs. 900 + Rs.1200 = Rs.2100 

Total received amount = Rs. 990 + Rs. 1140

= Rs. 2130 

So, his profit = Rs.2130- Rs.2100 = Rs.30 in transaction.

Hence, option (c) is correct.

18. A TV set was bought for t 26250 including 5% VAT. The original price of the TV set is

(a) Rs. 27562.50 

(b) Rs. 25000

(c) Rs. 24937.50

(d) Rs. 26245

Ans: Cost price of TV set = Rs. 26250.

VAT including = 5%

Original price = Cost price of article including VAT = 26250 -  $\frac{5}{100}$ × 26250

= 26250-1312.5

= Rs. 24937.5

So, the original price of the TV set = Rs. 24937.5 

Hence, option (c) is correct.

19. 40% of [100 – 20% of 300] is equal to

(a) 20 

(b) 16

(c) 140

(d) 64

Ans: 40% of [100-20% of 300]

\[\Rightarrow \]$\frac{40}{100}\times $ [100 - $\frac{20}{100}\times $300]

\[\Rightarrow \]$\frac{40}{100}\times $[100-60]

\[\Rightarrow \]$\frac{40}{100}\times $40 

\[\Rightarrow \]16

Hence, option (c) is correct.

20. Radhika bought a car for Rs. 250000. Next year, its price decreased by 10% and further next year, it decreased by 12%. In the two years, overall decrease per cent in the price of the car is

(a) 3.2% 

(b) 22% 

(c) 20.8% 

(d) 8%

Ans:  Radhika bought a car for Rs. 250000.

Cost price of a car = Rs.250000

Its price decreased next year by 10%.

So, Price becomes = 250000 - $\frac{10}{100}\times $250000

                              = 250000 - 25000 

                              = Rs225000

Next year , Price decreases by 12%  , price becomes =  225000 - $\frac{10}{100}\times $225000

                                                                                     = 225000 - 27000 

                                                                                       =Rs198000

Overall decreased % in two years = $\frac{250000~-~1980000}{250000}$ $\times $ 100

                                                       = 20.8%

Hence the correct option is (c) 

Fill in the blanks 

21. ……………. is a reduction on the marked price of the article.

Ans: Discount is a reduction on the marked price of the article.

22. Increase of a number from 150 to 162 is equal to an increase of ………………..percent.

Ans: Initial number = 150

Final number = 162

Increased number = 162 -150 = 12

Percent of increased number = $\frac{12}{150}$ x 100 = 8%

Therefore , Increase of a number from 150 to 162 is equal to an increase of 8 percent.

23. 15% increase in price of an article, which is Rs. 1620, is the increase of ……………..?

Ans:  Let the price of the article be Rs. x.

It is given that after 15% increase in price , price became Rs1620

So,  x + $\frac{15}{100}$ $\times $ x = 1620

 x + $\frac{3}{20}$ $\times $ x = 1620

$\frac{23x}{20}$  = 1620 

x = Rs1408

Increase in price = Rs1620 - Rs1408 

                                         = Rs212

Therefore, 15% increase in price of an article, which is Rs. 1620, is the increase Rs212

24. Discount =…………….

Ans: Discount = Market Price (MP) – Selling Price (SP)

Here, MP = Marked price, and SP = Selling price

25.Discount = Discount % of ……………

Ans: Discount = Discount % of marked price

 Discount is referred to a reduction given on marked price

26. ………is charged on the sale of an item by the government and is added to the bill amount.

Ans: Sales tax is charged on the sale of an item by the government and is added to the bill amount.

Sales tax = Tax % of bill amount

27. Amount when interest is compounded annually, is given by the formula……………….

Ans:  Amount when interest is compounded annually, is given by the formula

            A = $~P~{{\left( 1+~\frac{R}{100} \right)}^{T}}^{{}}$

where, P = principal, R = rate per- annum and T = time

28. Sales tax = Tax% of……………….

Ans: Sales tax=Tax % of bill amount

29. The time period after which the interest is added each time to form a new principal, is called the ……………

Ans: The time period after which the interest is added each time to form a new principal, is called the conversion period.

30.……………… expenses are the additional expenses incurred by a buyer for an item over and above its cost of purchase.

Ans: Overhead expenses are the additional expenses incurred by a buyer for an item over and above its cost of purchase.

31. The discount on an item for sale is calculated on the ……………..

Ans: The discount on an item for sale is calculated on the marked price.

32. When principal P is compounded semi-annually at r% per annum for t years, then amount = ……………..

Ans: When principal P is compounded semi-annually at r% per annum for t years.

         i.e Rate = $\frac{r}{2}$ and Time = 2t

Then , Amount (A) =  $~Principal\left( P \right)~{{\left( 1+~\frac{Rate\left( r \right)}{200} \right)}^{2t\left( Time \right)}}^{{}}$

A = $~\left( P \right)~{{\left( 1+~\frac{\left( r \right)}{200} \right)}^{2t}}^{{}}$

33. Percentages are to fractions with ………………. equal to 100.

Ans: Percentages are equal to fractions with denominators  equal to 100.

34. The marked price of an article when it is sold for  880 after a discount of 12%, is ……………..

Ans:  Selling price of an article = Rs.880 

Discount % = 12%

We know that, discount is calculated on the marked price. 

Let the marked price be Rs. x.

x - $\frac{12}{100}$ $\times $  x = 880

$\frac{88x}{100}$ = 880

x = Rs1000

Marked Price =  Rs1000

Therefore , The marked price of an article when it is sold for  880 after a discount of 12%, is  Rs1000.

35. The compound interest on Rs. 8000 for one year at 16% per annum compounded half-yearly is …………… , given that  ${{1.08}^{2}}$ = 1.1664.

Ans: We have, 

Principal(P) = Rs.8000

Time period = 1 yr

Rate = 16% per annum compounded half-yearly

A = $~P~{{\left( 1+~\frac{R}{100} \right)}^{T}}^{{}}$

A $=~P~{{(1+~\frac{0.16}{2})}^{2}}$

A = 8000 $\times $ ${{1.08}^{2}}$ 

A = 8000$\times $ ${{1.08}^{2}}$ 

A = 8000 $\times $ 1.1664

A = Rs9331.2

Therefore, The compound interest on Rs. 8000 for one year at 16% per annum compounded half-yearly is  Rs9331.2

36. In the first year on an investment of Rs 6,00,000 the loss is 5% and in the second year the gain is 10%, the net result is _________.

Ans: Investment amount = Rs6,00,000 

Loss in first year = 5%

1st year Investment = 600000 - $\frac{5}{100}\times $600000

                                   =  Rs570000

Net Investment when gain is 10% =  570000 +$\frac{10}{100}$ x 570000= 570000 + 57000

                                                                   = Rs7627000

37. If amount on the principal of Rs 6,000 is written as 600($1+{{\frac{5}{100}}^{{}}}^{{}}{{)}^{3}}$  and compound interest payable half yearly, then rate of interest p.a. is _________ and time in years is _________.

Ans: Here  amount on the principal of  6000 is written as 600($1+{{\frac{5}{100}}^{{}}}^{{}}{{)}^{3}}$  

 of and compound interest payable half-yearly, then rate of interest per annum is 10% and time (in years) is 1$\frac{1}{2}$yr.

38. By selling an article for Rs 1,12,000 a girl gains 40%. The cost price of the article was _________. 

Ans: Selling Price of Article = Rs 1,12,000 

         Gain% = 40%

Let the cost price of an article be x 

x + 40% of x = Selling price of an article 

x + $\frac{40}{100}$x = 1,12,000

x + $\frac{2}{5}$x = 1,12,000

$\frac{7}{5}$x =  1,12,000

x = Rs 80,000

Therefore , By selling an article for Rs 1,12,000 a girl gains 40%. The cost price of the article was Rs 80,000

39.  The loss per cent on selling 140 geometry boxes at the loss of SP of 10 geometry boxes is equal to ………………..

Ans: Suppose, the selling price of 1 geometry box = 1.

Now, the selling price for 140 geometry boxes = 1 × 140 = Rs. 140 

Similarly, selling price of 10 geometry boxes = 1 × 10 = Rs. 10

Loss = selling price of 10 geometry boxes = Rs. 10 

So, loss percentage =  $\frac{Loss}{CP}$ x 100   

By using this formula,

Loss percentage = 6$\frac{2}{3}$% 

Hence, The loss per cent on selling 140 geometry boxes at the loss of SP of 10 geometry boxes is equal to 6$\frac{2}{3}$% 

40. The cost price of 10 tables is equal to the sale price of 5 tables. The profit per cent in this transaction is ……………..

Ans: Let the cost price of 1 table be Rs. 1.

The cost price of 10 tables = Sale price of 5 tables Profit 

= Cost price of 5 tables 

= Rs. 5

Profit percentage = $\frac{Profit}{CP}$ × 100   = $\frac{5}{5}$ × 100 = 100%

Hence, The cost price of 10 tables is equal to the sale price of 5 tables. The profit per cent in this transaction is 100%

41. Abida bought 100 pens at the rate of Rs. 3.50 per pen and paid a sales tax of 4%. The total amount paid by Abida is ___________

Ans: Number of pens bought by Abida = 100

Rate of per pen = Rs.3.50 So, cost of 100 pens = 100 x 3.50 = 135

Abida also paid 4% sales tax on Rs. 350.

Hence ,the total amount paid by Abida = 350 x $\frac{4}{100}$ + 350  =  Rs 364

Therefore, Abida bought 100 pens at the rate of Rs. 3.50 per pen and paid a sales tax of 4%. The total amount paid by Abida is  Rs 364

42. The cost of a tape recorder is Rs. 10800 inclusive of sales tax charged at 8%. The price of the tape recorder before sales tax was charged, is ……………….

Ans:  Suppose the price of the tape recorder before sales tax be Rs. x.

The cost of a tape recorder ,  inclusive of sales tax charged at 8%. = Rs. 10800 

According to the question 

x +  $\frac{8}{100}$  ×  $x$ =  10800

$\frac{108x}{100}~$ = 10800

x = Rs10,000

Hence, The cost of a tape recorder is Rs. 10800 inclusive of sales tax charged at 8%. The price of the tape recorder before sales tax was charged, is Rs10000

43. 2500 is greater than 500 by …………..%.

Ans: Difference between 2500 and 500 = 2500 – 500 = 2000

Greater % =     $\frac{Difference}{500}~$ × 100   =  $\frac{2000}{500}~$× 100  = 400%

Hence, 2500 is greater than 500 by 400%

44. Four times a number is a …………….% increase in the number.

Ans:  Let the number be x

Four times of x  = 4x.

Hence, 4x is greater than x by 4x – x = 3x

Percentage increase in x =  $\frac{3x}{x}$ x 100 = 300%

45. 5% sales tax is charged on an article marked X 200 after allowing a discount of 5%, then the amount payable is …………….

Ans: Given marked price of the article = 1200 Discount = 5%

Selling price = 200 – $\frac{5}{100}$ × 200 =200 -10 = Rs.190

Selling price (including 5% sales tax) = 190 + $\frac{5}{100}$ × 190= 190+ 9.5 = Rs.199.5

Amount to be paid = Rs. 199.50

Therefore, 5% sales tax is charged on an article marked X 200 after allowing a discount of 5%, then the amount payable is  Rs. 199.50

State whether the statements are true (T) or false (F).

46. To calculate the growth of bacteria if the rate of growth is known, the formula for calculation of amount in compound interest can be used.

Ans: For calculating the growth of a bacteria for the rate of growth is known, then formula for calculation of amount in compound interest.where, A = growth after n years, P = initial number of bacteria and R = rate of growth can be used .

Hence the given statement is true.

47.Additional expenses made after buying an article are included in the cost price and are known as Value Added Tax. 

Ans: The given statement is false. VAT is always included in the selling price. Therefore, Value Added Tax is always added to the selling price. 

48. Discount is a reduction given on the cost price of an article.

Ans: Discount is termed as the reduction given on market price of an article , so the statement is False .

49. Compound interest is the interest calculated on the previous year’s amount.

Ans: Compound interest is referred to as  the interest calculated on the previous year’s amount.

Hence the given statement is true.

50. C.P. = M.P. – Discount.

Ans: The given statement is False as 

Selling price = Market price – discount 

51. A man purchased a bicycle for Rs 1,040 and sold it for Rs 800. His gain percent is 30%.

Ans: Given, CP of  a bicycle = Rs. 1,040

SP of this bicycle = Rs. 800 

We know that, loss = cost price – selling price = 1040 = 800 = Rs. 240

Now we know that ,

Loss% =  $\frac{Loss}{CP}$ × 100  = $\frac{240}{1040}$ × 100  =  23.07%

Hence, the given statement is false. 

52. Three times a number is a 200% increase in the number, then one-third of the same number is a 200% decrease in the number.

Ans: Let us suppose  x be the number.

So, three times of x is given by  3x

Difference = 3x-x = 2x

Percentage increase in x = $\frac{2x}{x}$ x 100 = 200%

One third of x is given by  $\frac{x}{3}$

Difference = x - $\frac{x}{3}$

                  = $\frac{2x}{3}$

Decreased % is given by  = $\left( \frac{2x}{3}\div x \right)$ $\times $ 100

                                          = $\frac{2}{3}$×100

                                          = 66.66%

53.  Simple interest on a given amount is always less than or equal to the compound interest on the same amount for the same time period and at the same rate of interest per annum. 

Ans: The S.I. and C.I. For some amount the equal rate of interest is always equal for the first year.

The S.I. is less than the C.I. for an equal amount on the same rate of interest for the second year. 

Hence, the given statement is false.

54. The cost of a sewing machine is Rs. 7000. Its value depreciates at 8% per annum. Then, the value of the machine after 2 yr is Rs. 5924.80.

Ans: Given, Principal = Rs.7000

Depreciation Rate  = 3% per annum

Time period = 2 yr

According to the Question ,

A = $~P{{\left( 1-~\frac{R}{100} \right)}^{n}}$

A = $~7000{{\left( 1-~\frac{8}{100} \right)}^{2}}$

A = $7000\times \frac{23}{25}\times \frac{23}{25}$

A =  Rs5924.80

Hence the given statement is True.

55. If the discount of Rs. y is available on the marked price of Rs. x, then the discount percent is $\frac{x}{y}$ x 100%.

Ans: Given, 

Marked Price = Rs x

Discount available = Rs y

Discount%  =  $\frac{Discount~}{Marked~Price~}$ x 100  =  $\frac{y}{x}$ x 100%

Hence the given statement is False .

56.  Number of students appearing for class X CBSE examination increased from 91422 in 1999-2000 to 116054 in 2008-09. Increase in the number of students who appeared is approximately 27%.

Ans: Increase in students  from 2008-09 to 1999-2000

= 116054 – 91422 = 24632

%Increase in students =  $\frac{no~of~students~increase~}{no~of~students~in~previous~year}$ × 100

                                   =$\frac{24632~}{91422}$ ×100

                                   = 27%(approx)

Hence the given statement is True..

57. Selling price of 9 articles is equals to the cost price of 15 articles .In this transaction the profit of 66$\frac{2~}{3}$%

Ans:  SP of 9 articles =CP of 15 articles 

Here in transaction,   cost price of 6 articles is the profit 

Profit% = $\frac{6~}{9}$×100 =  $\frac{200~}{3}$ =  $66\frac{2~}{3}$%

Hence, the given statement is True.

58. The compound interest on a sum of Rs. P for T years at R% per annum compounded annually is given by the formula, $P~{{\left( 1+~\frac{R}{100} \right)}^{{}}}^{{}}$

Ans:  The Formula for compound interest on a sum of Rs. P for T years at 

R% per annum compounded annually is given by $P~{{\left( 1+~\frac{R}{100} \right)}^{T}}^{{}}$

Hence the given statement is False .

59. In the case of gain, SP= $\frac{\left( 100+gain \right)}{100}$

Ans: The statement given is true. 

We know that,

Gain is given by = Selling price - Cost price 

Therefore now gain % = $\frac{Gain~}{Cost~price~}\times 100$

Therefore Selling price = $\frac{100+Gain\%}{100}\times 100$

It should be noted that gain or the loss is always calculated based on the cost price. 

60.In the case of loss,  CP= $\frac{100\times SP}{100+Loss~}$

Ans: The statement is false.

Loss is given by = Cost price - Selling price.

Therefore Loss % = $\frac{Loss~}{Cost~price~}\times 100~$

Therefore , Cost price = $\frac{100}{100-Loss%~}\times Selling~price~$

61. The value of a car, bought for Rs. 440000 depreciates each year by 10% of its value at the beginning of that year. So, its value becomes Rs. 308000 after three years.

Ans: The above statement if false, 

The value of the car which is the principal= Rupees 440000 Rate of depreciation (R%) =10% per annum Time period (T) = 3 yr

The value of the car after depreciation in 3 years is given by 

A= P${{\left( 1-\frac{R}{100} \right)}^{T}}$

   =  440000${{\left( 1-\frac{10}{100} \right)}^{3}}$

  = 440 $\times 729=Rupees~~320760$

62. The cost of a book marked at Rs. 190 after paying a sales tax of 2% is Rs. 192.

Ans: The statement given is false. 

The marked price of the book = Rs.190

Sales tax = 2% 

The cost price of the book after 2% sales tax = 190 + $\frac{2}{10}\times 190$

                                                                           = 190+38 = rupees 193.8

63. The buying price of 5 kg of flour with the rate Rs. 20 per kg, when 5% sales tax is added on the purchase, is Rs. 21. 

Ans: The above statement is true. 

The total flour bought = 5 kg 

Rate of one kg flour = 5 kg

The cost of 5 kg flour with 5% sales tax = 5 \[\times 20+\frac{5}{10}\times \left ( 5\times 20 \right )\]    

                                                                        =  100\[+\frac{5}{10}\times \left ( 100 \right )\]  

                                                                        = 105 rupees. 

The per kg flour rate after 5% sales tax =\[\frac{105}{5}\] = Rupees 21

64. The original price of a shampoo bottle bought for Rs. 324, if 8% VAT is included in the price, is Rs. 300.

Ans: The above statement is false. 

The original price of a shampoo bottle = rupees 300 

The cost price of the shampoo bottle after 8% VAT 

= \[300+ \frac{8}{100}\times 300\]

= 300 + 24 = Rupees 324. 

65. Sales tax is always calculated on the cost price of an item and is added to the value of the bill.

Ans: The above statement is false as the sales tax is always calculated on the selling price of an item and is added to the value of the bill.

66. In a factory, women are 35% of all the workers, the rest of the workers being men. The number of men exceeds that of women by 252. Find the total number of workers in the factory.

Ans:

It is given that the percentage of women in the factory = 35%

The percentage of men in the factory = 100 -35 = 65%

Let the number of the  persons in the factory be x. 

Based on the question,

\[x\times \frac{65}{100}-x\times \frac{35}{100}\]=252

\[\Rightarrow \frac{65x-35x}{100}=252\]

\[\Rightarrow \frac{30x}{100}=252\]

\[\Rightarrow \frac{2520}{3}\]=840

So therefore the total number of workers in the factory. 

67. Three bags contain 64.2 kg of sugar. The second bag contains \[\frac{4}{5}\] of the contents of the first and the third contains 45 ½  % of what there is in the second bag. How much sugar is there in each bag?

Ans: From the question we can say that the total weight of sugar in three bags = 64.2 kg.

Now let us assume that the first bag contains x kg sugar. 

The second bag contains =\[x\times \frac{4}{5}=\frac{4x}{5}\] kg

The third bag contains =\[x\times \frac{4}{5}\times \frac{91}{2}%=\frac{4x}{5}=\frac{91x}{250}kg\]

As per the question, 

\[x\times \frac{4}{5}\times \frac{91}{2}% = 64.2\]

\[x\times \frac{4}{5}\times \frac{91}{2}% \]= 64.2

541x =  64.2\[\times 250\]

\[\Rightarrow x = \frac{16050}{541}=29.67 kg\]

\[\Rightarrow x=\frac{16050}{541}\]=29.67 kg

So now the first bag contains the sugar = 29.67\[\times \frac{4}{5}\]=23.73 kg and

The third bag contains the sugar = \[\frac{91}{250}\times 29.67=10.8\] kg

68. Find the SP, if

(a) MP = Rs. 5450 and discount = 5%

(b) MP = Rs.1300 and discount = 15%

Ans: 

(a) Here from the question Marked price = 5450 and the discount percentage is = 5% 

Therefore the selling price = Marked price - \[\frac { Discount % }{100}\times Marked price\]

\[1300-\frac{15}{100}\times 1300= 1300-19.5= Rupees 1280.5\]

69. Find the MP, if

(a) SP = Rs. 495 and discount = 1%

(b) SP = Rs. 9250 and discount = 7 ½ %

\[9250= x-\frac{15}{2\times 100}\times x\]

Ans: (a) Selling price (SP) = 7495 and discount % = 1% 

Now let the marked price be rupees x

Therefore selling price = \[ Marked price - \frac{Discount%}{100}\times MP\]

\[\Rightarrow 495= x-\frac{1}{100}\times x\], on solving we get  

 x = 500 

Hence the marked price = Rupees 500. 

(b) SP = Rs. 9250 and discount = 7 ½ %

The selling price (SP) = Rupees 9250

Discount % = 7 ½ % =\[\frac{15}{2}%\]

Let the marked price be rupees x.

Therefore the selling price =\[ Marked price - \frac{Discount%}{100}\times MP\] 

\[9250= x-\frac{15}{2\times 100}\times x\]

9250 =\[ \frac{185x}{200}\]

x= rupees 10000

Hence the marked price = rupees 10000

70. Find discount in percent when

(a) MP = Rs.625 and SP = Rs.562.50

(b) MP = Rs.900 and SP = Rs.873

Ans:

(a) MP = Rs.625 and SP = Rs.562.50

Since discount = marked price - selling price = 625-562.5 = rupees 62.5 

Therefore discount % = \[\frac{Discount}{Marked price}\times 100=\frac{62.5}{625}\times 100 = 10%\]

(b) MP = Rs.900 and SP = Rs.873

The mark price (MP) = Rupees 900

Selling price (SP) = 873

Therefore discount = marked price -selling price = 900-873= Rupees 27 

Therefore discount % = \[\frac{Discount}{Marked price}\times 100= \frac{27}{900}\times 100= 3%\]

71. The marked price of an article is Rs. 500. The shopkeeper gives a discount of 5% and still makes a profit of 25%. Find the cost price of the article.

Ans: It is given that the marked price of an article = Rs.500 Discount % = 5%

It is given that the profit made by the owner = 25%

So now let the cost price of the article be Rs. x 

The cost price after 5% discount = 500 - \[\frac{5}{100}\times 500\]

                                                          = 500 - 25 = Rupees 475.

As per the question, 

(100+25)% of x = 475 

So now after solving, x = Rupees 380.

Hence the cost price of the article is Rupees 380. 

72. In 2007-08, the number of students who appeared for Class X examination was 105332 and in 2008-09 the number was 116054. If 88151 students passed the examination in 2007-08 and 103804 students in 2008-09. What is the increase or decrease in pass percentage in class X result?

Ans: From the question the number of students who appeared in 2007-08 = 105332

 Number of students appeared in 2008-09 = 116054  

The number of students passed in 2007-08 = 88151

The number of students passed in 2008-09 = 103804

The pass percentage of students for the period of  2007-08

= \[\frac{\textrm{Number of student passed in 2007-08}}{Number of student appeared in 2008-09}\times 100\]

= \[\frac{88151}{105332}\times 100\]

= 83.68% 

The passed percentage of students in 2008-09

= \[\frac{\textrm{Number of student passed in 2008-09}}{Number of student appeared in 2008-09}\times 100\]

= \[\frac{103804}{116054}\times 100\]

= 89.44% 

Therefore the total increase in percentage would be = 89.44 - 83.68 = 5.76% 

73. A watch worth Rs. 5400 x is offered for sale at Rs. 4500. What percent discount is offered during the sale?

Ans: The marked price of the watch = Rs.5400

The selling price = Rs.4500

Discount = Marked price – Selling price = Rs.5400 – Rs.4500 = Rs.900

Therefore discount % = \[\frac{Discount}{Marked \: price}\times 100\]

=\[\frac{900}{54}=\frac{150}{9}=\frac{50}{3}%\]

74. In the year 2001, the number of malaria patients admitted in the hospitals of a state was 4375. Every year this number decreases by 8%. Find the number of-patients in 2003.

Solution. The number of malaria patients admitted in a hospital in 2001 = 4375 Rate of decrement of malaria patients = 8%

Time period = 2 yr i.e.2003-2001=2 yr

Let the number of patients in 2003 be A.

Ans: From the question we can say that the number of malaria patients which were admitted in a hospital in 2001 = 4375 

The rate of decrement of malaria patients = 8% 

Time period = 2 year which is between 2003 -2001

Let the number of patients in 2003 be A. 

Let us use the formula,

A=\[P\left ( 1-\frac{R}{100} \right )^{T}\]

=\[4375\left ( 1-\frac{8}{100} \right )^{2}\]

=\[4375\times \left ( \frac{23}{25} \right )^{2}\] 

=  3703 

Therefore the number of patients in 2003 was 3703. 

75. Jyotsana bought a product for Rs. 3155 including 4.5% sales tax. Find the price before tax was added.

Ans: From the question we can say that the product was bought by Jyotsana for Rs. 3155 including 4.5% sales tax.

Let the price of the product before sales tax be Rs. x . 

So now, \[x+x\times \frac{4.5}{100}= 3155\]

On solving we get x= Rs 3019.14 

76. An average Urban Indian uses about 150 L of water everyday.

(a) What percent of water is used for bathing and sanitation together per day?

Ans: From the given details, water used for bathing per day = 20 L

Water used for sanitation = 40 L

Total water used per day = 150 L

The percentage of water that is used for bathing and sanitation together per day

=\[ \frac{20+40}{150}\times 100= \frac{60}{150}\times 100\]

=\[\frac{60}{150}\]= 40% 

(b) How much less per cent of water is used for cooking in comparison to that used for bathing?

Ans: Water which is been used to cook per day = 4L 

Water which is been used for bathing per day = 20L

The total difference between the water used for cooking and bathing = 20-4 = 16 L 

Therefore 16L of water is less used for cooking in comparison to bathing. 

In percentage =\[\frac{16}{150}\times 100 = \frac{32}{3}%\]

(c) What percent of water- is used for drinking, cooking and gardening together?

Ans: The water which is been used for drinking per day = 3L 

Water used for cooking per day = 4L 

Water used for gardening per day = 23L 

Total water which has been used for drinking , cooking and gardening = 3+4+23 = 30L.

In percentage the value is =\[\frac{30}{150}\times 100 = 20%\]

77. In 1975, the consumption of water for human use was about 3850 cu km/yr. It increased to about 6000 cu km/yr in the year 2000.

Find the percent increase in the consumption of water from 1975 to 2000. Also, find the annual per cent increase in consumption

(assuming water consumption increases uniformly).

Ans: The consumption of water for human in 1975 = 3850 cu km/yr

The consumption of water for human in 2000 = 6000 cu km/yr

Increase in consumption of water in 1975 to 2000 = 6000 - 3850 =2150 cu km/yr

In percentage = \[\frac{2150}{3850}\times 100= 55.84%\]

In 25 years total increase in water consumption = 2150 cu km/yr 

Therefore per year annual consumption = \[\frac{2150}{50}\]= 86 cu km/yr 

Therefore now, consumption in percentage is given by = \[\frac{86}{3850}\times 100=\frac{8600}{3850}= 2.23%\]

78.Harshna gave her car for service at service station on 27-05-2009 and was charged as follows

(a)3.10 L engine oil @ Rs. 178.75 per liter and VAT @ 20%.

(b)Rs. 1105.12 for all other services and VAT @ 12.5%.

(c)Rs. 2095.80 as labor charges and service tax @ 10%.

(d)3% cess on service tax.

Find the bill amount.

Ans:

(a) The total liters of engine oil used = 3.10L 

Rate of engine oil per liters =Rs. 178.75

The cost of engine oil = 3.10 x 17875= Rs. 554.125

The cost of engine oil including 20% VAT = 554.125 + 554.125\[\times \frac{20}{100}\]

                                                                    =   554.125 +\[ \frac{554.125}{5}\]

                                                                    =  Rs. 664.95

(b) Amount paid for all the services = Rs. 1105.12 

Amount paid including 12.5% VAT = 1105.12 +\[\frac{12.5}{100}\times 1105.12\]

                                                          = Rs.1243.26 

(c) Labor charges = Rs. 2095.90 

Service tax = 10% 

The total labor charges including 10% service tax

= 2095.80+ \frac{10}{100}\times 2095.8 = 2095.80 + 209.58= Rs. 2305.38

(d) Cess on service tax at 3% = 209.58\[\times \frac{3}{100}=2.095\times 3\]

                                              =  Rs. 6.29

Thus the total bill amount = Rs. 664.95+ Rs.1243.26+ Rs.2305.38+Rs.6.29 = Rs. 4219.88

79. Given, the principal = Rs.40000, rate of interest = 8% per annum compounded annually. Find

(a) Interest if the period is one year.

(b) Principal for the 2nd year.

(c) Interest for 2nd year.

(d) Amount if the period is two year.

Ans: Given, principal (P)= Rs.40000

Rate of interest (R) = 8% per annum

a) Compound interest for one year,

A=\[P\left ( 1-\frac{R}{100} \right )^{n}\]

=\[40000\left ( 1+\frac{8}{100} \right )^{1}\]        \[[\because n = 1 \, year]\]

=\[40000\left ( \frac{108}{100} \right )

So, A= 400(108) = Rs. 43200 

Compound Interest, CI = A - P = 43200- 40000 = Rs. 3200

b) Amount of first year = Principal of second year = Rs. 43200

c) Now, For second year,

Principal = Rs. 43200

Rate of interest, R = 8% per annum

Time, n = 1 year

A=\[P\left ( 1-\frac{R}{100} \right )^{n}\]

=\[43200\left ( 1+\frac{8}{100} \right )^{1}\]         \[[\because n = 1 \, year]\]

=\[43200\left ( \frac{108}{100} \right )\]

So, A = 432(108) = Rs. 46656

Compound Interest, CI = A - P = 46656 - 43200 = Rs. 3456

d) For period of 2 years, Amount is A= Rs 46656

80. In Delhi University, in the year 2009-10, 49000 seats were available for admission to various courses at graduation level. Out of these 28200 seats were for the students of General Category while 7400 seats were reserved for SC and 3700 seats for ST. Find the percentage of seats available for

(a) students of General Category.

(b) students of SC Category and ST Category taken together.

Ans: The total number of seats which are available for admission in 2009-10 = 49000

Seats reserved for General Category students = 28200

Seats reserved for SC Category students = 7400

Seats reserved for ST Category students = 3700

(a) Percentage of seats for the students of General Category.=\[\frac{28200\times 100}{49000}\]= 57.55%

(b)The percentage of seats  students of SC Category and ST Category taken together.

Seats reserved for SC Category students = 7400

Seats reserved for ST Category students = 3700

Taken together = 7400+3700 = 11100

Therefore now the percentage of seats =\[\frac{11100}{49000}\]= 22.65%

81. Prachi bought medicines from a medical store as prescribed by her doctor for Rs 36.40 including 4% VAT. Find the price before VAT was added.

Ans: As per question,

We know that, Selling price = cost price +VAT

So, Cost price = 36.40-\[\frac{4}{100}\times\] 36.40

=36.40-4\[\times\] 0.364

= 36.40- 1.456= Rs. 35 (Approx)

82. Kritika ordered one pizza and one garlic bread from a pizza store and paid Rs 387 inclusive of taxes of Rs 43. Find the tax%.

Ans: From the question we can figure out that the cost of one pizza and a garlic bread inclusive of tax = Rs. 43 

Therefore the cost of one pizza and a garlic bread without adding any tax = 387 -43 = Rs.344

Therefore Tax % = 12.5% \[\frac{43}{344}\times 100=\frac{100}{8}= 12.5%\]

83. Arunima bought household items whose marked price and discount % is as follows

Find the total amount of the bill she has to pay.

Ans:

Based on the data given above in the table we can say that 

The rate of one packet of atta = Rs.200

Discount % = 16%

So now price= 200 - \[\frac{16}{100}\times 200\]= 200-32= Rs.168

The rate of one packet of detergent = Rs.371

Discount % =22.10%

So now the price = 371-371\[\times \frac{22.10}{100}\]= Rs.289.009

Rate of one packet of namkeen = 153 

Discount % = 18.30% 

So now, price = 153-153\[\times\frac{18.30}{100}\]=Rs.125.001

Therefore the total bill amount = 168+ 289.009+125.001 =Rs.582.01

84. Devangi’s phone subscription charges for the period 17-02-09 to 16-03-09 were as follows.

Find the final bill amount, if 3% education cess was also charged on service tax.

Ans:

From the data given above in the table we can say that,

The amount for period 17-02-09 to 23-02-09 = Rs 199.75

Therefore the amount with service tax 12% = 199.75 + \[\frac{12}{100}\times 199.75\] = Rs 233.72

Amount for period 24-02-09 to 16-03-09 = Rs 599.25

Amount with service tax at 10% = 599.25+599.25 \[\times \frac{10}{100}\] = Rs 659.175

The total bill amount = Rs . 223.72 +650.175 = Rs. 882.895

Total bill amount including education cess of 3% 

= 882.895+3% of 882.895 

= 882.895 + \[\frac{3}{100}\times 882.895\]

= Rs. 909.39.

85. If principal = Rs 100000, rate of interest = 10% compounded half-yearly. Find.

(a) Interest for 6 months. (b) Amount after 6 months.

(c) Interest for next 6 months, (d) Amount after one year.

Ans: From the question, Principal(P) = Rs. 100000

Rate of interest (R) = 10% compounded half yearly.

a)  Interest for 6 months.

Given, n = 6 months

We know that, CI = A - P

And where for six months amount, A=\[P\left ( 1-\frac{R}{100} \right )^{n}\]

A=\[P\left ( 1-\frac{R}{100} \right )^{n}\] = \[100000\left ( 1+\frac{10}{100} \right )^{1}\]         (As n=1, for 6 month)

A = Rs. 105000

Now CI =  A - P

CI = 105000 - 100000 = Rs.5000

(b)The amount after 6 months = Rs. 105000

(c) Interest for next 6 months.

Principal = Amount after 6 months 

Therefore principal(P) = Rs.105000

Rate of interest (R)= 10% 

A=\[P\left ( 1-\frac{R}{100} \right )^{n}\]

=\[100000\left ( 1+\frac{10}{100} \right )^{1}\] 

   =  Rs.110250.

Compound interest, CI =  A - P

CI = 110250 - 10500 = Rs. 5250

(d) Amount after one year = Rs. 110250. 

86. Babita bought 160 kg of mangoes at Rs 48 per kg. She sold 70% of the mangoes at Rs 70 per kg and the remaining mangoes at Rs 40 per kg. Find Babita’s gain or loss per cent on the whole deal.

Ans:

Babita bought 160 kg of mangoes = Rs. 48 per kg

So now the total amount she paid = \[48 \times 160 = Rs. 7680\]

She sold 70% of the mangoes at Rs.70 per kh.

Therefore the cost of 70% mangoes = \[160 \times \frac{70}{100}\times 70 = Rs. 7890\]

Remaining mangoes = (100-70)% = 30%

Cost remaining at Rs. 40 per kg =160\[\times \frac{30}{100}\times\] 40= Rs.1920

The total amount received after selling the mangoes = 7840+1920 = Rs. 9760

Therefore SP > CP, Hence there is a gain.

Gain = SP-CP = 9760 - 7680 =Rs,2080

Gain% = \[\frac{Gain}{CP}\times 100=\frac{2080}{7680}\times 100\]=27.08%

87. A shopkeeper was selling all his items at a 25% discount. During the off season, he offered a 30% discount over and above the existing discount. If Pragya bought a skirt which was marked for Rs 1200, how much did she pay for it?

Ans:

From the question we know that the marked price of the skirt = Rs. 1200

During normal season discount at 25% = \[\frac{25}{100}\times 1200\]= Rs. 300

The price of the skirt after discount = Rs. 1200-Rs 300= RS.900

During off season time the shopkeeper also offers discount at 30 % = \[\frac{30}{100}\times 900= Rs. 270\]

The price of the skirt after 30% discount = Rs. 900-270 = Rs.630. 

Therefore Pragya paid Rs.630 while purchasing the skirt. 

88. Ayesha announced a festival discount of 25% on all the items in her mobile phone shop. Ramandeep bought a mobile phone for himself. He got a discount ? 1960. What was the marked price of the mobile phone?

Ans:

Let us assume that the marked price of the mobile phone be Rs. x 

We know that the festival discount on the mobile phone = 25% 

The total discount which Ramandeep accepted = Rs. 1960

So according to the given data we can say that, 

1960 =\[ x\times \frac{25}{100}\]

So now, x = Rs.7840.

Hence the marked price of the mobile phone was Rs. 7840. 

89. Find the difference between compound interest and simple interest on Rs 45000 at 12% per annum for 5 yr.

Ans:

From the question we know that 

Principal (P) = Rs. 45000

Rate of interest (R) = 12% per annum 

Time period (T) = 5 years 

Simple Interest = \[\frac{PRT}{100}\]=\[\frac{4500\times 12\times 5}{100}\]= Rs. 27000

Compound interest is given by, 

CI = A - P 

Now , A=\[P\left ( 1-\frac{R}{100} \right )^{T}\]

A=\[4500\left ( 1-\frac{12}{100} \right )^{5}\]

On calculating we get Amount, A as Rs. 79200

Therefore now the Compound interest is given by, 

CI = 79200 - 45000

CI = Rs. 34200.

Therefore now the difference between SI and CI =  34200- 27000 = Rs. 7200. 

90. A new computer costs Rs 100000. The depredation of computers is very high as new models with better technological advantages are coming into the market. The depredation is as high as 50% every year. How much will the cost of the computer be after two years?

Ans: From the question, 

The cost of the new computer = Rs. 100000

The depreciation rate = 50% per annum 

Time period (T) = 2 years 

Now let the cost of the computer after 2 years be Rs. A 

A=\[P\left ( 1-\frac{R}{100} \right )^{T}\]

   =\[100000\left ( 1-\frac{50}{100} \right )^{2}\]

A = Rs. 25000

Therefore the cost of the computer after 2 years will be Rs. 25000.

91. The population of a town was decreasing every year due to migration, poverty and unemployment. The present population of the town is 6,31,680. Last year the migration was 4% and the year before last, it was 6%. What was the population two years ago? 

Ans: As per question,

Suppose, two years ago the population = P

We know that,

A=\[P\left ( 1-\frac{R}{100} \right )\left ( 1-\frac{R}{100} \right )\]

So,

\[\Rightarrow 631680=P\left ( 1-\frac{4}{100} \right )\left ( 1-\frac{6}{100} \right )\]

\Rightarrow 631680=P\left (\frac{24}{25}  \right )\left ( \frac{47}{50} \right )

\[\Rightarrow P=\frac{631680\times 25\times 50}{24\times 47}\]= 700000

92. Lemons were bought at Rs 48 per dozen and sold at the rate of Rs 40 per 10. Find the gain or loss per cent.

Ans: As per question,

Cost of one dozen lemons = Rs. 48

We know that, 1 dozen = 12 pieces.

So cost of 1 lemon = \[Rs.\frac{48}{12}\]= Rs.4

Also 10 lemons sold for Rs. 40. So, Selling price of one lemons = \[\frac{40}{10}\]= Rs.4

Now the cost price of one lemon = selling price of one lemon.

So zero profit and zero loss.

93. If the price of petrol, diesel and LPG is slashed as follows: 

Complete the above table.

Ans: From the above table,

For per liter petrol, old price = Rs. 45.62 and 

New price = Rs. 40.62

Decrement in price = Rs. 45.62 - Rs. 40.62 = Rs. 5

So, Decrease percentage =\[\frac{5}{45.62}\times 100\]=10.96%

For per liter diesel, old price = Rs. 32.86 and

New price = Rs. 30.86

Decrement in price = Rs. 32.86 - Rs. 30.86 = Rs. 2

So, Decrease percentage =\[\frac{2}{32.86}\times 100\]=6.09%

For LPG, old price = Rs. 304.70 and

New price = Rs. 279.70

Decrement in price = Rs. 304.70 - Rs. 279.70 = Rs. 25

So, Decrease percentage =\[\frac{25}{304.70}\times 100=8.20%\]

94. What is the percentage increase or decrease in the number of seats won by A, B, C and D in the general elections of 2009 as compared to the results of 2004?

Ans: For political party A,

Number of seats won in 2004 = 206

Number of seats won in 2009 = 145

Decreased number of seats won by the party A, = 206 - 145 = 61 seats

So, Decreased percentage =\[\frac{61}{206}\times 100\]=29.61%

 For political party B,

Number of seats won in 2004 = 116

Number of seats won in 2009 = 138

Increased number of seats won by the party B, = 138 - 116 = 22 seats

So, Increased percentage =\[\frac{22}{116}\times 100\] =18.96%

For political party C,

Number of seats won in 2004 = 4

Number of seats won in 2009 = 24

Increased number of seats won by the party C, = 24 - 4 = 20 seats

So, Increased percentage =\[\frac{20}{4}\times 100\]=500%

For political party D,

Number of seats won in 2004 = 11

Number of seats won in 2009 = 12

Increased number of seats won by the party D, = 12 - 11 = 1 seats

So, Increased percentage =\[\frac{1}{11}\times 100\]=9.09%

95. How many more percent seats were won by X as compared to Y in Assembly Election in the state based on the data given below.

Ans: As per question,

Net number of seats won by the party X = 158

Net number of seats won by the party Y = 105

So, the total number of seats in election = 294

And the % of seats won by party X =\[\frac{158}{294}\times 100=53.74%\]

And also, the % of seats won by party Y =\[\frac{105}{294}\times 100=35.71%\]

Now, the difference of percentage = 53.74%-35.71%=18.03%

Therefore, party X won 18.03% as compared to party Y.

96. Ashima sold two coolers for Rs 3,990 each. On selling one cooler she gained 5% and on selling the other she suffered a loss of 5%. Find her overall gain or loss % in the whole transaction.

Ans: SP of each cooler = Rs. 3990

Suppose, the CP of both coolers for Ashima = x

We know that, Profit = SP - CP

So,

\[\Rightarrow 3990 = x+x\times \frac{5}{100}\]

\[\Rightarrow 3990=\frac{21x}{20}\]

\[\Rightarrow x=\frac{3990\times 20}{21}\]= Rs. 3800

And also, on another transaction of other cooler she has a loss = 5%

So,

\[\Rightarrow 3990=x-x\times \frac{5}{100} \]

\[\Rightarrow 3990=\frac{19x}{20}\]

\[\Rightarrow \frac{3990\times 20}{19}\]= Rs 4200

Now, the net CP for Ashima = Rs.3800 + Rs.4200 = Rs.8000

Ashima sold both coolers = Rs.3990  \[\times \] 2 = Rs.7980

Here, CP > SP.

So, Ashima has loss her whole transaction.

Now, Loss = Rs.8000 - Rs.7980 = Rs.20

And, loss percentage =\[\frac{20}{8000}\times 100=\frac{1}{4}%=0.25%\]

97. A lady buys some pencils for Rs 3 and an equal number for Rs 6. She sells them for Rs 7. Find her gain or loss%.

Ans: As per question,

cost price of some pencils = Rs. 3

For other equal no. of pencils = Rs. 6

Net selling price = Rs.7

Suppose, the lady buys ‘n’ pencils for Rs = 3. (Type - 1 pencil)

CP for one such pencil = \[\frac{3}{n}\]

And for ‘n’ pencils of other type, she paid = Rs 6 (Type -2 pencil)

CP for one such pencil  = \[\frac{6}{n}\]

Net selling price of ‘2n’ pencils = Rs.7

Now, Calculation for type - 1

We know that, Gain = selling price - cost price

By using above formula,

Gain = \[\frac{7}{2n}-\frac{3}{n}\]

=\frac{7-6}{2n}=\frac{1}{2n}

Also, gain percentage =\[\frac{Gain}{CP}\times 100\]

=\[\frac{\frac{1}{2n}}{\frac{3}{n}}\times100=\frac{50}{3} %\]

Now, Calculation for type - 2

We know that, Loss = cost price - selling price 

By using above formula,

Loss = \[\frac{6}{n}-\frac{7}{2n}\]

=\[\frac{12-7}{2n}=\frac{5}{2n}\]

Also, loss percentage = \[\frac{loss}{CP}\times 100\]

=\[\frac{\frac{5}{2n}}{\frac{6}{n}}\times100=\frac{125}{3} %\]

Net loss percentage = \[\frac{125}{3}-\frac{50}{3}=\frac{75}{3}=25%\]

98. On selling a chair for Rs 736, a shopkeeper suffers a loss of 8%. At what price should he sell it so as to gain 8%?

Ans: Given, selling price of chair = Rs.736,

This led to a loss of 8%.

Suppose, the cost price of a chair = Rs. x

As per question,

Selling price = Cost price - loss

\[\Rightarrow 736=x-\left ( \frac{8}{100} \times x\right )\]

\[\Rightarrow 736=\frac{92x}{100}\]

\[\Rightarrow x=\frac{73600}{92}\]= Rs.800

To gain 8% profit the price should be,

=\[800+\left ( \frac{8}{100}\times 800 \right )\]=800+64=Rs.864

99. A dining table is purchased for Rs 3,200 and sold at a gain of 6%. If a customer pays sales tax at the rate of 5%. How much does the customer pay in all for the table?

Ans: As per question,

Selling price of the dining table = \[3200+\left ( \frac{6}{100} \times 3200\right )= Rs. 3392\]

Selling price with sales tax =\[3392+\left ( \frac{5}{100} \times 3392\right )\]= Rs. 3561.6

100. Achal bought a second-hand car for Rs 2,25,000 and spent Rs 25,000 for repairing. If he sold it for Rs 3,25,000, what is his profit percent?

Ans: As per question,

Achal cost for the car = Rs. 2,25,000 + Rs. 25,000

= Rs. 2,50,000

Achal sold his car = Rs. 3,25,000

Now, profit = Rs. 3,25,000 - Rs. 2,50,000 = 75,000

So, profit percentage =\[\frac{Profit}{CP}\times 100%\]

=\[\frac{75000}{250000}\times 100%\]

=30%

101. A lady bought an air-conditioner for Rs 15,200 and spent Rs 300 and Rs 500 on its transportation and repair respectively. At what price should she sell it to make a gain of 15%?

Ans: Actual cost price of air conditioner with transportation charge and repair charges = Rs. 15,200 + Rs. 300 + Rs. 500

= Rs. 15,500 + Rs. 500

= Rs. 16,000

For getting gain 15% she should sell it for Rs = \[16,000 + \frac{15}{100}\times 16,000\]

= 16,000 + 2,400 = Rs 184000

102. What price should a shopkeeper mark on an article that costs him Rs 600 to gain 20%, after allowing a discount of 10%.

Ans: Given, gain percentage = 20% and the CP of an article = Rs. 600

 Now, Gain =\[ \frac{600\times 20}{100} = Rs. 120\]

By using formula SP = Gain + CP

\[\Rightarrow SP = 10 + 600 = Rs. 720\]

Suppose, the MP = x

Since, he allows a 10% discount. So,

\[\Rightarrow x-\frac{10}{100}\times x = 720\]

\[\Rightarrow \frac{9x}{10} = 720\]

\[\Rightarrow x =\frac{7200}{9} = Rs. 800\]

103. Brinda purchased 18 coats at the rate of Rs 1,500 each and sold them at a profit of 6%. If a customer is to pay sales tax at the rate of 4%, how much will one coat cost to the customer and what will be the total profit earned by Brinda after selling all coats?

Ans: As per question,

Net cost of 18 coats = \[1500 \times 18 = Rs. 27000\]

The amount received by Brinda,

= \[27,000 + 27,000 \times \frac{6}{100} = Rs. 28,620\]

If customer pay sale tax = 4%

Now, CP with sale tax = 28,620 + \[\frac{4}{100}\times\] 28,620 = Rs 29764.80

CP for 1 coat for customer = \[\frac{29,764.80}{18} = Rs. 1653.60\]

Now, profit earned by Brinda,

= Rs. 28620 - Rs.27,000 = Rs. 1620

104. Rahim borrowed Rs 10,24,000 from a bank for one year. If the bank charges interest of 5% per annum, compounded half-yearly, what amount will he have to pay after the given time period. Also, find the interest paid by him.

Ans: As per question, 

Suppose, amount = A

We know that, in half yearly, \[ R = \frac{R}{2}\] and T = 2T

So, for compounded half-yearly,

\[A=P\left ( 1-\frac{R}{200} \right )^{2T} = 10,24,000\left ( 1 + \frac{5}{200} \right )^{2}\]

\[\Rightarrow A = Rs. 10,75,840\]

Also, CI = A - P

= Rs. 10,75,840 - Rs. 10, 24, 000

= Rs.51,840

105. The following items are purchased from showroom: 

T-Shirt worth Rs 1200. Jeans worth Rs 1000. 2 Skirts worth Rs 1350 each. 

What will these items cost to Shikha if the sales tax is 7%?

Ans: As per question,

Net cost = Rs. 1200 + Rs. 1000 + Rs. 1350 = Rs. 3550

Shikha have to pay sale tax = 7%

Now, the net amount to pay = 3550 + \[\frac{7}{100}\times 3550 = Rs. 3798.5\]

106. The food labels given below give information about 2 types of soup: cream of tomato and sweet corn. Use these labels to answer the given questions. (All the servings are based on a 2000 calorie diet.)

Sweet Corn  Nutrition Facts  Serving Size 1 cup (240ml)  About 2 serving per Container	Cream of Tomato Nutrition Facts Serving  Size 1 cup (240ml)  About 2 serving per Container
Amount Per Serving  Calories 90           Calories from Fat 9	Amount Per Serving  Calories 100       Calories from Fat 20
% Daily Value* Total Fat 2g                      -         2% Saturated Fat-0g             -         0% Cholesterol 0mg             -         0% Sodium 540mg                -         22% Total Carbohydrate 17g -         6% Dietary Fiber 3 gram      -         14% Sugar 5g  Protein 3g	% Daily Value*  Total Fat 2g                       -           3% Saturated Fat-1.5g           -          6% Cholesterol 10mg            -          3% Sodium 690 mg                -          29% Total Carbohydrate 17g  -          6% Dietary Fiber 4 gram       -          18% Sugar 11g Protein 2g
Vitamin A 30%          Vitamin C 10%	Vitamin A 20%          Vitamin C 20%
Calcium 2%                          Iron 6%	Calcium 0%                          Iron 8%
*Percent Daily Values are based on a 2,000 calorie diet.	*Percent Daily Values are based on a 2,000 calorie diet.

(a) Which can be measured more accurately : the total amount of fat in cream of tomato soup or the total amount of fat in sweet corn soup? Explain. 

(b) One serving of cream of tomato soup contains 29% of the recommended daily value of sodium for a 2000 calorie diet. What is the recommended daily value of sodium in milligrams? Express the answer upto 2 decimal places. 

(c) Find the increased percent of sugar consumed if cream of tomato soup is chosen over sweet corn soup. 

(d) Calculate ratio of calories from fat in sweet corn soup to the calories from fat in cream of tomato soup.

Ans: As per question,

a) Serving size of one cup of sweet corn = 240mL

Net fat = 2g on 2%

The total amount of fat in sweet corn soup, = \[\frac{2}{100}\times 240 = 4.8 g\]

Now, for one serving = \[\frac{4.8}{2}\] = 2.4 g

Given, serving cost of one cup of tomato cream, = \[\frac{3}{100} \times 240\] = 7.2 g

Now, for one serving = \[\frac{7.2}{2}\] = 3.6 g

b) According to the question,

29% of 2000 calories = 690 mg

c) The increase percent of sugar consumed = 11g - 5g = 6g

So, increased percentage = \[\frac{6}{5}\times 100 % = 120 %\]

d) fat in sweet corn soup in calories = 9

And fat in cream tomato soup in calories = 20

The ratio = \[\frac{9}{20}\]

107. Music CD originally priced at Rs 120 is on sale for 25% off. What is the S.P.? Sonia and Rahul have different ways of calculating the sale price for the items they bought. 

As you work on the next problem, try both of these methods to see which you prefer.

Ans: As per question,

Original price of CD = Rs. 120

25% discount on Rs. 120.

If the sale is applicable, Discount = \[ 120 \times \frac{25}{100} = Rs.30\]

So, selling price after discount = Rs. 120 - Rs. 30 = Rs. 90

108. Store A and Store B both charge Rs 750 for a video game. This week the video game is on sale for Rs 600 at Store B and for 25% off at Store A. At which store is the game less expensive?

Ans: As per question, 

20% discount at store A. So,

Selling price at store A =\[750-\frac{20}{100}\times 750\]

= 750 - 150

= Rs.600

Given, selling price at store B = Rs.600

So, both are equally expensive.

109. At a toy shop the price of all the toys is reduced to 66% of the original price. 

(a) What is the sale price of a toy that originally costs Rs 90? 

(b) How much money would you save on a toy costing Rs 90? 

Ans: As per question,

a) When price reduced to 66% of the original price, 

Then the price = 90-\[\frac{66}{100}\times 90\] = Rs. 30.6

b) Saved money = \[\frac{66}{100}\times 90\] = Rs. 59.4

110. A store is having a 25% discount sale. Sheela has a Rs 50 gift voucher and wants to use it to buy a board game marked for Rs 320. She is not sure how to calculate the concession she will get. The sales clerk has suggested two ways to calculate the amount payable. 

Method 1: Subtract Rs 50 from the price and take 25% off the resulting price.

Method 2: Take 25% off the original price and then subtract Rs 50. 

a. Do you think both the methods will give the same result? If not, predict which method will be beneficial for her. 

b. For each method, calculate the amount Sheela would have to pay. Show your work. 

c. Which method do you think stores actually use? Why?

Ans: As per question,

a) In method 1,

Rs. 320 - Rs. 50 = Rs. 270

25% discount on Rs. 270 = 270 - \[\frac{25}{100}\times 270\] = Rs.202.5

In method 2,

25% discount on Rs. 320 = 320 - \[\frac{25}{100}\times 320\] = Rs.240

Price = Rs. 240 - Rs. 50 = Rs. 190

So, method 2 is beneficial for her.

b) In method 1, Amount paid = Rs. 202.5

In method 2, Amount paid = Rs. 190

c)  Method 1. This method shows actual discount in loss.

111. Living on your own: Sanjay is looking for a one-bedroom apartment on rent. At Neelgiri apartments, rent for the first two months is 20% off. The one bedroom rate at Neelgiri is Rs 6,000 per month. At Savana apartments, the first month is 50% off. The one bedroom rate at Savana apartments is Rs 7000 per month. Which apartment will be cheaper for the first two months? By how much?

Ans: As per question,

Rent for first two months,

= \[2\times \left ( 6000-\frac{20}{100}\times 6000 \right ) = Rs.9600\]

By comparison of Savana apartment, it offers 50% off for her first month, where the rent for bedroom = Rs. 7000/ month

= 7000-\[\frac{50}{100}\times\] 7000 = Rs. 3500

So, the rent for two months in Savana apartment,

= 3500 + 7000 = Rs. 10500

Therefore, Neelgiri apartment will be cheaper by,

= Rs. 10500- Rs.9600 = Rs.900

112. For an amount, explain why, a 20% increase followed by a 20% decrease is less than the original amount.

Ans: Suppose, the original price = x

20% increase in original price =\[x+ \frac{20}{100}\times x = \frac{6x}{5}\]

Now, 20% decrease in \[\frac{6x}{5}= \frac{6x}{5}- \frac{20}{100}\times \frac{6x}{5}\]

= \[\frac{30x}{25}-\frac{6x}{25}= \frac{24x}{25}\]

So the decreased price is less than the original price because decrement is calculated on increased price and increment is calculated on original price. So Decrement is more than increment.

113. Sunscreens block harmful ultraviolet (UV) rays produced by the sun. Each sunscreen has a Sun Protection Factor (SPF) that tells you how many minutes you can stay in the sun before you receive one minute of burning UV rays. For example, if you apply sunscreen with SPF 15, you get 1 minute of UV rays for every 15 minutes you stay in the sun. 

1. A sunscreen with SPF 15 allows only \[\frac{1}{15}\] of the sun’s UV rays. What percent of UV rays does the sunscreen abort?

2. Suppose a sunscreen allows 25% of the sun’s UV rays. 

a. What fraction of UV rays does this sunscreen block? Give your answer in lowest terms. 

b. Use your answer from Part (a) to calculate this sunscreen’s SPF. Explain how you found your answer.

3. A label on a sunscreen with SPF 30 claims that the sunscreen blocks about 97% of harmful UV rays. Assuming the SPF factor is accurate, is this claim true? Explain.

Ans: i) According to the question, \[\frac{14}{15}\] of the sun’s UV rays aborted by sunscreen.

In percentage = \[\frac{\frac{14}{15}}{1}\times 100 =93.33%\]

ii) a) Lowest fraction of blocked UV rays,

= 100 -25 = 75% = \[\frac{75}{100} = \frac{3}{4}\]

b) Sunscreen allows 25% or \[\frac{3}{4}\] of UV rays. Means, it protects UV rays 

= \[1 - \frac{3}{4} = \frac{1}{4}\]

Therefore, its SPF = 4

iii) The given statement is false.

114. A real estate agent receives Rs 50,000 as commission, which is 4% of the selling price. At what price does the agent sell the property?

Ans: Let the selling price = Rs. x

According to question, 

4% of x is equal to Rs. 50,000.

\[\Rightarrow \frac{4}{100}\times x = 50,000\]

\[\Rightarrow x= 25 \times 50,000\]

\[\Rightarrow x= 12,50,000\]

115. With the decrease in prices of tea by 15% Tonu, the chaiwallah, was able to buy 2 kg more of tea with the same Rs 45 that he spent each month on buying tea leaves for his chai shop. What was the reduced price of tea? What was the original price of tea? 

Ans: As per question,

Suppose, purchased tea = y kg

Price of tea per kg = Rs. x

Discount 15% per kg,

=\[ x - \frac{15}{100}\times 100 = \frac{85x}{100}\]

A chaiwala can buy 2 kg extra with 15% of discount.

But without discount, xy = 45 .....(i)

And \[\left ( \frac{85x}{100} \right )\left ( y+2 \right )\] = 45………..(ii)

By solving equation (i) and (ii):

\[\Rightarrow \left ( \frac{85xy}{100} \right ) + \frac{85\times 2x}{100}= 45\]

\[\Rightarrow \frac{85\times 2x}{100}= 45- \left ( \frac{85\times45 }{100} \right )\]

\[\Rightarrow 170x = 4500 - (85\times 45)\]

\[\Rightarrow x = \frac{45\times 100-45\times 85}{100} = \frac{45\times 15}{170} = 3.97 per kg\]

so, the reduced price = \[\frac{85\times 3.97}{100} = 3.33 per kg\]

\[\Rightarrow 170x = 4500 - (85\times 45)\]

\[\Rightarrow x = \frac{45\times 100-45\times 85}{100} = \frac{45\times 15}{170} = 3.97 per kg\]

so, the reduced price = \[\frac{85\times 3.97}{100} = 3.33 per kg\]

116. 116 Below is the report card of Vidit Atrey. Vidit’s teacher left the last column blank. Vidit is not able to make out, in which subject he performed better and in which he needs improvement. Complete the table to help Vidit know his comparative performance.Assessment report for- 2009-21

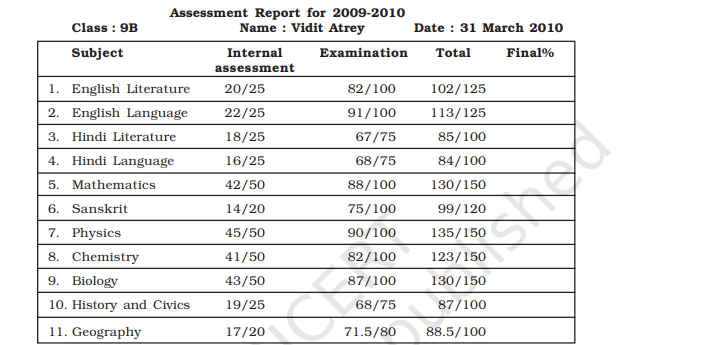
Ans:

From the data which has been given in the table , we can calculate the final percentage of each subject. 

1. English Literature = \[\frac{102}{125}\times 100=\frac{408}{5}= 81.6%\]

2. English language = \[\frac{113}{125}\times 100=\frac{452}{5}= 90.4%\]

3. Hindi literature = \[\frac{85}{100}\times 100 = 85%\]

4. Hindi literature = \[\frac{84}{100}\times 100 = 84%\]

5. Mathematics = \[\frac{130}{150}\times 100 = \frac{1300}{15} = 86.67%\]

6. Sanskrit = \[\frac{89}{100}\times 100 = \frac{890}{5} = 74.16%\]

7. Physics =  \[\frac{135}{150}\times 100 = \frac{1350}{15} = 90%\]

8. Chemistry =  \[\frac{123}{150}\times 100 = 82%\]

9. Biology = \[\frac{130}{150}\times 100 = \frac{1300}{15} = 86.66%\]

10. History and Civics = \[\frac{87}{100}\times 100 = 87%\]

11. Geography = \[\frac{88.5}{100}\times 100 = \frac{452}{5} = 88.5%\]

117.Sita’s practicing basketball. She has managed to score 32 baskets in 35 attempts. What is her success rate in percentage?

Ans:

It is said that Sita managed to score 32 baskets in 35 attempts. 

Now her success rate will be = \[\frac{32}{35}\times 100\]= 91.428%= 91.43%

118. During school hours, Neha finished 73% of her homework and Minakshi completed \[\frac{5}{8}\] of her homework. Who must finish a greater percent of 8 homework?

Ans:

It is given in the question that during school hours, Neha finished 73% of her homework and Minakshi completed 58% of her homework.

In percentage Neha finished her homework = 73%= \[\frac{73}{100}\]

Similarly Minakshi completed \[\frac{5}{8}\] of her homework. 

Homework left for Minakshi = 1- \[\frac{5}{8} = \frac{3}{8}\]

In percentage = \[\frac{3}{8}\times 100\] = 37.5 %

Homework left for Neha = (100-73) = 27% = \[\frac{27}{100}\]

Hence from the calculation we can say that Minashi finishes a greater percentage of homework compared to Neha.

119. Rain forests are home to 90000 of the 250000 identified plant species in the world. What percent of the world’s identified plant species are found in rainforests?

Ans:

It is given that rainforests are home to 90000 of the 250000 identified plant species in the world.

Percentage =\[\frac{90000}{250000}\times 100=\frac{900}{25}=36%\]

120. Madhu’s room measures 6m x 3m. Her carpet covers 8 m2. What percent of the floor is covered by the carpet?

Ans:

From the question we know that, 

Madhu’s room measures = 6m\times 3

Area of the room = 6\[\times 3\]=18\[m^{2}\](From area of the rectangle =\[1\times b\])

Madhu’s carpet covers = 8\[m^{2}\]

Therefore area covered by the carpet in percentage = \[\frac{8}{18}\times 100\]=44.44%

121. The human body is made up mostly of water. In fact about 67% of a person's total body weight is water. If Jyoti weighs 56 kg, how much of her weight is water?

Ans:

From the question we can say that 

Jyoti’s weight = 56 kg 

We know that 67% of a person total body weight is water

Water in Jyoti body =\[\frac{67}{100}\times 56\]=37.52Kg 

122. The percent of pure gold in 14 carat gold is about 58.3%. A 14 carat gold ring weighs 7.6 grams. How many grams of pure gold are in the ring?

Ans:

The percentage of gold in 14 carat gold = 58.3% 

Weight of 14 carat gold = 7.6 g 

Pure gold in 14 carat gold of 7.6 g = 76\[\times \frac{58.3}{100}=\frac{443.08}{100}=4.431g\]

Hence, pure gold in 7.6 g 0f 14 carat gold is equal to 4.431 g. 

123. A student used the proportion \[n^{100}=5^{32}\] to find 5% of 32. What did the student do wrong?

Ans: It is given in the question that the student used the proportion \[n^{100}=5^{32}\] to find 5% of 32 , which is an incorrect approach. 

5% of 32 will be calculated as = \[\frac{5}{100}\times 32=1.6\]

124. The table shows the cost of sunscreen of two brands with and without sales tax. Which brand has a greater sales tax rate? Give the sales tax rate of each brand?

		Cost in Rs	Cost + Tax in Rs
1	X (100 g)	70	75
2	Y (100 g)	62	65

Ans:

From the question we can say that, 

The brand X sunscreen cost = Rs. 70

With sales tax = Rs.75

Sales tax paid = Rs.75-Rs.70 = Rs.5 

The cost of Brand Y sunscreen = Rs. 62

Including sales tax = Rs.65

Sales tax for Y =  Rs.65 - Rs. 62 =Rs.3

Therefore brand X sales tax is more compared to brand Y.

Sales tax for brand X = \[\frac{5}{70}\times 100=7.14%\] 

Sales tax brand Y = \[\frac{3}{62}\times 100\]=4.84%

Comparing Quantities - Class 8 Science Chapter 9

Chapter Comparing Quantities is full of Mathematical calculations, whether it is to find the profits/losses, simple and compounding interest, discount,, or anything else. And by solving all the questions in this chapter, the students will be able to take their calculations skills to the next level.

 

This chapter is quite vast but the students should not are get discouraged by its size. The chapter includes 9 exercises and the students have to complete all these exercises, Students can find solutions to all the questions that appear in this chapter on Vednatu’s official website.

 

Moreover, this chapter 16 marks in the board exams, hence the students need to thoroughly prepare this chapter Comparing Quantities. This chapter is also important for students to get a basic understanding of the Profits/Loses and various types of Interest.

 

Most Important concepts

Let us look at some of the most important topics covered in this chapter of Class 8 Comparing Quantities.

 

Ratios and Percentage

The chapter makes the students engage with Ratios and percentages to compare the values of various problems, which have been discussed in the chapter. The first exercise of the chapter explains the concept of ratios and percentages in a very detailed manner.

 

Discounts

“Discounts” I strongly believe that you must have heard about this term at least once in your life. When you go shopping or orders things online, the term Discounts keeps coming quite often, The chapter Comparing Quantities talks about this term(Discounts) and teaches the student how to calculate discounts in different situations. 

 

Profits and Losses

In this chapter, The student comes across various new terms like selling prices, cost prices and overhead prices. Based on these new terms, students can determine the profits/losses in different circumstances. The students get to learn about the different formulas for finding profits and losses.