NCERT Exemplar for Class 9 Maths Chapter 8 - Quadrilaterals (Book Solutions)

Sample question 1: Diagonals of a parallelogram ABCD intersect at O. If \[\angle \mathbf{BOC}=\mathbf{90}{}^\text{o}\] and \[\angle \mathbf{BDC}=\mathbf{50}{}^\text{o}\] , then ∠OAB is 

(A) 90º 

(B) 50º 

(C) 40º 

(D) 10º

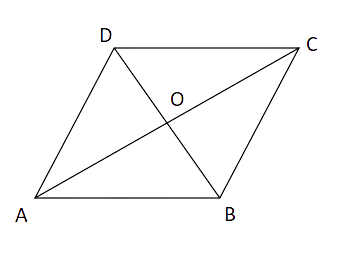
Ans: Option C is correct.

\[\angle BOC=90{}^\text{o}\]

\[\angle BOC+\angle COD=180{}^\text{o}\] (angles in a linear pair)

\[{{90}^{o}}+\angle COD=180{}^\text{o}\]

\[\angle COD=90{}^\text{o}\]

Also,

\[\angle BDC=50{}^\text{o}\] i.e. \[\angle ODC=50{}^\text{o}\]

Now, In $\Delta ODC$ ,

\[\angle ODC+\angle COD+\angle DCO={{180}^{o}}\]

\[{{50}^{o}}+{{90}^{o}}+\angle DCO={{180}^{o}}\]

\[\angle DCO={{40}^{o}}\]

DC || AB and AC is the transversal

$\therefore \angle DCA=\angle CAB$ (Alternate angles)

i.e. $\angle DCO=\angle OAB$

$\angle OAB={{40}^{o}}$

Exercise 8.1

1. Three angles of a quadrilateral are 75º, 90º and 75º. The fourth angle is 

(A) 90º 

(B) 95º 

(C) 105º 

(D) 120º 

Ans: The correct answer is option D.

The sum of all angles of a quadrilateral is 360º. The three angles are 75º, 90º and 75º. Let the fourth angle be xº. 

\[{{360}^{o}}=\left( {{75}^{o}}+{{90}^{o}}+{{75}^{o}}+{{x}^{o}} \right)\]

\[{{360}^{o}}=\left( {{240}^{o}}+{{x}^{o}} \right)\]

\[{{x}^{o}}={{360}^{o}}-{{240}^{o}}={{120}^{o}}\]

Thus, the fourth angle is 120º. 

2. A diagonal of a rectangle is inclined to one side of the rectangle at 25º. The acute angle between the diagonals is 

(A) 55º 

(B) 50º 

(C) 40º 

(D) 25º

Ans: Option B is correct.

Quadrilateral ABCD is a rectangle. The diagonals of a rectangle are equal and bisect each other. Diagonal AC is inclined to the side AB at an angle of 25º. 

Side AO = Side OB 

$\angle OAB=\angle OBA$

$\angle OAB=25{}^\text{o}$

$\angle OBA=~25{}^\text{o}$

In $\vartriangle OAB$,

$\angle OAB+\angle OBA+\angle AOB={{180}^{o}}$

$25{}^\text{o}+25{}^\text{o}+\angle AOB={{180}^{o}}$

$50{}^\text{o}+\angle AOB={{180}^{o}}$

$\angle AOB={{180}^{o}}-50{}^\text{o}=130{}^\text{o}$

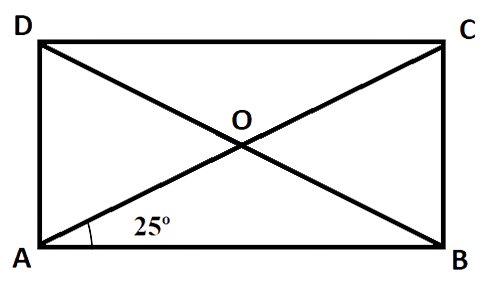
Now, $\angle AOB\text{ and }\angle BOC$ are angles in a linear pair.

$\Rightarrow \therefore \angle AOB+\angle BOC={{180}^{o}}$

$\Rightarrow {{130}^{o}}+\angle BOC={{180}^{o}}$

$\Rightarrow \angle BOC={{50}^{o}}$

Angle between the diagonals is 50º.

3. ABCD is a rhombus such that ∠ACB = 40º. Then ∠ADB is 

(A) 40º 

(B) 45º 

(C) 50º 

(D) 60º 

Ans: Option C is correct.

$\square ABCD$ is a rhombus and the diagonals of a rhombus are congruent and perpendicular bisectors of each other. 

$\therefore \angle BOC={{90}^{o}}$

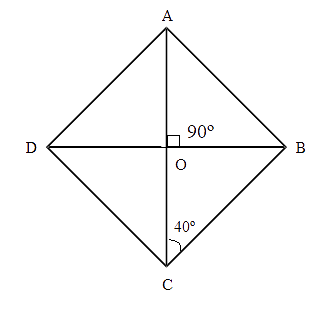
In $\vartriangle BOC$,

$\angle OBC+{{40}^{o}}+{{90}^{o}}={{180}^{o}}$

$\angle OBC+{{130}^{o}}={{180}^{o}}$

$\therefore \angle OBC={{50}^{o}}$

$\angle OBC\text{ and }\angle ADB$ are alternate interior angles. 

$\therefore \angle OBC=\angle ADB$

$\therefore \angle ADB={{50}^{o}}$

4. The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle, if 

(A) PQRS is a rectangle 

(B) PQRS is a parallelogram 

(C) diagonals of PQRS are perpendicular 

(D) diagonals of PQRS are equal. 

Ans: The correct answer is option C.

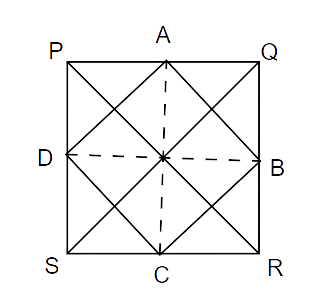
The rectangle ABCD is formed by joining the midpoints of quadrilateral PQRS. We know that the diagonals of a rectangle are equal. So, AC = BD. 

Similarly, PQ = QR.

Therefore, quadrilateral PQRS is a rhombus. In a rhombus, the diagonals are perpendicular. Hence, diagonals of PQRS are perpendicular.

5. The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rhombus, if 

(A) PQRS is a rhombus 

(B) PQRS is a parallelogram 

(C) diagonals of PQRS are perpendicular 

(D) diagonals of PQRS are equal.

Ans: The correct answer is option D.

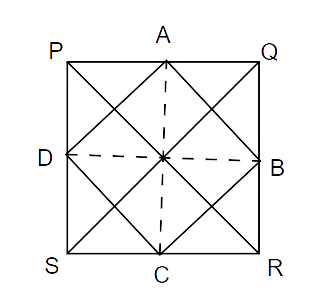
The rhombus ABCD is formed by joining the midpoints of quadrilateral PQRS. In a rhombus the diagonals are equal and bisect each other. So, in order for quadrilateral ABCD to be a rhombus the diagonals of quadrilateral PQRS should be equal.

6. If angles A, B, C and D of the quadrilateral ABCD, taken in order, are in the ratio 3:7:6:4, then ABCD is a

(A) rhombus 

(B) parallelogram 

(C) trapezium 

(D) kite

Ans: Option C is correct.

The angles A, B, C and D are in the ratio 3:7:6:4. 

Let x be the common multiple.

$\therefore 3x+7x+6x+4x={{360}^{o}}$

$\Rightarrow 20x={{360}^{o}}$

\[\Rightarrow x=\dfrac{{{360}^{o}}}{20}={{18}^{o}}\]

Thus, the angles are $\therefore 3x={{54}^{o}},7x={{126}^{o}},6x={{108}^{o}}\text{ and }4x={{72}^{o}}$

In a rhombus, parallelogram and kite the opposite angles are equal. So, the quadrilateral ABCD will be a trapezium.

7.If bisectors of \[\angle \mathbf{A}\] and \[\angle \mathbf{B}\] of a quadrilateral ABCD intersect each other at P, of \[\angle \mathbf{B}\] and \[\angle C\] at Q, of \[\angle C\] and \[\angle D\] at R and of \[\angle D\] and \[\angle \mathbf{A}\] at S, then PQRS is a 

(A) rectangle 

(B) rhombus 

(C) parallelogram 

(D) quadrilateral whose opposite angles are supplementary 

Ans: Option D is correct.

The required figure is as follows:

$\angle PQR=\angle BQC$ (Vertically opposite angles) ..(i)

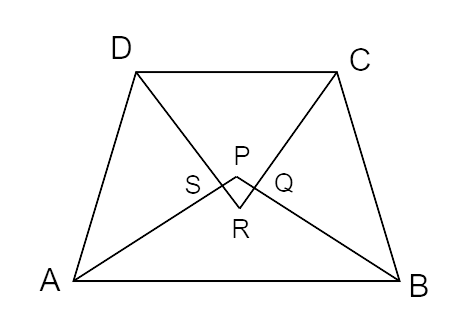
Now, In $\Delta BQC$

$\angle BQC+\angle QCB+\angle QBC={{180}^{o}}$

$\angle BQC+\dfrac{1}{2}\angle C+\dfrac{1}{2}\angle B={{180}^{o}}$ 

$\angle BQC={{180}^{o}}-\dfrac{1}{2}\left( \angle B+\angle C \right)$ ..(ii)

From (i) and (ii) we get,

$\angle PQR={{180}^{o}}-\dfrac{1}{2}\left( \angle B+\angle C \right)$ ..(iii)

Similarly, 

$\angle PSR={{180}^{o}}-\dfrac{1}{2}\left( \angle A+\angle D \right)$.. (iv)

By adding (iii) and (iv) we get,

$\angle PSR+\angle PQR={{180}^{o}}+{{180}^{o}}-\dfrac{1}{2}\left( \angle A+\angle B+\angle C+\angle D \right)$

$\angle PSR+\angle PQR={{360}^{o}}-\dfrac{1}{2}\left( {{360}^{o}} \right)$

\[\angle PSR+\angle PQR={{360}^{o}}-{{180}^{o}}\]

\[\angle PSR+\angle PQR={{180}^{o}}\]

Therefore, the opposite angles in quadrilateral PQRS are supplementary.

8. If APB and CQD are two parallel lines, then the bisectors of the angles APQ, BPQ, CQP and PQD form 

(A) a square 

(B) a rhombus 

(C) a rectangle 

(D) any other parallelogram 

Ans: Option C is correct.

The required figure is as follows:

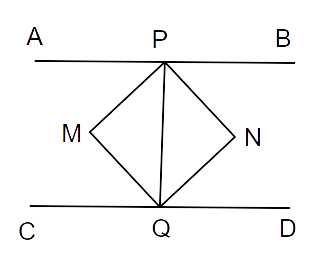
Lines APB and CQD are parallel.

$\therefore \angle APQ=\angle PQD$ ..(alternate interior angles)

Here, MP and NQ are the angle bisectors of $\angle APQ$ and $\angle PQD$

$\angle APQ=2\angle NQP$

Dividing both the sides by 2 we get,

$\angle MPQ=\angle NQP$

But these are alternate angles. So, MP || QN.

Similarly,

$\angle BPQ=\angle CQP$

So, PN || QM.

Thus, quadrilateral PNQM is a parallelogram.

As, CQD is a line. 

$\therefore \angle CQD={{180}^{o}}$

$\angle CQP+\angle PQD={{180}^{o}}$

MQ and NQ are the bisectors of $\angle CQP$ and $\angle PQD$

$2\angle MPQ+2\angle NQP={{180}^{o}}$

$2\left( \angle MPQ+\angle NQP \right)={{180}^{o}}$

$\angle MQN={{90}^{o}}$

Therefore, quadrilateral PNQM is a rectangle.

9. The figure obtained by joining the mid-points of the sides of a rhombus, taken in order, is

(A) a rhombus 

(B) a rectangle 

(C) a square 

(D) any parallelogram 

Ans: Option B is correct.

The required figure is as follows:

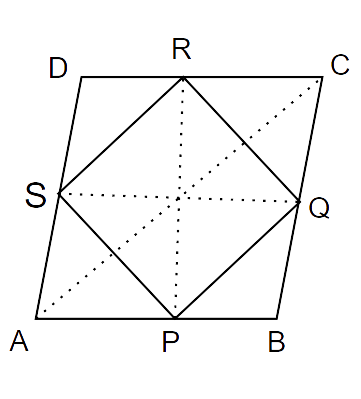
In \[\Delta ABC\] ,

P and Q are the midpoints of AB and BC respectively.

By Midpoint theorem,

PQ || AC and $PQ=\dfrac{1}{2}AC$ ..(i)

Similarly,

In \[\Delta ADC\] ,

S and R are the midpoints of AD and DC respectively.

By Midpoint theorem,

AC || SR and $SR=\dfrac{1}{2}AC$ ..(ii)

From (i) and (ii) we get,

PQ || SR and PQ = SR

Thus, quadrilateral PQRS is a parallelogram.

Now, 

ASQB is a parallelogram. So, AB = SQ. 

Also,

PRCB is a parallelogram. So, BC = PR.

But, BC = AB (Sides of a rhombus are equal)

AB = PR

So, SQ = PR.

A parallelogram with equal diagonals is a rectangle.

Therefore, the figure obtained by joining the mid-points of the sides of a rhombus will be a rectangle. 

10. D and E are the mid-points of the sides AB and AC of ABC and O is any point on side BC. O is joined to A. If P and Q are the mid-points of OB and OC respectively, then DEQP is 

(A) a square 

(B) a rectangle 

(C) a rhombus 

(D) a parallelogram 

Ans: Option D is correct.

The required figure is as follows:

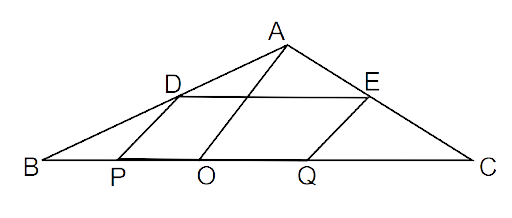
Since the line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is half of it.

So, DE || BC i.e. DE || PQ ..(i)

Now, In $\Delta AOB $ ,

Points D and P are the midpoints of AB and BO respectively.

Thus, DP || AO ..(ii)

Similarly,

In $\Delta AOC$ ,

Points E and Q are the midpoints of AC and CO respectively.

Thus, EQ || AO ..(iii)

From (ii) and (iii)

DP || EQ ..(iv)

From (i) and (iv)

DE || PQ and DP || EQ (opposite sides of quadrilateral DEQP)

This quadrilateral DEQP is a parallelogram.

11. The figure formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a square only if, 

(A) ABCD is a rhombus 

(B) diagonals of ABCD are equal 

(C) diagonals of ABCD are equal and perpendicular 

(D) diagonals of ABCD are perpendicular

Ans: Option C is correct.

The required figure is as follows:

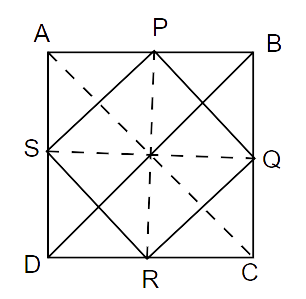
Given: In quadrilateral ABCD,

P, Q, R and S are the mid-points of sides AB, BC, CD and AD respectively.

Thus, PQRS is a square.

So, PQ = RQ = RS = SP ..(i)

And PR = SQ 

But, SQ = AB and PR = BC 

Thus, AB = BC

Hence, all the sides of quadrilateral ABCD are equal. 

So, the quadrilateral ABCD can either be a rhombus or a square. 

In $\Delta ABC$ , 

By mid-point theorem,

PQ || AC so, $PQ=\dfrac{1}{2}AC$ .. (ii)

Similarly, In $\Delta ADB$

By mid-point theorem,

SP || DB so, $SP=\dfrac{1}{2}DB$ ..(iii)

But PQ = SP ..(from i)

From (ii) and (iii),

$\dfrac{1}{2}DB=\dfrac{1}{2}AC$

$\therefore DB=AC$

Here the diagonals of quadrilateral ABCD are equal. So, quadrilateral ABCD is a square. 

In a square the diagonals are equal and perpendicular.

12. The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC = 32º and ∠AOB = 70º, then ∠DBC is equal to 

(A) 24º 

(B) 86º 

(C) 38º 

(D) 32º

Ans: Option C is correct.

Given: \[\angle DAC=32{}^\text{o}\]

\[\angle AOB=70{}^\text{o}\]

AD is parallel to BC and AC is the transversal.

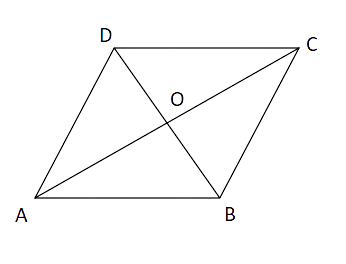
\[\angle DAC=\angle ACB\] (alternate interior angles)

\[\therefore \angle ACB={{32}^{o}}\] i.e. \[\therefore \angle OCB={{32}^{o}}\]

In $\Delta BOC$ ,

$\angle BOA$ is an exterior angle.

So, by exterior angle property,

$\Rightarrow \angle BOA=\angle OCB+\angle OBC$

$\Rightarrow {{70}^{o}}=\angle OBC+{{32}^{o}}$

$\Rightarrow \angle OBC={{38}^{o}}$

Thus, $\angle DBC={{38}^{o}}$

13. Which of the following is not true for a parallelogram? 

(A) opposite sides are equal 

(B) opposite angles are equal 

(C) opposite angles are bisected by the diagonals 

(D) diagonals bisect each other. 

Ans: Option C is correct.

In a parallelogram opposite sides and angles are equal. The diagonals bisect each other. Thus, opposite angles bisected by the diagonals is not true. 

14. D and E are the mid-points of the sides AB and AC respectively of ABC. DE is produced to F. To prove that CF is equal and parallel to DA, we need an additional information which is 

(A) \[\angle \mathbf{DAE}=\angle \mathbf{EFC}\]

(B) AE = EF 

(C) DE = EF 

(D) \[\angle \mathbf{ADE}=\angle \mathbf{ECF}\]

Ans: Option C is correct.

The required figure is as follows:

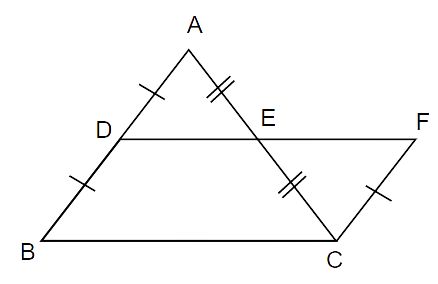
Given: AD = DB and AE = EC

CF is parallel to AD and D is the midpoint of AB

Thus, AD = DB = FC 

Now, In $\Delta AED$ and $\Delta EFC$ ,

(i) AD = FC ..(given)

(ii) $\angle AED=\angle FEC$ (vertically opposite angles)

(iii) AE = CE ..(E is the midpoint of AC)

Thus, by SAS test

$\Delta AED\cong \Delta EFC$ 

DE = EF (C.P.C.T)

$\angle DAE=\angle ECF$ (these are alternate angles formed by lines AD and CF and AC is the transversal)

Thus, AD || CF 

The additional information we need is DE = EF. 

Short Answer Questions with Reasoning

Sample Question 1: ABCD is a parallelogram. If its diagonals are equal, then find the value of \[\angle ABC\]. 

Ans: A parallelogram with equal diagonals is a rectangle. So, ABCD is a rectangle. Hence, \[\angle ABC=90{}^\text{o}\] .

Sample Question 2: Diagonals of a rhombus are equal and perpendicular to each other. Is this statement true? Give reason for your answer. 

Ans: The given statement is false. It is because in a rhombus the diagonals are perpendicular bisectors of each other but they are not equal.

Sample Question 3: Three angles of a quadrilateral ABCD are equal. Is it a parallelogram? Why or why not? 

Ans: The quadrilateral ABCD will not be a parallelogram if the three equal angles are acute angles. Because then the fourth angle will be greater than the three angles.

Sample Question 4: Diagonals AC and BD of a quadrilateral ABCD intersect each other at O such that OA: OC = 3: 2. Is ABCD a parallelogram? Why or why not? 

Ans: Diagonals of a parallelogram are perpendicular bisectors of each other. But, here the ratio of OA to OC is not equal. Hence, quadrilateral ABCD is not a parallelogram.

Exercise 8.2

1. Diagonals AC and BD of a parallelogram ABCD intersect each other at O. If OA = 3 cm and OD = 2 cm, determine the lengths of AC and BD.

Ans: The diagonals of a parallelogram bisect each other. 

$AC=2OA$ and $BD=2OD$ .

$\therefore AC=2\times 3cm=6cm$ and $BD=2\times 2cm=4cm$

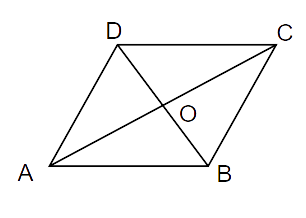
2. Diagonals of a parallelogram are perpendicular to each other. Is this statement true? Give reason for your answer. 

Ans: The given statement is false. The diagonals of a parallelogram bisect each other but not at 90º. 

3. Can the angles \[{{110}^{o}},80{}^\text{o},70{}^\text{o}\text{ and }95{}^\text{o}\] be the angles of a quadrilateral? Why or why not?

Ans: The sum of all angles of a quadrilateral is 360º. 

The sum of the given four angles = \[{{110}^{o}}+80{}^\text{o}+70{}^\text{o}+95{}^\text{o}=355\text{ }{}^\text{o}\]

Therefore, the angles \[{{110}^{o}},80{}^\text{o},70{}^\text{o}\text{ and }95{}^\text{o}\] cannot be the angles of a quadrilateral.

4. In quadrilateral ABCD, \[\angle \mathbf{A}+\angle \mathbf{D}=\mathbf{180}{}^\text{o}\] . What special name can be given to this quadrilateral? 

Ans: In \[\square ABCD\] , \[\angle A+\angle D=180{}^\text{o}\] which is the sum of two consecutive angles. This means the opposite sides are parallel and the \[\square ABCD\] is a trapezium.

Hence, the special name of the quadrilateral ABCD is trapezium.

5. All the angles of a quadrilateral are equal. What special name is given to this quadrilateral? 

Ans: A quadrilateral's angles are all equal. A quadrilateral's sum of angles is also 360º. As a result, each quadrilateral angle is 90º. As a result, the quadrilateral in question is a rectangle. As a result, the special term for a quadrilateral is rectangle.

6. Diagonals of a rectangle are equal and perpendicular. Is this statement true? Give reason for your answer. 

Ans: In a rectangle the diagonals are equal but not perpendicular bisectors of each other. Hence, the given statement is false. 

7. Can all the four angles of a quadrilateral be obtuse angles? Give reason for your answer.

Ans: No, since the quadrilateral's total of four angles will be more than 360º, but the sum of four angles of a quadrilateral is always 360º.

8. In $\Delta ABC$ , AB = 5 cm, BC = 8 cm and CA= 7 cm. If D and E are respectively the midpoints of AB and BC, determine the length of DE.

Ans: Given:

In $\Delta ABC$ ,

AB = 5 cm

BC = 8 cm

AC= 7 cm

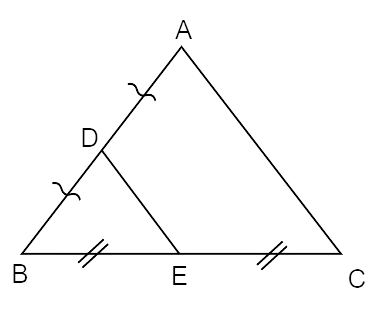
Thus, Using the midpoint theorem,

DE is half of AC.

$\therefore DE=\dfrac{1}{2}\times AC$

$\Rightarrow DE=\dfrac{1}{2}AC=\dfrac{1}{2}\times 7=3.5cm$

Therefore, DE = 3.5 cm.

9. In Fig.8.1, it is given that BDEF and FDCE are parallelograms. Can you say that BD = CD? Why or why not? 

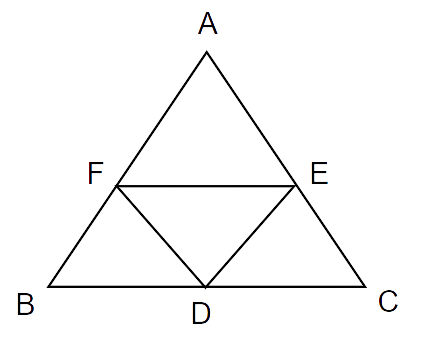
Ans: Here we have two parallelograms, BDEF and DFEC.

We know that opposite sides of a parallelogram are equal.

In parallelogram BDEF,

BD = FE ..(i)

Similarly, 

In parallelogram DFEC

CD = FE ..(ii)

From (i) and (ii),

BD = CD

10. In Fig.8.2, ABCD and AEFG are two parallelograms. If \[\angle C=55{}^\text{o}\] , determine \[\angle \mathbf{F}\] . 

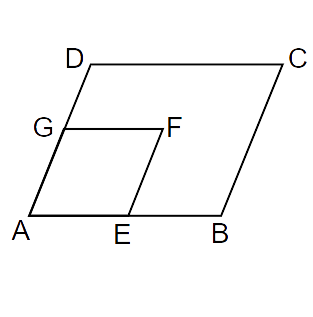
Ans: In parallelogram ABCD,

\[\angle C=55{}^\text{o}\]

Opposite angles of a parallelogram are equal.

$\therefore \angle A=\angle C$

\[\angle A=55{}^\text{o}\]

Now, In parallelogram AEFG,

$\angle A=\angle F$

\[\therefore \angle F=55{}^\text{o}\]

11. Can all the angles of a quadrilateral be acute angles? Give reason for your answer. 

Ans: An acute angle measures less than 90º. if all the angles of the quadrilateral will be acute then the total sum of the angles will be less than 360º. Therefore, all the angles of a quadrilateral cannot be acute.

12. Can all the angles of a quadrilateral be right angles? Give reason for your answer. 

Ans: Yes, a quadrilateral's angles can all be right angles. The total of the angles of a quadrilateral will equal 360º.

13. Diagonals of a quadrilateral ABCD bisect each other. If \[\angle \mathbf{A}=\mathbf{35}{}^\text{o}\] ,determine \[\angle \mathbf{B}\] . 

Ans: In quadrilateral ABCD the diagonals bisect each other. Thus, the given quadrilateral ABCD is a parallelogram.

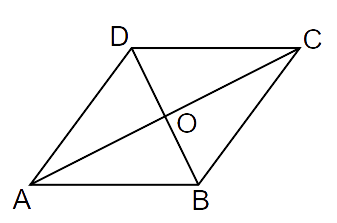
In a parallelogram the adjacent angles are supplementary.

\[\angle A=35{}^\text{o}\]

$\therefore \angle A+\angle B={{180}^{o}}$

$\therefore {{35}^{o}}+\angle B={{180}^{o}}$

$\angle B={{145}^{o}}$

14. Opposite angles of a quadrilateral ABCD are equal. If AB = 4 cm, determine CD. 

Ans: If the opposite angles of quadrilateral ABCD are equal then the given quadrilateral ABCD is a parallelogram.

In a parallelogram opposite sides are equal.

AB and CD are opposite sides of the quadrilateral ABCD.

AB = CD

Therefore, CD = 4cm

(D) Short Answer Questions

Sample Question 1: Angles of a quadrilateral are in the ratio 3: 4: 4: 7. Find all the angles of the quadrilateral. 

Ans: The angles of a quadrilateral are in the ratio 3: 4: 4: 7.

Let x be the common multiple. So, the angles will be 3x, 4x, 4x and 7x.

The sum of all angles of a quadrilateral is 360º.

\[~\therefore 3x+4x+4x+7x=360{}^\text{o}\]

$\Rightarrow 18x={{360}^{o}}$

$\Rightarrow x={{20}^{o}}$

The angles are,

$3x=3\times {{20}^{o}}={{60}^{o}}$

$4x=4\times {{20}^{o}}={{80}^{o}}$

$7x=7\times {{20}^{o}}={{140}^{o}}$

So the angles of the quadrilateral are 60º, 80º, 80º and 140º.

Sample Question 2: In Fig.8.3, X and Y are respectively the mid-points of the opposite sides AD and BC of a parallelogram ABCD. Also, BX and DY intersect AC at P and Q, respectively. Show that AP = PQ = QC. 

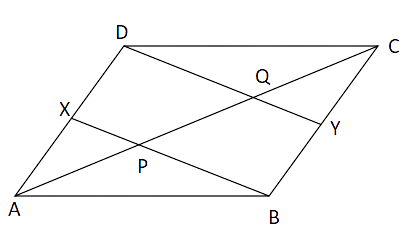
Ans: Y is the midpoint of BC and X is the midpoint of AD.

ABCD is a parallelogram.

So, AD = BC

$\therefore \dfrac{1}{2}AD=\dfrac{1}{2}BC$

DX = BY

$\therefore $ DX || BY (since AD || BC)

Thus, XDYB is a parallelogram

$\therefore $ XP || QD 

In $\Delta AQD$ , X is the midpoint of AD

$\therefore $ AP = PQ  (i)

Also, in $\Delta CPB$ ,

CQ = PQ (ii)

From (i) and (ii)

AP = PQ = QC. 

Sample Question 3: In Fig.8.4, AX and CY are respectively the bisectors of the opposite angles A and C of a parallelogram ABCD. Show that AX || CY.

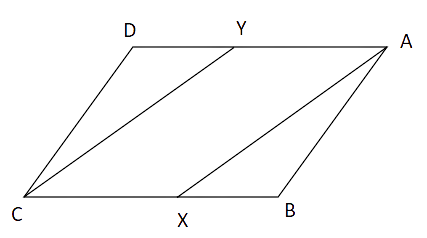
Ans: ABCD is a parallelogram.

$\therefore \angle A=\angle C$

$\dfrac{1}{2}\angle A=\dfrac{1}{2}\angle C$

(AX and CY )are the bisectors of $\angle A$ and $\angle C$  )

\[\angle YAX=\angle YCX\] (i)

Now, YA || CX

\[\angle AYC+\angle YCX=180{}^\text{o}\] (Corresponding angles are supplementary)

\[\angle AYC+\angle YAX=180{}^\text{o}\] (from i)

We know that,

Interior angles of the same side of the transversal are supplementary.

Therefore, AX || CY

Exercise 8.3

1. One angle of a quadrilateral is of \[{{108}^{o}}\] and the remaining three angles are equal. Find each of the three equal angles.

Ans: The sum of all angles of a quadrilateral is \[{{360}^{o}}\]. One angle is \[{{108}^{o}}\]. 

Let the other three angles be x.

$\therefore {{108}^{o}}+x+x+x={{360}^{0}}$

${{108}^{o}}+3x={{360}^{0}}$

$3x={{252}^{0}}$

$x=\dfrac{{{252}^{0}}}{3}={{84}^{o}}$

Each of the three angles will be of \[{84}^{o}\] each.

2. ABCD is a trapezium in which AB || DC and \[\angle \mathbf{A}=\angle \mathbf{B}=\mathbf{4}{{\mathbf{5}}^{\mathbf{o}}}\] . Find angles C and D of the trapezium.

Ans: Quadrilateral ABCD is a trapezium. 

$\angle A\text{ and }\angle \text{D}$ and $\angle B\text{ and }\angle C$ are the angles present on the same side of the trapezium.

Angles on the same side of the trapezium are supplementary.

$\therefore {{45}^{o}}+\angle \text{D=18}{{\text{0}}^{0}}$

$\therefore \angle \text{D=18}{{\text{0}}^{0}}-{{45}^{o}}={{135}^{o}}$

Similarly, 

$\therefore \angle C={{135}^{o}}$

Therefore, \[\angle A=\angle B={{45}^{o}}\] and $\angle D\text{ and }\angle C={{135}^{o}}$

3. The angle between two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 60º. Find the angles of the parallelogram.

Ans: Given: DP and DQ are the perpendicular to side AB and BC respectively. 

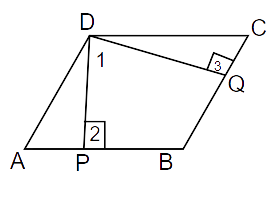
In quadrilateral DPBQ,

$\angle DPB=DQB={{90}^{o}}$

$\angle PDQ={{60}^{o}}$

$\therefore \angle DPB+DQB+\angle PDQ+\angle PBQ={{360}^{o}}$

${{90}^{o}}+{{90}^{o}}+{{60}^{o}}+\angle PBQ={{360}^{o}}$

$\angle PBQ={{360}^{o}}-{{240}^{o}}={{120}^{o}}$

$\therefore \angle PBQ=\angle ABC={{120}^{o}}$

$\therefore \angle ADC=\angle ABC={{120}^{o}}$ (Opposite angles of parallelogram are equal)

Now,

Adjacent angles of parallelogram are supplementary.

$\therefore \angle DAB+\angle ABC={{180}^{o}}$

$\therefore {{120}^{o}}+\angle DAB={{180}^{o}}$

\[\therefore \angle DAB={{180}^{o}}-{{120}^{o}}={{60}^{o}}\]

\[\therefore \angle DAB\text{ and }\angle DCB={{60}^{o}}\](Opposite angles of parallelogram are equal)

4. ABCD is a rhombus in which altitude from D to side AB bisects AB. Find the angles of the rhombus.

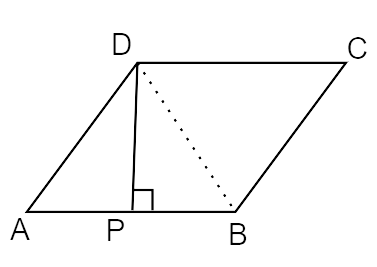
Ans: According to the question,

DP is perpendicular to side AB and AP = PB

Now,

In $\Delta APD\text{ and }\Delta \text{BPD}$ ,

$\angle DPA=\angle DPB={{90}^{o}}$

AP = PB (given)

DP = PD (common side)

$\therefore \Delta APB\cong \Delta \text{BPD}$ (SAS test)

$\therefore \angle DAB=\angle DBA$  (CPCT) ..(i)

Also, diagonals of a rhombus bisect the angles.

$\therefore \angle DBC=\angle DBA$ ..(ii)

From (i) and (ii)

$\therefore \angle DBC=\angle DBA=\angle DAB={{x}^{o}}$

Sum of adjacent angles in a rhombus is supplementary.

$\therefore \angle DAB+\angle ABC={{180}^{o}}$

$\therefore \angle DAB+\left( \angle DBC+\angle DBA \right)={{180}^{o}}$

$\therefore 3x={{180}^{o}}$

$x=\dfrac{{{180}^{o}}}{3}={{60}^{o}}$

$\therefore \angle DBC=\angle DBA=\angle DAB={{60}^{o}}$

$\angle ABC=\left( \angle DBC+\angle DBA \right)=\left( {{60}^{o}}+{{60}^{o}} \right)={{120}^{o}}$

Opposite angles of a rhombus are congruent.

$\therefore \angle DCB=\angle DAB={{60}^{o}}$

$\angle ABC=\angle ADC={{120}^{o}}$

5. E and F are points on diagonal AC of a parallelogram ABCD such that AE = CF. Show that BFDE is a parallelogram.

Ans: Given: Quadrilateral ABCD is a parallelogram. 

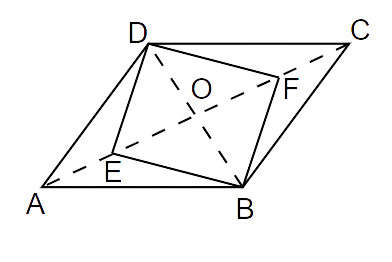
Diagonals of a parallelogram bisect each other.

$\therefore $ AO = OC and DO = OB

According to the diagram, A - E – O – F - C

AE + OE = CF + OF

Also, AE = CF (given)

$\therefore $ EO = OF

And OD = OB

Hence, BEDF is a parallelogram.

6. E is the mid-point of the side AD of the trapezium ABCD with AB || DC. A line through E drawn parallel to AB intersects BC at F. Show that F is the mid-point of BC. [Hint: Join AC]

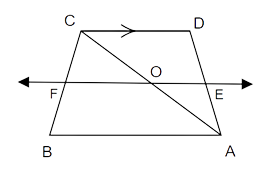
Ans: In trapezium ABCD, AB || CD and FE are drawn parallel to CD. 

$\therefore AB||CD||\text{ }FE$

In $\Delta ADC$, E is the midpoint of AD and $EO||DC$

By converse of Midpoint theorem,

O is the midpoint of AC.

Now, 

In $\Delta ABC$ , O is the midpoint of AC and $FO||AB$

By converse of Midpoint theorem,

F is the midpoint of BC.

7. Through A, B and C, lines RQ, PR and QP have been drawn, respectively parallel to sides BC, CA and AB of a ABC as shown in Fig.8.5. Show that $BC=\dfrac{1}{2}QR$ .

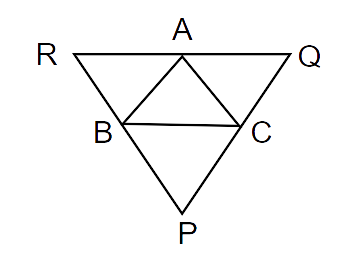
Ans: Given: AB||PQ, BC || RQ and AB || PQ

TPT: $BC=\dfrac{1}{2}QR$

Proof: In parallelogram ACBR,

BC = AR (Opposite sides of a parallelogram are equal) ..(i)

Also, 

In parallelogram ABCQ,

BC = AQ (Opposite sides of a parallelogram are equal) ..(ii)

From (i) and (ii)

BC = AR = AQ ..(iii)

Now,

In the above figure, R – A – Q ,

$\therefore RQ=AR+AQ$ 

\[\Rightarrow RQ=BC+BC\] .. (from iii)

$\Rightarrow RQ=2BC$

$\Rightarrow BC=\dfrac{1}{2}RQ$

Hence proved.

8. D, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral triangle ABC. Show that DEF is also an equilateral triangle. 

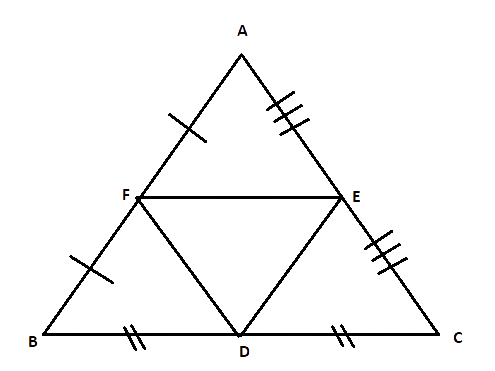
Ans: Given: $\Delta ABC$ is an equilateral triangle.

D is the midpoint of BC, E is the midpoint of AC and F is the midpoint of AB.

According to midpoint theorem,

$DE=\dfrac{1}{2}AB$ 

Also, 

$DF=\dfrac{1}{2}AC$

Similarly,

$FE=\dfrac{1}{2}BC$

But, AB = BC = AC

$\therefore $ DF = DE = FE 

Hence, $\Delta DFE$ is an equilateral triangle.

9. Points P and Q have been taken on opposite sides AB and CD, respectively of a parallelogram ABCD such that AP = CQ (Fig. 8.6). Show that AC and PQ bisect each other.

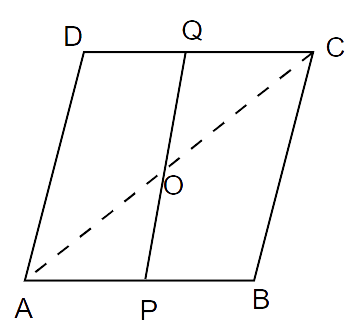
Ans: In $\Delta AOP\text{ and }\Delta COQ$ 

$\angle PAO=\angle OCQ$ (Alternate interior angles)

AP = CQ (given)

$\angle POA=\angle QOC$ (Vertically opposite angles)

By ASA test,

$\Delta AOP\cong \Delta COQ$

$\therefore $ OP = OQ and OC = OA

Therefore, PQ and AC bisect each other.

10. In Fig. 8.7, P is the mid-point of side BC of a parallelogram ABCD such that \[\angle \mathbf{BAP}=\angle \mathbf{DAP}\] . Prove that AD = 2CD.

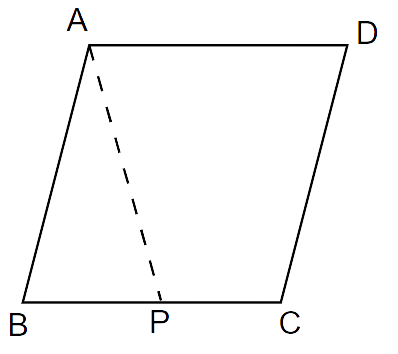
Ans: In the parallelogram ABCD, 

BP = PC

$\angle BAP=\angle PAD$ (Given)..(i)

Adjacent angles in a parallelogram are supplementary.

$\therefore \angle A+\angle B={{180}^{o}}$ (ii)

Now,

In $\Delta BAP$ ,

Sum of angles in a triangle is \[{180}^{o}\]

$\angle BAP+\angle APB+\angle ABP={{180}^{o}}$

$\dfrac{1}{2}\angle A+\angle APB+\angle B=\angle A+\angle B$ [from (i) and (ii)]

$\angle APB=\dfrac{1}{2}\angle A$

$\therefore \angle BAP=\angle APB$

PB = AB (sides opposite to congruent angles are equal) ..(iii)

AD = BC (Opposite sides of a parallelogram are equal)

$\therefore \dfrac{1}{2}AD=\dfrac{1}{2}BC$

Also, P is the midpoint of BC

$\Rightarrow \dfrac{1}{2}AD=BP$

From (iii)

$\Rightarrow \dfrac{1}{2}AD=AB$

But AD = CD (Opposite sides of a parallelogram are equal)

$\Rightarrow \dfrac{1}{2}AD=CD$

$\Rightarrow AD=2CD$

(E) Long Answer Questions

Sample Question 1: PQ and RS are two equal and parallel line-segments. Any point M not lying on PQ or RS is joined to Q and S and lines through P parallel to QM and through R parallel to SM meet at N. Prove that line segments MN and PQ are equal and parallel to each other.

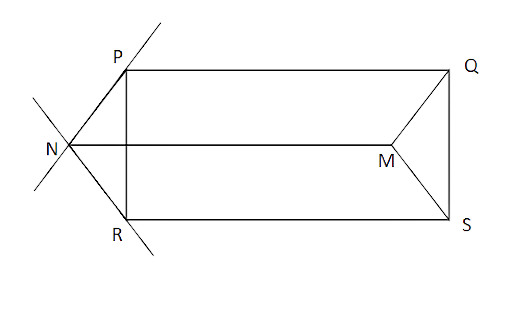
Ans: Given: PQ = RS and PQ || RS. 

PQSR is a parallelogram.

Thus, PR = QS and PR || QS  (i)

Now, PR || QS 

Interior angles on the same side of the transversal are supplementary.

Therefore, \[\angle RPQ+\angle PQS=180{}^\text{o}\]

\[\angle RPQ+\angle PQM+\angle MQS=180{}^\text{o}\] (ii) 

Also, PN || QM

Therefore, \[\angle NPQ+\angle PQM=180{}^\text{o}\]

\[\angle NPR+\angle RPQ+\angle PQM=180{}^\text{o}\]  (iii) 

Thus, \[\angle NPR=\angle MQS\] [from (ii) and (iii)] (iv) 

Similarly, \[\angle NRP=\angle MSQ\] (v) 

By ASA test of congruence and (from i, iv and v)

Therefore, \[\Delta PNR\cong \Delta QMS~\]

Thus, PN = QM and NR = MS (by CPCT) 

Since, PN = QM and PN || QM, 

Thus, PQMN is a parallelogram.

Therefore, MN = PQ and MN || PQ

Sample Question 2: Prove that a diagonal of a parallelogram divides it into two congruent triangles.

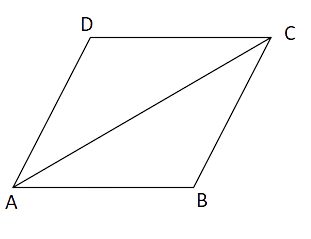
Ans: In $\Delta ABC$ and $\Delta ACD$

(i) \[\angle ~ACB=~\angle ~CAD\] (Alternate interior angles, AB || CD and AC is the transversal) 

(ii) AC =CA (common side)

(iii) \[\angle CAB=~\angle ~ACD\] (angles opposite to equal sides)

By ASA test of congruence,

\[\Delta ABC~\cong ~\Delta ACD\]

Sample Question 3: Show that the quadrilateral formed by joining the mid-points the sides of a rhombus, taken in order, forms a rectangle.

Ans: Quadrilateral ABCD is a rhombus

P, Q, R and S be the mid-points of sides AB, BC, CD and DA, respectively

Construction: Join BD and AC

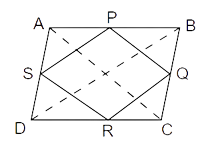
In \[\Delta ABD\] , 

S and P are the midpoints of AD and AB

By midpoint theorem,

$SP=\dfrac{1}{2}BD$ and SP || BD

Similarly,

$RQ=\dfrac{1}{2}BD$ and RQ || BD

Thus, SP || RQ

Therefore, PQRS is a parallelogram.

We know that diagonals of a rhombus are perpendicular to each other.

\[AC\bot BD\]

Now, \[\Delta BAC\]

SP || BD and PQ || AC 

Also, \[AC\bot BD\]

Thus, \[SP\bot PQ\] so, \[\angle SPQ=90{}^\text{o}\]

Therefore, PQRS is a rectangle.

Sample Question 4: A diagonal of a parallelogram bisects one of its angle. Prove that it will bisect its opposite angle also.

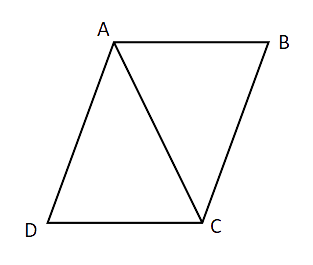
Ans: AC bisects $\angle A$

$\therefore \angle BAC=\angle DAC$ (i)

AB || CD and AC is a transversal

\[\angle BAC=\angle DCA\] (alternate angles) (ii)

Similarly,

AD || BC and AD is the transversal

\[\therefore \angle DAC\text{ }=\angle BCA\] (iii)

From (i), (ii) and (iii)

$\angle BCA\text{ }=\angle DCA$ 

Exercise 8.4

1. A square is inscribed in an isosceles right triangle so that the square and the triangle have one angle in common. Show that the vertex of the square opposite the vertex of the common angle bisects the hypotenuse.

Ans: Given: Quadrilateral CPQR is inscribed in the isosceles right triangle \[~\Delta ABC\]

Quadrilateral CPQR is a square

\[\therefore CP=PQ=RC=PR\]

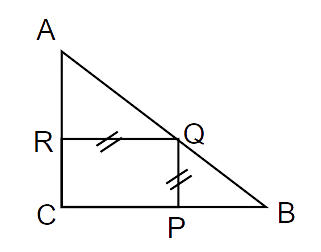
Also, \[~\Delta ABC\] is an isosceles triangle

\[\therefore BC=AC\]

\[\Rightarrow AR+RC=CP+BP\]

But RC = CP

\[\Rightarrow \therefore AR=BP~\]

Now, 

In \[\Delta QPB\text{ }and\text{ }\Delta ARQ\]

BP = AR

\[\angle QPB=\angle ARQ={{90}^{o}}\] (given)

PQ = RQ

\[\therefore \Delta QPB\cong \Delta ARQ\]

Thus, QB = AQ (CPCT)

This infers hypotenuse AB is bisected by Q.

2. In a parallelogram ABCD, AB = 10 cm and AD = 6 cm. The bisector of \[\angle \mathbf{A}\] meets DC in E. AE and BC produced meet at F. Find the length of CF.

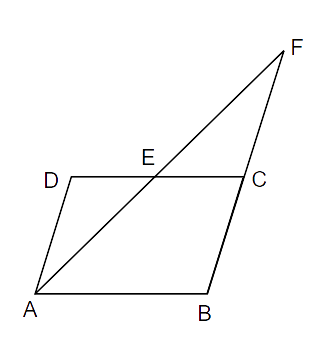
Ans: Given: Quadrilateral ABCD is a parallelogram.

AB = 10 cm

AD = 6 cm

AF is the bisector of \[\angle A\]

$\therefore \angle BAE=\angle DAE$

Also, AD || BC and AF is the transversal

$\therefore \angle DAE=\angle BFE$ (alternate interior angles)

Thus,

$\therefore \angle BAE=\angle BFE$

$\therefore FB=AB$(opposite sides of equal angles are equal)

FB = 10 cm

AD = BC = 6 cm (Opposite sides of a parallelogram are equal)

\[\Rightarrow FB=FC+BC\]

\[\Rightarrow 10cm=FC+6cm\]

\[\Rightarrow FC=4cm\]

Therefore, CF = 4 cm.

3. P, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.

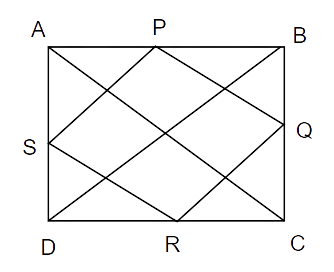
Ans: In quadrilateral ABCD,

P, Q, R and S are the mid-point of the sides AB, BC, CD and AD respectively.

$\therefore AC=BD$ (i)

Now, 

In \[\Delta ABC\] and \[\Delta ADC\]

PQ ||AC and SR || AC 

$\therefore PQ||SR$

$\therefore PQ=\dfrac{1}{2}AC$ ..(ii)

and $SR=\dfrac{1}{2}AC$ (given)

Thus,

PQ = SR 

In quadrilateral PQRS,

PQ = SR and $PQ||SR$. 

Thus, quadrilateral PQRS is a parallelogram.

Now, In \[\Delta ABC\]

$PQ=\dfrac{1}{2}AC$ (from ii)

$2PQ=AC$ ..(iii)

Similarly, In \[\Delta ABD\]

P and S are the midpoints of AB and AD respectively.

By midpoint theorem,

$PS=\dfrac{1}{2}BD$ 

$2PS=BD$ ..(iv)

But, AC = BD [From (i)]

From (iii) and (iv) we get,

$2PS=2PQ$

$\therefore PS=PQ$

A parallelogram with adjacent sides equal is a rhombus.

Therefore, quadrilateral PQRS is a rhombus.

4. P, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD such that \[\mathbf{AC}\bot \mathbf{BD}\] . Prove that PQRS is a rectangle.

Ans: We know that,

\[AC\bot BD\]

$\therefore \angle COD=\angle COB=\angle BOA=\angle DOA={{90}^{o}}$ 

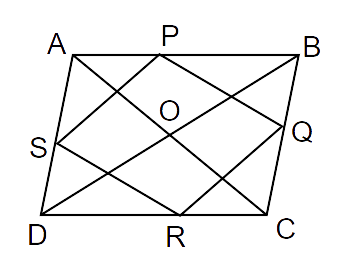
Now,

In $\Delta ABC$ and $\Delta ADC$ ,

PQ || AC and SR || AC

$\therefore $ PQ || SR

Also, By midpoint theorem,

$PQ=\dfrac{1}{2}AC$ and $SR=\dfrac{1}{2}AC$

 $\therefore $ PQ = SR

Similarly,

PS || RQ and PS = RQ

A quadrilateral with opposite sides equal and parallel and diagonals bisect at \[{90}^{o}\] is a rectangle.

Thus quadrilateral PQRS is a rectangle.

5. P, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC = BD and \[\mathbf{AC}\bot \mathbf{BD}\] . Prove that PQRS is a square.

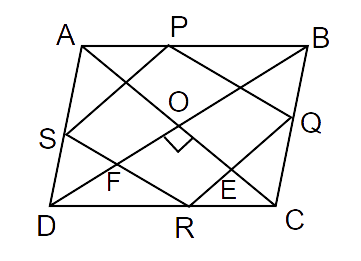
Ans: In $\Delta ABC$ and $\Delta ADC$ ,

PQ || AC and SR || AC

$\therefore $ PQ || SR

Also, By midpoint theorem,

$PQ=\dfrac{1}{2}AC$ and $SR=\dfrac{1}{2}AC$

 $\therefore $ PQ = SR

Similarly,

PS || RQ and \[PS=RQ=\dfrac{1}{2}BD\]

$\therefore $ PS = RQ

But, AC = BD

PQ = SR = PS = RQ

Thus, all the sides are equal.

Now, in EOFR,

\[\angle EOF={{90}^{o}}\]

So, \[\angle FRE={{90}^{o}}\] (opposite angles of a parallelogram are equal)

\[\angle SRQ={{90}^{o}}\]

Similarly, \[\angle RQP={{90}^{o}}\]

Therefore, Quadrilateral PQRS is a square.

6. A diagonal of a parallelogram bisects one of its angles. Show that it is a rhombus

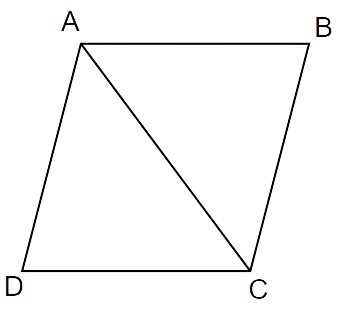
Ans: Diagonal AC bisects $\angle A$ 

$\angle DAC=\angle BAC$ (i)

Now, AD || BC and AC is the transversal

$\angle DAC=\angle ACB$ (ii)

From (i) and (ii)

$\angle BAC=\angle ACB$

Thus, AC = BC (opposite sides of equal angles)

But, AD = BC 

$\therefore $AB = BC = AD = AC

Hence ABCD is a rhombus. 

7. P and Q are the mid-points of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PRQS is a parallelogram.

Ans: Given: P is the midpoint of AB and Q is the midpoint of DC. 

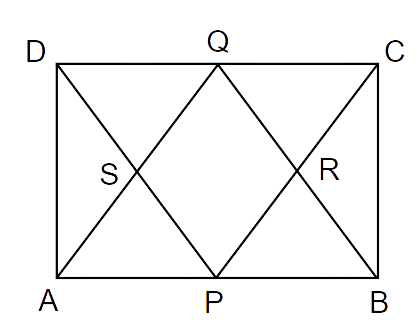
ABCD is a parallelogram.

AB = CD

$\therefore \dfrac{1}{2}AB=\dfrac{1}{2}CD$

AP = QC

$\therefore $ Quadrilateral APCQ is a parallelogram

AQ || PC and PR || QS ..(i)

Also, AB || DC and BP || DQ 

AB = DC 

$\therefore \dfrac{1}{2}AC=\dfrac{1}{2}DC$

As P and Q are the midpoints of AB and DC

BP = QD and BP || DQ

Thus, BQDP is a parallelogram.

So, DP || BQ and PS || QR.. (ii)

From (i) and (ii)

QS || PR and PS || RQ

Therefore, quadrilateral PRQS is a parallelogram.

8. ABCD is a quadrilateral in which AB || DC and AD = BC. Prove that \[\angle \mathbf{A}=\angle \mathbf{B}\] and \[\angle \mathbf{C}=\angle \mathbf{D}\]

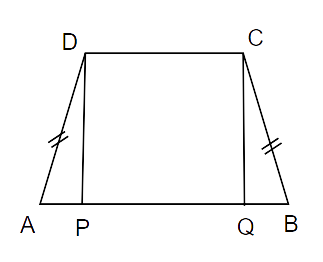
Ans: Given: AB || DC 

AD = BC 

Draw AP and CQ perpendicular to AB.

In $\Delta APD$ and $\Delta AQB$

(i) $\angle APD=\angle BQC$ ( \[{90}^{o}\] each)

(ii) AD = BC (given)

(iii) DP = CQ (distance between two parallel lines)

By RHS criterion of congruence,

$\Delta APD\cong \Delta AQB$ 

$\therefore \angle A=\angle B$ ..(I)

Now, AB || CD, AD and CB are transversals 

The sum of corresponding angles is supplementary.

$\angle A+\angle D={{180}^{o}}$  and $\angle B+\angle C={{180}^{o}}$

$\therefore \angle A+\angle D=\angle B+\angle C$

$\therefore \angle D=\angle C$ (from I)

Hence proved.

9. In Fig. 8.11, AB || DE, AB = DE, AC || DF and AC = DF. Prove that BC || EF and BC = EF. 

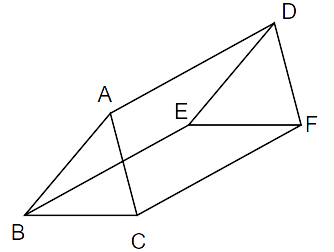
Ans: Given: AB || DE and AB = DE

AC||DF and AC = DF

TPT: BC||EF and BC = EF

Proof: In $\square ACFD$ ,

CA || FD and CA = FD

Thus, $\square ACFD$ is a parallelogram.

So, DA || CF and DA = CF ..(i)

Also, in $\square ABED$ ,

BA || ED and BA = ED 

Thus, $\square ABED$ is a parallelogram.

So, AD || EB and AD = BE (ii)

From (i) and (ii) we get,

DA = CF = BE and FC || BE (iii)

Now,

In $\square BCFE$ ,

CF = BE (from iii)

FC || BE

Thus, $\square BCFE$ is a parallelogram.

So, CB = EF and CB || EF.

Therefore, proved.

10. E is the mid-point of a median AD of ABC and BE is produced to meet AC at F. Show that $AF=\dfrac{1}{3}AC$ .

Ans: Given: AE = ED 

Construction: BE is produced to meet AC at F and is parallel to DG.

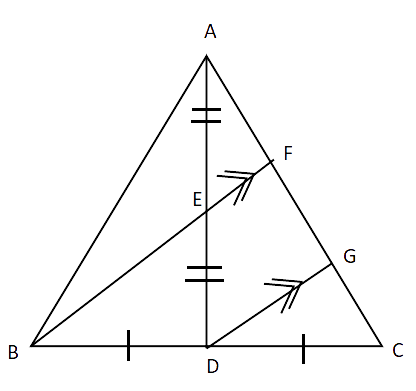
Proof: In $\Delta ADG$ ,

E is the midpoint of AD so AE = ED and EF || GD 

By converse of midpoint theorem,

AF = FG ..(i)

Similarly, in $\Delta FCB$ ,

D is the midpoint of BC so BD = DC and BF || DC

By converse of midpoint theorem,

FG = GC ..(ii)

From equation (i) and (ii) we get,

AF = FG = GC ..(iii)

Now, for side AC, A-F-G-C

\[\therefore AC=AF+FG+GC\]

  \[\Rightarrow AC=AF+AF+AF\] (from iii)

\[\Rightarrow AC=3AF\]

\[\Rightarrow AF=\dfrac{1}{3}AC\]

Hence proved.

11. Show that the quadrilateral formed by joining the mid-points of the consecutive sides of a square is also a square.

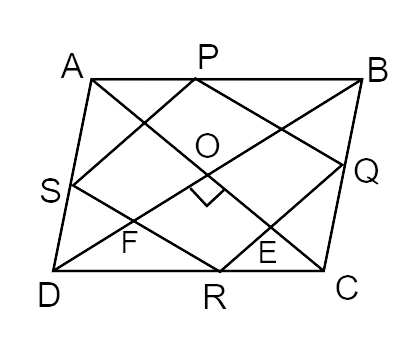
Ans: In $\Delta ABC$ and $\Delta ADC$ ,

PQ || AC and SR || AC

$\therefore $ PQ || SR

Also, By midpoint theorem,

$PQ=\dfrac{1}{2}AC$ and $SR=\dfrac{1}{2}AC$

 $\therefore $ PQ = SR

Similarly,

PS || RQ and \[PS=RQ=\dfrac{1}{2}BD\]

$\therefore $ PS = RQ

But, we know that diagonals of a square are equal and bisect each other.

So, AC = BD

$\therefore $ PQ =RQ = SR = PS 

Thus, all the sides are equal.

Now, in EOFR,

\[\angle EOF={{90}^{o}}\]

So, \[\angle FRE={{90}^{o}}\] (opposite angles of a parallelogram are equal)

\[\angle SRQ={{90}^{o}}\]

Similarly, \[\angle RQP={{90}^{o}}\]

Therefore, Quadrilateral PQRS is a square.

12. E and F are respectively the mid-points of the non-parallel sides AD and BC of a trapezium ABCD. Prove that EF || AB and $EF=\dfrac{1}{2}\left( AB+CD \right)$ .

Ans: Given: E is the midpoint of AD and F is the midpoint of BC

Construction: Join CE produced at G to meet AB.

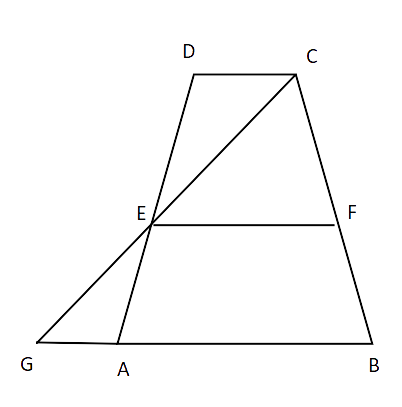
Proof: In \[\Delta EAG\] and \[\Delta EDC~\]

(i) \[\angle EGA=\angle ECD~\] (Alternate angles)

(ii) \[\angle GEA=\angle CED\] (vertically opposite angles) 

(iii) EA = ED (E is the midpoint of AD)

By AAS test of congruence,

\[\Delta EAG\cong \Delta EDC~\]

Thus, AG = DC and EG = EC (by CPCT)

Now, in \[\Delta CGB\] ,

F is the midpoint of BC and E is the midpoint of CG,

So, by midpoint theorem,

EF || AB

Also, by midpoint theorem

$EF=\dfrac{1}{2}BG$

But, BG = AG + AB

$EF=\dfrac{1}{2}\left( AG+AB \right)$

$EF=\dfrac{1}{2}\left( CD+AB \right)$ (since AG = DC)

Hence proved.

13. Prove that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.

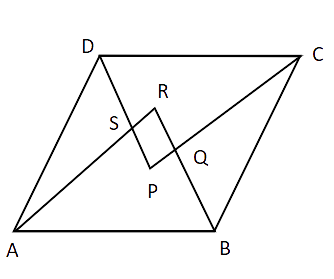
Ans: Quadrilateral ABCD is a parallelogram.

The adjacent angles of a parallelogram are supplementary.

$\therefore \angle A+\angle D={{180}^{o}}$ 

$\therefore \dfrac{\angle A}{2}+\dfrac{\angle D}{2}=\dfrac{{{180}^{o}}}{2}$

AR and DP are the bisectors of $\angle A$ and $\angle D$ respectively.

\[\angle SAD+\angle SDA={{90}^{o}}\]

Now, In $\Delta SAD$ ,

\[\angle SAD+\angle SDA+\angle DSA={{180}^{o}}\] (angle sum property)

\[{{90}^{o}}+\angle DSA={{180}^{o}}\]

\[\angle DSA={{90}^{o}}\] 

Thus, \[\angle RSP={{90}^{o}}\]

Similarly,

\[\angle RQP={{90}^{o}}\] 

All the four vertices of quadrilateral PQRS have a right angle.

Therefore, quadrilateral PQRS is a rectangle.

14. P and Q are points on opposite sides AD and BC of a parallelogram ABCD such that PQ passes through the point of intersection O of its diagonals AC and BD. Show that PQ is bisected at O.

Ans: In $\Delta AOP$ and $\Delta COQ$ ,

(i) $\angle AOP=\angle COQ$ (Vertically opposite angles)

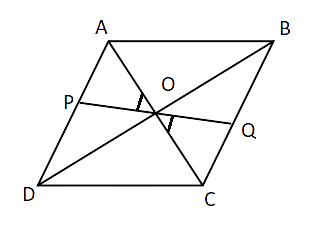
(ii) AO = OC (Diagonals of a parallelogram bisect each other)

(iii) $\angle PAO=\angle QCO$ (Alternate interior angles)

By ASA test of congruence,

$\Delta AOP\cong \Delta COQ$ 

PO = QO (by CPCT)

Therefore, PQ is bisected at O.

15. ABCD is a rectangle in which diagonal BD bisects \[\angle \mathbf{B}\] . Show that ABCD is a square.

Ans:  ABCD is a rectangle. 

Diagonal BD bisects \[\angle B\]

In $\Delta BCD$ and $\Delta BAD$

(i) \[\angle CBD=\angle ABD\] (BD is the angle bisector of \[\angle B\] )

(ii) $\angle BCD=\angle BAD$ (angles of a rectangle)

(iii) BD = DB (common side)

By AAS test of congruence,

$\Delta BCD\cong \Delta BAD$

DC = AB and BC = AD (by CPCT) ..(i)

Also, opposite sides of a rectangle are congruent.

$\therefore BA=CD$ and $BC=AD$ ..(ii)

From (i) and (ii) we get,

AB = BC = CD = AD

Therefore, ABCD is a square.

16. D, E and F are respectively the mid-points of the sides AB, BC and CA of a triangle ABC. Prove that by joining these mid-points D, E and F, the triangles ABC is divided into four congruent triangles.

Ans:  Sides AB, BC and CA have midpoints D, E and F respectively. 

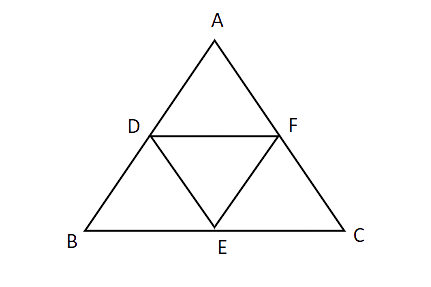
TPT: $\Delta DEF\cong \Delta CFE\cong \Delta EDB\cong \Delta FAD$

Proof: Segment DF joins the midpoints of AB and AC respectively.

By midpoint theorem,

DF || BC 

$\therefore $ DF || BE

Also, EF || DB 

$\therefore $ Quadrilateral BEFD is a parallelogram.

We know that, a diagonal divides a parallelogram in two congruent triangles.

$\therefore $ $\Delta DEF\cong \Delta EDB$ ..(i)

Similarly,

$\Delta DEF\cong \Delta CFE$ ..(ii)

And,

$\Delta DEF\cong \Delta FAD$ ..(iii)

From (i), (ii) and (iii)

$\Delta DEF\cong \Delta CFE\cong \Delta EDB\cong \Delta FAD$

Hence proved.

17. Prove that the line joining the mid-points of the diagonals of a trapezium is parallel to the parallel sides of the trapezium.

Ans: Given: ABCD is a trapezium

AB || CD

TPT: AB || CD || EF

Construction: Join DF and produce it at G to meet AB.

Proof: EF is joining the midpoints of unparalleled sides AD and BC respectively.

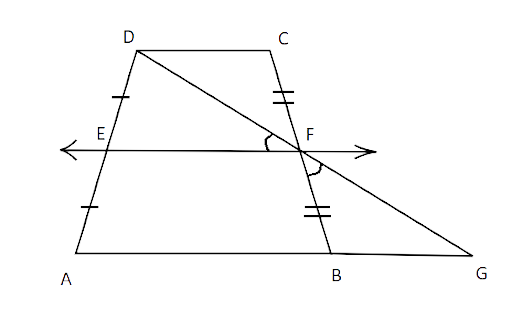
In \[\Delta DCF\] and \[\Delta GBF\]

(i) \[\angle CDF=\angle BGF\] (Alternate angles)

(ii) \[\angle DFC=\angle BFG\] (vertically opposite angles) 

(iii) FC = FB (F is the midpoint of BC)

By AAS test of congruence,

\[\Delta DCF\cong \Delta GBF\]

Thus, DF = GF and DC = BG (by CPCT)

Now, in \[\Delta DAG\] ,

F is the midpoint of BC and E is the midpoint of AD,

So, by midpoint theorem,

EF || AB

But, AB || DC

$\therefore $ AB || DC || EF 

Hence proved.

18.P is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.

Ans: Given: DP = PC 

AP || RC 

TPT: DA = AR and CQ = QR

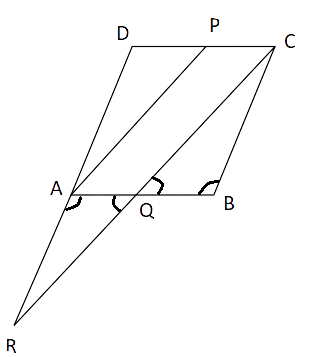
Proof: In $\Delta DCR$ ,

DP = CD (P is the midpoint of CD) and AP || CR

Thus, A is the midpoint of DR 

$\therefore $ AD = AR

But AD = BC

So, AR = BC..(a)

Now, in $\Delta RAQ$ and $\Delta CBQ$

(i) $\angle RAQ=\angle CBQ$ (alternate angles)

(ii) $\angle AQR=\angle CQB$ (vertically opposite angles)

(iii) AR = BC (from a)

By AAS test of congruence,

$\Delta RAQ\cong \Delta CBQ$ 

CQ = QR (by CPCT)

Therefore, AD = AR and CQ = QR

Hence proved.

If any of the Exemplar problems appear to be troublesome then referring to the NCERT Exemplar Solutions Class 9 Math Chapter 8 by Vedantu will be very helpful. Vedantu created the best study material for the Quadrilaterals through NCERT Exemplar Solutions to make your study time simple. These materials will assist you with upgrading your understanding in regards to the Chapter and consequently will help you achieve more marks in your tests.