Important Questions for CBSE Class 10 Maths Chapter 6 - Triangles 2024-25

1 Mark Question

1. In the figure \[\mathbf{\vartriangle ABC\sim\vartriangle EDC,}\]if we have \[\mathbf{\text{AB}=4~\text{cm},\text{ED}=3~\text{cm},\text{CE}=4.2~\text{cm}}\]and \[\mathbf{\text{CD}=4.8~\text{cm},}\]then the values of \[\mathbf{\text{CA}\,\,and\,\,\text{CB}}\] are

(image will be uploaded soon)

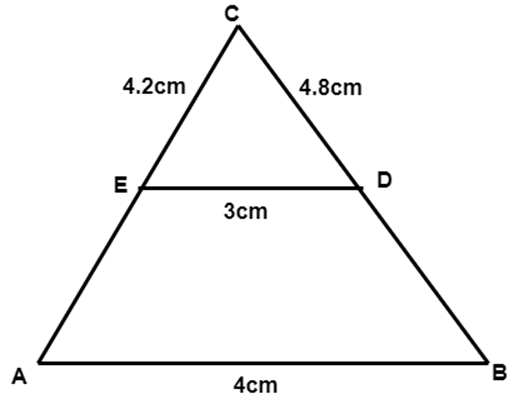
1. \[\mathbf{6~\text{cm},6.4~\text{cm}}\]

2. \[\mathbf{4.8~\text{cm},6.4~\text{cm}}\]

3. \[\mathbf{5.4~\text{cm},6.4~\text{cm}}\]

4. \[\mathbf{5.6~\text{cm},6.4~\text{cm}}\]

Ans: (d)  $ 5.6~\text{cm},6.4~\text{cm} $ 

As the triangles are similar,

 $ \dfrac{AB}{ED}=\dfrac{CA}{CE}=\dfrac{CB}{CD}=\dfrac{4}{3} $ 

 $ \dfrac{CA}{CE}=\dfrac{CA}{4.2}=\dfrac{4}{3} $ 

 $ CA=5.6 $ 

Then,

 $ \dfrac{CB}{CD}=\dfrac{CB}{4.8}=\dfrac{4}{3} $ 

 $ CB=6.4 $ 

2. The areas of two similar triangles are respectively  $ \mathbf{9~\text{c}{{\text{m}}^{2}} }$ and $ \mathbf{16~\text{c}{{\text{m}}^{2}}} $ . Then ratio of the corresponding sides are

1. 3:4  

2. 4:3  

3. 2:3 

4. 4:5 

Ans: (a)  $ 3:4 $ 

Ratio of area of triangle is equal to the square the ratio of the corresponding sides

Therefore,  $ \sqrt{\dfrac{9}{16}}=\dfrac{3}{4} $ 

3. Two isosceles triangles have equal angles and their areas are in the ratio \[\mathbf{16:\text{ }25,}\]then the ratio of their corresponding heights is

1. $ \mathbf{\dfrac{4}{5} }$ 

2. $ \mathbf{\dfrac{5}{4}} $ 

3. $ \mathbf{\dfrac{3}{6} }$ 

4. $ \mathbf{\dfrac{5}{7}} $ 

Ans: (a)  $ \dfrac{4}{5} $ 

Ratio of area of triangle is equal to the square the ratio of the corresponding sides

Therefore,  $ \sqrt{\dfrac{16}{25}}=\dfrac{4}{5} $ 

4. If  $ \mathbf{\vartriangle ABC\sim\vartriangle DEF} $ and  $ \mathbf{AB=5~\text{cm}, }$ area  $ \mathbf{(\Delta ABC)=20~\text{c}{{\text{m}}^{2}}, }$ area  $\mathbf{ (\Delta DEF)=45~\text{c}{{\text{m}}^{2}}, }$ then  $ \mathbf{\text{DE}= }$ 

1. $ \mathbf{\dfrac{4}{5}~\text{cm}} $ 

2. $ \mathbf{7.5~\text{cm} }$ 

3. $ \mathbf{8.5~\text{cm}} $ 

4. $ \mathbf{7.2~\text{cm}} $ 

Ans: (b)  $ 7.5~\text{cm} $ 

Ratio of area of triangle is equal to the square the ratio of the corresponding sides

Therefore,  $ \sqrt{\dfrac{(\Delta ABC)}{(\Delta DEF)}}=\dfrac{AB}{DE} $ 

 $ \sqrt{\dfrac{20}{45}}=\dfrac{5}{DE}\Rightarrow DE=7.5 $ 

 $ \dfrac{(\Delta ABC)}{(\Delta DEF)}=\dfrac{20}{45}=\dfrac{5}{7.5} $ 

5. A man goes  $ 15~\text{m} $ due west and then  $ 8~\text{m} $ due north. Find distance from the starting point.

1. 17 

2. 18

3. 16

4. 7

Ans: (A)  $ 17~\text{m} $ 

Square of the distance = square of the sum of two distances.

 $ =\sqrt{{{15}^{2}}+{{8}^{2}}}=\sqrt{225+64}=\sqrt{289}=17m $ 

6. In a triangle  $ \text{ABC}, $ if  $ \text{AB}=12~\text{cm},\text{BC}=16~\text{cm},\text{CA}=20~\text{cm}, $ then  $ \vartriangle ABC $ is

1. Acute angled

2. Right angled

3. Isosceles triangle

4. Equilateral triangle

Ans: (b) Right angled

(image will be uploaded soon)

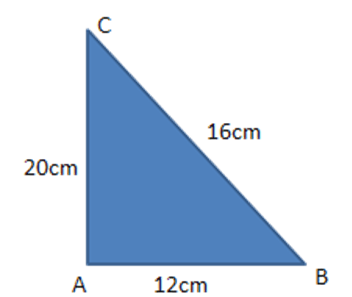
By law of Pythagoras triangle,

 $ A{{C}^{2}}=B{{C}^{2}}+A{{B}^{2}}={{\left( 16 \right)}^{2}}+{{\left( 12 \right)}^{2}}=400 $ 

 $ AC=20 $ 

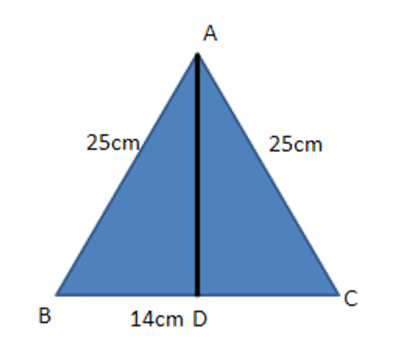
7. In an isosceles triangle  $ \text{ABC},\text{AB}=\text{AC}=25~\text{cm} $ and  $ \text{BC}=14~\text{cm}, $ then altitude from  $ \text{A} $ on  $ \text{BC}= $ 

1. 20

2.  24

3. 12

4. None of these

Ans: (b)  $ 24~\text{cm} $ 

(image will be uploaded soon)

8. The side of square who's diagonal is  $ 16~\text{cm} $ is

1. $\mathbf{ 16~\text{cm} }$ 

2. $ \mathbf{8\sqrt{2}~\text{cm} }$ 

3. $ \mathbf{5\sqrt{2}~\text{cm} }$ 

4. None of these

Ans: (a) \[8\sqrt{2}~\text{cm}\]

Length of diagonal = sum of both sides of square.

 $ {{\left( 16 \right)}^{2}}={{s}^{2}}+{{s}^{2}} $ 

 $ 2{{s}^{2}}=16*16 $ 

 $ {{s}^{2}}=8\left( 16 \right) $ 

 $ s=8\sqrt{2} $ 

9.In an isosceles triangle  $ \text{ABC}, $ if  $ \text{AC}=\text{BC} $ and  $ A{{B}^{2}}=2A{{C}^{2}}, $ then  $ \angle C= $ 

1. $ \mathbf{{{45}^{{}^\circ }}} $ 

2. $ \mathbf{{{60}^{{}^\circ }} }$ 

3. $\mathbf{ {{90}^{{}^\circ }} }$ 

4. $ \mathbf{{{30}^{{}^\circ }} }$ 

Ans: (c)  $ {{90}^{{}^\circ }} $ 

(image will be uploaded soon)

If two sides of a triangle are congruent, then angles opposite to those sides are congruent.

So  $ \angle C=90{}^\circ  $ 

10. If  $ \vartriangle ABC\sim\Delta EDF $ and  $ \vartriangle ABC $ is not similar to  $ \vartriangle DEF, $ then which of the following is not true?

1.  $\mathbf{ BC\times EF=AC\times FD }$ 

2.  $ \mathbf{AB\times EF=AC\times DE }$ 

3.  $ \mathbf{BC\times DE=AB\times EF }$ 

4. $ \mathbf{BC\times DE=AB\times FD }$ 

Ans: c)  $ BC\times DE=AB\times EF $ 

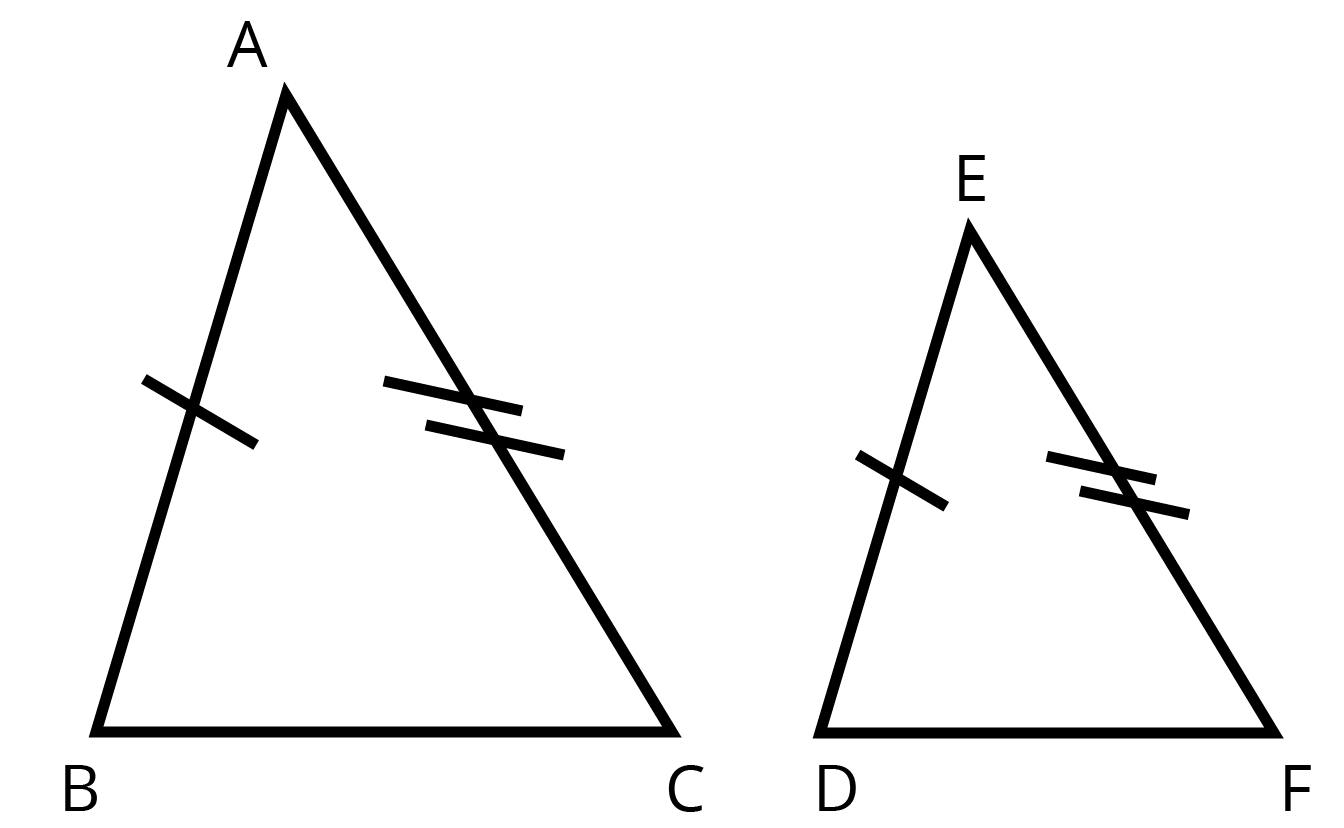
11.A certain right-angled triangle has its area numerically equal to its perimeter. The length of each side is an even integer, what is the perimeter?

1. 24 units

2. 36 units

3. 32 units

4. 30 units

Ans: 24 units

Length of each side is even integer amd also area is numerically equal its perimeter.

 $ \therefore \left( 6,8,10 \right) $  make a Pythagorean triplet.

 $ {{8}^{2}}+{{6}^{2}}={{10}^{2}} $ 

Sum of all sides =perimeter

 $ 6+8+10=24 $ 

12. In the given figure, if  $ \text{AB}||\text{CD}, $ then  $ x= $ 

(image will be uploaded soon)

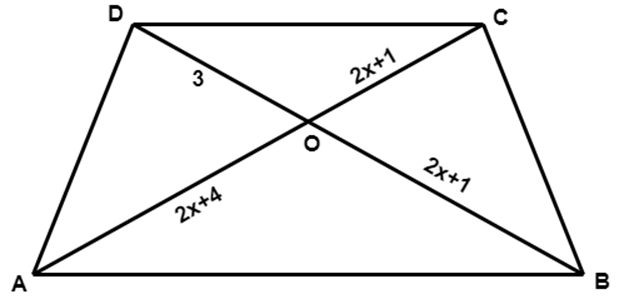
1. 3

2. 4

3. 5

4. 6

Ans: (a) 3

From the figure it is clear that the triangles  $ \text{ }\!\!\Delta\!\!\text{ OAB}\sim \text{ }\!\!\Delta\!\!\text{ OCD} $  because all the corresponding angles are equal.

So, we have,

 $ \dfrac{OA}{OC}=\dfrac{OB}{OD} $ 

 $ \dfrac{2x+4}{2x+1}=\dfrac{2x+1}{3} $ 

 $ 3\left( 2x+4 \right)=\left( 2x+1 \right)\left( 2x+1 \right) $ 

 $ 6x+12=4{{x}^{2}}+4x+1 $ 

Now, by rearranging the terms to one side of the equation we get,

 $ 4{{x}^{2}}-2x-11=0 $ …….(1)

Now, by using the formula of finding roots of quadratic equation

 $ \text{a}{{\text{x}}^{\text{2}}}\text{+bx+c=0} $  we get,

 $  X = \dfrac {{-b}\pm{(\sqrt{{b^2} - 4ac)}}}{2a}  $ 

By using this formula for equation (1) we get,

\[x=\dfrac{-\left( -2 \right)\pm \sqrt{{{\left( -2 \right)}^{2}} + 4\left( -11 \right)\left( 4 \right)}}{2\left( 4 \right)}\]

 $ \text{x=}\dfrac{\text{2 }\!\!\pm\!\!\text{ 6}\sqrt{\text{5}}}{\text{8}} $  

Here, the two values of  $ \text{x} $  are,

 $  \text{x=1}\text{.92}  $ 

 $  \text{x=-1}\text{.42}  $  

As the length cannot be negative so, the required value of  $ \text{x} $  is  $ 1.92 $ .

13.Length of an altitude of an equilateral triangle of side '  $ 2\text{a} $ '  $ \text{cm} $ is

1. $\mathbf{ 3\text{acm}} $ 

2. $ \mathbf{\sqrt{3}a~\text{cm} }$ 

3. $ \mathbf{\dfrac{\sqrt{3}}{2}a~\text{cm}} $ 

4. $\mathbf{ 2\sqrt{3}a~\text{cm} }$ 

Ans: (b)  $ \sqrt{3}a~\text{cm} $ 

(image will be uploaded soon)

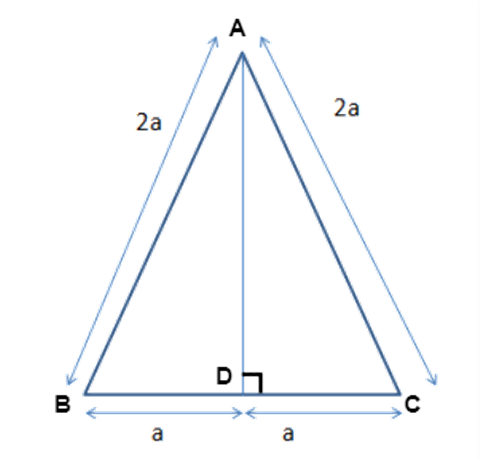
In the right angled  $ \vartriangle ABC $ 

 $ A{{B}^{2}}=A{{D}^{2}}+D{{B}^{2}} $ 

 $ A{{D}^{2}}=A{{B}^{2}}-D{{B}^{2}}=4{{a}^{2}}-{{a}^{2}}=3{{a}^{2}} $ 

 $ AD=\sqrt{3}acm $ 

14. If in two triangles  $ \text{ABC} $ and  $ \text{PQR},\dfrac{AB}{QR}=\dfrac{BC}{PR}=\dfrac{CA}{PQ} $ 

1. $ \mathbf{\vartriangle PQR\sim\vartriangle CAB} $ 

2. $\mathbf{ \vartriangle PQR\sim\Delta ABC }$ 

3. $ \mathbf{\Delta CBA=\vartriangle PQR }$ 

4. $ \mathbf{\Delta BCA\sim\Delta PQR }$ 

Ans: a)  $ \vartriangle PQR\sim\Delta CAB $ 

(image will be uploaded soon)

15. The area of two similar triangles are  $ 81~\text{c}{{\text{m}}^{2}} $ and  $ 49~\text{c}{{\text{m}}^{2}} $  respectively. If the altitude of the bigger triangle is  $ 4.5~\text{cm}, $ then the corresponding altitude of the smaller triangle is

1. $ \mathbf{2.5~\text{cm}} $ 

2. $ \mathbf{2.8~\text{cm} }$ 

3. $ \mathbf{3.5~\text{cm}} $ 

4. $ \mathbf{3.7~\text{cm} }$ 

Ans: c)  $ 3.5~\text{cm} $ 

 $ \dfrac{Area\,\,of\,\,l\arg er\vartriangle }{Area\,\,of\,\,smaller\vartriangle }={{\left( \dfrac{altitude\,\,\,of\,\,l\arg er\vartriangle }{altitude\,\,\,of\,\,smaller\vartriangle } \right)}^{2}} $ 

 $ \dfrac{81}{49}=\dfrac{{{\left( 4.5 \right)}^{2}}}{{{x}^{2}}} $ 

 $ \dfrac{9}{7}=\dfrac{4.5}{x} $ 

 $ x=3.5 $ 

16.In figure,  $ \text{DF}||\text{BC} $ and  $ \text{AD}=1~\text{cm},\text{BD}=2~\text{m}. $ The ratio of the area of  $ \vartriangle ABC $ to the area of  $ \vartriangle ADE $ is

1. 9:1

2. 1: 9

3. 3:1

4. none of these

Ans: (a) 9:1

(image will be uploaded soon)

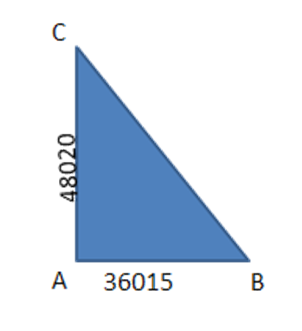
$ \dfrac{Area\,of\,\vartriangle ABC}{Area\,of\,\vartriangle ADF}=\dfrac{A{{B}^{2}}}{A{{D}^{2}}} $ 

 $ AB=AB+DB=1+2=3 $ 

 $ \dfrac{A{{B}^{2}}}{A{{D}^{2}}}=\dfrac{{{3}^{2}}}{1}=\dfrac{9}{1} $ 

17.In the given figure,  $ \vartriangle ABC\sim\vartriangle PQR, $ then the value of  $ x $  and  $ y $  are

(image will be uploaded soon)

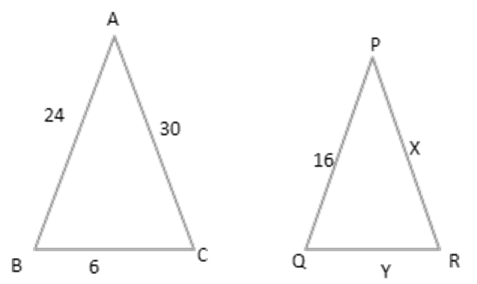
1. $\mathbf{ \left( x,y \right)=\left( 6,20 \right) }$ 

2. $ \mathbf{(20,60)} $ 

3. $ \mathbf{(x,y)=(3,10)} $ 

4. none of these

Ans: (d)none of these

 $ \dfrac{AB}{PQ}=\dfrac{AC}{PR}=\dfrac{BC}{QR} $ 

 $ \dfrac{24}{16}=\dfrac{30}{x}=\dfrac{6}{y} $ 

 $ \dfrac{24}{16}=\dfrac{30}{x}\Rightarrow x=20 $ 

 $ \dfrac{24}{16}=\dfrac{6}{y}\Rightarrow y=4 $ 

 $ \therefore \left( x,y \right)=\left( 20,4 \right) $ 

18.In figure,  $ \text{P} $  and  $ \text{Q} $  are points on the sides  $ \text{AB} $  and AC respectively of  $ \vartriangle ABC $  such that  $ \text{AP}=3.5~\text{cm},\text{AQ}=3~\text{cm} $ and $ \text{QC}=6~\text{cm} $ . If  $ \text{PQ}=4.5~\text{cm}, $ then  $ \text{BC} $ is

(image will be uploaded soon)

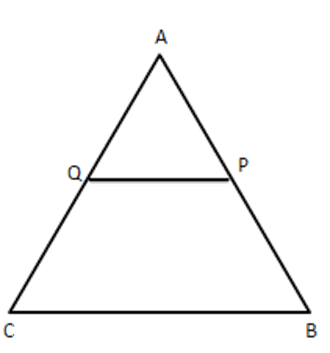
1. $\mathbf{ 12.5~\text{cm}} $ 

2. $ \mathbf{5.5~\text{cm} }$ 

3. $ \mathbf{13.5~\text{cm} }$ 

4. none of these

Ans: d)none of these.

 $ \dfrac{AC}{AP}=\dfrac{CB}{PQ}=\dfrac{AB}{AQ} $ 

 $ \dfrac{3+6}{3.5}=\dfrac{BC}{4.5}\Rightarrow BC=11.5 $ 

19.D, E, F are the mid-points of the sides  $ \text{AB},\text{BC}, $  and CA respectively of  $ \vartriangle ABC, $  then  $ \dfrac{\operatorname{ar}(\Delta DEF)}{\operatorname{ar}(\Delta ABC)} $ is

1. 1: 4

2. 4: 1

3. 1: 2

4. none of these

Ans: (a) 1: 4

(image will be uploaded soon)

 $ AB=2AD $ 

 $ \dfrac{\operatorname{ar}(\Delta DEF)}{\operatorname{ar}(\Delta ABC)}={{\left( \dfrac{DE}{AB} \right)}^{2}} $ 

 $ ={{\left( \dfrac{1}{2} \right)}^{2}}=\dfrac{1}{4} $ 

2 Marks Questions

1. In the given figures,  $ \vartriangle ODC\sim\vartriangle OBA,\angle BOC={{125}^{{}^\circ }} $  and  $ \angle CDO={{70}^{{}^\circ }}. $  Find

(image will be upload soon)

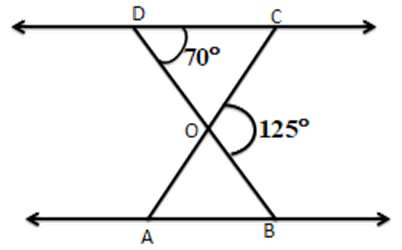
(i)  $ \mathbf{\angle DOC }$ 

Ans:  The sum of each interior angle and its adjacent exterior angle is equal to 180 degrees

 $ \angle DOC={{180}^{{}^\circ }}-{{125}^{{}^\circ }}={{55}^{{}^\circ }} $ 

(ii)  $\mathbf{ \angle DCO} $ 

Ans:   $ \angle DCO={{180}^{{}^\circ }}-\left( {{70}^{{}^\circ }}+{{55}^{{}^\circ }} \right)[\because DOB $ is a straight line and OC stands on it]

 $ ={{180}^{{}^\circ }}-{{125}^{{}^\circ }}={{55}^{{}^\circ }}\left[ \because  \right. $ sum of angles of a triangle  $ \left. ={{180}^{{}^\circ }} \right] $ 

(iii)  $ \mathbf{\angle OAB }$ 

Ans:  $ \left[ \begin{array}{*{35}{l}} \because \vartriangle ODC\sim\vartriangle OBA(\text{ given })  \\ \therefore \angle DOC=\angle AOB,\angle ODC=\angle OBA,\angle DCO=\angle OAB  \\ \end{array} \right] $ 

(iv)  $ \mathbf{\angle AOB }$ 

Ans:  $ \angle AOB=\angle DOC={{55}^{{}^\circ }} $ 

(v)  $\mathbf{ \angle OBA }$ 

Ans:  $ \angle OBA=\angle ODC={{70}^{{}^\circ }} $

2.  $ \vartriangle ABC\sim\vartriangle DEF $  and their areas are respectively  $ 64~\text{c}{{\text{m}}^{2}} $  and  $ 121~\text{c}{{\text{m}}^{2}}. $ If  $ \text{EF}=15.4~\text{cm}, $ find  $ \text{BC}. $ 

(image will  be uploaded soon)

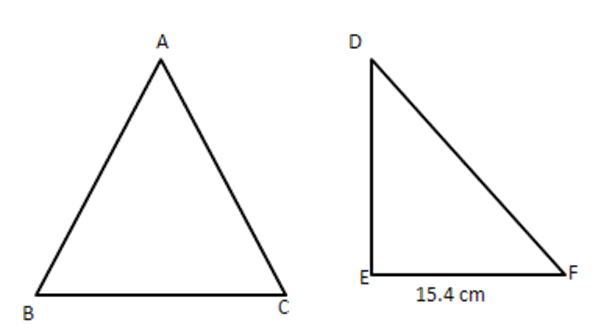
Ans: $ \text{ Since }\vartriangle ABC\sim\Delta DEF\therefore \dfrac{\operatorname{area}(\Delta ABC)}{\operatorname{area}(\Delta DEF)}=\dfrac{B{{C}^{2}}}{E{{F}^{2}}} $ 

 $ [\because  $ the ratio of the areas of two similar triangles is equal to the ratio of the squares of the corresponding sides]

 $ \Rightarrow \dfrac{64}{121}=\dfrac{B{{C}^{2}}}{{{(15.4)}^{2}}} $ 

 $ \Rightarrow B{{C}^{2}}=\dfrac{64\times 154\times 154}{121\times 10\times 10}=\dfrac{64\times 14\times 14}{100} $ 

 $ \Rightarrow BC=\dfrac{8\times 14}{10}=11.2~\text{cm} $ 

3.  $ \text{ABC} $ is an isosceles right triangle right-angled at  $ \text{B}\text{.} $ Prove that  $ A{{C}^{2}}=2A{{B}^{2}} $ 

(image will be uploaded soon)

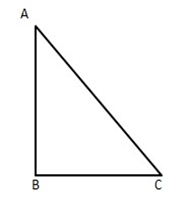
Ans: In right-angled  $ \vartriangle ABC, $ right  $ \angle A\,\,at\,\,B $ 

 $ A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}[ $ By Pythagoras theorem]

 $ =A{{B}^{2}}+A{{B}^{2}}=2A{{B}^{2}}\quad [\because BC=AB(given)] $ 

 $ =A{{C}^{2}}=2A{{B}^{2}} $ 

(image will be uploaded soon)

4. In the figure,  $ \text{DE}||\text{AC}  $  and  $ \dfrac{BE}{EC}=\dfrac{BC}{CP}, $  prove that

Ans: In  $ \Delta ABC,DE\|AC $ 

 $ \therefore \dfrac{BD}{DA}=\dfrac{BE}{EC}\ldots \ldots (i) $  [By Thales's Theorem]

Also  $ \dfrac{BE}{EC}=\dfrac{BC}{CP}(given)\ldots \ldots .(ii) $ 

 $ \therefore  $ from (i) and (ii), we get

 $ \dfrac{BD}{DA}=\dfrac{BC}{CP}\therefore DC\|AP $ 

 (By the converse of Thales's Theorem)

5.The hypotenuse of a right triangle is  $ 6~\text{m} $  more than twice of the shortest side. If the third side is  $ 2~\text{m} $  less than the hypotenuse. Find the side of the triangle.

Ans: Let shortest side be  $ Xm $  in length

Then hypotenuse  $ =(2x+6)m $ 

And third side  $ =(2x+4)m $ 

We have,

 $ {{(2x+6)}^{2}}={{x}^{2}}+{{(2x+4)}^{2}} $ 

 $ \Rightarrow 4{{x}^{2}}+24x+36={{x}^{2}}+4{{x}^{2}}+16+16x $ 

 $ \Rightarrow {{x}^{2}}-8x-20=0 $ 

 $ \Rightarrow x=10\text{ or }x=-2\text{ } $ 

 $ \Rightarrow x=10 $ 

Hence, the sides of triangle are  $ 10~\text{m},26~\text{m} $  and  $ 24~\text{m}. $ 

6. PQR is a right triangle right angled at P and M is a point on QR such that \[\text{PM}\bot \]QR. Show that \[P{{M}^{2}}=QM.MR\]

Ans: Given PQR is a right triangle right angled at P and  $ PM\bot QR $ 

(image will be uploaded soon )

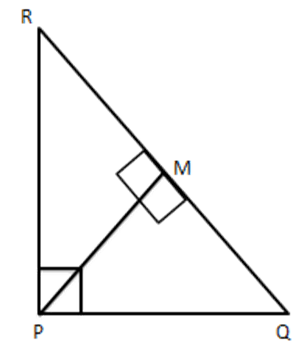
 $ \therefore \vartriangle PMR\sim\vartriangle PMQ $  

 $ \therefore \dfrac{PR}{PQ}=\dfrac{PM}{QM}=\dfrac{MR}{PM} $ 

 $ \Rightarrow \dfrac{PM}{QM}=\dfrac{MR}{PM} $ 

 $ \text{ i}\text{. e}\text{., }P{{M}^{2}}=QM.MR $ 

7. In the given figure, \[\mathbf{D}\text{ }\mathbf{E}\text{ }\left\| \mathbf{O}\text{ }\mathbf{Q}\text{ }\mathbf{and}\text{ }\mathbf{D}\text{ }\mathbf{F}\text{ }\left\| OR \right. \right.\text{ },\]Prove that \[\mathbf{E}\text{ }\mathbf{F}\text{ }\left\| OQ \right.\]

(image will be uploaded soon)

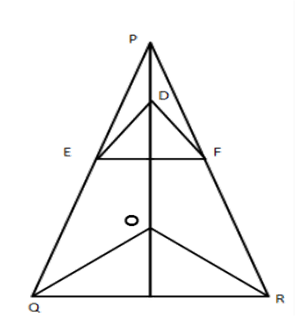
Ans: In  $ \vartriangle OQR,DE\|OQ $ 

 $ \dfrac{PE}{EQ}=\dfrac{PD}{DO}\,\,\,\,.....\left( 1 \right) $ 

In  $ \vartriangle OPR,DF\|OR $ 

 $ \dfrac{PD}{DO}=\dfrac{PF}{FR}\ldots \left( ii \right) $ 

From (i) and (ii), we get

 $ \dfrac{PE}{EQ}=\dfrac{PF}{FR} $ 

 $ \therefore From\,\,\vartriangle PQR $ 

 $ EF\|QR $ 

8. In figure,  $ \text{DE}||\text{BC} $ . Find EC

(image will be uploaded soon)

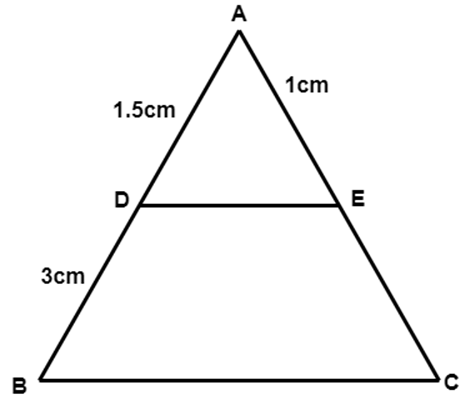
Ans:  $ \because DE\|BC $ 

 $ \therefore \dfrac{AD}{DB}=\dfrac{AE}{EC} $ 

 $ \Rightarrow \dfrac{1.5}{3}=\dfrac{1}{EC} $ 

 $ \therefore EC=2~\text{cm} $ 

9. In the given figure,  $ \text{ABC} $ and AMP are two right-angled triangles, right angled at  $ \text{B} $ and M respectively, prove that

 $ (i)\vartriangle ABC\sim\vartriangle AMP $ 

 (ii)  $ \dfrac{CA}{PA}=\dfrac{BC}{MP} $ 

(image will be uploaded soon)

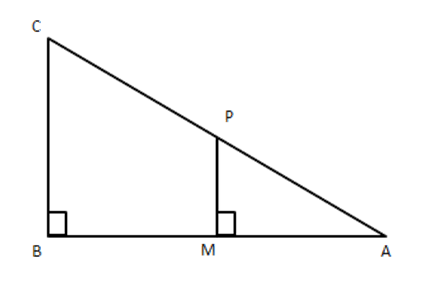
Ans: In  $ \vartriangle ABC $ and DAMP,

 $ \angle B=\angle M\left( {} \right. $ 

Each  $ \left. {{90}^{{}^\circ }} \right) $   

 $ \angle A=\angle A(\text{common}) $  

 $ \therefore \angle ACB=\angle APM $ 

 $ \therefore \Delta S $ are equiangular 

i.e.,  $ \vartriangle ABC\sim\vartriangle AMP $ 

 $ \therefore \dfrac{BC}{MP}=\dfrac{CA}{PA} $ 

10. In the given figure,  $ \text{OA}\times \text{OB}=\text{OC}\times OD $  or  $ \dfrac{OA}{OC}=\dfrac{OD}{OB} $ , prove that  $ \angle A=\angle C\,\,and\,\,\angle B=\angle D $ 

(image will be uploaded soon)

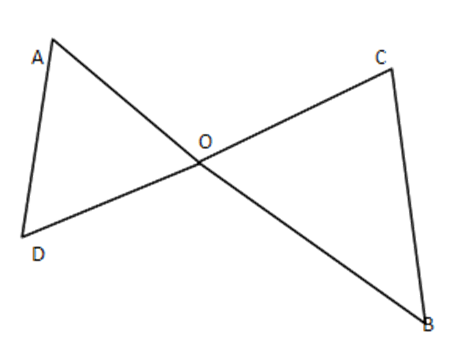
Ans: In  $ \vartriangle AOD\,\, $ and  $ \vartriangle BOC, $ 

 $ OA\times OB=OC\times OD $ 

 $ \text{ i}\text{.e }\dfrac{OA}{OC}=\dfrac{OD}{OB} $ 

And  $ \angle AOD=\angle BOC $  (Vertically opposite Angles)

 $ \therefore \vartriangle AOD\sim\Delta BOC(BySAS) $ 

 $ \therefore \angle A=\angle C $  and  $ \angle B=\angle D $  (Corresponding angles of similar  $ \Delta  $ )

11. In the given figure, 

 $ \text{DE}\|\text{BC} $ and $ \text{AD}=1~\text{cm},\text{BD}=2~\text{cm}. $ What is the ratio of the area of  $ \vartriangle ABC $ to the area of $ \vartriangle ADE $ ?

(image will be uploaded soon)

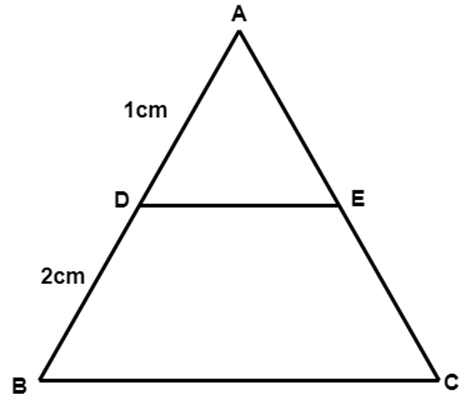
Ans:  $ \because DE\|BC $ in  $ \vartriangle ABC $  $ \therefore \angle ADE=\angle ABC $ 

 $ \angle AED=\angle ACB $ 

Also  $ \angle DAE=\angle DAC $ 

 $ \therefore \vartriangle ADE\sim\Delta ABC $ 

 $ \therefore \vartriangle ADE\sim\vartriangle ABC $ 

 $ \therefore\dfrac{A{{D}^{2}}}{A{{B}^{2}}}=\dfrac{\operatorname{area}(\vartriangle ADE)}{\operatorname{area}(\vartriangle ABC)} $ 

 $ \Rightarrow \dfrac{{{1}^{2}}}{{{3}^{2}}}=\dfrac{\operatorname{area}(\Delta ADE)}{\text{ area }(\Delta ABC)}[\because AB=AD+OB=1+2=3] $ 

 $ \text{ Hence, }\dfrac{\operatorname{area}(\Delta ABC)}{\operatorname{area}(\Delta ADE)}=\dfrac{9}{1} $ 

12. A right-angle triangle has hypotenuse of length  $ \text{p }cm $  and one side of length  $ \text{qcm}. $ If  $ \mathbf{p}-q=1, $ Find the length of third side of the triangle.

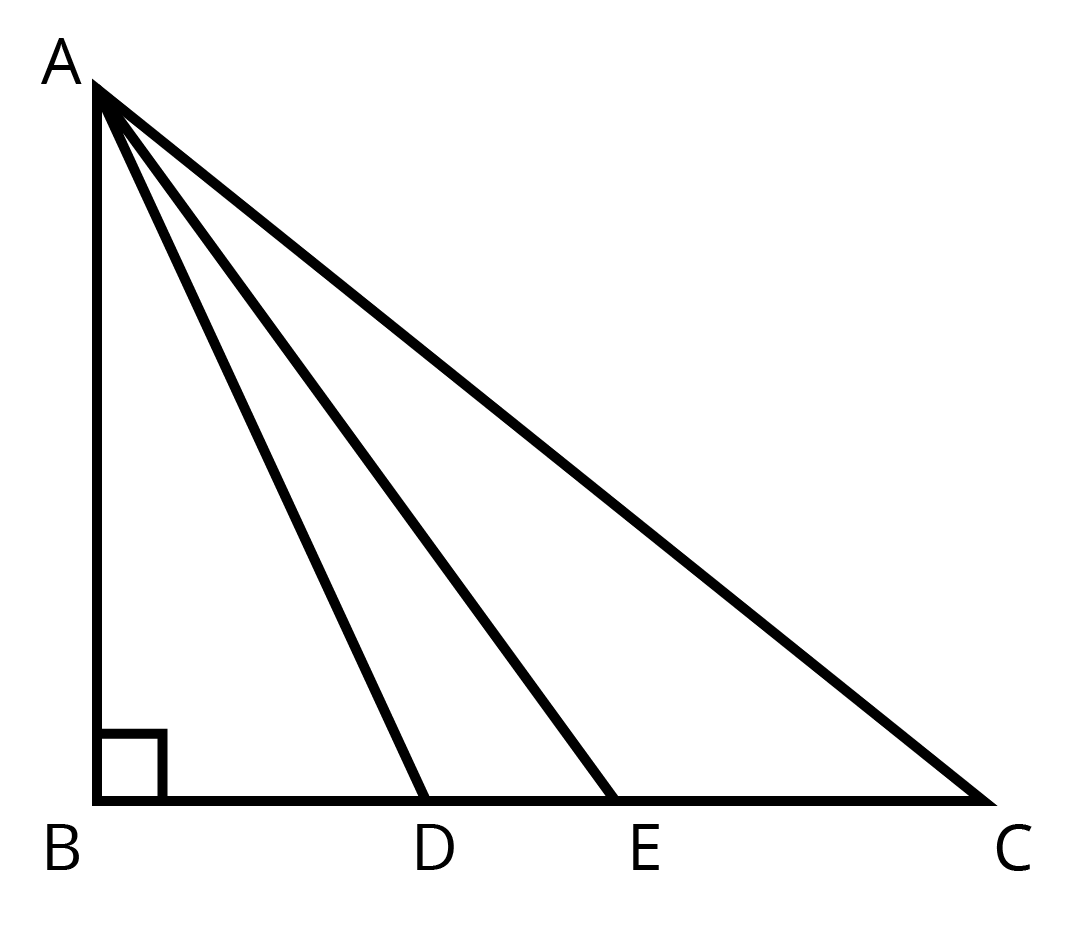
Ans: Let third side  $ =\text{xcm} $ 

Then by Pythagoras theorem.

 $ {{p}^{2}}={{q}^{2}}+{{x}^{2}} $ 

 $ {{x}^{2}}={{p}^{2}}-{{q}^{2}} $  

 $ =(p+q)\times 1(\because p-q=1) $ 

\[=q+1+q\]

\[=2\text{ }q+1\]

 $ \therefore x=\sqrt{2q+1} $ 

13. The length of the diagonals of a rhombus are  $ 24~\text{cm} $ and $ 10~\text{cm} $ . Find each side of rhombus.

Ans:  $ AC=24~\text{cm}\therefore AO=12~\text{cm} $ 

 $ BD=10~\text{cm}\therefore OD=5~\text{cm} $ 

(image will be uploaded soon)

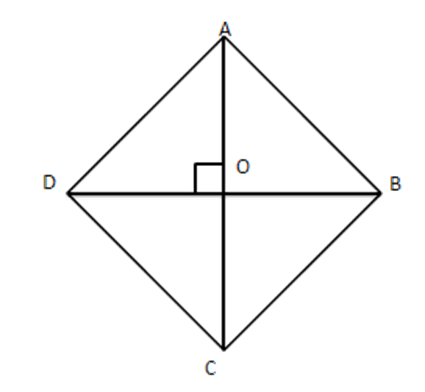
From right-angled  $ \vartriangle AOD\,\,\,A{{D}^{2}}=A{{O}^{2}}+O{{D}^{2}} $ 

 $ \Rightarrow A{{D}^{2}}={{12}^{2}}+{{5}^{2}} $ 

 $ \Rightarrow A{{D}^{2}}=169 $ 

 $ \Rightarrow AD=13~\text{cm} $ 

Hence each side  $ =13~\text{cm} $ 

14. In an isosceles right-angled triangle, prove that hypotenuse is  $ \sqrt{2} $ times 

Ans: Let hypotenuse of right-angled  $ \Delta =h $ units and equal sides of triangle  $ x $ units

 $ \therefore  $ By Pythagoras theorem,

 $ {{h}^{2}}={{x}^{2}}+{{x}^{2}} $ 

 $ \Rightarrow {{h}^{2}}=2{{x}^{2}} $ 

 $ \Rightarrow h=\sqrt{2}x $ 

15. In figure, express  $ \text{x} $  in terms of  $ \mathbf{a},\mathbf{b},\mathbf{c}. $ 

(image will be uploaded soon)

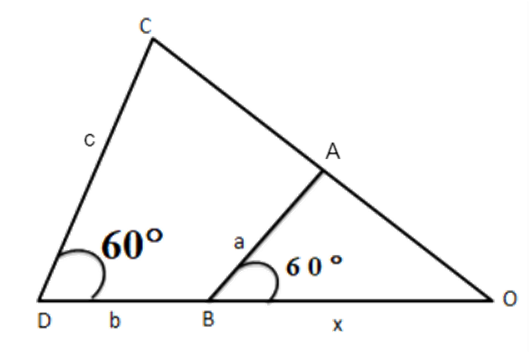
Ans:  $ \vartriangle ABO\sim\vartriangle OCD $ 

 $ \Rightarrow \dfrac{x}{a}=\dfrac{x+b}{c} $ 

 $ \Rightarrow x=ax+ab $ 

 $ \Rightarrow x(c-a)=ab $ 

 $ \Rightarrow x=\dfrac{ab}{c-a} $ 

16. The perimeter of two similar triangle ABC and PQR are respectively  $ 36~\text{cm} $ and  $ 24\text{cm}. $ If  $ \text{PQ}=10~\text{cm}, $  find  $ \text{AB}. $ 

Ans:  $ \vartriangle ABC\sim\Delta PQR $ 

 $ \therefore \dfrac{AB}{PQ}=\dfrac{BC}{QR}=\dfrac{AC}{PR} $ 

 $ \Rightarrow \dfrac{AB+BC+AC}{PQ+QR+PR}=\dfrac{\text{ perimeter of }\Delta ABC}{\text{ perimeter of }\Delta PQR} $ 

 $ \Rightarrow \dfrac{AB}{10}=\dfrac{36}{24} $ 

 $ \Rightarrow AB=\dfrac{36\times 10}{24}=15~\text{cm} $ 

17. In the given figure,  $ \text{DE}||\text{BC}. $  If  $ AD=x,DB=x-2,AE=x+2,EC=x-1 $ find the value of \[\mathbf{x}.\]

(image will be uploaded soon)

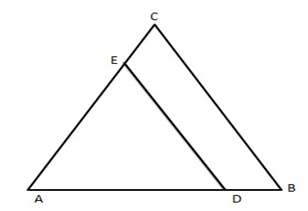
Ans: In the given figure,

\[D\text{ }E\text{ }\left\| BC \right.\]

 $ \therefore \dfrac{AD}{DB}=\dfrac{AE}{EC} $ 

 $ \Rightarrow \dfrac{x}{x-2}=\dfrac{x+2}{x-1} $ 

 $ \Rightarrow {{x}^{2}}-x={{x}^{2}}-4 $ 

 $ \Rightarrow x=4 $ 

18. In the given figure,  $ \dfrac{AO}{OC}=\dfrac{BO}{OD}=\dfrac{1}{2} $ and  $ \text{AB}=5~\text{cm}, $ find the value of  $ \text{DC}. $ 

(image will be uploaded soon )

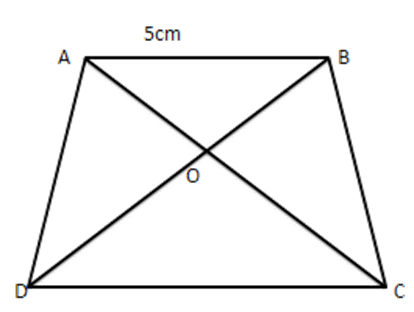
Ans: In  $ \vartriangle AOB $ and  $ \vartriangle COD, $ 

 $ \angle AOB=\angle COD $  [Vertically opposite angles]

 $ \dfrac{AO}{OC}=\dfrac{BO}{OD}\Rightarrow \dfrac{AO}{OB}=\dfrac{OC}{OD} $  [Given]

 $ \therefore \vartriangle AOB\sim\vartriangle COD $  [By SAS similarity]

 $ \therefore \dfrac{AO}{CO}=\dfrac{BO}{DO}=\dfrac{AB}{CD} $ 

 $ \dfrac{1}{2}=\dfrac{AB}{DC}\left[ \dfrac{AO}{OC}=\dfrac{BO}{OD}=\dfrac{1}{2} \right.is\,\,\,given] $ 

 $ \Rightarrow \dfrac{1}{2}=\dfrac{5}{DC} $ 

 $ \Rightarrow DC=10~\text{cm} $ 

19. In  $ \vartriangle ABC,AB=AC $ and  $ \text{D} $ is a point on side  $ \text{AC}, $ such that  $ \text{B}{{\text{C}}^{2}}=AC\times CD\cdot  $ Prove that  $ \text{BD}=\mathbf{BC}. $ 

(image will be uploaded soon)

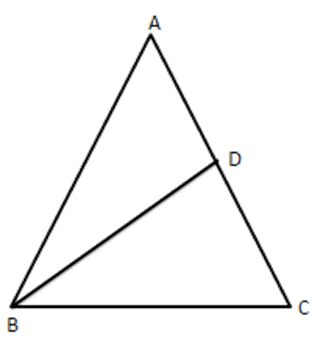
Ans: Given:  $ \Delta ABC $ in which  $ AB=AC,D $ is a point on  $ BC $ 

To prove:  $ \text{BD}=\text{BC } $ 

Proof:  $ B{{C}^{2}}=AC\times CD $ [given] 

 $ \Rightarrow \dfrac{BC}{AC}=\dfrac{DC}{BC} $ 

 $ \text{ In }\vartriangle ABC\text{ and }\vartriangle BDC, $ 

 $ \Rightarrow \dfrac{BC}{CA}=\dfrac{DC}{CB}\text{ and }\angle C=\angle C[\text{ Common }] $ 

 $ \therefore \vartriangle ABC\sim\vartriangle BDC[\text{SASsimilarity}] $ 

 $ \Rightarrow \dfrac{AB}{BD}=\dfrac{AC}{BC}\Rightarrow \dfrac{AC}{BD}=\dfrac{AC}{BC}[\because AB=AC] $ 

 $ \Rightarrow BD=BC $ 

3 Marks Questions

1. In the given figure,  $ \dfrac{QT}{PR}=\dfrac{QR}{QS} $  and  $ \angle 1=\angle2 $ . Prove that  $ \Delta PQS\sim\Delta TQR $ 

(image will be uploaded soon)

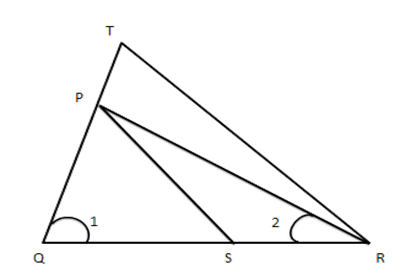
Ans: Since  $ \dfrac{QT}{PR}=\dfrac{QR}{QS} $ [Given]

 $ \therefore \dfrac{QT}{QR}=\dfrac{PR}{QS} $ 

Since  $ \angle 1=\angle 2\,\,\,[Given] $ 

 $ PQ=PR $ 

 (In  $ \Delta PQR $ sides opposites to opposite angles are equal)

 $ \therefore \dfrac{QT}{QR}=\dfrac{PQ}{QS}\ldots \ldots .(iii)[\operatorname{Form}(i)\text{ and }(ii)] $ 

Now in  $ \vartriangle PQS $ and  $ \vartriangle TQR $ 

From (iii), \[\dfrac{PQ}{QS}=\dfrac{QT}{QR}i.e.\dfrac{PQ}{QT}=\dfrac{QS}{QR}\]

And  $ \angle Q=\angle Q $ [Common]

 $ \therefore \Delta PQS\sim\Delta TQR $  [By S.A.S. Rule of similarity]

2. In the given figure, PA, QB and RC are each perpendicular to AC. Prove that  $ \dfrac{1}{x}+\dfrac{1}{2}=\dfrac{1}{y} $ 

(image will be uploaded soon)

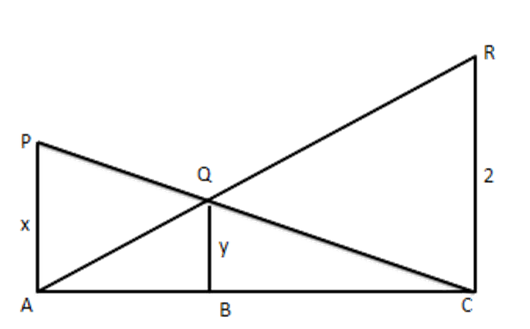
Ans: In   $ \vartriangle PAC\text{ and }\Delta QBC\text{ } $ 

 $ \angle PAC=\angle QBC\left[ \text{ Each }={{90}^{{}^\circ }} \right] $ 

 $ \angle PCA=\angle QCB[\text{Common}] $ 

 $ \therefore \vartriangle PAC\sim\Delta QBC $ 

 $ \dfrac{x}{y}=\dfrac{AC}{BC}\text{ i}\text{.e}\text{. }\dfrac{y}{x}=\dfrac{BC}{AC}\ldots \ldots .(i) $ 

 $ \text{ Similarly, }\dfrac{z}{y}=\dfrac{AC}{AB}\text{ i}\text{.e}\text{. }\dfrac{y}{z}=\dfrac{AB}{AC}\ldots \ldots .(ii) $ 

 $ \text{Adding (i) and (ii), we get } $ 

 $ \Rightarrow \dfrac{BC+AB}{AC}=\dfrac{y}{x}+\dfrac{y}{z}=y\left( \dfrac{1}{x}+\dfrac{1}{z} \right) $ 

 $ \Rightarrow \dfrac{AC}{AC}=y\left( \dfrac{1}{x}+\dfrac{1}{z} \right)\Rightarrow 1=\left( \dfrac{1}{x}+\dfrac{1}{z} \right) $ 

 $ \Rightarrow \dfrac{1}{y}=\dfrac{1}{x}+\dfrac{1}{z} $ 

3. In the given figure,  $ \text{DE}||\text{BC} $ and AD:DB \[=\mathbf{5}:\text{ }\mathbf{4},\]find  $ \dfrac{\text{ area }(\Delta DFE)}{\text{ area }(\Delta CFB)} $ .

(image will be uploaded soon)

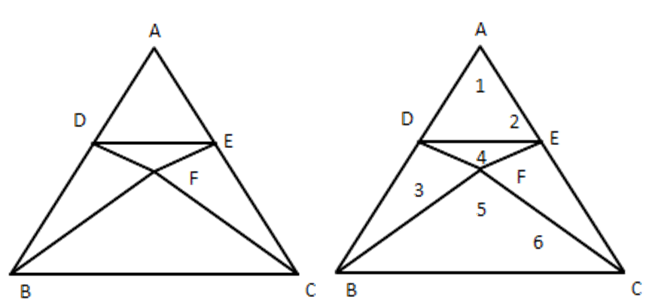
Ans: In  $ \vartriangle ADE $ and  $ \vartriangle ABC, $   $ \angle 1=\angle 1 $ (Common)

 $ \angle 2=\angle ACB $  [Corresponding angles]

 $ \therefore \vartriangle ADE\sim\vartriangle ABC $  [By A.A Rule]

 $ \therefore \dfrac{DE}{BC}=\dfrac{AD}{AB}\ldots \ldots ..i) $ 

Again in  $ \vartriangle DEF $ and  $ \vartriangle CFB, $ 

 $ \angle 3=\angle 6\,\,[Alternate\,\,\,angles] $ 

 $ \angle 4=\angle 5 $  [Vertically oppositeangles]

 $ \therefore \Delta DFE\sim\vartriangle CFB $  [By A.A Rule]

 $ \therefore \dfrac{\text{ Area }(\Delta DFE)}{\text{ area }(\Delta CFB)}=\dfrac{D{{E}^{2}}}{B{{C}^{2}}}={{\left( \dfrac{AD}{AB} \right)}^{2}} $  [From (i)]

 $ ={{\left( \dfrac{5}{9} \right)}^{2}}\left[ \because \dfrac{AD}{DB}=\dfrac{5}{4}\Rightarrow \dfrac{AD}{AD+DB}=\dfrac{5}{5+4}\Rightarrow \dfrac{AD}{DB}=\dfrac{5}{9} \right] $ 

 $ \therefore \dfrac{\operatorname{area}(\Delta DFE)}{\operatorname{area}(\Delta CFB)}=\dfrac{25}{81} $ 

3. Determine the length of an altitude of an equilateral triangle of side ‘2a’ cm.

(image will be uploaded soon)

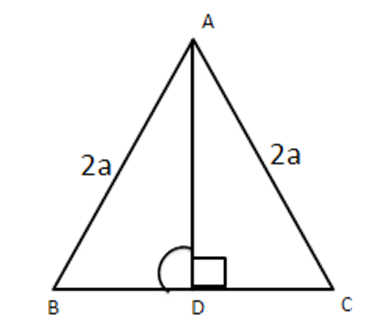
Ans: In right triangles  $ \vartriangle ADB $ and  $ \vartriangle ADC, $ 

\[A\text{ }B=A\text{ }C\] 

\[A\text{ }D=A\text{ }D\]

 $ \therefore \angle ADB=\angle ADC\left( {} \right.Each\left. ={{90}^{{}^\circ }} \right) $ 

 $ \therefore \vartriangle ADB\cong \vartriangle ADC(RHS) $ 

 $ \therefore BD=DC(CPCT) $ 

 $ \therefore BD=DC=a[\because BC=2a] $ 

In right  $ \vartriangle ADB,A{{D}^{2}}+B{{D}^{2}}=A{{B}^{2}} $ (By Pythagoras Theorem)

 $ \Rightarrow A{{D}^{2}}+{{a}^{2}}={{(2a)}^{2}} $ 

 $ \Rightarrow A{{D}^{2}}=4{{a}^{2}}-{{a}^{2}}=3{{a}^{2}} $ 

 $ \Rightarrow AD=\sqrt{3}a~\text{cm} $ 

4. In the given figure, if  $ \angle 1=\angle 2 $ and  $ \vartriangle NSQ\cong \vartriangle MTR. $  Then prove that  $ \Delta PTS\sim\Delta PRO $ 

(image will be uploaded soon)

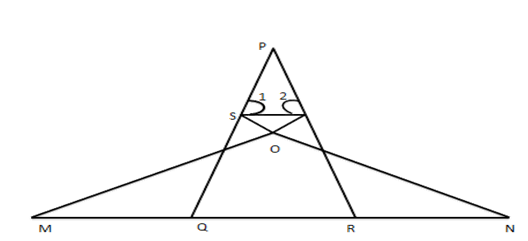
Ans:  $ \Rightarrow \angle Q=\angle R(\text{ in }\Delta PQR) $ 

 $ ={{90}^{{}^\circ }}-\dfrac{1}{2}\angle P $ 

 $ \text{Again }\angle 1=\angle 2[\text{given}\,\,\,\text{in}\,\,\vartriangle \text{PST}] $ 

 $ \therefore \angle 1=\angle 2=\dfrac{1}{2}\left( {{180}^{{}^\circ }}-\angle P \right) $ 

 $ ={{90}^{{}^\circ }}-\dfrac{1}{2}\angle P $ 

Thus, in  $ \Delta PTS $ and  $ \vartriangle PRQ $ 

 $ \angle 1=\angle Q\left[ \text{ Each }={{90}^{{}^\circ }}-\dfrac{1}{2}\angle P \right] $ 

 $ \angle 2=\angle R,\angle P=\angle P(\text{ Common }) $ 

 $ \Delta PTS\sim\Delta PRQ $ 

5. In the given figure the line segment XY||AC and XY divides triangular region ABC into two points equal in area, Determine $ \dfrac{AX}{AB} $ .

(image will be uploaded soon)

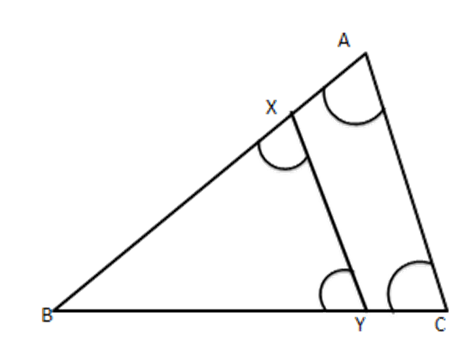
Ans: Since  $ XY\|AC $ 

 $ \therefore \angle BXY=\angle BAC $  

 $ \angle BYX=\angle BCA $  [Corresponding angles]

 $ \therefore \Delta BXY\sim\vartriangle BAC $  [A.A. similarity]

 $ \therefore \dfrac{\operatorname{ar}(\Delta BXY)}{\operatorname{ar}(\Delta BAC)}=\dfrac{B{{X}^{2}}}{B{{A}^{2}}} $ 

But  $ \operatorname{ar}(\Delta BXY)=\operatorname{ar}(XYCA) $ 

 $ \therefore 2(\Delta BXY)=\operatorname{ar}(\Delta BXY)+\operatorname{ar}(XYCA) $ 

 $ =\operatorname{ar}(\Delta BAC) $ 

 $ \therefore \dfrac{\operatorname{ar}(\Delta BXY)}{ar(\Delta BAC)}=\dfrac{1}{2} $ 

 $ \therefore \dfrac{B{{X}^{2}}}{B{{A}^{2}}}=\dfrac{1}{2} $ 

 $ \Rightarrow \dfrac{BX}{BA}=\dfrac{1}{\sqrt{2}} $ 

 $ \therefore \dfrac{BA-BX}{BA}=\dfrac{\sqrt{2}-1}{\sqrt{2}} $ 

 $ \Rightarrow \dfrac{AX}{AB}=\dfrac{\sqrt{2}-1}{\sqrt{2}}=\dfrac{2-\sqrt{2}}{2} $ 

6. BL and CM are medians of  $ \vartriangle ABC $ right angled at A. Prove that  $ 4\left( \text{B}{{\text{L}}^{2}}+\text{C}{{\text{M}}^{2}} \right)=5\text{B}{{\text{C}}^{2}} $ 

(image will be uploaded soon)

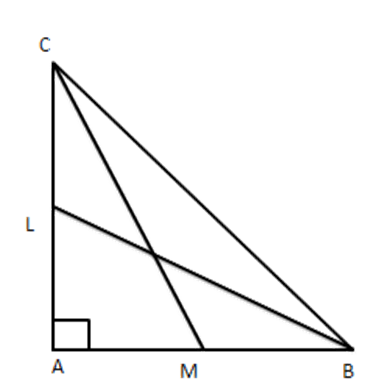
Ans: BL and CM are medians of a  $ \vartriangle ABC $  in which  $ \angle A={{90}^{{}^\circ }} $ 

From  $ \Delta ABC,B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}} $ 

From right angled  $ \vartriangle ABL, $ 

 $ B{{L}^{2}}=A{{L}^{2}}+A{{B}^{2}} $ 

 $ i.e.,B{{L}^{2}}={{\left( \dfrac{AC}{2} \right)}^{2}}+A{{B}^{2}} $ 

 $ \Rightarrow 4B{{L}^{2}}=A{{C}^{2}}+4A{{B}^{2}} $ 

 (ii)

From right-angled  $ \vartriangle CMA $ 

 $ C{{M}^{2}}=A{{C}^{2}}+A{{M}^{2}} $ 

i.e.  $ C{{M}^{2}}=A{{C}^{2}}+{{\left( \dfrac{AB}{2} \right)}^{2}} $ [ mid-point] 

 $ \Rightarrow C{{M}^{2}}=A{{C}^{2}}+\dfrac{A{{B}^{2}}}{4} $ 

 $ \Rightarrow 4C{{M}^{2}}=4A{{C}^{2}}+A{{B}^{2}} $ 

Adding (ii) and (iii), we get

i.e.  $ 4\left( B{{L}^{2}}+C{{M}^{2}} \right)=5B{{C}^{2}} $ [From (i)]

7.  $ \text{ABC} $ is a right triangle right angled at  $ \text{C}. $ Let  $ \text{BC}=\text{a},\text{CA}=\mathbf{b},\text{AB}=\text{c} $ and let  $ \text{p} $ be the length of perpendicular from C on AB, prove that

(i)  $ \mathbf{cp}=\mathbf{ab} $ 

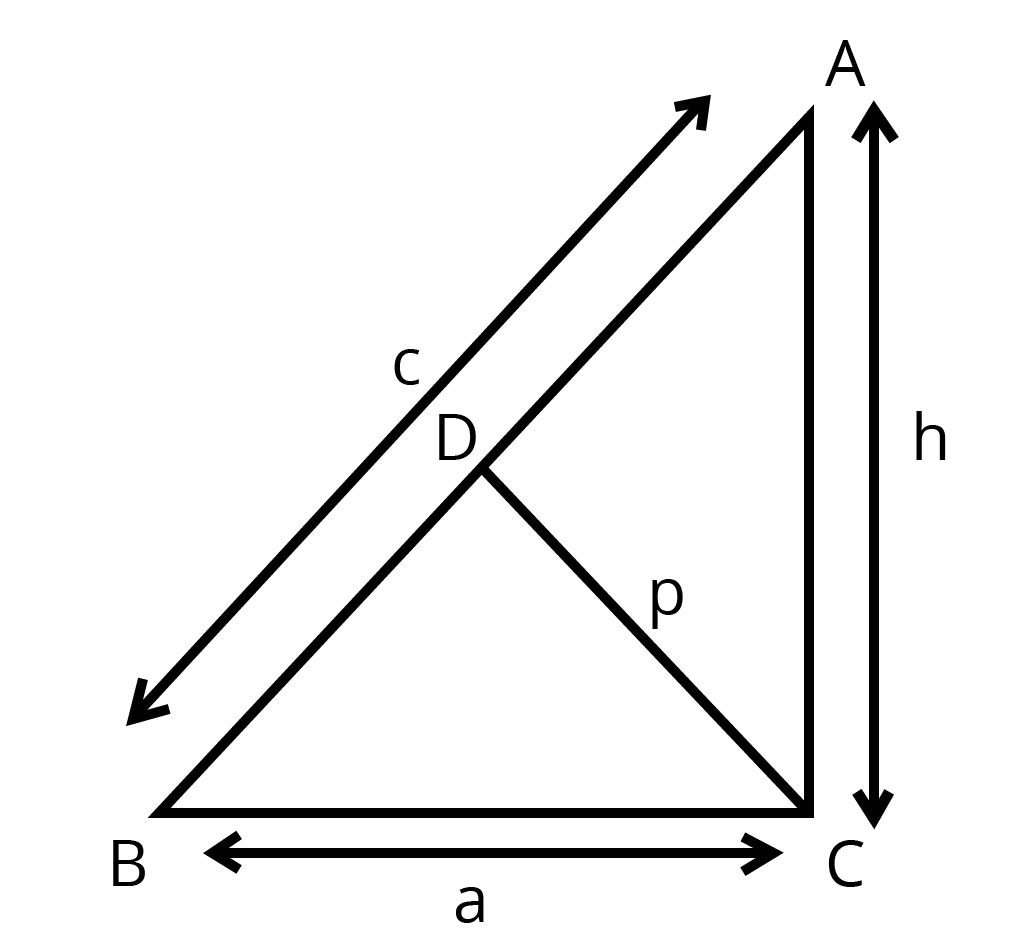
Ans:  Draw  $ CD\bot AB $ 

Then,  $ CD=p $ 

Now area of  $ \vartriangle ABC=\dfrac{1}{2}(BC\times CA) $ 

 $ =\dfrac{1}{2} a b $ 

Also area of  $ \Delta ABC=\dfrac{1}{2}AB\times CD $ 

 $ =\dfrac{1}{2}cp $ Then,  $ \dfrac{1}{2}ab=\dfrac{1}{2}cp $ 

 $ \Rightarrow cp=ab $ 

(ii)  $ \dfrac{1}{{{p}^{2}}}=\dfrac{1}{{{a}^{2}}}+\dfrac{1}{{{b}^{2}}} $ 

Ans: Since  $ \vartriangle ABC $ is a right-angled triangle with  $ \angle C={{90}^{{}^\circ }} $ 

 $ \therefore A{{B}^{2}}=B{{C}^{2}}+A{{C}^{2}} $ 

 $ \Rightarrow {{c}^{2}}={{a}^{2}}+{{b}^{2}} $ 

 $ \Rightarrow {{\left( \dfrac{ab}{p} \right)}^{2}}={{a}^{2}}+{{b}^{2}} $ 

 $ \therefore cp=ab $ 

 $ \Rightarrow c=\dfrac{ab}{p} $ 

 $ \Rightarrow \dfrac{1}{{{p}^{2}}}=\dfrac{{{a}^{2}}+{{b}^{2}}}{{{a}^{2}}{{b}^{2}}} $ 

 $ \Rightarrow \dfrac{1}{{{p}^{2}}}=\dfrac{1}{{{b}^{2}}}+\dfrac{1}{{{a}^{2}}} $ 

Thus  $ \dfrac{1}{{{p}^{2}}}=\dfrac{1}{{{a}^{2}}}+\dfrac{1}{{{b}^{2}}} $ 

8. In figure, a triangle  $ \text{ABC} $ is right-angled at B. side BC is trisected at points  $ \text{D} $ and  $ \text{E}, $ prove that  $ 8A{{E}^{2}}=3A{{C}^{2}}+5A{{D}^{2}} $ .

(image will be uploaded soon)

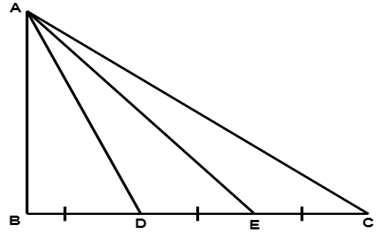
Ans: Given:  $ \vartriangle ABC $ is right-angled at \[B.\]Side BC is trisected at D and E.

To Prove:  $ 8A{{E}^{2}}=3A{{C}^{2}}+5A{{D}^{2}} $ 

Proof: D and E are the paints of trisection of BC

 $ BD=\dfrac{1}{3}BC\text{ and }BE=\dfrac{2}{3}BC $ 

In right-angled triangle  $ \text{ABD} $ 

 $ A{{D}^{2}}=A{{B}^{2}}+B{{D}^{2}}\ldots \ldots \ldots .(ii) $  [Using Pythagoras theorem]

In  $ \vartriangle ABE $ 

 $ A{{E}^{2}}=A{{B}^{2}}+B{{E}^{2}}\ldots \left( iii \right) $ 

In  $ \vartriangle ABC $ 

 $ A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}\ldots \left( iv \right) $ 

From (ii) and (iii), we have

 $ A{{D}^{2}}-A{{E}^{2}}=B{{D}^{2}}-B{{E}^{2}} $ 

 $ \Rightarrow A{{D}^{2}}-A{{E}^{2}}={{\left( \dfrac{1}{3}BC \right)}^{2}}-{{\left( \dfrac{2}{3}BC \right)}^{2}} $ 

 $ \Rightarrow A{{D}^{2}}-A{{E}^{2}}=\dfrac{1}{9}B{{C}^{2}}-\dfrac{4}{9}B{{C}^{2}}=\dfrac{-3}{9}B{{C}^{2}} $ 

 $ \Rightarrow A{{E}^{2}}-A{{D}^{2}}=\dfrac{1}{3}B{{C}^{2}}\ldots \ldots .(v) $ 

From (iii) and (iv), we have

 $ A{{C}^{2}}-A{{E}^{2}}=B{{C}^{2}}-B{{E}^{2}} $ 

 $ =B{{C}^{2}}-\dfrac{4}{9}B{{C}^{2}} $ 

 $ \Rightarrow A{{C}^{2}}-A{{E}^{2}}=\dfrac{5}{9}B{{C}^{2}} $ 

From (v) and (vi), we get

 $ A{{C}^{2}}-A{{E}^{2}}=\dfrac{5}{3}\left( A{{E}^{2}}-A{{D}^{2}} \right) $ 

 $ \Rightarrow 3A{{C}^{2}}-3A{{E}^{2}}=5A{{E}^{2}}-5A{{D}^{2}} $ 

 $ \Rightarrow 8A{{E}^{2}}=5A{{D}^{2}}+3A{{C}^{2}} $ 

9. In figure, DEFG is a square and  $ \angle BAC={{90}^{{}^\circ }}, $ show that $ D{{E}^{2}}=BD\times EC $ .

(image will be uploaded soon)

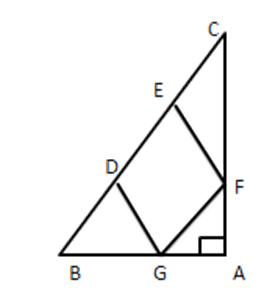
Ans: Given:  $ \vartriangle ABC $ is right-angled at A and DEFG is a square To Prove:  $ D{{E}^{2}}=BD\times EC $ 

Proof: Let  $ \angle C=x\ldots \ldots ..(i) $ 

Then,  $ \angle ABC={{90}^{{}^\circ }}-x[\because \Delta ABC $ is right angled ] 

Also  $ \Delta BDG $ is right-angled at D.

 $ \angle BGD={{90}^{{}^\circ }}-\left( {{90}^{{}^\circ }}-x \right)=x\ldots \ldots .(ii) $ 

From (i) and (ii), we get

 $ \angle BGD=\angle C\ldots \ldots ..(iii) $ 

Consider  $ \Delta BDG\,\,and\,\,\Delta CEF $ 

 $ \angle CEF=\angle BDG=90[\because DEFG $ is square ]

 $ \angle BGD=\angle C $  [From (iii) ]

 $ \therefore \vartriangle BDG\sim\vartriangle FEC\,\,[ByAAsimilarity] $ 

 $ \therefore \dfrac{BD}{EF}=\dfrac{DG}{EC} $ 

 $ \Rightarrow EF\times DG=BD\times EC $ 

But  $ EF=DG=DE[\because  $ side of a square]

 $ \Rightarrow DE\times DE=BD\times EC $ 

 $ \Rightarrow D{{E}^{2}}=BD\times EC $ 

10.In a quadrilateral  $ \text{ABCD},\text{P},\text{Q},\text{R},\text{S} $ are the mid-points of the sides  $ \text{AB},\text{BC},\text{CD} $ and DA respectively. Prove that PQRS is a parallelogram.

(image will be uploaded soon)

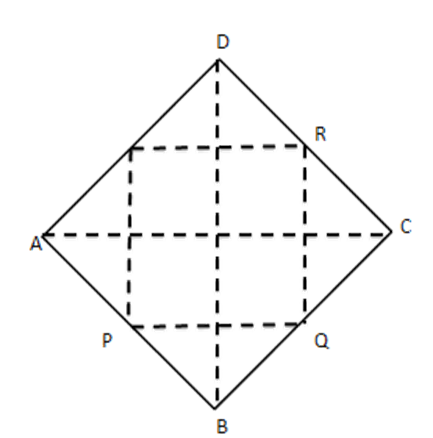
Ans: To Prove: PQRS is a parallelogram

Construction: Join AC

Proof: In  $ \vartriangle DAC, $ 

 $ \dfrac{DS}{SA}=\dfrac{DR}{RC}=1[\because \text{S} $ and R are mid-points of AD and DC ]

 $ \Rightarrow SR\|AC $ ....... (i) [by converse of B.P.T]

In  $ \Delta BAC,\dfrac{PB}{AP}=\dfrac{BQ}{QC}=1[\because \text{P} $ and  $ \text{Q} $ are mid points of  $ \text{AB} $ and BC]

 $ \Rightarrow PQ\|AC $  .......(ii) [By converse of B.P.T]

From (i) and (ii), we get

 $ SR\|PQ\ldots \ldots .(iii) $ 

Similarly, join B to D and PS| |QR

 $ \Rightarrow \therefore PQRS $ is a parallelogram.

11. Triangle  $ \text{ABC} $ is right-angled at  $ \text{C} $ and  $ \text{CD} $ is perpendicular to  $ \text{AB}, $ prove that  $ B{{C}^{2}}\times AD=A{{C}^{2}}\times BD $ 

(image will be uploaded soon)

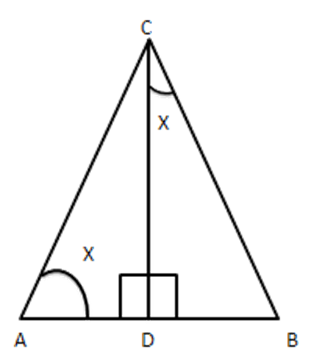
Ans: Given: A  $ \vartriangle ABC $ right angled at  $ \text{C} $ and  $ CD\bot AB $ 

To Prove:  $ B{{C}^{2}}\times AD=A{{C}^{2}}\times BD $ 

Proof: Consider  $ \vartriangle ACD\,\,\,and\,\,\Delta DCB $ 

Let  $ \angle A=x $ 

Then $ \angle B={{90}^{{}^\circ }}-x[\because \Delta ACB $ is right angled]

 $ \Rightarrow \angle DCB=x[\because \Delta CDB $ is right angled ]

In  $ \vartriangle ADC $ and  $ \vartriangle CDB, $ 

 $ \angle ADC=\angle CDB\left[ {{90}^{{}^\circ }}\text{ each } \right] $ 

 $ \angle A=\angle DCB=x $ 

 $ \vartriangle ACD\sim\vartriangle CBD $  [By AA similarity ]

 $ \Rightarrow \dfrac{\operatorname{ar}\Delta ACD}{\operatorname{ar}\Delta CBD}=\dfrac{A{{C}^{2}}}{B{{C}^{2}}} $ 

 $ \Rightarrow \dfrac{\dfrac{1}{2}AD\times CD}{\dfrac{1}{2}BD\times CD}=\dfrac{A{{C}^{2}}}{B{{C}^{2}}} $ 

 $ \Rightarrow \dfrac{AD}{BD}=\dfrac{A{{C}^{2}}}{B{{C}^{2}}} $ 

 $ \Rightarrow B{{C}^{2}}\times AD=A{{C}^{2}}\times BD $ 

12. Triangle  $ \text{ABC} $ is right angled at  $ \text{C} $ and  $ \text{CD} $ is perpendicular to  $ \text{AB}. $  Prove that  $ B{{C}^{2}}\times AD=A{{C}^{2}}\times BD $ 

(image will be uploaded soon)

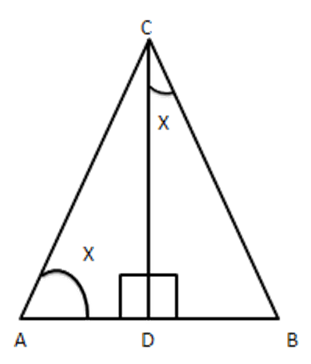
Ans: Given: \[\vartriangle ABC\]right-angled at C and  $ CD\bot AB $ 

To prove:  $ B{{C}^{2}}\times AD=A{{C}^{2}}\times BD $ 

Proof: Consider  $ \vartriangle ACD $ and  $ \vartriangle DCB $ 

(image will be uploaded soon)

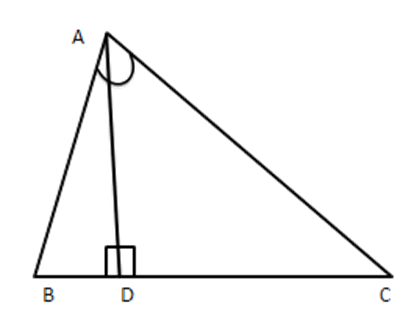
Let  $ \angle A=x $ 

Then  $ \angle B=90-x[\because \Delta ACB $ is right angled ]

 $ \Rightarrow \angle DCB=x[\because \Delta CDB $ is right angled ]

In  $ \vartriangle ADC $ and  $ \Delta CDB $ 

 $ \angle ADC=\angle CDB\left[ {{90}^{{}^\circ }} \right. $ each ]

 $ \angle A=\angle DCB=x[ $ from above ]

 $ \therefore \vartriangle ACD\sim\Delta CBD[ $ AA similarity]

 $ \Rightarrow \dfrac{\operatorname{ar}(\Delta ACD)}{ar(\Delta VBD)}=\dfrac{A{{C}^{2}}}{B{{C}^{2}}} $ 

 $ \Rightarrow \dfrac{\dfrac{1}{2}\times AD\times CD}{\dfrac{1}{2}\times BD\times CD}=\dfrac{A{{C}^{2}}}{B{{C}^{2}}} $ 

 $ \Rightarrow \dfrac{AD}{BD}=\dfrac{A{{C}^{2}}}{B{{C}^{2}}} $ 

 $ \Rightarrow B{{C}^{2}}\times AD=A{{C}^{2}}BD $ 

13. In figure,  $ \text{ABC} $ and DBC are two triangles on the same base BC. If AD intersect EC at 0, prove that  $ \dfrac{\operatorname{ar}(\Delta ABC)}{ar(\Delta DBC)}=\dfrac{AO}{DO} $ 

(image will be uploaded soon)

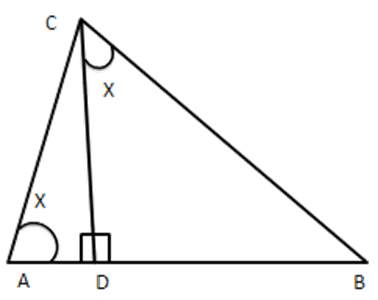
Ans: Given: ABC and DBC are two triangles on the same base BC but on the opposite sides of BC, AD intersects BC at O.

Construction: Draw  $ AL\bot BC $ and  $ DM\bot BC $ 

To prove:  $ \dfrac{ar(\Delta ABC)}{\operatorname{ar}(\Delta DBC)}=\dfrac{AO}{EO} $ 

Proof: In  $ \vartriangle ALO\,\,\,and\,\,\,\vartriangle DMO $ 

 $ \angle ALO=\angle DMO\left[ each \right. $   $ \left. {{90}^{{}^\circ }} \right] $ 

 $ \angle AOL=\angle DOM[Vertically\,\,\,opposite\,\,angles] $ 

 $ \therefore \vartriangle ALO\sim\Delta DMO[ $ By AA similarily]

 $ \Rightarrow \dfrac{AL}{DM}=\dfrac{AO}{DO} $ 

 $ \therefore \dfrac{\operatorname{ar}(\Delta ABC)}{ar(\Delta DBC)}=\dfrac{AO}{DO} $ 

14. In figure, ABC is a right triangle right-angled at B. Medians AD and CE are of respective lengths 5 cm and  $ 2\sqrt{5}cm $ , find length of AC.

(image will be uploaded soon)

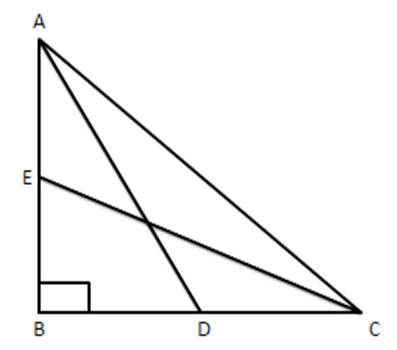
Ans: Given:  $ \vartriangle ABC $ with  $ \angle B={{90}^{{}^\circ }},\text{AD} $ and  $ \text{CE} $ are medians 

To find: Length of AC

Proof: In  $ \vartriangle ABD $ right-angled at B,

 $ A{{D}^{2}}=A{{B}^{2}}+B{{D}^{2}}[By\text{ pythagoras theorem }] $ 

 $ =A{{B}^{2}}+{{\left( \dfrac{1}{2}BC \right)}^{2}}\left[ \because BD=\dfrac{1}{2}BC \right] $ 

 $ =A{{B}^{2}}+\dfrac{1}{4}B{{C}^{2}} $ 

 $ 4A{{D}^{2}}=4A{{B}^{2}}+B{{C}^{2}}\ldots \ldots ..(i) $ 

In  $ \Delta BCE $ right-angled at B

 $ C{{E}^{2}}=B{{E}^{2}}+B{{C}^{2}} $ 

 $ \Rightarrow C{{E}^{2}}={{\left( \dfrac{1}{2}AB \right)}^{2}}+B{{C}^{2}} $ 

 $ \Rightarrow C{{E}^{2}}=\dfrac{1}{4}A{{B}^{2}}+B{{C}^{2}} $ 

 $ \Rightarrow 4C{{E}^{2}}=A{{B}^{2}}+4B{{C}^{2}}\ldots \ldots .(ii) $ 

 $ \Rightarrow 4A{{D}^{2}}+4C{{E}^{2}}=5A{{B}^{2}}+5B{{C}^{2}}=5\left( A{{B}^{2}}+B{{C}^{2}} \right) $ 

 $ \Rightarrow 4A{{D}^{2}}+4C{{E}^{2}}=5A{{C}^{2}} $ 

Given that  $ \text{AD}=5 $ and  $ CE=2\sqrt{5} $ 

 $ 4{{(5)}^{2}}+4{{(2\sqrt{5})}^{2}}=5A{{C}^{2}} $ 

 $ \Rightarrow 100+80=5A{{C}^{2}} $ 

 $ \Rightarrow A{{C}^{2}}=\dfrac{180}{5} $ 

 $ \Rightarrow A{{C}^{2}}=36\Rightarrow AC=6~\text{cm} $ 

15. In the given figure,  $ \dfrac{QR}{OS}=\dfrac{QT}{PR} $ and  $ \angle 1=\angle 2, $ show that  $ \vartriangle PQS\sim\Delta TQR. $ 

(image will be uploaded soon)

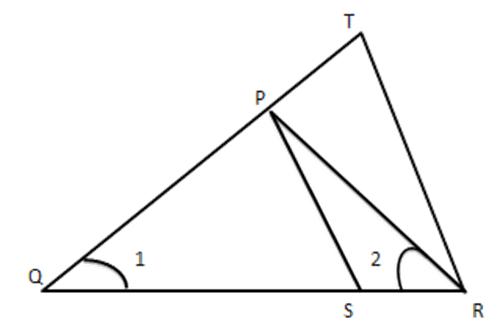
Ans: Given:  $ \dfrac{QR}{QS}=\dfrac{QT}{PR} $ and  $ \angle 1=\angle 2 $ 

Proof: As  $ \angle 1=\angle 2 $ 

 $ PQ=PR\ldots ..(i)[ $ side opposite to equal angles are equal]

Also  $ \dfrac{QR}{QS}=\dfrac{QT}{PR}( $ given)  $ \ldots \ldots .(ii) $ 

 $ \Rightarrow \dfrac{QR}{QS}=\dfrac{QT}{PQ} $ From (i) and (ii)

In  $ \vartriangle PQS $ and TQR, we have

 $ \dfrac{QR}{QS}=\dfrac{QT}{QP}=\dfrac{QS}{QT}\Rightarrow \dfrac{QR}{QP}[ $ From (ii)]

16. Given a triangle ABC. 0 is any point inside the triangle  $ \text{ABC},\text{X},\text{Y},\text{Z} $ are points on  $ \text{OA}, $ OB and OC, such that  $ \text{XY}||\text{AB}\,\,\,and\,\,\,\text{XZ}||\text{AC}, $ show that  $ \text{YZ}\|AC. $ 

(image will be uploaded soon)

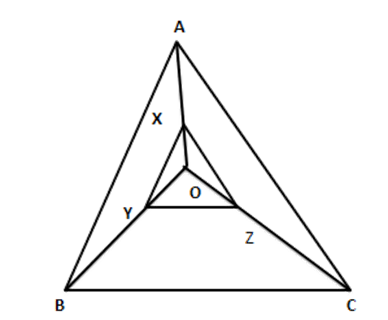
Ans: Given: A  $ \vartriangle ABC,O $ is a point inside  $ \vartriangle ABC,X,Y $ and  $ Z $ are points on  $ OA,OB $ and OC respectively such that  $ \text{XY}||\text{AB} $ and  $ \text{XZ}\|\text{AB} $ and  $ \text{XZ}||\text{AC} $ 

To show: YZ| | BC

Proof: In  $ \vartriangle OAB,XY\|AB $ 

 $ \dfrac{OX}{AX}=\dfrac{OY}{BY}\ldots \ldots .(i)[By\text{B}.\text{P}.\text{T}] $ 

In  $ \Delta OAC,XZ\|AC $ 

 $ \therefore \dfrac{OX}{AX}=\dfrac{OZ}{CZ}\ldots \ldots ..(ii)[By\text{B}.\text{P}.\text{T}] $ 

From (i) and (ii), we get  $ \dfrac{OY}{BY}=\dfrac{OZ}{CZ}\ldots \ldots \ldots . $  (iii)

Now in  $ \vartriangle OBC\dfrac{OY}{BY}=\dfrac{OZ}{CZ}(from(iii)) $ 

 $ \Rightarrow YZ\|BC $  [Converse of B.P.T]

17. PQR is a right triangle right angled at Q. If QS = SR, show that  $ P{{R}^{2}}=4P{{S}^{2}}-3P{{Q}^{2}} $ 

(image will be uploaded soon)

Ans: Given: PQR is a right Triangle, right-angled at Q Also  $ QS=SR $ 

To prove:  $ P{{R}^{2}}=4P{{S}^{2}}-3P{{Q}^{2}} $ 

Proof: In right-angled triangle PQR right angled at Q.

  $ P{{R}^{2}}=P{{Q}^{2}}+Q{{R}^{2}} $ [By Pythagoras theorem]

Also  $ QS=\dfrac{1}{2}QR[\because QS=QR] $ 

In right-angled triangle PQS, right angled at Q.

 $ P{{S}^{2}}=P{{Q}^{2}}+Q{{S}^{2}} $ 

 $ \Rightarrow P{{S}^{2}}=P{{Q}^{2}}+{{\left( \dfrac{1}{2}QR \right)}^{2}}[\text{ From }(ii)] $ 

 $ \Rightarrow 4P{{S}^{2}}=4P{{Q}^{2}}+Q{{R}^{2}}\ldots \ldots .(iii) $ 

From (i) and (iii), we get

 $ P{{R}^{2}}=P{{Q}^{2}}+4P{{S}^{2}}-4P{{Q}^{2}} $ 

 $ \Rightarrow P{{R}^{2}}=4P{{S}^{2}}-3P{{Q}^{2}} $ 

18. A ladder reaches a window which is 12 m above the ground on one side of the street. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window 9 m high. Find the width of the street if the length of the ladder is 15 m.

(image will be uploaded soon)

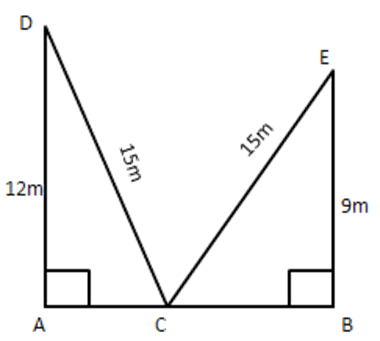
Ans: Let AB be the width of the street and C be the foot of ladder.

Let D and E be the windows at heights  $ 12~\text{m} $ and  $ 9~\text{m} $ respectively from the ground.

In  $ \Delta CAD, $ right angled at A, we have

 $ C{{D}^{2}}=A{{C}^{2}}+A{{D}^{2}} $ 

 $ \Rightarrow {{15}^{2}}=A{{C}^{2}}+{{12}^{2}} $ 

 $ \Rightarrow A{{C}^{2}}=225-144=81 $ 

 $ \Rightarrow AC=9~\text{m} $ 

In  $ \Delta CBE, $ right angled at B, we have

 $ C{{E}^{2}}=B{{C}^{2}}+B{{E}^{2}} $ 

 $ \Rightarrow {{15}^{2}}=B{{C}^{2}}+{{9}^{2}} $ 

 $ \Rightarrow B{{C}^{2}}=225-81 $ 

 $ \Rightarrow B{{C}^{2}}=144 $ 

 $ \Rightarrow BC=12m $ 

Hence, width of the street  $ \text{AB}=\text{AC}+\text{BC}=9+12=21~\text{m} $ 

19. In figure,  $ \dfrac{XP}{PY}=\dfrac{XQ}{QZ}=3 $ , if the area of\[\vartriangle XYZ\] is  $ 32c{{m}^{2}} $  then find the area of the quadrilateral PYZQ.

(image will be uploaded soon)

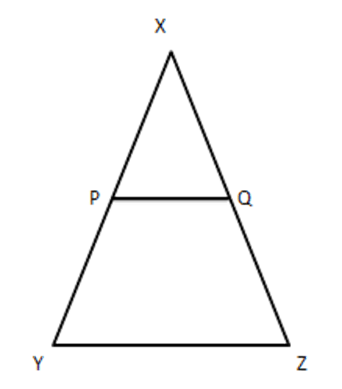
Ans: Given  $ \dfrac{XP}{PY}=\dfrac{XQ}{QZ} $ (given)

 $ \Rightarrow PQ\|YZ..... $  (i) (By converse of B.P.T)

In  $ \vartriangle XPQ $ and $ \vartriangle XYZ $ , we have

($ \angle XPQ=\angle Y $) (From (i) corresponding angles)

 $ \angle X=\angle Y[\text{common}] $ 

 $ \therefore \Delta XPQ\sim\Delta XYZ $  (By AA similarity)

 $ \therefore \dfrac{\operatorname{ar}(\Delta XYZ)}{ar(\Delta XPQ)}=\dfrac{X{{Y}^{2}}}{X{{P}^{2}}} $ 

We have  $ \dfrac{PY}{XP}=\dfrac{1}{3}\Rightarrow \dfrac{PY}{XP}+1=\dfrac{1}{3+1}\Rightarrow \dfrac{PY+XP}{XP}=\dfrac{4}{3} $ 

 $ \Rightarrow \dfrac{XY}{XP}=\dfrac{4}{3} $ 

Substituting in (i), we get

 $ \dfrac{\operatorname{ar}(\Delta XYZ)}{\operatorname{ar}(\Delta XPQ)}={{\left( \dfrac{4}{3} \right)}^{2}}=\dfrac{16}{9} $ 

 $ \Rightarrow \dfrac{32}{\operatorname{ar}(XPQ)}=\dfrac{16}{9} $ 

 $ \operatorname{ar}(XPQ)=\dfrac{32\times 9}{16}=18~\text{c}{{\text{m}}^{2}} $ 

Area of quadrilateral  $ PYZQ=32-18=14~\text{c}{{\text{m}}^{2}} $ 

4 Marks Questions

1. Prove that if a line is drawn parallel to one side of a triangle to intersect the other two sides in district points, ten other two sides are divided in the same ratio. By using this theorem, prove that in\[\vartriangle ABC\] if  $ DE\left\| BC \right. $  then,  $ \dfrac{AD}{BD}=\dfrac{AE}{AC} $ 

(image will be uploaded soon)

Ans: Given: In  $ \vartriangle ABC\,\,\,\,DE\|BC $ intersect AB at D and AC at E. To Prove:  $ \dfrac{AD}{DB}=\dfrac{AE}{EC} $ 

Construction: Draw  $ EF\bot AB $ and  $ DG\bot AC $  and join DC and  $ \text{BE}. $ 

Proof:  $ \operatorname{ar}\vartriangle ADE=\dfrac{1}{2}AD\times EF $ 

 $ \operatorname{ar}\Delta DBE=\dfrac{1}{2}DB\times EF $ 

 $ \therefore \dfrac{\operatorname{ar}\vartriangle ADE}{\operatorname{ar}\Delta DBE}=\dfrac{\dfrac{1}{2}AD\times EF}{\dfrac{1}{2}DB\times EF}=\dfrac{AD}{DB}\ldots \ldots .(i) $ 

Similarly,  $ \dfrac{\operatorname{ar}\Delta ADE}{\operatorname{ar}\Delta DEC}=\dfrac{\dfrac{1}{2}AE\times DG}{\dfrac{1}{2}EC\times DG}=\dfrac{AE}{EC}\ldots \ldots ..(ii) $ 

Since  $ \vartriangle DBE $ and  $ \vartriangle DEC $ are on the same base and between the same parallels

 $ \therefore \operatorname{ar}(\Delta DBE)=\operatorname{ar}(\Delta DEC) $ 

 $ \Rightarrow \dfrac{1}{\operatorname{ar}(\Delta DBE)}=\dfrac{1}{\operatorname{ar}(\Delta DEC)} $ 

 $ \therefore \dfrac{\operatorname{ar}\Delta ADE}{\operatorname{ar}\Delta DBF}=\dfrac{\operatorname{ar}\Delta ADE}{ar\Delta DFC} $ 

 $ \Rightarrow \dfrac{AD}{DB}=\dfrac{AB}{EC} $ 

 $ \because DE\|BC $ 

 $ \Rightarrow \dfrac{AD}{AD+DB}=\dfrac{AE}{AE+EC}\left[ \because \dfrac{p}{q}=\dfrac{r}{s}\Rightarrow \dfrac{p}{p+q}=\dfrac{r}{r+s} \right] $ 

 $ \Rightarrow \dfrac{AD}{AB}=\dfrac{AE}{AC} $ 

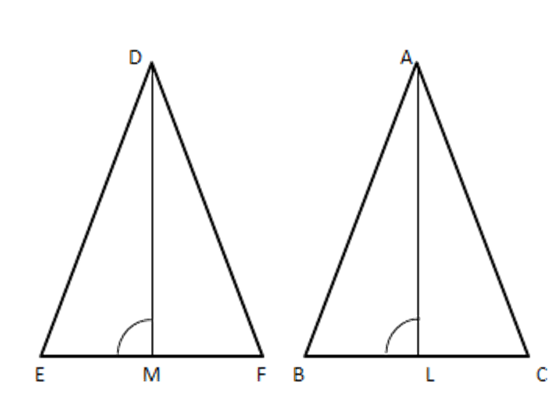
2. Prove that the ratio of areas of two similar triangles are in the ratio of the squares of the corresponding sides. By using the above theorem solve in two similar triangles PQR and LMN, QR = 15cm and MN = 10 cm. Find the ratio of areas of two triangles.

(image will be uploaded soon)

Ans: Given: Two triangles ABC and DEF

Such that  $ \vartriangle ABC\sim\vartriangle DEF $ 

To Prove:  $ \dfrac{\operatorname{ar}(\Delta ABC)}{\operatorname{ar}(\Delta DEF)}=\dfrac{A{{B}^{2}}}{D{{E}^{2}}}=\dfrac{B{{C}^{2}}}{E{{F}^{2}}}=\dfrac{A{{C}^{2}}}{D{{F}^{2}}} $ 

Construction: Draw  $ AL\bot BC\,\,\,and\,\,\,DM\bot EF $ 

 $ \text{Proof: }\dfrac{\operatorname{ar}(\Delta ABC)}{\operatorname{ar}(\Delta DEF)}=\dfrac{\dfrac{1}{2}(BC)(AL)}{\dfrac{1}{2}(EF)(DM)} $ 

 $ \left[ \because ar\text{ of }\Delta =\dfrac{1}{2}b\times h \right] $ 

 $ \Rightarrow \dfrac{Area(\Delta ABC)}{Area(\Delta DEF)}=\dfrac{BC}{EF}\times \dfrac{AL}{DM}\ldots \ldots ..\left( i \right) $ 

Again, in  $ \vartriangle ALB $  and  $ \vartriangle DME $ we have

 $ \angle ALB=\angle DME\left[ \text{ Each }={{90}^{{}^\circ }} \right] $ 

$ \angle ABL=\angle DEM\left[ \begin{array}{*{35}{l}} \because \vartriangle ABC\sim\vartriangle DEF  \\ \therefore \angle B=\angle E  \\ \end{array} \right] $

 $ \therefore \vartriangle ALB-\vartriangle DME $  [By AA rule]

 $ \therefore \dfrac{AB}{DE}=\dfrac{AL}{DM}[\because  $ Corresponding sides of similar triangles are proportional] Further,  $ \vartriangle ABC\sim\Delta DEF $ 

 $ \therefore \dfrac{AB}{DE}=\dfrac{BC}{EF}=\dfrac{AC}{DF} $ 

From (ii) and (iii),

 $ \dfrac{BC}{EF}=\dfrac{AL}{DM} $ 

Putting in (i), we get

 $ \dfrac{\text{ Area }(\Delta ABC)}{\text{ Area }(\Delta DEF)}=\dfrac{Al}{DM}\times \dfrac{AL}{DM} $ 

 $ =\dfrac{A{{L}^{2}}}{D{{M}^{2}}}=\dfrac{A{{B}^{2}}}{D{{E}^{2}}} $ 

 $ =\dfrac{A{{C}^{2}}}{D{{F}^{2}}} $ 

 $ \text{Hence, }\dfrac{\operatorname{ar}(\Delta ABC)}{ar(\Delta DEF)}=\dfrac{A{{B}^{2}}}{D{{E}^{2}}}=\dfrac{B{{C}^{2}}}{E{{F}^{2}}}=\dfrac{A{{C}^{2}}}{D{{F}^{2}}} $ 

Since  $ \vartriangle PQR\sim\vartriangle LMN $ 

 $ \therefore \dfrac{\operatorname{ar}(\Delta PQR)}{ar(\Delta LMN)}=\dfrac{Q{{R}^{2}}}{M{{N}^{2}}}=\dfrac{{{(15)}^{2}}}{{{(10)}^{2}}} $ 

 $ =\dfrac{225}{100}=\dfrac{9}{4} $ 

Hence, required ratio is 9: 4.

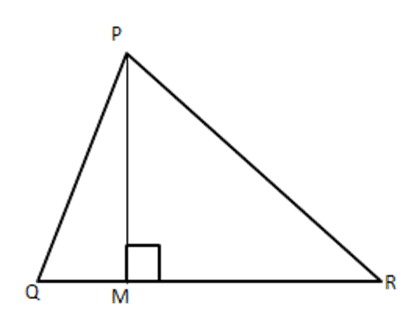
3. Prove that in a right-angled triangle the square of the hypotenuse is equal to the sum 45 of the squares of the other two sides. Use the above theorem in the given figure to prove that

 $ P{{R}^{2}}=P{{Q}^{2}}+Q{{R}^{2}}-2QM.QR $ 

(image will be uploaded soon)

Ans: Given:  $ \vartriangle ABC $ right-angled at A

To Prove:  $ B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}} $ 

Construction: Draw  $ AD\bot BC $ from A to BC

Proof: In  $ \vartriangle BAD $ and $ \vartriangle ABC $ ,

 $ \angle B=\angle B $  [Common]  $ \angle BAC=\angle BDA={{90}^{{}^\circ }} $ 

 $ \therefore \vartriangle BAD\sim\vartriangle BCA[ $ By AA similarity ]

  $ \therefore \dfrac{AB}{BC}=\dfrac{BD}{AB} $ 

 $ \Rightarrow A{{B}^{2}}=BC\times AD\quad \ldots \ldots .(i) $ 

Similarly, in  $ \vartriangle ADC $ and  $ \vartriangle BAC $ 

 $ \angle ADC=\angle BAC\left[ {{90}^{{}^\circ }}\text{ each } \right] $ 

 $ \angle C=\angle C[\text{Common}] $ 

 $ \therefore \vartriangle ADC\sim\vartriangle BAC[\text{ByAAsimilarity}] $ 

 $ \therefore \dfrac{DC}{AC}=\dfrac{AC}{BC} $ 

 $ \Rightarrow A{{C}^{2}}=DC\times BC\ldots \ldots .(ii) $ 

 $ (i)+(ii) $ 

 $ A{{B}^{2}}+A{{C}^{2}}=BC\times BD+DC\times BC $ 

 $ \quad =BC[BD+DC] $ 

 $ =BC\times BC $ 

 $ \Rightarrow A{{B}^{2}}+A{{C}^{2}}=B{{C}^{2}} $ 

To Prove:  $ P{{R}^{2}}=P{{Q}^{2}}+QR2-2QM\cdot QR $ 

Proof: In  $ \vartriangle PMR $ 

 $ P{{R}^{2}}=P{{M}^{2}}+M{{R}^{2}}[ $ Using above theorem]

 $ =P{{M}^{2}}+{{(QR-QM)}^{2}} $ 

 $ =P{{M}^{2}}+Q{{R}^{2}}+Q{{M}^{2}}-2QM\cdot QM $ 

 $ =\left( P{{M}^{2}}+Q{{M}^{2}} \right)+Q{{R}^{2}}-2QM\cdot QR $ 

 $ =P{{Q}^{2}}+Q{{R}^{2}}-2QM\cdot QR\left[ \because P{{Q}^{2}}=Q{{M}^{2}}+P{{M}^{2}} \right] $

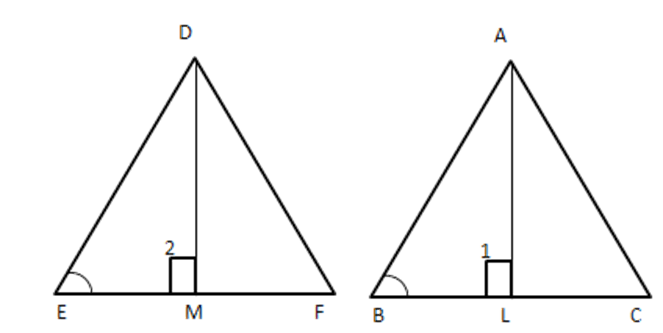
4. Prove that the ratio of areas of two similar triangles is equal to the square of their corresponding sides. Using the above theorem do the following the area of two similar triangles are  $ 81c{{m}^{2}} $ and  $ 144c{{m}^{2}} $ , if the largest side of the smaller triangle is 27 cm, then find the largest side of the largest triangle.

(image will be uploaded soon)

Ans: Given: Two triangles ABC and DEF such that  $ \vartriangle ABC\sim \vartriangle DEF $ 

To prove:  $ \dfrac{\operatorname{ar}(\Delta ABC)}{\operatorname{ar}(\Delta DEF)}=\dfrac{A{{B}^{2}}}{D{{E}^{2}}}=\dfrac{B{{C}^{2}}}{E{{F}^{2}}}=\dfrac{A{{C}^{2}}}{D{{F}^{2}}} $ 

Construction: Draw  $ AL\bot BC $ and  $ DM\bot EF $ 

Proof: Since similar triangles are equiangular and their corresponding sides are proportional

 $ \therefore \vartriangle ABC\sim\Delta DEF $ 

 $ \Rightarrow \angle A=\angle D,\angle B=\angle E,\angle C=\angle F $ 

And  $ \dfrac{AB}{DE}=\dfrac{BC}{EF}=\dfrac{AC}{DF}\ldots \ldots .(i) $ 

In  $ \vartriangle ALB $ and $ \vartriangle DMB $ ,

 $ \angle 1=\angle 2\text{ and }\angle B=\angle E $ 

 $ \Rightarrow \vartriangle ALB-\vartriangle DME[\text{ByAAsimilarity}] $ 

 $ \Rightarrow \dfrac{AL}{DM}=\dfrac{AB}{DE}\cdots \ldots ...(ii) $ 

From (i) and (ii), we get

 $ \dfrac{AB}{DE}=\dfrac{BC}{EF}=\dfrac{AC}{DF}=\dfrac{AL}{DM} $ 

Now  $ \dfrac{\text{ area }(\Delta ABC)}{\operatorname{area}(\Delta DEF)}=\dfrac{\dfrac{1}{2}(BC\times AL)}{\dfrac{1}{2}(BF\times DM)} $ 

 $ \Rightarrow \dfrac{\text{ Area }(\Delta ABC)}{\text{ Area }(\Delta DEF)}=\dfrac{BC}{EF}\times \dfrac{AL}{DM} $ 

 $ \Rightarrow \dfrac{\text{ Area }(\Delta ABC)}{\text{ Area }(\Delta DEF)}=\dfrac{BC}{EF}\times \dfrac{BC}{EF}=\dfrac{B{{C}^{2}}}{E{{F}^{2}}} $ 

Hence,  $ \dfrac{\text{ Area }\vartriangle ABC}{\text{Area}\vartriangle DEF}=\dfrac{A{{B}^{2}}}{D{{E}^{2}}}=\dfrac{B{{C}^{2}}}{E{{F}^{2}}}=\dfrac{A{{C}^{2}}}{D{{F}^{2}}} $ 

Let the largest side of the largest triangle be  $ x~\text{cm} $ 

Using above theorem,

 $ \dfrac{{{x}^{2}}}{{{27}^{2}}}=\dfrac{144}{81}\Rightarrow \dfrac{x}{27}=\dfrac{12}{9} $ 

 $ \Rightarrow x=36~\text{cm} $ 

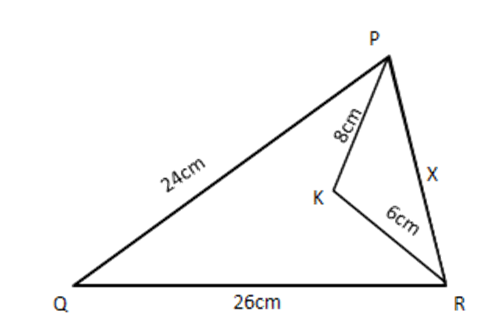
5. In a triangle if the square of one side is equal to the sum of the squares on the other two sides. Prove that the angle apposite to the first side is a right angle. Use the above theorem to find the measure  $ \angle PKR $ of in figure given below.

(image will be  uploaded soon)

Ans: Given: A  $ \vartriangle ABC $ such that

 $ A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}} $ 

To prove: Triangle ABC is right angled at B

Construction: Construct a triangle DEF such that

 $ DE=AB,EF=BC\text{ and D}E={{90}^{{}^\circ }} $ 

Proof:  $ \because \Delta DEF $ is a right angled triangle right angled at E[construction]

 $ \therefore  $ By Pythagoras theorem, we have

 $ D{{F}^{2}}=D{{E}^{2}}+E{{F}^{2}} $ 

 $ \Rightarrow D{{F}^{2}}=A{{B}^{2}}+B{{C}^{2}}[\because DE=AB\text{ and }EF=BC] $ 

 $ \Rightarrow D{{F}^{2}}=A{{C}^{2}}\left[ \because A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}} \right] $ 

 $ \Rightarrow D{{F}^{2}}=A{{C}^{2}}\left[ \because A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}} \right] $ 

 $ \Rightarrow DF=AC $ 

Thus, in  $ \vartriangle ABC $ and $ \vartriangle DEF $ , we have

(images will be uploaded soon)

 $ AB=DE,BC=EF\,\,and\,\,\,AC=DF $  [By Construction and (i)]

 $ \therefore \vartriangle ABC\cong \vartriangle DEF $ 

 $ \Rightarrow \angle B=\angle E={{90}^{{}^\circ }} $ 

Hence,  $ \vartriangle ABC $ is a right triangle.

Hence,  $ \vartriangle ABC $ is a right triangle.

 $ \text{ In }\Delta QPR,\angle QPR={{90}^{{}^\circ }} $ 

 $ \Rightarrow {{24}^{2}}+{{x}^{2}}={{26}^{2}} $ 

 $ \Rightarrow x=10\Rightarrow PR=10~\text{cm} $ 

Now in  $ \Delta PKR,P{{R}^{2}}=P{{K}^{2}}+K{{R}^{2}}\left[ {} \right. $ as  $ \left. {{10}^{2}}={{8}^{2}}+{{6}^{2}} \right] $ 

 $ \therefore \Delta PKR $ is right angled at  $ \text{K} $ 

 $ \Rightarrow \angle PKR={{90}^{{}^\circ }} $ 

Download Important Questions for Class 10 Maths Chapter 6

Students continuing with math in their higher students will require this knowledge to solve complex sums. Triangles class 10 important questions are available in a compiled pdf form to download on any device and use to prepare for their exams. The pdf will also ask as a model question paper and help students get an insight into what to expect in their actual board exam. Triangles class 10 extra questions with solutions will focus on more theoretical-based questions. They will act as revision notes to help you to revise the entire triangles chapter in a short span right before the math exam.

Maths Class 10 Triangles Important Questions

Introduction

The triangles class 10 notes chapter 6 provided here is a crucial study resource for the students studying in class 10. These CBSE class 10 maths triangles important questions are brief, and it also covers all the theories from this lesson. Questions from these theories are likely to be asked in the board exam. You will also learn about theorems that are based on comparable concepts. In your preceding year's classes, you must have studied the basics of triangles, for example, the perimeter of a triangle and its area, etc.

Triangle

A triangle can be characterized as a polygon that has three points and three sides. The inside points of a triangle total up to 180 degrees, and the outside points total up to 360 degrees. Based on the length and its angle, it can be classified into the following kinds-

• Scalene Triangle – Each side of the triangle is of different measure.

• Isosceles Triangle – Any two different sides of the triangle are of equivalent length. 

• Symmetrical Triangle – All the three sides of a triangle are equivalent, and each angle is 60 degrees. 

• Acute Angled Triangle – All the angles are not more than 90 degrees.

• Right Angle Triangle – Any of the three angles is equivalent to 90 degrees. 

• Obtuse-Angled Triangle – One out of the three angles is more than 90 degrees.

Similar Figures

• Two forms having an identical shape, but not necessarily identical, are referred to as similar figures.

• All congruent forms are similar, but not all similar forms are congruent.

• Example- any two squares since their sides are proportional.

Triangles Similarity Criteria

To determine if the two triangles are similar or not, you need to check the following four criteria:

• Side-Side-Side (SSS) Similarity Criterion – When the relating sides of any two triangles are in a similar proportion, at that point, their comparing angles will be equivalent, and the triangle will be considered as similar triangles. 

• Point Angle (AAA) Similarity Criterion – When the relating angles of any two triangles are equivalent, at that point, their comparing side will be in similar proportion, and the triangles are viewed as similar.

• Point Angle (AA) Similarity Criterion – When two angles of one triangle are separately equivalent to the two angles of the other triangle, at that point, the two triangles are considered as similar. 

• Side-Angle-Side (SAS) Similarity Criterion – When one angle of a triangle is equal to one angle of another triangle and the sides incorporating these angles are in a similar proportion (relative), at that point, the triangles are supposed to be similar.

Thales Theorem

Statement: A-line that is drawn parallel to any side of a triangle will intercross the other two remaining sides in separate points. The other two remaining sides are then declared to be divided in an equivalent ratio."

Proof:

In ∆ABC, DE || BC.

To prove: ADDB=AEEC

Construction: Draw EM perpendicular AD and DN perpendicular AE. Join point B to point E and point C to point D.

Proof: In ∆ADE and ∆BDE,

ar(ΔADE)ar(ΔBDE)=12×AD×EM12×DB×EM=ADDB (i) [Area of ∆ = 12 x base x corresponding altitude

In ∆ADE and ∆CDE,

ar(ΔADE)ar(ΔCDE)=12×AE×DN12×EC×DN=AEEC

∵ DE || BC …[Given

∴ ar(∆BDE) = ar(∆CDE)

From (i), (ii) and (iii),

ADDB=AEEC

Example - If point D is the center/radius of the circle and BC is 4 cm, and AC is 3 cm, What is the diameter of the circle?

Solution

According to Thales theorem, triangle ABC is considered as a right triangle where ∠ACB = 90°.

To determine the diameter of the given circle, one should apply the Pythagorean theorem.

BC2 + AC2 =AB2

4*4 + 3*3 = AB2

16 + 9 = AB2

25 = AB2

AB = 5 cm

Hence, the diameter of the circle is 5 cm

Area of Triangles

Statement- "The ratios of the areas of any two comparable triangles is equivalent to the square of the ratio of their similar sides."

Proof

Given: ∆ABC ~ ∆DEF

To prove: ar(ΔABC)ar(ΔDEF) = AB2 DE2 = BC2 EF2 = AC2 DF2

Construction: Draw AM perpendicular BC and DN perpendicular EF.

Proof: In ∆ABC and ∆DEF

ar(ΔABC)ar(ΔDEF)=12×BC×AM12×EF×DN=BCEF.AMDN …(i) 

[Area of ∆ = 12 x base x corresponding altitude]

∵ ∆ABC ~ ∆DEF

∴ ABDE=BCEF …..(ii) …[Sides are proportional]

∠B = ∠E ……..[∵ ∆ABC ~ ∆DEF]

∠M = ∠N …..[each 90°]

∴ ∆ABM ~ ∆DEN ……[AA similarity]

∴ ABDE=AMDN …..(iii) …[Sides are proportional]

From (ii) and (iii), we can deduce- BCEF=AMDN …(iv)

From (i) and (iv), we can deduce- ar(ΔABC)ar(ΔDEF)=BCEF.BCEF=BC2 EF2

Similarly, it can be proven that

ar(ΔABC)ar(ΔDEF)=AB2 DE2 = AC2 DF2

∴ar(ΔABC)ar(ΔDEF)=AB2 DE2=BC2 EF2=AC2 DF2 

Example -In ΔABC andΔAPQ, the length of the sides are given as AP = 4 cm , PB = 8 cm and BC = 6 cm. Determine the ratio of the areas of triangle ABC and triangle APQ.

 In triangle ABC and triangle APQ, ∠PAQ is common 

and 

∠APQ = ∠BAC (corresponding angles)

ΔABC ~ ΔAPQ (AA criterion for similar triangles)

Since the two triangles are comparable, we can use the theorem based on the areas of similar triangles,

area of ΔABC / area of ΔAPQ = (AB/AP)2 = (12/6)2 = 4

Pythagoras’ Theorem

Statement: In a right-angled triangle, the total of the squares of the remaining two sides of the triangle is equivalent to the square of the hypotenuse.

Proof 

Given: ABC is a right triangle that is right-angled at point B.

To prove: AB² + BC² = AC²

Construction: Draw BD ⊥ AC

Proof: In ∆s ABC and ADB

∠A = ∠A (common)

∠ABC = ∠ADB (each angle 90°)

∴ ∆ABC ~ ∆ADB (AA Similarity rule)

∴ ABAD=ACAB (sides are proportional)

⇒ AB² = AC.AD

Now in ∆ABC and ∆BDC

∠C = ∠C (common)

∠ABC = ∠BDC (each 90°)

∴ ∆ABC ~ ∆BDC (AA similarity)

∴ BCDC=ACBC (sides are proportional)

BC² = AC.DC (ii)

On adding (i) and (ii), we get

AB² + BC² = ACAD + AC.DC

⇒ AB² + BC² = AC.(AD + DC)

AB² + BC² = AC.AC

∴AB² + BC² = AC²

Example:

The height of the triangle is 4 and the breadth is 3, find the hypotenuse.

Solution 

EG and GF are the two given sides of the right-angled Triangle.

EG = 5 cm and GF = 12 cm 

From Pythagoras Theorem, we have:

EF2 = EG2 + GF2

= (5)2 + (12)2

= 25 + 144

So, EF2 = 169

EF = 13 cm

Converse of Pythagoras’ Theorem

Statement: In a triangle, if the sum of the squares of the other two remaining sides of the triangle is equivalent to the square of one side of the triangle then the angle opposite the primary side is definitely a right angle."

Proof 

To prove: ∠ABC = 90°

Construction: Draw a right-angled ∆DEF in which DE = AB and EF = BC

Proof: In ∆ABC,

AB² + BC² = AC² …(i) (given)

In rt. ∆DEF

DE² + EF² = DF² …(By pythagoras theorem)

AB² + BC² = DF² …..(ii) …(DE = AB, EF = BC)

From (i) and (ii), we get

AC² = DF²

⇒ AC = DF

Now, DE = AB …(by cont)

EF = BC …(by cont)

DF = AC …….(proved above)

∴ ∆DEF ≅ ∆ABC ……(sss congruence)

∴ ∠DEF = ∠ABC …..(CPCT)

∠DEF = 90° …(by cont)

∴ ∠ABC = 90°

Why Choose Vedantu? 

Vedantu is a prominent educational forum that delivers accurate and easily understandable academic content for students from each grade. From sample papers to CBSE solutions, you can find any exam or study material on Vedantu, which subject experts curate. Class 10 math ch 6 important questions are a study guide for many students who are cramming in the last-minute revision session before the exam. Besides helping students understand what kind of questions to expect in their final examination, it will also enhance their confidence and sharpen their conceptual understanding. Each of the solutions provided by Vedantu for important questions of chapter 6 maths class 10 is verified and is based on the latest updated CBSE syllabus. Register with Vedantu to be updated on the latest study material and get professional help for your exam preparation.

Benefits of Important Questions for CBSE Class 10 Maths Chapter 6 - Triangles 2024-25

The benefits of Important Questions for CBSE Class 10 Maths Chapter 6 - "Triangles" for the academic year 2024-25 are multifaceted. These questions serve as a strategic tool to aid students in their exam preparation by offering a focused and efficient way to revise crucial concepts and theorems related to triangles. By concentrating on key topics, they help students identify the most relevant material for their exams, saving time and ensuring a comprehensive understanding. Moreover, these important questions often mimic the examination format and challenge levels, enabling students to gauge their preparedness and build confidence. They promote a deeper grasp of the subject, enhance problem-solving skills, and foster the ability to apply geometric principles in practical scenarios, ultimately leading to improved performance in Class 10 mathematics examinations.

Important Related Links for CBSE Class 10 Maths

Conclusion

Vedantu's Important Questions for CBSE Class 10 Maths Chapter 6 - Triangles offer a valuable resource for students seeking to excel in their mathematics studies. With a comprehensive selection of essential questions and in-depth explanations, Vedantu equips learners with the necessary tools to master the concept of triangles. By practicing these questions, students can strengthen their problem-solving skills and gain confidence in tackling various triangle-related problems. Furthermore, Vedantu's user-friendly platform and expert faculty ensure a seamless learning experience. Whether preparing for exams or aiming for a deeper understanding of the subject, Vedantu's Important Questions provide an effective and convenient learning aid, empowering students to achieve academic success in mathematics.