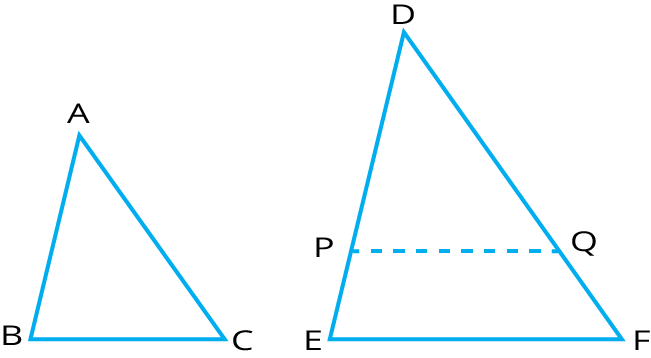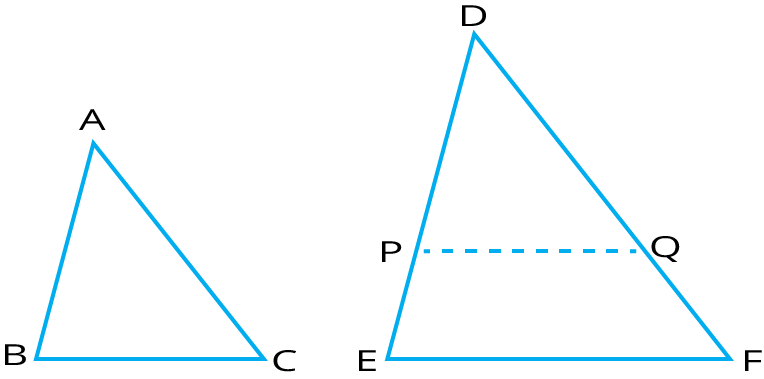Class 10 Maths Chapter 6 Summary Notes PDF Download
Triangles Class 10 Maths Chapter 6 CBSE Notes - 2025-26



FAQs on Triangles Class 10 Maths Chapter 6 CBSE Notes - 2025-26
1. What are the key concepts summarized in the Triangles Class 10 Revision Notes as per the CBSE 2025–26 syllabus?
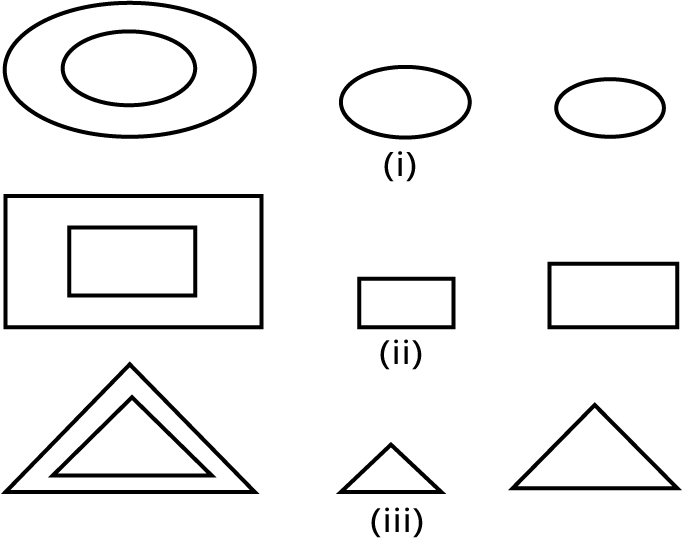
The Triangles Class 10 Revision Notes focus on properties of triangles, criteria for similarity (AAA, SSS, SAS), the Basic Proportionality Theorem (Thales), classification of triangles based on sides and angles, and key theorems like the Pythagorean theorem, all structured for quick revision.
2. How can students use revision notes for effective last-minute preparation of Chapter 6: Triangles?
For efficient revision, students should:
- Review all key theorems and proofs listed in the notes,
- Go through formula summaries,
- Memorise important properties and similarity criteria,
- Practice sample problems highlighted in the notes,
- Connect new theorems to those studied in previous classes for deeper understanding.
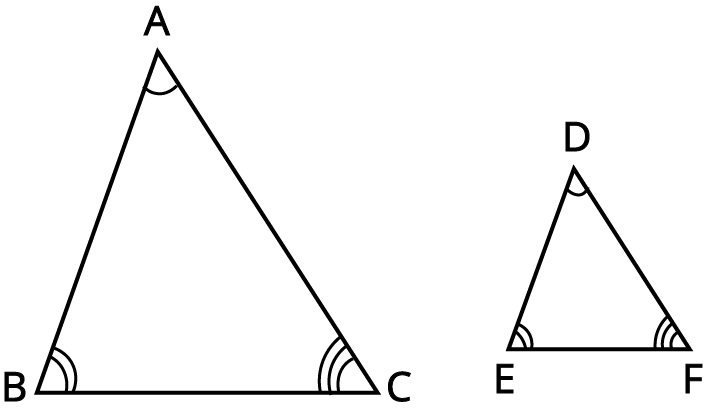
3. How are similar triangles identified as per the revision notes in the CBSE syllabus?
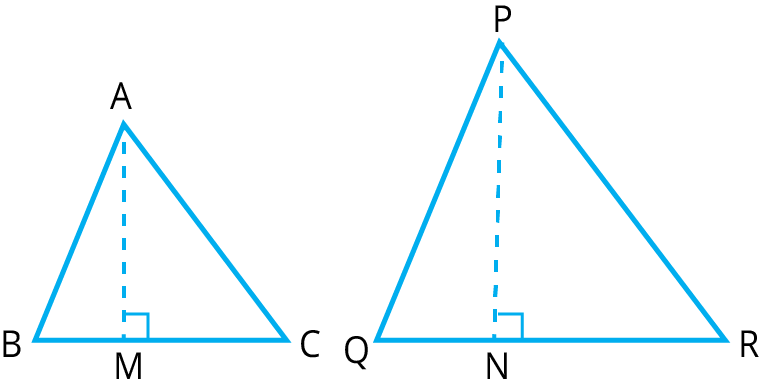
Similar triangles are identified when their corresponding angles are equal and their corresponding sides are in the same ratio. The criteria used include the AAA (Angle-Angle-Angle), SSS (Side-Side-Side), and SAS (Side-Angle-Side) similarity criteria.
4. What are the main differences between congruent and similar figures highlighted in the Triangles Class 10 Notes?
Congruent figures have equal corresponding sides and angles (same size and shape), while similar figures have equal corresponding angles but proportional sides (same shape, not necessarily the same size).
5. Which theorems should students focus on when revising the Triangles chapter for exams?
Students should focus on:
- Basic Proportionality Theorem (Thales Theorem),
- Criteria for similarity (AAA, SSS, SAS),
- Pythagorean Theorem and its converse,
- The relationship between areas of similar triangles.
6. Why is understanding similar triangles important in solving real-life and higher-level geometry problems?
Understanding similar triangles is crucial because they form the basis for solving indirect measurement problems, trigonometry, and applications in fields like engineering and physics, making future math learning and problem solving more accessible.
7. How does the summary in Triangles Class 10 Notes help clarify misconceptions about triangle similarity and congruence?
The summary clearly differentiates that all congruent figures are similar, but not all similar figures are congruent. It highlights common student errors, such as assuming equal sides means similarity, reminding that angle correspondence must be checked as well.
8. What is the significance of Thales' (Basic Proportionality) Theorem in the revision notes?
Thales’ Theorem states that when a line is drawn parallel to one side of a triangle, it divides the other two sides in the same ratio. This theorem is fundamental for establishing the similarity of triangles and solving many geometry problems in exams.
9. How are triangles classified according to their sides and angles in the revision notes?
Triangles are classified by:
- Sides: Equilateral (all sides equal), Isosceles (two sides equal), Scalene (no sides equal).
- Angles: Acute triangle (all angles less than 90°), Right triangle (one angle 90°), and Obtuse triangle (one angle above 90°).
10. What common errors should students avoid when revising for Chapter 6 Triangles using quick notes?
Students should avoid:
- Confusing similarity with congruence,
- Ignoring the requirement for proportional sides in similar triangles,
- Missing out on reviewing the converses of key theorems (like Pythagoras),
- Overlooking the need to practice proof-based questions,
- Memorising without understanding connections between theorems.




















 Watch Video
Watch Video