Force Solutions for ICSE Board Class 10 Physics (Concise - Selina Publishers)

Exercise – 1 (A)

1. State the condition when on applying a force, a body has:

(a) Translational motion,

Ans: A body produces translational motion when it is free to move

(b) Rotational motion.

Ans: A body produces rotational motion when it is pivoted at a point.

2. Define moment of force and state its S.I. unit

Ans: The moment of force is defined as the product of the magnitude of the force applied to the distance of the line of action of the force from the axis of rotation. S.I. the unit of moment of force is Newton meter (Nm). 

3. State whether the moment of force is a scalar or vector quantity? 

Ans: Vector Quantity

4. State two factors affecting the turning effect of a force.

Ans: The moment of a force about a point depends on the two factors given below: 

(a) The magnitude of the force applied and, 

(b) The perpendicular distance of the line of action of a force from the axis of rotation.

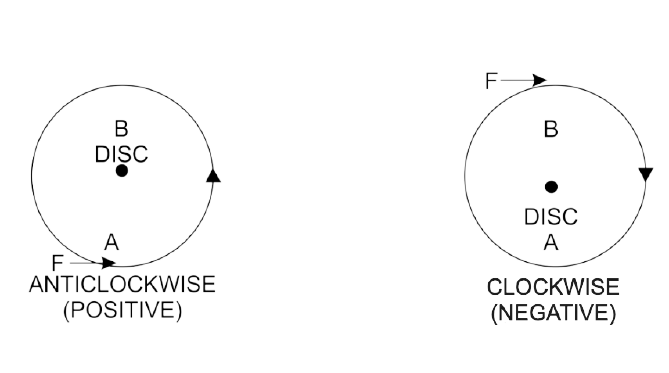
5. When does a body rotate? State one way to change the direction of rotation of the body. Give a suitable example to explain your answer. 

Ans: When a force is given to a body that is pivoted at an appropriate point, the body spins about the axis that passes through the pivoted point. On changing the point of application of force, the direction of rotation can be changed.

The figure given below shows the anticlockwise and clockwise moments produced in a disc pivoted at its center by changing the point of application of force F from A to B

6. Write the expression for the moment of a given force about a given axis. 

Ans: Moment of a force about a given axis of rotation = Magnitude of the force applied $\times$ perpendicular distance of force from the axis of rotation

7. What do you understand by the clockwise and anticlockwise moment of force? When is it positive? 

Ans: When the turning effect on the body is anticlockwise, the moment of force is termed the anticlockwise moment, and it is treated as negative, but when the turning impact on the body is clockwise, the moment of force is called the clockwise moment, and it is taken as positive.

8. State one way to reduce the moment of a given force about a given axis of rotation. 

Ans: As the moment of force depends on the distance of the line of action of the force from the axis of rotation. Decreasing the perpendicular distance from the axis decreases the moment of a given force.

9. State on the way to obtain a greater moment of a force about a given axis of rotation. 

Ans: As the moment of force depends on the distance of the line of action of the force from the axis of rotation. Increasing the perpendicular distance from the axis increases the moment of a given force. 

10. Why is it easier to open a door by applying force at the free end of it? 

Ans: It is easier to open a door by applying the force at the free end of it because the less force needed to turn the body is less when the perpendicular distance is large. 

11. The stone of hand flour grinder is provided with a handle near its rim. Give a reason. 

Ans: The stone handle is provided near the rim of a hand flour grinder so that by just applying a small force at the handle it can be easily rotated about the iron pivot at its center.

12. It is easier to turn the steering wheel of a large diameter than that of a small diameter. Give a reason. 

Ans: Because the force applied on the steering of a large diameter is less as it is at a large distance from the center of the rim.

13. A spanner (or wrench) has a long handle. Why? 

Ans: To produce a larger turning moment so that the nut can be easily turned with less force a spanner (or wrench) has a long handle

14. A jackscrew is provided with a long arm. Explain why?

Ans: A jackscrew, which is used to lift heavy loads like vehicles, is provided with a long arm so that less amount of effort is required to raise or lower the jack.

15. A, B, and C are the three forces each of magnitude 4 N acting in the plane of paper as shown in Fig. 1.26. Point O lies in the same plane.  

(i) Which force has the least moment about O? Give a reason. 

Ans: (i) We know that,

Moment of force = Force × distance 

As the perpendicular distance of vector ‘C’ is minimum from the point O. Hence, Vector C will have the minimum moment about O.

(ii) which force has the greatest moment about O? Give a reason. 

Ans: We know that, 

Moment of force = Force $\times$ perpendicular distance 

As the distance of vector ‘A’ is largest from the point O, Vector A will have the largest moment about O.

(iii) Name the forces producing (a) Clockwise, (b) anticlockwise moments. 

Ans: (a) The vectors ‘A’ and ‘B’ will produce clockwise moments because the turning effect on the body is clockwise, and hence the moment of force is called clockwise moment and it will be taken as negative.

(b) Vector ‘C’ will produce an anticlockwise moment because the turning effect on the body is anticlockwise and hence the Moment of force is called anticlockwise moment and hence it is taken as positive.

(iv) what is the resultant torque about the point O?

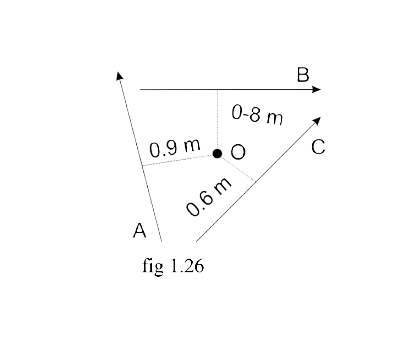
Ans: Here, the resultant torque about point O = sum of all the torques due to vectors A, B, and C

∴ Resultant torque about point O 

= [−(4 × 0.9) – (4 × 0.8) + (4×0.6)] Nm

= [− 3.6 – 3.2 + 2.4] Nm

= − 4.4 Nm 

The negative sign here suggests that the resultant torque will be in the clockwise direction.

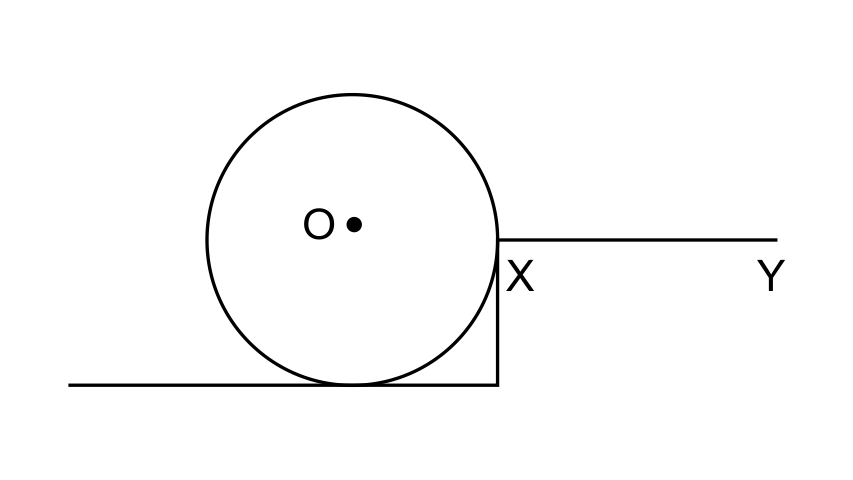
16. The adjacent diagram (Fig. 1.31) Shows a heavy roller, with its axle at O, which is to be raised on a pavement XY. If there is friction between the roller and pavement, show by an arrow on the diagram the point of application and the direction of force to be applied. If pivoted at O, will it go up?

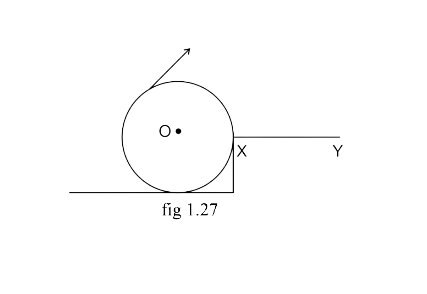
Ans:

The force 'F' must be applied in the direction shown in the diagram.

No, if pivoted at O, it will not go up.

17. A body is acted upon by two forces each of magnitude F, but in

opposite direction. State the effect of the forces if 

(a) both forces act at the same point of the body. 

Ans: As, both the forces are in opposite directions.

Hence, resultant force acting on the body 

= F − F = 0 

moment of forces = 0 

i.e., no motion of the body

(b) the two forces act at two different points of the body at a separation r. 

Ans: Resultant force = F – F = 0

The force tends to rotate the body about the midpoint between the two forces,

Moment of forces = $F \times r$

18. Draw a neat and labelled diagram to show the direction of two forces acting on a body to produce rotation in it. Also mark the point about which rotation takes place, by the letter O.

Ans:

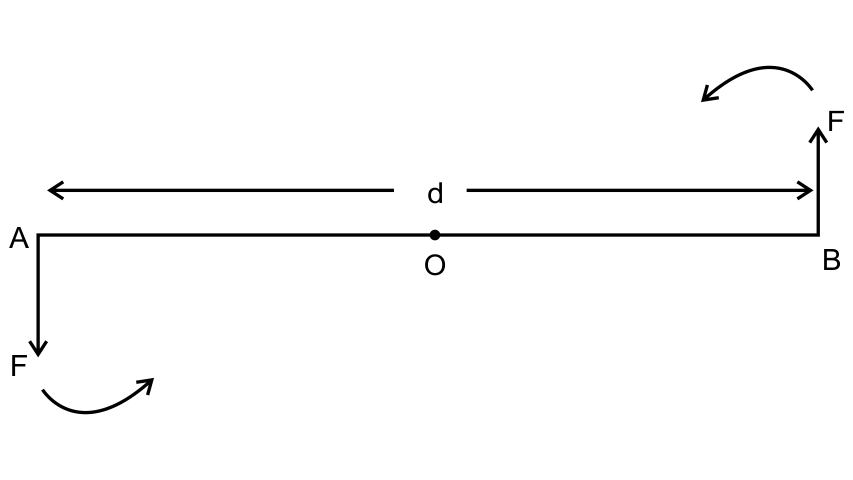
At points A and B, two equal and opposite forces each of magnitude F are applied. 

The two forces will rotate the bar in an anticlockwise direction.

19. What do you understand by the term couple? State its effect on a body. Give two examples in our daily life where a couple is applied to turn a body. 

Ans: Two equal and opposite parallel forces which are not acting along with the same line of action form a couple. To produce the rotation a couple of force is always needed. For example, turning a key inside a lock and rotation of a steering wheel.

20. Define the moment of a couple. Write its S.I. unit. 

Ans:  The moment of a couple is equal to the product of either of the force and the ⟂ distance between the line of action of the forces. S.I unit of moment of a couple is Nm.

21. Prove that 

Moment of couple = Force × couple arm.

Ans:

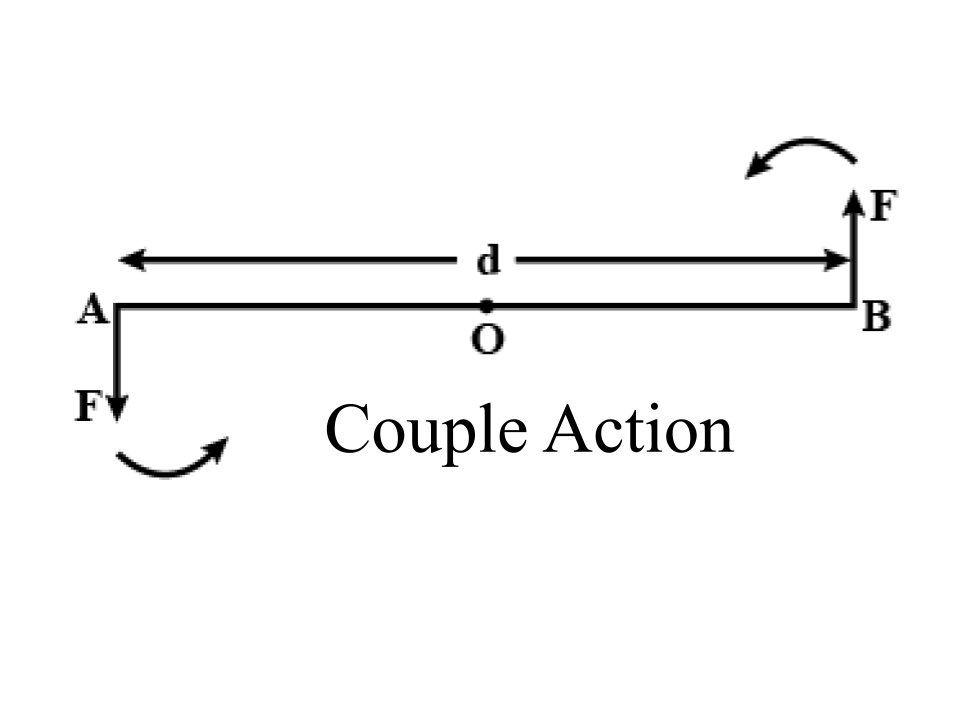
At ‘A’ and ‘B’ points, two equal and opposite forces each of magnitude F are applied. The bar will be turned in an anticlockwise direction by the two forces. The ⟂ the distance between the two forces is AB which is called the couple arms. 

The Moment of force F at the end ‘A’ 

= F × OA (anticlockwise) 

The Moment of force F at the end ‘B’ 

= F × OB (anticlockwise) 

Total moment of couple 

=F × OA + F × OB 

= F × (OA + OB) 

= F × AB 

= F × d (anticlockwise) 

= Either of the force x perpendicular distance between the two forces (or couple arms)

Thus, The moment of couple = Either Force × Couple arm

22. What do you mean by equilibrium of a body? 

Ans: When a few forces acting on a body produce no change in its state of motion or of rest, the body is said to be in equilibrium. 

23. State the condition when a body is in (i) static (ii) dynamic, equilibrium. Give one example each of static and dynamic equilibrium. 

Ans: (i) Even under the influence of the applied forces when a body remains at the state of rest, then the body is said to be in static equilibrium. For example, a book lying on a table.

(ii) When a body remains in the same state of motion (i.e., translational, or rotational), under the influence of the applied forces, the body is in dynamic equilibrium. For example, a raindrop reaches the earth surface with a constant velocity 

24. State two conditions for a body, acted upon by several forces, to be

in equilibrium. 

Ans: For a body to be in equilibrium: 

(i) All forces acting on the body should result in a zero resultant.

(ii) All of the forces acting on the body around the point of rotation should result in a zero resultant moment.

25. State the principle of moments. Name one device based on it.

Ans: The principle of moments states that The body is in equilibrium if the algebraic sum of moments of all forces acting on it around the axis of rotation is zero. The principle of moments governs the operation of a beam balance (or physical balance).

26. Describe a simple experiment to verify the principle of moments, if you are supplied with a metre rule, a fulcrum and two springs with slotted weights. 

Ans: From fixed support suspend a meter rule horizontally by means of a strong thread at ‘O’ as shown.

Now suspend two spring balances with some slotted weights W1 and W2 on them, on either side of the thread. The scale may tilt to one side. Adjust the distances of two spring balances from the support by keeping one at 'A' and the other at 'B' until the scale is horizontal once more.

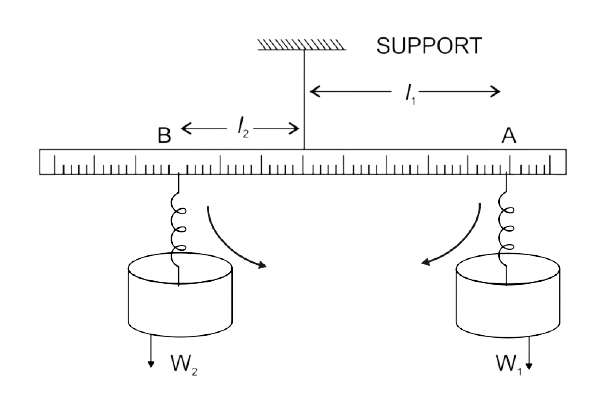
Allow the weight (W1) to be suspended from the spring balance on the right side of the thread at 'A' at a distance of OA = l1, while the weight hanging on the left side of the thread from the spring balance at 'B' is W2 at OB = l2,

The weight W1 has a tendency to turn the scale clockwise, whereas the weight W2 has a tendency to turn it anticlockwise.

Clockwise moment = W1 × l1 

Anticlockwise moment = W2 × l2 

When the scale is horizontal and the scale is in equilibrium, it is discovered that 

Clockwise moment = Anticlockwise moment 

i.e., W1× l1 = W2 × l2 

This verifies the principle of moments.

27. Complete the following sentences: 

(i) The S.I. unit of moment of force is ……………..

Ans: Nm

(ii) In equilibrium, the algebraic sum of moments of all forces about the point of rotation is ………...

Ans: zero

(iii) In a beam balance when the beam is balanced in a horizontal position, it is in …………… equilibrium.

Ans: static

(iv) The moon revolving around the earth is in ………… equilibrium.

Ans: dynamic

Multiple Choice Type

1. The moment of a force about a given axis depends: 

(a) only on the magnitude of force 

(b) only on the perpendicular distance of force from the axis. 

(c) neither on the force nor on the perpendicular distance of force from the axis 

(d) both on the force and its perpendicular distance from the axis. 

Ans: Option (d)

The moment of a force about a given axis depends on both on the 

force and its perpendicular distance from the axis. 

As, Moment of force = Force x Perpendicular distance 

2. A body is acted upon by two unequal forces in opposite directions, but not in the same line. The effect is that: 

(a) The body will have only the rotational motion 

(b) The body will have only the translational motion 

(c) The body will have neither rotational motion nor translational motion. 

(d) The body will have rotational as well as translational motion. 

Ans: Option (d) 

Resultant force ≠ 0

The force tends to rotate the body about the mid-point between the two forces,

Moment of forces = F x r

Numericals

1. The moment of a force of 10 N about a fixed point O is 5 N m. 

Calculate the distance of the point O from the line of action of the force. 

Ans: Moment of force = force x perpendicular distance of force from point O 

Moment of force = F x r 

5 Nm = 10 × r 

r = 5/10 = 0.5 m 

2. A nut is opened by a wrench of length 10 cm. if the least force required is 5.0 N, find the moment of force needed to turn the nut. 

Ans: Given,

Length, r = 10 cm = 0.1 m 

Force, F= 5N 

Moment of force = F × r = 5 × 0.1 = 0.5 Nm 

3. A Wheel of diameter 2 m is shown in Fig. 1.28 with axle at O. A force F = 2 N is applied at B in the direction shown in figure. Calculate the 

moment of force about (i) Centre O, and (ii) point

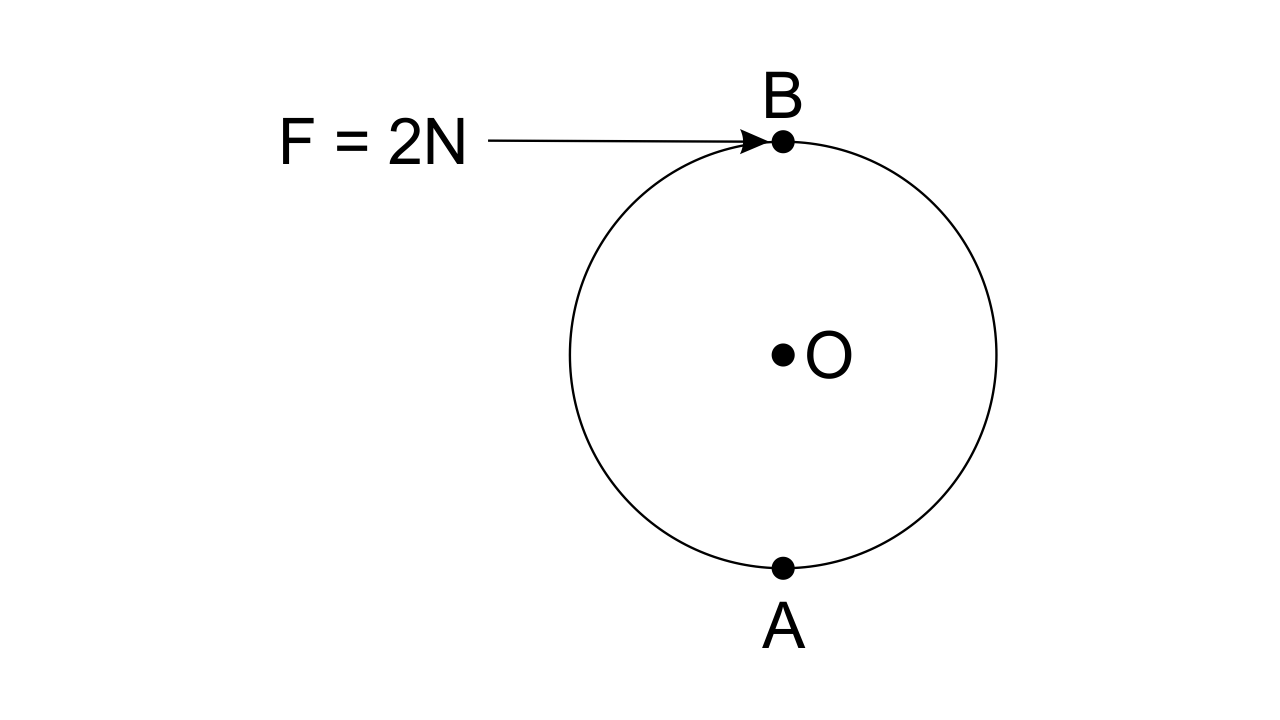
Force, F = 2N 

Diameter = 2m 

The perpendicular distance between B and O is 1m 

(i) Moment of force at point O = F x r 

= 2 x 1 

= 2 Nm (clockwise)

(ii) Moment of force at point A = F × r

=2 × 2 

= 4 Nm (clockwise) 

4. The diagram in fig.1.29 shows two forces F1 = 5 N and F2 = 3N acting at points A and B of a rod pivoted at a point O, such that OA = 2m and OB = 4m.

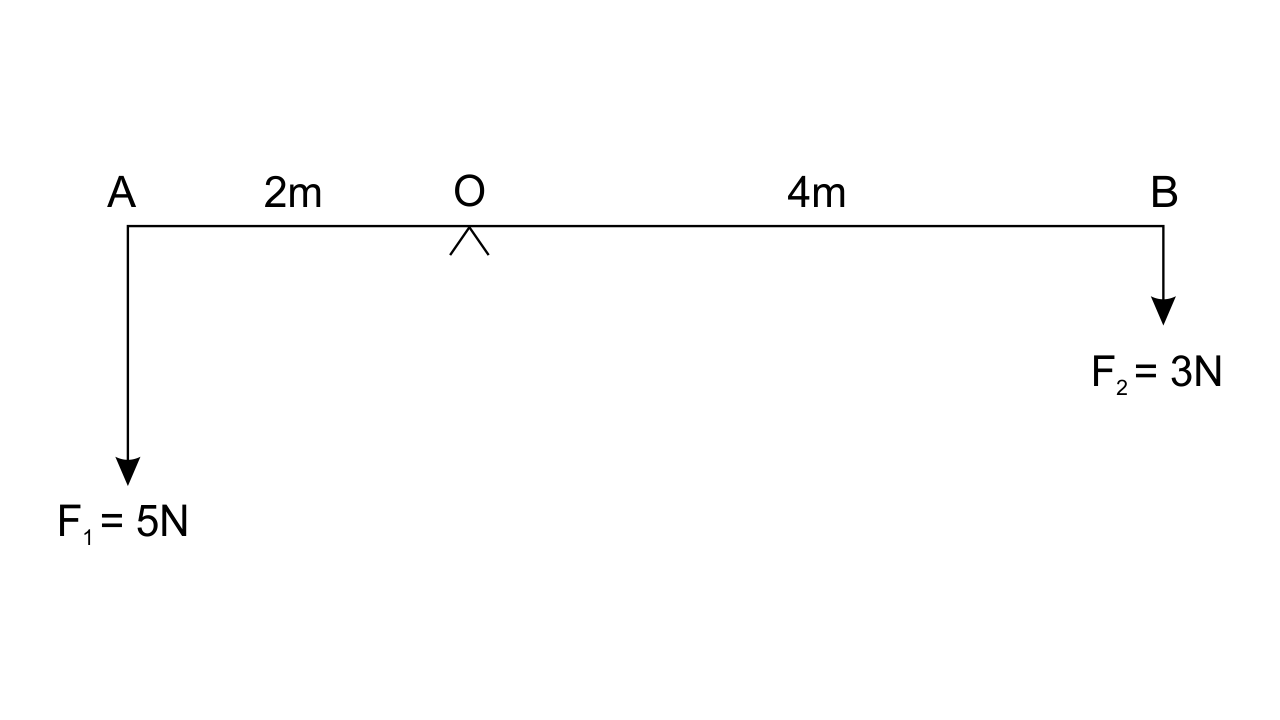
Calculate: 

(i) Moment of force F1 about O. 

Ans: Given AO = 2m and OB = 4m 

(i) Moment of force F1(= 5N) at A about the point O 

= F1 × OA 

= 5 × 2 

= 10 Nm in anticlockwise direction

(ii) Moment of force F2 about O. 

Ans: Moment of force F2 (= 3N) at B about the point O 

= F2 × OB 

= 3 × 4 

=12 Nm in a clockwise direction

(iii) Total moment of the two forces about O.

Ans: Total moment of forces about the mid-point O.

= 12 – 10 

= 2 Nm in clockwise direction

5. Two forces each of magnitude 10 N act vertically upwards and downwards respectively at the two ends of a uniform road of length 4 m which is pivoted at its midpoint as shown in fig 1.30. Determine the magnitude of resultant moment of forces about the pivot O.

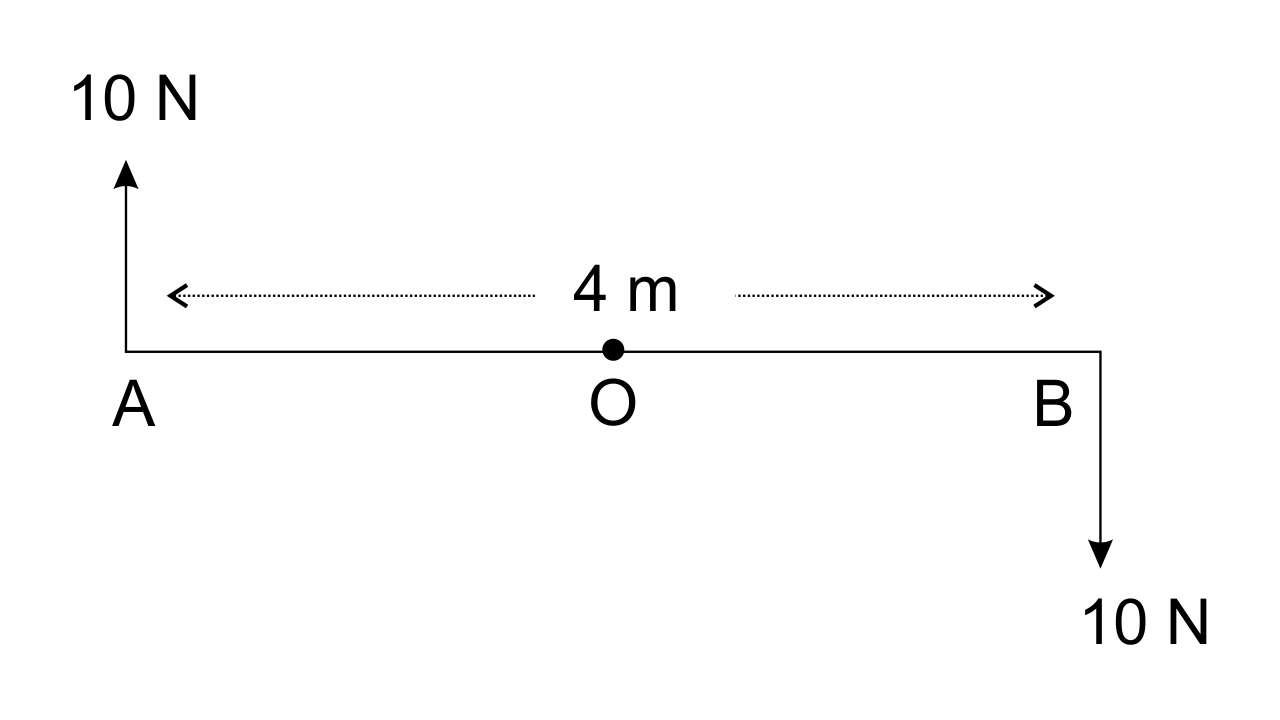
Ans: Given, AB = 4 m 

Hence, OA = 2 m and OB = 2 m 

Moment of force F (=10N) at A about the point O

= F × OA 

= 10 × 2 

= 20 Nm in clockwise direction 

Moment of force F (=10N) at point B about the point O 

= F × OB

= 10 × 2 

= 20 Nm in clockwise direction

Total moment of forces about the mid-point O 

= 20 + 20 

= 40 Nm in clockwise direction 

6. Fig 1.31 shows two forces each of magnitude 10 N acting at the points A and B at a separation of 50 cm, in opposite directions. Calculate the resultant moment of the two forces about the point (i) A, (ii) B, and (iii) O, situated exactly at the middle of the two forces.

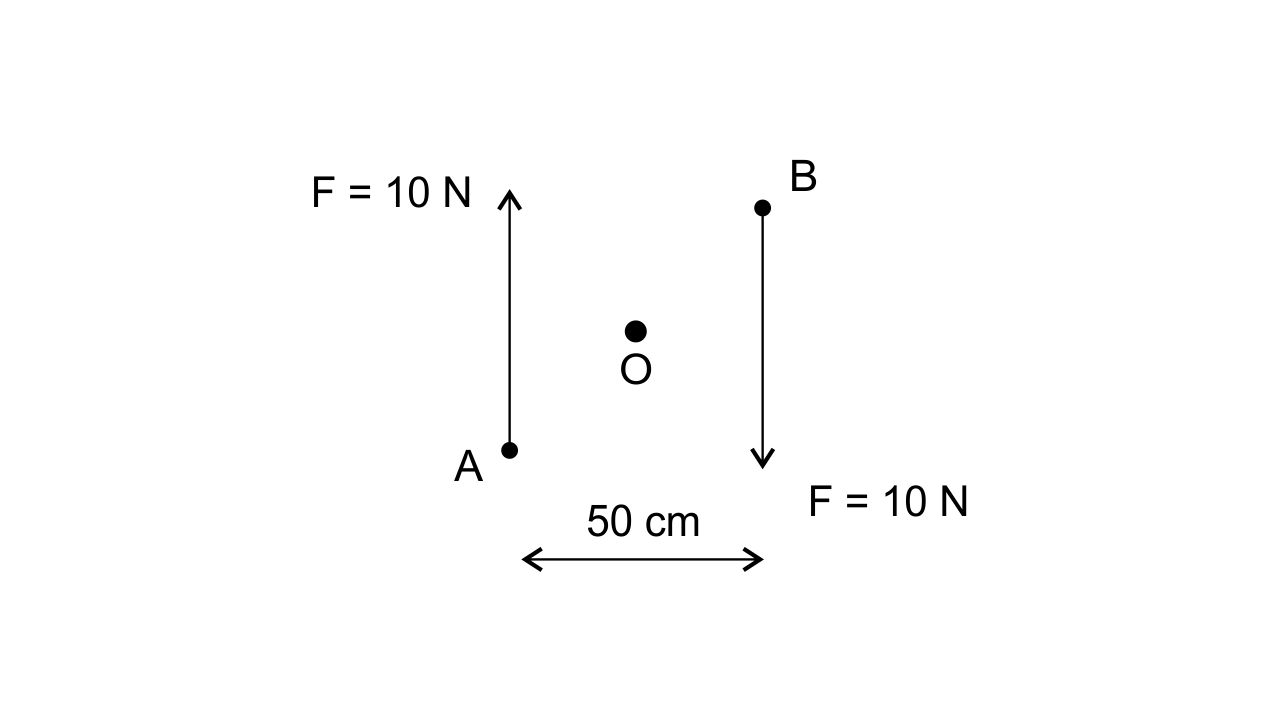
Ans: (i) Perpendicular distance of point A from the force (F = 10 N) at B is 0.5m, 

The perpendicular distance of point A is zero from the force (F = 10 N) at A 

Hence, the moment of the force about A is 

= 10 N × 0.5m 

= 5 Nm (clockwise)

(ii) Perpendicular distance of point B from the force (F = 10 N) at A is 0.5m, 

Perpendicular distance of point B is zero from the force (F = 10) N at B 

Hence, the moment of the force about B is 

= 10 N × 0.5m 

= 5 Nm (clockwise)

(iii) Perpendicular distance of point O from either of the forces (F = 10N) is 

0.25m 

Moment of force F (=10N) at A about O 

= 10N × 0.25m 

= 2.5 Nm (clockwise) 

And,

Moment of force F (=10N) at B about O 

= 10N × 0.25m

=2.5 Nm (clockwise) 

Hence, total moment of the two forces about O 

= 2.5 + 2.5 = 5 Nm (clockwise)

7. A steering wheel of diameter 0.5 m is rotated anticlockwise by applying two forces each of magnitude 5 N. Draw a diagram to show the application of forces and calculate the moment of forces applied. 

Ans:

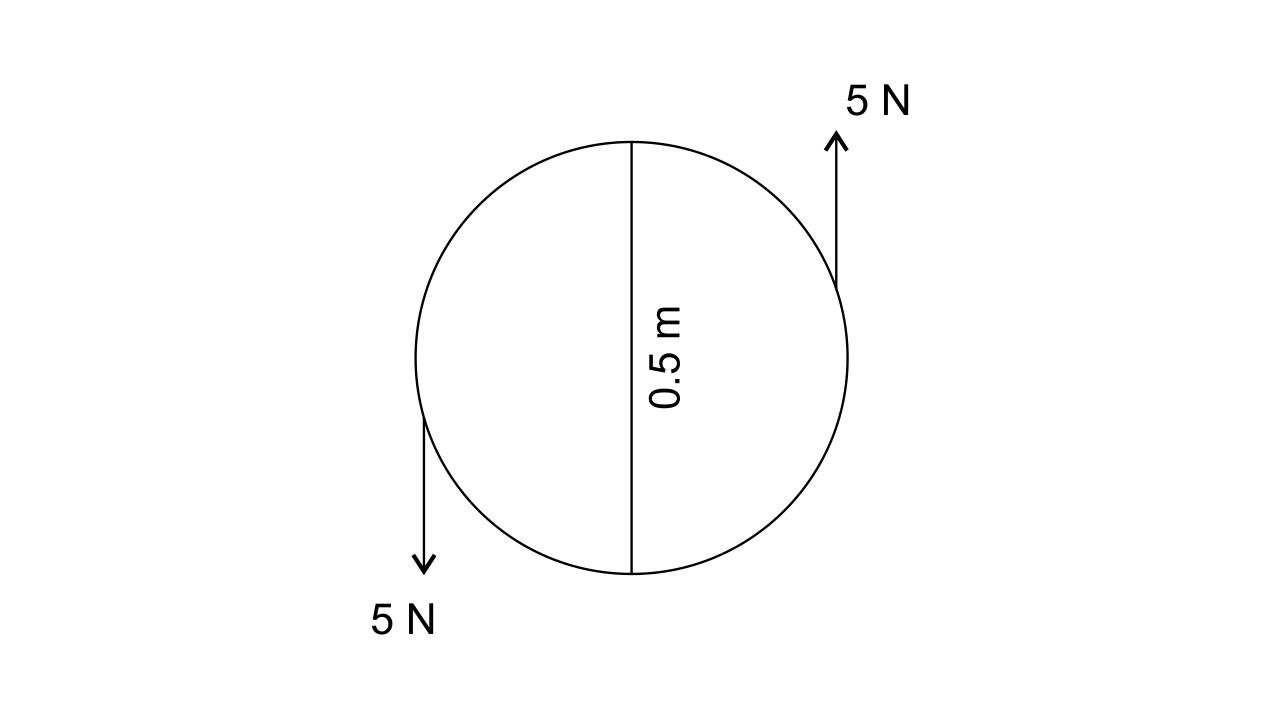
Moment of couple = either force × couple arm 

= 5 N × 0.5 m 

= 2.5 Nm 

8. A uniform metre rule is pivoted at its mid-point. A weight of 50 gf is suspended at one end of it. Where should a weight of 100 gf be suspended to keep the rule horizontal? 

Ans:

Let us assume that the 50-gf weight produce an anticlockwise moment about the 

the middle point of meter rule i.e., at 50cm.

Let a weight of 100gf produce a clockwise moment about the middle point. 

Let its distance from the middle be ‘d’ cm. 

Then, according to principle of moments, 

Anticlockwise moment = Clockwise moment 

50gf × 50 cm = 100gf × d 

So, d = (50×50) /100 = 25cm from the other end

9. A uniform metre rule balances horizontally on a knife edge placed at the 58 cm mark when a weight of 20 gf is suspended from one end. 

(i) Draw a diagram of the arrangement 

Ans: Weight mg (W) of rule produces an anti-clockwise moment about the knife 

edge O. To balance it, 20gf must be suspended at the end B to produce 

clockwise moment about the knife-ed

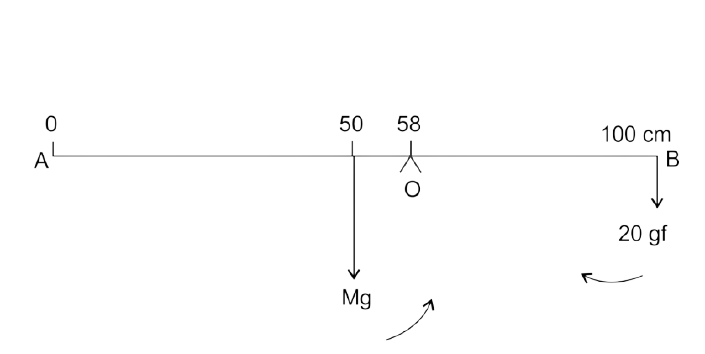
(ii) What is the weight of the rule? 

Ans: From the principle of moments, 

Anticlockwise moment = Clockwise moment 

W × (58-50) = 20gf × (100 − 58) 

W × 8 = 20gf × 42 

W = (20gf × 42) /8 = 105 gf

10. The diagram below (Fig 1.32) shows a uniform bar supported at the middle point O. A weight of 40 gf is placed at a distance 40 cm to the left of point O. How can you balance the bar with a weight of 80 gf?

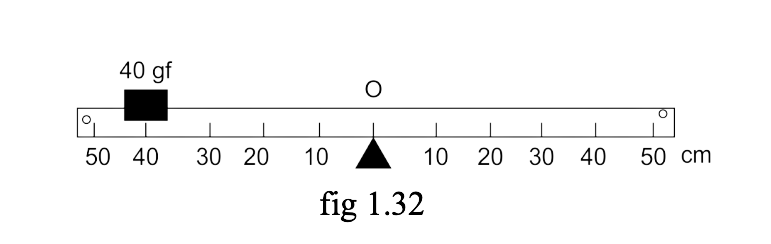
Ans: Anticlockwise moment = 40gf × 40 cm 

Clockwise moment = 80 gf × d cm 

From the principle of moments, 

Anticlockwise moment = Clockwise moment 

40 gf × 40 cm = 80 gf × d 

So, d = (40gf ×40)/80 

= 20 cm to the right of point O.

11. Fig 1.33 shows a uniform metre rule placed on a fulcrum at its mid-point O and having a weight 40 gf at the 10 cm mark and a weight of 20 gf at the 90 cm mark. 

(i) Is the metre rule in equilibrium? If not, how will the rule turn? 

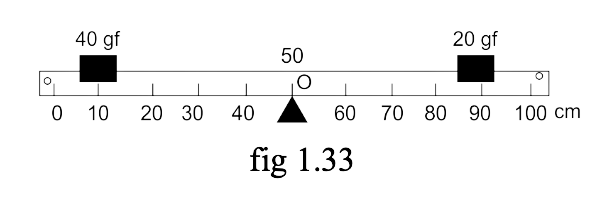
Ans:  Anticlockwise moment = 40 gf × (50 − 10) cm 

= 40gf × 40cm = 1600 gf × cm 

Clockwise moment = 20gf × (90- 50) 

= 20 gf × 40cm 

= 800 gf × cm 

The anticlockwise moment is not equal to the clockwise moment. 

Hence the metre rule is not in equilibrium, and it will turn anticlockwise.

(ii) How can the rule be brought in equilibrium by using an additional weight of 40 gf?

Ans: To balance it, 40gf weight should be kept on right-hand side to 

produce a clockwise moment about the middle point. Let its distance from the 

middle be ‘d’ cm. 

Then, clockwise moment = 20 gf × 40cm + 40gf × d cm 

From the principle of moments, 

Anticlockwise moment= Clockwise moment 

40 gf × 40 cm = 20gf × 40 + 40 × d cm 

1600 – 800 = 40gf × d cm

So, d = 800gf cm /40gf 

= 20 cm (on the other side)

Hence, by placing the additional weight of 40 gf at the 70 cm mark the rule can 

be brought in equilibrium. 

12. When a boy weighing 20 kgf sits at one end of a 4 m long see-saw, it gets depressed at this end. How can it be brought to the horizontal position by a man weighing 40 kgf.

Ans: From the principle of moments, 

Anticlockwise moment = Clockwise moment 

20 kgf × 2m = 40kgf × d 

So, d = (20 kgf ×2m)/ 40 kgf = 1m from the centre on the side opposite to the 

boy.

13. A physical balance has its arms of length 60 cm and 40 cm. What weight kept on the pan of the longer arm will balance an object of weight 100 gf kept on another pan? 

Ans: From the principle of moments, 

Anticlockwise moment = Clockwise moment 

100 gf × 40 cm = W × 60 cm 

So, weight on the longer pan,

W = (100gf ×40cm)/ 60cm = 200gf /3 = 66.67 gf

14. The diagram in Fig 1.34 shows a uniform metre rule weighing 100gf, pivoted as its centre O. Two weights 150 gf and 250 gf hang from the points A and B respectively of the metre rule such that OA = 40 cm and OB = 20 cm. 

Calculate: 

(i) the total anticlockwise moment about o, 

Ans: Total anticlockwise moment about O = 150 gf × 40 cm = 6000 gf cm 

(ii) the total clockwise moment about O, 

Ans: Total clockwise moment about O, = 250gf × 20 cm = 5000 gf cm 

(iii) the difference of anticlockwise and clockwise moments, and 

Ans: The difference of anticlockwise and clockwise moment = 6000 – 5000 = 1000gf cm 

(iv) the distance from O where a 100 gf weight should be placed to balance the metre rule.

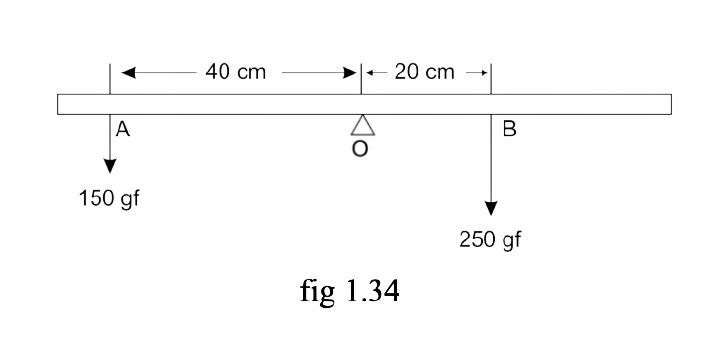
Anticlockwise moment = Clockwise moment

To balance it, 100gf weight should be kept on the right-hand side so as to produce a clockwise moment about the O. 

Let its distance from the point O be ‘d’ cm. 

Then, 150gf × 40 cm = 250gf × 20 cm + 100gf × d 

6000gf cm = 5000gf cm + 100gf × d 

1000gf cm = 100 gf × d 

So, d= 1000gf cm /100gf = 10 cm on the right side of O.

15. A uniform metre rule of weight 10 gf is pivoted at its 0 mark. 

(i) What moment of force depresses the rule? 

Ans: Anticlockwise moment= 10gf × 50 cm = 500gf cm

(ii) How can it be made horizontal by applying a least force? 

Ans: From the principle of moments, 

Anticlockwise moment = Clockwise moment 

10gf × 50 cm = W × 100cm 

So, W = (10gf ×50cm)/100cm = 5gf 

By applying a force 5 gf upwards at the 100 cm mark, the rule can be made 

horizontal.

16. A uniform half metre rule can be balanced at the 29.0 cm mark when a mass of 20 g is hung from its one end. 

(a) Draw a diagram of the arrangement. 

Ans: Diagram of the arrangement is shown below:

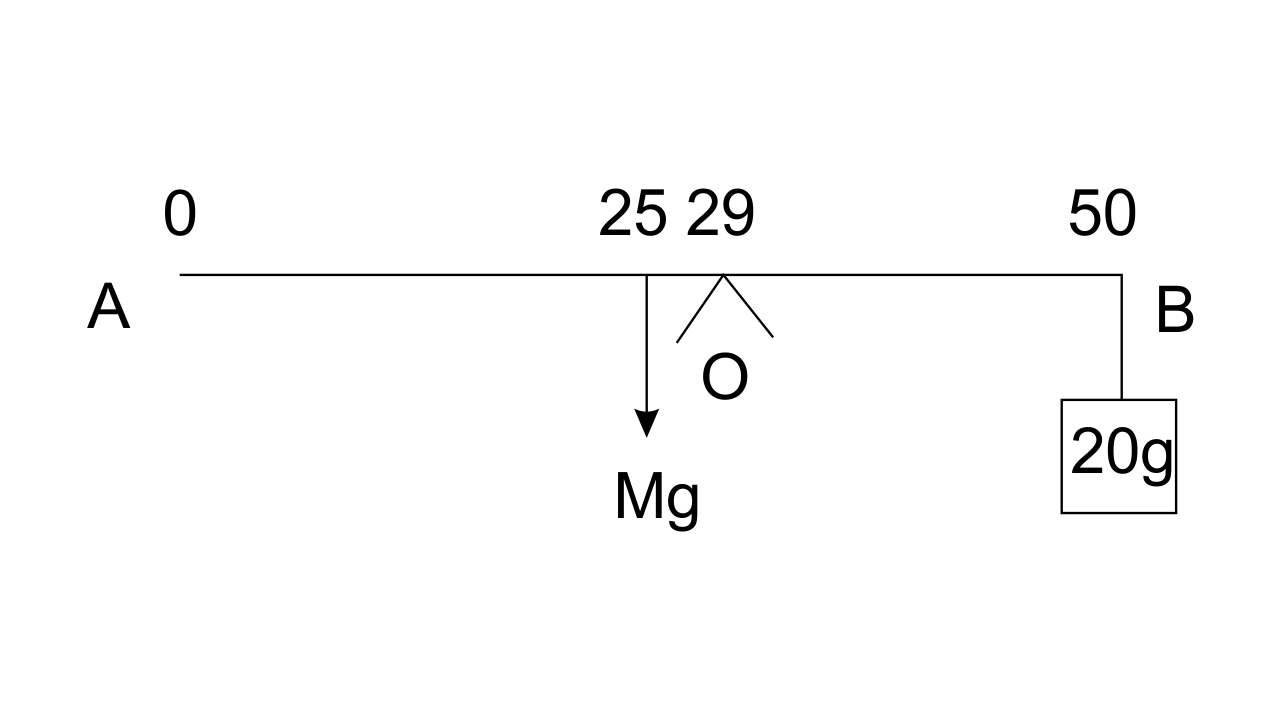
(b) Find the mass of the half metre rule.

Ans: Suppose the mass of the meter rule be M.

Given, uniform meter rule, so weight (Mg) will act at 25 cm.

Mg produces an anticlockwise moment about point o.

Now, to balance the 20g weight is tied at 50cm point and it acts in the clockwise direction.

As we know, the principle of moments states that

Anticlockwise moment = Clockwise moment

Mg (29 - 25) = 0.02 g (50-29) 

M = $\frac{21\times{0.02}}{4}$

M = 0.105 Kg

M = 105 g

The weight of half the meter rule is 105 g.

(c) In which direction would the balancing point shift if 20 g is shifted inside from its one end? 

Ans: The balancing point will shift towards the 25 cm mark.

17. A uniform metre rule of mass 100 g is balanced on a fulcrum at mark 40 cm by suspending an unknown mass m at the mark 20 cm. 

(i) Find the value of m. 

Ans: From the principle of moments, 

Clockwise moment = Anticlockwise moment 

100g × (50 − 40) cm = m × (40 − 20) cm 

100g × 10 cm = m × 20 cm = m = 50 g
 

(ii) To which side the rule will tilt if the mass m is moved to the mark 10 cm? 

Ans: The rule will tilt on the side of mass m (anticlockwise) if the mass m is 

moved to the mark 10cm.

(iii) What is the resultant moment now? 

Ans: Anticlockwise moment if mass m is moved to the mark 

10 cm = 50g × (40−10) cm = 50 × 30 = 1500 g cm 

Clockwise moment = 100g × (50 − 40) cm = 1000g cm 

Resultant moment = 1500g cm − 1000g cm = 500gf cm (anticlockwise)

(iv) How can it be balanced by another mass of 50 g? 

Ans: From the principle of moments, 

Clockwise moment = Anticlockwise moment 

To balance it, 50g weight should be kept on the right-hand side so as to produce a clockwise moment. Let its distance from the fulcrum be ‘d’ cm. 

So, 100g × (50 − 40) cm + (50g × d) = 50g × (40 − 10) cm 

1000g cm + (50g × d) = 1500 g cm 

50 g × d = 500g cm 

So, d =10 cm 

By suspending the mass 50g at the mark 50 cm, it can be balanced.

18. In Fig. 1.35, a uniform bar of length l m is supported at its end and loaded by a weight W kgf at its middle. In equilibrium, find the reactions R1 and R2 at the ends.

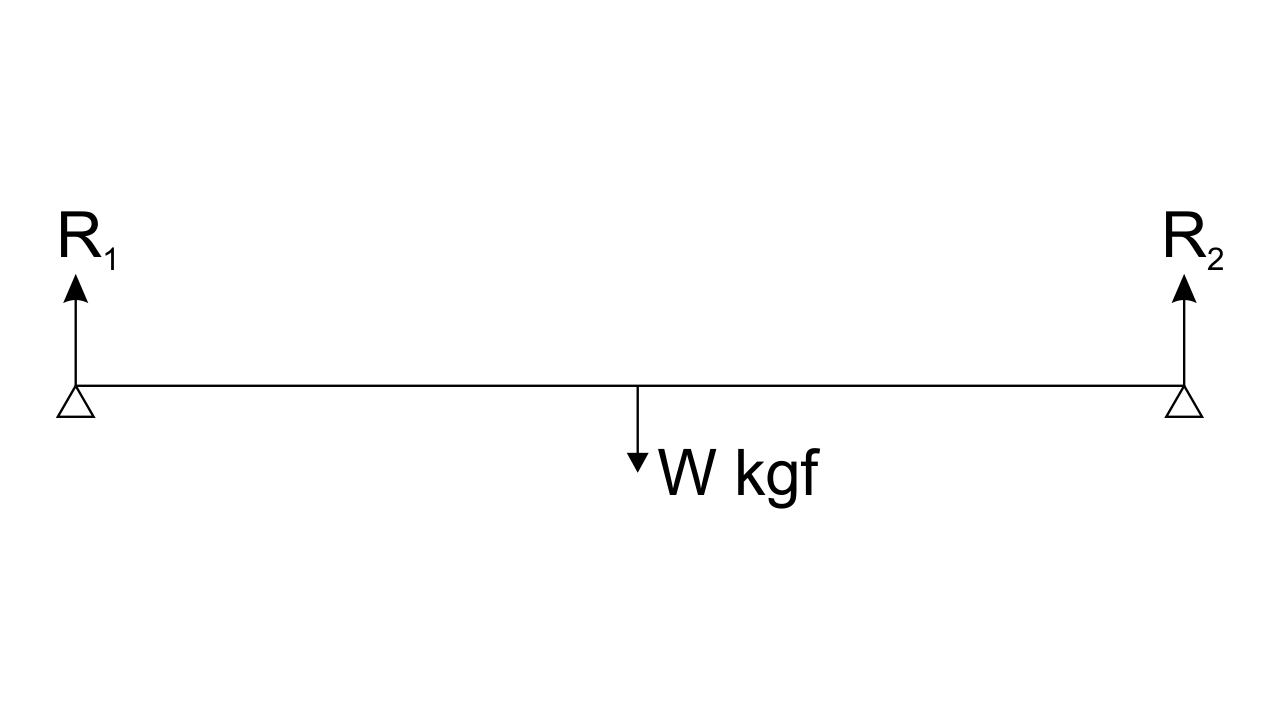
(Hint: in equilibrium R1 + R2 = W and R1 x $\frac{1}{2}$= R2 x $\frac{1}{2}$)

Ans:

Balancing the forces on Y-axis

R1 + R2 = W ……………… (1)

The equation for torque about the centre of bar:

R1(0.5) + W (0) – R2(0.5) = 0

• R1 = R2 …………………… (2)

From eq., (1) and (2)

R1 = R2 = $\frac{W}{2}$ kgf

Exercise – 1 (B)

1. Define the term ‘centre of gravity of a body’. 

Ans:

Centre of gravity is the point about which the algebraic sum of moments of weights of particles constituting the body are zero and the entire weight of the body is considered to act at this point. 

2. Can the centre of gravity be situated outside the material of the 

body? Give an example. 

Ans:

Yes, the center of gravity can be situated outside the material of the body. For example, the center of gravity of the ring.

3. State a factor on which the position of centre of gravity of a body depends? Explain your answer with an example. 

Ans:

The position of a body's centre of gravity is determined by its shape, or the distribution of mass within it.

For example, the center of gravity of a uniform wire is at its midpoint. The centre of gravity of this wire, however, will be at the centre of the circle if it is bent into a circle.

4. What is the position of centre of gravity of a: 

(a) rectangular lamina 

Ans: The position of centre of gravity of a 

(a) Rectangular lamina is the junction of the diagonals of the rectangular lamina.

(b) cylinder

Ans: Cylinder is on the cylinder's axis, at the midpoint

5. At which point is the centre of gravity situated in: 

(a) a triangular lamina 

Ans: A triangular lamina's centre of gravity is located at the intersection of its medians:

(b) a circular lamina? 

Ans: A circular lamina's centre of gravity is in the centre of the circular lamina.

6. Where is the centre of gravity of a uniform ring situated? 

Ans: Centre of gravity of a uniform ring is situated at the centre of the ring.

7. A square cardboard is suspended by passing a pin through a narrow hole at its one corner. Draw a diagram to show its rest position. In the diagram, mark the point of suspension by the letter S and centre of gravity by the letter G. 

Ans:

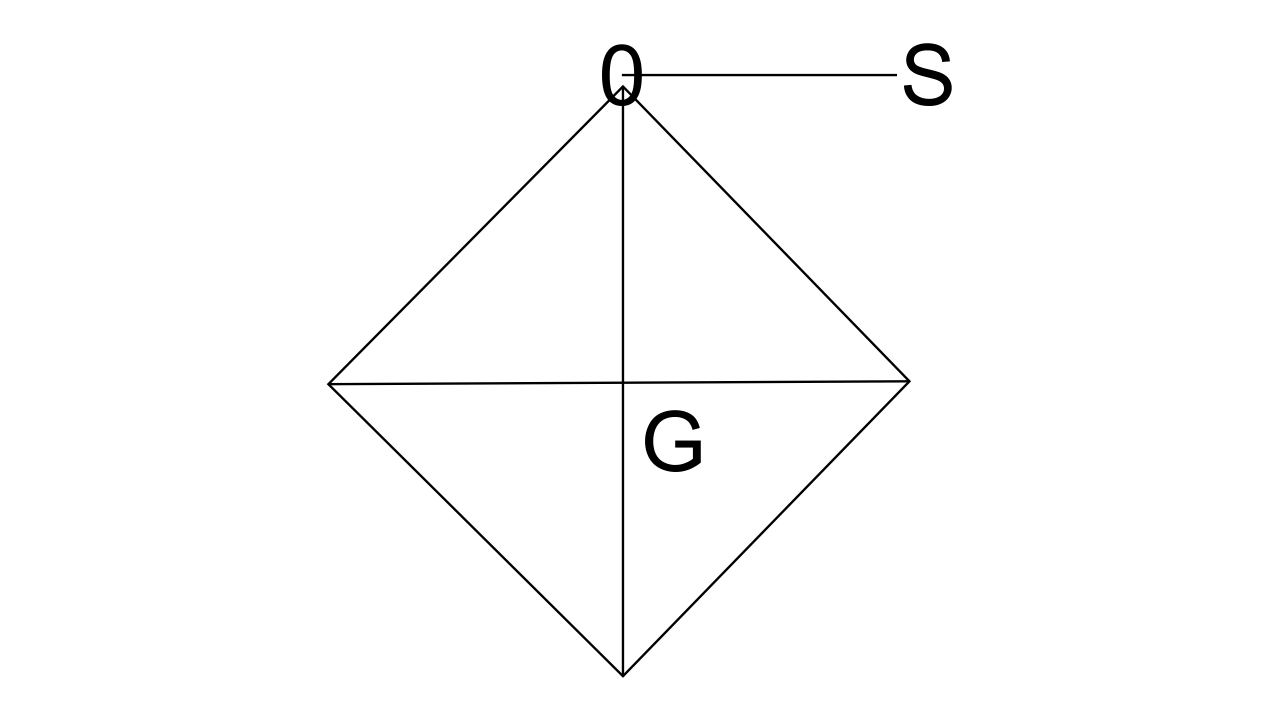
G is the centre of gravity, and S is the point of suspension, on a square cardboard in the rest position.

8. Explain how you will determine experimentally the position of centre of gravity for a triangular lamina (or a triangular piece of cardboard) 

Ans:

Take a triangular lamina. Make three fine holes along the edge of the triangular lamina at a, b, and c. Suspend the supplied lamina from hole 'a' with a plumb line. Verify that the lamina is free to oscillate around the suspension point. Draw a straight-line ad along the plumb line once the lamina has come to rest. Experiment again by dangling the lamina through hole 'b' and subsequently through hole 'c,' yielding straight lines be and cf, respectively. 

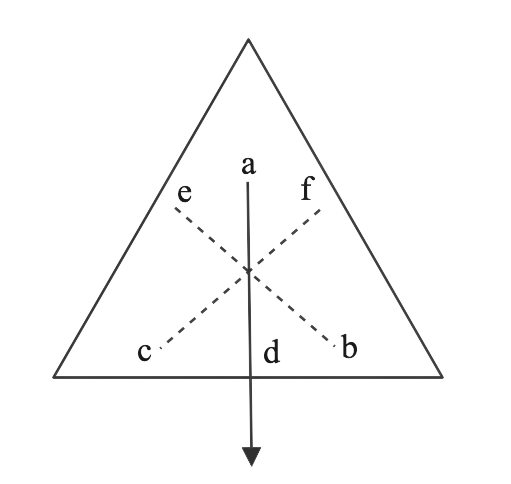
The lines ad, be, and cf intersect at a common point G, which is the position of the triangular lamina's centre of gravity, i.e., the point of intersection of mediAns:

9. State whether the following statements are true or false. 

(i) ‘The position of centre of gravity of a body remains unchanged even when the body is deformed’ 

Ans: False. The position of centre of gravity of a body of given mass depends on 

its shape i.e., on the distribution of mass in it.

(ii) ‘Centre of gravity of a freely suspended body always lies vertically below the point of suspension’

Ans: True. 

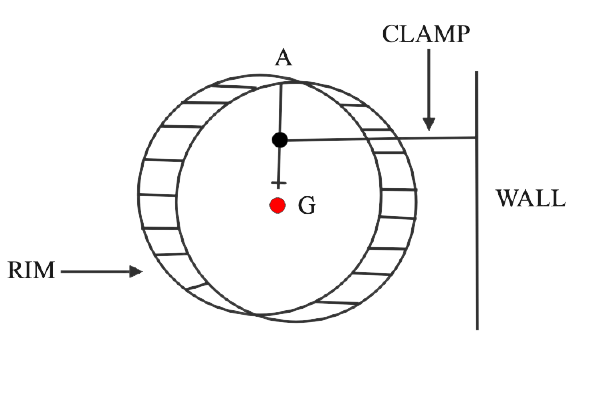
10. A uniform flat circular rim is balanced on a sharp vertical nail by supporting it at point A, as shown in fig 1.41. Mark the position of centre of gravity of the rim in the diagram by the letter G.

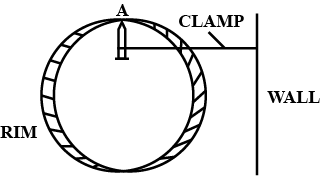
Ans:

11. Fig. 1.42 shows three pieces of card board of uniform thickness cut into three different shapes. On each diagram draw two lines to indicate the position of centre of gravity G.

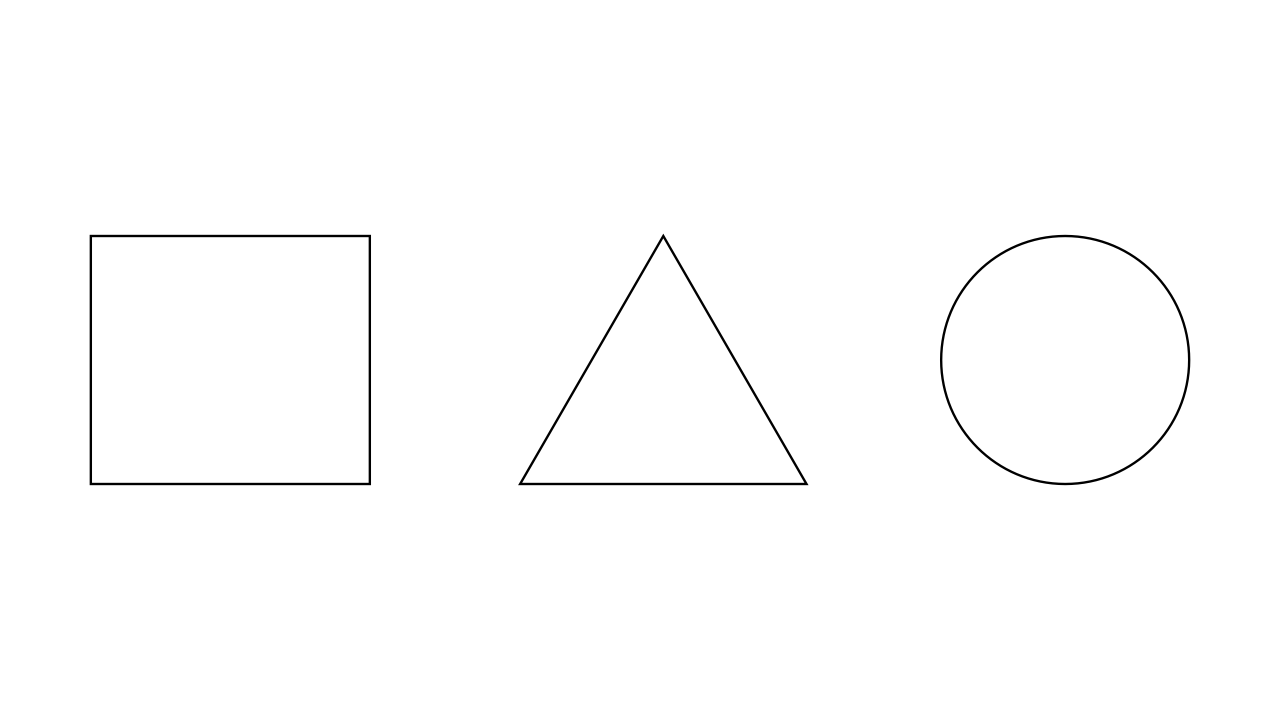
Fig. 1.42

Ans:

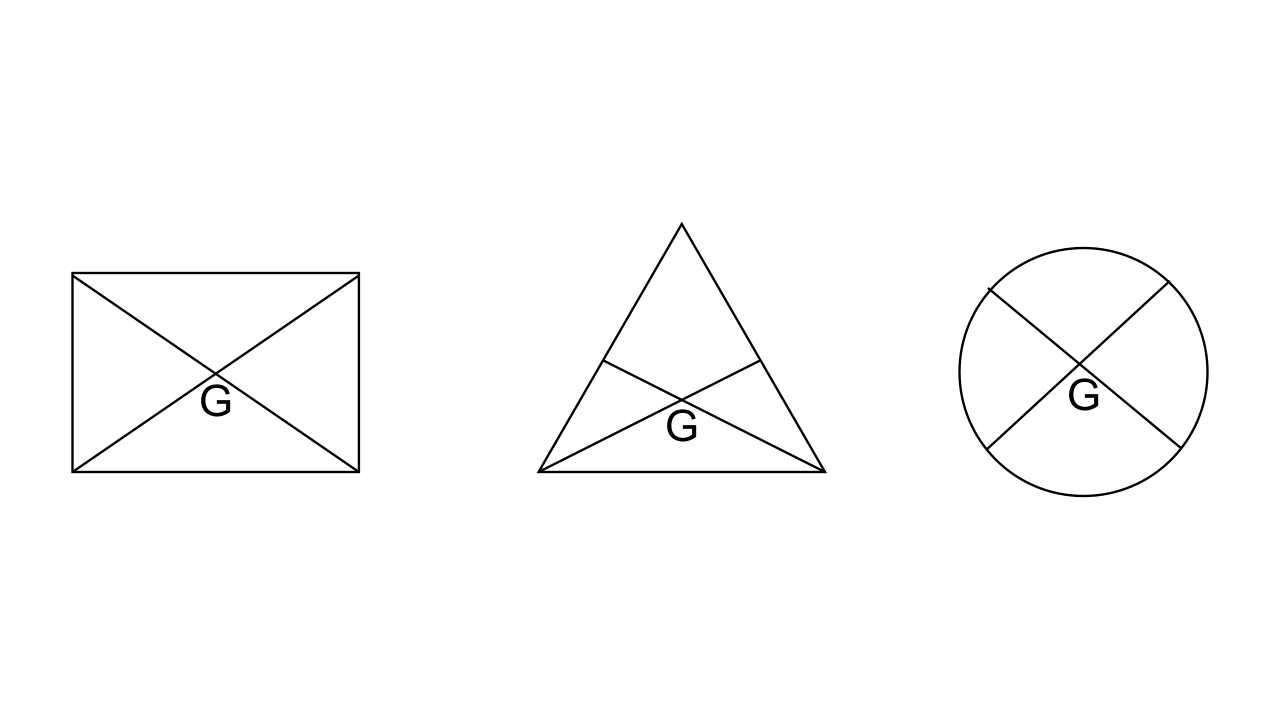
Multiple Choice Type:

1. The centre of gravity of a uniform ball is 

(a) at its geometrical centre 

(b) at its bottom 

(c) at its topmost point 

(d) at any point on its surface 

Ans: The correct answer is option (a).

(a) At its geometrical centre

2. The centre of gravity of a hollow cone of height h is at distance x from its vertex where the value of x is:

(a) h/3 

(b) h/4

(c) 2h/3 

(d) 3h/4

Ans: The correct answer is option (c).

The centre of gravity of a hollow cone is at a height of h/3 from the base. Hence, from the vertex the height is 

h - $\frac{\text {h}}{3}=\frac{\text{2h}}{3}$

Hence, the correct answer is (c) 2h/3 

Exercise 1(C)

1. Explain the meaning of uniform circular motion. Why is such motion said to be accelerated?

Ans: A particle's motion is said to be uniform circular motion when it moves at a constant speed in a circular route. The revolution of the earth around the sun, for example, is an example of uniform circular motion.

Because the velocity changes due to the continuous change in motion direction, uniform circular motion is accelerated. As a result, even when the body moves at a constant speed, its velocity varies. As a result, the velocity of a body moving in a circular path at a constant speed varies continuously. The change in velocity causes the moving body to accelerate. As a result, even when the speed remains constant, circular motion is an acceleration motion.

2. Draw a neat labelled diagram for a particle moving in a circular path with a constant speed. In your diagram show the direction of velocity at any instant. 

Ans: A particle moving in a circular path with a constant speed.

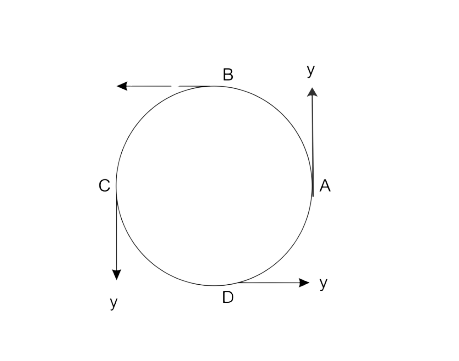
3. Is it possible to have an accelerated motion with a constant speed? Name such type of motion. 

Ans: Yes, the uniform circular motion has an accelerated motion with a constant speed. 

4. Give an example of motion in which speed remains uniform, but the velocity changes. 

Ans: A cyclist on a circular track is an example of motion in which the velocity fluctuates but the speed remains constant.

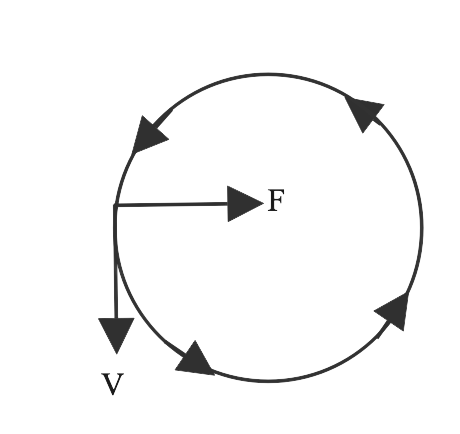
5. A uniform circular motion is an accelerated motion. State whether the acceleration is uniform or variable? Name the force responsible to cause this acceleration. What is the direction of force at any instant? Draw a diagram in support of your answer.

Ans: The speed of a uniform circular motion is increased because the direction changes frequently. As a result, it is described as an evenly accelerated motion.

This acceleration requires centripetal force, which is directed toward the circular path's centre.

6. Differentiate between a uniform linear motion and uniform circular motion.

Ans:

7. Name the force required for circular motion. State its direction. 

Ans: Centripetal force is required for circular motion. It is always directed towards the centre of the circle.

8. What is a centripetal force? 

Ans: Force acting on a body that is in circular motion is called centripetal force. It acts towards the centre of the circular path.

9. Explain the motion of a planet around the sun in a circular path.

Ans: A planet orbits the sun in a circular route, with the requisite centripetal force provided by the sun's gravitational attraction on the planet. The centripetal force, which is responsible for the planet's round motion, is always directed towards the sun's centre at each point along its journey. 

10. (a) How does a centripetal force differ from a centrifugal force with reference to the direction in which they act?

Ans: Centripetal force acts in the centre of the rotational motion whereas the centrifugal force is the kind of the rotational force that acts away from the centre. Both the force acts in the direction opposite to each other.

(b) Is centrifugal force the force of reaction of the centripetal force?

Ans: The centripetal force and the centrifugal force possess the same magnitude but opposite directions to each other. Though they behave as the reaction force, they do not form the pair of the action and the reaction as given by Newton's third law of motion. Newton's third law states that for every action produced by one object will have an equal and opposite direction produced by the other object. But these centripetal and the centrifugal force act on the same body.

(c) Compare the magnitudes of centripetal and centrifugal force.

Ans: The magnitude of the centripetal and the centrifugal force are equal but their direction varies.

11. Is centrifugal force a real force?

Ans: No, centrifugal force is a fictitious force.

12. A small pebble tied at one end of a string is placed near the periphery of a circular disc, at the centre of which the other end of the string is tied to a peg. The disc is rotating about an axis passing through its centre. 

(a) What will be your observation when you are standing outside the disc? Explain. 

Ans: On standing outside the disc, we find that the pebble is moving on a circular path.

(b) What will be your observation when you are standing at the centre of the disc. Explain.

Ans: On standing at the centre of the disc, we find that the pebble is stationary placed just in front of us. 

13. A piece of stone tied at the end of a thread is whirled in a horizontal circle with uniform speed by hand. Answer the following questions:

(a) Is the velocity of stone uniform or variable?

Ans: Velocity of the stone is variable.

(b) Is the acceleration of stone uniform or variable?

Ans: Acceleration of stone is variable.

(c) What is the direction of acceleration at any instant?

Ans: The direction of acceleration of stone at any instance is to the centre of the circular path.

(d) Which force provides the centripetal force required for circular motion?

Ans: The frictional force provides the centripetal force.

(e) Name the force and its direction which acts on the hand.

Ans: Centrifugal force acts on the hand and its direction is away from the centre.

14. State two differences between centripetal and centrifugal force.

Ans:

15. State whether the following statements are true or false by writing T/F against them. 

(a) Earth moves around the sun with a uniform velocity.

Ans: False

(b) The motion of the moon around the earth in a circular path is an accelerated motion. 

Ans: True

(c) A uniform linear motion is un-accelerated, while a uniform circular motion is an accelerated motion. 

Ans: True

(d) In a uniform circular motion, the speed continuously changes because the direction of motion changes. 

Ans: False

(e) A boy experiences a centrifugal force on his hand when he rotates a piece of stone tied at one end of a string, holding the other end in his hand.

Ans: True

Multiple Choice Type:

1. Which of the following quantity remains constant in a uniform circular motion:

(a) Velocity

(b) speed

(c) acceleration

(d) both velocity and speed.

Ans: The correct option is option (b). 

Speed is a scalar quantity, whereas velocity and acceleration are vectors. As a result, while speed remains constant, velocity and acceleration change as the direction changes, and in a circular motion, the direction of motion changes at each point.

2. Centrifugal force is:

(a) A real force 

(b) The force of reaction of centripetal force

(c) A fictitious force

(d) Directed towards the centre of the circular path.

Ans: The correct option is option (c). 

Force Solutions for ICSE Board Class 10 Physics

Introduction:

Force Solutions for ICSE Board Class 10 Physics (Concise - Selina Publishers) provides students a solution that contains accurate answers for all of the questions that are mentioned in the NCERT Class 10 textbook and are as per the ICSE board. These solutions are provided by the Physics expert at Vedantu. Selina Solutions that are provided are also in such a language that provides students a better and logical understanding of the topics. Selina Solutions for Class 10 are also quite helpful in analyzing the answers and checking their performance. Using the method of smart study will help you score better marks in Class 10 and by using the tips provided in Selina Solutions we can also perform much better in examinations.

Benefits of Force Solutions for ICSE Board Class 10 Physics (Concise - Selina Publishers):

1. Selina Solutions prepared for students of ICSE Class 10 are one of the best learning resources that help students to stimulate their exam preparations

2. Solutions that are provided consist of step by step points so that students understand each of the steps involved in the process

3. The help that the students get makes it easier for them to understand the topics easily and explain the answers in their own words.