Concise Mathematics Class 10 ICSE Solutions for Chapter 12 - Reflection

Exercise 12A

1. Complete the following table:

Ans: If the point is reflected with respect to the origin then the sign for both the coordinates will change.

If the point is reflected with respect to the y-axis then the sign of the x coordinate will change.

If the point is reflected with respect to the x-axis then the sign of the y coordinate will change.

So the new table will be

2. A point A is its own image under the reflection in the line l. Describe the position of the point P with respect to the line l.

Ans: In the question, it is given that the point P has its own image under the reflection of the line l.

Therefore the point P is a fixed point.

Thus, the position of point P with respect to the line l is unchanged.

3. State the coordinates of the following points under reflection in x-axis:

(i) (3,2)

Ans: If the point is reflected with respect to the x-axis then the sign of the y coordinate will change.

(3,2) after reflection under x-axis will be (3,-2)

(ii) (-5,4)

Ans: If the point is reflected with respect to the x-axis then the sign of the y coordinate will change.

(-5,4) after reflection under x-axis will be (-5,-4)

(iii) (0,0)

Ans: If the point is reflected with respect to the x-axis then the sign of the y coordinate will change.

(0,0) after reflection under x-axis will be (0,0)

4. State the coordinates of the following points under reflection in y-axis:

(i) (6,-3)

Ans: If the point is reflected with respect to the y-axis then the sign of the x coordinate will change.

(6,-3) after reflection under y-axis will be (-6,-3)

(ii) (-1,0)

Ans: If the point is reflected with respect to the y-axis then the sign of the x coordinate will change.

(-1,0) after reflection under y-axis will be (1,0)

(iii) (-8,-2)

Ans: If the point is reflected with respect to the y-axis then the sign of the x coordinate will change.

(-8,-2) after reflection under y-axis will be (8,-2)

5. State the coordinates of the following points under reflection in origin:

(i) (-2,-4)

Ans: If the point is reflected with respect to the origin then the sign for both the coordinates will change.

(-2,-4) after reflection under origin will be (2,4)

(ii) (-2,7)

Ans: If the point is reflected with respect to the origin then the sign for both the coordinates will change.

(-2,7) after reflection under origin will be (2,-7)

(iii) (0,0)

Ans: If the point is reflected with respect to the origin then the sign for both the coordinates will change.

(0,0) after reflection under origin will be (0,0)

6. State the coordinates of the following points under reflection in the line x=0:

(i) (-6,4)

If a point is reflected with respect to the line x=0, then the sign of the x-coordinate will change.

(-6,4) after reflection will be (6,4).

(ii) (0,5)

If a point is reflected with respect to the line x=0, then the sign of the x-coordinate will change.

(0,5) after reflection will be (0,5).

(iii) (3,-4)

If a point is reflected with respect to the line x=0, then the sign of the x-coordinate will change.

(3,-4) after reflection will be (-3,-4).

7. State the coordinates of the following points under reflection in the line y=0:

(i) (-3,0)

If a point is reflected with respect to the line y=0, then the sign of the y-coordinate will change.

(-3,0) after reflection will be (-3,0).

(ii) (8,-5)

If a point is reflected with respect to the line y=0, then the sign of the y-coordinate will change.

(8,-5) after reflection will be (8,5).

(iii) (-1,-3)

If a point is reflected with respect to the line y=0, then the sign of the y-coordinate will change.

(-1,-3) after reflection will be (-1,3).

8. A point P is reflected in the x-axis. Coordinates of its image are (-4,5).

(i) Find the coordinates of P.

(ii) Find the coordinates of the image of P under reflection in the y-axis.

Ans: Given that the Coordinates of point P are reflected in x-axis, which means the sign of the y coordinate is changed.

Original coordinates of P will be (-4,-5).

Coordinates of point under reflection of y-axis will be a change in the sign of x coordinate which is equal to (4,5)

9. A point P is reflected in the origin. Coordinates of its image are (-2,7).

(i) Find the coordinates of point P.

(ii) Find the coordinates of the image of P under reflection in the x-axis.

Ans: Given that the coordinates are reflected under origin. Therefore both the coordinates are changed.

Original coordinates of the point P are (2,-7)

Coordinates of point under reflection of x-axis will be a change in the sign of y coordinate which is equal to (-2,-7)

10. The point P(a,b) is first reflected in the origin and then reflected in the y-axis to $\mathbf{P}'$. If $\mathbf{P}'$ has the coordinates (4,6); evaluate a and b.

Ans: If a point is reflected in the origin then signs of both the coordinates will change.

If a point is reflected in the y-axis then the sign of x coordinate will change.

P(a,b) when reflected under origin will be (-a,-b)

(-a,-b) when reflected under y-axis will be (a,-b)

$\text{P}'$=(a,-b)

Given $\text{P}'$ has coordinates (4,6)

(a,-b)=(4,6)

Therefore a=4 and b=-6.

11. The point P(x,y) is first reflected in the x-axis and then reflected in the origin to $\mathbf{P}'.$ If $\mathbf{P}'$ has coordinates (-8,5); evaluate x and y.

Ans: Reflection of point P(x,y) with respect to x-axis is (x,-y).

Reflection of (x,-y) with respect to origin is $\text{P }\!\!'\!\!\text{ }$=(-x,y)

Given the coordinates of $\text{P }\!\!'\!\!\text{ }$ as (-8,5)

Comparing (-x,y) to (-8,5), we get x=8 and y=5.

12. The point A(-3,2) is reflected in the x-axis to the point $\mathbf{A}'.$ Point $\mathbf{A}'$ is then reflected in the origin to point $\mathbf{A}''.$

(i) Write down the coordinates of  $\mathbf{A}''.$

Ans: When a point is reflected in the x-axis, the sign of the y coordinate will change. So $\text{A }\!\!'\!\!\text{ }$=(-3,-2)

$\text{A }\!\!'\!\!\text{ }$=(-3,-2) is reflected in the origin to form $\text{A}''.$ So $\text{A}''$=(3,2).

(ii) Write a single transformation that maps $\mathbf{A}$ onto $\mathbf{A}''.$

Ans: Reflection of a point P(x,y) with respect to y-axis is P(-x,y)

Reflection of (-3,2) with respect to y-axis is (3,2)

Therefore, the reflection of point A with respect to y-axis is point $\text{A}''.$ 

13. The point A(4,6) is first reflected in the origin to point $\mathbf{A}'.$ Point $\mathbf{A}'$ is then reflected in the y-axis to point $\mathbf{A}''.$

(i) Write down the coordinates of  $\mathbf{A}''.$

Ans: When a point is reflected in the origin, the sign of both coordinates will change. So $\text{A }\!\!'\!\!\text{ }$=(-4,-6)

$\text{A }\!\!'\!\!\text{ }$=(-4,-6) is reflected in the y-axis to form $\text{A}''.$ So $\text{A}''$=(4,-6).

(ii) Write a single transformation that maps $\mathbf{A}$ onto $\mathbf{A}''.$

Ans: Reflection of a point P(x,y) with respect to x-axis is P(x,-y)

Reflection of (4,6) with respect to x-axis is (3,-2)

Therefore, the reflection of point A with respect to x-axis is point $\text{A}''.$ 

14. The triangle ABC, where A is (2,6), B is (-3,5) and C is (4,7), is reflected in the y-axis to triangle $\mathbf{A}'\mathbf{B}'\mathbf{C}'$. Triangle $\mathbf{A}'\mathbf{B}'\mathbf{C}'$ is then reflected in the origin to triangle $\mathbf{A}''\mathbf{B}''\mathbf{C}''.$

(i) Write down the coordinates of $\mathbf{A}'',\mathbf{B}'',\mathbf{C}''.$

Ans: Reflection in y-axis is given by the change in the sign of x-axis.

$\text{A }\!\!'\!\!\text{ }$=(-2,6); $\text{B }\!\!'\!\!\text{ }$=(3,5); $\text{C }\!\!'\!\!\text{ }$=(-4,7)

Reflection in origin is given by the change in the sign of both the coordinates.

$\text{A}''$=(2,-6); $\text{B}''$=(-3,-5); $\text{C}''$=(4,-7)

(ii) Write down a single transformation that maps triangle $\mathbf{ABC}$ onto triangle $\mathbf{A}''\mathbf{B}''\mathbf{C}''.$

Ans: Reflection of a point P(x,y) with respect to x-axis is P(x,-y)

Reflection of (2,6), (-3,5) and (4,7) with respect to the x-axis is (3,-6), (-3,-5) and (4,-7).

Therefore, the reflection of triangle ABC with respect to x-axis is point $\text{A}''\text{B}''\text{C}''.$

15. P and Q have coordinates (-2,3) and (5,4) respectively. Reflect P in the x-axis to $\mathbf{P}'$ and Q in the y-axis to $\mathbf{Q}'.$ State the coordinates of $\mathbf{P}'$ and $\mathbf{Q}'.$

Ans: Reflection of a point A(x,y) with respect to x-axis is A(x,-y).

So P(-2,3) will become $\text{P }\!\!'\!\!\text{ }$(-2,-3)

Reflection of a point A(x,y) with respect to y-axis is A(-x,y)

So Q(5,4) will become $\text{Q }\!\!'\!\!\text{ }$(-5,4)

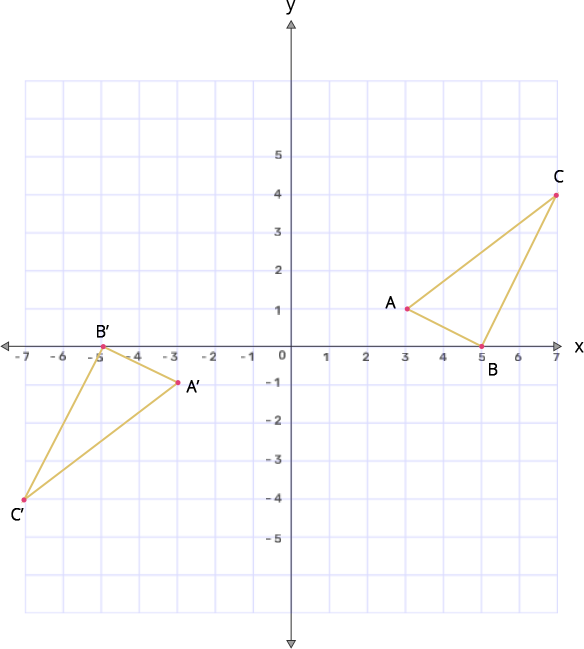
16. On a graph paper, plot the triangle ABC, whose vertices are at the points A(3,1), B(5,0) and C(7,4).

On the same diagram, draw the image of the triangle ABC under reflection in the origin O(0,0).

Ans: Given the points of triangle ABC and another triangle $\text{A }\!\!'\!\!\text{ B }\!\!'\!\!\text{ C }\!\!'\!\!\text{ }$ is formed when it is reflected with respect to the origin forming $\text{A }\!\!'\!\!\text{ B }\!\!'\!\!\text{ C }\!\!'\!\!\text{ }.$

Reflection of a point P(x,y) with respect to origin is P(-x-y).

So, coordinates of the reflected triangle are $\text{A }\!\!'\!\!\text{ }$(-3,-1), $\text{B }\!\!'\!\!\text{ }$(-5,0) and $\text{C }\!\!'\!\!\text{ }$(-7,-4).

So the graph formed will be as shown below.

17. Point $\mathbf{A}$(4,-1) is reflected as $\mathbf{A}'$ in the y-axis. Point $\mathbf{B}$ on reflection in the x-axis is mapped as $\mathbf{B}'$(-2,5). Write the coordinates of $\mathbf{A}'$ and $\text{B}$.

Ans: Reflection of a point P(x,y) with respect to x-axis is P(x,-y).

Reflection of a point P(x,y) with respect to the y-axis is P(-x,y).

So point A(4,-1) will become $\text{A }\!\!'\!\!\text{ }$(-4,-1)

Given B when reflected in x-axis gives $\mathbf{B}'$(-2,5)

So B=(-2,-5)

18. The point (-5,0) on reflection in a line is mapped as (5,0) and the point (-2,-6) on reflection in the same line is mapped as (2,-6).

(a) Name the line of reflection.

Ans: If we observe only the sign of the x-coordinate is changed for the point (-5,0) and (-2,-6).

We know that the reflection of a point P(x,y) with respect to the y-axis is P(-x,y).

Therefore the reflection is in the y-axis.

(b) Write the coordinates of the image of (5,-8) in the line obtained in (a).

Ans: In (a) we found that the reflection is in the y-axis.

Reflection of a point P(x,y) with respect to the y-axis is P(-x,y).

Therefore the coordinates of the image of (5,-8) in the line obtained is (-5,-8).

Exercise 12B

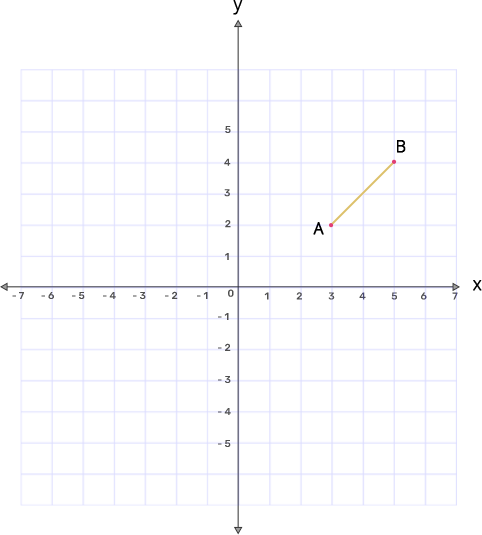
1. Attempt this question on graph paper

(a) Plot A(3,2) and B(5,4) on graph paper. Take 1cm=1unit on both the axes.

Ans: 

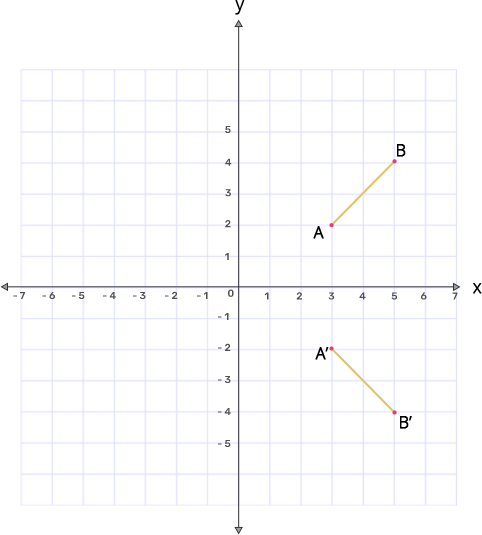
(b) Reflect A and B in the x-axis to $\mathbf{A}'$ and $\mathbf{B}'$ respectively. Plot these points also on the same graph paper.

Ans: A(3,2) when reflected in x-axis will be $\text{A }\!\!'\!\!\text{ }$(3,-2)

B(5,4) when reflected in x-axis will be $\text{B }\!\!'\!\!\text{ }$(5,-4)

(c) Write down

(i) Geometrical name of the figure $\mathbf{AB{B}'{A}'}.$

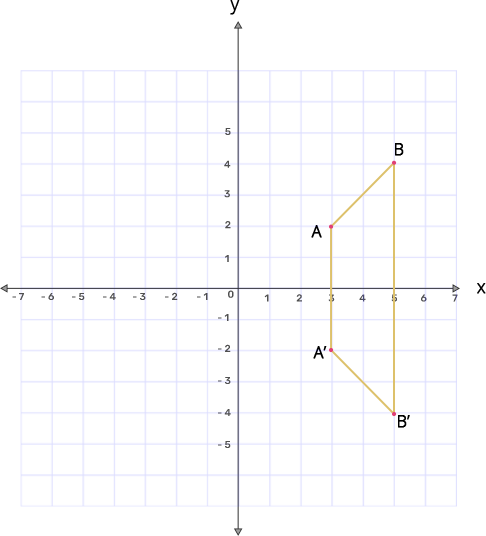
From the graph, the shape of $\mathbf{ABB}'\mathbf{A}'$ will be an isosceles trapezium.

(ii) The measure  of angle $\mathbf{ABB}'.$

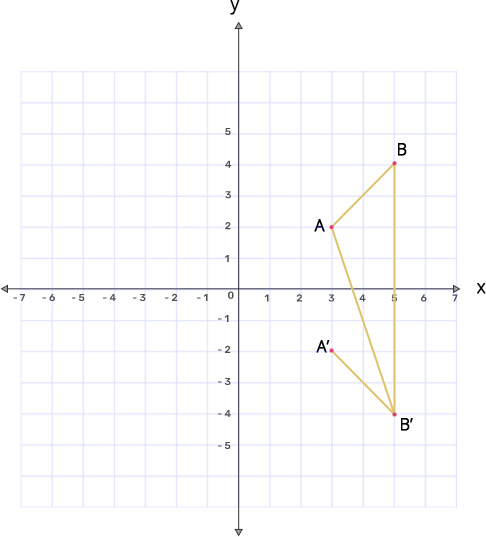
Drop a perpendicular line from A such that it meets the line B, then the point will be a right angle and the other two points from the figure will be at ${{45}^{\text{o}}}.$

Therefore the measure of angle $\text{ABB }\!\!'\!\!\text{ }$ is ${{45}^{\text{o}}}.$

(iii) The image $\mathbf{A}''$ of $\mathbf{A},$ when A is reflected in origin.

A(3,2) when reflected in origin will be $\text{A}''$(-3,-2)

(iv) The single transformation that maps $\mathbf{A}'$ to $\mathbf{A}''.$

$\mathbf{A}'$ (3,-2) and $\text{A}''$(-3,-2)

Only the sign of the x-coordinate is changed.

Reflection in the y-axis will give a change in the sign of the x-coordinate.

2. Points (3,0) and (-1,0) are invariant points under the reflection in the line ${{\mathbf{L}}_{1}};$ points (0,-3) and (0,1) are invariant points on reflection in line ${{\mathbf{L}}_{2}}.$

(i) Name or write equations for the lines ${{\mathbf{L}}_{1}}$ and ${{\mathbf{L}}_{2}}.$

Ans: Given points (3,0) and (-1,0) have y-coordinate as 0 and so they lie in the x-axis. Therefore the points (3,0) and (-1,0) are invariant in points under the reflection in the x-axis.

Thus the equation of line ${{\text{L}}_{1}}$ is y=0.

Given points (0,-3) and (0,1) have x-coordinates as 0 and so they lie in the y-axis. Therefore the points (0,3) and (0,1) are invariant in points under the reflection in the y-axis.

Thus the equation of line ${{\text{L}}_{2}}$ is x=0.

(ii) Write down the images of points P(3,4) and Q(-5,-2) on reflection in ${{\mathbf{L}}_{1}}.$ Name the images as $\mathbf{P}'$ and $\mathbf{Q}'$ respectively.

Ans: We know that line ${{\text{L}}_{1}}$ is a reflection in the x-axis.

Point P(3,4) when reflected in x-axis will be $\text{P }\!\!'\!\!\text{ }$(3,-4) and point Q(-5,-2) when reflected in x-axis will be $\text{Q }\!\!'\!\!\text{ }$(-5,2).

(iii) Write down the images of P and Q on reflection in ${{\mathbf{L}}_{2}}.$ Name the images as $\mathbf{P}''$ and $\mathbf{Q}''$ respectively.

Ans: We know that line ${{\text{L}}_{2}}$ is a reflection in the y-axis.

Point P(3,4) when reflected in y-axis will be $\text{P}''$(-3,4) and point Q(-5,-2) when reflected in y-axis will be $\text{Q}''$(5,-2).

(iv) State or describe a single transformation that maps $\mathbf{P}'$ onto $\mathbf{P}''.$

Ans: $\text{P }\!\!'\!\!\text{ }$ is (3,-4) and $\text{P}''$ is (-3,4)

Signs of both the coordinates are changed, which means the reflection took place in the origin.

(x,y) when reflected in origin gives (-x,-y).

3. (i) Point P(a,b) is reflected in the x-axis to $\mathbf{P}'$(5,-2). Write down the values of a and b.

Ans: When P(a,b) is reflected in x-axis, point P will transform to (a,-b)

So $\text{P }\!\!'\!\!\text{ }$(a,-b)=$\mathbf{P}'$(5,-2)

Therefore, a=5 and b=2

(ii) $\mathbf{P}''$ is the image of P when reflected in the y-axis. Write down the coordinates of $\mathbf{P}''.$

Ans: When P(a,b) is reflected in y-axis, point P will transform to (-a,b)

So $\text{P}''$=(-5,2)

(iii) Name a single transformation that maps $\mathbf{P}'$ to $\mathbf{P}''.$

Ans: When a point P(a,b) is reflected in origin then the point transforms to (-a,-b).

$\text{P }\!\!'\!\!\text{ }$=(5,-2) and $\text{P}''$=(-5,2)

Here the signs of both the coordinates are changed.

So when $\text{P }\!\!'\!\!\text{ }$ is reflected in origin, we get $\text{P}''.$

4. The point (-2,0) on reflection in a line is mapped to (2,0) and the point (-5,6) on reflection in the same line is mapped to (-5,-6).

(i) State the name of the mirror line and write its equation.

Ans: The reflection in the y-axis is given by ${{\text{M}}_{\text{y}}}$(x,y) = (-x,y).

Hence, the point (-2,0) when reflected in the y-axis is mapped to (-2,0).

Thus, the mirror line is the y-axis and its equation is x = 0.

(ii) State the coordinates of the image (-8,-5) in the mirror line.

Ans: Coordinates of the image of (-8, -5) in the mirror line (i.e., y-axis) 

are (-8,5).

5. The points P(4,1) and Q(-2,4) are reflected in line y=3. Find the coordinates of $\mathbf{P}',$ the image of $\mathbf{P}$ and $\mathbf{Q}',$ the image of $\mathbf{Q}.$

Ans: Line y=3 is parallel to x-axis which is at a distance of 3 units.

Mark the points P and Q on the graph and also draw the line y=3 and let us consider it as XY.

Given P(4,1) is below the line XY and the point Q(-2,4) is above the line.

Mark another point $\text{P }\!\!'\!\!\text{ }$ such that it is the exact image of the point P and mark another point $\text{Q }\!\!'\!\!\text{ }$ such that it is the exact image of the point Q.

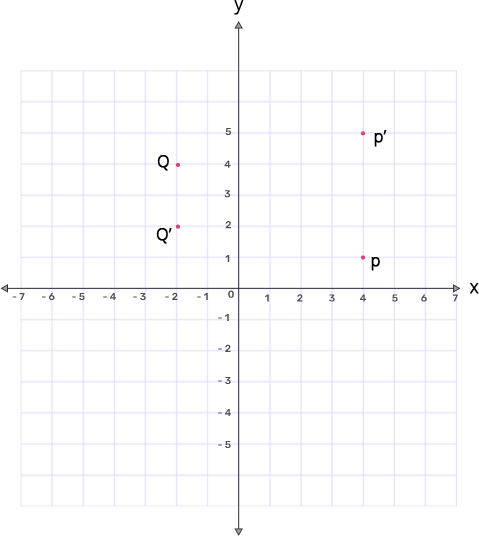
Thus the coordinates of the points $\text{P }\!\!'\!\!\text{ }$ and $\text{Q }\!\!'\!\!\text{ }$ are (4,5) and (-2,2) respectively.

6. A point P(-2,3) is reflected in the line x=2 to the point $\mathbf{P}'.$ Find the coordinates of $\mathbf{P}'.$

Ans: Line x=2 is parallel to y-axis which is at a distance of 2 units.

Mark the point P on the graph and also draw the line x=2 and let us consider it as XY.

Given P(-2,3) is on the left side of the line XY and the point.

Mark another point $\text{P }\!\!'\!\!\text{ }$ such that it is the exact image of the point P.

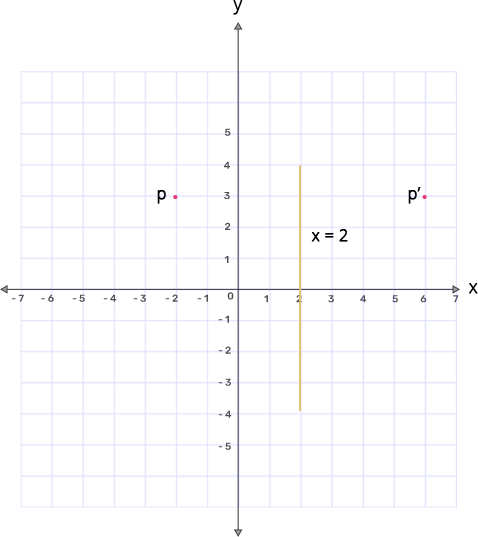
Thus the coordinates of the points $\text{P }\!\!'\!\!\text{ }$ is (6,3).

7. A point $\mathbf{P}$(a,b) is reflected in the x-axis to $\mathbf{P}'$(2,-3). Write down the values of a and b. $\mathbf{P}''$ is the image of $\mathbf{P}$, reflected in the y-axis. Write down the coordinates of $\mathbf{P}''.$ Find the coordinates of $\mathbf{P}'''$ when $\mathbf{P}$ is reflected in the line, parallel to the y-axis such that x=4.

Ans: A point $\text{P}$(a,b) is reflected in the x-axis to $\text{P }\!\!'\!\!\text{ }$(2,-3).

We know ${{\text{M}}_{\text{x}}}$(x,y) =(x,-y)

Thus, coordinates of $\text{P}$ are (2,3).

Hence, a=2 and b=3.

Image of $\text{P}$ reflected in the y-axis is $\text{P}''$(−2,3) .

Reflection of P in the line x = 4 is $\text{P}''\text{ }\!\!'\!\!\text{ }$(6,3).

8. Points A and B have coordinates (3,4) and (0,2) respectively. Find the image:

(a) $\mathbf{A}'$ of $\mathbf{A}$ under reflection in the x-axis.

Ans: When A(3,4) is reflected in the x-axis, we get $\text{A }\!\!'\!\!\text{ }$(3,-4).

(b) $\mathbf{B}'$ of $\mathbf{B}$ under reflection of the line $\mathbf{AA}'.$

Ans: Image of B(0,2) under reflection in the line $\text{AA }\!\!'\!\!\text{ }$ is $\text{B }\!\!'\!\!\text{ }$(6,2).

(c) $\mathbf{A}''$ of $\mathbf{A}$ under reflection in the y-axis.

Ans: When A(3,4) is reflected in the y-axis, we get $\text{A}''$(-3,4).

(d) $\mathbf{B}''$ of $\mathbf{B}$ under reflection in the line $\mathbf{AA}''.$

Ans: Image of B(0,2) under reflection in the line $\text{AA}''$ is $\text{B}''$(0,6).

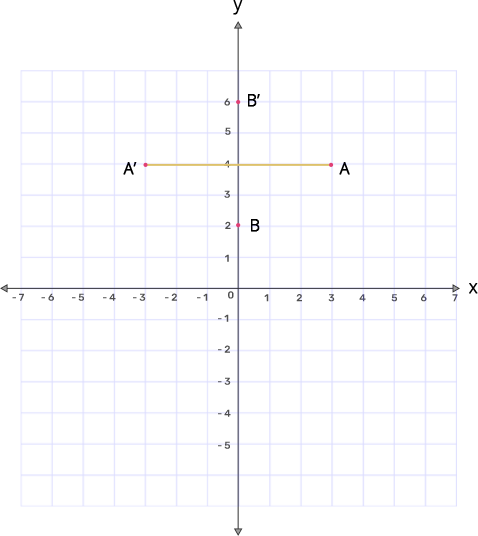
9. (i) Plot the points A(3,5) and B(-2,-4). Use 1cm=1unit on both the axes.

Ans: 

(ii) $\mathbf{A}'$ is the image of $\mathbf{A}$ when reflected in the x-axis. Write down the coordinates of $\mathbf{A}'$ and plot it on the graph paper.

Ans: A(3,5) when reflected in x-axis gives $\text{A }\!\!'\!\!\text{ }$(3,-5)

(iii) $\mathbf{B}'$ is the image of $\mathbf{B}$ when reflected in the y-axis, followed by the reflection in the origin. Write down the coordinates of $\mathbf{B}'$ and plot it on the graph paper.

Ans: When B(-2,-4) is reflected in y-axis, we get $\text{B }\!\!'\!\!\text{ }$(2,-4)

When $\text{B }\!\!'\!\!\text{ }$(2,-4) is reflected in origin, we get $\text{B }\!\!'\!\!\text{ }$(-2,4)

(iv) Write down the geometrical name of the figure $\mathbf{AA}'\mathbf{BB}'.$

Ans: After plotting all the points and connecting the lines, we get the graph as

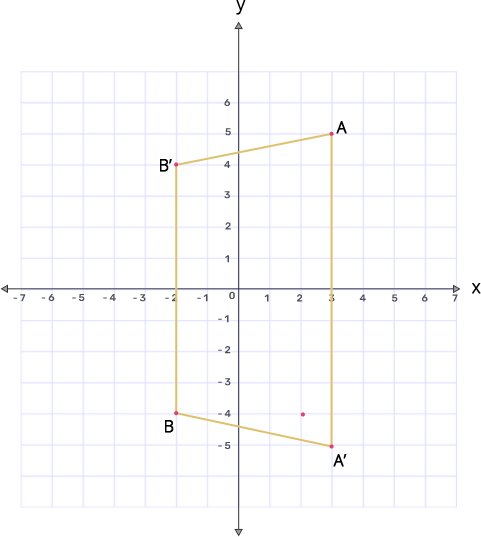
From the graph $\mathbf{AA}'\mathbf{BB}'$ is an isosceles trapezium.

(v) Name 2 invariant points under reflection in x-axis.

Ans: Any point which remains unchanged under the given reflection is known as an invariant point.

We know that for reflection in the x-axis, the sign of the y coordinate will change.

So 2 invariant points can be (5,0) and (-6,0).

10. The point $\mathbf{P}$(5,3) was reflected in the origin to get the image $\mathbf{P}'$

(a) Write down the coordinates of $\mathbf{P}'.$

Ans: Point P(5,3) when reflected in origin gives $\text{P }\!\!'\!\!\text{ }$(-5,-3)

(b) If M is the foot of perpendicular from P to the x-axis, find the coordinates of M.

Ans: Coordinates of M will be (5,0)

(c) If N is the foot of perpendicular from $\mathbf{P}'$ to the x-axis, find the coordinates of N.

Ans: Coordinates of N will be (-5,0)

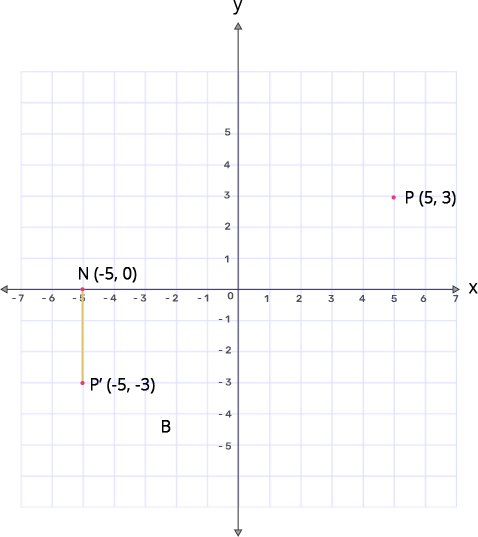
(d) Name the figure $\mathbf{PMP}'\mathbf{N}$

Ans: $\text{PMP }\!\!'\!\!\text{ N}$ is a Parallelogram.

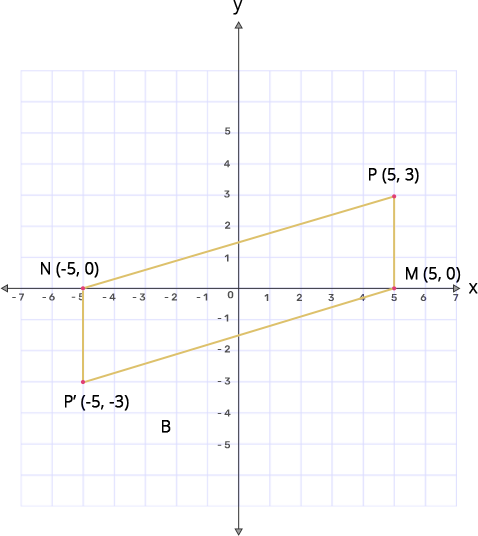
(e) Find the area of the figure $\mathbf{PMP}'\mathbf{N}$.

Ans: Area of $\text{PMP }\!\!'\!\!\text{ N}$=Area of $\text{PMN}$ + Area of $\text{P }\!\!'\!\!\text{ MN}$

$\Rightarrow \text{PMP }\!\!'\!\!\text{ N}=\dfrac{1}{2}\times 10\times 3+\dfrac{1}{2}\times 10\times 3$

$\Rightarrow \text{PMP }\!\!'\!\!\text{ N}=15+15$

$\Rightarrow \text{PMP }\!\!'\!\!\text{ N}=30$

Therefore the area of $\text{PMP }\!\!'\!\!\text{ N}$ is 30 sq.units.

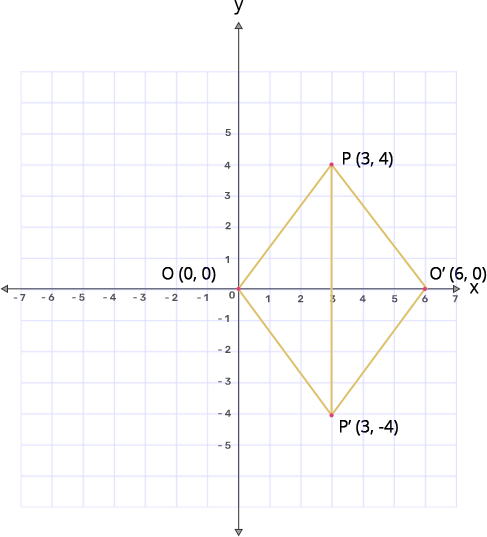
11. The point $\mathbf{P}$(3,4) is reflected to $\mathbf{P}'$ in the x-axis; and $\mathbf{O}'$ is the image of $\mathbf{O}$(the origin) when reflected in the line $\mathbf{PP}'.$ Write:

(i) the coordinates of $\mathbf{P}'$ and $\mathbf{O}'$

Ans: P(3,4) when reflected in x-axis gives $\text{P }\!\!'\!\!\text{ }$(3,-4)

O(0,0) when reflected in the line $\mathbf{PP}'$ gives $\mathbf{O}'$(6,0).

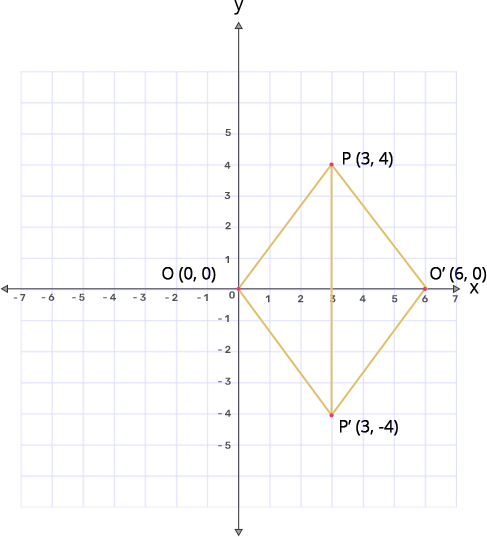
(ii) the length of the segments $\mathbf{PP}'$ and $\mathbf{OO}'$

Ans: Length of segment $\text{PP }\!\!'\!\!\text{ }$ is 8 and the length of segment $\text{OO }\!\!'\!\!\text{ }$ is 6.

(iii) the perimeter of the quadrilateral $\mathbf{POP}'\mathbf{O}',$

Ans: From the figure it is clear that all the sides are equal in length.

So $\text{OP}=\sqrt{{{(3)}^{2}}+{{(4)}^{2}}}=\sqrt{25}=5$

Perimeter of the quadrilateral $\mathbf{POP}'\mathbf{O}'=4\left( \mathbf{side} \mathbf{OP} \right)$

$\Rightarrow $Perimeter=4(5)

$\Rightarrow $Perimeter=20

Therefore the perimeter of the quadrilateral $\text{POP }\!\!'\!\!\text{ O }\!\!'\!\!\text{ }$ is 20units.

(iv) the geometrical name of $\mathbf{POP}'\mathbf{O}'$ is

Ans: $\text{POP }\!\!'\!\!\text{ O }\!\!'\!\!\text{ }$ is a Rhombus.

12. A(1,1), B(5,1), C(4,2) and D(2,2) are vertices of a quadrilateral. Name the quadrilateral ABCD. $\mathbf{A},\mathbf{B},\mathbf{C},\mathbf{D}$ are reflected in the origin on to $\mathbf{A}',\mathbf{B}',\mathbf{C}',\mathbf{D}'$ respectively. Locate  $\mathbf{A}',\mathbf{B}',\mathbf{C}',\mathbf{D}'$ on the graph sheet and write their coordinates. Are $\mathbf{D},\mathbf{A},\mathbf{A}',\mathbf{D}'$ collinear?

Ans: $\text{A}$(1,1) when reflected in origin gives $\text{A }\!\!'\!\!\text{ }$(-1,-1)

$\text{B}$(5,1) when reflected in origin gives $\text{B }\!\!'\!\!\text{ }$(-5,-1)

$\text{C}$(4,2) when reflected in origin gives $\text{C }\!\!'\!\!\text{ }$(-4,-2)

$\text{D}$(2,2) when reflected in origin gives $\text{D }\!\!'\!\!\text{ }$(-2,-2)

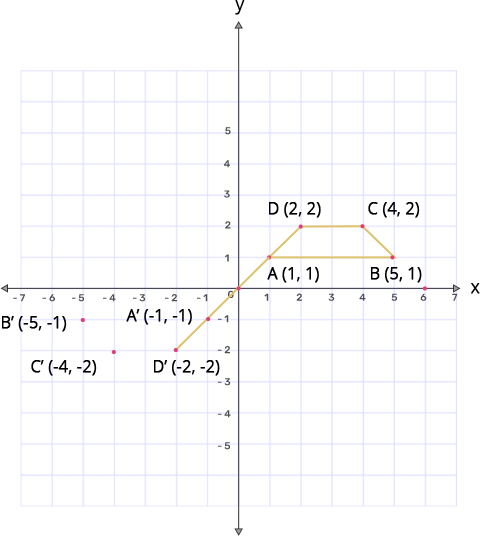
From the graph it is clear that $\mathbf{D},\mathbf{A},\mathbf{A}',\mathbf{D}'$ are collinear.

13. $\mathbf{P}$ and $\mathbf{Q}$ have coordinates (0,5) and (-2,4).

(a) P is invariant when reflected in an axis. Name the axis.

Ans: Point P is invariant when reflected in the y-axis.

When a point is reflected in the y-axis, the sign of the x coordinate changes.

Thus the required axis is y axis.

(b) Find the image of Q on reflection in the axis found in (a).

Ans: Q(-2,4) when reflected in y axis gives the image of Q which is (2,4).

(c) (0,k) on reflection in the origin is invariant. Write the value of k.

Ans: Any point which remains unchanged under the given reflection is known as an invariant point.

When a point is reflected in the origin signs of both the coordinates will change.

For the point to be invariant when reflected in the origin, the value of k must be equal to zero.

(d) Write the coordinates of the image of Q, obtained by reflecting it in the origin followed by the reflection in the x-axis.

Ans: When Q(-2,4) is reflected in origin, we get (2,-4)

When (2,-4) is reflected in the x-axis, we get (2,4).

14. (a) The point P(2,-4) is reflected about the line x=0 to get the image Q. Find the coordinates of Q.

Ans: When P(2,-4) is reflected in the line x=0, we get Q as (-2,-4).

(b) The point Q is reflected about the line y=0 to get the image R. Find the coordinates of R.

Ans: When Q(-2,-4) is reflected in the line y=0, we get R as (-2,4)

(c) Name the figure PQR.

Ans: After plotting the points P(2,-4); Q(-2,-4) and R(-2,4), we get the graph as

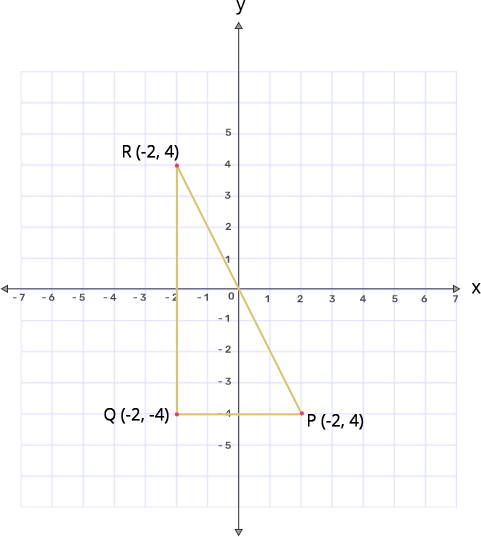
From the graph it is clear that the figure formed is a Right angled triangle.

(d) Find the area of figure PQR.

Ans: Area of $\text{ }\!\!\Delta\!\!\text{ PQR}=\dfrac{1}{2}\times \text{PQ}\times \text{QR}$

Area=$\dfrac{1}{2}\times 4\times 8$

Area=16

Therefore, the area of triangle PQR is 16sq.units.

15. Using a graph paper, plot the points $\mathbf{A}$(6,4) and $\mathbf{B}$(0,4).

(a) Reflect $\mathbf{A}$ and $\mathbf{B}$ in the origin to get the images $\mathbf{A}'$ and $\mathbf{B}'.$

Ans: $\mathbf{A}$(6,4) when reflected in origin gives $\mathbf{A}'$(-6,-4)

$\mathbf{B}$(0,4) when reflected in origin gives $\mathbf{B}'$(0,-4)

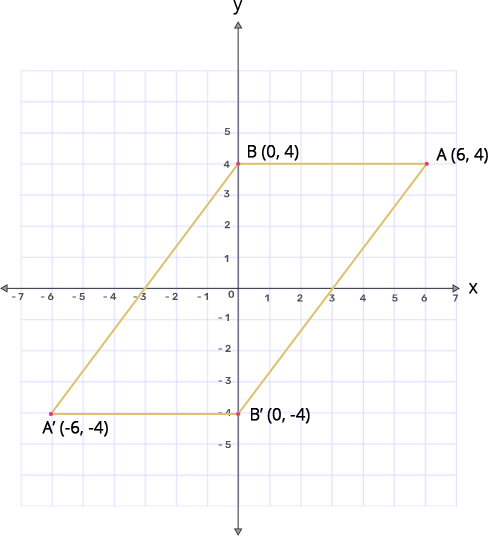
(b) Write the coordinates of $\mathbf{A}'$ and $\mathbf{B}'$.

Ans: Coordinates of $\text{A }\!\!'\!\!\text{ }$ and $\text{B }\!\!'\!\!\text{ }$ are (-6,-4) and (0,-4) respectively.

(c) State the geometrical name for the figure $\mathbf{ABA}'\mathbf{B}'.$

Ans: $\text{ABA }\!\!'\!\!\text{ B }\!\!'\!\!\text{ }$ is a parallelogram.

(d) Find its perimeter.

Ans: In $\text{ }\!\!\Delta\!\!\text{ BAB }\!\!'\!\!\text{ },$

$\text{BB }\!\!'\!\!\text{ }=8\text{ }\!\! \!\!\text{ }$units

$\text{A }\!\!'\!\!\text{ B }\!\!'\!\!\text{ }=$6 units

$\text{BA }\!\!'\!\!\text{ }=\sqrt{{{6}^{2}}+{{8}^{2}}}=\sqrt{100}=10$

From the figure,

$\text{BA }\!\!'\!\!\text{ }=\text{B }\!\!'\!\!\text{ A}=10$ and $\text{A }\!\!'\!\!\text{ B }\!\!'\!\!\text{ }=\text{AB}=6$

Perimeter = $\text{BA }\!\!'\!\!\text{ }+\text{B }\!\!'\!\!\text{ A}+\text{AB}+\text{A }\!\!'\!\!\text{ B }\!\!'\!\!\text{ }$

$\Rightarrow $Perimeter = $10+10+6+6$

$\Rightarrow $Perimeter = 32

Therefore the perimeter of the parallelogram is 32 units.

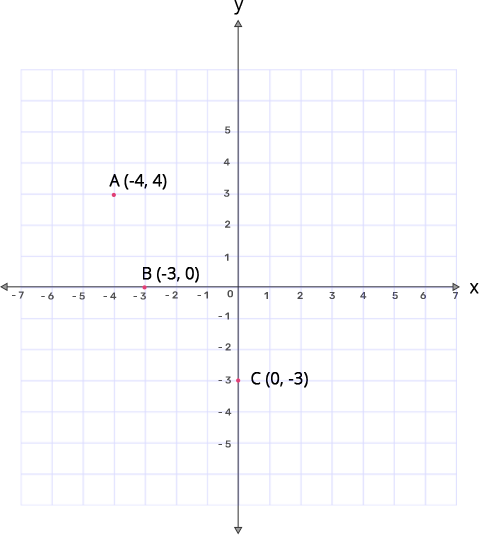
16. Using graph paper for this question, plot the points O(0,0), A(-4,4), B(-3,0) and C(0,-3).

Ans: 

(i) Reflect points A and B on the y-axis and name them $\mathbf{A}'$ and $\mathbf{B}'$ respectively. Write down their coordinates.

Ans: A(-4,4) when reflected in y-axis gives $\text{A }\!\!'\!\!\text{ }$(4,4)

B(-3,0) when reflected in y-axis gives $\text{B }\!\!'\!\!\text{ }$(3,0)

(ii) Name the figure $\mathbf{OABCB}'\mathbf{A}'.$

Ans: After plotting all the points on the graph

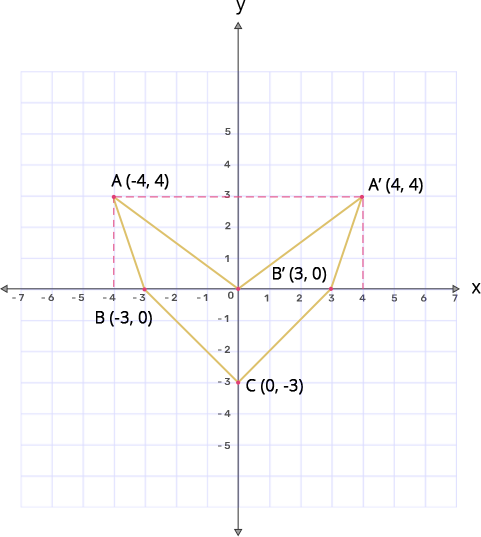
Therefore the diagram formed is an Arrowhead.

(iii) State the line of symmetry of this figure.

Ans: Line of symmetry is the line which divides the given figure into 2 equal parts.

Therefore the line of symmetry for the above figure is the y-axis.

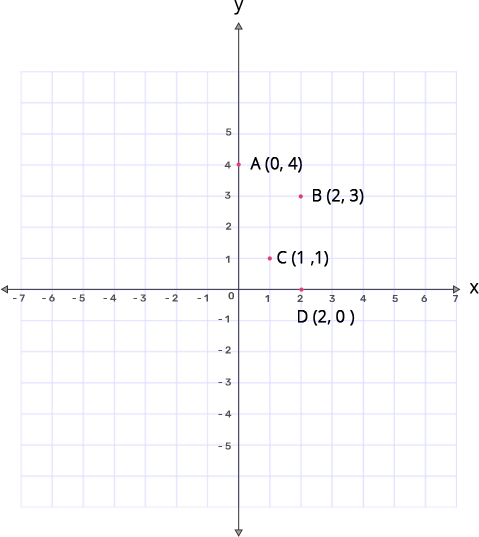
17. Use a graph paper for this question.

(i) Plot the following points $\mathbf{A}\left( 0,4 \right),\mathbf{B}\left( 2,3 \right),\mathbf{C}\left( 1,1 \right),\mathbf{D}\left( 2,0 \right)$

Ans: 

(ii) Reflect points B,C,D on the y-axis and write down their coordinates. Name the images as $\mathbf{B}',\mathbf{C}',\mathbf{D}'$ respectively.

Ans: B(2,3) when reflected in y-axis gives $\text{B }\!\!'\!\!\text{ }$(-2,3)

C(1,1) when reflected in y-axis gives $\text{C }\!\!'\!\!\text{ }$(-1,1)

D(2,0) when reflected in y-axis gives $\text{D }\!\!'\!\!\text{ }$(-2,0)

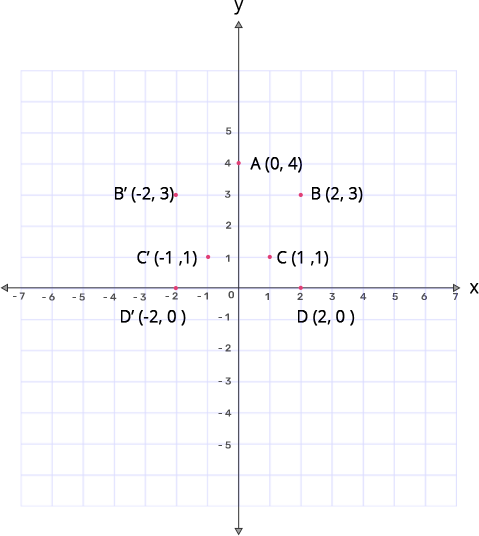
(iii) Join the points $\mathbf{A},\mathbf{B},\mathbf{C},\mathbf{D},\mathbf{D}',\mathbf{C}',\mathbf{B}',\mathbf{A}$ in order, so as to form a closed figure. Write down the equation of the line about which if this closed figure obtained is folded, the two parts of the figure exactly coincide.

Ans: Joining the points, we get the graph as

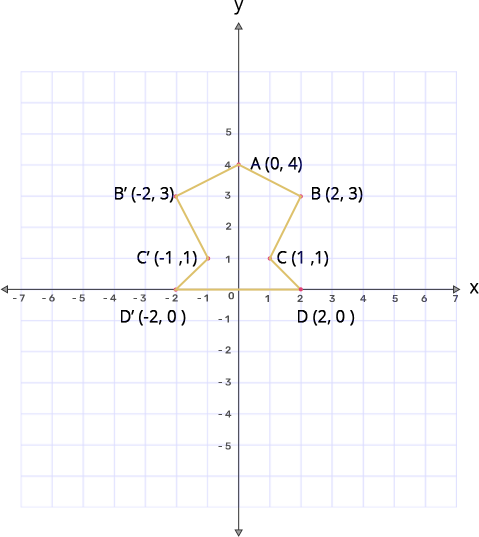
The given figure is symmetrical about the line x=0(i.e y-axis).

Importance of the Chapter - Reflection in the Mathematics Subject

The two mutually perpendicular number lines intersecting each other at their zeroes are called coordinate axes. The horizontal line is called the x-axis and the vertical line is called the y  axis, the point where axes intersect each other is called the origin.

1. Reflection 

As it suggests by name, reflection is the image of any point by coordinate Axis. In other words, reflection is the image of a point. Its properties are :

• Distance from the line of point and its image is always the same.

• Reflection can be observed by any of the axes also. It may be the x-axis and y-axis.

2. Coordinates of a Point

The position of a point in a place is expressed by a pair of two numbers called coordinates. The first number of the pair is called x coordinate or abscissa and the second number is called y coordinate or ordinate.

To know the abscissa and ordinate of any point on the plane, we need to find simply the distance of it from the origin. 

3. Coordinate Axis 

The plane which consists of the X-axis and Y-axis is called the XY plane. X-axis and y-axis are two mutually perpendicular lines that denote the position of any point on the plane.  The origin is the intersection point of the X and the axis is denoted by O.

The direction of the OX ray on the horizontal lines shows the direction of positive numbers. The ray OX' points towards the direction of negative numbers. Similarly, OY points the direction of positive numbers on the Y-axis whereas soy points towards the direction of negative numbers.

4. Reflection

When an object is placed in front of a plane mirror, its image is formed at the same distance behind the mirror. This is called reflection.

• Reflection of a Point on the x-axis: The reflection of a point, Mx (y, x) in the x-axis is (x, -y).

• Reflection of a Point in the y-axis: The reflection of a point, My (y, x) in the y-axis is (-x, y).

• Reflection of a Point in Origin: The reflection of a point, M0 (y, x) in the origin is (-x, -y).

• The reflections of a point P (3, 3) in the x-axis, y.

5. Invariant Point

A point is known as the invariant point concerning a given line if and only if it lies on the line. The image of a figure under reflection is congruent to the original figure. Reflection in the x-axis, followed by a reflection in the y  axis is equivalent to reflection in the origin.

Exercises in Selina Concise Mathematics Class 10 Solutions Chapter 12 - Reflection:

One can refer to the following exercises given in the ICSE Class 10 Chapter 12 - Reflection: 

Exercise 12 (A) Solutions

Exercise 12 (B) Solutions

Tips to Prepare for Exams using Selina Concise Class 10 Chapter 12 Maths Solution

By referring to the Selina notes of this chapter students will be familiar with formulas, concepts and definition of this chapter, revising all these things are very advantageous for the last-minute preparation.

Students can solve various types of problems related to the reflection, which will make you more confident to solve any kind of problem asked in the examination. So, if you are trying to score more marks in the examination, you must solve the questions independently at least three or four times.

Example:

Reflection of a Point P

Let there is a point P then we can find the Reflection of a point 

1. On the line y = 0, ( On x-axis )

• If the point has coordinates ( a, b ) then the points of reflection will be ( a, - b)

• Only the sign of coordinates changes.

2. On the line x = 0 ( On the y-axis)

• If the point has coordinates ( a, b ) then the points of reflection will be ( a, - b)

• Only the signs of abscissa change.

1. Going through stepwise solutions of Selina Class 10 Maths will help the students to understand the steps in detail, as in Mathematics along with the answers step used to solve is also important and carries marks. Students have to understand their strengths and weaknesses and work to improve both.

2. If you notice any questions that seem to be critical when practicing, make a note of them and you can solve those questions again while revising this chapter. This would help you to understand the concept in a better way.

3. Using graphs and figures with focus and neatness will also help you achieve complete marks in the 10 board examinations.

Advantages of Using the Selina Notes

There are several advantages to the students referring to the Selina Maths notes, some of them are discussed below:

• Easy & reliable solutions.

• Available free of cost.

• Highlight important examination questions.

• Step-by-step solutions for all questions.

• Prepared by subject-matter experts.

• Designed according to the latest ICSE syllabus pattern.

• Available online 24/7.

Selina ICSE Chapter 12 Reflection solutions contains answers of all the questions and it is solved by the subject experts of Vedantu who follow the recent ICSE guidelines and syllabus. Referring to the Selina ICSE Solutions of Class 10 students can easily score good marks in 10 Class board examinations.

Conclusion

Selina Concise Maths Solutions for Class 10 is perfect for preparing for the board examinations because ICSE Class 10 syllabus is extensive and needs a lot of concentration and efforts on the part of the students so that they can face the examinations and ace their tests easily. The Selina Concise Maths Class 10 ICSE solutions PDF includes a detailed explanation for all the chapters topic-wise for all the subjects. Each explanation is given with all the assumptions and logic used to determine the conclusion that would help the student to examine and understand important concepts.