Concise Mathematics Class 10 ICSE Solutions for Chapter 4 - Linear Inequations (In one variable)

Exercise- 4(A)

1. State, true or false:

(i) \[\mathbf{x}<-\mathbf{y}~\Rightarrow ~-\mathbf{x}>\mathbf{y}\]

Ans: This statement is true, because when each term of an inequation be multiplied by the same negative number, the sign of inequality reveres.

Therefore, when  $\text{x}<-\text{y}$ is multiplied by $\left( -1 \right)$, we get $-\text{x}>\text{y}$.

(ii) $-5\mathbf{x}\ge 15\Rightarrow ~\mathbf{x}\ge 3$

Ans: Here, we have  $-5\text{x}\ge 15$

Now, divide by 5 in given inequality

$\frac{-5\text{x}}{5}\text{ }\!\!~\!\!\text{ }\ge \text{ }\!\!~\!\!\text{ }\frac{15}{5}$

$-\text{x }\!\!~\!\!\text{ }\ge \text{ }\!\!~\!\!\text{ }3$

Multiply by $\left( -1 \right)$, we get

$\text{x }\!\!~\!\!\text{ }\le \text{ }\!\!~\!\!\text{ }-3$  

Because when each term of an inequation be multiplied by the same negative number, the sign of inequality reveres.

Therefore, $-5\text{x}\ge 15\Rightarrow \text{ }\!\!~\!\!\text{ x}\le 3$

Hence, given statement is false.

(iii) $2\mathbf{x}\le -7\Rightarrow ~\frac{2\mathbf{x}}{-4}\ge \frac{-7}{-4}$

Ans: Here, we have  $2\text{x}\le -7$

Now, divide by $\left( -4 \right)$ in given inequality, we get

⇒ $\frac{2\text{x}}{-4}\text{ }\!\!~\!\!\text{ }\ge \text{ }\!\!~\!\!\text{ }\frac{-7}{-4}$ 

Because when each term of an inequation be divided by the same negative number, the sign of inequality reveres.

Therefore, $2\text{x}\le -7\Rightarrow \text{ }\!\!~\!\!\text{ }\frac{2\text{x}}{-4}\ge \frac{-7}{-4}\text{ }\!\!~\!\!\text{ }$

Hence, given statement is true.

(iv) $7>5\Rightarrow ~\frac{1}{7}<\frac{1}{5}$

Ans: Here, we have  $7>5$

Now, taking reciprocals in given inequality, we get

⇒ $\frac{1}{7}<\frac{1}{5}$

Because, when we take the reciprocals of each term in inequality, then the sign of inequality reverses. 

Therefore, $\text{ }\!\!~\!\!\text{ }7>5\Rightarrow \text{ }\!\!~\!\!\text{ }\frac{1}{7}<\frac{1}{5}$

Hence, given statement is true.

2. State, whether the following statements are true or false.

(i) If $\mathbf{a}<\mathbf{b},~$then $\mathbf{a}-\mathbf{c}<\mathbf{b}-\mathbf{c}$ 

Ans: Here, we have  $\text{a}<\text{b}$

Now, subtract ‘c’ from both side of given inequality, we get

⇒ $\text{a}-\text{c}<\text{b}-\text{c}$

Because when we subtract the same number from each term of inequality, the sign of inequality is the same.

Therefore, $\text{a}<\text{b }\!\!~\!\!\text{ }\Rightarrow \text{a}-\text{c}<\text{b}-\text{c}$

Hence, the given statement is true.

(ii) If $\mathbf{a}>\mathbf{b},$ then $\mathbf{a}+\mathbf{c}>\mathbf{b}+\mathbf{c}$ 

Ans: Here, we have  $\text{a}>\text{b}$

Now, add ‘c’ to both side of given inequality, we get

⇒ $\text{a}+\text{c}>\text{b}+\text{c}$

Because when we add the same number in each term of the inequality, the sign of inequality is the same.

Therefore, $\text{a}+\text{c}>\text{b}+\text{c}$

Hence, the given statement is true.

(iii) If $\mathbf{a}<\mathbf{b},$ then $\mathbf{ac}>\mathbf{bc}$

Ans: Here, we have  $\text{a}<\text{b}$

Now, multiply by ‘c’ in given inequality, we get

⇒ $\text{ac}<\text{bc}$  [if c is a positive number]

Or $\text{ac}>\text{bc}$  [if c is a negative number]

Because when we multiply by the same positive number in each term of the inequality, the sign of inequality is the same.

But when we multiply by the same negative number in each term of the inequality, the sign of inequality reverses.

Here, the sign of c is not mentioned. Therefore, the given statement is false.

(iv) If $\mathbf{a}>\mathbf{b},~$then $\frac{\mathbf{a}}{\mathbf{c}}<\frac{\mathbf{b}}{\mathbf{c}}$

Ans: Here, we have  $\text{a}>\text{b}$

Now, multiply by ‘c’ in given inequality, we get

⇒ $\frac{\text{a}}{\text{c}}>\frac{\text{b}}{\text{c}}$  (if c is a positive number)

Or $\frac{\text{a}}{\text{c}}<\frac{\text{b}}{\text{c}}$  (if c is a negative number)

Because when we divide by the same positive number in each term of the inequality, the sign of inequality is the same.

But when we divide by the same negative number in each term of the inequality, the sign of inequality reverses.

Here, the sign of c is not mentioned. Therefore, the given statement is false.

(v) If $\mathbf{a}-\mathbf{c}>\mathbf{b}-\mathbf{d};$ then $\mathbf{a}+\mathbf{d}>\mathbf{b}+\mathbf{c}$

Ans: Here, we have  $\text{a}-\text{c}>\text{b}-\text{d}$

Now, transfer ‘c’ and ‘d’ to its other sides in given inequality, we get

⇒ $\text{a}+\text{d}>\text{b}+\text{c}$

Because when we transfer numbers to other sides of inequality, the sign of inequality is the same.

Therefore, the given statement is true.

(vi) If $\mathbf{a}<\mathbf{b},$ and $\mathbf{c}>0,$ then $\mathbf{a}-\mathbf{c}>\mathbf{b}-\mathbf{c}$ , where a, b, c and d are real numbers and $\mathbf{c}\ne 0$.

Ans: Here, we have  $\text{a}<\text{b}$

Now, subtract ‘c’ from both side of given inequality, we get

⇒ $\text{a}-\text{c}<\text{b}-\text{c}$

Because when we subtract the same number from each term of inequality, the sign of inequality is the same.

Therefore, $\text{a}<\text{b }\!\!~\!\!\text{ }\Rightarrow \text{a}-\text{c}<\text{b}-\text{c}$

Hence, the given statement is false.

3. If $\mathbf{x}\in \mathbf{N},$ Find the solution set of inequations.

(i) $5\mathbf{x}+3\le 2\mathbf{x}+18$

Ans: Here, we have  $5\text{x}+3\le 2\text{x}+18$

⇒ $5\text{x}+3\le 2\text{x}+18$

⇒ $5\text{x}-2\text{x}\le 18-3$

⇒ $3\text{x}\le 15$

⇒ $\text{x}\le 5$

Since $\text{x}\in \text{N}$ (Natural number), thus possible values of $\text{x}$ are 1, 2, 3, 4 and 5.

Therefore, the required solution set is {1, 2, 3, 4, 5}.

(ii) $3\mathbf{x}-2<19-4\mathbf{x}$

Ans: Here, we have  $3\text{x}-2<19-4\text{x}$

⇒ $3\text{x}-2<19-4\text{x}$

⇒ $3\text{x}+4\text{x}<19+2$

⇒ $7\text{x}<21$

⇒ $\text{x}<3$

Since $\text{x}\in \text{N}$ (Natural number), thus possible values of $\text{x}$ are 1 and 2.

Therefore, the required solution set is {1, 2}.

4. If the replacement set is the set of whole numbers, solve:

(i) $\mathbf{x}+7\le 11$ 

Ans: Here, we have  $\text{x}+7\le 11$

⇒ $\text{x}+7\le 11$

⇒ $\text{x}\le 4$

Since the replacement set is the set of whole numbers. Thus, possible values of $\text{x}$ are 0, 1, 2, 3 and 4. Therefore, the required solution set is {0, 1, 2, 3, 4}.

(ii) $3\mathbf{x}-1>8$

Ans: Here, we have  $3\text{x}-1>8$

⇒ $3\text{x}-1>8$

⇒ $3\text{x}>9$

⇒ $\text{x}>3$

Since the replacement set is the set of whole numbers. Therefore, the required solution set is {4, 5, 6, 7, ……….}.

(iii) $8-\mathbf{x}>5$

Ans: Here, we have  $8-\text{x}>5$

⇒ $8-5>\text{x}$

⇒ $3>\text{x}$

⇒ $\text{x}<3$

Since the replacement set is the set of whole numbers. Therefore, the required solution set is {0, 1, 2}.

(iv) $7-3\mathbf{x}\ge -\frac{1}{2}$

Ans: Here, we have  $7-3\text{x}\ge -\frac{1}{2}$

⇒ $7-3\text{x}\ge -\frac{1}{2}$

⇒ $-3\text{x}\ge -\frac{1}{2}-7$

⇒ $-3\text{x}\ge -\frac{15}{2}$

⇒ $\text{x}\le \frac{15}{6}$

⇒ $\text{x}\le 2.5$

Since the replacement set is the set of whole numbers. Therefore, the required solution set is {0, 1, 2}.

(v) $\mathbf{x}-\frac{\text{3}}{\text{2}}\text{}\frac{\text{3}}{\text{2}}-\mathbf{x}$

Ans: Here, we have  $\text{x}-\frac{3}{2}<\frac{3}{2}-\text{x}$

⇒ $\text{x}-\frac{3}{2}<\frac{3}{2}-\text{x}$

⇒ $\text{x}+\text{x}<\frac{3}{2}+\frac{3}{2}$

⇒ $2\text{x}<\frac{6}{2}$

⇒ $2\text{x}<3$

⇒ $\text{x}<\frac{3}{2}$

⇒ $\text{x}<1.5$

Since the replacement set is the set of whole numbers. Therefore, the required solution set is {0, 1}.

(vi) \[\text{18}\le \text{3x-2}\]

Ans: Here, we have  $18\le 3\text{x}-2$

⇒ $18\le 3\text{x}-2$

⇒ $18+2\le 3\text{x}$

⇒ $20\le 3\text{x}$

⇒ $3\text{x}\ge 20$

⇒ $\text{x}\ge \frac{20}{3}$

⇒ $\text{x}\ge 6.67$

Since the replacement set is the set of whole numbers. Therefore, the required solution set is {7, 8, 9,…}.

5. Solve the inequation:  $\text{3-2x}\ge \text{x-12}$ given that $\mathbf{x}\in \mathbf{N}$. 

Ans: Here, we have  $3-2\text{x}\ge \text{x}-12$

⇒ $3-2\text{x}\ge \text{x}-12$

⇒ $-2\text{x}-\text{x}\ge -12-3$

⇒ $-3\text{x}\ge -15$

⇒ $3\text{x}\le 15$

⇒ $\text{x}\le 5$

Since $\text{x}\in \text{N}$ (Natural number), thus possible values of $\text{x}$ are 1, 2, 3, 4 and 5.

Therefore, the required solution set is {1, 2, 3, 4, 5}.

6. If \[\text{25-4x}\le \text{16,}\] find: 

(i) The smallest value of $\mathbf{x},$ when $\mathbf{x}$ is a real number.

Ans: Here, we have  $25-4\text{x}\le 16$

⇒ $25-4\text{x}\le 16$

⇒ $-4\text{x}\le 16-25$

⇒ $-4\text{x}\le -9$

⇒ $4\text{x}\ge 9$

⇒ $\text{x}\ge \frac{9}{4}$

⇒ $\text{x}\ge 2.25$

Thus, the smallest value of $\text{x},$ when $\text{x}$ is real number is 2.25.

(ii) The smallest value of $\mathbf{x}$, when $\mathbf{x}$ is an integer

Ans: Here, we have  $25-4\text{x}\le 16$

⇒ $25-4\text{x}\le 16$

⇒ $-4\text{x}\le 16-25$

⇒ $-4\text{x}\le -9$

⇒ $4\text{x}\ge 9$

⇒ $\text{x}\ge \frac{9}{4}$

⇒ $\text{x}\ge 2.25$

Thus, the smallest value of $\text{x},$ when $\text{x}$ is an integer is 3.

7. If the replacement set is the set of real numbers, solve:

(i) $\text{-4x}\ge \text{-16}$ 

Ans: Here, we have  $-4\text{x}\ge -16$

⇒ $-4\text{x}\ge -16$

⇒ $4\text{x}\le 16$

⇒ $\text{x}\le \frac{16}{4}$

⇒ $\text{x}\le 4$

Since the replacement set is the set of real numbers. Therefore, required solution set is {$\text{x}:\text{x}\in \text{R}$ and $\text{x}\le 4$}.

(ii) $\text{8-3x}\le \text{20}$

Ans: Here, we have  $8-3\text{x}\le 20$

⇒ $-3\text{x}\le 20-8$

⇒ $-3\text{x}\le 12$

⇒ $3\text{x}\ge -12$

⇒ $\text{x}\ge -\frac{12}{3}$

⇒ $\text{x}\ge -4$

Since the replacement set is the set of real numbers. Therefore, required solution set is {$\text{x}:\text{x}\in \text{R}$ and $\text{x}\ge -4$}.

(iii) $\text{5+}\frac{\text{x}}{\text{4}}\text{}\frac{\text{x}}{\text{5}}\text{+9}$

Ans: Here, we have  $5+\frac{\text{x}}{4}>\frac{\text{x}}{5}+9$

⇒ $5+\frac{\text{x}}{4}>\frac{\text{x}}{5}+9$

⇒ $\frac{\text{x}}{4}-\frac{\text{x}}{5}>9-5$

⇒ $\frac{5\text{x}-4\text{x}}{20}>4$

⇒ $\frac{\text{x}}{20}>4$

⇒ $\text{x}>80$

Since the replacement set is the set of real numbers. Therefore, required solution set is {$\text{x}:\text{x}\in \text{R}$ and $\text{x}>80$}.

(iv) $\frac{\mathbf{x}+3}{8}<\frac{\mathbf{x}-3}{5}$

Ans: Here, we have  $\frac{\text{x}+3}{8}<\frac{\text{x}-3}{5}$

⇒ $\frac{\text{x}+3}{8}<\frac{\text{x}-3}{5}$

⇒ $5\left( \text{x}+3 \right)<8\left( \text{x}-3 \right)$

⇒ $5\text{x}+15<8\text{x}-24$

⇒ $5\text{x}-8\text{x}<-24-15$

⇒ $-3\text{x}<-39$

⇒ $3\text{x}>39$

⇒ $\text{x}>\frac{39}{3}$

⇒ $\text{x}>13$

Since the replacement set is the set of real numbers. Therefore, required solution set is {$\text{x}:\text{x}\in \text{R}$ and $\text{x}>13$}.

8. Find the smallest value of x for which $\text{5-2x5}\frac{\text{1}}{\text{2}}\text{-}\frac{\text{5}}{\text{3}}\text{x}$,  where $\mathbf{x}$ is an integer.

Ans: Here, we have  $5-2\text{x}>5\frac{1}{2}-\frac{5}{3}\text{x}$

⇒ $5-2\text{x}>\frac{11}{2}-\frac{5\text{x}}{3}$

⇒ $-2\text{x}+\frac{5\text{x}}{3}>\frac{11}{2}-5$

⇒ $\frac{-6\text{x}+5\text{x}}{3}>\frac{11-10}{2}$

⇒ $\frac{-\text{x}}{3}>\frac{1}{2}$

⇒ $\frac{\text{x}}{3}<-\frac{1}{2}$

⇒ $\text{x}<-\frac{3}{2}$

⇒ $\text{x}<-1.5$

Since $\text{x}$ is an integer. Therefore, the smallest value of $\text{x}$ is $\text{ }\!\!~\!\!\text{ }-1.$

9. Find the largest value of x for which $\text{2}\left( \text{x-1} \right)\le \text{9-x}$ and $\mathbf{x}\in \mathbf{W}$.

Ans: Here, we have  $2\left( \text{x}-1 \right)\le 9-\text{x}$

⇒ $2\left( \text{x}-1 \right)\le 9-\text{x}$

⇒ $2\text{x}-2\le 9-\text{x}$

⇒ $2\text{x}+\text{x}\le 9+2$

⇒ $3\text{x}\le 11$

⇒ $\text{x}\le \frac{11}{3}$

⇒ $\text{x}\le 3.67$ 

Since $\text{x}\in \text{W}$ . Therefore, the largest value of $\text{x}$ is 3.

10.  Solve the inequations: $\text{12+1}\frac{\text{5}}{\text{6}}\text{x}\le \text{5+3x}$ and $\mathbf{x}\in \mathbf{R}~.$

Ans: Here, we have  $12+1\frac{5}{6}\text{x}\le 5+3\text{x}$

⇒ $12+1\frac{5}{6}\text{x}\le 5+3\text{x}$

⇒ $12+\frac{11\text{x}}{6}\le 5+3\text{x}$

⇒ $\frac{11\text{x}}{6}-3\text{x}\le 5-12$

⇒ $\frac{11\text{x}-18\text{x}}{6}\le -7$

⇒ $\frac{-7\text{x}}{6}\le -7$

⇒ $-7\text{x}\le -42\text{ }\!\!~\!\!\text{ }$

⇒ $7\text{x}\ge 42$

⇒ $\text{x}\ge \frac{42}{7}$

⇒ $\text{x}\ge 6$

Since $\text{x}\in \text{R}$.

Therefore, the solution set is {$\text{x}:\text{x}\in \text{R}$ and $\text{x}\ge 6$}

11.  Given $\mathbf{x}\in $ {integers}, find the solution set of: \[\text{-5}\le \text{2x-3x+2}\]

Ans: Here, we have  $-5\le 2\mathbf{x}-3<\mathbf{x}+2$

We can write it into two different inequalities i.e.,

⇒$-5\le 2\text{x}-3$ and $2\text{x}-3<\text{x}+2$

⇒ $-5+3\le 2\text{x}$ and $2\text{x}-\text{x}<2+3$

⇒ $-2\le 2\text{x}$ and $\text{x}<5\text{ }\!\!~\!\!\text{ }$

⇒ $\text{x}\ge -1$ and $\text{x}<5$

Since $\text{x}\in $ {integers}. Therefore, required solution set is {$-1,\text{ }\!\!~\!\!\text{ }0,\text{ }\!\!~\!\!\text{ }1,\text{ }\!\!~\!\!\text{ }2,\text{ }\!\!~\!\!\text{ }3,\text{ }\!\!~\!\!\text{ }4$}.

12.  Given $\mathbf{x}\in $ {whole numbers}, find the solution set of: $\text{-1}\le \text{3+4x23}$

Ans: Here, we have  $-1\le 3+4\text{x}<23$

We can write it into two different inequalities i.e.,

⇒$-1\le 3+4\text{x}$ and $3+4\text{x}<23$

⇒$-1-3\le 4\text{x}$ and $4\text{x}<23-3$

⇒$-4\le 4\text{x}$ and $4\text{x}<20$

⇒$-1\le \text{x}$ and $\text{x}<5$

⇒$\text{x}\ge -1$ and $\text{x}<5$

Since $\text{x}\in $ {whole numbers}. 

Therefore, required solution set is {$\text{ }\!\!~\!\!\text{ }0,\text{ }\!\!~\!\!\text{ }1,\text{ }\!\!~\!\!\text{ }2,\text{ }\!\!~\!\!\text{ }3,\text{ }\!\!~\!\!\text{ }4$}.

Exercise- 4(B)

1. Represent the following inequalities on real number line:

(i) $\text{2x-15}$

Ans: Here, we have  $2\text{x}-1<5$

⇒ $2\text{x}<5+1$

⇒ $2\text{x}<6$

⇒ $\text{x}<\frac{6}{2}$

⇒ $\text{x}<3$

Thus, the solution on the number line is as shown below:

(ii) $\text{3x+1}\ge \text{-5}$

Ans: Here, we have  $3\text{x}+1\ge -5$

⇒ $3\text{x}\ge -5-1$

⇒ $3\text{x}\ge -6$

⇒ $\text{x}\ge -\frac{6}{3}$

⇒ $\text{x}\ge -2$

Thus, the solution on the number line is as shown below:

(iii) $\text{2}\left( \text{2x-3} \right)\le \text{6}$

Ans: Here, we have  $2\left( 2\text{x}-3 \right)\le 6$

⇒ $\left( 2\text{x}-3 \right)\le \frac{6}{2}$

⇒ $2\text{x}-3\le 3$

⇒ $2\text{x}\le 6$

⇒ $\text{x}\le \frac{6}{3}$

⇒ $\text{x}\le 3$

Thus, the solution on the number line is as shown below:

(vi) $\text{-4x4}$

Ans: Here, we have  $-4<\text{x}<4$

Thus, the solution on the number line is as shown below:

(v) $\text{-2}\le \text{x5}$

Ans: Here, we have  $-2\le \text{x}<5$

Thus, the solution on the number line is as shown below:

(vi) \[\text{8}\ge \text{x-3}\]

Ans: Here, we have  $8\ge \text{x}>-3$

Thus, the solution on the number line is as shown below:

(vii) $\text{-5x}\le \text{-1}$

Ans: Here, we have  $-5<\text{x}\le -1$

Thus, the solution on the number line is as shown below:

2. For each graph given alongside, write an inequation taking x as the variable: 

(i) 

Ans: Here, from the given graph, it is observed that value of $\text{x}$ is less than or equal to $\left( -1 \right)$.

Thus, it can be written as $\{\text{x}:\text{x}\le -1$ and $\text{x}\in \text{R}$}

(ii)    

Ans: Here, from the given graph, it is observed that value of $\text{x}$ is greater than or equal to $2$.

Thus, it can be written as $\left\{ \text{x}:\text{x}\ge 2\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{ x}\in \text{R} \right\}$

(iii)  

Ans: Here, from the given graph, it is observed that value of $\text{x}$ is greater than or equal to $-\text{ }\!\!~\!\!\text{ }4$ but less than $3$.

Thus, it can be written as $\{\text{x}:-4\le \text{x}<3\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{ x}\in \text{R}\}$

(iv)  

Ans: Here, from the given graph, it is observed that value of $\text{x}$ is greater than $-1$ but less than or equal to $5$.

Thus, it can be written as $\{\text{x}:-1<\text{x}\le 5\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{ x}\in \text{R}\}$

3. For the following inequations, graph the solution set on the real number line:

(i)  $\text{-4}\le \text{3x-18}$

Ans: Here, we have  $-4\le 3\text{x}-1<8$

We can write it into two different inequalities i.e.,

⇒$-4\le 3\text{x}-1$ and $3\text{x}-1<8$

⇒$-4+1\le 3\text{x}$ and $3\text{x}<8+1$

⇒$-3\le 3\text{x}$ and $3\text{x}<9$

⇒$-1\le \text{x}$ and $\text{x}<3$

⇒$\text{x}\ge -1$ and $\text{x}<3$

Thus, $\text{x}$ is greater than or equal to $-1$ but less than 3.

Therefore, graphical representation on number line is:

(ii) $\text{x-13-x}\le \text{5}$

Ans: Here, we have  $\text{x}-1<3-\text{x}\le 5$

We can write it into two different inequalities i.e.,

⇒$\text{ }\!\!~\!\!\text{ x}-1<3-\text{x}$ and $3-\text{x}\le 5$

⇒$\text{ }\!\!~\!\!\text{ x}+\text{x}<3+1$ and $-\text{x}\le 5-3$

⇒ $2\text{x}<4$ and $-\text{x}\le 2$

⇒ $\text{x}<2$ and $\text{x}\ge -2$

Thus, $\text{x}$ is greater than or equal to $-2$ but less than 2.

Therefore, graphical representation on number line is:

4. Represent the solution of each of the following inequations inequalities on the number line:

(i) $\text{4x-1x+11}$

Ans: Here, we have  $4\text{x}-1>\text{x}+11$

⇒ $4\text{x}-\text{x}>11+1$

⇒ $3\text{x}>12$

⇒ $\text{x}>\frac{12}{3}$

⇒ $\text{x}>4$

Thus, the solution on the number line is as shown below:

(ii) $7-\mathbf{x}\le 2-6\mathbf{x}$

Ans: Here, we have  $7-\text{x}\le 2-6\text{x}$

⇒ $-\text{x}+6\text{x}\le 2-7$

⇒ $5\text{x}\le -5$

⇒ $\text{x}\le -\frac{5}{5}$

⇒ $\text{x}\le -1$

Thus, the solution on the number line is as shown below:

(iii) $\text{x+3}\le \text{2x+9}$

Ans: Here, we have  $\text{x}+3\le 2\text{x}+9$

⇒ $\text{x}-2\text{x}\le 9-3$

⇒ $-\text{x}\le 6$

⇒ $\text{x}\ge -6$

Thus, the solution on the number line is as shown below:

(iv) $\text{2-3x7-5x}$

Ans: Here, we have  $2-3\text{x}>7-5\text{x}$

⇒ $-3\text{x}+5\text{x}>7-2$

⇒ $2\text{x}>5$

⇒ $\text{x}>\frac{5}{2}$

⇒ $\text{x}>2.5$

Thus, the solution on the number line is as shown below:

(V) $\text{1+x}\ge \text{5x-11}$

Ans: Here, we have  $1+\text{x}\ge 5\text{x}-11$

⇒ $\text{x}-5\text{x}\ge -11-1$

⇒ $-4\text{x}\ge -12$

⇒ $4\text{x}\le 12$

⇒ $\text{x}\le \frac{12}{4}$

⇒ $\text{x}\le 3$

Thus, the solution on the number line is as shown below:

(vi) $\frac{\text{2x+5}}{\text{3}}\text{3x-3}$

Ans: Here, we have  $\frac{2\text{x}+5}{3}>3\text{x}-3$

⇒ $2\text{x}+5>3\left( 3\text{x}-3 \right)$

⇒ $2\text{x}+5>9\text{x}-9$

⇒ $2\text{x}-9\text{x}>-9-5$

⇒ $-7\text{x}>-14$

⇒ $7\text{x}<14$

⇒ $\text{x}<\frac{14}{7}$

⇒ $\text{x}<2$

Thus, the solution on the number line is as shown below:

5. $\mathbf{x}\in $ {real numbers} and \[\text{-13-2x}\le \text{7,}\] evaluate $\mathbf{x}$ and represent it on a number line.

Ans: Here, we have  $-1<3-2\text{x}\le 7$

We can write it into two different inequalities i.e.,

⇒$\text{ }\!\!~\!\!\text{ }-1<3-2\text{x}$ and $3-2\text{x}\le 7$

⇒$\text{ }\!\!~\!\!\text{ }2\text{x}<3+1$ and $-2\text{x}\le 7-3$

⇒$\text{ }\!\!~\!\!\text{ }2\text{x}<4$ and $-2\text{x}\le 4$

⇒$\text{ }\!\!~\!\!\text{ x}<2$ and $-\text{x}\le 2$

⇒$\text{ }\!\!~\!\!\text{ x}<2$ and $\text{x}\ge -2$

Thus, $\text{x}$ is greater than or equal to $-2$ but less than 2.

Therefore, the solution set is {$-2\le \text{x}<2,\text{x}\in \text{R}$}and solution on the number line is as shown below:

6. List the elements of the solution set of the inequation: $\text{-3x-2}\le \text{9-2x}$; $\mathbf{x}\in \mathbf{N}.$

Ans: Here, we have  $-3<\text{x}-2\le 9-2\text{x}$

We can write it into two different inequalities i.e.,

⇒$\text{ }\!\!~\!\!\text{ }-3<\text{x}-2$ and $\text{x}-2\le 9-2\text{x}$

⇒$\text{ }\!\!~\!\!\text{ }-3+2<\text{x}$  and $\text{x}+2\text{x}\le 9+2$

⇒$-1<\text{x}$ and $\text{ }\!\!~\!\!\text{ }3\text{x}\le 11$

⇒$-1<\text{x}$ and $\text{ }\!\!~\!\!\text{ x}\le \frac{11}{3}$

Now, we can say,

⇒$-1<\text{ }\!\!~\!\!\text{ x}\le \frac{11}{3}$

⇒$-1<\text{ }\!\!~\!\!\text{ x}\le 3.67$

Since, $\text{x}\in \text{N}$ (Natural number)

Thus, the required solution set is {1, 2, 3}

7. Find the range of values of $\mathbf{x}$ which satisfies $\text{-2}\frac{\text{2}}{\text{3}}\le \mathbf{x}+\frac{\text{1}}{\text{3}}\text{3}\frac{\text{1}}{\text{3}}\text{ }\!\!~\!\!\text{ },~\mathbf{x}\in \mathbf{R}$. Graph these values of $\text{x}$ on the number line.

Ans: Here, we have  $-2\frac{2}{3}\le \text{x}+\frac{1}{3}<3\frac{1}{3}$

We can write it into two different inequalities i.e.,

⇒$\text{ }\!\!~\!\!\text{ }-2\frac{2}{3}\le \text{x}+\frac{1}{3}$ and $\text{x}+\frac{1}{3}<3\frac{1}{3}$

⇒$\text{ }\!\!~\!\!\text{ }-\frac{8}{3}\le \text{x}+\frac{1}{3}$ and $\text{x}+\frac{1}{3}<\frac{10}{3}$

⇒$-\frac{8}{3}-\frac{1}{3}\le \text{x}$ and $\text{ }\!\!~\!\!\text{ x}<\frac{10}{3}-\frac{1}{3}$

⇒$-\frac{9}{3}\le \text{x}$ and $\text{ }\!\!~\!\!\text{ x}<\frac{9}{3}$

⇒$-3\le \text{x}$ and $\text{ }\!\!~\!\!\text{ x}<3$

Thus, $\text{x}$ is greater than or equal to $-3$ but less than 3.

Therefore, required range of  $\text{x}$ is $-3\le \text{x}<3\text{ }\!\!~\!\!\text{ }$ and solution on the number line is as shown below:

8. Find the values of $\text{x}$, which satisfy the inequation:$\text{-2}\le \frac{\text{1}}{\text{2}}\text{-}\frac{\text{2x}}{\text{3}}\le \text{1}\frac{\text{5}}{\text{6}}$ , x∈N Graph the solution on the number line.

Ans: Here, we have  $-2\le \frac{1}{2}-\frac{2\text{x}}{3}\le 1\frac{5}{6}$

We can write it into two different inequalities i.e.,

⇒$\text{ }\!\!~\!\!\text{ }-2\le \frac{1}{2}-\frac{2\text{x}}{3}$ and $\frac{1}{2}-\frac{2\text{x}}{3}\le 1\frac{5}{6}$

⇒$\text{ }\!\!~\!\!\text{ }\frac{2\text{x}}{3}\le \frac{1}{2}+2$ and $\frac{1}{2}-\frac{2\text{x}}{3}\le \frac{11}{6}$

⇒$\text{ }\!\!~\!\!\text{ }\frac{2\text{x}}{3}\le \frac{5}{2}$ and $-\frac{2\text{x}}{3}\le \frac{11}{6}-\frac{1}{2}$

⇒$\text{ }\!\!~\!\!\text{ }2\text{x}\le \frac{15}{2}$ and $-\frac{2\text{x}}{3}\le \frac{11-3}{6}$

⇒$\text{ }\!\!~\!\!\text{ x}\le \frac{15}{4}$ and $-\frac{2\text{x}}{3}\le \frac{8}{6}$

⇒$\text{ }\!\!~\!\!\text{ x}\le 3.75$ and $-\frac{2\text{x}}{3}\le \frac{4}{3}$

⇒$\text{ }\!\!~\!\!\text{ x}\le 3.75$ and $-\text{x}\le 2$

⇒$\text{ }\!\!~\!\!\text{ x}\le 3.75$ and $\text{x}\ge -2$

⇒$-2\le \text{x}\le 3.75$ 

Since, $\text{x}\in \text{N}$ (Natural number)

Thus, the required solution set is {1, 2, 3}

Therefore, solution on the number line is as shown below

9. Given $\mathbf{x}\in $ {real numbers}, find the range of values of $\mathbf{x}$ for which $\text{-5}\le \text{2x-3x+2}$ and represent it on a real number line.

Ans: Here, we have  $-5\le 2\text{x}-3<\text{x}+2\text{ }\!\!~\!\!\text{ }$

We can write it into two different inequalities i.e.,

⇒$\text{ }\!\!~\!\!\text{ }-5\le 2\text{x}-3$ and $2\text{x}-3<\text{x}+2\text{ }\!\!~\!\!\text{ }$

⇒$\text{ }\!\!~\!\!\text{ }-5+3\le 2\text{x}$ and $2\text{x}-\text{x}<2+3\text{ }\!\!~\!\!\text{ }$

⇒$\text{ }\!\!~\!\!\text{ }-2\le 2\text{x}$ and $\text{x}<5\text{ }\!\!~\!\!\text{ }$

⇒$\text{ }\!\!~\!\!\text{ }-1\le \text{x}$ and $\text{x}<5\text{ }\!\!~\!\!\text{ }$

Thus, $\text{x}$ is greater than or equal to $-1$ but less than 5.

Since $\text{x}\in ${real numbers}

Therefore, required range of  $\text{x}$ is $-1\le \text{x}<5\text{ }\!\!~\!\!\text{ }$ and solution on the number line is as shown below:

10.  If $\text{5x-3}\le \text{5+3x}\le \text{4x+2,}$ express, it as $\mathbf{a}\le \mathbf{x}\le \mathbf{b}$ and then state the values of $\mathbf{a}$ and $\mathbf{b}$.

Ans: Here, we have  $5\text{x}-3\le 5+3\text{x}\le 4\text{x}+2$

We can write it into two different inequalities i.e.,

⇒$\text{ }\!\!~\!\!\text{ }5\text{x}-3\le 5+3\text{x}$ and $5+3\text{x}\le 4\text{x}+2\text{ }\!\!~\!\!\text{ }$

⇒$\text{ }\!\!~\!\!\text{ }5\text{x}-3\text{x}\le 5+3$ and $3\text{x}-4\text{x}\le 2-5\text{ }\!\!~\!\!\text{ }$

⇒$\text{ }\!\!~\!\!\text{ }2\text{x}\le 8$ and $-\text{x}\le -3$

⇒$\text{ }\!\!~\!\!\text{ x}\le 4$ and $\text{x}\ge 3$

⇒$\text{ }\!\!~\!\!\text{ }3\le \text{x}\le 4$ 

Now, on comparing with $\text{a}\le \text{x}\le \text{b}$, we get $\text{a}=3$ and $\text{b}=4.$

Thus, the values of $\text{a}$ and $\text{b}$ are 3 and 4 respectively. 

11.  Solve the following inequation and graph the solution set on the number line:  \[\text{2x-3x+2}\le \text{3x+5;x}\in \mathbf{R}.\]

Ans: Here, we have  $2\text{x}-3<\text{x}+2\le 3\text{x}+5$

We can write it into two different inequalities i.e.,

⇒$\text{ }\!\!~\!\!\text{ }2\text{x}-3<\text{x}+2$ and $\text{x}+2\le 3\text{x}+5\text{ }\!\!~\!\!\text{ }$

⇒$\text{ }\!\!~\!\!\text{ }2\text{x}-\text{x}<2+3$ and $\text{x}-3\text{x}\le 5-2\text{ }\!\!~\!\!\text{ }$

⇒$\text{ }\!\!~\!\!\text{ x}<5$ and $-2\text{x}\le 3\text{ }\!\!~\!\!\text{ }$

⇒$\text{ }\!\!~\!\!\text{ x}<5$ and $-\text{x}\le \frac{3}{2}$

⇒$\text{ }\!\!~\!\!\text{ x}<5$ and $-\text{x}\le 1.5$

⇒$\text{ }\!\!~\!\!\text{ x}<5$ and $\text{x}\ge -1.5$

Thus, $\text{x}$ is greater than or equal to $-1.5$ but less than 5.

Therefore, the solution set is {$-1.5\le \text{x}<5,\text{x}\in \text{R}$}and solution on the number line is as shown below:

12.  Solve and graph the solution set of: 

(i) $\text{2x-97}$ and $\text{3x+9}\le \text{25}$; $\mathbf{x}\in \mathbf{R}$.

Ans: Here, we have  $2\text{x}-9<7$ and $3\text{x}+9\le 25$

⇒$\text{ }\!\!~\!\!\text{ }2\text{x}-9<7$  and $3\text{x}+9\le 25\text{ }\!\!~\!\!\text{ }$

⇒$\text{ }\!\!~\!\!\text{ }2\text{x}<7+9$   and $3\text{x}\le 25-9\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$

⇒$\text{ }\!\!~\!\!\text{ }2\text{x}<16$ and $3\text{x}\le 16\text{ }\!\!~\!\!\text{ }$

⇒$\text{ }\!\!~\!\!\text{ x}<8$ and $\text{x}\le \frac{16}{3}$

⇒$\text{ }\!\!~\!\!\text{ x}<8$ and $\text{x}\le 5.34$

Therefore, the solution set is {$\text{x}\le 5.34,\text{x}\in \text{R}$}and solution on the number line is as shown below:

(ii) \[\text{2x-9}\le \text{7}\] and $\text{3x+925}$

Ans: Here, we have  $2\text{x}-9\le 7$ and $3\text{x}+9>25$

⇒$\text{ }\!\!~\!\!\text{ }2\text{x}-9\le 7$  and $3\text{x}+9>25\text{ }\!\!~\!\!\text{ }$

⇒$\text{ }\!\!~\!\!\text{ }2\text{x}\le 7+9$   and $3\text{x}>25-9\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$

⇒$\text{ }\!\!~\!\!\text{ }2\text{x}\le 16$ and $3\text{x}>16\text{ }\!\!~\!\!\text{ }$

⇒$\text{ }\!\!~\!\!\text{ x}\le 8$ and $\text{x}>\frac{16}{3}$

⇒$\text{ }\!\!~\!\!\text{ x}\le 8$ and $\text{x}>5.34$

⇒$\text{ }\!\!~\!\!\text{ }5.34<\text{x}\le 8$ , Since $\text{x}\in \text{I}$ (integers)

Therefore, the solution set is {$6,\text{ }\!\!~\!\!\text{ }7,\text{ }\!\!~\!\!\text{ }8$}and solution on the number line is as shown below:

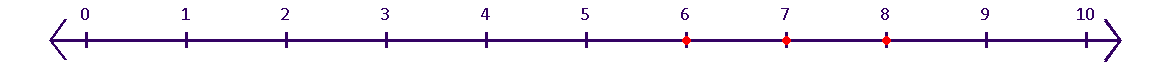
(iii) $\text{x+5}\ge \text{4}\left( \text{x-1} \right)$ and $\text{3-2x-7;}\mathbf{x}\in \mathbf{R}$

Ans: Here, we have  $\text{x}+5\ge 4\left( \text{x}-1 \right)\text{ }\!\!~\!\!\text{ }$ and $3-2\text{x}<-7$

⇒$\text{ }\!\!~\!\!\text{ x}+5\ge 4\left( \text{x}-1 \right)\text{ }\!\!~\!\!\text{ }$ and $3-2\text{x}<-7$

⇒$\text{ }\!\!~\!\!\text{ x}+5\ge 4\text{x}-4\text{ }\!\!~\!\!\text{ }$ and $-2\text{x}<-7-3$

⇒$\text{ }\!\!~\!\!\text{ x}-4\text{x}\ge -4-5\text{ }\!\!~\!\!\text{ }$ and $-2\text{x}<-10$

⇒$-3\text{x}\ge -9\text{ }\!\!~\!\!\text{ }$ and $-\text{x}<-5$

⇒$\text{x}\le 3\text{ }\!\!~\!\!\text{ }$ and $\text{x}>5$ 

It is not possible.

Therefore, the solution set is empty set or $\varnothing .$

13.  Solve and graph the solution set of:

(i) $\text{3x-219}$ or $\text{3-2x}\ge \text{-7}$; $\mathbf{x}\in \mathbf{R}.$

Ans: Here, we have  $3\text{x}-2>19\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$or $3-2\text{x}\ge -7$

⇒$\text{ }\!\!~\!\!\text{ }3\text{x}-2>19\text{ }\!\!~\!\!\text{ }$ or $3-2\text{x}\ge -7$

⇒$\text{ }\!\!~\!\!\text{ }3\text{x}>19+2\text{ }\!\!~\!\!\text{ }$ or $-2\text{x}\ge -7-3$

⇒$\text{ }\!\!~\!\!\text{ }3\text{x}>21\text{ }\!\!~\!\!\text{ }$ or $-2\text{x}\ge -10$

⇒$\text{ }\!\!~\!\!\text{ x}>\frac{21}{3}\text{ }\!\!~\!\!\text{ }$ or $-\text{x}\ge -\frac{10}{2}$

⇒$\text{ }\!\!~\!\!\text{ x}>7\text{ }\!\!~\!\!\text{ }$ or $-\text{x}\ge -5$

⇒$\text{ }\!\!~\!\!\text{ x}>7\text{ }\!\!~\!\!\text{ }$ or $\text{x}\le 5$

Thus, graph of points which belong to $\text{x}>7$ or $\text{x}\le 5$ is shown as below:

(ii) $\text{5p-12}$ or $\text{7}\le \text{2p-1}\le \text{17;}$ $\mathbf{p}\in \mathbf{R}.$

Ans: Here, we have  $5>\text{p}-1>2\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$or $7\le 2\text{p}-1\le 17$

Now, 

Case 1:  When $5>\text{p}-1>2\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$

Adding 1 in given inequation, we get

⇒$\text{ }\!\!~\!\!\text{ }5+1>\text{p}-1+1>2+1\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$

⇒$\text{ }\!\!~\!\!\text{ }6>\text{p}>3$

⇒$\text{ }\!\!~\!\!\text{ }3<\text{p}<6$

Case 2: When $7\le 2\text{p}-1\le 17$

Adding 1 in given inequation, we get

⇒$7+1\le 2\text{p}-1+1\le 17+1\text{ }\!\!~\!\!\text{ }$

⇒$8\le 2\text{p}\le 18\text{ }\!\!~\!\!\text{ }$

Now, dividing by 2

⇒$\frac{8}{2}\le \frac{2\text{p}}{2}\le \frac{18}{2}\text{ }\!\!~\!\!\text{ }$

⇒$\text{ }\!\!~\!\!\text{ }4\le \text{p}\le 9\text{ }\!\!~\!\!\text{ }$

Here, from case 1 and case 2, we get

⇒$\text{ }\!\!~\!\!\text{ }3<\text{p}\le 9\text{ }\!\!~\!\!\text{ }$

Thus, the graph of the solution set is:

14.  The diagram represents two inequations A and B on real number lines: 

A =

B =

(i) Write down A and B in set builder notation.

Ans: Here, in set A, $\text{x}$ is greater than or equal to $-2$ but less than 5.

Thus, set builder notation of set A is {$\text{x}:\text{x}\in \text{R},-2\le \text{x}<5$}

Now, in set B, $\text{x}$ is greater than or equal to $-4$ but less than 3.

Therefore, set builder notation of set B is {$\text{x}:\text{x}\in \text{R},-4\le \text{x}<3$}

(ii) Represent $\mathbf{A}\cap \mathbf{B}$ and $\mathbf{A}\cap \mathbf{{B}'}$ on two different number lines.

Ans: Here, set A = {$\text{x}:\text{x}\in \text{R},-2\le \text{x}<5$}

                   set B = {$\text{x}:\text{x}\in \text{R},-4\le \text{x}<3$}

                   set $\text{{B}'}$ = {$\text{x}:\text{x}\in \text{R},\text{x}<-4$ and $\text{x}\ge 3$}

Thus, the intersection of set A and set B in set builder notation is written as below:

$\text{A}\cap \text{B}=\{\text{x}:\text{x}\in \text{R},\text{ }\!\!~\!\!\text{ }-2\le \text{x}<3\}$ 

Here, the intersection of set A and set $\text{{B}'}$ in set builder notation is written as below:

$\text{A}\cap \text{{B}'}=\{\text{x}:\text{x}\in \text{R},\text{ }\!\!~\!\!\text{ }3\le \text{x}<5\}$

15.  Use real number line to find the range of values of x for which: 

(i) $\text{x3}$ and $\text{0x6}$

Ans: Here, we have $\text{x}>3$ and $0<\text{x}<6$

Case 1: - When $\text{x}>3$

Case 2: - When $0<\text{x}<6$

Now, from both graphs, we have $3<\text{x}<6$.

Therefore, required range of $\text{x}$ is $3<\text{x}<6.$

(ii) $\mathbf{x}<0$ and $-3\le \mathbf{x}<1$

Ans: Here, we have $\text{x}<0$  and $-3\le \text{x}<1$

Case 1: - When $\text{x}<0$

Case 2: - When $-3\le \text{x}<1$

Now, from both graphs, we have $-3\le \text{x}<0$.

Therefore, required range of $\text{x}$ is $-3\le \text{x}<0.$

(iii) $-1<\mathbf{x}\le 6$ and $-2\le \mathbf{x}\le 3$

Ans: Here, we have $-1<\text{x}\le 6\text{ }\!\!~\!\!\text{ }$  and $-2\le \text{x}\le 3$

Case 1: - When $-1<\text{x}\le 6$ 

Case 2: - When $-2\le \text{x}\le 3$

Now, from both graphs, we have $-1<\text{x}\le 3$.

Therefore, required range of $\text{x}$ is $-1<\text{x}\le 3.$

16.  Illustrate the set {$\mathbf{x}:-3\le \mathbf{x}<0$ or $\mathbf{x}>2$; $\mathbf{x}\in \mathbf{R}$} on a real number line.

Ans: Here, we have a set {$\text{x}:-3\le \text{x}<0$ or $\text{x}>2$; $\text{x}\in \text{R}$}

It means we must take the union of $-3\le \text{x}<0$ and $\text{x}>2$.

Thus, the above sets on the number line are shown below:

17.  Given \[\text{A= }\!\!\{\!\!\text{ x }\!\!~\!\!\text{ : }\!\!~\!\!\text{ -1x}\le \text{5,x}\in \text{R}\}\] and $\text{B= }\!\!\{\!\!\text{ x }\!\!~\!\!\text{ : }\!\!~\!\!\text{ -4}\le \text{x3,x}\in \text{R}\}$

Represent on different number lines: (xxx) $\mathbf{A}\cap \mathbf{B}$

Ans: Here, set A = {$\text{x}:-1<\text{x}\le 5,\text{x}\in \text{R}$}

                   set B = {$\text{x}:\text{ }\!\!~\!\!\text{ }-4\le \text{x}<3,\text{ }\!\!~\!\!\text{ x}\in \text{R}\}$

Thus, the intersection of set A and set B in set builder notation is written as below:

(i) $\text{A}\cap \text{B}=\{\text{x}:-1<\text{x}<3\}$ 

(ii) \[\text{{A}'}\cap \text{B}\]

Ans: Here, set A = {$\text{x}:-1<\text{x}\le 5,\text{x}\in \text{R}$}

                   set $\text{{A}'}$ = {$\text{x}:\text{x}\le -1\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{ x}>5\text{ }\!\!~\!\!\text{ },\text{x}\in \text{R}$}

                   set B = {$\text{x}:\text{ }\!\!~\!\!\text{ }-4\le \text{x}<3,\text{ }\!\!~\!\!\text{ x}\in \text{R}\}$

Thus, the intersection of set A and set B in set builder notation is written as below:

$\text{{A}'}\cap \text{B}=\left\{ \text{x}:-4\le \text{x}\le -1 \right\}$ 

(iii) $\mathbf{A}-\mathbf{B}$

Ans: Here, set A = {$\text{x}:-1<\text{x}\le 5,\text{x}\in \text{R}$}

                   set B = {$\text{x}:\text{ }\!\!~\!\!\text{ }-4\le \text{x}<3,\text{ }\!\!~\!\!\text{ x}\in \text{R}\}$

set $\text{{B}'}$ = {$\text{x}:\text{ }\!\!~\!\!\text{ x}<-4\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{ x}\ge 3\text{ }\!\!~\!\!\text{ },\text{ }\!\!~\!\!\text{ x}\in \text{R}\}$

We know that $\text{A}-\text{B}=\text{A}\cap \text{{B}'}$

Thus, $\text{A}\cap \text{{B}'}=\left\{ \text{x }\!\!~\!\!\text{ }:3\le \text{x}\le 5,\text{ }\!\!~\!\!\text{ x}\in \text{R} \right\}$

18.  P is the solution set of $\text{7x-24x+1}$ and Q is the solution set of $\text{9x-45}\ge \text{5}\left( \text{x-5} \right)\text{;}$ where $\mathbf{x}\in \mathbf{R}$. Represent on different number lines:

(i) $\mathbf{P}\cap \mathbf{Q}$

Ans: Here, set P = solution set of $7\text{x}-2>4\text{x}+1$

                   set Q = solution set of $9\text{x}-45\ge 5\left( \text{x}-5 \right)$

Now, 

Case 1: When $7\text{x}-2>4\text{x}+1$

⇒ $7\text{x}-4\text{x}>1+2$

⇒ $3\text{x}>3$

⇒ $\text{x}>\frac{3}{3}$

⇒ $\text{x}>1$

Thus, set P = {$\text{x }\!\!~\!\!\text{ }:\text{x}>1,\text{ }\!\!~\!\!\text{ x}\in \text{R}\}$

Case 2:  When $9\text{x}-45\ge 5\left( \text{x}-5 \right)$

⇒ $9\text{x}-45\ge 5\text{x}-25$

⇒ $9\text{x}-5\text{x}\ge -25+45$

⇒ $4\text{x}\ge 20$

⇒ $\text{x}\ge \frac{20}{4}$

⇒ $\text{x}\ge 5$

Thus, set Q = {$\text{x }\!\!~\!\!\text{ }:\text{x}\ge 5,\text{ }\!\!~\!\!\text{ x}\in \text{R}\}$

Therefore, from case 1 and case 2, we have 

⇒ $\text{P}\cap \text{Q}=\left\{ \text{x }\!\!~\!\!\text{ }:\text{ }\!\!~\!\!\text{ x}\ge 5,\text{ }\!\!~\!\!\text{ x}\in \text{R} \right\}$

(ii) $\mathbf{P}-\mathbf{Q}~$

Ans: Here, set P = {$\text{x }\!\!~\!\!\text{ }:\text{x}>1,\text{ }\!\!~\!\!\text{ x}\in \text{R}\}$

                   set Q = {$\text{x }\!\!~\!\!\text{ }:\text{x}\ge 5,\text{ }\!\!~\!\!\text{ x}\in \text{R}\}$

                   set $\text{{Q}'}$ = {$\text{x}:\text{ }\!\!~\!\!\text{ x}<5\text{ }\!\!~\!\!\text{ },\text{ }\!\!~\!\!\text{ x}\in \text{R}\}$

We know that $\text{P}-\text{Q}=\text{P}\cap \text{{Q}'}$

Thus, $\text{P}\cap \text{{Q}'}=\{\text{x }\!\!~\!\!\text{ }:1<\text{x}<5,\text{ }\!\!~\!\!\text{ x}\in \text{R}\}$

(iii) $\mathbf{P}\cap \mathbf{{Q}'}~$

Ans: Here, set P = {$\text{x }\!\!~\!\!\text{ }:\text{x}>1,\text{ }\!\!~\!\!\text{ x}\in \text{R}\}$

                   set Q = {$\text{x }\!\!~\!\!\text{ }:\text{x}\ge 5,\text{ }\!\!~\!\!\text{ x}\in \text{R}\}$

                   set $\text{{Q}'}$ = {$\text{x}:\text{ }\!\!~\!\!\text{ x}<5\text{ }\!\!~\!\!\text{ },\text{ }\!\!~\!\!\text{ x}\in \text{R}\}$

Thus, $\text{P}\cap \text{{Q}'}=\{\text{x }\!\!~\!\!\text{ }:1<\text{x}<5,\text{ }\!\!~\!\!\text{ x}\in \text{R}\}$

19.  If $\mathbf{P}=\{\mathbf{x}~:7\mathbf{x}-4>5\mathbf{x}+2,~\mathbf{x}\in \mathbf{R}\}$ and $\mathbf{Q}=\left\{ \mathbf{x}~:\mathbf{x}-19\ge 1-3\mathbf{x},~\mathbf{x}\in \mathbf{R} \right\}$; find the range of set $\mathbf{P}\cap \mathbf{Q}$ and represent it on a number line.

Ans: Here, set P = solution set of $7\text{x}-4>5\text{x}+2$

set Q = solution set of $\text{x}-19\ge 1-3\text{x}$

Now, 

Case 1: When $7\text{x}-4>5\text{x}+2$

⇒ $7\text{x}-5\text{x}>2+4$

⇒ $2\text{x}>6$

⇒ $\text{x}>\frac{6}{2}$

⇒ $\text{x}>3$

Thus, set P = {$\text{x }\!\!~\!\!\text{ }:\text{x}>3,\text{ }\!\!~\!\!\text{ x}\in \text{R}\}$

Case 2:  When $\text{x}-19\ge 1-3\text{x}$

⇒ $\text{x}+3\text{x}\ge 1+19$

⇒ $4\text{x}\ge 20$

⇒ $\text{x}\ge \frac{20}{4}$

⇒ $\text{x}\ge 5$

Thus, set Q = {$\text{x }\!\!~\!\!\text{ }:\text{x}\ge 5,\text{ }\!\!~\!\!\text{ x}\in \text{R}\}$

Therefore, from case 1 and case 2, we have 

⇒ $\text{P}\cap \text{Q}=\left\{ \text{x }\!\!~\!\!\text{ }:\text{ }\!\!~\!\!\text{ x}\ge 5,\text{ }\!\!~\!\!\text{ x}\in \text{R} \right\}$

20. Find the range of values of $\mathbf{x}$, which satisfy: $\text{-}\frac{\text{1}}{\text{3}}\le \frac{\text{x}}{\text{2}}\text{+1}\frac{\text{2}}{\text{3}}\text{5}\frac{\text{1}}{\text{6}}$ 

Graph, in each of the following cases, the values of $\text{x}$ on the different real number lines:

(i) $\mathbf{x}\in \mathbf{W}$

Ans: Here, we have  $-\frac{1}{3}\le \frac{\text{x}}{2}+1\frac{2}{3}<5\frac{1}{6}$

We can write it into two different inequalities i.e.,

⇒$\text{ }\!\!~\!\!\text{ }-\frac{1}{3}\le \frac{\text{x}}{2}+1\frac{2}{3}$ and $\frac{\text{x}}{2}+1\frac{2}{3}<5\frac{1}{6}$

⇒$\text{ }\!\!~\!\!\text{ }-\frac{1}{3}\le \frac{\text{x}}{2}+\frac{5}{3}$ and $\frac{\text{x}}{2}+\frac{5}{3}<\frac{31}{6}$

⇒$\text{ }\!\!~\!\!\text{ }-\frac{1}{3}-\frac{5}{3}\le \frac{\text{x}}{2}$ and $\frac{\text{x}}{2}<\frac{31}{6}-\frac{5}{3}$

⇒$\text{ }\!\!~\!\!\text{ }-\frac{6}{3}\le \frac{\text{x}}{2}$ and $\frac{\text{x}}{2}<\frac{31-10}{6}$

⇒$\text{ }\!\!~\!\!\text{ }-2\le \frac{\text{x}}{2}$ and $\frac{\text{x}}{2}<\frac{21}{6}$

⇒$\text{ }\!\!~\!\!\text{ }-4\le \text{x}$ and $\text{x}<\frac{42}{6}$

⇒$\text{ }\!\!~\!\!\text{ x}\ge -4$ and $\text{x}<7$

⇒$-4\le \text{x}<7$

Since, $\text{x}\in \text{W}$ (Whole number)

Thus, the required solution set is {0, 1, 2, 3, 4, 5, 6}

Therefore, solution on the number line is as shown below:

(ii) $\mathbf{x}\in \mathbf{Z}$

Ans: Here, we have  $-4\le \text{x}<7\text{ }\!\!~\!\!\text{ }$

Since, $\text{x}\in \text{Z}$ (Integer)

Thus, the required solution set is {-4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6}

Therefore, solution on the number line is as shown below:

(iii)$\mathbf{x}\in \mathbf{R}$

Ans: Here, we have  $-4\le \text{x}<7\text{ }\!\!~\!\!\text{ }$

Since, $\text{x}\in \text{R}$(Real number)

Thus, the required solution set is {$\text{x }\!\!~\!\!\text{ }:\text{ }\!\!~\!\!\text{ }-4\le \text{x}<7,\text{ }\!\!~\!\!\text{ x}\in \text{R}$}

Therefore, solution on the number line is as shown below:

21. Given: $\mathbf{A}=\{\mathbf{x}~:~-8<5\mathbf{x}+2\le 17,~\mathbf{x}\in \mathbf{I}\}$

$~\mathbf{B}=\{\mathbf{x}~:~-2\le 7+3\mathbf{x}<17,~\mathbf{x}\in \mathbf{R}\}$

Where, R = {real numbers} and I = {integers}. Represent A and B on two different number lines. Write down the elements of $\text{A}\cap \text{B}.\text{ }\!\!~\!\!\text{ }$

Ans: Here, set A = solution set of $-8<5\text{x}+2\le 17$, $\text{x}\in \text{I}$

set B = solution set of $-2\le 7+3\text{x}<17$, $\text{x}\in \text{R}$

Now, 

Case 1: When $-8<5\text{x}+2\le 17$, $\text{x}\in \text{I}$

On subtracting 2 from given inequation, we get

⇒ $-8-2<5\text{x}+2-2\le 17-2$

⇒ $-10<5\text{x}\le 15$

Dividing by 5 in given inequation, we get

⇒ $-\frac{10}{2}<\frac{5\text{x}}{5}\le \frac{15}{5}$

⇒ $-2<\text{x}\le 3$

Therefore, set A = {$\text{x}:\text{ }\!\!~\!\!\text{ }-2<\text{x}\le 3,\text{ }\!\!~\!\!\text{ x}\in \text{I}$}

Since, $\text{x}\in \text{I}${integers}

Thus, required solution set is {-1, 0, 1, 2, 3}

Case 2:  When $-2\le 7+3\text{x}<17$, $\text{x}\in \text{R}$

On subtracting 7 from given inequation, we get

⇒ $-2-7\le 7+3\text{x}-7<17-7$

⇒ $-9\le 3\text{x}<10$

Dividing by 3 in given inequation, we get

⇒ $-\frac{9}{3}\le \frac{3\text{x}}{3}<\frac{10}{3}$

⇒ $-3\le \text{x}<3.34$

Therefore, set B = {$\text{x}:\text{ }\!\!~\!\!\text{ }-3\le \text{x}<3.34,\text{ }\!\!~\!\!\text{ x}\in \text{R}$}

Thus, $\text{A}\cap \text{B}=\left\{ -1,\text{ }\!\!~\!\!\text{ }0,\text{ }\!\!~\!\!\text{ }1,\text{ }\!\!~\!\!\text{ }2,\text{ }\!\!~\!\!\text{ }3 \right\}.$

22 . Solve the following inequation and represent the solution set on the number line $\text{2x-5}\le \text{5x+411}$, where $\mathbf{x}\in \mathbf{I}.$

Ans: Here, we have $2\text{x}-5\le 5\text{x}+4<11$

We can write it into two different inequalities i.e.,

⇒ $2\text{x}-5\le 5\text{x}+4$ and $5\text{x}+4<11$

⇒$\text{ }\!\!~\!\!\text{ }2\text{x}-5\text{x}\le 4+5$ and $5\text{x}<11-4$

⇒$-3\text{x}\le 9$ and $5\text{x}<7$

⇒$-\text{x}\le \frac{9}{3}$ and $\text{x}<\frac{7}{5}$

⇒$-\text{x}\le 3$ and $\text{x}<1.4$

⇒$\text{x}\ge -3$ and $\text{x}<1.4$

⇒$-3\le \text{x}<1.4$ , Since $\text{x}\in \text{I}$ (integers)

Therefore, the solution set is {$-3,\text{ }\!\!~\!\!\text{ }-2,\text{ }\!\!~\!\!\text{ }-1,\text{ }\!\!~\!\!\text{ }0,\text{ }\!\!~\!\!\text{ }1$}and solution on the number line is as shown below:

23. Given that $\mathbf{x}\in \mathbf{I}$, solve the inequation and graph the solution on the number line: $\text{3}\ge \frac{\text{x-4}}{\text{2}}\text{+}\frac{\text{x}}{\text{3}}\ge \text{2}$.

Ans: Here, we have  $3\ge \frac{\text{x}-4}{2}+\frac{\text{x}}{3}\ge 2$

We can write it into two different inequalities i.e.,

⇒$3\ge \frac{\text{x}-4}{2}+\frac{\text{x}}{3}$ and $\frac{\text{x}-4}{2}+\frac{\text{x}}{3}\ge 2$

⇒$3\ge \frac{3\left( \text{x}-4 \right)+2\text{x}}{6}$ and $\frac{3\left( \text{x}-4 \right)+2\text{x}}{6}\ge 2$

⇒$18\ge 3\text{x}-12+2\text{x}$ and $3\text{x}-12+2\text{x}\ge 12$

⇒$18+12\ge 5\text{x}$ and $5\text{x}\ge 12+12$

⇒$30\ge 5\text{x}$ and $5\text{x}\ge 24$

⇒$\frac{30}{5}\ge \text{x}$ and $\text{x}\ge \frac{24}{5}$

⇒$6\ge \text{x}$ and $\text{x}\ge 4.8$

⇒$\text{x}\le 6$ and $\text{x}\ge 4.8$

⇒$4.8\le \text{x}\le 6$, Since $\text{x}\in \text{I}$ (integers)

Therefore, the solution set is {$5,\text{ }\!\!~\!\!\text{ }6$}and solution on the number line is as shown below:

24.  Given: $\text{A= }\!\!\{\!\!\text{ x }\!\!~\!\!\text{ :11x-57x+3},~\mathbf{x}\in \mathbf{R}$} and 

$\text{B= }\!\!\{\!\!\text{ x }\!\!~\!\!\text{ :18x-9}\ge \text{15+12x},~\mathbf{x}\in \mathbf{R}$}

Find the range of set $\text{A}\cap \text{B}$ and represent it on a number line.

Ans: Here, set A = solution set of $11\text{x}-5>7\text{x}+3,\text{ }\!\!~\!\!\text{ x}\in \text{R}$

set B = solution set of $18\text{x}-9\ge 15+12\text{x},\text{ }\!\!~\!\!\text{ x}\in \text{R}$

Now, 

Case 1: When $11\text{x}-5>7\text{x}+3$

⇒ $11\text{x}-7\text{x}>3+5$

⇒ $4\text{x}>8$

⇒ $\text{x}>\frac{8}{2}$

⇒ $\text{x}>2$

Thus, set A = {$\text{x }\!\!~\!\!\text{ }:\text{x}>2,\text{ }\!\!~\!\!\text{ x}\in \text{R}\}$

Case 2:  When $18\text{x}-9\ge 15+12\text{x}$

⇒ $18\text{x}-12\text{x}\ge 15+9$

⇒ $6\text{x}\ge 24$

⇒ $\text{x}\ge \frac{24}{6}$

⇒ $\text{x}\ge 4$

Thus, set B = {$\text{x }\!\!~\!\!\text{ }:\text{x}\ge 4,\text{ }\!\!~\!\!\text{ x}\in \text{R}\}$

Therefore, from case 1 and case 2, we have 

⇒ $\text{A}\cap \text{B}=\left\{ \text{x }\!\!~\!\!\text{ }:\text{ }\!\!~\!\!\text{ x}\ge 4,\text{ }\!\!~\!\!\text{ x}\in \text{R} \right\}$

25.  Find the set of values of x, satisfying: 

$\text{7x+3}\ge \text{3x-5}$ and $\frac{\mathbf{x}}{4}-5\le \frac{5}{4}-\mathbf{x}$, where  $\mathbf{x}\in \mathbf{N}.~$

Ans: Here, we have  $7\text{x}+3\ge 3\text{x}-5\text{ }\!\!~\!\!\text{ }$ and $\text{ }\!\!~\!\!\text{ }\frac{\text{x}}{4}-5\le \frac{5}{4}-\text{x}$

⇒$\text{ }\!\!~\!\!\text{ }7\text{x}+3\ge 3\text{x}-5\text{ }\!\!~\!\!\text{ }$   and $\frac{\text{x}}{4}-5\le \frac{5}{4}-\text{x}$

⇒$\text{ }\!\!~\!\!\text{ }7\text{x}-3\text{x}\ge -5-3\text{ }\!\!~\!\!\text{ }$   and $\frac{\text{x}}{4}+\text{x}\le \frac{5}{4}+5$

⇒$\text{ }\!\!~\!\!\text{ }4\text{x}\ge -8\text{ }\!\!~\!\!\text{ }$   and $\frac{\text{x}+4\text{x}}{4}\le \frac{5+20}{4}$

⇒$\text{ }\!\!~\!\!\text{ x}\ge -\frac{8}{4}\text{ }\!\!~\!\!\text{ }$ and $\frac{5\text{x}}{4}\le \frac{25}{4}$

⇒$\text{ }\!\!~\!\!\text{ x}\ge -2\text{ }\!\!~\!\!\text{ }$ and $5\text{x}\le 25$

⇒$\text{ }\!\!~\!\!\text{ x}\ge -2\text{ }\!\!~\!\!\text{ }$ and $\text{x}\le \frac{25}{5}$

⇒$\text{ }\!\!~\!\!\text{ x}\ge -2\text{ }\!\!~\!\!\text{ }$ and $\text{x}\le 5$

⇒$\text{ }\!\!~\!\!\text{ }-4\le $ $\text{x}\le 5$

Since $\text{x}\in \text{N}$ (Natural number)

Therefore, the solution set is {$1,\text{ }\!\!~\!\!\text{ }2,\text{ }\!\!~\!\!\text{ }3,\text{ }\!\!~\!\!\text{ }4,\text{ }\!\!~\!\!\text{ }5$}. 

26.  Solve:  

(i) $\frac{\text{x}}{\text{2}}\text{+5}\le \frac{\text{x}}{\text{3}}\text{+6}$, where $\mathbf{x}$ is a positive odd integer.

Ans: Here, we have  $\frac{\text{x}}{2}+5\le \frac{\text{x}}{3}+6$

⇒ $\frac{\text{x}}{2}-\frac{\text{x}}{3}\le 6-5$

⇒ $\frac{3\text{x}-2\text{x}}{6}\le 1$

⇒ $\frac{\text{x}}{6}\le 1$

⇒ $\text{x}\le 6$

Since $\text{x}$ is a positive odd integer.

Therefore, the solution set is {$1,\text{ }\!\!~\!\!\text{ }3,\text{ }\!\!~\!\!\text{ }5$}. 

(ii) $\frac{2\mathbf{x}+3}{3}\ge \frac{3\mathbf{x}-1}{4}$, where $\mathbf{x}$ is a positive even integer.

Ans: Here, we have  $\frac{2\text{x}+3}{3}\ge \frac{3\text{x}-1}{4}$

⇒ $4\left( 2\text{x}+3 \right)\ge 3\left( 3\text{x}-1 \right)$

⇒ $8\text{x}+12\ge 9\text{x}-3$

⇒ $8\text{x}-9\text{x}\ge -3-12$

⇒ $-\text{x}\ge -15$

⇒ $\text{x}\le 15$

Since $\text{x}$ is a positive even integer.

Therefore, the solution set is {$2,\text{ }\!\!~\!\!\text{ }4,\text{ }\!\!~\!\!\text{ }6,\text{ }\!\!~\!\!\text{ }8,\text{ }\!\!~\!\!\text{ }10,\text{ }\!\!~\!\!\text{ }12,\text{ }\!\!~\!\!\text{ }14$}. 

27.  Solve the inequation: $-2\frac{1}{2}+2\mathbf{x}\le \frac{4\mathbf{x}}{5}\le \frac{4}{3}+2\mathbf{x},~\mathbf{x}\in \mathbf{W}.$ 

Graph the solution set on the number line.

Ans: Here, we have  $-2\frac{1}{2}+2\text{x}\le \frac{4\text{x}}{5}\text{ }\!\!~\!\!\text{ }$ and $\text{ }\!\!~\!\!\text{ }\frac{4\text{x}}{5}\le \frac{4}{3}+2\text{x}$

⇒$\text{ }\!\!~\!\!\text{ }-\frac{5}{2}+2\text{x}\le \frac{4\text{x}}{5}\text{ }\!\!~\!\!\text{ }$   and $\frac{4\text{x}}{5}\le \frac{4}{3}+2\text{x}$

⇒$\text{ }\!\!~\!\!\text{ }2\text{x}-\frac{4\text{x}}{5}\le \frac{5}{2}\text{ }\!\!~\!\!\text{ }$   and $\frac{4\text{x}}{5}-2\text{x}\le \frac{4}{3}$

⇒$\text{ }\!\!~\!\!\text{ }\frac{10\text{x}-4\text{x}}{5}\le \frac{5}{2}\text{ }\!\!~\!\!\text{ }$   and $\frac{4\text{x}-10\text{x}}{5}\le \frac{4}{3}$

⇒$\text{ }\!\!~\!\!\text{ }\frac{6\text{x}}{5}\le \frac{5}{2}\text{ }\!\!~\!\!\text{ }$   and $-\frac{6\text{x}}{5}\le \frac{4}{3}$

⇒$\text{ }\!\!~\!\!\text{ }12\text{x}\le 25\text{ }\!\!~\!\!\text{ }$   and $-18\text{x}\le 20$

⇒$\text{ }\!\!~\!\!\text{ x}\le \frac{25}{12}\text{ }\!\!~\!\!\text{ }$   and $-\text{x}\le \frac{20}{18}$

⇒$\text{ }\!\!~\!\!\text{ x}\le 2.08$   and $\text{x}\ge -1.11$

⇒$\text{ }\!\!~\!\!\text{ }-1.11\le $ $\text{x}\le 2.08$

Since $\text{x}\in \text{W}$ (Whole number)

Therefore, the solution set is {$0,\text{ }\!\!~\!\!\text{ }1,\text{ }\!\!~\!\!\text{ }2$}. 

Thus, the solution on the number line is as shown below:

28.  Find three consecutive largest positive integers such that the sum of one – third of first, one – fourth of second and one – fifth of third is at most 20.

Ans: Let the required three consecutive integers are $\text{x},\text{ }\!\!~\!\!\text{ x}+1\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{ x}+2$.

Now, according to question

⇒ $\frac{1}{3}\text{x}+\frac{1}{4}\left( \text{x}+1 \right)+\frac{1}{5}\left( \text{x}+2 \right)\le 20$

⇒ $\frac{20\text{x}+15\left( \text{x}+1 \right)+12\left( \text{x}+2 \right)}{60}\le 20$

⇒ $\frac{20\text{x}+15\text{x}+15+12\text{x}+24}{60}\le 20$

⇒ $47\text{x}+39\le 1200$

⇒ $47\text{x}\le 1200-39$

⇒ $47\text{x}\le 1161$

⇒ $\text{x}\le \frac{1161}{47}$

⇒ $\text{x}\le 24.70$

Here, the largest value of positive integer $\text{x}$ is 24.

Thus, the required three consecutive integers are 24, 25 and 26.

29.  Solve the given inequation and graph the solution on the number line. $2\mathbf{y}-3<\mathbf{y}+1\le 4\mathbf{y}+7,~\mathbf{y}\in \mathbf{R}$ 

Ans: Here, we have $2\text{y}-3<\text{y}+1\le 4\text{y}+7$ 

We can write it into two different inequalities i.e.,

⇒$2\text{y}-3<\text{y}+1\text{ }\!\!~\!\!\text{ }$and $\text{y}+1\le 4\text{y}+7$

⇒$2\text{y}-\text{y}<1+3\text{ }\!\!~\!\!\text{ }$and $\text{y}-4\text{y}\le 7-1$

⇒$\text{y}<4\text{ }\!\!~\!\!\text{ }$and $-3\text{y}\le 6$

⇒$\text{y}<4\text{ }\!\!~\!\!\text{ }$and $-\text{y}\le \frac{6}{3}$

⇒$\text{y}<4\text{ }\!\!~\!\!\text{ }$and $-\text{y}\le 2$

⇒$\text{y}<4\text{ }\!\!~\!\!\text{ }$and $\text{y}\ge -2$

⇒$-2\le \text{y}<4$

Therefore, the solution set is {$\text{y}:\text{ }\!\!~\!\!\text{ }-2\le \text{y}<4,\text{ }\!\!~\!\!\text{ y}\in \text{R}$}and solution on the number line is as shown below:

30. Solve the inequation: $3\mathbf{z}-5\le \mathbf{z}+3<5\mathbf{z}-9;\mathbf{z}\in \mathbf{R}.$Graph the solution set on the number line. 

Ans: Here, we have $3\text{z}-5\le \text{z}+3<5\text{z}-9$ 

We can write it into two different inequalities i.e.,

⇒$3\text{z}-5\le \text{z}+3\text{ }\!\!~\!\!\text{ }$and $\text{z}+3<5\text{z}-9$

⇒$3\text{z}-\text{z}\le 3+5\text{ }\!\!~\!\!\text{ }$and $\text{z}-5\text{z}<-9-3$

⇒$2\text{z}\le 8\text{ }\!\!~\!\!\text{ }$and $-4\text{z}<-12$

⇒$\text{z}\le \frac{8}{2}\text{ }\!\!~\!\!\text{ }$and $-\text{z}<-\frac{12}{4}$

⇒$\text{z}\le 4\text{ }\!\!~\!\!\text{ }$and $-\text{z}<-3$

⇒$\text{z}\le 4\text{ }\!\!~\!\!\text{ }$and $\text{z}>3$

⇒$3<\text{z}\le 4$

Therefore, the solution set is {$\text{z}:\text{ }\!\!~\!\!\text{ }3<\text{z}\le 4,\text{ }\!\!~\!\!\text{ z}\in \text{R}$}and solution on the number line is as shown below:

31.  Solve the following inequation and represent the solution set on number line: $\text{-3-}\frac{\text{1}}{\text{2}}\text{-}\frac{\text{2x}}{\text{3}}\le \frac{5}{6}~,~\mathbf{x}\in \mathbf{R}.$ 

Ans: Here, we have $-3<-\frac{1}{2}-\frac{2\text{x}}{3}\le \frac{5}{6}\text{ }\!\!~\!\!\text{ }$ 

We can write it into two different inequalities i.e.,

⇒$-3<-\frac{1}{2}-\frac{2\text{x}}{3}\text{ }\!\!~\!\!\text{ }$and $-\frac{1}{2}-\frac{2\text{x}}{3}\le \frac{5}{6}$

⇒$-3+\frac{1}{2}<-\frac{2\text{x}}{3}\text{ }\!\!~\!\!\text{ }$and $-\frac{2\text{x}}{3}\le \frac{5}{6}+\frac{1}{2}$

⇒$\frac{-6+1}{2}<-\frac{2\text{x}}{3}\text{ }\!\!~\!\!\text{ }$and $-\frac{2\text{x}}{3}\le \frac{5+3}{6}$

⇒$\frac{-5}{2}<-\frac{2\text{x}}{3}\text{ }\!\!~\!\!\text{ }$and $-\frac{2\text{x}}{3}\le \frac{8}{6}$

⇒$\frac{2\text{x}}{3}<\frac{5}{2}\text{ }\!\!~\!\!\text{ }$and $-\text{x}\le \frac{24}{12}$

⇒$\text{x}<\frac{15}{4}\text{ }\!\!~\!\!\text{ }$and $-\text{x}\le 2$

⇒$\text{x}<3.75\text{ }\!\!~\!\!\text{ }$and $\text{x}\ge -2$

⇒$-2\le \text{x}<3.75$

Therefore, the solution set is {$\text{x}:\text{ }\!\!~\!\!\text{ }-2\le \text{x}<3.75,\text{ }\!\!~\!\!\text{ x}\in \text{R}$}and solution on the number line is as shown below:

32.  Solve the following inequation and represent the solution set on the number line: $\text{4x-19}\frac{\text{3x}}{\text{5}}\text{-2}\le \text{-}\frac{\text{2}}{\text{5}}\text{+x, }\!\!~\!\!\text{ }\mathbf{x}\in \mathbf{R}.$ 

Ans: Here, we have $4\text{x}-19<\frac{3\text{x}}{5}-2\le -\frac{2}{5}+\text{x}$

We can write it into two different inequalities i.e.,

⇒$4\text{x}-19<\frac{3\text{x}}{5}-2\text{ }\!\!~\!\!\text{ }$and  $\frac{3\text{x}}{5}-2\le -\frac{2}{5}+\text{x}$

⇒$4\text{x}-\frac{3\text{x}}{5}<-2+19\text{ }\!\!~\!\!\text{ }$and $\text{ }\!\!~\!\!\text{ }\frac{3\text{x}}{5}-\text{x}\le -\frac{2}{5}+2$

⇒$\frac{20\text{x}-3\text{x}}{5}<17\text{ }\!\!~\!\!\text{ }$and  $\frac{3\text{x}-5\text{x}}{5}\le \frac{-2+10}{5}$

⇒$\frac{17\text{x}}{5}<17\text{ }\!\!~\!\!\text{ }$and  $\frac{-2\text{x}}{5}\le \frac{8}{5}$

⇒$\text{x}<5\text{ }\!\!~\!\!\text{ }$and  $-2\text{x}\le 8$

⇒$\text{x}<5\text{ }\!\!~\!\!\text{ }$and  $-\text{x}\le \frac{8}{2}$

⇒$\text{x}<5\text{ }\!\!~\!\!\text{ }$and  $-\text{x}\le 4$

⇒$\text{x}<5\text{ }\!\!~\!\!\text{ }$and  $\text{x}\ge -4$

⇒$-4\le \text{x}<5$

Therefore, the solution set is {$\text{x}:\text{ }\!\!~\!\!\text{ }-4\le \text{x}<5,\text{ }\!\!~\!\!\text{ x}\in \text{R}$}and solution on the number line is as shown below:

33.  Solve the following inequation, write the solution set and represent it on the number line:  $\text{-}\frac{\text{x}}{\text{3}}\le \frac{\text{x}}{\text{2}}\text{-1}\frac{\text{1}}{\text{3}}\text{}\frac{\text{1}}{\text{6}},~\mathbf{x}\in \mathbf{R}.$ 

Ans: Here, we have $-\frac{\text{x}}{3}\le \frac{\text{x}}{2}-1\frac{1}{3}<\frac{1}{6},\text{ }\!\!~\!\!\text{ x}\in \text{R}$

We can write it into two different inequalities i.e.,

⇒$-\frac{\text{x}}{3}\le \frac{\text{x}}{2}-1\frac{1}{3}\text{ }\!\!~\!\!\text{ }$and  $\frac{\text{x}}{2}-1\frac{1}{3}<\frac{1}{6}$

⇒$-\frac{\text{x}}{3}-\frac{\text{x}}{2}\le -\frac{4}{3}\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$and  $\frac{\text{x}}{2}-\frac{4}{3}<\frac{1}{6}$

⇒$\frac{-2\text{x}-3\text{x}}{6}\le -\frac{4}{3}\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$and  $\frac{\text{x}}{2}<\frac{1}{6}+\frac{4}{3}$

⇒$\frac{-5\text{x}}{6}\le -\frac{4}{3}\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$and  $\frac{\text{x}}{2}<\frac{1+8}{6}$

⇒$\frac{5\text{x}}{2}\ge 4\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$and  $\text{x}<\frac{9}{3}$

⇒$\text{x}\ge \frac{8}{5}\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$and  $\text{x}<3$

⇒$\text{x}\ge 1.6\text{ }\!\!~\!\!\text{ }$and  $\text{x}<3$

⇒$1.6\le \text{x}<3$

Therefore, the solution set is {$\text{x}:\text{ }\!\!~\!\!\text{ }1.6\le \text{x}<3,\text{ }\!\!~\!\!\text{ x}\in \text{R}$}and solution on the number line is as shown below:

34.  Find the values of $\mathbf{x},~$which satisfy the inequation $\text{-2}\frac{\text{5}}{\text{6}}\text{}\frac{\text{1}}{\text{2}}\text{-}\frac{\text{2x}}{\text{3}}\le 2,~\mathbf{x}\in \mathbf{W}.$ Graph the solution set on the number line.

Ans: Here, we have $-2\frac{5}{6}<\frac{1}{2}-\frac{2\text{x}}{3}\le 2,\text{ }\!\!~\!\!\text{ x}\in \text{W}$

We can write it into two different inequalities i.e.,

⇒$-2\frac{5}{6}<\frac{1}{2}-\frac{2\text{x}}{3}\text{ }\!\!~\!\!\text{ }$and  $\frac{1}{2}-\frac{2\text{x}}{3}\le 2$

⇒$-\frac{17}{6}<\frac{1}{2}-\frac{2\text{x}}{3}\text{ }\!\!~\!\!\text{ }$and  $-\frac{2\text{x}}{3}\le 2-\frac{1}{2}$

⇒$\frac{2\text{x}}{3}<\frac{1}{2}+\frac{17}{6}\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$and  $-\frac{2\text{x}}{3}\le \frac{4-1}{2}$

⇒$\frac{2\text{x}}{3}<\frac{3+17}{6}\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$and  $-\frac{2\text{x}}{3}\le \frac{3}{2}$. 

⇒$2\text{x}<\frac{20}{2}\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$and  $-\text{x}\le \frac{9}{4}$

⇒$2\text{x}<10\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$and  $-\text{x}\le 2.25$

     $\text{x}<5\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$and  $\text{x}\ge -2.25$

⇒$-2.25\le \text{x}<5$

Since $\text{x}\in \text{W}$(whole number)

Therefore, the solution set is {$0,\text{ }\!\!~\!\!\text{ }1,\text{ }\!\!~\!\!\text{ }2,\text{ }\!\!~\!\!\text{ }3,\text{ }\!\!~\!\!\text{ }4$}and solution on the number line is as shown below:

35.  Solve the following inequation and write the solution set:

$\text{13x-515x+47x+12, }\!\!~\!\!\text{ x}\in \mathbf{R}$ Represent the solution on a real number line.

Ans: Here, we have $13\text{x}-5<15\text{x}+4<7\text{x}+12,\text{ }\!\!~\!\!\text{ x}\in \text{R}$

We can write it into two different inequalities i.e.,

⇒$13\text{x}-5<15\text{x}+4\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$and  $15\text{x}+4<7\text{x}+12$

⇒$13\text{x}-15\text{x}<4+5\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$and  $15\text{x}-7\text{x}<12-4$

⇒$-2\text{x}<9\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$and  $8\text{x}<8$

⇒$-\text{x}<\frac{9}{2}\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$and  $\text{x}<\frac{8}{8}$

⇒$-\text{x}<4.5\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$and  $\text{x}<1$

⇒$\text{x}>-4.5\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$and  $\text{x}<1$

⇒$-4.5<\text{x}<1$

Therefore, the solution set is {$\text{x }\!\!~\!\!\text{ }:\text{ }\!\!~\!\!\text{ }-4.5<\text{x}<1,\text{x}\in \text{R}$}and solution on the number line is as shown below:

36.  Solve the following inequation, write the solution set and represent it on the number line.$\text{-3}\left( \text{x-7} \right)\ge \text{15-7x}\frac{\text{x+1}}{\text{3}},~\mathbf{x}\in \mathbf{R}.$ 

Ans: Here, we have $-3\left( \text{x}-7 \right)\ge 15-7\text{x}>\frac{\text{x}+1}{3},\text{ }\!\!~\!\!\text{ x}\in \text{R}$

We can write it into two different inequalities i.e.,

⇒$-3\left( \text{x}-7 \right)\ge 15-7\text{x }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$and  $15-7\text{x}>\frac{\text{x}+1}{3}$

⇒$-3\text{x}+21\ge 15-7\text{x }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$and  $3\left( 15-7\text{x} \right)>\text{x}+1$

⇒$-3\text{x}+7\text{x}\ge 15-21\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$and  $45-21\text{x}>\text{x}+1$

⇒$4\text{x}\ge -6\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$and  $-21\text{x}-\text{x}>1-45$

⇒$\text{x}\ge -\frac{6}{4}\text{ }\!\!~\!\!\text{ }$and  $-22\text{x}>-44$

⇒$\text{x}\ge -1.5\text{ }\!\!~\!\!\text{ }$and  $22\text{x}<44$

⇒$\text{x}\ge -1.5\text{ }\!\!~\!\!\text{ }$and  $\text{x}<2$

⇒$-1.5\le \text{x}<2$

Therefore, the solution set is {$\text{x }\!\!~\!\!\text{ }:\text{ }\!\!~\!\!\text{ }-1.5\le \text{x}<2,\text{x}\in \text{R}$}and solution on the number line is as shown below:

37.  Solve the following inequation and represent the solution set on a number line. $\text{-8}\frac{\text{1}}{\text{2}}\text{-}\frac{\text{1}}{\text{2}}\text{-4x}\le \text{7}\frac{\text{1}}{\text{2}}\text{, }\!\!~\!\!\text{ }\mathbf{x}\in \mathbf{I}$. 

Ans: Here, we have -8\[\frac{1}{2}< -\frac{1}{2}-4x\leq 7\frac{1}{2},x\epsilon\] I

We can write it into two different inequalities i.e.,

⇒ -8\[\frac{1}{2}< -\frac{1}{2}\]-4x and -\[\frac{1}{2}-4x\leq 7\frac{1}{2}\]

⇒ -\[\frac{17}{2}< -\frac{1}{2}\]-4x and -\[\frac{1}{2} -4x\leq \frac{15}{2}\]

⇒ 4x < -\[\frac{1}{2} + \frac{17}{2}\] and 4x\[\leq\]  -\[\frac{15}{2} + \frac{1}{2}\]

⇒ 4x < \[\frac{16}{2}\] and 4x\[\leq\]  \[\frac{16}{2}\]

⇒ x < \[\frac{16}{8}\] and -x\[\leq\]  \[\frac{16}{8}\]

⇒ x < 2 and -x \[\leq\]  2

⇒ x < and x \[\geq\]  -2

⇒ -2 \[\leq\]  x < 2

Since x∈I (integers)

Therefore, the solution set is {-2, -1, 0.1}and solution on the number line is as shown below:

ICSE Class 10 Mathematics Chapter 4 Selina Concise Solutions - Free PDF Download

Class 9 is the gateway to the board class and the concepts of this class have their place in the higher-level exams like JEE, BITSAT, and so on; for this, you need to be crystal clear in all the concepts. Keeping in mind the understanding level of students, we have provided all the resources from Selina Concise ICSE Class 9 Maths Solutions to PYQP so that you can score 90+ in your upcoming Maths exam.

Now, we will look at the list of exercises included in Chapter 10 of Class 9.

Solutions To Selina Class 9 Maths Chapter 10 Triangles

Selina Class 9 Chapter 10 Triangles, contains 2 exercises, and solutions to all the questions present in these exercises are available on this page. Now, let us have a look at topics that are being covered in this chapter in a tabular format:

Now, let’s understand what this chapter talks about in detail:

Selina ICSE Board Class 9 ICSE Chapter 10 Triangles

Exercise 10.1: Introduction 

A polygon that is formed by the intersection of three lines and has three common points is said to be a triangle or trigon. A triangle has three vertices, three sides, and three angles, where all the sides or angles may be the same or vary depending on the triangle type.

(Image will be Uploaded Soon)

In the above figure, triangles ABC has three sides, viz: AB, BC, AC, and three angles, viz: ∠ A, ∠B, ∠ C.

First Figure: ∠ A = ∠B = ∠ C: Equilateral triangle.

Second Figure: ∠B = 90°, right-angled isosceles triangle

Third figure: ∠ A ≠ ∠B ≠ ∠ C: Scalene triangle

Exercise 10.2: The Relation Between Sides and Angles of Triangles

• Inequality Relations In a Triangle

If two sides of a triangle are not equal, the longer side has a greater angle to the side opposite to it. If there is a triangle ΔABC, where BC > AB, then:

 ∠ CAB > ∠ ACB.

The Triangle Inequality Theorem states that the sum of the lengths of any two sides of a triangle is greater than the length of the third side of a triangle.

Exercise 10.3: Some Important Terms on Triangles

• Median

• Altitude

• Orthogonal

• Sides

• Angles

• Congruence of triangles

Exercise 10.4: Conditions for Congruency of Triangles

Two triangles have congruence when the sides and angles of one triangle equal the corresponding sides and angles of the other triangle.

(Image will be Uploaded Soon)

From the figure, Δ ABC  ≅ Δ DEF, now, let’s understand how:

Here: ∠ A = ∠ D, ∠ B = ∠ E, and ∠ C = ∠ F 

Also,

AB = DE 

BC = EF 

AC = DF

Exercise 10.5: Congruent Triangles

Below are the different Conditions for the congruency of triangles:

1. SAS (Side-Angle-Side) congruence rule

2. ASA (Angle-Side-Angle) congruence rule

3. AAS (Angle-Angle-Side) congruence rule

4. SSS (Side-Side-Side) congruence rule

5. RHS (Right angle-Hypotenuse-Side) congruence rule

Download ICSE Selina Class 9 Maths Chapter 10 Triangles Solutions PDF

Free PDF of the solutions to Selina ICSE Class 9 Mathematics Chapter 10 Triangles is available on our website, click on the following link:

Class 10 board tests are an essential stage in students' lives. It is the stage that requires a decent look over the multitude of ideas since these ideas are the structure points of one's career. And, one of the essential subjects in the tenth ICSE is Mathematics. STEM competitors should know that the chart of their professional development relies significantly upon Mathematics. Also, Vedantu will leave no stones unturned for students to be prepared for their tests.

Why Choose Vedantu For ICSE Selina Class Maths Solutions?

Following are the Salient features of referring to Vedantu’s ICSE Class 9 Solutions to Selina Maths textbook:

• Subject-matter experts at Vedantu design ICSE Selina Concise Solutions in a concise format explaining all the important concepts included in the latest syllabus of the ICSE Board. Also, all the contents are consistently updated because variations occur every day around.

• Vedantu follows the Back-to-Basics rule; therefore, the Solutions to Selina Class 9 Chapter 10 Triangles will help you understand the basic concepts of triangles, congruent triangles, and various criteria for congruence for a lifetime.

• Many students face difficulty understanding the applications of triangles. However, Vedantu Selina Solutions are easy-to-understand and concise that will help you in the quick understanding of tough concepts. 

• Also, you will find numerous examples that will help you gain confidence in solving challenging problems on triangles during exams with ease.

• With convenient arrangements by Vedantu, students don't need to lose the speed of addressing questions. Suppose you are stuck on a question and assuming that you need to skim through the pages of your course books to comprehend the idea and afterward sort out the arrangement it would break the stream. In addition to the fact that it causes interference is tedious. Furthermore, when you have tests on your head, losing a particle of time can cause losing marks.

• Addressing Mathematics questions is a bit-by-bit process and staggering after a species is probably going to occur. Furthermore, as an inquisitive student, you should know where you committed the error. Going through a weighty course reading isn't simply time taking however you may now see precisely which place you committed the error. With Vedantu it is extremely straightforward. With Vedantu arrangements of Class 10, you can see each progression minutely.

• Vedantu comprehends the quandary of students when they are hindered because of a question and henceforth it intricately clarifies each question with sufficient articulations and theory so a student doesn't lose marks in light of ICSE step marking. Selina Concise is viewed as the base book for the ICSE boards arrangement and Vedantu assists students with endeavoring better.

There is no choice rather than troublesome work for accomplishment. Students essentially need to practice in this subject of Mathematics. Vedantu accepts that no one has a substitute way or technique for dominating a field. Simply tireless practice can prepare us to achieve achievement through faultlessness in any field. Thus, the solution of Selina Mathematics Class X through students can achieve a decent score. The practice assists us with accomplishing higher targets and goals.

The act of different issues is just the consistent usage of one's psychological capacities. With preparation, you can tame your entire self to achieve any score and focus easily and reasonably. To dominate, Vedantu gives Selina Concise Mathematics Class 10 ICSE Solutions for Chapter 4 - Linear Inequations (In one variable). Goal, certainty, obstruction, courage, and responsibility. This one aid will assist you with arriving at your objective.

There are many books one can propose for Class tenth Mathematics ICSE. Nonetheless, skimming through all will be problematic as there are many subjects to oversee during your boards. It would be amazingly somber and bumbling to comprehend through a heap of books. Accordingly, Vedantu recommends the key and proposed book that would cover all prospectuses and activities as demonstrated by the Class 10 ICSE question plan, which is, Selina Concise. Assuming that students practice all question types from Selina Concise Class 10 Mathematics, then, at that point, it would not be difficult to get extraordinary marks. Vedantu henceforth concocts Solutions for Class 10 Mathematics ICSE.

Best of Both Worlds

The best part of Vedantu is that you can access all the study materials at free-of-cost without paying a single penny. 

Besides study materials, our academicians are also available 24 by 7 for your assistance.

Now, let’s look at some of the FAQs being asked by many of your peers