Electrochemistry JEE Advanced 2026 Revision Notes - Free PDF Download
FAQs on Electrochemistry JEE Advanced 2026 Notes
1. How many types of electrochemical cells are there?
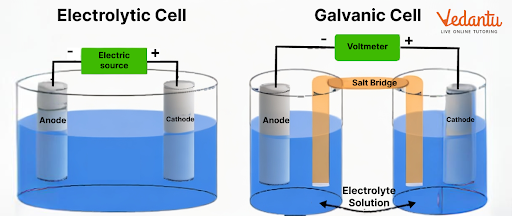
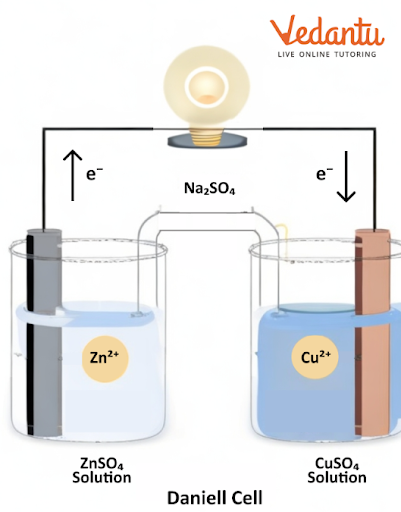
There are two types of cells we can find in this chapter, galvanic and electrolytic cells. A galvanic cell converts chemical energy into electrical energy. An electrolytic cell converts electrical energy to chemical energy.
2. What is an electrochemical series?
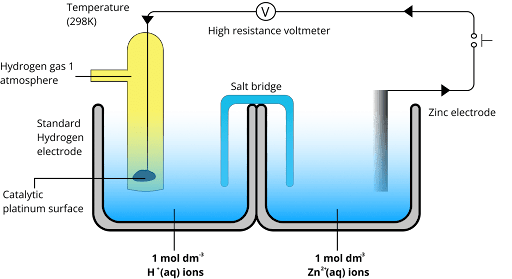
It is an activity series that determines the position of radicals and elements based on their electrode potential values. The values are measured by using the standard hydrogen electrode as a reference frame.
3. What is the application of the electrochemical series?
The prime application of the electrochemical series is to determine the reactivity of elements; reducing and oxidising strengths of elements and ions. This series enables us to identify the reducing and oxidising agents in an electrochemical system.
4. What is the importance of an electrochemical cell diagram?
A cell diagram explains the different parts of an electrochemical cell. It is used to explain how an electrochemical reaction will take place in a system.
5. Is electrochemistry difficult?
The complex concepts of electron transfer and redox reactions in electrochemistry can make it difficult at first, but with the right knowledge and practice, it can be made easier and more enjoyable.
6. Why is electrochemistry useful?
Electrochemistry is useful because it may be utilised in batteries, prevent corrosion, and industrial processes like electroplating. It also provides metal polishing, material protection, and energy storage options.
7. Who is the father of electrochemistry?
Allen J. Bard, who has served as the Norman Hackerman – Welch Regents Chair in Chemistry for 63 years and is regarded as "the father of modern electrochemistry," is retiring from the Department of Chemistry.
8. Who designed the first electrochemical cell?
The voltaic pile, a kind of electrochemical cell, was created in 1800 by Italian physicist Alessandro Volta. It produced a constant electrical current by alternating copper and zinc discs spaced by cardboard soaked in salt.
9. What are the key points of electrochemistry?
Electrochemistry mainly highlights the understanding of redox reactions that involve electron transfer, and application in electrolysis and gives insights of electrode potentials.
10. How many types of electrochemical cells are there?
There are two types of cells we can find in this chapter, galvanic and electrolytic cells. A galvanic cell converts chemical energy into electrical energy. An electrolytic cell converts electrical energy to chemical energy.
11. What is the importance of an electrochemical cell diagram?
A cell diagram explains the different parts of an electrochemical cell. It is used to explain how an electrochemical reaction will take place in a system.
12. What is an electrochemical series?
Based on the values of their electrode potentials, the reactivity series is essential in identifying the locations of radicals and elements. In order to provide a consistent frame of comparison, these values are usually measured using the standard hydrogen electrode as a reference point.