Question

Calculate the equivalent resistance between X and Y.

A) $1\Omega $
B) $2\Omega $
C) $3\Omega $
D) $4\Omega $

Answer 1

Hint: Equivalent resistance of two resistances connected in series combination is equal sum of individual resistances. Multiplicative inverse of equivalent resistance of two resistances connected in parallel combination is equal sum of multiplicative inverse of individual resistance. Here to find equivalent resistance between X and Y, we divide the complete circuit in parts and solve the parts and combine them again.

Complete step by step solution:
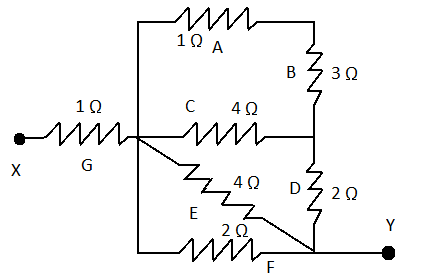
Given, ${R_A} = 1\Omega $, ${R_B} = 3\Omega $, ${R_C} = 4\Omega $, ${R_D} = 2\Omega $, ${R_E} = 4\Omega $, ${R_F} = 2\Omega $ and ${R_G} = 1\Omega $.
First, we take ${R_A}$ and ${R_B}$, these are connected in series then their equivalent resistance is ${R_{AB}} = {R_A} + {R_B} = 1 + 3 = 4\Omega $.
Now, resistance ${R_{AB}}$ and ${R_C}$ are connected in parallel and their equivalent resistance is ${R_{ABC}} = \dfrac{{{R_{AB}} \times {R_C}}}{{{R_{AB}} + {R_C}}} = \dfrac{{4 \times 4}}{{4 + 4}} = 2\Omega $.
Now, ${R_{ABC}}$ and \[{R_D}\] are connected in series and their equivalent resistance is ${R_{ABCD}} = {R_{ABC}} + {R_D} = 2 + 2 = 4\Omega $.
Now, resistance ${R_{ABCD}}$, ${R_E}$ and ${R_F}$ are connected in parallel combination and their equivalent resistance is \[{R_{ABCDEF}} = \dfrac{1}{{\dfrac{1}{{{R_{ABCD}}}} + \dfrac{1}{{{R_E}}} + \dfrac{1}{{{R_F}}}}} = \dfrac{1}{{\dfrac{1}{4} + \dfrac{1}{4} + \dfrac{1}{2}}} = 1\Omega \].
Finally, we have two resistance \[{R_{ABCDEF}}\] and \[{R_G}\] connected in series and their equivalent resistance is ${R_{Eq}} = {R_{ABCDEF}} + {R_G} = 1 + 1 = 2\Omega $.

Hence equivalent resistance between X and Y is $2\Omega $ and the correct answer is option B.

Note: For better understanding we can assume that after every step combination of resistances is replaced by their equivalent resistance. After all steps we find that there is only one resistance between X and Y and this resistance is equivalent resistance of all resistances.