Question

Heights of transmitting and receiving antennas from earth surface are \[{h_t}\] and \[{h_R}\] respectively. Write the relation for the maximum line of sight (LOS) distance between two antennas.

Answer 1

Hint: The maximum line of sight is the maximum distance between the transmitting and the receiving antenna beyond which they would no longer be able to send or receive signals from one another. The curvature of the earth is what causes the distance to be finite i.e. a flat earth would have no maximum line of sight.

Formula used: In this solution we will be using the following formula;
\[hy{p^2} = op{p^2} + ad{j^2}\] where \[hyp\] is the hypotenuse of a right angled triangle, \[opp\] is the opposite side and \[adj\] is the adjacent side

Complete Step-by-Step Solution:
We shall draw two antennae on the surface of a round earth as shown in the figure

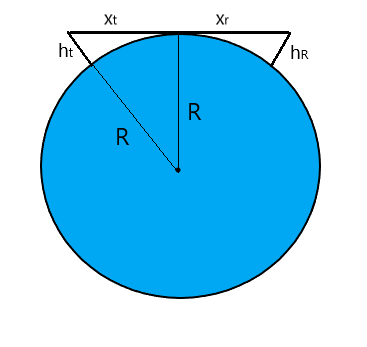
The maximum line of sight by diagram is given by
\[S = {x_t} + {x_r}\]
From Pythagoras theorem which states that
\[hy{p^2} = op{p^2} + ad{j^2}\] where \[hyp\] is the hypotenuse of a right angled triangle, \[opp\] is the opposite side and \[adj\] is the adjacent side
Hence,
\[{\left( {R + {h_t}} \right)^2} = {R^2} + x_t^2\]
\[ \Rightarrow x_t^2 = {\left( {R + {h_t}} \right)^2} - {R^2}\]
By opening the bracket and subtracting in the right hand side, we have
\[x_t^2 = {R^2} + {h_t}^2 + 2{h_t}R - {R^2}\]
\[ \Rightarrow x_t^2 = {h_t}^2 + 2{h_t}R\]
Now, if the height of the transmission antennae is taken to be small with respect to the radius of the earth, then the square of the height can be dropped as in
For \[{h_t} < < R\]. Then \[{h_t}^2 + 2{h_t}R = 2{h_t}R\].
Then the transmission antennae height can be given as
\[x_t^2 = 2{h_t}R\],
By finding the square root of both sides, we have
\[{x_t} = \sqrt {2{h_t}R} \]
Similarly, for the receiving antennae, we have that
\[{x_r} = \sqrt {2{h_R}R} \].
Then, the maximum line of sight is given by
\[S = {x_t} + {x_r} = \sqrt {2{h_t}R} + \sqrt {2{h_R}R} \]

Note: For clarity, the dropping of the square of the height can be justified through the following analysis; The equation \[{h_t}^2 + 2{h_t}R\] can be written as \[{R^2}\left( {\dfrac{{{h^2}}}{{{R^2}}} + \dfrac{{2h}}{R}} \right)\], now since, the height is small relative to the radius of the earth, then \[\dfrac{h}{R} < < 0\]. Now, from maths, we observe that when a number is less than zero, then the square of the number is even far less than zero. Hence, the first term in the bracket \[{\left( {\dfrac{h}{R}} \right)^2} \to 0\] and hence can be neglected. If we multiply \[{R^2}\], we have
\[{R^2}\left( {0 + \dfrac{{2{h_R}}}{R}} \right)\]
\[ \Rightarrow 2hR\]