Question

In a circular grassy plot, a quadrilateral shape with its corners touching the boundary of the plot is to be paved with the bricks. Find the area of the quadrilateral when the sides of the quadrilateral are $36{\text{m,77m,75m and 40m}}$.
A) $4686{\text{ square meter}}$
B) ${\text{2886 square meter}}$
C) ${\text{3856 square meter}}$
D) ${\text{none of these}}$

Answer 1

Hint: As we know that it forms a cyclic quadrilateral and we know that if sides of the cyclic quadrilateral is given for example a, b, c, d then the area is given by
${\text{area}} = \sqrt {(s - a)(s - b)(s - c)(s - d)} $
Where $s$is the semi-perimeter of the quadrilateral which means $s = \dfrac{{a + b + c + d}}{2}$

Complete step by step solution:
Here as we are given that in a circular grassy plot, a quadrilateral shape with its corners touching the boundary of the plot is to be paved with the bricks. So it will form the cyclic quadrilateral.

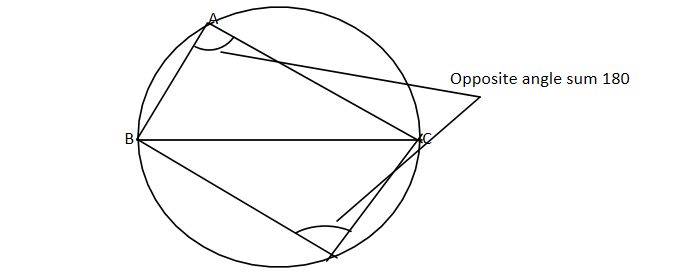
Let $ABCD$ be the quadrilateral.
Let us assume that $AB = a,BC = b,CD = c,AD = d$
Upon joining $AC$ let us assume that $AC = x$
$\angle ABC = \theta $
And we know that in the cyclic quadrilateral sum of the opposite angle sis equal to $180^\circ $
So $\angle ABC + \angle ADC = 180^\circ $
$\theta + \angle ADC = 180^\circ $
$\angle ADC = 180^\circ - \theta $
Now we can apply cosine formula in $\Delta ADC$ and $\Delta ABC$
Now in $\Delta ABC$
$\cos B = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}$
And we know that $\angle B = \theta $
$\cos \theta = \dfrac{{{a^2} + {b^2} - {x^2}}}{{2ab}}$$ - - - - - (1)$
And in $\Delta ADC$
$\cos D = \dfrac{{{c^2} + {d^2} - {x^2}}}{{2cd}}$ and we know that $\angle D = 180 - \theta $
And $\cos (180 - \theta ) = - \cos \theta $
$ - \cos \theta = \dfrac{{{c^2} + {d^2} - {x^2}}}{{2cd}}$$ - - - - (2)$
Now we can write equation (1) as
${x^2} = {a^2} + {b^2} - 2ab\cos \theta $
And from equation (2), we get
${x^2} = {c^2} + {d^2} + 2cd\cos \theta $
Equating both we get that
${a^2} + {b^2} - 2ab\cos \theta $$ = {c^2} + {d^2} + 2cd\cos \theta $
So we get
$\cos \theta (2cd + 2ab) = {a^2} + {b^2} - {c^2} - {d^2}$
$\cos \theta = \dfrac{{{a^2} + {b^2} - {c^2} - {d^2}}}{{2(ab + cd)}}$
And we know that the area of the quadrilateral is given as
Area of quadrilateral $ABCD$$ = $ area of$\Delta ABC$+area of $\Delta ADC$
And if we are given two sides and the included angle, then the area is given by $\dfrac{1}{2}ab\sin \theta $ where $\theta $ is the included angle
So we get that
Area of quadrilateral $ABCD$$ = $ area of$\Delta ABC$+area of $\Delta ADC$
                                                     $ = \dfrac{1}{2}ab\sin \theta + \dfrac{1}{2}cd\sin (180 - \theta)$
And we know $\sin (180 - \theta ) = \sin \theta $
So Area of quadrilateral $ABCD$$ = \dfrac{1}{2}ab\sin \theta + \dfrac{1}{2}cd\sin \theta $
$A = = \dfrac{1}{2}(ab + cd)\sin \theta $
Upon squaring both the sides we get
${A^2} = \dfrac{1}{4}{(ab + cd)^2}{\sin ^2}\theta $
And we know that ${\sin ^2}\theta = 1 - {\cos ^2}\theta $
${A^2} = \dfrac{1}{4}{(ab + cd)^2}(1 - {\cos ^2}\theta )$
Now we know that $\cos \theta = \dfrac{{{a^2} + {b^2} - {c^2} - {d^2}}}{{2(ab + cd)}}$
So on putting this value we get that
${A^2} = \dfrac{1}{4}{(ab + cd)^2}(1 - \dfrac{{{{({a^2} + {b^2} - {c^2} - {d^2})}^2}}}{{4{{(ab + cd)}^2}}})$
${A^2} = \dfrac{1}{4}\left( {\dfrac{{4{{(ab + cd)}^2} - {{({a^2} + {b^2} - {c^2} - {d^2})}^2}}}{4}} \right)$
We can write it as
$16{A^2} = {(2(ab + cd))^2} - {({a^2} + {b^2} - {c^2} - {d^2})^2}$
On applying ${a^2} - {b^2} = (a + b)(a - b)$
$16{A^2} = (2(ab + cd) + {a^2} + {b^2} - {c^2} - {d^2})(2(ab + cd) - {a^2} - {b^2} + {c^2} + {d^2})$$16{A^2} = ({a^2} + {b^2} + 2ab - ({c^2} + {d^2} - 2cd)( - ({a^2} + {b^2} - 2ab) + {c^2} + {d^2} + 2cd)$
$16{A^2} = ({(a + b)^2} - {(c + d)^2})({(c + d)^2} - {(a + b)^2})$
Again solving we get that
$16{A^2} = ((a + b + c + d)(a + b - c - d)(c + d + a + b)(c + d - a - b))$
And we know that $s$ is the semi-perimeter and
${\text{area}} = \sqrt {(s - a)(s - b)(s - c)(s - d)} $
$s = \dfrac{{a + b + c + d}}{2}$
So as we know that $s = \dfrac{{a + b + c + d}}{2}$
$2s = a + b + c + d$
$2s - 2d = a + b + c - d$
$2s - 2c = a + b + d - c$
$2s - 2b = a + c + d - b$
$2s - 2a = c + b + d - a$
We get that
$16{A^2} = 2(s - a)2(s - c)2(s - b)2(s - d)$
${A^2} = (s - a)(s - c)(s - b)(s - d)$
So for the cyclic quadrilateral the area is given by
${\text{area}} = \sqrt {(s - a)(s - b)(s - c)(s - d)} $
Here sides are given as $a = 36m,b = 77m,c = 75m,d = 40m$
 $s = \dfrac{{a + b + c + d}}{2}$
$s = \dfrac{{36 + 77 + 75 + 40}}{2} = 114$
${\text{area}} = \sqrt {(114 - 36)(114 - 77)(114 - 75)(114 - 40)} $
${\text{area}} = \sqrt {78.37.39.74} $
On solving this we get that

${\text{area}} = \sqrt {39.2.37.39.37.2} = (39)(37)(2) = 2886{m^2}.$

Note: for the triangle if all the sides are given then the area of the triangle is given by the formula
${\text{area}} = \sqrt {s(s - a)(s - b)(s - c)} $
Where $s = \dfrac{{a + b + c}}{2}$
And this is called the Heron’s formula.