Question

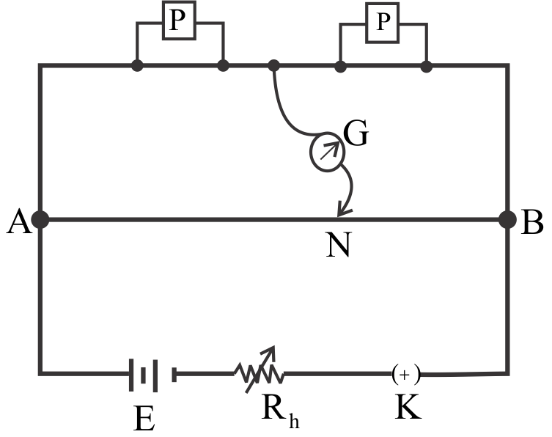
In a meter bridge experiment resistances are connected as shown in figure. Initially resistance $P = 4\Omega $ and the neutral point $N$ is at $60cm$ from $A$. Now an unknown resistance $R$ is connected in series to $P$ and the new position of the neutral point is at $80cm$ from $A$. The value of unknown resistance $R$ is:
    
(A) $6\Omega $
(B) $7\Omega $
(C) $\dfrac{{33}}{5}\Omega $
(D) $\dfrac{{20}}{3}\Omega $

Answer 1

Hint: Using the formula of a meter bridge, first calculate the value of the resistance $Q$. Then with this value of $Q$ we can determine the value of the unknown resistance $R$ using the same formula.
Formula used
$\dfrac{X}{l} = \dfrac{R}{{100 - l}}$, where $X$ is the known resistance and $R$is the unknown resistance and $l$ is in $cm$.

Complete step by step solution
A meter bridge is an electrical instrument that works on the principle of a Wheatstone bridge. It is used in finding the unknown resistance of a conductor.
It consists of a long wire of $1m$ which is separated into two sections. In the left section we attach the known resistance and in the right section, we attach the unknown resistance. A jockey is present to detect the balance point. The galvanometer indicates the balance point. The balance point is the point on the wire where the galvanometer shows zero deflection.
Let $X$ be the known resistance and $R$ be the unknown resistance.
Then we can write,
$\dfrac{X}{l} = \dfrac{R}{{100 - l}}$
Using this formula we can determine the value of the unknown resistance.
The distance between $A$ and $B$ is $100cm$
It is given that $AN = 60cm$
So, $NB$ would be equal to $\left( {100 - 60} \right)cm = 40cm$
From this diagram we can see that,
$
  \dfrac{P}{{AN}} = \dfrac{Q}{{NB}} \\
   \Rightarrow \dfrac{4}{{60}} = \dfrac{Q}{{40}} \\
   \Rightarrow Q = \dfrac{{16}}{6} \\
   \Rightarrow Q = \dfrac{8}{3}\Omega \\
 $
Now when another resistance $R$ is connected in series with $P$, $AN$ becomes $80cm$
So, the value of the unknown resistance becomes,
$
  \dfrac{{P + R}}{{80}} = \dfrac{Q}{{20}} \\
   \Rightarrow \dfrac{{4 + R}}{4} = \dfrac{8}{3} \\
   \Rightarrow 12 + 3R = 32 \\
   \Rightarrow 3R = 20 \\
   \Rightarrow R = \dfrac{{20}}{3}\Omega \\
 $
So, the value of the unknown resistance $R$ is $\dfrac{{20}}{3}\Omega $

Therefore, the correct option is D.

Note: The main function of a meter bridge is to find the value of an unknown resistance. Another one of its functions is to compare two different resistances.