Question

In a potentiometer a standard cell of EMF 5V and of negligible resistance maintains a steady current through the potentiometer wire of length 5 meter. Two primary cells of emf ${E_1}$ and ${E_2}$, are joined in series. (i) same polarity, (ii) opposite polarity. The configuration is connected to a galvanometer and a jockey to the potentiometer. The balancing lengths in the two cases are found to be 350 cm and 5 cm respectively.
A) Draw the necessary circuit diagram.
B) Find the value of the emf’s of the two cells,

Answer 1

Hint: In a potentiometer the jockey is used to slide over the wire to find the balancing length. The polarity is different in the two cases.

Complete step by step solution:
Here the first step is to understand the questions and the conditions given.
There is wire AB of length 5 meter. It is connected to a 5 volt cell. So let us start drawing the circuit.
The first part of the circuit:

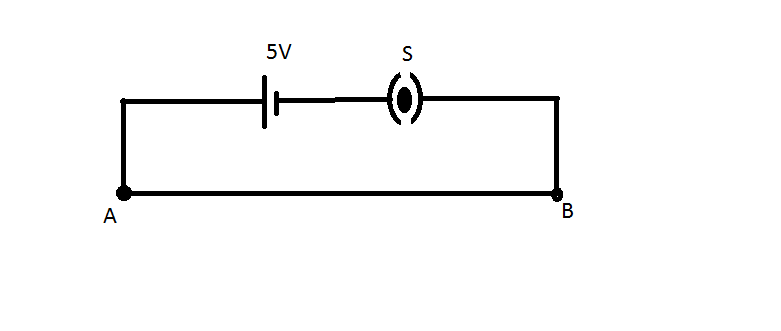
The above diagram is the first part of the circuit.
Now for the second part the two cells are connected in series. So for the next part we are going to add them to the first part directly without drawing it separately.

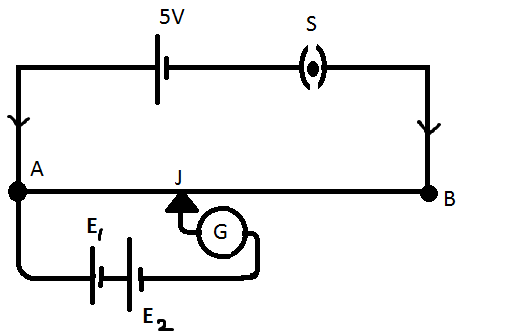
The above diagram shows the final circuit for the given condition.
Now for the second part of the question;
The potential gradient is to be calculated.
Hence if emf is 5 volts and length is 5 meters the potential gradient of AB is given by;
$k = \dfrac{V}{{{l_{cm}}}}$ here V is potential difference across the length and ${l_{cm}}$ is the length of AB in centimeter
So $k = \dfrac{{5V}}{{500cm}} = \dfrac{{1}}{{100}}$
Now case 1: the cells have same polarity-
Thus ${E_1} + {E_2} = kl$, here, l is the balancing length for the same polarity, so, l= 350cm.
Hence, ${E_1} + {E_2} = \dfrac{1}{{100}} \times 350 = 3.5$ (equation: 1)
Now for Case 2: the polarities of the cell are opposite-
Hence, ${E_1} - {E_2} = kl'$ here $l'$ is the balancing length for opposite polarity, so $l' = 5cm$.]
Thus, ${E_1} - {E_2} = \dfrac{1}{{100}} \times 5 = 0.05$ (equation: 2)
Now we solve the equations 1 and 2;
First adding equation 2 to equation 1, we get;
$2{E_1} = 3.55$
Thus, ${E_1} = \dfrac{{3.55}}{2} = 1.78V$
Now substituting the value of ${E_1}$ in equation 1 we get;
$1.78 + {E_2} = 3.5$
Hence, ${E_2} = 3.5 - 1.78 = 1.72V$

Therefore, the emf’s are 1.78 and 1.72 volts respectively.

Note: The polarity is a very important character. It should be carefully considered.
Whenever a question of a potentiometer like this comes, the first step should be to draw the diagram for better understanding of the conditions and the second step should be finding the potential gradient.